不完全市场下投资组合选择的鞅方法
不完备市场上基于虚拟证券的鞅测度

不完备市场上基于虚拟证券的鞅测度
朱捷;王生喜;王杰
【期刊名称】《哈尔滨商业大学学报:自然科学版》
【年(卷),期】2022(38)5
【摘要】基于多维扩散过程所驱动的不完备市场,引入虚拟证券,研究了不同准则下的最优鞅测度问题.首次提出了均方误差次优准则及相对均方差次优准则,并在上述两个准则下,得到了鞅测度的显式表达,验证了上述鞅测度在二阶矩意义上与极小鞅测度、相对熵极小鞅测度以及方差最优鞅测度无差异.
【总页数】7页(P604-609)
【作者】朱捷;王生喜;王杰
【作者单位】广东科技学院;厦门大学嘉庚学院
【正文语种】中文
【中图分类】O211.63
【相关文献】
1.跳扩散半鞅的最小鞅测度与最小熵鞅测度
2.最小对称熵鞅测度和不完备市场中的定价问题
3.右连续信息域下连续半鞅的方差最优鞅测度
4.证券市场上虚假陈述行不的法律责任
5.虚拟资本与我国公司在证券市场上的融资
因版权原因,仅展示原文概要,查看原文内容请购买。
投资组合的选择(1)

清华大学 经济管理学 系 朱宝宪
八、风险与无风险资产的结构变化
投资者希望将所持有的风险资产组合比重从0.7降为 0.55。投资者的投资资金的配置则为
投资于股票: y=500 000×0.55=275 000(元) 投资于国库券:1-y=500 000×0.45=225 000(元)
雨较多的年份
股市的牛市 股市的熊市
0.4
0.3
பைடு நூலகம்17%
1%
少雨年份 冷饮需求大增
0.3 5%
新组合的期望收益为8.6%,标准差为7.03%。互补的选择效果比 与无风险资产构成的组合还好。
资产组合 全部投资于伞公司股票 一半伞股票一半国库券 一半伞股票一半冷饮股票
期望收益 9.6% 6.3% 8.6%
标准差 20.76% 10.38% 7.03%
–由于10万的效用值为11.51,比公平游戏的 11.37要大,
–风险厌恶型投资者不会进行这一投资。即不 投资于公平游戏。
清华大学 经济管理学 系 朱宝宪
二十、效用公式
这里有一个金融界广泛运用的一个投资效用计 算公式,资产组合的期望收益为E(r),其收益 方差为2,其效用值为:
U=E(r)-0.005A2
所以,投资者对风险的厌恶程度十分关键。
清华大学 经济管理学 系 朱宝宪
二十二、均值-方差准则
–风险厌恶型的投资者承担风险是要报酬的, 这个风险报酬就是超额收益或风险溢价。
–因此对于风险厌恶型的投资者来说,存在着 选择资产的均值-方差准则:当满足下列(a)、 (b)条件中的任何一个时,投资者将选择资产 A作为投资对象:
–(a) –(b)
投资组合选择,Merton问题

u( x) x bx2 (b 0), a( x) 2b / (1 2bx);
18
3.2 期望效用理论 常见风险厌恶效用函数(继续)
HARA ( Hyperbolic absolute risk aversion ) utility function
1 ax u ( x) b , b 0. 1
3.2 期望效用理论
如何得到投资者的效用函数??
1 )首先指定投资者效用函数的形状,如指数型,对 数型等,然后对其中的参数进行估计。
2 )直接估计:选择两个固定点 A和B ,并假设 u(A)=A , u(B)=B ;构造一个以概率 p 获得 A , 概率 1−p 获得 B 的彩票(lottery) x;向投资者询问其愿意用来交换此彩 票的财富水平C。
称为u的等价效用函数。 u
单调性(monotone)
若x y a.s. 则x y.
数值表示满足单调性当且仅当u为严格单调增函数。
13
3.2 期望效用理论 St. Petersburg Paradox(Nicholas Bernoulli 1713)
这是一个掷硬币的游戏,参加者先付门票,然后开始 掷硬币,直至第一个正面出现时为止。总的掷币次数 n决定参加者的报酬,计算报酬r的公式为
其中 u(.)为u(.)的一阶导数。
25
3.3 期望效用最大化模型
当一个资产为无风险资产时
1 0 假设第一个资产为无风险资产,其回报率为 rf P / P 1 1 , 有
L 1 0 1 E[u( P1 ) P ] P 0, r E [ u ( P )]. 1 1 f 1
15
3.2 期望效用理论
Lévy市场下保险公司的最优投资策略

Lévy市场下保险公司的最优投资策略作者:孙海霞来源:《财会学习》 2017年第18期文 / 孙海霞摘要:本文假设投资者是损失厌恶的,保险公司的盈余和风险资产价格过程都是列维过程。
保险公司的目标是当最终财富超过他的期望水平时,期望效用最大。
本文主要通过鞅方法,把动态问题转化为静态问题,求出最优投资策略和最终财富的确切表达式。
关键词:鞅方法;最优投资;损失厌恶一、引言随着保险公司可以在资本市场进行投资,越来越多的投资者关注保险公司的投资组合问题,在现实生活中保险公司投资决策者并不是完全理性的,最著名的就是累积前景理论 (CPT) 来弥补 EUM 的缺陷,在 Guo(2014) 之前没有人把 CPT 引入保险公司的投资决策中,Guo(2014) 即引入进来,并指出保险公司的盈余是服从列维过程,然而在保险公司在资本市场进行投资的时候,价格过程由于受到很多因素的影响,不是一个连续的过程,而是存在一个跳的的过程,至今还没有文章在CPT 原理中加入保险公司的风险资产价格服从列维过程。
本文假设者是损失厌恶的,满足 S- 型效用函数,为了使模型更具有现实性,我们假定保险公司投资于一种无风险资产和 n 种风险资产,风险资产的价格过程服从列维过程,并且假定保险公司的盈余过程也是服从列维过程的。
再运用鞅方法,得出最优投资策略和最优财富过程。
二、模型假设保险公司在时间 [0,T] 内在资本市场投资 n+1 种资产,一种无风险资产和 n 种风险资产,其中无风险资产的价格满足根据效用最大化准则,保险公司的最优投资问题可以表示成如下形式:三、最优模型的求解用鞅方法去解决这一问题,定义折现因子为:结果表明,最终财富是一个不连续的过程,在好的状态下的时候不会超过最终财富时,投资者将获得超过参考点的财富。
在不好的状态下的时候,会超过最终财富时,投资者的最终财富为零。
这是由于对于损失厌恶投资而言,面对损失时是风险喜好的,投资者为了获得更大的收益,可以接受更大的损失。
随机过程--鞅
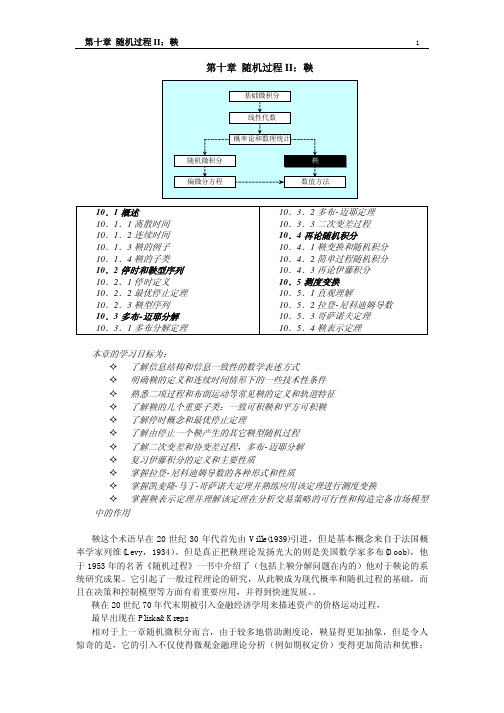
并且由于可以借助现代数值计算技术,它还提供了更为强大的运算能力,而这对于实际工 作又是至关重要的。
在本章中,我们首先在离散时间下,使用在概率基础一章中接触到的分割、条件数学 期望等概念来严格地给出鞅的定义。然后澄清一些性技术要求并给出连续时间鞅的概念。 介绍一些常见的鞅的例子。在讨论了鞅的两个重要子类之后,
F a = {{uu},{ud},{du},{dd}} F b = {uu, ud , du, dd}
F c = {{uu,ud},{du},{dd}} F d = {{uu},{uu,ud},{du},{dd}}
F e = {{uu},{ud},{du}} 根据我们在概率论一章中学习过的知识,我们知道 F a , F b 和 F c 都是对样本空间 Ω 的一种分割。这是因为按照分割的定义,它们各自包含的所有元素的并集构成了整个状 态空间,而它们所包含的元素两两相交的结果是空集。 F d 和 F e 则不是分割,因为 F d 中前两个元素的交集不是空集,而是{uu} ;而 fe 的所有元素的并也没有构成整个状态空 间,缺少了{dd} 。
10.3.2 多布-迈耶定理 10.3.3 二次变差过程 10.4 再论随机积分 10.4.1 鞅变换和随机积分 10.4.2 简单过程随机积分 10.4.3 再论伊藤积分 10.5 测度变换 10.5.1 直观理解 10.5.2 拉登-尼科迪姆导数 10.5.3 哥萨诺夫定理 10.5.4 鞅表示定理
如果不做什么手脚他的运气应当是同他以前的赌博经历无关的用表示他在赌完第n次后拥有的赌本数如果对于任何n都有成立即赌博的期望收获为0仅能维持原有财富水平不变就可以认为这种赌博在统计上是公平的ex就是对这种价格运动的预测而恰好鞅就是用条件数学期望来定义的这种相似性就激发了使用鞅和与之相关的数学概念来描述金融资产价格运动过程特征的热情鞅在20世纪80年代以后迅速成为主流金融经济学研究中标准的时髦
资金管理之反等价鞅策略

剀利公式:在反等价鞅策略下,每次下赌注的百分之多少,才可以实现最快的盈利?答案:K = W - (1-W)/RK:每次下注所占总资金的比例, W:你的策略的胜率, R下注的赔率投硬币游戏:W=0.5 R=2 那么 K = 0.5-(1-0.5)/2 = 0.25也就是说,投硬币游戏中,只要你每次投入你的总资金的四分之一,永远遵守这个几率的玩下去,那么,你将以最快的速度成为亿万富翁。
这个公式是引用自Ed Seykota 的风险管理文章。
外汇市场和期货市场呢?我们引用剀利公式的基础方程:K = (W*R-1)/(R-1)K,W, R的定义同上。
于是,我们发现,盈利有一个基本的前提,那就是你的胜率乘以你的赔率,结果必须大于1,否则无论如何都不可能盈利。
投硬币游戏中W*R=1,正好期望值是持平的。
但是由于我们“永远亏不光”,而且我们总有“停手”的那一天,所以,我们可以选择我们赚到一亿美元时候停手,所以,成为亿万富翁仍然是可能的。
根据剀利公式的基础方程,来考虑外汇市场和期货市场。
假设我每一单的胜率是W=0.5,每一单的止赢和止损的比例是2:1,也就是说,赔率R=3。
这样,根据剀利基础方程,K=(0.5*3-1)/(3-1) = 25%,也就是说,每一单的仓位设置,需要达到总资金的25%时候是最优解。
如果胜率是0.4,那么K=10%如果止赢和止损比是3:1,那么赔率R=4, 胜率W=0.4 那么K = (0.4*4-1)/(4-1) = 20%胜率W=0.3的话K = (0.3*4-1)/(4-1) = 6.7%看到这里,我想你应该明白了为什么无数的汇市和期市的老手告诉我们:“每次投入资金的10%-20%,止赢和止损的比例设置成2:1和3:1,这样即使你的胜率是40%甚至30%,你都可以稳定盈利!"这就是最最普遍的资金管理技巧的数学基础--剀利公式!看到这里,你可能为说,要是这么简单的话,为什么股市汇市期市里面有90%的人赔钱呢?注意到,剀利公式只有战略上的指导意义,而并不具有操作意义。
简析等价鞅测度及其应用

式 5;05"IJC)
+’ +!&;)* ’就等于 C $
6 : : 6 0 3
这
个特征阐明了在不丧失一般性条件下! 为什么可将人们的注意力限定在隐含锥 空间 % 的特殊概率测度类型上 $ 重要的 是 要 指 出 ) 鞅 概 率 测 度 (: 不 是 为 了 将 股 票价格实际波动观测值模型化而外生引 入的 $ 相反的是 ! 它应该被看作是衍生证 券套利估价中非常有用的技术工具 $ 评价 ! 鞅测度 & 或风险中性概率 ’ 概 念本质上取决于基数资产的选择 $ 可以 确 认 相 对 股 票 价 格 ?:0? > 5 的 唯 一 鞅 测 度为 C 类 的 唯 一 因 子 ( ! 且 ( 与 C 的 以 下值一致 )C0C0) 3 % 3 + 79 $
!"#"$
!"#$ RS45S4&TQUV4Q
!""# !" $ # $ %" %&& #&
!" !"#$%&’()
-王 俊
罗 猛
自从 !" 世纪 #" 年代后数理分析工 具广泛应用于金融分析领域 ! 其中最为 知名的当属 $%$ 定 理 "&’$( 以 及 无 套 利 )’(*+ 定 理 和 鞅 等 价 定 理 等 # 在 这 当 中 ! 鞅等价定理直至目前仍然是金融分 析中的前沿课题 $ 并且 ! 等价鞅测度定理 还是人们在分析金融产品定价 % 消除金 融投机套利机会 " 降低金融产品投资风 险的主要工具 $ 等价鞅测度定理在金融 市场分析中的很多领域都可以得到应 用 $ 剖析等价鞅测度定理及其应用无疑 对掌握金融产品定价方法 " 优化金融产 品投资组合 " 降低金融产品投资风险将 有所裨益 $ 一 ! 鞅的定义及含义 一个关于 ,!-.-"" 适应的过程 /0)/-+-"" 称 为 一 个 & 关 于 ,!-.-"" 的 ’ 鞅 ! 如 每 个 /可 积 ! 且 /-01)/-23 4 !-+ !-0"!3 ### &3 ’ 称 为 一 个 上 鞅 ! 如 式 &3 ’ 换 为 /-$1)/-23 4 量族 !3! ( ( (!!* 生成而致 ! 从 而 更 精 确 而 言 !B; 0B &!"!!3!( ( (!!;’! &; )* ! 等 式 中
鞅、鞅差和市场有效性

弱式有效
可实施性。 [参 考 文 献]
[1]陈灯塔,洪永森.中 国 股 市 是 弱 式 有 效 的 吗 —基 于 一 种
同理可以证明半强式有效市场 强式有效市场
新方法的实证研究[J].经济学(季刊),2003(3)
性质二: 定义在(Ω,I,P)以及滤基(In)n 上的市场 M 是有效的市
[2]张亦春,周颖刚。中国股市弱式有效吗[J].金融研究,2001 (3)
1965 年 Fama 在 总 结 前 人 研 究 的 基 础 上 , 在 The Theory Of Stock Market Price 中 定 义 了 有 效 市 场 的 价 格 行 为,Samuelson(1965)、Mandelbrot(1966)和 Roberts(1967)在不 同的领域完善了市场有效性理论, 并根据价格对信息的 反应程度,把有效市场分为:弱有效市场、半强式有效市 场和强式有效市场。 Fama(1970)最终完成了有效市场的完 整框架,正式形成了有效市场理论,认为有效市场的核心 是能够及时、准确的对市场信息做出反应的市场,信息是 有效市场的核心。
第 2012 年第 11 期 ( 总第 409 期)
[文章 编 号] 1009- 6043( 2012)11- 0030- 02
商业经济 SHANGYE JINGJI
鞅、鞅差和市场有效性
No.11,2012 Total No.409
刘辉
( 上海理工大学 管理学院 , 上海 200093)
[摘 要] 市场有效性理论是现代经济学和金融学的基础定理之一,主流的资本市场理论均以其为基础。 通过探
随着分析技术的发展, 随机分析技术被广泛应用于 价格行为研究和金融指标分析, 但这些研究却发现价格 Pt 的对数增量 Xt=lnPt-lnPt-1 似乎是独立的(满足特定的假 设的条件下),Cowles(1933)以及随后的 Working(1934)等均 得出了类似结论 。 随后,Kendall 发现金融市场价 格 波动 具 有 完 全 随 机 性 ,无 周 期 、无 趋 向 行(即 Sn=S0Exp(∑Xt), 其中 Xt=lnPt-lnPt-1,Xt 独立同分 布), 并在 The Analys is Of Economic Time-Serial 中描述了市场价格行为的形态及其 随机过程特征。 在其基础上,学者不断完善分析的方法并 构 造 随 机 过 程 模 型 来 描 述 价 格 行 为 (Robert,Osborne 和 Samuelson 等)。 这 一 系 列 研 究初 步 构 建 了 有效 市 场 理 论 (Efficient Capital Market Theory)的雏形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
不完全市场下投资组合选择的鞅方法
【摘要】介绍了投资组合选择理论的产生和新的发展,在总结不完全市场下假设下投资组合选择的鞅方法的基础上,对其理论进行了详细的描述。
【关键词】不完全市场,投资组合选择,随机控制论,鞅方法1、引言
投资组合选择理论被定义为最佳风险管理的定量分析。
投资组合选择主要是投资者把拥有的财富投资到不同的资产中,以达到风险和确保收益的目的。
其本质上就是一个金融优化问题的研究。
1952年,美国经济学家markowitz(1952)首次提出投资组合理论,并进行了全面深入和开创性的研究,他利用了均值和方差的概念来分析资产的收益和风险[1]。
它极大地推动了现代金融学的产生和发展,也掀起了华尔街的第一次革命。
投资组合选择理论最大的应用就是证券投资上面,尤其是基金管理行业。
证券投资基金起源于英国投资信托公司,发展与美国证券投资市场。
在markowitz之前,基金经理很难去风险有很好的刻画,均值方差投资理论给基金管理行业提供了重要的理论依据。
随着各种理论模型的提出,极大地促进了投资组合选择理论的发展,也推动了证券投资行业的兴起和繁荣。
金融市场可以分为完全市场和不完全市场,从50年代以来,投资组合的研究主要集中在完全市场,并且已经有了很多丰富的理论成果。
但是现实的市场多数都是不完全的,完全市场的假设往往和
实际相违背,于是80年代末90年代初起,开始进行了对不完全市场下的投资组合的研究[2-4]。
研究的方法主要集中在两种:(1)控制论方法,(2)鞅方法。
本文主要是在研究大量文献的基础上,总结和分析在不完全市场下投资组合选择的鞅方法。
2、鞅和对偶方法
鞅方法主要就是思想是把一个动态的最优问题,转化为一个静态的最优问题。
pagès(1987)最早采用鞅方法来研究不完全市场下的投资组合选择问题,并且提出了等价鞅测度的思想[2]。
he和pearson(1988)继续了pagès的工作,重点讨论了如何需找最大的等价鞅测度,并且定义了arrow-debreu状态价格[3]。
karatzas、lehoczky、shreves和xu(1991)用鞅和对偶的方法,通过增加“虚拟”股票,得到了与完全市场相一致的最优投资组合。
这几位学者都通过假设股票数量小于brownian运动个数来刻画市场的不完全性[4]。
总结起来,可以概括为:
求解时可以利用对偶原理进行求解。
上述方法其实和不完全市场下的期权定价的需找一个相对最优
的等价鞅测度来进行定价的思想很像,实际上期权定价也等价于一个如何寻找一个资产组合来复制这个期权。
所以我们可以采用处理不完全市场下期权定价的方法,来确定鞅方法中的状态价格密度过程。
比如可以用最优鞅测度定价方法、一般均衡框架定价方法等。
3、总结与讨论
鞅方法最大的优点就是把一个动态问题转化为一个静态问题的,
计算量相对较少,可以利用对偶理论等技巧来计算该静态问题。
但是对于不同的处理方式,难易程度有很大不同。
比如对于通过寻找一个相对最优的等价鞅测度来计算状态价格密度过程这种处理方
法就带来比较繁琐的计算,会用到鞅论的一些理论。
参考文献:
[1]markowitz h m. portfolio selection. journal of finance,1952, 7:.
[2]h. pagès, optimal consumption and portfolio policies when markets are incomplete, mit mimeo, massachusetts institute of technology, cambridge, ma, 1987
[3]h. he and n. pearson, consumption and portfolio policies with incomplete markets and short-sale constraints: the finite dimensional case, working paper, simon graduate school of business administration, university of rochester,rochester, ny, 1988
[4]i. karatzas, j. lehoczky, s.e. shreve and g.l. xu,martingale and duality methods for utility maximization in incomplete markets, siam j. control and optimization, 1991,29(3):702-730
[5]d. duffie, m. jackson, optimal hedging and equilibrium in a dynamic futures market, journal economic dynamics control, 1990, 14: 21-33.。
