容斥原理习题加答案
完整版容斥原理习题加答案

1. 现有50名学生都做物理、化学实验,如果物理实验做正确的有40人,化学实验做正确的有31人,两种实验都错的有4人,则两种实验都做对的有()【答案】B【解析】直接代入公式为:50=31+40+4- A H B得A H B=25,所以答案为B。
2. 某服装厂生产出来的一批衬衫大号和小号各占一半。
其中25%是白色的, 75%是蓝色的。
如果这批衬衫共有100件,其中大号白色衬衫有10件,小号蓝色衬衫有多少件?()A 、15B、25C 、35D40【答案】C【解析】这是一种新题型,该种题型直接从求解出发,将所求答案设为A H B,本题设小号和蓝色分别为两个事件A和B,小号占50%蓝色占75%直接代入公式为:100=50+75+10- A H B,得:A H B=353. 某高校对一些学生进行问卷调查。
在接受调查的学生中,准备参加注册会计师考试的有63人,准备参加英语六级考试的有89人,准备参加计算机考试的有47人,三种考试都准备参加的有24人,准备只选择两种考试都参加的有46人,【解析】本题画图按中路突破原则,先填充三集合公共部分数字 24,再推其他部分数字:根据每个区域含义应用公式得到:总数=各集合数之和-两两集合数之和+三集合公共数+三集合之外数=63+89+47— {(x+24)+(z+24)+(y+24)}+24+15=199— { (x+z+y ) +24+24+24}+24+15根据上述含义分析得到:x+z+y 只属于两集合数之和,也就是该题所讲的只选择两种考试都参加的人数,所以 x+z+y 的值为46人;得本题答案为120.4. 对某单位的100名员工进行调查,结果发现他们喜欢看球赛和电影、戏剧。
其中58人喜欢看球赛,38人喜欢看戏剧,52人喜欢看电影,既喜欢看球赛又喜 欢看戏剧的有18人,既喜欢看电影又喜欢看戏剧的有16人,三种都喜欢看的有 12人,则只喜欢看电影的有多少人( )A.22 人B.28 人C.30 人D.36 人【答案】A【解析】本题画图按中路突破原则,先填充三集合公共部分数字 12,再推其他部分数字:根据各区域含义及应用公式得到:总数=各集合数之和-两两集合数之和+三集合公共数+三集合之外数100= 58+38+52- {18+16+ (12+ x ) }+12+0,因为该题中,没有三种都不喜 欢的人,所以三集合之外数为 0,解方程得到:x = 14。
小学四年级奥数第35讲 容斥原理(含答案分析)

第35讲容斥原理一、专题简析:容斥问题涉及到一个重要原理——包含与排除原理,也叫容斥原理。
即当两个计数部分有重复包含时,为了不重复计数,应从它们的和中排除重复部分。
容斥原理:对n个事物,如果采用不同的分类标准,按性质a分类与性质b 分类(如图),那么具有性质a或性质b的事物的个数=N a+N b-N ab。
Nab NbNa二、精讲精练:例1:一个班有48人,班主任在班会上问:“谁做完语文作业?请举手!”有37人举手。
又问:“谁做完数学作业?请举手!”有42人举手。
最后问:“谁语文、数学作业都没有做完?”没有人举手。
求这个班语文、数学作业都完成的人数。
练习一1、五年级有122名学生参加语文、数学考试,每人至少有一门功课取得优秀成绩。
其中语文成绩优秀的有65人,数学优秀的有87人。
语文、数学都优秀的有多少人?2、四年级一班有54人,订阅《小学生优秀作文》和《数学大世界》两种读物的有13人,订《小学生优秀作文》的有45人,每人至少订一种读物,订《数学大世界》的有多少人?例2:某班有36个同学在一项测试中,答对第一题的有25人,答对第二题的有23人,两题都答对的有15人。
问多少个同学两题都答得不对?练习二1、五(1)班有40个学生,其中25人参加数学小组,23人参加科技小组,有19人两个小组都参加了。
那么,有多少人两个小组都没有参加?2、一个班有55名学生,订阅《小学生数学报》的有32人,订阅《中国少年报》的有29人,两种报纸都订阅的有25人。
两种报纸都没有订阅的有多少人?例3:某班有56人,参加语文竞赛的有28人,参加数学竞赛的有27人,如果两科都没有参加的有25人,那么同时参加语文、数学两科竞赛的有多少人?练习三1、一个旅行社有36人,其中会英语的有24人,会法语的有18人,两样都不会的有4人。
两样都会的有多少人?2、一个俱乐部有103人,其中会下中国象棋的有69人,会下国际象棋的有52人,这两种棋都不会下的有12人。
容斥原理练习题解析版

容斥原理练习题【练习 1】47 名学生参加数学和语文考试,其中语文得分 95 分以上的 14 人, 数学得分 95 分以上的 21 人,两门都不在 95 分以上的有 22 人.问:两门都在 95 分以上的有多少人?【解析】如图,用长方形表示这47 名学生, A 圆表示语文得分95 分以上的人数,B 圆表示数学得95 分以上的人数,A 与B 重合的部分表示两门都在95 分以上的人数,长方形内两圆外的部分表示两门都不在95 分以上的人数.由图中可以看出,全体人数是至少一门在95 分以上的人数与两门都不在95 分以 上的人数之和,则至少一门在95 分以上的人数为: 47 - 22 = 25 (人).根据包含排除法,两门都在95 分以上的人数为:14 + 21 - 25 = 10 (人).【练习 2】某班有 42 人,其中 26 人爱打篮球,17 人爱打排球,19 人爱踢足球, 9 人既爱打篮球又爱踢足球,4 人既爱打排球又爱踢足球,没有一个人三种球都爱好,也没有一个人三种球都不爱好.问:既爱打篮球又爱打排球的有几人?【解析】由于全班42 人没有一个人三种球都不爱好,所以全班至少爱好一种球的有42 人.根据包含排除法, 42 =(26 + 17 + 19)-(9 + 4 + 既爱打篮球又爱打排球的人数)+ 0 ,得到既爱打篮球又爱打排球的人数为: 49 - 42 = 7 (人).95分以上的 数学95分以上的 B不在两门95分以上的 语文95分以上的 A 两门都【练习 3】四(二)班有48 名学生,在一节自习课上,写完语文作业的有30 人,写完数学作业的有20 人,语文数学都没写完的有6 人.(1)问语文数学都写完的有多少人?(2)只写完语文作业的有多少人?【解析】(1)由题意,有48 - 6 = 42 (人)至少完成了一科作业,根据包含排除原理,两科作业都完成的学生有:30 + 20 - 42 = 8 (人).(2)只写完语文作业的人数=写完语文作业的人数-语文数学都写完的人数,即30 - 8 = 22 (人)【练习 4】某班学生手中分别拿红、黄、蓝三种颜色的小旗,已知手中有红旗的共有34 人,手中有黄旗的共有26 人,手中有蓝旗的共有18 人.其中手中有红、黄、蓝三种小旗的有6 人.而手中只有红、黄两种小旗的有9 人,手中只有黄、蓝两种小旗的有4 人,手中只有红、蓝两种小旗的有3 人,那么这个班共有多少人?【解析】如图,用A 圆表示手中有红旗的,B 圆表示手中有黄旗的,C 圆表示手中有蓝旗的.如果用手中有红旗的、有黄旗的与有蓝旗的相加,发现手中只有红、黄两种小旗的各重复计算了一次,应减去,手中有三种颜色小旗的重复计算了二次,也应减去,那么,全班人数为:(34+ 26 +18)-(9+ 4 + 3)- 6 ⨯ 2 = 50 (人).A BC。
(完整版)容斥原理习题加答案

1.现有50名学生都做物理、化学实验,如果物理实验做正确的有40人,化学实验做正确的有31人,两种实验都错的有4人,则两种实验都做对的有( )A、27人B、25人C、19人D、10人【答案】B【解析】直接代入公式为:50=31+40+4-A∩B得A∩B=25,所以答案为B。
2.某服装厂生产出来的一批衬衫大号和小号各占一半。
其中25%是白色的,75%是蓝色的。
如果这批衬衫共有100件,其中大号白色衬衫有10件,小号蓝色衬衫有多少件?()A、15B、25C、35D、40【答案】C【解析】这是一种新题型,该种题型直接从求解出发,将所求答案设为A∩B,本题设小号和蓝色分别为两个事件A和B,小号占50%,蓝色占75%,直接代入公式为:100=50+75+10-A∩B,得:A∩B=35。
3.某高校对一些学生进行问卷调查。
在接受调查的学生中,准备参加注册会计师考试的有63人,准备参加英语六级考试的有89人,准备参加计算机考试的有47人,三种考试都准备参加的有24人,准备只选择两种考试都参加的有46人,不参加其中任何一种考试的都15人。
问接受调查的学生共有多少人?()A.120B.144C.177D.192【答案】A【解析】本题画图按中路突破原则,先填充三集合公共部分数字24,再推其他部分数字:根据每个区域含义应用公式得到:总数=各集合数之和-两两集合数之和+三集合公共数+三集合之外数=63+89+47-{(x+24)+(z+24)+(y+24)}+24+15=199-{(x+z+y)+24+24+24}+24+15根据上述含义分析得到:x+z+y只属于两集合数之和,也就是该题所讲的只选择两种考试都参加的人数,所以x+z+y的值为46人;得本题答案为120.4.对某单位的100名员工进行调查,结果发现他们喜欢看球赛和电影、戏剧。
其中58人喜欢看球赛,38人喜欢看戏剧,52人喜欢看电影,既喜欢看球赛又喜欢看戏剧的有18人,既喜欢看电影又喜欢看戏剧的有16人,三种都喜欢看的有12人,则只喜欢看电影的有多少人()A.22人B.28人C.30人D.36人【答案】A【解析】本题画图按中路突破原则,先填充三集合公共部分数字12,再推其他部分数字:根据各区域含义及应用公式得到:总数=各集合数之和-两两集合数之和+三集合公共数+三集合之外数100=58+38+52-{18+16+(12+ x)}+12+0,因为该题中,没有三种都不喜欢的人,所以三集合之外数为0,解方程得到:x=14。
容斥原理(二)(含答案)-
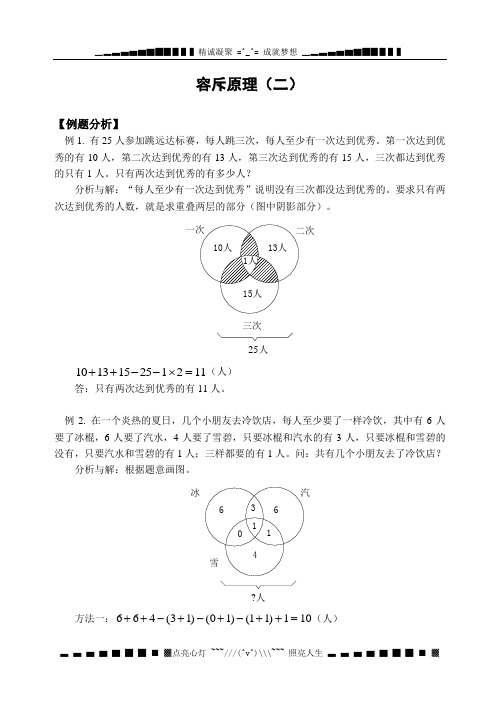
容斥原理(二)【例题分析】例1. 有25人参加跳远达标赛,每人跳三次,每人至少有一次达到优秀。
第一次达到优秀的有10人,第二次达到优秀的有13人,第三次达到优秀的有15人,三次都达到优秀的只有1人。
只有两次达到优秀的有多少人?例2. 在一个炎热的夏日,几个小朋友去冷饮店,每人至少要了一样冷饮,其中有6人要了冰棍,6人要了汽水,4人要了雪碧,只要冰棍和汽水的有3人,只要冰棍和雪碧的++---⨯=(人)方法二:664311210答:共有10个小朋友去了冷饮店。
例3. 有28人参加田径运动会,每人至少参加两项比赛。
已知有8人没参加跑的项目,参加投掷项目的人数与参加跑和跳两项的人数都是17人。
问:只参加跑和投掷两项的有多少人?30人参的有3人,既参加数学又参加英语和既参加英语又参加语文的人数均为质数,而三种全参7。
答:既参加英语又参加数学小组的为2人或7人。
例5. 某班同学参加升学考试,得满分的人数如下:数学20人,语文20人,英语20人,数学、英语两科满分者8人,数学、语文两科满分者7人,语文、英语两科满分者9人,三科都没得满分者3人。
问这个班最多多少人?最少多少人?满分的人数,即x x ≤≤78,且x ≤9,由此我们得到x ≤7。
另一方面x 最小可能是0,即没有三科都得满分的。
当x 取最大值7时,全班有()39746+=人,当x 取最小值0时,全班有()390+=39人。
答:这个班最多有46人,最少有39人。
【模拟试题】(答题时间:30分钟)1. 六年级共有96人,两种刊物每人至少订其中一种,有23的人订《少年报》,有12的人订《数学报》,两种刊物都订的有多少人?2. 小明和小龙两家合住一套房子,门厅、厨房和厕所为公用,在登记住房面积时,两家他们住的一套房子共有多少平方米?3. 某班45名同学参加体育测试,其中百米得优者20人,跳远得优者18人,又知百米、跳远都得优者7人,跳高、百米得优者6人,跳高、跳远均得优者8人,跳高得优者22人,全班只有1名同学各项都没达优秀,求三项都是优秀的人数。
容斥原理练习答案

容斥原理1.一个俱乐部,会下象棋的有69人,会下围棋的有58人,两种棋都不会下的人有12人,两种棋都会下的有30人,问这个俱乐部一共有多少人?【答案】109人.2.一个班有48人,班主任在班会上问:“谁做完语文作业?请举手!”有37人举手.又问:“谁做完数学作业?请举手!”有42人举手.最后问:“谁语文、数学作业都没有做完?”没有人举手.求这个班语文、数学作业都完成的人数.【答案】31人.3.调查一群小朋友最喜欢吃的水果中,有三种水果最喜欢(苹果、香蕉、草莓),每人都有自己喜欢吃的。
其中喜欢吃苹果的有20人,喜欢吃香蕉的有25人,喜欢吃草莓的有30人,既喜欢苹果又喜欢香蕉的有8人,既喜欢苹果又喜欢草莓的有7人,既喜欢香蕉又喜欢草莓的有6人,三种都喜欢的有4人,请问一共有多少个小朋友?【答案】58个.4.对39种食物中是否含有甲、乙、丙三种维生素进行调查,结果如下:含甲的有17种,含乙的有18种,含丙的含有15种,含甲、乙的有7种,含甲、丙的有6种,含乙、丙的有9种,三种维生素都不含的有7种,则三种维生素都含的有多少种?【答案】4种.5.一次考试共有两题,第一题做对有20人,其中5人第二题错了;第二题总共30人做对,有3人一道题都没做对,请问一共有多少人报名参加?【答案】38人.6.光明小学举办学生书法展览.学校的橱窗里展出了每个年级学生的书法作品,其中有24幅不是五年级的,有22幅不是六年级的,五、六年级参展的书法作品共有10幅,其他年级参展的书法作品共有多少幅?【答案】18幅.7.在某个风和日丽的日子,10个同学相约去野餐,每个人都带了吃的,其中6个人带了汉堡,6个人带了鸡腿,4个人带了芝士蛋糕,有3个人既带了汉堡又带了鸡腿,1个人既带了鸡腿又带了芝士蛋糕。
2个人既带了汉堡又带了芝士蛋糕.问:(1)三种都带了的有几人?(2)只带了一种的有几个?【答案】(1)0人(2)4人.8.有100名学生,按照1-100编号,面对老师站成一排,第一次让编号是2的倍数的学生向后转,第二次让编号为5的学生向后转,那么最后面对老师的学生有多少名?【答案】50名.9.某学校五年二班参加语文、数学、英语三科考试,语文90分以上的有21人,数学有19人,英语有20人,语文数学都在90分以上的有9人,数学英语在90分以上的有7人,语文英语都在90分以上的有8人,另外有5人三科都在90分以下,这个班最多有多少人?【答案】48人.10.一小偷藏匿于某商场,三名警察甲、乙、丙分头行动搜查商场的100家商铺.已知甲检查过80家,乙检查过70家,丙检查过60家,则三人都检查过的商铺至少有多少家?【答案】10家.。
2024小升初专项训练容斥原理练习及答案解析
第3讲容斥原理第一关两量重叠问题【知识点】在日常生活中,人们常常需要统计一些数量,在统计的过程中,往往会发现有些数量重复出现,为了使重复出现的部分不致被重复计算,人们研究出一种新的计数方法,既先不考虑重复的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排除出去,使计算的结果既无遗漏又无重复.这种计数方法称为包含排除法,也叫做容斥原理或重叠问题.一般方法:在解答有关包含排除问题时,我们常常利用圆圈图(韦恩图)来帮助分析思考.容斥原理1:两量重叠问题A类与B类元素个数的总和=A类元素的个数+B类元素个数-既是A类又是B类的元素个数用符号可表示成:A∪B=A+B-A∩B (其中符号“∪”读作“并”,相当于中文“和”或者“或”的意思,符号“∩”读作“交”,相当于中文“且”的意思).【例1】“两会”是“全国人民代表大会”和“中国人民政治协商会议”的简称,如果2017年“人大会议”和“政协会议”均历时11天,并且两个会议有9天同时进行.那么,2017年的“两会”将一共进行多少天?【答案】13【例2】三(1)班同学给“手拉手”小伙伴捐物品,捐衣物的有26人,捐文具的有32人,两样都捐的有18人.捐物品的同学一共有几人?【答案】40【例3】同学们去动物园游玩,每人至少参观一个馆.参观大象馆的有10人,参观猴子馆的有15人,两个馆都参加的有6人,一共有多少人去动物园?【答案】19【例4】某班老师建议学生读A、B两本课外读物,结果有25人没有读A,有19人没有读B,20人只读了1本书,11人读过2本书,那么该班共有多少人?【答案】43【例5】假期中,王老师给三(1)班同学推荐了《冰雪奇缘》和《疯狂原始人》两部动画片供大家选择观看.两部电影都看的有36人,两部电影都没看的只有2人;看了《冰雪奇缘》的有40人,看了《疯狂原始人》的有38人.三(1)班一共有多少人?【答案】44【例6】光辉小学六年级在一次语、数联赛中,语文及格的有24人,数学及格的有27人,其中语、数都及格的有14人,另外还有8人语、数都没及格,六年级共有学生多少人?【答案】45【例7】三(5)班同学参加了音乐、美术这两个课外兴趣小组,已知参加音乐小组的有32人,参加美术组的有30人,两个小组都参加的有10人,三(5)班共有学生多少人?【答案】52【例8】四(1)班每个同学至少参加一项兴趣小组,参加美术小组的有32人,参加书法小组的有36人,两项都参加的有15人,四(1)班有多少人?【答案】53【例9】五年级(1)班每人都至少参加一个兴趣小组,参加语文兴趣小组的有45人,参加数学兴趣小组的有37人,有20人两个小组都参加.这个班共有多少人?【答案】62【例10】一次竞赛有2题,答对第一题的有186人,答对第二题的有143人,全错的有21人,全对的51人,问参加竞赛的共有多少人?【答案】299【例11】新东方在“五一劳动节”即将发行新版积分卡.如果旧版积分卡上共出现300位老师,新版积分卡上共出现400位老师,其中有150位老师在新旧两版积分卡中都出现了,那么,在新旧两版积分卡上共出现了多少位老师?【答案】550【例12】六年级一班春游,带矿泉水的有18人,带水果的有16人,这两种至少带一种的有28人,求两种都带的有多少人?【答案】6【例13】空军突击队共有25名士兵,每个人都擅长射击和武术中的一项或者两项,如果士兵中擅长射击的有20人,擅长武术的有12人,则两项均擅长的士兵有多少人?【答案】7【例14】某天的放学路上,甲和乙交流起各自玩过的电子游戏,他们回想起了20个不同的游戏,其中甲玩过8个,乙玩过16个,那么他们都玩过的游戏有几个?【答案】4【例15】三(2)班第一小组共有8人,在一次语文和数学测验中,他们均至少有一门得了95分以上,其中语文得95分以上的有5人,数学得95分以上的有7人,语文和数学均得95分以上的有多少人?【答案】4【例16】一次考试,语文得100分的有5人,数学得100分的8人,老师发现这次考试得100分的只有10人,那么,得双100分的有多少人?【答案】3【例17】某校五年一班有40人,其中有28人参加了数学小组,30人参加了外语小组,有6人两个小组都没有参加,两个小组都参加的有多少人?【答案】24【例18】六(3)班同学有23人参加了舞蹈和击剑兴趣小组,其中参加舞蹈兴趣小组的有17人,参加击剑兴趣小组的有20人,两个兴趣小组都参加的有多少人?【答案】14【例19】五(1)班40名同学采集标本,每个同学至少要采集一种标本.采集昆虫标本的有28人,采集植物标本的有19人,两种标本都采集的有多少人?【答案】7【例20】学校开运动会,某班有30名学生,其中20人报名参加赛跑项目,11人报名参加跳跃项目,两项都没有报名的有4人,问两项都参加的有几人?【答案】5【例21】全班50人做2道数学题,其中第一道做对的有40人,第二道做对的有30人,两道都做错的有5人,则两道都做对的有多少人?【答案】25【例22】六(1)班有45名同学,17人参加了象棋兴趣小组,22人参加了围棋兴趣小组,13人两个小组都没有参加,两个小组都参加的有多少人,多少人只参加了象棋兴趣小组?【答案】7;10【例23】一个班有48个人,班主任在班会上问:“谁完成了语文作业?请举手!”有37人举手,又问:“谁完成了数学作业?请举手!”有42人举手,最后问:“谁语文、数学作业都没有完成?”没有人举手,求这个班语文、数学作业都完成的人数。
容斥原理练习题解析版
容斥原理练习题【练习 1】47 名学生参加数学和语文考试,其中语文得分 95 分以上的 14 人, 数学得分 95 分以上的 21 人,两门都不在 95 分以上的有 22 人.问:两门都在 95 分以上的有多少人?【解析】如图,用长方形表示这47 名学生, A 圆表示语文得分95 分以上的人数,B 圆表示数学得95 分以上的人数,A 与B 重合的部分表示两门都在95 分以上的人数,长方形内两圆外的部分表示两门都不在95 分以上的人数.由图中可以看出,全体人数是至少一门在95 分以上的人数与两门都不在95 分以 上的人数之和,则至少一门在95 分以上的人数为: 47 - 22 = 25 (人).根据包含排除法,两门都在95 分以上的人数为:14 + 21 - 25 = 10 (人).【练习 2】某班有 42 人,其中 26 人爱打篮球,17 人爱打排球,19 人爱踢足球, 9 人既爱打篮球又爱踢足球,4 人既爱打排球又爱踢足球,没有一个人三种球都爱好,也没有一个人三种球都不爱好.问:既爱打篮球又爱打排球的有几人?【解析】由于全班42 人没有一个人三种球都不爱好,所以全班至少爱好一种球的有42 人.根据包含排除法, 42 =(26 + 17 + 19)-(9 + 4 + 既爱打篮球又爱打排球的人数)+ 0 ,得到既爱打篮球又爱打排球的人数为: 49 - 42 = 7 (人).95分以上的 数学95分以上的 B不在两门95分以上的 语文95分以上的 A 两门都【练习 3】四(二)班有48 名学生,在一节自习课上,写完语文作业的有30 人,写完数学作业的有20 人,语文数学都没写完的有6 人.(1)问语文数学都写完的有多少人?(2)只写完语文作业的有多少人?【解析】(1)由题意,有48 - 6 = 42 (人)至少完成了一科作业,根据包含排除原理,两科作业都完成的学生有:30 + 20 - 42 = 8 (人).(2)只写完语文作业的人数=写完语文作业的人数-语文数学都写完的人数,即30 - 8 = 22 (人)【练习 4】某班学生手中分别拿红、黄、蓝三种颜色的小旗,已知手中有红旗的共有34 人,手中有黄旗的共有26 人,手中有蓝旗的共有18 人.其中手中有红、黄、蓝三种小旗的有6 人.而手中只有红、黄两种小旗的有9 人,手中只有黄、蓝两种小旗的有4 人,手中只有红、蓝两种小旗的有3 人,那么这个班共有多少人?【解析】如图,用A 圆表示手中有红旗的,B 圆表示手中有黄旗的,C 圆表示手中有蓝旗的.如果用手中有红旗的、有黄旗的与有蓝旗的相加,发现手中只有红、黄两种小旗的各重复计算了一次,应减去,手中有三种颜色小旗的重复计算了二次,也应减去,那么,全班人数为:(34+ 26 +18)-(9+ 4 + 3)- 6 ⨯ 2 = 50 (人).A BC。
奥数 容斥原理(例题+详解)
容斥原埋在很多计数问题中常用到数学上的一个包含与排除原理,也称为容斥原理.为了说明这个原理,我们先介绍一些集合的初步知识。
例1、桌上有两张圆纸片A、B.假设圆纸片A的面积为30平方厘米,圆纸片B的面积为20平方厘米.这两张圆纸片重叠部分的面积为10平方厘米.则这两张圆纸片覆盖桌面的面积由容斥原理的公式(1)可以算出为:|A∪B|=30+20-10=40(平方厘米)。
例2、求在1至100的自然数中能被3或7整除的数的个数。
分析解这类问题时首先要知道在一串连续自然数中能被给定整数整除的数的个数规律是:在n个连续自然数中有且仅有一个数能被n整除.根据这个规律我们可以很容易地求出在1至100中能被3整除的数的个数为33个,被7整除的数的个数为14个,而其中被3和7都能整除的数有4个,因而得到解:设A={在1~100的自然数中能被3整除的数},B={在1~100的自然数中能被7整除的数},则A∩B={在1~100的自然数中能被21整除的数}。
∵100÷3=33…1,∴|A|=33。
∵100÷7=14…2,∴|B|=14。
∵100÷21=4…16,∴|A∩B|=4。
由容斥原理的公式(1):|A∪B|=33+14-4=43。
答:在1~100的自然数中能被3或7整除的数有43个。
例3、求在1~100的自然数中不是5的倍数也不是6的倍数的数有多少个?分析如果在1~100的自然数中去掉5的倍数、6的倍数,剩下的数就既不是5的倍数也不是6的倍数,即问题要求的结果。
解:设A={在1~100的自然数中5的倍数的数},B={在1~100的自然数中6的倍数的数},数.为此先求|A∪B|。
∵100÷50=20,∴|A|=20又∵100÷6=16…4,∴|B|=16∵100÷30=3…10,∴|A∩B|=3,|A∪B|=|A|+|B|-|A∩B|=20+16-3=33。
初中数学竞赛《容斥原理》练习题及答案 (34)
初中数学竞赛《容斥原理》练习题
1.把7个两两不同的球分给两个人,使得每人至少分得2个球,则不同的分法共有112种.
【分析】首先算出7个两两不同的球分给两个人,共有多少种分法,去掉一个人没有分得物件的分法以及有一个人恰好分得一件物体的分法,由此可以解答问题.
【解答】解:因为把7件彼此相异的物件分给两个人,每件物件都有2种分法,故不同的分法共有27×4=128种,
其中,使得一个人没有分得物件的分法有2种,
使得有一个人恰好分得一件物体的分法有2×7=14种,
故使得每人至少分得2件物件的分法共有128﹣2﹣14=112种.
故答案为112.
【点评】此题关键理解7个两两不同的球分给两个人,包含了一个人没有分得物件,一个人恰好分得一件物体,每人至少分得2个球,算出总数,去掉前两者问题得解.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.现有50名学生都做物理、化学实验,如果物理实验做正确的有40人,化学实验做正确的有31人,两种实验都错的有4人,则两种实验都做对的有( )
A、27人
B、25人
C、19人
D、10人
【答案】B
【解析】直接代入公式为:50=31+40+4-A∩B
得A∩B=25,所以答案为B。
2.某服装厂生产出来的一批衬衫大号和小号各占一半。
其中25%是白色的,75%是蓝色的。
如果这批衬衫共有100件,其中大号白色衬衫有10件,小号蓝色衬衫有多少件()
A、15
B、25
C、35
D、40
【答案】C
【解析】这是一种新题型,该种题型直接从求解出发,将所求答案设为A∩B,本题设小号和蓝色分别为两个事件A和B,小号占50%,蓝色占75%,直接代入公式为:100=50+75+10-A∩B,得:A∩B=35。
3.某高校对一些学生进行问卷调查。
在接受调查的学生中,准备参加注册会计师考试的有63人,准备参加英语六级考试的有89人,准备参加计算机考试的有47人,三种考试都准备参加的有24人,准备只选择两种考试都参加的有46人,
不参加其中任何一种考试的都15人。
问接受调查的学生共有多少人()A.120
B.144
C.177
D.192
【答案】A
【解析】本题画图按中路突破原则,先填充三集合公共部分数字24,再推其他部分数字:
根据每个区域含义应用公式得到:
总数=各集合数之和-两两集合数之和+三集合公共数+三集合之外数
=63+89+47-{(x+24)+(z+24)+(y+24)}+24+15
=199-{(x+z+y)+24+24+24}+24+15
根据上述含义分析得到:x+z+y只属于两集合数之和,也就是该题所讲的只选择两种考试都参加的人数,所以x+z+y的值为46人;得本题答案为120.
4.对某单位的100名员工进行调查,结果发现他们喜欢看球赛和电影、戏剧。
其中58人喜欢看球赛,38人喜欢看戏剧,52人喜欢看电影,既喜欢看球赛又喜欢看戏剧的有18人,既喜欢看电影又喜欢看戏剧的有16人,三种都喜欢看的有12人,则只喜欢看电影的有多少人()
人人人人
【答案】A
【解析】本题画图按中路突破原则,先填充三集合公共部分数字12,再推其他部分数字:
根据各区域含义及应用公式得到:
总数=各集合数之和-两两集合数之和+三集合公共数+三集合之外数
100=58+38+52-{18+16+(12+ x)}+12+0,因为该题中,没有三种都不喜欢的人,所以三集合之外数为0,解方程得到:x=14。
52=x+12+4+Y=14+12+4+Y,得到Y=22人。
5.某班统计考试成绩,数学得90分上的有25人;语文得90分以上的有21人;两科中至少有一科在90分以上的有38人。
问两科都在90分以上的有多少人
解:设A={数学成绩90分以上的学生}
B={语文成绩90分以上的学生}
那么,集合A∪B表示两科中至少有一科在90分以上的学生,由题意知,
∣A∣=25,∣B∣=21,∣A∪B∣=38
现要求两科均在90分以上的学生人数,即求∣A∩B∣,由容斥原理得
∣A∩B∣=∣A∣+∣B∣-∣A∪B∣=25+21-38=8
点评:解决本题首先要根据题意,设出集合A,B,并且会表示A∪B,A∩B,再利用容斥原理求解。
6. 某班同学中有39人打篮球,37人跑步,25人既打篮球又跑步,问全班参加篮球、跑步这两项体育活动的总人数是多少
解:设A={打篮球的同学};B={跑步的同学}
则A∩B={既打篮球又跑步的同学}
A∪B={参加打篮球或跑步的同学}
应用容斥原理∣A∪B∣=∣A∣+∣B∣-∣A∩B∣=39+37-25=51(人)
7. 某年级的课外学科小组分为数学、语文、外语三个小组,参加数学小组的有23人,参加语文小组的有27人,参加外语小组的有18人;同时参加数学、语文两个小组的有4人,同时参加数学、外语小组的有7人,同时参加语文、外语小组的有5人;三个小组都参加的有2人。
问:这个年级参加课外学科小组共有多少人
解1:设A={数学小组的同学},B={语文小组的同学},C={外语小组的同学},A∩B={数学、语文小组的同学},A∩C={参加数学、外语小组的同学},B∩C={参加语文、外语小组的同学},A∩B∩C={三个小组都参加的同学}
由题意知:∣A∣=23,∣B∣=27,∣C∣=18
∣A∩B∣=4,∣A∩C∣=7,∣B∩C∣=5,∣A∩B∩C∣=2
根据容斥原理二得:
∣A∪B∪C∣=∣A∣+∣B∣+∣C∣-∣A∩B∣-∣A∩C|-∣B∩C|+|A∩B∩C∣
=23+27+18-(4+5+7)+2
=54(人)
山东公务员行测:数量关系之容斥问题解题原理及方法
解2:利用图示法逐个填写各区域所表示的集合的元素的个数,然后求出最后结果。
设A、B、C分别表示参加数学、语文、外语小组的同学的集合,其图分割成七个互不相交的区域,区域Ⅶ(即A∩B∩C)表示三个小组都参加的同学的集合,由题意,应填2。
区域Ⅳ表示仅参加数学与语文小组的同学的集合,其人数为4-2=2(人)。
区域Ⅵ表示仅参加数学与外语小组的同学的集合,其人数为7-2=5(人)。
区域Ⅴ表示仅参加语文、外语小组的同学的集合,其人数为5-2=3(人)。
区域Ⅰ表示只参加数学小组的同学的集合,其人数为
23-2-2-5=14(人)。
同理可把区域Ⅱ、Ⅲ所表示的集合的人数逐个算出,分别填入相应的区域内,则参加课外小组的人数为;
14+20+8+2+5+3+2=54(人)
点评:解法2简单直观,不易出错。
由于各个区域所表示的集合的元素个数都计算出来了,因此提供了较多的信息,易于回答各种方式的提问。
8.某车间有工人100人,其中有5个人只能干电工工作,有77人能干车工工作,86人能干焊工工作,既能干车工工作又能干焊工工作的有多少人
解:工人总数100,只能干电工工作的人数是5人,除去只能干电工工作的人,这个车间还有95人。
利用容斥原理,先多加既能干车工工作又能干焊工工作的这一部分,其总数为163,然后找出这一公共部分,即163-95=68
9.某次语文竞赛共有五道题(满分不是100分),丁一只做对了(1)、(2)、(3)三题得了16分;于山只做对了(2)、(3)、(4)三题,得了25分;王水只做对了(3)、(4)、(5)三题,得了28分,张灿只做对了(1)、(2)、(5)三题,得了21分,李明五个题都对了他得了多少分
解:由题意得:前五名同学合在一起,将五个试题每个题目做对了三遍,他们的总分恰好是试题总分的三倍。
五人得分总和是16+25+30+28+21=120。
因此,五道题满分总和是120÷3=40。
所以李明得40分。
10.某大学有外语教师120名,其中教英语的有50名,教日语的有45名,教法语的有40名,有15名既教英语又教日语,有10名既教英语又教法语,有8名既教日语又教法语,有4名教英语、日语和法语三门课,则不教三门课的外语教师有多少名
解:本题只有求出至少教英、日、法三门课中一种的教师人数,才能求出不教这三门课的外语教师的人数。
至少教英、日、法三门课中一种教师人数可根据容斥原理求出。
根据容斥原理,至少教英、日、法三门课中一种的教师人数为50+45+40-15-10-8+4=106(人)不教这三门课的外语教师的人数为120-106=14(人)。
