方差分析显著性检验实例分析-推荐下载
方差分析报告

方差分析报告引言方差分析(Analysis of Variance,简称ANOVA)是一种用于比较两个或更多个样本均值的统计方法。
通过方差分析,我们可以确定不同组别之间是否存在显著差异,以及这种差异是否是由随机因素引起的。
本文将对方差分析的原理、应用场景以及实施过程进行详细介绍,并通过一个案例来展示如何进行方差分析并解读结果。
原理方差分析基于总体均值和个体观测值的关系进行推断,其基本思想是将总体方差分解为组内方差(Within-group Variance)和组间方差(Between-group Variance),然后通过比较这两部分方差的大小来判断是否存在组别间的显著差异。
方差分析的假设: - 原假设(H₀):各组别样本均值没有显著差异。
- 备择假设(H₁):各组别样本均值存在显著差异。
应用场景方差分析常用于以下场景: - 不同治疗方法的疗效比较 - 不同教育水平对工资的影响分析 - 不同广告投放策略的销售效果比较实施步骤进行方差分析的基本步骤如下:1.收集数据:根据实际需求,收集符合要求的样本数据。
2.建立假设:明确原假设和备择假设。
3.计算总体均值:计算每个组别的样本均值和总体均值。
4.计算组间方差:计算组间平方和、组间均方和和组间自由度。
5.计算组内方差:计算组内平方和、组内均方和和组内自由度。
6.计算F值:根据组间均方和和组内均方和计算F值。
7.判断显著性:根据F值和显著性水平对结果进行判断。
8.结果解读:根据显著性水平,判断组别间的差异是否显著。
案例分析我们以某个电商平台的不同广告投放策略的销售额数据为例,进行方差分析。
首先,我们从该电商平台收集到了三个组别的销售额数据,分别为A组、B组和C组。
我们的目标是比较这三个组别的销售额是否存在显著差异。
数据组别销售额(万元)A组15.6A组13.2A组16.5B组12.3B组11.8B组10.9C组14.6C组16.2C组15.8首先,我们要计算每个组别的样本均值和总体均值。
15.1.115方差分析

3
21
28
19
26
26
4
13
27
15
23
27
方差分析
方差分析从观测变量的方差入手,研究诸多控制变量中哪些变量对观测变量 具有显著影响,以及对这些显著的控制变量的不同水平的影响程度进行分析。
方差分析认为,观测变量的数据差异由两部分组成: 第一类是控制因素造成的差异,也称系统误差。 第二类是随机ቤተ መጻሕፍቲ ባይዱ素的造成的差异,也称随机误差。
“机器Z”的F值为10.835,显著性水平为0.000说 明各机器间的完工时间存在显著性差异。
工人与机器的交互作用的F值为13.670,显著性水 平为0.000,说明工人Y与机器Z之间的交互作用对 完工时间具有影响。
双因素方差分析结果
4)工人Y两两对比检验结果 由于方差齐次检验已经证明分 组数据具有方差齐次性,所以 应该采用表格的上半部分数据。 数据显示工人甲与丙、甲与丁、 乙与丙、乙与丁、丁与丙之间 的完工时间存在显著性差异。
双因素方差分析结果
5)机器Z两两对比检验结果 由于方差齐次检验已经证明分 组数据具有方差齐次性,所以 应该采用表格的上半部分数据。 数据显示机器A与B、A与C、 B与D、C与D之间的完工时间 存在显著性差异。
感谢观看
一元方差分析的软件实现及应用
案例:某电池厂设计了4种不同的生产工艺A、B、C、D,生产了4批电池, 在每批电池中随机抽取12个为样本, 现检验其寿命是否相同,具体数据如下 所示。
1.单击按钮使变量“电池寿命” 和“生产工艺”分别进入因变 量列表和因子列表。
2.对比:对平均数的变动进行趋势检验,比 较专业。
一元方差分析的结果
4)多重比较检验结果显示: A与C、A与D、B与C、B与 D这几种生产工艺生产的电 池使用寿命有无显著性的差 异。
方差分析介绍及案例分析

P
(6) <0.05 >0.05 >0.05
q0.05,(57,3)=3.40
q0.05,(57,2)=2.83
结论
总的说来,三种治疗方案的治疗婴幼儿贫血 疗效有差别。而这种差别主要来自A方案和C
方案。这一结论可用下列形式表示:
A 1.840 B 1.415 C 0.930
多个实验组与一个对照组均数间的 两两比较
单因素多个样本均数的比较 (analysis of one way variance)
处理因素只有一个 属于完全随机设计:随机抽样 随机分组 随机试验
C X
2
N
2
SS总 X C
SS组间 ni X i X
2
2
Xi
ni
2
C
SS组内 si ni 1 SS总 SS组间
总=总例数-1=20-1=19 处理=处理组数-1=4-1=3 配伍=配伍组数-1=5-1=4 误差=总-处理-配伍=19-3-4=12
列方差分析表
变异来源 总 处理 配伍 误差 表 6.8 两因素方差分析表 SS MS 0.74128 19 0.41084 3 0.13695 0.11233 4 0.02808 0.21811 12 0.01818 F 7.53 1.54 P < 0.01 > 0.05
1.840 0.913 15.8482
1.415 1.297 31.9669 59.3755
0.930 0.78 11.5626
变异分解
组间变异
总变异
组内变异
SS总=SS组间+SS组内
生物统计学-方差分析

: :
: :
: :
: :
: :
x1j x1n
x2j
x3j
xij
验方法,是将总变异按照来源分为处理效应和试验
误差,并做出其数量估计。
发现各变异原因在总变异中相对重要程度的一
种统计分析方法。
二、方差分析的基本原理
总变异分解为组间变异和组内变异。 组内变异是个体差异所致,是抽样误差。 组间变异可能由两种原因所致, 一是抽样误差; 二是处理不同。 在抽样研究中抽样误差是不可避免的,故 导致组间变异的第一种原因肯定存在;第二种原因 是否存在,需通过假设检验作出推断
上述模型中,包括两类不同的处理效应。 第一类处理效应称为固定效应(fixed effect), 它是由固定因素(fixed factor)所引起的效应。 若因素的a个水平是经过特意选择的,则该 因素称为固定因素。例如,几个不同的实验 温度,几个不同的化学药物或一种药物的几
种不同浓度,几个作物品种以及几个不同的
第二类处理效应称为随机效应(random effect),它是由随机因素(random factor)所引起的效应。若因素的a 个水平, 是从该因素全部水平的总体中随机抽出的样 本,则该因素称为随机因素。从随机因素的 a 个水平所得到的结论,可以推广到这个因 素的所有水平上。处理随机因素所用的模型 称为随机效应模型(random effect model)。例2.2 的动物窝别,是从动物所有可 能的窝别中随机选出来的,实验的目的是考 查在窝别之间,出生重是否存在差异,因而 “窝别”是随机因素。
方差分析例题及作业参考答案2015.10.22

第六章 例题及作业参考答案【 P101-例1】 方差齐性检验:242322210:σσσσ===H 05.0981.0>=p 方差齐。
43210:μμμμ===H方差分析表方差来源 离差平方和 由度方差 F 值P 结论 组间 5.399 3 1.800 505.4880.000 * 组内 0.043120.004*:P<0.05不同工艺处理间的氨基酸百分含量有显著性差异。
两两比较:各组按平均值由好到差依次排序,4213x x x x>>> 05.0000.0:05.030.0:210130<==>==p H p H μμμμ破壁和酸处理对氨基酸的百分含量的影响无显著差异。
酸处理和碱处理对氨基酸的百分含量的影响有显著差异。
最佳工艺为破壁和酸处理。
【 P105-例3】 方差齐性检验:242322210:σσσσ===H 05.0079.0>=p 方差齐。
43210:μμμμ===H方差分析表方差来源 离差平方和 由度方差 F 值P 结论 A138.21 3 46.07 10.13 0.000 * 误差e 104.57234.55*:P<0.05不同剂量的葛根素对心脏冠脉血流量有显著性差异。
两两比较:各组按平均值由好到差依次排序,1234x x x x>>> 05.0002.0:05.0122.0:05.049.0:05.036.0:120420230430<==>==>==>==p H p H p H p H μμμμμμμμ1.5g,3g,5g 剂量的葛根素对心脏冠脉血流量彼此之间无显著性差异,与1g 均有显著性差异。
【本题讨论】1、 第一组:建议删除第4、第7个数据,补充试验,以满足大鼠支数的最低要求。
2、 第二组:数据波动过大52.2,25.2==S x,建议补充试验,确定有效试验数据。
3、 鉴于存在以上问题,最终结论可能不客观。
方差分析举例
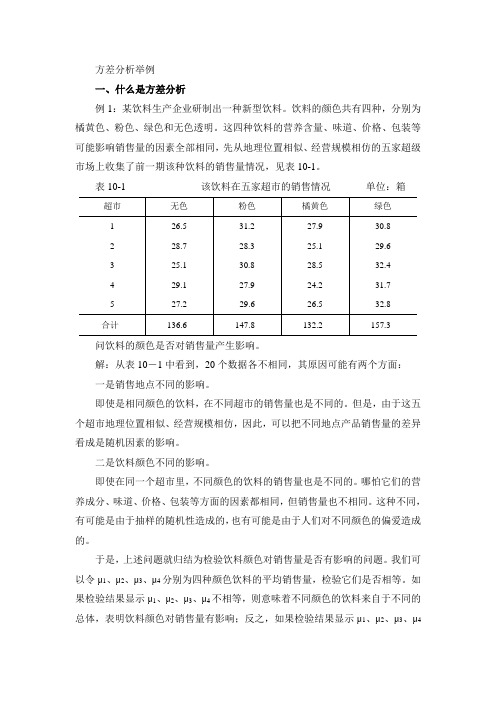
方差分析举例一、什么是方差分析例1:某饮料生产企业研制出一种新型饮料。
饮料的颜色共有四种,分别为橘黄色、粉色、绿色和无色透明。
这四种饮料的营养含量、味道、价格、包装等可能影响销售量的因素全部相同,先从地理位置相似、经营规模相仿的五家超级市场上收集了前一期该种饮料的销售量情况,见表10-1。
表10-1 该饮料在五家超市的销售情况单位:箱问饮料的颜色是否对销售量产生影响。
解:从表10-1中看到,20个数据各不相同,其原因可能有两个方面:一是销售地点不同的影响。
即使是相同颜色的饮料,在不同超市的销售量也是不同的。
但是,由于这五个超市地理位置相似、经营规模相仿,因此,可以把不同地点产品销售量的差异看成是随机因素的影响。
二是饮料颜色不同的影响。
即使在同一个超市里,不同颜色的饮料的销售量也是不同的。
哪怕它们的营养成分、味道、价格、包装等方面的因素都相同,但销售量也不相同。
这种不同,有可能是由于抽样的随机性造成的,也有可能是由于人们对不同颜色的偏爱造成的。
于是,上述问题就归结为检验饮料颜色对销售量是否有影响的问题。
我们可以令μ1、μ2、μ3、μ4分别为四种颜色饮料的平均销售量,检验它们是否相等。
如果检验结果显示μ1、μ2、μ3、μ4不相等,则意味着不同颜色的饮料来自于不同的总体,表明饮料颜色对销售量有影响;反之,如果检验结果显示μ1、μ2、μ3、μ4之间不存在显著性差异,则意味着不同颜色的饮料来自于相同的总体,可认为饮料颜色对销售量没有影响。
这就是一个方差分析问题。
在方差分析中常用到一些术语。
1.因素因素是一个独立的变量,也就是方差分析研究的对象,也称为因子。
如:例1中,我们要分析饮料的颜色对饮料的销售量是否有影响,在这里,“饮料的颜色”是所要检验的对象,它就是一个因素。
在有的书中把因素称为“因子”。
2.水平因素中的内容称为水平,它是因素的具体表现。
如:例1中“饮料的颜色”这一因素中的水平有四个,即饮料的四种不同颜色:无色、粉色、桔黄色、绿色;它们是“饮料的颜色”这一因素的四种具体表现。
方差分析--实例

例6.1 测定东北、内蒙古、河北、安徽、贵州5个地区黄鼬冬季针毛的长度,每个地区随机抽取4个样本,测定的结果列于表6-1。
试比较各地区黄鼬针毛长度的差异显著性。
表6-1 不同地区黄鼬冬季针毛长度(单位:mm)
地区东北内蒙古河北安徽贵州合计
1 32.0 29.
2 25.5 23.
3 22.3
2 32.8 27.4 26.1 25.1 22.5
3 31.2 26.3 25.8 25.1 22.9
4 30.4 26.7 26.7 25.
5 23.7
∑x126.4 109.6 104.1 99.0 91.4 530.5
n 4 4 4 4 4 20
x31.60 27.40 26.03 24.75 22.85 26.53 ∑X23997.44 3007.98 2709.99 2453.16 2089.64 14258.21
例6.2 园艺研究所调查了3个品种草莓的维生素C含量(mg/100g),测定结果列于表6-2。
试分析不同品种之间维生素C含量是否有显著性差异。
表6-2 不同品种草莓维生素C含量(单位:mg/100g)
例6.3 研究三种不同日粮对猪日增重的影响,每种日粮饲喂5头猪,三种日粮分别用TR1、TR2、TR3表示。
相关数据如下表所示:
TR1 TR2 TR3
270 290 290
300 250 340
280 280 330
280 290 300
270 280 300 总和 1400 1390 1560 4350
n 5 5 5 15
y280 278 312 290。
方差分析

方差分析方差分析是对多个总体均值是否相等这一假设进行检验。
下面通过一个例子说明方差分析的内容。
例:某化妆品生产公司研制出一种饮料。
饮料的颜色共有四种,分别为橘黄色、粉色、绿色和无色透明。
随机从五家专卖市场上收集了前一期该种饮料的销售量,如表9-1所示。
这是一个方差分析问题,即对四种不同颜色的饮料的销售量均值是否相等进行检验。
我们把四种不同颜色的饮料的销售量均值分别记为,由题意知,要检验假设;不全相等如果检验结果为不全相等,则表明饮料颜色对销售量产生影响。
反之,如果检验结果为不存在显著影响,则可以认为饮料颜色对销售量没有影响,他们来自于相同的总体。
方差分析的基本概念在方差分析中,常常用到一些术语。
我们把要考察的对象的某种特征称为指标。
试验条件分为可控制的和不可控制的两类,称可控制的试验条件为因素;因素所处的状态称为该因素的水平。
如果在一项试验中只有一个因素在变化,称他为单因素试验。
若试验中变化因素多于一个,称他为双因素以及多因素试验。
在上例中,饮料的销售量为指标,饮料的颜色为因素,饮料的四种颜色为该因素的四个水平,该例是一个单因素四水平试验。
上一章所讲的对两个总体均值的比较,实际上就是单因素两水平试验。
下面,我们简单阐述单因素方差分析的基本原理。
1.2单因素方差分析1.2.1 单因素方差分析的基本原理单因素方差分析是研究一个因素的变化对试验指标的影响是否显著的统计分析方法,是方差分析中最简单的情形。
设因素A有r个水平在水平下进行次独立试验,试验记录如表9-2其中表示第i水平进行第j次试验的可能结果。
假设,。
待检假设为:,不全相等。
如果成立,那么r个总体间无显著差异,即是说因素A对试验结果的影响不显著,所有可视为来自同一个总体,各间的差异只是由随机因素引起的。
若不成立,则在所有的总变差中,除随机波动引起的变差外,还应包括由于因素A的不同水平作用产生的差异。
如果不同水平作用产生的差异比随机因素引起的差异大得多,就认为因素A 对试验结果有显著影响,否则就认为因素A对试验的影响不显著。
