组合逻辑电路中的竞争与冒险.
组合逻辑电路中的竞争与冒险

组合逻辑电路中的竞争与冒险前面分析组合逻辑电路时,都没有考虑门电路的延迟时间对电路产生的影 响。
实际上,从信号输入到稳定输出需要一定的时间。
由于从输入到输出的过程 中,不同通路上门的级数不同,或者门电路平均延迟时间的差异, 使信号从输入 经不同通路传输到输出级的时间不同。
由于这个原因,可能会使逻辑电路产生错 误输出,通常把这种现象称为竞争冒险。
竞争:在组合逻辑电路中,某个输入变量通过两条或两条以上途径传到输出 门的输入端,由于每条途径的延迟时间不同帮到达输出门的时间就有先有后, 这种现象称为竞争。
冒险:是指数字电路中,某个瞬间出现了非预期信号的现象, 即某一瞬间数 字电路出现了违背真值表所规定的逻辑电平。
这样就出现了不该出现的尖脉冲,这个尖脉冲可能对后面的电路产生干扰一、竞争冒险的概念及其产生的原因以图示电路为例可看出,大多数组合电路都存在竞争,但所有竞争不一定都 产生错误的干扰脉冲。
竞争是产生冒险的必然条件,而冒险并非竞争的必然结果。
由以上分析可知,只要两个互补的信号送入同一门电路, 就可能出现竞争冒 险。
因此把冒险现象分为两种:1•“ 0”型冒险A +A 冒险在理想情况下输出电平为“ 1”,由于竞争输出产生低电平窄脉冲。
第二 AA=0 % 二A A=12•“ T 型冒险A A 冒险在理想情况下输出电平为“ 0”,由于竞争输出产生高电平窄脉冲。
二、竞争冒险的判断方法判断竞争冒险是否存在的方法很多,最常见的方法有:1 •代数法A »——& _________ p Yi(a)A------- > 1 _____ i> Y2(a)A _____ : ____ :_____A ―订|~?1I III IYi ___________________________(b)A—— __ LA —LdJ _L_U Y2 --------------- U —U(b)在逻辑函数表达式中,是否存在某变量的原变量和反变量。
探索组合逻辑电路的竞争冒险现象及消除方法

探索组合逻辑电路的竞争冒险现象及消除方法随着电子技术的不断发展和应用,组合逻辑电路作为数字电路中最简单的一种电路,在电子设备中应用广泛。
然而,在实际应用中,我们常常会遇到一些竞争冒险的问题。
那么,究竟什么是竞争冒险呢?它又是如何产生的呢?如何消除这种现象呢?下面就来一一解答。
一、竞争冒险的定义竞争冒险(Race Hazard)是指输入信号有多条路径到达输出端,而输出信号的正确性与哪条输入路线先到达输出端有关的一种现象。
简而言之,竞争冒险就是同一信号在不同的路径上到达目的地的时间不同,导致信号的正确性无法得到保证。
二、竞争冒险的产生原因竞争冒险通常是在异步电路中产生的。
异步电路是一种没有时钟信号的电路。
因为没有时钟信号控制,异步电路的输入信号会在任何时间到达电路中。
如果异步电路的不同信号路径的延时不相等,就会产生竞争冒险。
三、竞争冒险的消除方法为了消除竞争冒险,我们有以下几种方法:1.插入缓冲器插入缓冲器是一种最基本的解决竞争冒险问题的方法。
在信号到达目的地之前,可以在较长的信号路径中插入缓冲器,使延时较短的信号路径延迟与较长的信号路径相同的时间,达到信号的同步。
2.加强约束条件加强约束条件也可以消除竞争冒险的问题。
在设计电路的时候,我们可以设置更为严格的约束条件,使得各个信号路径的延迟时间尽量相近,从而避免产生竞争冒险。
3.优化电路结构优化电路结构也可以解决竞争冒险的问题。
我们可以在电路设计过程中尽量避免存在长短不一的信号路径,或者在架构设计时就考虑到延迟问题,在电路结构设计时保持信号路径相对简单结构,减少信号传输延迟时间。
总之,竞争冒险是组合逻辑电路中不可避免的现象,我们应该在电路设计与实现中充分考虑其存在,采取相应的措施来消除竞争冒险带来的风险和影响。
组合逻辑电路中的竞争冒险

消除冒险的方法: 1. 加封锁脉冲 2. 加选通脉冲 3. 修改逻辑设计
4. 接入滤波电容 由于尖峰干扰脉冲的宽度很窄,在可能产生尖 峰干扰脉冲的门电路输出端与地之间接入一个容量 为几十皮法的电容就可吸收掉尖峰干扰脉冲。
本章小结
组合逻辑电路指任一时刻的输出仅取决于
该时刻输入信号的取值组合,而与电路原
以逻辑门为基本单元的电路设计,其最简含义 是:逻辑门数目最少,且各个逻辑门输入端的
数目和电路的级数也最少,没有竟争冒险。 以 MSI 组件为基本单元的电路设计,其最简含 义是:MSI 组件个数最少,品种最少,组件之 间的连线最少。
编码器的作用是将具有特定含义的信息编成 相应二进制代码输出,常用的有二进制编码 器、二-十进制编码器和优先编码器。 译码器的作用是将表示特定意义信息的二进 制代码翻译出来,常用的有二进制译码器、 二-十进制译码器和数码显示译码器。
将两式对比只要令数据选择器的输入为:
A1 A, A0 G, D0 R, D1 D2 R , D3 1
则数据选择出逻辑式为: 将给定的逻辑函数式化为与上式对应的形式:
令数据选择器的输入结成如下形式:
A1 A, A0 B, D0 C , D1 1, D2 C , D3 C
尖峰干扰脉冲的现象,称为冒险。 可能导致错误动作
二、竞争冒险的产生原因及消除方法
负尖峰脉冲冒险举例 G1
A Y=A+A G2 Y A 理A 想Y A 考虑门延时 Y 正尖峰脉冲冒险举例
G1 A
1
A G2 理A Y想 Y0 A Y 1tpd
1tpd
1
Y=A· A 考虑门延时
可见,在组合逻辑电路中,当一个门电路(如 G2) 输入两个向相反方向变化的互补信号时,则在输出端 可能会产生尖峰干扰脉冲。
第四章 组合逻辑电路的竞争冒险

3.4组合逻辑电路中竞争--冒险现象理想情况电路中的连线和逻辑门都没有延迟。
电路的多个输入信号发生变化时都是同时瞬间完成的。
实际情况信号通过逻辑门需要响应时间。
信号的变化需要一定的过渡时间。
多个信号发生变化时有先后快慢的差异。
冒险逻辑冒险功能冒险不同的冒险,产生的原因不同,消除冒险的方法也不相同。
3.4.1 竞争 冒险现象及其成因两个输入信号(一个从1将出现毛刺竞争不一定都会产生尖峰脉冲不产生毛刺t pd2<t pd1+t 出现毛刺检查逻辑冒险的方法稳态时输出1,输入变化瞬间输出0的冒险,称为偏1型冒险。
稳态时输出0,输入变化瞬间输出1的冒险,称为偏0型冒险。
方法代数法卡诺图法方法比较繁琐,适用范围广,对两级(含)以上电路都适用。
注意:不能对函数进行化简。
方法简单,只适用于两级电路。
计算机模拟检查法实验检查法功能冒险输入从Ii 变到Ij时产生功能冒险的条件:2、有P个(P≥2)变量同时发生变化;1、输入变量变化前后函数值相同。
即F( I i)=F( I j);3 、由P个变量组合所构成的2P个格,既有1又有0。
例3-14:判断下面卡诺图所示逻辑函数,当输入ABCD从0110→1100,1111→1010,0011→0100,1000→1101变化时,是否存在功能冒险。
功能冒险的消除方法选通脉冲加入的位置和极性的确定:与非门实现函数F=AB+CD正极性脉冲加在第二级功能冒险的消除方法或非门实现函数F=(A+B)(C+D)负极性脉冲加在第一级功能冒险的消除方法负极性脉冲加在一个与门上功能冒险的消除方法方法二:在对输出波形边沿要求不高的情况下,可以在输,滤除毛刺。
出端接一个几十到几百皮法的滤波电容CL在输出端加小电容可以消除毛刺。
但是输出波形的前后沿将变坏,只适用于低速电路,在对波形要求较严格时,应再加整形电路。
3.4.2 消除竞争 冒险的方法加冗余项:只能消除逻辑冒险,而不能消除功能冒险,适用范围有限。
组合逻辑电路中的竞争与冒险现象

F DD
此处两卡诺圈相切, 有两个最小项相邻 但又不在一个卡诺
圈中,会出现
F BB
1.2 组合逻辑电路中的竞争与冒险现象的消除
1.改变逻辑设计(增加冗余项)
使得表达式无论在什么样的逻辑值组合下不会出现 AA 或者 A A 的形式
例 判断F BC AC是否存在冒险,如果有,通过增加冗余项消除冒险
不考虑门电路的延时, 无论A取什么值,输出F
总是为1,不可能为0
考虑门电路的延时产生
“冒险”,因为这个毛刺 是负向的,而逻辑函数F本 身应该为1,所以称为“0
冒险”
上述分析竞争冒险产生的例子都是由于门电路的延时产生了冒险,在逻辑关系上是
由于 AA 或 A A 引起的,因此我们可以根据表达式中某个变量是否同时以原变量
F BC AC AB
2.吸收法(滤波电容)
增加的沉余项,即使A=B=1,C发生 改变,电路有延迟,F始终为1。这
样就避免了冒险现象的发生
3.取样法
数字电路与逻辑设计
和反变量出现来判断是否具备了竞争条件
代数判别法
例 逻辑表达式为 F BC AC AB ,判断是否可能存在竞争冒险。 解:表达式中,变量C和B都存在着原变量和反变量,是否有可能出现 F C C 或者
是 F B B 的取值组合?
当A=1,B=1时,F C C ,出现“0冒险”。
当A=1,C=1时,F B B ,出辑电路中的竞争与冒险现象
以上所讨论的组合逻辑电路都假设逻辑门电路是理想的。即没有延时时间对信号波形的影响。 在实际电路设计中,我们必须考虑延时因素。 因为按理想条件设计的电路,在信号的瞬变时刻有可能在电路的输出端出现不应有的毛刺,使电 路处于不稳定状态,我们称这种现象为“冒险”。 在有多个输入信号的组合电路中,当有两个或两个以上信号同时发生变化时,由于同一个信号通 过不同路径到达某一个门的输入端的先后时间有差别,这种现象称为“竞争”
5组合逻辑电路中的竞争冒险

(b)
L A A 1 稳态逻辑关系
竞争产生负尖脉冲:偏1冒险
产生竞争冒险的原因:门电路的传输延迟使同一变量经过 不同路径到达输出端的时间不同。
竞争冒险的危害性:使对脉冲敏感的系统出现误动作。
2 冒险现象的判别方法(分析法) 1) 代数法
分析输入变量的取值情况,看是否存在某些输入变量的特定 取值使表达式出现L=AA 或者L=A+A 例 判断 L AC AB AC 是否存在冒险现象
B=1, A=0时出现L=C+C
AC AB
C 00 01 11 10
0
1
AB
BC
L= BC+ AC +AB
B=1, A=0时出现L=C+C+1
2) 加滤波电容
A
A
&
C
A
1
&
≥1
L
C
1
&
C
C
B
B
(a)
L AC AB AC
L 冒险
(b)
3) 加选通控制 保证输出在输入信号稳定时有效
组合逻辑电路分析与设计小结
3.5 组合逻辑电路中的竞争冒险
1 竞争冒险的意义
竞争: 在组合逻辑电路中,若某个变量通过2条以上的途 径到达输出端,由于每条路径上的延迟时间不同,到达输 出端的时间有先后区别,这一现象叫做竞争。
A
B
1
G1 C
G3
&
G4
&
G2
L
&
冒险: 当某个变量发生变化时,如果真值表所描述的逻辑 关系受到短暂的破坏,并在输出端出现不应有的尖脉冲, 此种情况称为冒险。
组合逻辑电路中的竞争冒险

组合逻辑电路中的竞争冒险
前面分析组合逻辑电路时,都没有考虑门电路的延迟时间对电路产生的影响。
实际上,从信号输入到稳定输出需要一定的时间。
由于从输入到输出的过程中,不同通路上门的级数不同,或者门电路平均延迟时间的差异,使信号从输人经不同通路传输到输出级的时间不同。
由于这个原因,可能会使逻辑电路产生错误输出。
通常把这种现象称为竞争冒险。
一、产生竞争冒险的原因
首先来分析下图所示电路的工作情况,可以建立竞争冒险的概念。
在图中,与门G2的输入是A和两个互补信号。
由于G1的延迟,的下降沿要滞后于A的上升沿,因此在很短的时间间隔内,G2的两个输入端都会出现高电平,致使它的输出出现一个高电平窄脉冲(它是按逻辑设计要求不应出现的干扰脉冲),见图中的波形部分所示。
与门G2的2个输入信号分别由G1和A端两个路径在不同的时刻到达的现象,通常称为竞争,由此而产生输出干扰脉冲的现象称为冒险。
下面进一步分析组合逻辑电路产生竞争冒险的原因。
设有一个逻辑电路如上图所示,其工作波形如下图所示。
它的输出逻辑表达式为。
由此式可知,当A和B都为1时,L=1,与C的状态无关。
但是,由波形图可以看出,在C由1变0时,C由0变1有一延迟时间,在这个时间间隔内,G2和G3的输出AC和同时为0,而使输出出现一负跳变的窄脉冲,即冒险现象。
这是产生竞争冒险的原因之一,其他原因这里不作详述。
由以上分析可知,当电路中存在由反相器产生的互补信号,且在互补信。
数字电子技术基础34组合逻辑电路中的竞争-冒险现象
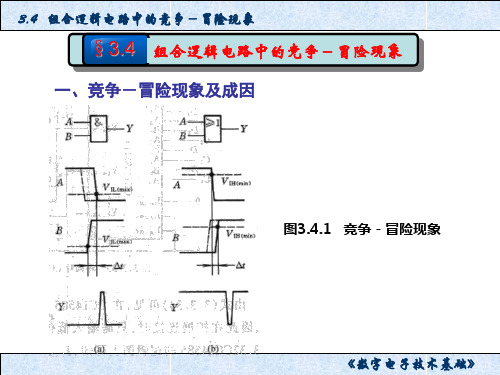
§3.4 组合逻辑电路中的竞争-冒险现象
一、竞争-冒险现象及成因
图3.4.1
竞争-冒险现象
《数字电子技术基础》
3.4 组合逻辑电路中的竞争-冒险现象
成因:当两个输入信号同时向相反的逻辑电平跳变 时(一个从1变为0,一个从0变为1) ,由于存在时刻上 的差异,使两个信号在 t 的极短时间内同时为高电平 或低电平,从而产生尖峰脉冲,不符合门电路稳态下的 逻辑功能,产生内部噪声。
《数字电子技术基础》
3.4 组合逻辑电路中的竞争-冒险现象
三、消除竞争-冒险现象的方法 (一)接入滤波电容 尖峰脉冲一般都很窄(几十ns以内),只要在输出 端并接一个很小的滤波电容 C f (TTL电路中通常为几 十~几百皮法),就足以将尖峰脉冲的幅度削弱至门电 路的阈值电压以下。 例:
图3.4.2 接入滤波电 容消除竞争-冒险现 象的示意图
优点: 简单易行。
缺点: 增加了输出电压波形的上升和下降时间,使波形变坏。
《数字电子技术基础》
3.4 组合逻辑电路中的竞争-冒险现象
(二)引入选通脉冲 例:
图3.4.3 引入选通脉 冲消除竞争-冒险现 象的示意图
优点: 简单,不需增加电路元件。 缺点: 正常的输出信号也将变成脉冲信号,宽度与选通 脉冲相同,且此选通脉冲必须与输入信号同步。
《数字电子技术基础》
3.4 组合逻辑电路中的竞争-冒险现象
(三)修改逻辑设计 有时可用增加冗余项的方法消除竞争-冒险现象。 例:将 Y AB AC 化成 Y AB AC BC ,可 使电路功能不变,而消去B=C=1时的竞争-冒险现象。
图3.4.4 修改逻辑设计消除竞争-冒险现象的示意图
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
组合逻辑电路中的竞争与冒险
前面分析组合逻辑电路时,都没有考虑门电路的延迟时间对电路产生的影响。
实际上, 从信号输入到稳定输出需要一定的时间。
由于从输入到输出的过程中, 不同通路上门的级数不同, 或者门电路平均延迟时间的差异, 使信号从输入经不同通路传输到输出级的时间不同。
由于这个原因, 可能会使逻辑电路产生错误输出,通常把这种现象称为竞争冒险。
竞争:在组合逻辑电路中, 某个输入变量通过两条或两条以上途径传到输出门的输入端, 由于每条途径的延迟时间不同帮到达输出门的时间就有先有后, 这种现象称为竞争。
冒险:是指数字电路中, 某个瞬间出现了非预期信号的现象, 即某一瞬间数字电路出现了违背真值表所规定的逻辑电平。
这样就出现了不该出现的尖脉冲,
一、
竞争冒险的概念及其产生的原因
以图示电路为例可看出, 大多数组合电路都存在竞争, 但所有竞争不一定都产生错误的干扰脉冲。
竞争是产生冒险的必然条件,
而冒险并非竞争的必然结果。
由以上分析可知, 只要两个互补的信号送入同一门电路, 就可能出现竞争冒险。
因此把冒险现象分为两种:
1. “ 0”型冒险
A A +冒险在理想情况下输出电平为“ 1” , 由于竞争输出产生低电平窄脉冲。
A A ⋅冒险在理想情况下输出电平为“ 0” ,由于竞争输出产生高电平窄脉冲。
二、竞争冒险的判断方法
判断竞争冒险是否存在的方法很多,最常见的方法有: 1.代数法
在逻辑函数表达式中, 是否存在某变量的原变量和反变量。
若去掉其他变量得到 A A Y +=,电路有可能产生“ 0”冒险;若得到 A A Y ⋅=,则可能产生“ 1” 冒险。
2.卡诺图法
画出逻辑函数的卡诺图, 当卡诺图中两个合并最小项圈相切, 即两个合并最小项圈相邻—有相邻项, 各合并最小项圈各自独立—不相交时, 这个逻辑函数有可能出现冒险现象。
三、消除竞争冒险的方法
1.修改逻辑设计 (1代数法
①逻辑变换消去互补量
((C A B A Y ++=当 B =C=0时, A A Y ⋅=, 存在竞争冒险。
若将逻辑函数表达式进行逻辑变换,则 BC B A AC Y ++=,这时消去了 A A ⋅互补量,从而不会产生竞争冒险。
②增加乘积项
C A AB Y +=当 B=C=1时, A A Y +=,存在竞争冒险。
若增加乘积项 BC , 则 BC C A AB Y ++=,消除了竞争冒险。
(2卡诺图法
将卡诺图中相切的圈用一个多余的圈连接起来,即可消除冒险现象。
2
为了消除竞争冒险产生的干扰脉冲,可引入封锁脉冲, 。
封锁脉冲要与信号
转换时间同步, 而且封锁脉冲宽度不应小于电路从一个稳态转换到另一个稳态的过渡时间。
3.引入选通脉冲
选通法是当有冒险脉冲时, 利用选通脉冲把输出级封锁住, 使冒险脉冲不能输出, 而当冒险脉冲消失之后, 选通脉冲又允许正常输出。
它出现的时间应与输入信号变化的时间错开, 从而避开了冒险, 在时间上则在干扰脉冲已经消失之后才加入,这样电路的输出不再是电位信号,而是一个脉冲信号。
4.输出端并联电容—滤波电容
因为竞争冒险所产生的干扰脉冲一般很窄,所以当电路工作频率不很高时, 在输出端并接一个电容, 可以吸收掉干扰脉冲, 将尖峰脉冲的幅度减小到不起影响的程度。
但应注意电容量不能太大,否则使波形变坏,影响电路的工作速度。
