2.4摩尔热容
合集下载
2-4热容,恒容变温过程、恒压变温过程

微分:
Qp dU nCp,mdT
积分:
Qp U nC p,mdT
T1
T2
恒压过程:W = -PΔV ΔU = ΔH - pΔV 对理想气体 W = -PΔV = -nRΔT
2.4 热容,恒容变温过程、恒压变温过程 4.凝聚态物质变温过程
微分:
QP dH nCp,mdT
5 = R 2
C p ,m
7 = R 2
2.4 热容,恒容变温过程、恒压变温过程 ⑤. 应用
U nCV ,m (T )dT
T1
T2
H nCp,m (T )dT
T1
T2
a. 应用体系为单纯的PVT变化。 b. 对于理想气体,U = f (T) H = f (T) 说明理想气体U和H只 是T的状态函数,不受过程是否恒容或恒压以及其它条件 的限制,但此过程的Q不一定等于QV,QP c. 对于凝聚态物质Cp,m — Cv,m = 0 (少数物质除外,如 C6H6,C2H5OH),因为液固态物质的摩尔体积随温度的 变化可忽略。
对于理想气体
U m 0 Vm T
Vm R T p
Cp,m - Cv,m = R Cp — Cv = nR 在具体应用中,对单、双原子理想气体可取以下值: 单原子分子 Cv ,m 双原子分子 Cv ,m
3 = R 2 C p ,m 5 = R 2
U m Vm U m p T p T p T V
再由 定压下 代入式,得
U U dU m m dT m dV T V V T
U m U m U m Vm V T T p T V m T p NhomakorabeaT1
Qp dU nCp,mdT
积分:
Qp U nC p,mdT
T1
T2
恒压过程:W = -PΔV ΔU = ΔH - pΔV 对理想气体 W = -PΔV = -nRΔT
2.4 热容,恒容变温过程、恒压变温过程 4.凝聚态物质变温过程
微分:
QP dH nCp,mdT
5 = R 2
C p ,m
7 = R 2
2.4 热容,恒容变温过程、恒压变温过程 ⑤. 应用
U nCV ,m (T )dT
T1
T2
H nCp,m (T )dT
T1
T2
a. 应用体系为单纯的PVT变化。 b. 对于理想气体,U = f (T) H = f (T) 说明理想气体U和H只 是T的状态函数,不受过程是否恒容或恒压以及其它条件 的限制,但此过程的Q不一定等于QV,QP c. 对于凝聚态物质Cp,m — Cv,m = 0 (少数物质除外,如 C6H6,C2H5OH),因为液固态物质的摩尔体积随温度的 变化可忽略。
对于理想气体
U m 0 Vm T
Vm R T p
Cp,m - Cv,m = R Cp — Cv = nR 在具体应用中,对单、双原子理想气体可取以下值: 单原子分子 Cv ,m 双原子分子 Cv ,m
3 = R 2 C p ,m 5 = R 2
U m Vm U m p T p T p T V
再由 定压下 代入式,得
U U dU m m dT m dV T V V T
U m U m U m Vm V T T p T V m T p NhomakorabeaT1
2.4热容QvQp

P1=100 kPa V1=50dm3
恒容加热
P2=200 kPa V2=50dm3
恒压冷却
T1=?
T2=?
解:P1V1=P3V3 ;P1V1=nRT1, P3V3=nRT3 T1=T3
所以:整个过程 ΔH=0;ΔU=0
根据热一定律 ΔU=Q+W 所以 :Q=-W
P3=200 kPa V3=25dm3 T3=?
14
例:某双原子例理想理气气体P1VmTo过l ,程由Δ始H态和20Δ0Uk的Pa计、3算50K 绝热
反抗 50 kPa恒外压一次膨胀到平衡态,求末态温度T2和过程 的Q、W、ΔH、ΔU。
解:要求出ΔH和ΔU,根据计算公式,末态温度T2的求取 是本题目的关键。 (1)求T2:绝热过程体系与外界没有热交换,则Q=0
提示:
读完题后,象教材例题上那样,先用框架流程图把题目的
条件(P、V、T)画出来,这样做题不容易出错。
19
课堂作业讲解
第一题: 2 mol 理想气体,Cp,m =7/2 R,由始态100 kPa、50dm3,
先恒容加热使得压力升至200 kPa,再恒压冷却使体积缩小到 25 dm3。求整个过程的Q、W、ΔH、ΔU。
W = U-Q =-9.98 kJ
9
4.4 凝聚态物质变温过程的热
• 对凝聚态物质的变温过程,
在恒压或压力变化不很大时, 可由Cp,m求得 Q
Q和p HH,
T2
T 1 nC p,mdT
如 果 Cp,m 为 常 数 , 则Qp nCp,m(T2-T1)
因V 0, 故W 0, U H.
注意:
20
课堂作业讲解
W=W1+W2 第一步为恒容过程,所以:W1=0 W=W2=-P2(V3-V2)
第二章热力学第一定律(2)

C p ,mCV ,m , cV =C p =nC p ,m , CV =nCV ,m , c p = MM
17
一些气体自25℃至某温度的平均摩尔定压热容Cp,m/(J⋅K-1⋅mol-1) t/℃ H2 空气 CH4 25 28.80 29.14 35.74 100 28.94 29.24 37.54 200 29.08 29.35 40.24 300 29.13 29.57 43.01 500 29.94 30.20 48.70 1000 29.80 31.74 60.86
代入数据得
ΔU = 9876 J = 9.876 kJ
QV = ΔU = 9.876 kJ ΔH = ΔU + Δ ( pV ) = ΔU + n(Ar,g) RΔT = 13.201 kJ
13
4. Cp,m(CV,m)随温度T的变化
是重要的基础热数据,是通过量热实验获得的。 往往随温度而变化。 表达Cp,m随T变化的方法有三种 (1) 数据列表: (2) Cp,m—T 曲线:直观 (3) 函数关系式:便于积分、应用 C p ,m = a + bT + cT 2 C p ,m = a + bT + cT 2 + dT 3
解: ΔU =n ∫T1 CV ,m dT
=2mol × 25.29J ⋅ mol−1 ⋅ K −1 × (352.15 − 298.15)K ΔU =nCV ,m (T2 − T1 ) =2731 J ΔH =nC p ,m (T2 − T1 ) =2mol × 33.60J ⋅ mol−1 ⋅ K −1 × (352.15 − 298.15)K =3629 J
解: 过程恒容 W£½0
ΔU = ΔU (Ar,g) + ΔU (Cu,s)
24摩尔热容
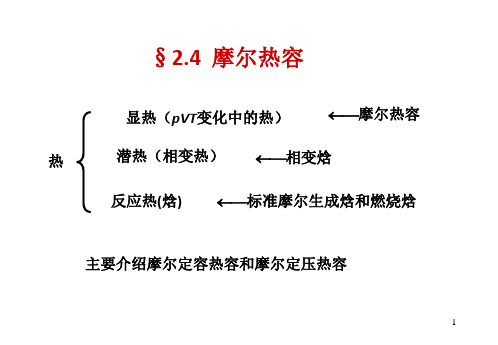
理想气体:
( Um V
) T
0,
(
Vm T
) p
R p
,
C p ,m CV ,m R
单原子分子 双原子分子
3
5
CV ,m 2 R,C p,m 2 R
5
7
CV ,m 2 R,C p,m 2 R
对pg混合物, Cp,m(mix)=∑y(B) Cp,m(B);
CV,m(mix)=∑y(B) CV,m(B)
22
解题步骤:a.先找为0 量;b.再计算状态函数
c.求功
d.求热
例 1. 在带活塞汽缸中有1mol He(g),起始状态为25℃、 500 kPa,若在恒温下将施加在活塞上的环境压力突然
加至1000kPa并达平衡,求压缩过程的Q、W、ΔU和
ΔH。
pg,n=1mol T1=298.15K p1 =500kPa V1 =
理想气体
n=1mol p1=101.325kPa
T1=300K V1
恒p外 dT=0
n=1mol p2= p外
T2=300K V2
U
n
T2 T1
CV ,mdT
=8729J
H
n
T2 T1
Cp,mdT
=14.55kJ
W2=0 dV=0
n=1mol V3=V2
W= W1+ W2=-p环(V2-V1)
T3=1000K
T2、p2、V2
ΔUT ΔUV
ΔUV ΔUT
n mol pg T2、p' 、V1
T1、p ' 、V2
T2
T2
U UV UT n CV ,mdT 0 n CV ,mdT
物理化学2-04摩尔热容

dp=0
2molH2 p2 =p1 = 100kPa
T2= 1000K
Qp = H nC p,mT
= 2 mol×29.2 J·mol1·K1(1000-400)K
= 35.04 kJ
U = H- (pV) = H-nR(T2-T1) = 25.06 kJ W = U-Q =-9.98 kJ
19
例17 0.2 mol某理想气体, 从273 K, 1 MPa恒压
23.529kJ
Or: W = U - Qp =56.6 - 80.129= -23.529 kJ
25
21
例18 3 mol某理想气体, 在101.3 kPa下恒压由20℃加热 到80℃, 计算此过程的Q, W, U, H. 已知该气体 CV, m = (31.38+13.4×103 T/K)J·mol1·K1.
n = 3 mol T1 = 20℃ p1 =101.3kpa
恒压
n = 3 mol T2 = 80℃ p2 = 101.3kpa
0,
Vm T
p
R p
Cp,m CV,m R 或 Cp-CV = nR
13
③注意:
单原子分子,如:Ar,He,etc.
C C 3 R , 5 R
V,m 2
P,m 2
ig.
双原子分子,如:N2,O2,H2,etc.
CV,m
5 2
R
,
CP,m
7 2
R
14
5.摩尔热容随温度变化的表达式
热容的大小与物种及其聚集状态和温度有关。
, T T1 T2 2
16
8.气体恒容变温过程
计算式:
QV VU
T2
第二章 热力学第一定律-kt

§2.1 基本概念及术语
4 热力学平衡态(thermodynamical equilibrium 热力学平衡态( state) )
一定条件下,系统中各个相的宏观性质不随时间变化的状态。 热平衡(thermal equilibrium):体系各部分温度相等 热平衡 : 力平衡(mechanical equilibrium) :体系各部的压力都相等 力平衡 相平衡(phase equilibrium):多相共存时,各相的组成和数 相平衡 : 量不随时间而改变 化学平衡(chemical equilibrium):反应体系中各物的数量不 化学平衡 : 再随时间而改变
16
§2.2 热力学第一定律
• 1 功(work) )
除了热传递以外,其它各种形式传递的能量, 用W或δW表示。包含体积功和非体积功。 单位: 单位 焦耳(J)
正负号规定: 正负号规定:系统对环境做功W<0,系统得到环 境的功W>0。 非体积功: 非体积功: 电功 W′= –nFE;表面功 W′=σAs
状态函 数法
过程中状态函数的变化的计算方法, 即状态函数变化只取决于始末态而 与途径无关。
11
§2.1 基本概念及术语
b 单相混合物系统
X = f ( x, y, n) = f (T , p, n)
c 多相系统
X (α ) = f (T , p, n)
X ( β ) = f (T , p, n)
12
10
§2.1 基本概念及术语
状态函数表征: 状态函数表征:
a 纯物质单相系统 X = f ( x, y )
∆X = ∫ dX = X 2 − X 1
X1 X2
状态2 状态
2 1
2.4 热容,恒容及恒压过程

重排,将 dp, dT 项分开,得:
dU ( U V U U V )T ( )T dp [( )V ( )T ( ) p ]dT V p T V T U U U V =( )T dp [( )V ( )T ( ) p ]dT p T V T U U )T dp ( ) p dT p T
C p CV ( H U ) p ( )V T T (U PV ) U ( ) p ( )V (代入H 定义式) T T U V U ( ) p p( ) p ( )V T T T 根据复合函数的偏微商公式(见下页)
(
U U U V ) p ( )V ( )T ( ) p T T V T
所以
V ( ) p nR / p T
Cp CV nR
下一内容 回主目录 返回
201与Cv之差
证明:( U ) p ( U ) ( U ) ( V ) p T T V V T T 设: U U (T ,V ), V V (T , p) U U dU ( )V dT ( )T dV T V
上一内容
下一内容 回主目录 返回
2014-7-4
1.5 热容 (heat capacity) 等压热容Cp: C p Qp ( H ) p
dT T
QP (T2 T1 ) H n CP,m dT T
1
T2
等容热容Cv:
QV U CV ( )V T dT
1.9
热容 (heat capacity)
对于组成不变的均相封闭体系,不考虑非膨 胀功,设体系吸热Q,温度从T1 升高到T2,则:
平均热容定义: C 真热容C :
Q C dT
Q T2 T1
dU ( U V U U V )T ( )T dp [( )V ( )T ( ) p ]dT V p T V T U U U V =( )T dp [( )V ( )T ( ) p ]dT p T V T U U )T dp ( ) p dT p T
C p CV ( H U ) p ( )V T T (U PV ) U ( ) p ( )V (代入H 定义式) T T U V U ( ) p p( ) p ( )V T T T 根据复合函数的偏微商公式(见下页)
(
U U U V ) p ( )V ( )T ( ) p T T V T
所以
V ( ) p nR / p T
Cp CV nR
下一内容 回主目录 返回
201与Cv之差
证明:( U ) p ( U ) ( U ) ( V ) p T T V V T T 设: U U (T ,V ), V V (T , p) U U dU ( )V dT ( )T dV T V
上一内容
下一内容 回主目录 返回
2014-7-4
1.5 热容 (heat capacity) 等压热容Cp: C p Qp ( H ) p
dT T
QP (T2 T1 ) H n CP,m dT T
1
T2
等容热容Cv:
QV U CV ( )V T dT
1.9
热容 (heat capacity)
对于组成不变的均相封闭体系,不考虑非膨 胀功,设体系吸热Q,温度从T1 升高到T2,则:
平均热容定义: C 真热容C :
Q C dT
Q T2 T1
物理化学第三章2-04摩尔热容

U m Vm V p T p m T
C p,m CV ,m 很小
U m ② 理想气体: V m
Vm 0 , R T T p p
PVm=RT
Cp,m CV,m R
1
T2
小结:
①对一定量的理想气体的任意pVT变化, 有:
U nCV ,mdT
T1 T2
H nCp,mdT
T1
T2
②一个十分常见的错误是: 将上两式运用于包含理想气体 的相变或化学变化过程, 因恒温, 得 U = 0! H = 0 ! ③在非恒容或非恒压条件下, U Q , H Q。如:压 缩绝热气缸内的理想气体, Q = 0; 而 T > 0, U > 0, H > 0。
代入前式,得: Cp ,m CV ,m
U m Vm V p T p m T
4. Cp , m与CV , m的关系:
⑵结论:
T p
C p ,m C V ,m
Vm ①凝聚态物质 很小
§2.4 摩 尔 热 容
1.热容 定义:一定量的物质温升1度所需的热量。 C=Q/ T
一定量:1mol 摩尔热容
C=Q/ dT
单位 : Jmol-1K-1 Cm=C/n
1kg 质量热容
单位 : Jkg-1K-1
§2.4摩 尔 热 容
2.摩尔定容热容
CV, m
单位 : Jmol-1K-1
C p ,m
1 δQ p = n dT
对恒压过程 δQ p = dH p = n dH m,p 代入有
C p ,m
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解: Q = T nCp ,m dT
T2
1
= n [ a(T2-T1)+b / 2(T22-T12)] 把数据代入,得Q = 1.14 kJ W = -pV = -nRT = -0.42 kJ U = Q+W = 0.72 kJ H = Q = 1.14 kJ
例. 某理想气体,其CV,m = 20 J· 1· 1, mol K 现有该气体10 mol处于283 K,采取下列不同途 径升温至566 K。试计算各个过程的Q,W,U, H,并比较之。 ( 1 )体积保持不变; ( 2 )系统与环境无热交换; ( 3 )压力保持不变。
W、Q、ΔU和ΔH。
解:n=1mol,理想气体 p1=2atm 恒容 V1=10L T1 W1 p2=20atm 恒压 V2=10L T2 W2 p3=20atm V3=1L T3
W1 =0 W2=- p ΔV=- p2 (V3- V2)=- 20 × (1-10)
=180 atm· L=180×101.325×10-3
Q p T
T2
1
nC p ,mdT
非恒压系统分理想气体和凝聚态物质两种情况。 a.理想气体: 理想气体的U=f(t),H=U+PV=U+nRT= f(t)
H T
T2
1
nC p ,mdT
b.凝聚态物质 凝聚态物质在T一定时,只要压力变化不大, 压力p对△H的影响往往可以忽略不计。
H nC p ,mdT
§2.4 摩尔热容
1.摩尔定容热容 CV ,m : (1)定义
在某温度T时,物质的量为n的物质在恒容且非 体积功为零时,不发生化学变化、相变化,温度
升高dT所需的热量为δQV,则该温度T下的摩尔定
容热容以表示 CV , m为:
CV ,m
1 δQV n dT
由于QV = dU=ndUm
dU m 1 dU CV ,m dT n dT V V
C p ,m a bT cT 2 C p ,m a bT c 'T 2 C p ,m a bT cT 2 dT 3
式中 a、b、c、 c’、 d 分别为经验系数,
其值由实验确定。应用以上两式时所取修正项
多少取决于要求的精确度。
5.平均摩尔定压热容
C p ,m
知气体的CV=20.92J· -1· -1。 mol K 解: n=1mol,理想气体 t1 =27 ℃ p1 = 1atm V1
(1) 恒温、恒外压
t2 =27 ℃ p2 = p环 V2
恒容
t3=97 ℃ p3 = 10atm V3 = V2
(2)
ΔU=nCV(T3-T2)=1×20.92 × (97-27)=1464J ΔH=nCP(T3-T1)=n(CV+R)(T3-T1) =1×(20.92+8.315)×(97-27)=2046J p环=p2=p3×T2/ T3 W1=- p环 ΔV= -p2(V2-V1)= -p2V2+p2V1=-nRT2 +p2(nRT1/p1)=- nRT2{1-(p3/ p2)×(T1/ T3)} =-1×8.31×300.15{1-(10/1)×300.15/370.15} =17740J
T2
n T2 T1
Qp
C p ,m C p ,mdT /(T2 T1 )
T1
不同温度范围内,物质的平均摩尔定压热容 不同。 在一般计算中若温度变化不大,常将摩尔定 压热容视为不变。
例题1:
1.1mol理想气体由2atm、10L时恒容升温,使压力
到20 atm。再恒压压缩至体积为1L。求整个过程的
解:( 1 )dV = 0,W = 0。 QV = U = n CV,m (T2-T1 ) = ( 10×20×283 ) J = 56.6 kJ H = n Cp,m (T2-T1 ) = {10×(20+8.314)×283} J = 80.129 kJ ( 2 )Q = 0, U2 = U1 = 56.6 kJ, H2 = H1 = 80.129 kJ W = U2 = 56.6 kJ ( 3 )dp = 0,U3 = U1 = 56.6 kJ, Qp = H = 80.129 kJ
=18.24kJ
W = W1 + W2 =18.24kJ
∵p3 V3= p1 V1
∴T3= T1,故ΔU=0 ΔH=0 Q=-W= - 18.24kJ
例. 3 mol单原子理想气体,从初态T1 = 300 K ,p1 = 100 kPa,反抗恒外压力50 kPa作不可逆 膨胀,至终态T2 = 300 K,p2 = 50 kPa,求这 一过程的Q,W,U,H。 解:U = 0,H = 0
对于理想气体 C p ,m CV ,m R
C 对单原子: V ,m 3R / 2, C p ,m 5R / 2 C 对双原子: V ,m 5R / 2, C p ,m 7 R / 2
对于凝聚态物质
CV ,m C p ,m
4.定压摩尔热容与温度的关系
热容随温度变化,常用级数形式表示热容 对温度的依赖关系:
升高dT所需的热量为δQV,则该温度T下的摩尔定
压热容以表示 C p ,m为:
1 δQp C p,m n dT
由于Qp = dH=ndHm
C p,m
1 dH dH m dT dT n p p
单位为: J K 1 mol1 。
(2)应用:单纯PVT变化 恒压: H
C p ,m CV ,m [(
U m Vm U m [( ) p p( )p ] ( )V T T T
U m U V V U U V )V ( m )T ( m ) p p( m ) p ] ( m )V [( m )T p]( m ) p T Vm T T T Vm T
单位为: J K 1 mol1 。
(2)应用:单纯PVT变化
恒容: U
QV T
T2
1
nCV ,mdT
非恒容理想气体:
U T
T2
1
nCV ,mdT
(理想气体的U=f(t))
2.摩尔定压热容 C p,m :
(1)定义
在某温度T时,物质的量为n的物质在恒压且非 体积功为零时,不发生化学变化、相变化,温度
W V12 pdV -p(V 2-V 1) = -nRT2 nRT1 V nR(T1 T2 ) 23.529kJ
例题: 1mol理想气体于27℃、1atm时受某恒定外压恒温 压缩到平衡,再于该状态下恒容升温至97℃则压
力达10atm。求整个过程的W、Q、ΔU、ΔH。已
T1
T2
过程的△U, U H
3.Cp,m与CV,m的关系
C p ,m CV ,m
U m U m dU m dT V d V T V T U m U m U m Vm 有 T V T T p V m T p
W = -pamb( V2-V1 )
= -pambnRT( 1 / p2-1 / p1 ) = -3.741 kJ Q = -W = 3.741 kJ
例. 2 mol H2从400 K,100 kPa定压加热到1000 K ,已知Cp,m(H2) = 29.2 J· 1· 1,求U,H, mol K Q,W各为多少? 解:Qp = H nC p ,m T
W2=0 W= W1+ W2=17740J Q=ΔU-W=1464-17740=16276J
= 2 mol×29.2 J· 1· 1( 1000-400 ) K mol K
= 35.04 kJ U = H - ( pV ) = H-nR( T2-T1 ) = 25.06 kJ W = U-Q = -9.98 kJ
例. 0.2 mol某理想气体,从273 K,1 MPa定压加 热到523 K,计算该过程的Q,W,U,H。已知该 气体的Cp,m = ( 20+7×10-3 T / K ) J· 1· 1。 mol K
T2
1
= n [ a(T2-T1)+b / 2(T22-T12)] 把数据代入,得Q = 1.14 kJ W = -pV = -nRT = -0.42 kJ U = Q+W = 0.72 kJ H = Q = 1.14 kJ
例. 某理想气体,其CV,m = 20 J· 1· 1, mol K 现有该气体10 mol处于283 K,采取下列不同途 径升温至566 K。试计算各个过程的Q,W,U, H,并比较之。 ( 1 )体积保持不变; ( 2 )系统与环境无热交换; ( 3 )压力保持不变。
W、Q、ΔU和ΔH。
解:n=1mol,理想气体 p1=2atm 恒容 V1=10L T1 W1 p2=20atm 恒压 V2=10L T2 W2 p3=20atm V3=1L T3
W1 =0 W2=- p ΔV=- p2 (V3- V2)=- 20 × (1-10)
=180 atm· L=180×101.325×10-3
Q p T
T2
1
nC p ,mdT
非恒压系统分理想气体和凝聚态物质两种情况。 a.理想气体: 理想气体的U=f(t),H=U+PV=U+nRT= f(t)
H T
T2
1
nC p ,mdT
b.凝聚态物质 凝聚态物质在T一定时,只要压力变化不大, 压力p对△H的影响往往可以忽略不计。
H nC p ,mdT
§2.4 摩尔热容
1.摩尔定容热容 CV ,m : (1)定义
在某温度T时,物质的量为n的物质在恒容且非 体积功为零时,不发生化学变化、相变化,温度
升高dT所需的热量为δQV,则该温度T下的摩尔定
容热容以表示 CV , m为:
CV ,m
1 δQV n dT
由于QV = dU=ndUm
dU m 1 dU CV ,m dT n dT V V
C p ,m a bT cT 2 C p ,m a bT c 'T 2 C p ,m a bT cT 2 dT 3
式中 a、b、c、 c’、 d 分别为经验系数,
其值由实验确定。应用以上两式时所取修正项
多少取决于要求的精确度。
5.平均摩尔定压热容
C p ,m
知气体的CV=20.92J· -1· -1。 mol K 解: n=1mol,理想气体 t1 =27 ℃ p1 = 1atm V1
(1) 恒温、恒外压
t2 =27 ℃ p2 = p环 V2
恒容
t3=97 ℃ p3 = 10atm V3 = V2
(2)
ΔU=nCV(T3-T2)=1×20.92 × (97-27)=1464J ΔH=nCP(T3-T1)=n(CV+R)(T3-T1) =1×(20.92+8.315)×(97-27)=2046J p环=p2=p3×T2/ T3 W1=- p环 ΔV= -p2(V2-V1)= -p2V2+p2V1=-nRT2 +p2(nRT1/p1)=- nRT2{1-(p3/ p2)×(T1/ T3)} =-1×8.31×300.15{1-(10/1)×300.15/370.15} =17740J
T2
n T2 T1
Qp
C p ,m C p ,mdT /(T2 T1 )
T1
不同温度范围内,物质的平均摩尔定压热容 不同。 在一般计算中若温度变化不大,常将摩尔定 压热容视为不变。
例题1:
1.1mol理想气体由2atm、10L时恒容升温,使压力
到20 atm。再恒压压缩至体积为1L。求整个过程的
解:( 1 )dV = 0,W = 0。 QV = U = n CV,m (T2-T1 ) = ( 10×20×283 ) J = 56.6 kJ H = n Cp,m (T2-T1 ) = {10×(20+8.314)×283} J = 80.129 kJ ( 2 )Q = 0, U2 = U1 = 56.6 kJ, H2 = H1 = 80.129 kJ W = U2 = 56.6 kJ ( 3 )dp = 0,U3 = U1 = 56.6 kJ, Qp = H = 80.129 kJ
=18.24kJ
W = W1 + W2 =18.24kJ
∵p3 V3= p1 V1
∴T3= T1,故ΔU=0 ΔH=0 Q=-W= - 18.24kJ
例. 3 mol单原子理想气体,从初态T1 = 300 K ,p1 = 100 kPa,反抗恒外压力50 kPa作不可逆 膨胀,至终态T2 = 300 K,p2 = 50 kPa,求这 一过程的Q,W,U,H。 解:U = 0,H = 0
对于理想气体 C p ,m CV ,m R
C 对单原子: V ,m 3R / 2, C p ,m 5R / 2 C 对双原子: V ,m 5R / 2, C p ,m 7 R / 2
对于凝聚态物质
CV ,m C p ,m
4.定压摩尔热容与温度的关系
热容随温度变化,常用级数形式表示热容 对温度的依赖关系:
升高dT所需的热量为δQV,则该温度T下的摩尔定
压热容以表示 C p ,m为:
1 δQp C p,m n dT
由于Qp = dH=ndHm
C p,m
1 dH dH m dT dT n p p
单位为: J K 1 mol1 。
(2)应用:单纯PVT变化 恒压: H
C p ,m CV ,m [(
U m Vm U m [( ) p p( )p ] ( )V T T T
U m U V V U U V )V ( m )T ( m ) p p( m ) p ] ( m )V [( m )T p]( m ) p T Vm T T T Vm T
单位为: J K 1 mol1 。
(2)应用:单纯PVT变化
恒容: U
QV T
T2
1
nCV ,mdT
非恒容理想气体:
U T
T2
1
nCV ,mdT
(理想气体的U=f(t))
2.摩尔定压热容 C p,m :
(1)定义
在某温度T时,物质的量为n的物质在恒压且非 体积功为零时,不发生化学变化、相变化,温度
W V12 pdV -p(V 2-V 1) = -nRT2 nRT1 V nR(T1 T2 ) 23.529kJ
例题: 1mol理想气体于27℃、1atm时受某恒定外压恒温 压缩到平衡,再于该状态下恒容升温至97℃则压
力达10atm。求整个过程的W、Q、ΔU、ΔH。已
T1
T2
过程的△U, U H
3.Cp,m与CV,m的关系
C p ,m CV ,m
U m U m dU m dT V d V T V T U m U m U m Vm 有 T V T T p V m T p
W = -pamb( V2-V1 )
= -pambnRT( 1 / p2-1 / p1 ) = -3.741 kJ Q = -W = 3.741 kJ
例. 2 mol H2从400 K,100 kPa定压加热到1000 K ,已知Cp,m(H2) = 29.2 J· 1· 1,求U,H, mol K Q,W各为多少? 解:Qp = H nC p ,m T
W2=0 W= W1+ W2=17740J Q=ΔU-W=1464-17740=16276J
= 2 mol×29.2 J· 1· 1( 1000-400 ) K mol K
= 35.04 kJ U = H - ( pV ) = H-nR( T2-T1 ) = 25.06 kJ W = U-Q = -9.98 kJ
例. 0.2 mol某理想气体,从273 K,1 MPa定压加 热到523 K,计算该过程的Q,W,U,H。已知该 气体的Cp,m = ( 20+7×10-3 T / K ) J· 1· 1。 mol K
