13-3 等体、等压过程,摩尔热容
合集下载
准静态过程 功 热量 内能 热力学第一定律 等体过程 等压过程 摩尔热容等温过程和绝热过程

V2 V
Qp
E2
E1
W
等压膨胀过程:气体吸收的热 量,一部分用于内能的增加, 一部分用于对外作功。
p
等 压
p
( p,V2 ,T2 )
2
( p,V1,T1)
1
压
W
缩
o V2
V1 V
Qp
E1
W
E2
等压压缩过程:外界对气体作 的功和内能的减少均转化为热 量放出。
等压过程中,W 与 △E始终同号
Q
m' M
解 1)等温过程
W12 '
RT ln V2 ' V1
2.80104 J
2)氢气为双原子气体
(i 2) i 1.40
T2
T1
(V1 V2
)
1
753K
p
p2
2 T2
p2' T2' T1
Q0
p1
2'
T1
T 常量 1
o V2 V2' V1 10 V1 V
怎么求?
由热力学第一定律
dQT dWT pdV
Q T
WT
p RT
V2 V1
pdV
V
p
p1
1 ( p1,V1,T )
p2
( p2 ,V2 ,T )
2
o V1 dV V2 V
恒
温
谁做功?
热
源
T
QT
WT
V2
V1
RT V
dV
RT
ln V2 V1
RT ln p1
大学物理-热力学基础-课件
Wa
CV m (T2
T1)
p1V1 p2V2
1
本题用 Wa E 计算较方便
关键用绝热方程
T2
T1
( V1 V2
)
1
先求出 T2
p
p2
2 T2
T2' T1
Q0
p2'
2'
p1
TC
T1
1
o V2 V2' V1 10 V1 V
18.
*四. 多方过程 — 实际过程( 满足 PV n C)
绝热 n = ( CPm / CVm )
等温 n = 1 等压 n = 0
W p1V1 p2V2 n 1
满足 E CV (T2 T1)
Q Cn (T2 T1)
等体 n = ∞
p
可以证明
n= n=∞
n=1
Cn
(
n
n 1
)CV
n=0
o
V
19.
13 – 5 循环过程 卡诺循环
一. 循环过程
1. 特点 E 0 W = Q ( 热功转换 )
1
2
W
(2)热一定律 dQP dE PdV
o V1
V2 V
QP
E
V2 PdV
V1
v
i 2
R(T2
T1 )
P(V2
V1 )
7.
2.摩尔定压热容 CPm
1mol
:
CPm
dQp dT
理论值:
CPm
dE pdV dT
CVm
R
i2R 2
(近似)
实验值:查表 (精确)
QP
dQP
10 13-3 理想气体的等体过程和等压过程 摩尔热容

实际上,气体所进行的过程,常常既 不是等温又不是绝热的,而是介于两 者之间,可表示为 PVn =常量 (n为多方指数) 凡满足上式的过程称为多方过程。 n =1 —— 等温过程 n = —— 绝热过程 n= 0 —— 等压过程 n = —— 等容过程 一般情况1 n ,多方过程可近似 代表气体内进行的实际过程。
PV RT PV RT
C p,m CV ,m R
理想气体的定压摩尔热容比定体摩尔热容大一个恒量R •在等体过程中,气体吸收的热量全部用来增加系统的内能 •等压过程中,气体吸收的热量,一部分用来增加系统的内能, 还有一部分用于气体膨胀时对外界作功 气体升高相同的温度,在等压过程吸收的热量要比在等温过 程中吸收的热量多。
3
水蒸气
m
蒸气 0.598kg m
3
水
100 C 热源
W pdV pV pm(
1
蒸气
1
1
水
1
)
E Q W m L pm(
蒸气
水
)
E 1 1 L p( ) 2.09106 J kg1 m 蒸气 水
四、多方过程
2、比热容:
单位质量的热容称为比热容。
C 1 dQ c m m dT
13-4 理想气体的等温过程和绝热过程
一、等温过程
•特点:
理想气体的温度保持不变, T=const
•过程曲线:
在PV图上是一条双曲线, 叫等温线。
恒 温 热 源 T
•过程方程:
p1V1 p2V2
p p1
p2
1 ( p1 ,V1 , T )
p
T 常量
Q0
papT
PV RT PV RT
C p,m CV ,m R
理想气体的定压摩尔热容比定体摩尔热容大一个恒量R •在等体过程中,气体吸收的热量全部用来增加系统的内能 •等压过程中,气体吸收的热量,一部分用来增加系统的内能, 还有一部分用于气体膨胀时对外界作功 气体升高相同的温度,在等压过程吸收的热量要比在等温过 程中吸收的热量多。
3
水蒸气
m
蒸气 0.598kg m
3
水
100 C 热源
W pdV pV pm(
1
蒸气
1
1
水
1
)
E Q W m L pm(
蒸气
水
)
E 1 1 L p( ) 2.09106 J kg1 m 蒸气 水
四、多方过程
2、比热容:
单位质量的热容称为比热容。
C 1 dQ c m m dT
13-4 理想气体的等温过程和绝热过程
一、等温过程
•特点:
理想气体的温度保持不变, T=const
•过程曲线:
在PV图上是一条双曲线, 叫等温线。
恒 温 热 源 T
•过程方程:
p1V1 p2V2
p p1
p2
1 ( p1 ,V1 , T )
p
T 常量
Q0
papT
计算各等值过程的热量功和内能的理论基础
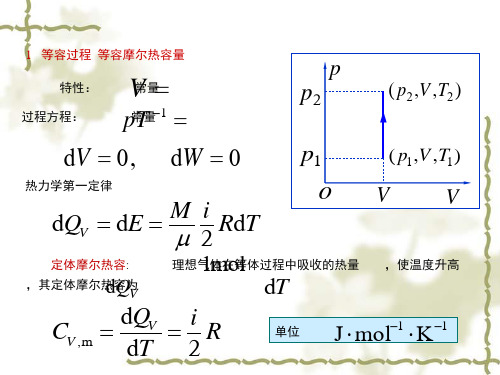
1 等容过程 等容摩尔热容量
特性: 过程方程:
V常量
p常T量1
p
p2
( p2,V ,T2 )
dV 0, dW 0 p1
( p1,V ,T1)
热力学第一定律
dQV
dE
M
i 2
RdT
oV
V
定体摩尔热容:
1mol 理想气体在等体过程中吸收的热量 ,使温度升高
,其定体摩尔热d容Q为V
dT
CV ,m
dQV dT
3)热能 Q E W 8.3 p0V0
二 绝热过程 与外界无热量交换的过程
特征: dQ 0
p
p1
1( p1,V1,T1)
热一律 dW dE 0
dW dE
p2
( p2,V2,T2 )
2
dE
M
CV ,mdT
W
V2 V1
pdV
T2 T1
M
CV
,m
dT
M
CV ,m (T2
T1)
o V1 dV V2 V
V
V
E1
QV
E2
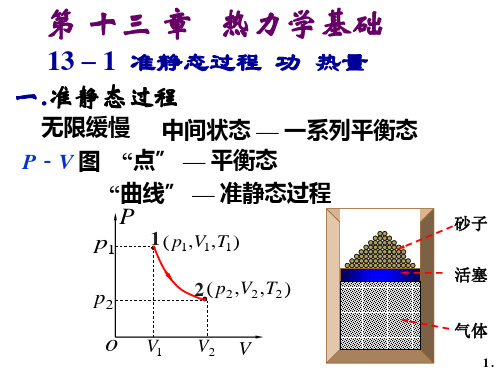
2 等压过程 等压摩尔热容量
特 性: 过程方程:
p常量
V常T量1
p
p
( p,1V1,T1)
( p,V2,T2) 2
功 W p(V2 V1)
W
热一律 dQp dE dW o V1 V2 V
定压摩尔热容: 理想气体1m在等o压l 过程中吸
收的热量
,温度升高 ,其定压摩尔热容为
dQp
绝热的汽缸壁和活塞
绝热过程方程的推导
dQ 0, dW dE
pdV CV ,mdT pV RT
特性: 过程方程:
V常量
p常T量1
p
p2
( p2,V ,T2 )
dV 0, dW 0 p1
( p1,V ,T1)
热力学第一定律
dQV
dE
M
i 2
RdT
oV
V
定体摩尔热容:
1mol 理想气体在等体过程中吸收的热量 ,使温度升高
,其定体摩尔热d容Q为V
dT
CV ,m
dQV dT
3)热能 Q E W 8.3 p0V0
二 绝热过程 与外界无热量交换的过程
特征: dQ 0
p
p1
1( p1,V1,T1)
热一律 dW dE 0
dW dE
p2
( p2,V2,T2 )
2
dE
M
CV ,mdT
W
V2 V1
pdV
T2 T1
M
CV
,m
dT
M
CV ,m (T2
T1)
o V1 dV V2 V
V
V
E1
QV
E2
2 等压过程 等压摩尔热容量
特 性: 过程方程:
p常量
V常T量1
p
p
( p,1V1,T1)
( p,V2,T2) 2
功 W p(V2 V1)
W
热一律 dQp dE dW o V1 V2 V
定压摩尔热容: 理想气体1m在等o压l 过程中吸
收的热量
,温度升高 ,其定压摩尔热容为
dQp
绝热的汽缸壁和活塞
绝热过程方程的推导
dQ 0, dW dE
pdV CV ,mdT pV RT
13-3理想气体的等体、等压和等温过程

第十三章 热力学基础
19
物理学
第五版
13- 理想气体的等体、 13-3 理想气体的等体、等压和等温过程 热容 摩尔热容比
γ = Cp,m CV,m
等压过程的三个量
W = p (V2 − V1 ) = ν R (T2 − T1 )
Q p = νC p,m (T2 − T1 )
E2 − E1 =νCV ,m (T2 − T1 )
由热力学第一定律
p2
2
V1
o
dQT = dWT = pdV
dV
V2 V
QT = W T =
∫
V2
V1
pdV
10
第十三章 热力学基础
物理学
第五版
13- 理想气体的等体、 13-3 理想气体的等体、等压和等温过程 热容
QT = WT = ∫ pdV
V1
V2
RT p =ν V
V2
p1V1 = p 2V2
RT V2 QT = W = ∫ ν dV = ν RT ln V1 V V1
p1 = νRT ln p2
第十三章 热力学基础
11
物理学
第五版
13- 理想气体的等体、 13-3 理想气体的等体、等压和等温过程 热容 等温过程热量与功的转换情况 等温膨胀 等温膨胀 等温压缩 等温压缩
p p1
1 ( p1 , V1 , T )
14
第十三章 热力学基础
物理学
第五版
13- 理想气体的等体、 13-3 理想气体的等体、等压和等温过程 热容
(一)摩尔定体热容
d 理想气体,等体过程, 1mol 理想气体,等体过程, QV ,dT 。
CV ,m
∵
19
物理学
第五版
13- 理想气体的等体、 13-3 理想气体的等体、等压和等温过程 热容 摩尔热容比
γ = Cp,m CV,m
等压过程的三个量
W = p (V2 − V1 ) = ν R (T2 − T1 )
Q p = νC p,m (T2 − T1 )
E2 − E1 =νCV ,m (T2 − T1 )
由热力学第一定律
p2
2
V1
o
dQT = dWT = pdV
dV
V2 V
QT = W T =
∫
V2
V1
pdV
10
第十三章 热力学基础
物理学
第五版
13- 理想气体的等体、 13-3 理想气体的等体、等压和等温过程 热容
QT = WT = ∫ pdV
V1
V2
RT p =ν V
V2
p1V1 = p 2V2
RT V2 QT = W = ∫ ν dV = ν RT ln V1 V V1
p1 = νRT ln p2
第十三章 热力学基础
11
物理学
第五版
13- 理想气体的等体、 13-3 理想气体的等体、等压和等温过程 热容 等温过程热量与功的转换情况 等温膨胀 等温膨胀 等温压缩 等温压缩
p p1
1 ( p1 , V1 , T )
14
第十三章 热力学基础
物理学
第五版
13- 理想气体的等体、 13-3 理想气体的等体、等压和等温过程 热容
(一)摩尔定体热容
d 理想气体,等体过程, 1mol 理想气体,等体过程, QV ,dT 。
CV ,m
∵
大学物理热学第十三章 热力学基础 PPT

Mayer公式
•摩尔热容比
CP,m i 2
CV ,m i
泊松比
CV ,m
i 2
R
Cp,m
CV ,m
R
i
2 2
R
单原子分子理想气体 i 3 1.67
双原子分子理想气体 i 5 1.40
多原子分子理想气体 i 6 1.33
pV m RT RT
M
Q CV ,m (T2 T1)
•过程曲线: p b T2
0
a T1 V
吸收得热量全部用来内能增加;或向外界放热以内能减小为代 价;系统对外不作功。
3、理想气体定体摩尔热容 CV ,m
•定义:1mol、等体过程升高1度所需得热量
•等体过程吸热 QV CV ,m (T2 T1)
•等体过程内能得增量
E
QV
i 2
R
T2
T1 CV ,m T2
13-1 准静态过程 功 热量
一、准静态过程
可用P-V 图上得一条有
方向得曲线表示。
二、功
准静态过程系统对外界做功:
元功: dW Fdl pSdl pdV
dl
系统体积由V1变 为V2,系统对外 界作总功为:
V2
W= pdV
V1
p F S pe
光滑
注意:
V2
W= pdV
V1
1、V ,W>0 ;V ,W<0或外界对系统作功 ,V不变时W=0
V2 PdV
V1
i CV ,m 2 R
CP,m
CV ,m
CP,m CV ,m R
等容 等压
WV 0
QV CV ,m (T2 T1) E
QP Cp,m (T2 T1) CV ,m (T2 T1) P(V2 V1) WP P(V2 V1) R(T2 T1)
1-理想气体的等体过程和等压过程摩尔热容

2019年10月25日星期五
理学院 物理系
大学物理
§13-3 理想气体的等体过程和等压过程 摩尔热容
4.摩尔热容量C 和热量 Q 的关系 dQ=νCdT
5.摩尔定容热容CV (molar heat capacity at constant volume) (1)CV 和热量的关系 (dQ)V=vCVdT (2)CV 和内能的关系 vCVdT=(dE)V (3)内能 E 和状态 (T, V, P) 的关系
PV RT
P dV RdT
d Q CV dT P dV
d Q CV dT R dT
CV RdT
d Q CP dT
CP CV R
2019年10月25日星期五
理学院 物理系
§13-3 理想气体的等体过程和等压过程 摩尔热容
7.迈耶公式及其物理意义
(1)迈耶公式
CP
CV
R
i 2
R
R
Байду номын сангаас
i 2
1
R
(2)迈耶公式的物理意义
(3)摩尔气体常数R
(4)热容比
CP
i 2
1
R
i2
CV
iR
i
2
2019年10月25日星期五
理学院 物理系
8.7
28.8 20.4
8.4
28.6 20.4
8.2
29.3 21.2
8.1
28.9 21.0
7.9
36.2 27.8
8.4
35.5 27.2
8.4
热力学基础1

0.1kg水蒸气自120℃加热升温至140℃, 水蒸气自120℃加热升温至140℃ 例3. 0.1kg水蒸气自120℃加热升温至140℃,求等 体过程和等压过程各吸收了多少热量?内能各变化多 体过程和等压过程各吸收了多少热量? 各作了多少功? 少?各作了多少功? 解: 已知 M = 18×10−3 kg⋅ mol −1 CV ,m = 27⋅ 82J ⋅ mol −1⋅ k −1
系统内能的增量只与系统起始和终了状态有 关,与系统所经历的过程无关 .
二 热力学第一定律
Q = (E2 − E1) +W
系统从外界吸收热量, 系统从外界吸收热量,一部分使系统内能 增加, 增加,另一部分使系统对外做功 —— 热力学第一定律
热力学第一定律 讨论: 讨论:
Q = (E2 − E1) +W
C p, m =
PV =
dQp dT
m RT M
m W = ∫ dW = ∫ pdV = p(V2 −V1 ) = R(T2 − T1 ) V1 M m m ∆E = Qp −W = (Cp,m − R)(T2 −T1)= CV ,m (T2 −T1 ) M M
V2
C p,m − CV ,m = R
p
A*
2 1 *B
p
A*
2 1 *B
WA1B +QA1B =WA2B +QA2B
∆EAB = C
o
V
WA1B2A + QA1B2A = 0
∆E A1B 2 A = 0
o
V
理想气体内能 : 表征系统状态的单值函数 , 理想气体的内能仅是温度的函数 .
E = E (T )
一般气体: 一般气体:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
m Qp Cp (T2 T1 ) Cp (T2 T1 ) M 1.50 5 36.2 300 9.05 10 J 3 18 10
所作的功为
m A R(T2 T1 ) R(T2 T1 ) M 1.50 5 8 . 31 300 2 . 08 10 J 3 18 10
(2)a→b →c ,先等压压缩,后等体升压
T1 T3 E3 E1 0 气体吸收的总热量和所作的总功为
Q A Ap AV
b→c 等体过程,不做功 AV 0 a→b 等压过程,做功为
p
c
a
Ap p1 (V2 V1 )
b
O
V
1.013 105 (20 106 100 106 ) 8.1J Q A Ap 8.1J
V1
p p
A
O V1 V2 V
定压摩尔热容Cp 在等压过程中, 1mol 理想气体经吸热 Q, 温度变化 T
Q E A E pV
Q E pV Cp lim ( ) lim ( ) lim ( ) T 0 T T 0 T T 0 T dE dV dV ( ) p ( ) CV p ( ) dT dT dT
内能增量为
E E2 E1 Qp A
9.05 10 2.08 10
5
5
6.97 10 J
5
1mol 理想气体的状态方程为 pV RT
两边对 T 求导,因 p = 常量,有
dV p( ) R dT
迈耶公式 比热容比
Cp CV R
C p / CV
E Cp (T2 T1 ) p(V2 V1 )
例1水蒸气的Cp=3.62J/(mol· K) 。今将1.50Kg 温 度100℃的水蒸气,在标准大气压下缓慢加热, 使其温度上升到400℃, 试求此过程中水蒸气吸 收的热量、对外所作的功和内能的改变。水蒸 气的摩尔质量 M = 18×10-3Kg/mol。 解 由于在标准大气压下加热, 这是一等压过程。 把水蒸气看成理想气体,注意到其ν=m/M,上升 的温度为T2-T1=300K, 则过程中吸收的热量为
几种分子的CV、Cp和γ
物理量
分子 单原子分子 刚性双原子分子
定体摩 尔热容
定压摩 尔热容
比热 容比
3R / 2
5R / 2
5R / 2
7R / 2
5/3 7/5 4/3
刚性多原子分子
3R
4R
比热容
dQ 热容 C dT
比热容
dQ C c mdT m
三、等温过程
1. 特征 T = C, dT = 0 ( dE = 0 )
V2 A RT ln V1
p p1
p2 O
6. 热量 dQ = dA = pdV
V2 QT A RT ln V1 由于 pV C
V2 p1 QT AT RT ln RT ln V1 p2
等温过程中系统吸收的热量全部用来对外 作功。
内 过 容 程
特征
过程方程
V2
V2
O
V
V
定体摩尔热容CV
在定体过程中,1mol 理想气体经吸热 Q, 温度变化 T Q CV lim ( ) T 0 T E dE CV lim ( ) Q E A T 0 T dT A0
p
p2
5. 热量
p1 O V V
dE dQ pdV
dE = d Q
c
a
b
O
E3 E1 0
V
气体吸收的热量和所作的功为
V2 V2 QT A RT ln p1V1 ln V1 V1
6 20 10 1.013 105 100 10 6 ln 6 100 10 16.3J
负号表示在等温压缩过程中, 外界向气体 做功而气体向外界放出热量。
1. 特征 p = C, dp = 0 2. 过程方程
pV RT
3. 过程曲线
ห้องสมุดไป่ตู้
V T
C (盖-吕萨克定律)
p p O
平行于V 轴的等压线。
V1
V2 V
4. 功 (A 等于等压线下的面积 )
A pdV p dV pV
V2
pV RT
A p(V2 V1 ) R(T2 T1 )
内能增量 ΔE
系统作功 A 0
吸收热量 Q
摩尔热容 C
p 恒量 等体 V= 恒量 T
V 恒量 等压 p= 恒量 T
CV T
i CV R 2
Cp CV R i2 R 2
CV T
pV 或 RT
RT ln
Cp T
等温
T= 恒量
pV 量
恒
0
p1 V2 RT ln 或 p2 V1
5. 热量
Q p E A E RT
dQP CP dT
p p
A
O V1 V2 V
dQ p C p dT
νmol理想气体
Q p Cp (T2 T1 )
6. 内能变化
E CV (T2 T1 )
E Qp A Cp (T2 T1 ) p(V2 V1 )
2. 过程方程
pV RT pV C (玻意耳定律)
3. 过程曲线 在 P — V 图上, 每 一个等温过程对应一条 双曲线, 称为等温线。
p p1 T V1 pdV V2 V
p2 O
4. 内能变化 dE = 0
5. 功 A pdV RT
V1
V2
V2
V1
dV V
T V1 pdV V2 V
理想气体的等体、等压、等温过程
例2 把压强为1.013×105pa, 体积为100cm3的氮 气压缩到20cm3时,气体内能的增量、吸收的热 量和所做的功各是多少?假设经历的是如下两 个过程: (1)等温过程;(2)先等压压缩,然后再 等体升压到同样状态。
p
解 (1) 如图所示, a→c,等温 度过程,若把氮气看成理想 气体,则其内能不变。
13.3 理想气体的等体过程和等压 过程 摩尔热容
一、等体过程 在等体过程中,理想气体的体积保持不变。
1. 特征 V = C,dV = 0
2.过程方程
pV RT
p T
C (查理定律)
3. 过程曲线 平行于p 轴的等体线。 4. 功
p2
p1
p
A dA pdV 0
V1 V1
QV E2 E1 CV (T2 T1 )
pV RT
pV T R
V QV CV ( p2 p1 ) R
6. 内能变化
νmol理想气体
E QV CV (T2 T1 )
(适应于理想气体的一切过程)
二、等压过程 在等压过程中, 理想气体的压强保持不变。
