2014年人教版数学八上能力培优11.1与三角形有关的线段
2014年秋人教版八年级数学上11.1与三角形有关的线段(1)同步习题精讲课件
习 题 精 讲
11．1 与三角形有关的线段
数 学 八年级上册 (人教版)
11．1 与三角形有关的线段
第1课时 三角形的边
1．由不在同一条直线上的三条线段首尾顺次
相接所组成的图形叫做 三角形 ．
2．三边都相等的三角形叫做等边三角形 ，有
两边相等的三角形叫做 等腰三角形 ．
3．三角形按边的相等关系分类：
三 三边都不相等的三角形 角 等腰 底边和腰不相等的等腰三角形 形 三角形 等边三角形
4．三角形两边之和 大于 第三边，两边之差小于第
三边．
三角形的有关概念 1．(5分)如图所示，三角形的个数为( B )
A．4个
B．5个
C．6个
D．7个
2．(5分)如图，用符号表示以点B为顶点的三角
三、解答题(共36分) 15．(8分)某木材市场上木棒规格与价格如下表： 规格 1m 2m 3m 4m 5m 6m
价格(元/根) 10
15
20
25
30
35
小明的爷爷要做一个三角形的木架养鱼用，现有两根 长度为3 m和5 m的木棒，还需要到某木材市场上购买一 根． (1)有几种规格的木棒可供小明的爷爷选择？ (2)在能做成三角架的情况下，选择哪一种规格的木棒 最省钱？
形：△BDF、△BDA、△BEA、△BCA .
3．(5分)如图，在△ACE中，∠CEA的
对边是 AC ．
三角形按边分类 4．(5分)下列叙述中正确的是( C )
A．三角形可分为等腰三角形和等边三角形
B．等腰三角形是等边三角形
C．等边三角形是特殊的等腰三角形
D．三角形可分为三边都不相等三角形和三边都相 等的三角形
人教版八年级上册11.1《与三角形有关的线段》说课稿
3.技术工具：网络资源、在线学习平台等，提供丰富的学习资料，拓展学生的学习视野。
它们在教学中的作用主要有：
1.直观展示几何图形和性质，降低学生的理解难度。
2.提供丰富的学习资源，满足学生的个性化学习需求。
3.创设生动、有趣的学习情境，激发学生的学习兴趣。
人教版八年级上册11.1《与三角形有关的线段》说课稿
一、教材分析
（一）内容概述
本节课选自人教版八年级上册11.1《与三角形有关的线段》，它是整个课程体系中几何部分的重要内容，主要介绍了三角形的中线、高线、角平分线等基本概念及其性质。这部分内容是对三角形知识的深入探究，旨在帮助学生巩固对三角形基本概念的理解，并为后续学习相似三角形、解直角三角形等知识打下基础。
（二）新知讲授
在新知讲授阶段，我将采用以下步骤逐步呈现知识点，引导学生深入理解：
1.通过动态PPT或几何画板展示三角形的中线、高线、角平分线的定义和性质，让学生直观地理解这些概念。
2.结合实际例题，讲解中线、高线、角平分线的判定方法和应用，让学生在具体情境中掌握知识。
3.分步骤演示如何准确地画出三角形的中线、高线、角平分线，并指导学生进行动手操作，加深对知识点的理解。
（三）巩固练习
为了帮助学生巩固所学知识并提升应用能力，我计划设计以下巩固练习或实践活动：
1.基础练习：布置一些基本的画图题目，如画出给定三角形的中线、高线、角平分线，让学生独立完成。
2.提高练习：设计一些综合性的题目，让学生运用所学知识解决实际问题，如求三角形的面积、判断三角形的类型等。
3.小组合作活动：组织小组讨论，让学生共同探究与三角形有关的线段在生活中的应用，培养学生的团队合作能力和创新思维。
初中数学人教版八年级上册 第十一章 11.1与三角形有关的线段
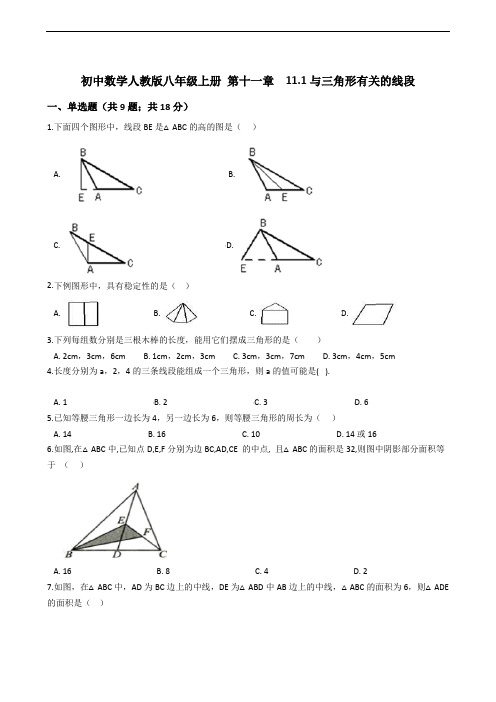
初中数学人教版八年级上册第十一章11.1与三角形有关的线段一、单选题（共9题；共18分）1.下面四个图形中，线段BE是△ABC的高的图是（）A. B.C. D.2.下例图形中，具有稳定性的是（）A. B. C. D.3.下列每组数分别是三根木棒的长度，能用它们摆成三角形的是（）A. 2cm，3cm，6cmB. 1cm，2cm，3cmC. 3cm，3cm，7cmD. 3cm，4cm，5cm4.长度分别为a，2，4的三条线段能组成一个三角形，则a的值可能是( ).A. 1B. 2C. 3D. 65.已知等腰三角形一边长为4，另一边长为6，则等腰三角形的周长为（）A. 14B. 16C. 10D. 14或166.如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE 的中点, 且△ABC的面积是32,则图中阴影部分面积等于（）A. 16B. 8C. 4D. 27.如图，在△ABC中，AD为BC边上的中线，DE为△ABD中AB边上的中线，△ABC的面积为6，则△ADE 的面积是（）A. 1B. 32C. 2 D. 528.若一个三角形三个内角的度数之比为3：4：5，则这个三角形是（）A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等腰三角形9.如图1，M是铁丝AD的中点，将该铁丝首尾相接折成△ABC，且∠B=30∘，∠C=100∘，如图2．则下列说法正确的是（）A. 点在上B. 点在的中点处C. 点在上，且距点较近，距点较远D. 点在上，且距点较近，距点较远二、填空题（共7题；共8分）10.三角形三条中线交于一点，这个点叫做三角形的________．11.若三角形的两边长是5 和2 ，且第三边的长度是偶数，则第三边长可能是________．12.三角形具有稳定性，要使一个四边形框架稳定不变形，至少需要钉________根木条.13.如图，AD是△ABC的中线，若AB：AC＝3：4，则S△ABD：S△ACD＝________．14.如图，在△ABC中(AB＞BC)，AC=2BC，BC边上的中线AD把△ABC的周长分成60和40两部分，则AC=________，AB=________.15.在△ABC中，若AB=5，AC=3．则中线AD的长的取值范围是________。
人教版八年级数学上册与三角形有关的线段复习及习题11.1解析答案教案
11.1小节复习及习题11.1练习指导备课人：备课日期：年月日较大的三角形，然后把三个小三角形合成的三角形，即按从小到大依次找出，做到不重复不遗漏。
2.长为10,7,5,3的四根木条，选其中三根组成三角形，有几种选法？为什么？【提示】先选两根较短的木条作为三角形的两边并计算它们的和，再根据“三角形任意两边的和大于第三边”考虑选第三根木条。
本题只有5+3＞7一种符合，故只有一种选法。
3.对于下面每个三角形，过顶点A画出中线、角平分线和高。
【提示】图(1)为等腰三角形，所画中线、角平分线和高重合；图(2)是直角三角形，高就是直角边AB；图(3)是钝角三角形，所画的高在CB的延长线上。
4.如图，在△ABC中，AE是中线，AD是角平分线，AF是高。
填空：(1)BE= =21；(2)∠BAD= =21；(3)∠AFB= =90°；(4)S△ABC= .【提示】(1)(2)(3)小题根据三角形的中线、角平分线、高的定义解答，(4)小题根据三角形的面积公式解答。
AB CE D F5.选择题。
下列图形中有稳定性的是（ ）A.正方形B.长方形C.直角三角形D.平行四边形【解析】三角形具有稳定性，四边形不具有稳定性。
故选C. 综合运用6.一个等腰三角形的一边长为6cm ，周长为20cm ，求其它两边的长.【提示】分两种情况解答：①6cm 的边为底边；②6cm 的边为腰.7.(1)已知等腰三角形的一边长等于5，一边长等于6，求它的周长.(2)已知等腰三角形的一边长等于4，一边长等于9，求它的周长.【提示】分两种情况解答：①第一条边为底，第二条边为腰；②第一条边为腰，第二条边为底。
注意判断是否能围成三角形。
8.如图，在△ABC 中，AB=2，BC=4，△ABC 的高AD 与CE 的比是多少？【提示】：利用三角形的面积公式9.如图，AD 是△ABC 的角平分线，DE//AC ，DE 交AB 于点E ，DF//AB ，DF 交AC 于点F.图中∠1与∠2有什么关系?为什么?【提示】利用“两直线平行，内错角相等”，得出∠1=∠DAC ，∠2=∠DAE ，再利用角平分线的性质得出∠1=∠2。
人教版八年级上册数学教学设计《11.1 与三角形有关的线段》
人教版八年级上册数学教学设计《11.1 与三角形有关的线段》一. 教材分析本节课的主题是“与三角形有关的线段”，这是人教版八年级上册数学的一个重要内容。
本节课主要让学生了解并掌握三角形的中线、角平分线、高线等概念，以及它们之间的关系。
通过对这些线段的性质和作用的学习，培养学生空间想象能力和逻辑思维能力，为学生进一步学习几何知识打下基础。
二. 学情分析学生在学习本节课之前，已经掌握了三角形的基本概念和性质，如三角形的内角和、三角形的分类等。
但学生对三角形的中线、角平分线、高线等概念及性质可能较为陌生，因此，教师在教学中要注重引导学生从已知知识出发，探索新知识，培养学生自主学习的能力。
三. 教学目标1.知识与技能：让学生掌握三角形的中线、角平分线、高线的概念，理解它们之间的关系。
2.过程与方法：通过观察、操作、猜想、验证等方法，培养学生的空间想象能力和逻辑思维能力。
3.情感态度与价值观：激发学生学习几何的兴趣，培养学生的合作意识，使学生感受到数学在生活中的应用。
四. 教学重难点1.重点：三角形的中线、角平分线、高线的概念及性质。
2.难点：三角形的中线、角平分线、高线之间的相互关系。
五. 教学方法1.情境教学法：通过设置问题情境，引导学生观察、操作、猜想、验证，激发学生的学习兴趣。
2.合作学习法：学生进行小组讨论，培养学生合作意识，提高学生解决问题的能力。
3.启发式教学法：教师引导学生从已知知识出发，探索新知识，培养学生的自主学习能力。
六. 教学准备1.教具：三角板、直尺、圆规、多媒体设备等。
2.学具：学生每人一份三角板、直尺、圆规等。
七. 教学过程1.导入（5分钟）教师通过提问方式引导学生回顾三角形的基本概念和性质，为新课的学习做好铺垫。
2.呈现（10分钟）教师利用多媒体展示三角形的中线、角平分线、高线的图片，引导学生观察并思考这些线段的特征。
3.操练（10分钟）教师学生进行小组讨论，让学生通过实际操作，探索三角形的中线、角平分线、高线之间的关系。
人教版八年级数学上册同步练习11.1与三角形有关的线段(word版,含答案解析)
11.1 与三角形有关的线段一、选择题（共10小题；共50分）1. 三角形按边可分为( )A. 等腰三角形、直角三角形、锐角三角形B. 直角三角形、不等边三角形C. 等腰三角形、不等边三角形D. 等腰三角形、等边三角形2. 已知a，b，c是△ABC的三边长，且(a+b+c)(a−b)=0，则△ABC一定是( )A. 等腰三角形B. 直角三角形C. 等边三角形D. 以上答案都不对3. 若钝角三角形ABC中，∠A=27∘，则下列哪个选项不可能是∠B的度数( )A. 37∘B. 57∘C. 77∘D. 97∘4. 根据定义，三角形的角平分线，中线和高线都是( )A. 直线B. 线段C. 射线D. 以上都对5. 在△ABC中，如果∠B−∠A=90∘，那么△ABC是( )A. 直角三角形B. 锐角三角形C. 钝角三角形D. 无法确定6. 已知某三角形第一条边长为(2a−b)cm，第二条边比第一条边长(a+b)cm，第三条边比第一条边的2倍少(a−b)cm，则这个三角形的周长为( )A. 3a cmB. (3a−b)cmC. (5a−b)cmD. (8a−2b)cm7. 如图，工人师傅做了一个长方形窗框ABCD，E，F，G，H分别是四条边上的中点，为了使它稳固，需要在窗框上钉一根木条，这根木条不应钉在( )A. A，C两点之问B. E，G两点之间C. B，F两点之间D. G，H两点之间8. 人字梯中间一般会设计一“拉杆”，这样做的道理是( )A. 两点之间，线段最短B. 垂线段最短C. 两直线平行，内错角相等D. 三角形具有稳定性9. 如图，在Rt△ABC中，∠C=90∘，以△ABC的一边为边画等腰三角形，使得它的第三个顶点在△ABC的其他边上，则可以画出的不同的等腰三角形的个数最多为( )A. 4B. 5C. 6D. 710. 已知三角形的两边长分别为4cm和9cm，则下列长度的四条线段中能作为第三边的是( )A. 13cmB. 6cmC. 5cmD. 4cm二、填空题（共6小题；共48分）11. 如果知道三角形的一边之长和这边上的高，三角形确定．（填“能”或“不能”）12. 三角形按边分类：三角形{三边都不等的三角形等腰三角形{ 的等腰三角形 的三角形13. 如图，在锐角三角形ABC中，AD⊥BC于点D，E是BC上一点，连接AE．图中：（1）锐角三角形有个；（2）直角三角形有个；（3）钝角三角形有个．14. 等腰三角形的、、三线合一．15. 如果等腰三角形的底边和一腰长分别为12cm，15cm．那么这个三角形的周长为cm．16. 如图，用六根木条钉成一个六边形框架ABCDEF，要使框架稳固且不活动，则至少还需要添加根木条．三、解答题（共4小题；共52分）17. 图中有几个不同的三角形?用符号表示这些三角形．18. 用9根同样的火柴棒在桌面上摆一个三角形（应首尾相接，不允许火柴棒折断，但允许将几根火柴棒连成一根作为一条线段，火柴要全部用完），你能摆出哪几种不同形状的三角形?19. 已知△ABC中两个内角的度数，判断△ABC的类型：（1）∠A=30∘，∠B=40∘．（2）∠B=32∘，∠C=58∘．（3）∠A=60∘，∠C=50∘．20. 为使五边形木架（用5根木条钉成）不变形，哥哥准备如图①那样再钉上两根木条，弟弟准备如图②那样再钉上两根木条，哪种方法能使木架不变形?为什么?答案第一部分1. C2. A3. C 【解析】∵钝角三角形△ABC中，∠A=27∘，∴∠B+∠C=180∘−27∘=153∘，又∵△ABC为钝角三角形，有两种可能情形如下：① ∠C>90∘，∴∠B<153∘−90∘=63∘，∴选项A，B合理；② ∠B>90∘，∴选项D合理，∴∠B不可能为77∘．4. B 【解析】三角形的角平分线，中线和高线都是线段．5. C6. D7. B8. D 【解析】人字梯中间一般会设计一“拉杆”，是为了形成三角形，利用三角形具有稳定性来增加其稳定性．故选：D．9. D10. B第二部分11. 不能【解析】画出简图比较容易判定．如图，知道三角形的一边之长和这边上的高，三角形不能确定．12. 底边和腰不相等，等边13. 2，3，114. 顶角平分线，底边上的中线，底边上的高15. 4216. 3第三部分17. △ABE，△BCE，△CDE，△ABC，△BCD．18. 三种（3，3，3；3，4，2；1，4，4）．19. （1）钝角三角形．（2）直角三角形．（3）锐角三角形．20. 两种方法都能使木架不变形．在图①中，△ABE，△BDE，△BCD的形状和大小不变．在图②中，△ABE，△ABC的形状和大小不变，故点D相对△ABE，△ABC的位置也不变．。
人教版数学 八年级上册11.1与三角形有关的线段 练习 (含答案)
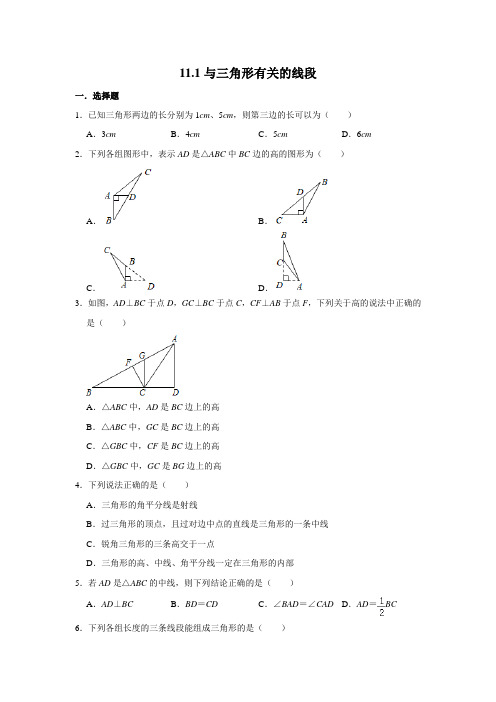
11.1与三角形有关的线段一．选择题1．已知三角形两边的长分别为1cm、5cm，则第三边的长可以为（）A．3cm B．4cm C．5cm D．6cm2．下列各组图形中，表示AD是△ABC中BC边的高的图形为（）A．B．C．D．3．如图，AD⊥BC于点D，GC⊥BC于点C，CF⊥AB于点F，下列关于高的说法中正确的是（）A．△ABC中，AD是BC边上的高B．△ABC中，GC是BC边上的高C．△GBC中，CF是BC边上的高D．△GBC中，GC是BG边上的高4．下列说法正确的是（）A．三角形的角平分线是射线B．过三角形的顶点，且过对边中点的直线是三角形的一条中线C．锐角三角形的三条高交于一点D．三角形的高、中线、角平分线一定在三角形的内部5．若AD是△ABC的中线，则下列结论正确的是（）A．AD⊥BC B．BD＝CD C．∠BAD＝∠CAD D．AD＝BC 6．下列各组长度的三条线段能组成三角形的是（）A．4cm，5cm，9cm B．4cm，4cm，8cmC．5cm，6cm，7cm D．3cm，5cm，10cm7．如果a、b、c分别是三角形的三条边，那么化简|a﹣c+b|+|b+c﹣a|的结果是（）A．﹣2c B．2b C．2a﹣2c D．b﹣c8．如图，在△ABC中，AB＝2020，AC＝2018，AD为中线，则△ABD与△ACD的周长之差为（）A．1B．2C．3D．49．如图，△ABC的BC边上的高是（）A．BE B．AF C．CD D．CF10．设三角形三边之长分别为3，8，1﹣2a，则a的取值范围为（）A．3＜a＜6B．﹣5＜a＜﹣2C．﹣2＜a＜5D．a＜﹣5或a＞2二．填空题11．如图，根据“两点之间线段最短”，可以判定AC+BC AB（填“＞”“＜”或“＝”）．12．从长度分别为3cm，4cm，5cm，6cm，9cm的线段中任意取3条，能构成的三角形个数为．13．△ABC的两边长分别是2和7，且第三边为奇数，则第三边长为．14．如图，AD是△ABC的一条中线，若BD＝3，则BC＝．15．如图所示，第1个图中有1个三角形，第2个图中共有5个三角形，第3个图中共有9个三角形，依此类推，则第6个图中共有三角形个．三．解答题16．在△ABC中，已知AB＝3，AC＝7，若第三边BC的长为偶数，求△ABC的周长．17．已知a＝m2+n2，b＝m2，c＝mn，且m＞n＞0．（1）比较a，b，c的大小；（2）请说明以a，b，c为边长的三角形一定存在．18．如图，在三角形ABC中，AB＝10cm，AC＝6cm，D是BC的中点，E点在边AB上，三角形BDE与四边形ACDE的周长相等．（1）求线段AE的长．（2）若图中所有线段长度的和是53cm，求BC+DE的值．参考答案一．选择题1．解：设第三边的长为xcm，则5﹣1＜x＜1+5，即4＜x＜6．故选：C．2．解：△ABC的高AD是过顶点A与BC垂直的线段，只有D选项符合．故选：D．3．解：∵AD⊥BC于点D，∴△ABC中，AD是BC边上的高，故A选项正确，B选项错误；∵CF⊥AB于点F，∴△GBC中，CF是BG边上的高，故C选项错误，D选项错误．故选：A．4．解：A．三角形的角平分线是线段，故A不符合题意；B．三角形的中线是线段，故B不符合题意；C．锐角三角形的三条高交于一点说法正确，故C符合题意；D．锐角三角形的三条高都在三角形内部；直角三角形有两条高与直角边重合，另一条高在三角形内部；钝角三角形有两条高在三角形外部，一条高在三角形内部．故D不符合题意；故选：C．5．解：∵AD是△ABC的中线，∴BD＝DC，故选：B．6．解：根据三角形的三边关系，A、4+5＝9，不能组成三角形，不符合题意；B、4+4＝8，不能够组成三角形，不符合题意；C、5+6＞7，能组成三角形，符合题意；D、3+5＝8＜10，不能组成三角形，不符合题意．故选：C．7．解：∵a、b、c分别是三角形的三条边，∴a﹣c+b＞0，b+c﹣a＞0，∴|a﹣c+b|+|b+c﹣a|＝a﹣c+b+b+c﹣a＝2b．故选：B．8．解：∵AD为中线，∴DB＝DC，∴△ABD与△ACD的周长之差为：（AB+AD+BD）﹣（AD+DC+AC）＝AB+AD+BD﹣AD﹣DC﹣AC＝AB﹣AC＝2020﹣2018＝2，故选：B．9．解：△ABC的BC边上的高是AF，故选：B．10．解：由题意得：8﹣3＜1﹣2a＜8+3，解得：﹣5＜a＜﹣2，故选：B．二．填空题11．解：如图，根据“两点之间线段最短”，可以判定AC+BC＞AB，故答案为：＞．12．解：其中的任意三条组合有：3cm、4cm、5cm；3cm、4cm、6cm；3cm、4cm、9cm；3cm、5cm、6cm；3cm、5cm、9cm；3cm、6cm、9cm；4cm、5cm、6cm；4cm、5cm、9cm；4cm、6cm、9cm；5cm、6cm、9cm十种情况．根据三角形的三边关系，其中的3cm、4cm、5cm；3cm、4cm、6cm；3cm、5cm、6cm；4cm、5cm、6cm；4cm、6cm、9cm；5cm、6cm、9cm能搭成三角形．故答案为：6．13．解：∵7﹣2＝5，7+2＝9，∴5＜第三边＜9，∵第三边为奇数，∴第三边长为7．故答案为：7．14．解：∵AD是△ABC的一条中线，BD＝3，∴BC＝2BD＝2×3＝6．故答案为：6．15．解：第n个图形中，三角形的个数是1+4（n﹣1）＝4n﹣3．所以当n＝6时，原式＝21，故答案为：21．三．解答题16．解：∵在△ABC中，AB＝3，AC＝7，∴第三边BC的取值范围是：4＜BC＜10，∴符合条件的偶数是6或8，∴当BC＝6时，△ABC的周长为：3+6+7＝16；当BC＝8时，△ABC的周长为：3+7+8＝18．∴△ABC的周长为16或18．17．解：（1）∵a＝m2+n2，b＝m2，c＝mn，且m＞n＞0，∴m2+n2＞m2＞mn，∴a＞b＞c；（2）∵m＞n＞0，∴mn＞n2，∴m2+mn＞m2+n2，∴a，b，c为边长的三角形一定存在．18．解：（1）∵三角形BDE与四边形ACDE的周长相等，∴BD+DE+BE＝AC+AE+CD+DE，∵BD＝DC，∴BE＝AE+AC，设AE＝x cm，则BE＝（10﹣x）cm，由题意得，10﹣x＝x+6．解得，x＝2，∴AE＝2cm；（2）图中共有8条线段，它们的和为：AE+EB+AB+AC+DE+BD+CD+BC＝2AB+AC+2BC+DE，由题意得，2AB+AC+2BC+DE＝53，∴2BC+DE＝53﹣（2AB+AC）＝53﹣（2×10+6）＝27，∴BC+DE＝（cm）．。
人教版八年级数学上册教学设计11.1 与三角形有关的线段
人教版八年级数学上册教学设计11.1 与三角形有关的线段一. 教材分析人教版八年级数学上册第11.1节“与三角形有关的线段”，主要包括三角形的两边之和大于第三边、三角形的两边之差小于第三边以及三角形的高的概念。
这些内容是学生进一步学习三角形性质的基础，对于培养学生的空间想象能力和逻辑思维能力具有重要意义。
二. 学情分析八年级的学生已经学习了平面几何的基本概念和性质，对图形的认识有一定的基础。
但是，对于三角形的高的概念和性质，以及如何运用三角形的性质解决实际问题，学生可能还比较陌生。
因此，在教学过程中，需要注重引导学生从实际问题中抽象出三角形的性质，并通过大量的实例来加深学生对三角形性质的理解。
三. 教学目标1.理解三角形的两边之和大于第三边、两边之差小于第三边的性质。
2.掌握三角形的高的概念，能画出一个三角形的所有高。
3.会运用三角形的性质解决一些实际问题。
四. 教学重难点1.教学重点：三角形的两边之和大于第三边、两边之差小于第三边的性质，三角形的高的概念。
2.教学难点：如何运用三角形的性质解决实际问题。
五. 教学方法1.采用问题驱动的教学方法，引导学生从实际问题中抽象出三角形的性质。
2.利用多媒体课件，生动形象地展示三角形的性质，帮助学生直观理解。
3.通过大量的练习，巩固学生对三角形性质的理解。
4.采用小组合作的学习方式，培养学生的团队合作能力。
六. 教学准备1.多媒体课件七. 教学过程1.导入（5分钟）利用多媒体课件，展示一些实际问题，如：在平面上有三个点，如何判断这三个点能否构成一个三角形？引导学生从实际问题中感受到三角形性质的重要性。
2.呈现（10分钟）介绍三角形的两边之和大于第三边、两边之差小于第三边的性质，并通过多媒体课件展示相应的图形，帮助学生直观理解。
3.操练（10分钟）让学生在纸上画出一个任意的三角形，然后用尺子量出三角形的三条边的长度，验证三角形的两边之和大于第三边、两边之差小于第三边的性质。
人教版数学八年级上册教案11.1《与三角形有关的线段》
人教版数学八年级上册教案11.1《与三角形有关的线段》一. 教材分析人教版数学八年级上册第11.1节《与三角形有关的线段》主要介绍了三角形的中线、角平分线和高的概念。
通过本节课的学习，学生能够理解三角形中线、角平分线和高的定义，掌握它们的基本性质，并为后续的三角形全等和三角形的证明打下基础。
二. 学情分析学生在七年级已经学习了线段的性质和三角形的基本概念，对线段和三角形有一定的认识。
但部分学生对概念的理解不够深入，对性质的运用不够熟练。
因此，在教学过程中，需要引导学生通过观察、操作、思考、交流等活动，加深对三角形中线、角平分线和高的理解，提高运用性质解决问题的能力。
三. 教学目标1.了解三角形的中线、角平分线和高的定义，掌握它们的基本性质。
2.能够运用中线、角平分线和高的性质解决一些简单问题。
3.培养学生的观察能力、操作能力、思考能力和交流能力。
四. 教学重难点1.重点：三角形的中线、角平分线和高的定义及基本性质。
2.难点：运用中线、角平分线和高的性质解决问题。
五. 教学方法1.采用问题驱动法，引导学生观察、操作、思考、交流，发现规律。
2.运用多媒体辅助教学，展示清晰的图形和动画，帮助学生形象地理解概念和性质。
3.采用案例分析法，精选典型例题，让学生在解决实际问题中掌握知识。
六. 教学准备1.多媒体教学设备。
2.三角板、直尺、量角器等绘图工具。
3.准备相关课件和教学素材。
七. 教学过程1. 导入（5分钟）利用多媒体展示一个三角形，引导学生观察并思考：三角形有哪些特殊的线段？2. 呈现（10分钟）介绍三角形的中线、角平分线和高的概念，并用多媒体展示它们的定义和性质。
让学生通过观察和思考，发现它们之间的关系。
3. 操练（10分钟）学生分组讨论，每组选择一个三角形，画出它的中线、角平分线和高，并观察它们之间的关系。
教师巡回指导，解答学生的疑问。
4. 巩固（10分钟）学生独立完成教材中的练习题，教师选取部分题目进行讲解和分析。
人教版八年级上数学11.1 与三角形有关的线段 同步练习及答案(含答案)
第11章《三角形》同步练习（§11.1 与三角形有关的线段A）班级学号姓名得分1、填空题：(1)由____________三条线段______所组成的图形叫做三角形．组成三角形的线段叫做______；相邻两边的公共端点叫做______，相邻两边所组成的角叫做______，简称______．(2)如图所示，顶点是A、B、C的三角形，记作______，读作______．其中，顶点A所对的边______还可用______表示；顶点B所对的边______还可用______表示；顶点C 所对的边______还可用______表示．(3)由“连接两点的线中，线段最短”这一性质可以得到三角形的三边有这样的性质______________________________．由它还可推出：三角形两边的差____________．(4)对于△ABC，若a≥b，则a＋b______c同时a－b______c；又可写成______＜c＜______．(5)若一个三角形的两边长分别为4cm和5cm，则第三边x的长度的取值范围是____________，其中x可以取的整数值为____________．2．已知：如图，试回答下列问题：(1)图中有______个三角形，它们分别是______________________________________.(2)以线段AD为公共边的三角形是_________________________________________.(3)线段CE所在的三角形是______，CE边所对的角是________________________．(4)△ABC、△ACD、△ADE这三个三角形的面积之比等于______∶______∶______．3．选择题：(1)下列各组线段能组成一个三角形的是( )．(A)3cm，3cm，6cm (B)2cm，3cm，6cm(C)5cm，8cm，12cm (D)4cm，7cm，11cm(2)现有两根木条，它们的长分别为50cm，35cm，如果要钉一个三角形木架，那么下列四根木条中应选取( )．(A)0.85m长的木条(B)0.15m长的木条(C)1m长的木条(D)0.5m长的木条(3)从长度分别为10cm、20cm、30cm、40cm的四根木条中，任取三根可组成三角形的个数是( )．(A)1个(B)2个(C)3个(D)4个(4)若三角形的两边长分别为3和5，则其周长l的取值范围是( )．(A)6＜l＜15 (B)6＜l＜16(C)11＜l＜13 (D)10＜l＜164.(1)一个等腰三角形的周长为18，若腰长的3倍比底边的2倍多6，求各边长．(2)已知等腰三角形的一边等于8cm，一边等于6cm，求它的周长．(3)一个等腰三角形的周长为30cm，一边长为6cm，求其它两边的长．(4)有两边相等的三角形的周长为12cm，一边与另一边的差是3cm，求三边的长．5．(1)若三角形三条边的长分别是7，10，x，求x的范围．(2)若三边分别为2，x－1，3，求x的范围．(3)若三角形两边长为7和10，求最长边x的范围．(4)等腰三角形腰长为2，求周长l的范围．(5)等腰三角形的腰长是整数，周长是10，求它的各边长．6．已知：如图，△ABC中，AB＝AC，D是AB边上一点．(1)通过度量AB 、CD 、DB 的长度，确定AB 与)(21DB CD 的大小关系.(2)试用你所学的知识来说明这个不等关系是成立的．7．已知：如图，P 是△ABC 内一点．请想一个办法说明AB ＋AC ＞PB ＋PC ．8．如图，D 、E 是△ABC 内的两点，求证：AB ＋AC ＞BD ＋DE ＋EC ．第11章《三角形》同步练习（§11.1 与三角形有关的线段B ）班级 学号 姓名 得分1．填空题：(1)从三角形一个顶点向它的对边画______，以______和______为端点的线段叫做三角形这边上的高．如图，若CD 是△ABC 中AB 边上的高，则∠ADC ______∠BDC ＝______，C 点到对边AB 的距离是______的长．(2)连结三角形的一个顶点和它______的______叫做三角形这边上的中线． 如右图，若BE 是△ABC 中AC 边上的中线，则AE ______.______21EC(3)三角形一个角的______与这个角的对边相交，以这个角的______和______为端点的线段叫做三角形的角平分线．一个角的平分线与三角形的角平分线的区别是________________________________ ______________________________________． 如图，若AD 是△ABC 的角平分线，则∠BAD ______∠CAD ＝21______或∠BAC ＝2______＝2______．2．已知：△GEF ，分别画出此三角形的高GH ，中线EM ，角平分线FN ．3．(1)分别画出△ABC 的三条高AD 、BE 、CF ．(∠A为锐角) (∠A为直角) (∠A为钝角)(2)这三条高AD、BE、CF所在的直线有怎样的位置关系?4．(1)分别画出△ABC的三条中线AD、BE、CF．(2)这三条中线AD、BE、CF有怎样的位置关系?(3)设中线AD与BE相交于M点，分别量一量线段BM和ME、线段AM和MD的长，从中你能发现什么结论?5．(1)分别画出△ABC的三条角平分线AD、BE、CF.(2)这三条角平分线AD、BE、CF有怎样的位置关系?(3)设△ABC的角平分线BE、CF交于N点，请量一量点N到△ABC三边的距离，从中你能发现什么结论?6．已知：△ABC中，AB＝AC，BD是AC边上的中线，如果D点把三角形ABC的周长分为12cm和15cm两部分，求此三角形各边的长．7．(1)如果将一个三角形的三边的长确定，那么这个三角形的形状和大小就不会改变了，三角形的这个性质叫做________________________. (2)四边形是否具有这种性质? 8．将一个三角形剖分成若干个面积相等的小三角形，称为该三角形的等积三角形的剖分(以下两问要求各画三个示意图)(1)已知一个任意三角形，并其剖分成3个等积的三角形． (2)已知一个任意三角形，将其剖分成4个等积的三角形．9．不等边△ABC 的两条高长度分别为4和12，若第三条高的长也是整数，试求它的长．参考答案（§11.1 与三角形有关的线段A ）1．(1)不在同一直线上的，首尾顺次相接，三角形的边，三角形的顶点，三角形的内角，三角形的角．(2)△ABC ，三角形ABC ，BC ，a ；AC ，b ；AB ，c (3)三角形两边之和大于第三边，小于第三边． (4)＞，＜，a －b ，a ＋b(5)1cm ＜x ＜9cm ，2cm 、3cm 、4cm 、5cm 、6cm 、7cm 、8cm ． 2．(1)六，△ABC 、△ABD 、△ABE 、△ACD 、△ACE 、△ADE ． (2)△ABD 、△ACD 、△ADE ． (3)△ACE ，∠CAE ． (4)BC ：CD ：DE ．3．(1)C ，(2)D ，(3)A ，(4)D4．(1)6，6，6；(2)20cm ，22cm ；(3)12cm ，12cm ；(4)5cm ，5cm ，2cm ． 5．(1)3＜x ＜17；(2)2＜x ＜6；(3)10≤x ＜17；(4)4＜e ＜8； (5)3，3，4或4，4，2 6．(1))(21DB CD AB +>． (2)提示：对于△ADC ，∵AD ＋AC ＞DC ， ∴(AD ＋DB )＋AC ＞CD ＋DB ， 即AB ＋AC ＞CD ＋DB ．又∵AB ＝AC ，∴2AB ＞CD ＋DB ． 从而AB ＞21(CD ＋DB )． 7．提示：延长BP 交AC 于D ．∵在△ABD 中，AB ＋AD ＞BD ＝BP ＋PD ，① 在△DPC 中，DP ＋DC ＞PC ，② 由①、②，∴AB ＋(AD ＋DC )＋DP ＞BP ＋PC ＋DP ． 即AB ＋AC ＞PB ＋PC ．8．证明：延长BP 交AC 于D ，延长CE 交BD 于F ． 在△ABD 中，AB ＋AD ＞BD ． ① 在△FDC 中，FD ＋DC ＞FC ． ② 在△PEF 中，PF ＋FE ＞PE ． ③①＋②＋③得AB ＋AD ＋FD ＋DC ＋PF ＋FE ＞BD ＋FC ＋PE ， 即：AB ＋AC ＋PF ＋FD ＋FE ＞BP ＋PF ＋FD ＋FE ＋EC ＋PE ， 所以AB ＋AC ＞BP ＋PE ＋EC ．（§11.1 与三角形有关的线段B ）1．(1)垂线，顶点、垂足，＝，90°，高CD 的长． (2)所对的边的中点、线段，＝，AC(3)平分线，顶点、交点，一个角的平分线是射线，而三角形的角平分线是线段． ＝，∠BAC ，∠BAD ，∠DAC 2．略．3．(1)略，(2)三条高所在直线交于一点．4．(1)略，(2)三条中线交于一点，(3)BM ＝2ME ．5．(1)略，(2)三条角平分线交于一点，(3)点N 到△ABC 三边的距离相等． 6．提示：有两种情况，分别运用方程思想，设未知数求解．⎩⎨⎧===,11,8BC AC AB 或⎩⎨⎧===.7,10BC AC AB 7．(1)三角形的稳定性，(2)不具有稳定性．8．(1)(2)下列各图是答案的一部分：9．它的长为5，或4．提示：设S △ABC ＝S ，第三条高为h ，则△ABC 的三边长可表示为：hSS S 212242、、，列不等式得：12242212242SS h S S S +<<- ∴3＜h ＜6．。
人教版八年级数学上册(教案)：11.1 与三角形有关的线段
教学目标：知识与技能：结合三角形的实例，探索、掌握三角形3条边之间的关系.会用符号表示三角形，了解按边关系对三角形进行分类.理解三角形三边之间的不等关系，并会初步应用它们来解决问题.过程与方法：结合具体实例，进一步认识三角形的概念及其基本要素，掌握三角形三边关系。
情感、态度和价值观：通过观察、操作、想象、推理、交流等活动，发展空间观念、推理能力和有条理地表达能力重点：三角形的三边之间的不等关系.难点：应用三角形的三边之间的不等关系判断3条线段能否组成三角形. 教学过程：一、问题情境：三角形是我们早已熟悉的图形，你能列举出日常生活中有什么物体是三角形吗？对于三角形，你了解了哪些方面的知识？你能画一个三角形吗？二、新课学习：⒈三角形的相关概念.⑴什么是三角形：如图⑴，由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.⑵三角形的有关概念：①边：组成三角形的三条线段叫做三角形的三条边.②角：三角形相邻两边的夹角叫做三角形的内角，简称三角形的角 .③顶点：三角形相邻两边的公共端点叫做三角形的顶点.⑶三角形的表示：如图⑴以A、B、C为顶点的三角形记作“⊿ABC ”，读作“三角形ABC”.⑷三角形的分类：如图⑵①等边三角形：图⑵中⑴的⊿ABC的边AB＝BC＝AC，⊿ABC是等边三角形.即：三条边都相等的三角形叫做等边三角形.②等腰三角形：图⑵中⑵的⊿ABC的边AB＝AC，但AB≠BC， AC≠BC，⊿ABC是等腰三角形.即：有两条边相等的三角形叫做等腰三角形.等腰三角形中，相等的边叫做腰，另一边叫做底，两腰的夹角叫做顶角，腰和底的夹角叫做底角.注意：等边三角形是特殊的等腰三角形，即腰和底相等的等腰三角形.③不等边三角形：图⑵中⑶的⊿ABC的边AB≠AC≠BC≠AB，⊿ABC是不等边三角形.即：三条边都不相等的三角形叫做不等边三角形.综上三角形按边分类关系如下三条边都不相等的三角形： .三角形腰和底不相等的： .有两条边相等的三角形⎧⎪⎧⎪⎪⎪⎧⎨⎨⎨⎪⎪⎩⎩⎪⎪⎩定义：由不在同一条直线上的三条线段首尾依次连接所组成的图形不等边三角形按边分类底边和腰不等的等腰三角形等腰三角形等边三角形三边不等关系：任意一边之小于其它两边的和而大于其它两边的差边腰和底相等的： .⑸练习：教材P65练习 “1”（口答）⑹讨论与交流： 如图⑶，存在AB 1,AB 2,AB 3,···AB 9,AB 10,10条线段，且B 1,B 2, ···B 10在同一条直线上，则，图中三角形共有45 个.⒉三角形三边关系： 阅读教材P64“探究”完成下列问题：⑴如图⑷，根据线段公里“两点之间线段最短”可得，⊿ABC 的三边 满足下列关系：AB ＋BC ＞AC ;AB ＋AC ＞BC ;BC ＋AC ＞AB .或：c ＋a ＞b ; c ＋b ＞a ; a ＋b ＞c .即：三角形任意两边的和 大于第三边 .上述关系也可表示为：a －b ＜c ; b －c ＜a ; c －a ＜b 或b －a ＜c ; c －b ＜a ; a －c ＜b .即：三角形任意两边的差 小于第三边 .注意：综合上可知：三角形任意一边小于 其他两边的和，并且大于 其他两边的差.⑵练习：教材P65练习“2” （口答）说明：应用三角形三边之间的关系判定三条线段能否构成三角形时，常常只要两条较短的线段长度之和大于第三条线段的长度即可.⑶例解与应用：阅读教材P64例，解答下列问题：一个等腰三角形的周长为28cm.①已知腰长是底边长的3倍，求各边的长；②已知其中一边的长为6cm,求其它两边的长.解：①设底边长为x cm ,则腰长为3x cm ，根据题意得x ＋3x ＋3x ＝28解得 x ＝4.所以 3x ＝3×4＝12.即：等腰三角形的三边长分别为4 cm ，12 cm ，12 cm .②若腰长为6cm ,则底边长为28－2×6＝16cm ,此时6＋6＜16，故不能组成三角形，所以腰长不能为6.若底边长为6cm ，则腰长为﹙28－6﹚÷2＝11cm ,它能构成三角形.所以它的其它边长为11cm 、11cm .⑷讨论与交流:①如果三条线段的比是①1∶3∶4；②1∶2∶3；③1∶4∶6；④3∶3∶6；⑤6∶6∶10；⑥3∶4∶5.其中能构成三角形的有 2 个.②若a ，b ，c 分别是三角形的三边，化简︱a －b －c ︱＋︱b －c －a ︱＋︱c －a ＋b ︱＝ .③已知一个等腰三角形的两边长分别为5cm 和9cm ，那么这个三角形的周长为19cm 或23cm. .三、课堂小结：四、课堂检测：1.如图⑸，共有个三角形，其中以AC为边的三角形有个.2.一个等腰三角形的两边分别为7cm和10cm，则它的周长为 .3.一个等腰三角形的两边分别为2cm和5cm；则它的周长为 .4.一个三角形的周长为15cm,且其中两边都等于第三边的2倍，，那么这个三角形的最短边长为 .5.已知一个三角形的两边长分别为5cm和9cm，那么这个三角形的第三边x的取值范围是＜x＜ .六、课后作业⒈书面作业：⑴课本P69习题7.1“1”（做书上）⑵课本P69习题7.1“2”（做书上）⑶等腰三角形底边为4.腰长为b,则b一定满足( )A．b＞2 B. 2＜b＜4 C. 2＜b＜8 D.b＜8 ⑷已知三条线段的比是：①2∶3∶4；②1∶2∶3；③2∶4∶6；④3∶3∶6；⑤6∶6∶10；⑥6∶8∶10.其中可构成三角形的有 ( )A. 1个B. 2个C. 3个D. 4个⑸已知三角形的三边长为连续的整数，且周长为12cm，则它的最短边长为( )A. 2cmB. 3cmC. 4cmD. 5cm⑹已知a,b,c为三角形的三边，则︱a＋b―c︱－︱b－c－a︱的化简结果是( )A.2aB. －2bC.2a＋2bD.2b－2c⑺已知等腰三角形的两边长分别为4cm和6cm,且它的周长大于14cm,则第三边长为⑻已知等腰三角形的两边长分别为4，9，求它的周长.⒉跟踪训练：⑴如图⑹所示，为估计池塘岸边A、B的距离，小方在池塘的一侧选取一点O，测得OA＝15cm，OB＝10cm,A、B间的距离不可能是（）A.20cmB.15cmC.10cmD.5cm⑵下列说法①等边三角形是等腰三角形；②三角形任意两边的和大于第三边；③三角形按边分类可分为等腰三角形、等边三角形和不等边三角形；④三角形按角分类应分为锐角三角形、直角三角形和钝角三角形.其中正确的有（）A. 1个B. 2个C. 3个D. 4个⑶已知三角形的两边长分别为4cm和9cm,则下列长度的四条线段中能作为第三边的是（）A.13cmB.6cmC.5cmD.4cm⑷三角形的一边长为5，一边长为13，则第三边x的取值范围是（）A. 5＜x＜ 13B. 8＜x＜18C.x＞8D. x＜18⑸已知三角形三边的比是3∶4∶5，其周长为48cm，那么它的三边长为 .⑹三角形有两边长为5和1，第三边为奇数，则此三角形的周长为 .⑺已知周长小于13的三角形三边长都是质数，且其中一条边a长为3，求符合条件的三角形的个数.⑻一个等腰三角形的一条边长为6，另两边长是不小于3且不大于13的奇数，求这个等腰三角形的周长.。
八年级数学人教版上册【能力培优】11.1与三角形有关的线段(含答案)
第十一章三角形11.1 与三角形相关的段一三角形个数确实定1．如，中三角形的个数（）A．2B． 18C．19D．202．如所示，第 1 个中有 1 个三角形，第 2 个中共有 5 个三角形，第 3 个中共有9个三角形，依此推，第 6 个中共有三角形__________个．3．资料，并填表：在△ ABC 中，有一点 P1，当 P1、A、 B、 C 没有任何三点在同向来上，可构成三个不重叠的小三角形（如）．当△ ABC 内的点的个数增添，若其余条件不，三角形内互不重叠的小三角形的个数状况怎？达成下表：△ABC 内点的个数123⋯1007构成不重叠的小三角形的个数35⋯二依据三角形的三不等关系确立未知字母的范4．三角形的三分3， 1－ 2a， 8， a 的取范是（）A ．－ 6＜ a＜－ 3B ．－ 5＜ a＜－ 2C． 2＜ a＜5D． a＜－ 5 或 a＞－ 25.在△ ABC 中，三分正整数 a、 b、 c，且 c≥ b≥ a＞ 0，假如 b=4 ，的三角形共有 ______个．6．若三角形的三分是2、 x、8，且 x 是不等式x2 ＞1 2 x的正整数解，求第23三 x 的．状元笔录【知识重点】1．三角形的三边关系三角形两边的和大于第三边，两边的差小于第三边．2．三角形三条重要线段(1)高：从三角形的极点向对边所在的直线作垂线，极点与垂足之间的线段叫做三角形的高．(2)中线：连结三角形的极点与对边中点的线段叫做三角形的中线．(3)角均分线：三角形内角的均分线与对边订交，极点与交点之间的线段叫做三角形的角均分线．3．三角形的稳固性三角形拥有稳固性．【温馨提示】1．以“能否有边相等”，能够将三角形分为两类：三边都不相等的三角形和等腰三角形．而不是分为三类：三边都不相等的三角形、等腰三角形、等边三角形，等边三角形是等腰三角形的一种．2．三角形的高、中线、角均分线都是线段，而不是直线或射线．【方法技巧】1．依据三角形的三边关系判断三条线段可否构成三角形时，要看两条较短边之和能否大于最长边．2．三角形的中线将三角形分红两个同底等高的三角形，这两个三角形面积相等．参照答案 :1．D 分析：段 AB 上有 5 个点，段 AB 与点 C 成 5×（ 5－1）÷2=10 个三角形；同，段 DE 上也有 5 个点，段 DE 与点 C 成 5×（ 5－ 1）÷2=10 个三角形，中三角形的个数 20 个．故 D．2． 21 分析：依据前的详细数据，再合形，不：后的比前多4，若把第一个形中三角形的个数看作是1=4 － 3，第 n 个形中，三角形的个数是4n－ 3．因此当 n=6 ，原式 =21 ．3．解：填表以下：△ABC 内点的个数123⋯1007构成不重叠的小三角形的个数357⋯2015分析：当△ABC 内有 1 个点，构成不重叠的三角形的个数是3=1×2＋ 1；当△ ABC 内有 2个点，构成不重叠的三角形的个数是5=2×2＋1；参照上边数据可知，三角形的个数与点的个数之的关系是：三角形内有 n 个点，三角形内互不重叠的小三角形的个数是2n+1，故当有 3 个点，三角形的个数是3×2＋ 1=7；当有 1007 个点，三角形的个数是1007×2＋1=2015 ．4． B分析：依据意，得8－3＜ 1－ 2a＜ 8＋ 3，即 5＜ 1－ 2a＜ 11，解得－ 5＜ a＜－ 2．故B ．5．10分析：∵在△ ABC中，三分正整数a、b、c，且 c≥b≥a＞ 0，∴ c＜a+b．∵b=4，∴a=1， 2，3， 4． a=1 ， c=4 ；a=2 ， c=4 或 5；a=3 ， c=4， 5， 6； a=4 ， c=4， 5，6， 7．∴ 的三角形共有1+2+3+4=10 个．6．解：原不等式可化3（ x+2）＞－ 2（ 1－ 2x），解得 x＜ 8．∵x 是它的正整数解，∴x可取 1， 2， 3， 5， 6， 7．再依据三角形三关系，得6＜x＜ 10，∴x=7．。
人教初中数学课标八年级上册 第十一章 11.1与三角形有关的线段(第二课时) 教案
11.1与三角形有关的线段（第二课时）一、内容和内容解析1.内容三角形的高、中线与角平分线，三角形的稳定性2.内容解析三角形的高、中线与角平分线是三角形内部的三条重要线段，也是“图形与几何”必备的知识基础。
既是对前面学过的线段的中点、垂线及角平分线等知识的内化，又为后面学习全等三角形及相似三角形等知识奠定了基础。
理解三角形的高、中线与角平分线的概念到用几何语言精确表述，这是学生在几何学习上的一个深入.基于以上分析，确定本节课的教学重点：理解三角形的高、中线与角平分线的概念，会用工具准确画出三角形的高、中线与角平分线。
二、目标和目标解析1.目标（1）理解三角形的高、中线与角平分线的概念，了解三角形的稳定性。
（2）会用工具准确画出三角形的高、中线与角平分线。
2.目标解析达成目标（1）的标志是：学生通过画图操作理解三角形的高、中线与角平分线的概念，并能用几何语言表述；通过教具展示感受三角形的稳定性。
达成目标（2）的标志是：能在具体的图形中利用工具作出三角形的高线、中线、角平分线。
三、教学问题诊断分析画钝角三角形的高时，有两个垂足落在边的延长线上，对于图形的这种特点学生不太适应，教学时可结合过线段外一点画已知线段的垂线（垂足在线段的延长线上）的知识帮助学生理解。
基于以上分析，确定本节课的教学难点是：画钝角三角形的高。
四、教学过程设计1.质疑展示，操作验证问题1.通过画三角形的中线，你有什么发现？师生活动：学生回答，三角形有三条中线。
追问1.教材中以三角形一条边上的中线为例介绍了三角形的中线，结合作图你能用语言描述三角形中线的定义吗？师生活动：学生通过讨论概括三角形中线的定义，教师加以完善。
设计意图：让学生通过亲自作图，先从形象上认识三角形中线的定义，然后用语言归纳出中线定义，这样做，不仅容易理解定义，同时也培养了他们的语言表达能力。
追问2.除此之外你还有什么发现？师生活动：学生回答，三角形三条中线交于一点追问3.在作图过程中三角形的三条中线都交于一点吗？师生活动：学生交流，提出质疑，教师提供技术帮助，学生亲自操作验证。
人教版八年级上册数学11.1与三角形有关的线段专题练习含答案
与三角形有关的线段一、选择题1、已知三角形的两边分别为4和9，则此三角形的第三边可能是（）A． 4 B．5 C．9 D． 132、下列长度的三根木棒首尾相接，不能做成三角形框架的是( )A．5 cm、7 cm、2 cm B．7 cm、13 cm、10 cmC．5 cm、7 cm、11 cm D．5 cm、10 cm、13 cm3、如图，已知BE，CF分别为△ABC的两条高，BE和CF相交于点H，若∠BAC=50°，则∠BHC 为（）A．115°B．120°C．125°D．130°4、下列长度的三条线段，不能组成三角形的是（）A．2、3、4 B．1、2、3 C．3、4、5 D．4、5、65、若△ABC内一点O到三角形三条边的距离相等，则O为△ABC（）的交点．A．角平分线B．高线C．中线D．边的中垂线6、如图，在△ABC中，BD、BE分别是高和角平分线，点F在CA的延长线上，FH⊥BE交BD于G，交BC于H，下列结论：①∠DBE=∠F；②2∠BEF=∠BAF+∠C；③∠F=（∠BAC﹣∠C）；④∠BGH=∠ABE+∠C其中正确的是（）A．①②③B．①③④C．①②④D．①②③④7、下列各组数可能是一个三角形的边长的是（）A．1，2，4 B．4，5，9 C．4，6，8 D．5，5，118、如图，CD，CE，CF分别是△ABC的高、角平分线、中线，则下列各式中错误的是（）A．AB=2BF B．∠ACE=∠ACB C．AE=BE D．CD⊥BE9、一个三角形中直角的个数最多有（）Ａ．3Ｂ．1Ｃ．2Ｄ．010、下列图形不具有稳定性的是（）11、下列各组中的三条线段能组成三角形的是（）Ａ．3，4，8 Ｂ．5，6，11Ｃ．5，6，10 Ｄ．4，4，812、如图所示，其中三角形的个数是（）Ａ．2个Ｂ．3个Ｃ．4个Ｄ．5个13、下列图形不具有稳定性的是（）A．正方形B．等腰三角形C．直角三角形D．钝角三角形14、如图，AC⊥BC，CD⊥AB，DE⊥BC，分别交BC，AB，BC于点C，D，E，则下列说法中不正确的是（）A．AC是△ABC和△ABE的高B．DE，DC都是△BCD的高C．DE是△DBE和△ABE的高D．AD，CD都是△ACD的高二、填空题15、在△ABC是AB＝5，AC＝3，BC边的中线的取值范围是。
人教版八年级上册数学11.1与三角形有关的线段(教案)
3.成果分享：每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上，以便全班都能看到。
（五）总结回顾（用时5分钟）
今天的学习，我们了解了三角形的基本概念、内角和、边长关系等重要性质，以及三角形在实际生活中的应用。同时，我们也通过实践活动和小组讨论加深了对三角形知识的理解。我希望大家能够掌握这些知识点，并在日常生活中灵活运用。最后，如果有任何疑问或不明白的地方，请随时向我提问。
2.在新课讲授环节，我采用了理论介绍、案例分析和重点难点解析相结合的方式。从学生的反馈来看，这种教学方法有助于他们深入理解三角形的基本性质和运用。但在讲解过程中，我发现部分学生对三角形边长关系这一难点理解不够透彻，需要在今后的教学中加强引导和讲解。
3.实践活动环节，学生分组讨论和实验操作，提高了他们的动手能力和团队协作能力。但在实验操作过程中，我发现部分学生对于三角形高、中线、角平分线的画法掌握不够熟练，需要在今后的教学中加强练习和指导。
4.学生小组讨论环节，大家积极参与，提出了很多有创意的想法。但在讨论过程中，我发现部分学生对于三角形在实际生活中的应用了解不够深入，需要在今后的教学中增加相关案例和实例。
5.总结回顾环节，学生对本次课程的知识点有了更加全面的掌握。但在这一环节，我发现部分学生对于课程内容的记忆不够牢固，需要在课后加强复习和巩固。
5.培养学生的团队合作和交流表达能力：在小组讨论和展示环节，鼓励学生积极参与，学会倾听他人意见，表达自己的观点，提高团队协作能力。
三、教学难点与重点
1.教学重点
（1）三角形的定义及其相关概念：理解三角形的三个顶点、三条边以及内角，这是学习三角形相关知识的基础。
人教版八年级数学上册11.1与三角形有关的线段.docx
初中数学试卷桑水出品11.1 与三角形有关的线段一．选择题（共18小题）1．（2015•长沙）如图，过△ABC的顶点A，作BC边上的高，以下作法正确的是（）A．B．C．D．2．（2015•广安）下列四个图形中，线段BE是△ABC的高的是（）A．B．C．D．3．（2015•宜昌）下列图形具有稳定性的是（）A．正方形B．矩形C．平行四边形D．直角三角形4．（2015•泉州）已知△ABC中，AB=6，BC=4，那么边AC的长可能是下列哪个值（）A．11 B．5 C．2 D． 15．（2015•大连）下列长度的三条线段能组成三角形的是（）A．1，2，3 B．1，，3 C．3，4，8 D．4，5，66．（2015•南通）下列长度的三条线段能组成三角形的是（）A．5，6，10 B．5，6，11 C．3，4，8 D．4a，4a，8a（a＞0）7．（2014•台湾）如图，D为△ABC内部一点，E、F两点分别在AB、BC上，且四边形DEBF为矩形，直线CD交AB于G点．若CF=6，BF=9，AG=8，则△ADC的面积为何？（）A．16 B．24 C．36 D．548．（2014•西宁）下列线段能构成三角形的是（）A．2，2，4 B．3，4，5 C．1，2，3 D．2，3，69．（2014•宜昌）已知三角形两边长分别为3和8，则该三角形第三边的长可能是（）A．5 B．10 C．11 D．1210．（2014•包头）长为9，6，5，4的四根木条，选其中三根组成三角形，选法有（）A．1种B．2种C．3种D．4种11．（2014•南平）下列每组数分别表示三根木棒的长，将它们首尾连接后，能摆成三角形的一组是（）A．1，2，1 B．1，2，2 C．1，2，3 D．1，2，412．（2013•温州）下列各组数可能是一个三角形的边长的是（）A．1，2，4 B．4，5，9 C．4，6，8 D．5，5，1113．（2013•宜昌）下列每组数分别表示三根木棒的长度，将它们首尾连接后，能摆成三角形的一组是（）A．1，2，6 B．2，2，4 C．1，2，3 D．2，3，414．（2013•长沙）如果一个三角形的两边长分别为2和4，则第三边长可能是（）A．2 B． 4 C．6 D．815．（2013•南通）有3cm，6cm，8cm，9cm的四条线段，任选其中的三条线段组成一个三角形，则最多能组成三角形的个数为（）A．1 B． 2 C．3 D． 416．（2013•河北）如图1，M是铁丝AD的中点，将该铁丝首尾相接折成△ABC，且∠B=30°，∠C=100°，如图2．则下列说法正确的是（）A．点M在AB上B．点M在BC的中点处C．点M在BC上，且距点B较近，距点C较远D．点M在BC上，且距点C较近，距点B较远17．（2013•梧州）下列各组线段的长为边，能组成三角形的是（）A．2cm，3cm，4cm B．2cm，3cm，5cm C．2cm，5cm，10cm D．8cm，4cm，4cm18．（2013•西藏）已知三角形两边长分别为3和9，则此三角形的第三边的长可能是（）A．4 B． 5 C．11 D．15二．填空题（共6小题）19．（2015•东莞）如图，△ABC三边的中线AD、BE、CF的公共点为G，若S△ABC=12，则图中阴影部分的面积是．20．（2015•佛山）各边长度都是整数、最大边长为8的三角形共有个．21．（2015•巴中）若a、b、c为三角形的三边，且a、b满足+（b﹣2）2=0，则第三边c的取值范围是．22．（2014•淮安）若一个三角形三边长分别为2，3，x，则x的值可以为（只需填一个整数）23．（2013•济南）如图，D、E分别是△ABC边AB、BC上的点，AD=2BD，BE=CE，设△ADC的面积为S1，△ACE的面积为S2，若S△ABC=6，则S1﹣S2的值为．24．（2013•贺州）如图，A、B、C分别是线段A1B，B1C，C1A的中点，若△ABC的面积是1，那么△A1B1C1的面积．11.1 与三角形有关的线段参考答案与试题解析一．选择题（共18小题）1．（2015•长沙）如图，过△ABC的顶点A，作BC边上的高，以下作法正确的是（）A．B．C．D．考点：三角形的角平分线、中线和高．分析：根据三角形高线的定义：过三角形的顶点向对边引垂线，顶点和垂足之间的线段叫做三角形的高线解答．解答：解：为△ABC中BC边上的高的是A选项．故选A．点评：本题考查了三角形的角平分线、中线、高线，熟记高线的定义是解题的关键．2．（2015•广安）下列四个图形中，线段BE是△ABC的高的是（）A．B．C．D．考点：三角形的角平分线、中线和高．分析：根据三角形高的画法知，过点B作AC边上的高，垂足为E，其中线段BE是△ABC的高，再结合图形进行判断．解答：解：线段BE是△ABC的高的图是选项D．故选D．点评：本题主要考查了三角形的高，三角形的高是指从三角形的一个顶点向对边作垂线，连接顶点与垂足之间的线段．熟记定义是解题的关键．3．（2015•宜昌）下列图形具有稳定性的是（）A．正方形B．矩形C．平行四边形D．直角三角形考点：三角形的稳定性；多边形．分析：根据三角形具有稳定性，四边形具有不稳定性进行判断．解答：解：直角三角形具有稳定性．故选：D．点评：此题考查了三角形的稳定性和四边形的不稳定性，正确掌握三角形的性质是解题关键．4．（2015•泉州）已知△ABC中，AB=6，BC=4，那么边AC的长可能是下列哪个值（）A．11 B．5 C．2 D． 1考点：三角形三边关系．分析：根据在三角形中任意两边之和大于第三边，任意两边之差小于第三边列出不等式即可．解答：解：根据三角形的三边关系，6﹣4＜AC＜6+4，即2＜AC＜10，符合条件的只有5，故选：B．点评：本题考查的是三角形的三边关系，掌握三角形形成的条件：任意两边之和大于第三边，任意两边之差小于第三边是解题的关键．5．（2015•大连）下列长度的三条线段能组成三角形的是（）A．1，2，3 B．1，，3 C．3，4，8 D．4，5，6考点：三角形三边关系．分析：根据三角形的三边满足任意两边之和大于第三边来进行判断．解答：解：A、1+2=3，不能组成三角形，故本选项错误；B、1+＜3，不能组成三角形，故本选项错误；C、3+4＜8，不能组成三角形，故本选项错误；D、4+5＞6，能组成三角形，故本选项正确．故选D．点评：本题考查了能够组成三角形三边的条件，简便方法是：用两条较短的线段相加，如果大于最长的那条线段就能够组成三角形．6．（2015•南通）下列长度的三条线段能组成三角形的是（）A．5，6，10 B．5，6，11 C．3，4，8 D．4a，4a，8a（a＞0）考点：三角形三边关系．分析：根据三角形的三边关系对各选项进行逐一分析即可．解答：解：A、∵10﹣5＜6＜10+5，∴三条线段能构成三角形，故本选项正确；B、∵11﹣5=6，∴三条线段不能构成三角形，故本选项错误；C、∵3+4=7＜8，∴三条线段不能构成三角形，故本选项错误；D、∵4a+4a=8a，∴三条线段不能构成三角形，故本选项错误．故选A．点评：本题考查的是三角形的三边关系，熟知三角形任意两边之和大于第三边，任意两边差小于第三边是解答此题的关键．7．（2014•台湾）如图，D为△ABC内部一点，E、F两点分别在AB、BC上，且四边形DEBF为矩形，直线CD交AB于G点．若CF=6，BF=9，AG=8，则△ADC的面积为何？（）A．16 B．24 C．36 D．54考点：三角形的面积；矩形的性质．分析：由于S△ADC=S△AGC﹣S△ADG，根据矩形的性质和三角形的面积公式计算即可求解．解答：解：S△ADC=S△AGC﹣S△ADG=×AG×BC﹣×AG×BF=×8×（6+9）﹣×8×9=60﹣36=24．故选：B．点评：考查了三角形的面积和矩形的性质，本题关键是活用三角形面积公式进行计算．8．（2014•西宁）下列线段能构成三角形的是（）A．2，2，4 B．3，4，5 C．1，2，3 D．2，3，6考点：三角形三边关系．专题：常规题型．分析：根据三角形的任意两边之和大于第三边，对各选项的数据进行判断即可．解答：解：A、2+2=4，不能构成三角形，故A选项错误；B、3、4、5，能构成三角形，故B选项正确；C、1+2=3，不能构成三角形，故C选项错误；D、2+3＜6，不能构成三角形，故D选项错误．故选：B．点评：本题考查了三角形的三边关系，熟记三角形的任意两边之和大于第三边，两边之差小于第三边是解题的关键．9．（2014•宜昌）已知三角形两边长分别为3和8，则该三角形第三边的长可能是（）A．5 B．10 C．11 D．12考点：三角形三边关系．专题：常规题型．分析：根据三角形的第三边大于两边之差，而小于两边之和求得第三边的取值范围，再进一步选择．解答：解：根据三角形的三边关系，得第三边大于：8﹣3=5，而小于：3+8=11．则此三角形的第三边可能是：10．故选：B．点评：本题考查了三角形的三边关系，即三角形的第三边大于两边之差，而小于两边之和，此题基础题，比较简单．10．（2014•包头）长为9，6，5，4的四根木条，选其中三根组成三角形，选法有（）A．1种B．2种C．3种D．4种考点：三角形三边关系．专题：常规题型．分析：要把四条线段的所有组合列出来，再根据三角形的三边关系判断能组成三角形的组数．解答：解：四根木条的所有组合：9，6，5和9，6，4和9，5，4和6，5，4；根据三角形的三边关系，得能组成三角形的有9，6，5和9，6，4和6，5，4．故选：C．点评：本题考查了三角形的三边关系，熟记三角形的任意两边之和大于第三边，两边之差小于第三边是解题的关键．11．（2014•南平）下列每组数分别表示三根木棒的长，将它们首尾连接后，能摆成三角形的一组是（）A．1，2，1 B．1，2，2 C．1，2，3 D．1，2，4考点：三角形三边关系．分析：根据三角形的三边关系：三角形两边之和大于第三边，计算两个较小的边的和，看看是否大于第三边即可．解答：解：A、1+1=2，不能组成三角形，故A选项错误；B、1+2＞2，能组成三角形，故B选项正确；C、1+2=3，不能组成三角形，故C选项错误；D、1+2＜4，不能组成三角形，故D选项错误；故选：B．点评：此题主要考查了三角形的三边关系，关键是掌握三角形的三边关系定理．12．（2013•温州）下列各组数可能是一个三角形的边长的是（）A．1，2，4 B．4，5，9 C．4，6，8 D．5，5，11考点：三角形三边关系．分析：看哪个选项中两条较小的边的和大于最大的边即可．解答：解：A、因为1+2＜4，所以本组数不能构成三角形．故本选项错误；B、因为4+5=9，所以本组数不能构成三角形．故本选项错误；C、因为4+6＞8，所以本组数可以构成三角形．故本选项正确；D、因为5+5＜11，所以本组数不能构成三角形．故本选项错误；故选C．点评：本题主要考查了三角形的三边关系定理：任意两边之和大于第三边，只要满足两短边的和大于最长的边，就可以构成三角形．13．（2013•宜昌）下列每组数分别表示三根木棒的长度，将它们首尾连接后，能摆成三角形的一组是（）A．1，2，6 B．2，2，4 C．1，2，3 D．2，3，4考点：三角形三边关系．分析：根据三角形的三边关系：三角形两边之和大于第三边，计算两个较小的边的和，看看是否大于第三边即可．解答：解：A、1+2＜6，不能组成三角形，故此选项错误；B、2+2=4，不能组成三角形，故此选项错误；C、1+2=3，不能组成三角形，故此选项错误；D、2+3＞4，能组成三角形，故此选项正确；故选：D．点评：此题主要考查了三角形的三边关系，关键是掌握三角形的三边关系定理．14．（2013•长沙）如果一个三角形的两边长分别为2和4，则第三边长可能是（）A．2 B． 4 C．6 D．8考点：三角形三边关系．分析：已知三角形的两边长分别为2和4，根据在三角形中任意两边之和＞第三边，任意两边之差＜第三边；即可求第三边长的范围．解答：解：设第三边长为x，则由三角形三边关系定理得4﹣2＜x＜4+2，即2＜x＜6．因此，本题的第三边应满足2＜x＜6，把各项代入不等式符合的即为答案．2，6，8都不符合不等式2＜x＜6，只有4符合不等式．故选B．点评：本题考查了三角形三边关系，此题实际上就是根据三角形三边关系定理列出不等式，然后解不等式即可．15．（2013•南通）有3cm，6cm，8cm，9cm的四条线段，任选其中的三条线段组成一个三角形，则最多能组成三角形的个数为（）A．1 B． 2 C．3 D． 4考点：三角形三边关系．分析：从4条线段里任取3条线段组合，可有4种情况，看哪种情况不符合三角形三边关系，舍去即可．解答：解：四条木棒的所有组合：3，6，8和3，6，9和6，8，9和3，8，9；只有3，6，8和6，8，9；3，8，9能组成三角形．故选：C．点评：此题主要考查了三角形三边关系，三角形的三边关系：任意两边之和＞第三边，任意两边之差＜第三边；注意情况的多解和取舍．16．（2013•河北）如图1，M是铁丝AD的中点，将该铁丝首尾相接折成△ABC，且∠B=30°，∠C=100°，如图2．则下列说法正确的是（）A．点M在AB上B．点M在BC的中点处C．点M在BC上，且距点B较近，距点C较远D．点M在BC上，且距点C较近，距点B较远考点：三角形三边关系．分析：根据钝角三角形中钝角所对的边最长可得AB＞AC，取BC的中点E，求出AB+BE＞AC+CE，再根据三角形的任意两边之和大于第三边得到AB＜AD，从而判定AD的中点M在BE上．解答：解：∵∠C=100°，∴AB＞AC，如图，取BC的中点E，则BE=CE，∴AB+BE＞AC+CE，由三角形三边关系，AC+BC＞AB，∴AB＜AD，∴AD的中点M在BE上，即点M在BC上，且距点B较近，距点C较远．故选：C．点评：本题考查了三角形的三边关系，作辅助线把△ABC的周长分成两个部分是解题的关键，本题需要注意判断AB的长度小于AD的一半，这也是容易忽视而导致求解不完整的地方．17．（2013•梧州）下列各组线段的长为边，能组成三角形的是（）A．2cm，3cm，4cm B．2cm，3cm，5cm C．2cm，5cm，10cm D．8cm，4cm，4cm考点：三角形三边关系．分析：根据在三角形中任意两边之和大于第三边，任意两边之差小于第三边．即可求解．解答：解：根据三角形任意两边的和大于第三边，可知A、2+3＞4，能组成三角形，故本选项正确；B、2+3=5，不能组成三角形，故本选项错误；C、2+5＜10，不能够组成三角形，故本选项错误；D、4+4=8，不能组成三角形，故本选项错误；故选A．点评：本题考查了能够组成三角形三边的条件，其实用两条较短的线段相加，如果大于最长的那条就能够组成三角形．18．（2013•西藏）已知三角形两边长分别为3和9，则此三角形的第三边的长可能是（）A．4 B．5 C．11 D．15考点：三角形三边关系．分析：已知三角形的两边长分别为3和9，根据在三角形中任意两边之和＞第三边，任意两边之差＜第三边；即可求第三边长的范围．解答：解：设第三边长为x，则由三角形三边关系定理得9﹣3＜x＜9+3，即6＜x＜12．因此，本题的第三边应满足6＜x＜12，把各项代入不等式符合的即为答案．只有11符合不等式，故答案为11．故选C．点评：此类求三角形第三边的范围的题，实际上就是根据三角形三边关系定理列出不等式，然后解不等式即可．二．填空题（共6小题）19．（2015•东莞）如图，△ABC三边的中线AD、BE、CF的公共点为G，若S△ABC=12，则图中阴影部分的面积是4．考点：三角形的面积．分析：根据三角形的中线把三角形的面积分成相等的两部分，知△ABC的面积即为阴影部分的面积的3倍．解答：解：∵△ABC的三条中线AD、BE，CF交于点G，∴S△CGE=S△AGE=S△ACF，S△BGF=S△BGD=S△BCF，∵S△ACF=S△BCF=S△ABC=×12=6，∴S△CGE=S△ACF=×6=2，S△BGF=S△BCF=×6=2，∴S阴影=S△CGE+S△BGF=4．故答案为4．点评：根据三角形的中线把三角形的面积分成相等的两部分，该图中，△BGF的面积=△BGD的面积=△CGD的面积，△AGF的面积=△AGE的面积=△CGE的面积．20．（2015•佛山）各边长度都是整数、最大边长为8的三角形共有20个．考点：三角形三边关系．分析：利用三角形三边关系进而得出符合题意的答案即可．解答：解：∵各边长度都是整数、最大边长为8，∴三边长可以为：1，8，8；2，7，8；2，8，8；3，6，8；3，7，8；3，8，8；4，5，8；4，6，8；4，7，8；4，8，8；5，5，8；5，6，8；5，7，8；5，8，8；6，6，8；6，7，8；6，8，8；7，7，8；7，8，8；8，8，8；故各边长度都是整数、最大边长为8的三角形共有20个．故答案为：20．点评：此题主要考查了三角形三边关系，正确分类讨论得出是解题关键．21．（2015•巴中）若a、b、c为三角形的三边，且a、b满足+（b﹣2）2=0，则第三边c的取值范围是1＜c＜5．考点：三角形三边关系；非负数的性质：偶次方；非负数的性质：算术平方根．分析：根据非负数的性质列式求出a、b，再根据三角形的任意两边之和大于第三边，两边只差小于第三边求解即可．解答：解：由题意得，a2﹣9=0，b﹣2=0，解得a=3，b=2，∵3﹣2=1，3+2=5，∴1＜c＜5．故答案为：1＜c＜5．点评：本题考查了非负数的性质：几个非负数的和为0时，这几个非负数都为0；三角形的三边关系．22．（2014•淮安）若一个三角形三边长分别为2，3，x，则x的值可以为4（只需填一个整数）考点：三角形三边关系．专题：开放型．分析：根据三角形的三边关系：三角形两边之和大于第三边，三角形的两边差小于第三边可得x的取值范围．解答：解：根据三角形的三边关系可得：3﹣2＜x＜3+2，即：1＜x＜5，所以x可取整数4．故答案为：4．点评：此题主要考查了三角形的三边关系，关键是掌握第三边的范围是：大于已知的两边的差，而小于两边的和．23．（2013•济南）如图，D、E分别是△ABC边AB、BC上的点，AD=2BD，BE=CE，设△ADC的面积为S1，△ACE的面积为S2，若S△ABC=6，则S1﹣S2的值为1．考点：三角形的面积．专题：压轴题．分析：根据等底等高的三角形的面积相等求出△AEC的面积，再根据等高的三角形的面积的比等于底边的比求出△ACD的面积，然后根据S1﹣S2=S△ACD﹣S△ACE计算即可得解．解答：解：∵BE=CE，∴S△ACE=S△ABC=×6=3，∵AD=2BD，∴S△ACD=S△ABC=×6=4，∴S1﹣S2=S△ACD﹣S△ACE=4﹣3=1．故答案为：1．点评：本题考查了三角形的面积，主要利用了等底等高的三角形的面积相等，等高的三角形的面积的比等于底边的比，需熟记．24．（2013•贺州）如图，A、B、C分别是线段A1B，B1C，C1A的中点，若△ABC的面积是1，那么△A1B1C1的面积7．考点：三角形的面积．专题：压轴题．分析：连接AB1，BC1，CA1，根据等底等高的三角形的面积相等求出△ABB1，△A1AB1的面积，从而求出△A1BB1的面积，同理可求△B1CC1的面积，△A1AC1的面积，然后相加即可得解．解答：解：如图，连接AB1，BC1，CA1，∵A、B分别是线段A1B，B1C的中点，∴S△ABB1=S△ABC=1，S△A1AB1=S△ABB1=1，∴S△A1BB1=S△A1AB1+S△ABB1=1+1=2，同理：S△B1CC1=2，S△A1AC1=2，∴△A1B1C1的面积=S△A1BB1+S△B1CC1+S△A1AC1+S△ABC=2+2+2+1=7．故答案为：7．点评：本题考查了三角形的面积，主要利用了等底等高的三角形的面积相等，作辅助线把三角形进行分割是解题的关键．。
八年级数学上册 11.1《与三角形有关的线段》三角形的高、中线与角平分线学习指导素材 新人教版(2
八年级数学上册11.1《与三角形有关的线段》三角形的高、中线与角平分线学习指导素材（新版）新人教版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（八年级数学上册11.1《与三角形有关的线段》三角形的高、中线与角平分线学习指导素材（新版）新人教版）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为八年级数学上册11.1《与三角形有关的线段》三角形的高、中线与角平分线学习指导素材（新版）新人教版的全部内容。
学习指导:三角形的高、中线与角平分线一、学习要点学习目标：知识目标：了解三角形的高、中线、角平分线及重心的有关概念。
能力目标：会用工具准确画出三角形的高、中线与角平分线, 通过画图了解三角形的三条高(及所在直线)交于一点,三角形的三条中线,三条角平分线等都交于一点.重难点剖析：重点：（1）了解三角形的高、中线与角平分线的概念，会用工具准确画出三角形的高、中线与角平分线。
（2）了解三角形的三条高、三条中线与三条角平分线分别交于一点.难点：（1)三角形平分线与角平分线的区别，三角形的高与垂线的区别.（2)钝角三角形高的画法。
（3）不同的三角形三条高的位置关系.二、学习引导预习形成知识点1：三角形的高(1）定义：(2）高的叙述方法(右图）：①____是△ABC的高；②____⊥BC,垂足为D;③D点在BC上,且_____=______=90°（3）几何语言：D C BA逆向:知识点2：①三角形的中线（1）定义：（2）几何语言（图2）:逆向： ②三角形的重心 （1）定义：（2)找出下列三角形的重心知识点3：三角形的角平分线（1）定义：（2）几何语言（图3）：逆向：(3）分别画出下列三角形的高、中线及角平分线预习检测1.三角形的三条高在( ）图2ABCD（1）（2）（3）图3ABCD1 2（1）（2）（3）A.三角形的内部B.三角形的外部C.三角形的边上D.三角形的内部，外部或边上2.下列说法正确的是（）①平分三角形内角的射线叫做三角形的角平分线；②三角形的中线,角平分线都是线段，而高是直线；③每个三角形都有三条中线，高和角平分线；④三角形的中线是经过顶点和对边中点的直线.A. ③④B. ③C. ②③ D。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第十一章三角形
11.1与三角形有关的线段（附答案）
专题一三角形个数的确定
1．如图，图中三角形的个数为（）
A．2 B．18 C．19 D．20
2．如图所示，第1个图中有1个三角形，第2个图中共有5个三角形，第3个图中共有9个三角形，依此类推，则第6个图中共有三角形__________个．
3．阅读材料，并填表：
在△ABC中，有一点P1，当P1、A、B、C没有任何三点在同一直线上时，可构成三个不重叠的小三角形（如图）．当△ABC内的点的个数增加时，若其他条件不变，三角形内互不重叠的小三角形的个数情况怎样？
专题二根据三角形的三边不等关系确定未知字母的范围
4．三角形的三边分别为3，1－2a，8，则a的取值范围是（）
A．－6＜a＜－3 B．－5＜a＜－2 C．2＜a＜5 D．a＜－5或a＞－2
5. 在△ABC中，三边长分别为正整数a、b、c，且c≥b≥a＞0，如果b=4，则这样的三角形共有______个．
6．若三角形的三边长分别是2、x、8，且x是不等式
2
2
x+
＞
12
3
x
-
-的正整数解，试求第
三边x的长．
状元笔记
【知识要点】
1．三角形的三边关系
三角形两边的和大于第三边，两边的差小于第三边．
2．三角形三条重要线段
(1)高：从三角形的顶点向对边所在的直线作垂线，顶点与垂足之间的线段叫做三角形的高．
(2)中线：连接三角形的顶点与对边中点的线段叫做三角形的中线．
(3)角平分线：三角形内角的平分线与对边相交，顶点与交点之间的线段叫做三角形的角平分线．
3．三角形的稳定性
三角形具有稳定性．
【温馨提示】
1．以“是否有边相等”，可以将三角形分为两类：三边都不相等的三角形和等腰三角形．而不是分为三类：三边都不相等的三角形、等腰三角形、等边三角形，等边三角形是等腰三角形的一种．
2．三角形的高、中线、角平分线都是线段，而不是直线或射线．
【方法技巧】
1．根据三角形的三边关系判定三条线段能否组成三角形时，要看两条较短边之和是否大于最长边．
2．三角形的中线将三角形分成两个同底等高的三角形，这两个三角形面积相等．
参考答案:
1．D 解析：线段AB上有5个点，线段AB与点C组成5×（5－1）÷2=10个三角形；同样，线段DE上也有5个点，线段DE与点C组成5×（5－1）÷2=10个三角形，图中三角形的个数为20个．故选D．
2．21 解析：根据前边的具体数据，再结合图形，不难发现：后边的总比前边多4，若把第一个图形中三角形的个数看作是1=4－3，则第n个图形中，三角形的个数是4n－3．所以当n=6时，原式=21．
3=1×2＋1；当△ABC内有2个点时，构成不重叠的三角形的个数是5=2×2＋1；参考上面数据可知，三角形的个数与点的个数之间的关系是：三角形内有n个点时，三角形内互不重叠的小三角形的个数是2n+1，故当有3个点时，三角形的个数是3×2＋1=7；当有1007个点时，三角形的个数是1007×2＋1=2015．
4．B 解析：根据题意，得8－3＜1－2a＜8＋3，即5＜1－2a＜11，解得－5＜a＜－2．故选B．
5．10 解析：∵在△ABC中，三边长分别为正整数a、b、c，且c≥b≥a＞0，∴c＜a+b．∵b=4，∴a=1，2，3，4．a=1时，c=4；a=2时，c=4或5；a=3时，c=4，5，6；a=4时，c=4，5，6，7．∴这样的三角形共有1+2+3+4=10个．
6．解：原不等式可化为3（x+2）＞－2（1－2x），解得x＜8．
∵x是它的正整数解，
∴x可取1，2，3，5，6，7．
再根据三角形三边关系，得6＜x＜10，
∴x=7．。