【江苏省苏州市】2017届高三上学期期末数学试卷-答案
【真题】2017-2018年江苏省苏州市高三(上)期末数学试卷(文科)与答案
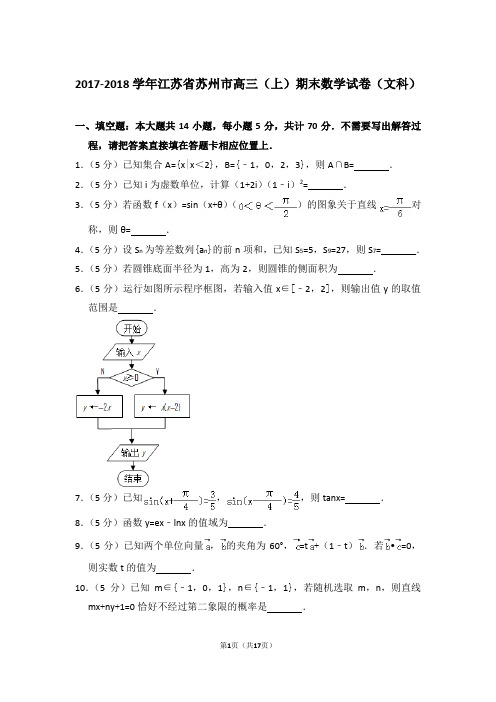
2017-2018学年江苏省苏州市高三(上)期末数学试卷(文科)一、填空题:本大题共14小题,每小题5分,共计70分.不需要写出解答过程,请把答案直接填在答题卡相应位置上.1.(5分)已知集合A={x|x<2},B={﹣1,0,2,3},则A∩B=.2.(5分)已知i为虚数单位,计算(1+2i)(1﹣i)2=.3.(5分)若函数f(x)=sin(x+θ)()的图象关于直线对称,则θ=.4.(5分)设S n为等差数列{a n}的前n项和,已知S5=5,S9=27,则S7=.5.(5分)若圆锥底面半径为1,高为2,则圆锥的侧面积为.6.(5分)运行如图所示程序框图,若输入值x∈[﹣2,2],则输出值y的取值范围是.7.(5分)已知,,则tanx=.8.(5分)函数y=ex﹣lnx的值域为.9.(5分)已知两个单位向量,的夹角为60°,=t+(1﹣t).若•=0,则实数t的值为.10.(5分)已知m∈{﹣1,0,1},n∈{﹣1,1},若随机选取m,n,则直线mx+ny+1=0恰好不经过第二象限的概率是.11.(5分)已知f(x)=,则不等式f(x2﹣x+1)<12解集是.12.(5分)在直角坐标系xOy中,已知A(﹣1,0),B(0,1),则满足PA2﹣PB2=4且在圆x2+y2=4上的点P的个数为.13.(5分)已知正实数x,y满足xy+2x+y=4,则x+y的最小值为.14.(5分)若(m≠0)对一切x≥4恒成立,则实数m的取值范围是.二、解答题:本大题共六小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.(14分)在△ABC中,设角A,B,C的对边分别为a,b,c,且acosC+=b.(Ⅰ)求角A的大小;(Ⅱ)若a=,b=4,求边c的大小.16.(14分)如图,在四棱锥P﹣ABCD中,四边形ABCD是矩形,平面PCD⊥平面ABCD,M为PC中点.求证:(1)PA∥平面MDB;(2)PD⊥BC.17.(14分)甲、乙两地相距1000km,货车从甲地匀速行驶到乙地,速度不得超过80km/h,已知货车每小时的运输成本(单位:元)由可变成本和固定成本组成,可变成本是速度平方的倍,固定成本为a元.(1)将全程运输成本y(元)表示为速度v(km/h)的函数,并指出这个函数的定义域;(2)为了使全程运输成本最小,货车应以多大的速度行驶?18.(16分)如图,已知椭圆的右顶点为A(2,0),点P (2e,)在椭圆上(e为椭圆的离心率).(1)求椭圆的方程;(2)若点B,C(C在第一象限)都在椭圆上,满足,且,求实数λ的值.19.(16分)设数列{a n}满足a n+1=2a n+n2﹣4n+1.(1)若a1=3,求证:存在f(n)=an2+bn+c(a,b,c为常数),使数列{a n+f(n)}是等比数列,并求出数列{a n}的通项公式;(2)若a n是一个等差数列{b n}的前n项和,求首项a1的值与数列{b n}的通项公式.20.(16分)已知a,b为常数,a≠0,函数.(1)若a=2,b=1,求f(x)在(0,+∞)内的极值;(2)①若a>0,b>0,求证:f(x)在区间[1,2]上是增函数;②若f(2)<0,f(﹣2)<e﹣2,且f(x)在区间[1,2]上是增函数,求由所有点(a,b)形成的平面区域的面积.2017-2018学年江苏省苏州市高三(上)期末数学试卷(文科)参考答案与试题解析一、填空题:本大题共14小题,每小题5分,共计70分.不需要写出解答过程,请把答案直接填在答题卡相应位置上.1.(5分)已知集合A={x|x<2},B={﹣1,0,2,3},则A∩B={﹣1,0} .【解答】解:∵A={x|x<2},B={﹣1,0,2,3},∴A∩B={﹣1,0}.故答案为:{﹣1,0}2.(5分)已知i为虚数单位,计算(1+2i)(1﹣i)2=4﹣2i.【解答】解:(1+2i)(1﹣i)2=(1+2i)(1﹣2i+i2)=(1+2i)(﹣2i)=﹣2i﹣4i2=4﹣2i.故答案为:4﹣2i.3.(5分)若函数f(x)=sin(x+θ)()的图象关于直线对称,则θ=.【解答】解:∵函数f(x)=sin(x+θ)的图象关于直线x=对称,∴+θ=kπ+,k∈Z,∴θ=kπ+,k∈Z,又0<θ<,∴θ=,故答案为:.4.(5分)设S n为等差数列{a n}的前n项和,已知S5=5,S9=27,则S7=14.【解答】解:∵数列{a n}是等差数列,S5=5,S9=27,∴,解得.∴S7==﹣7+21=14.故答案为:14.5.(5分)若圆锥底面半径为1,高为2,则圆锥的侧面积为π.【解答】解:∵圆锥的底面半径为1,高为2,∴母线长为:,∴圆锥的侧面积为:πrl=π×1×=π,故答案为:π.6.(5分)运行如图所示程序框图,若输入值x∈[﹣2,2],则输出值y的取值范围是[﹣1,4] .【解答】解:由程序框图知:算法的功能是求y=的值,当﹣2≤x<0时,函数为减函数,∴0<y≤4;当0≤x≤2时,函数y=x(x﹣2),∴﹣1≤y≤0.综上y的取值范围是[﹣1,4].故答案为:[﹣1,4].7.(5分)已知,,则tanx=﹣7.【解答】解:∵,,∴,两式相比得,即4sinx+4cosx=3sinx﹣3cosx,∴sinx=﹣7cosx,∴tanx=﹣7,故答案为:﹣78.(5分)函数y=ex﹣lnx的值域为[2,+∞).【解答】解:定义域为(0,+∞),=,当时y′<0,当时,y′>0,所以函数在区间(0,)上单调递减,在区间()上单调递增,所以f (x)≥,所以函数的值域为[2,+∞).故答案为:[2,+∞).9.(5分)已知两个单位向量,的夹角为60°,=t+(1﹣t).若•=0,则实数t的值为2.【解答】解:由题意可得,=||||cos60°=,∵,∴=t+(1﹣t)==1﹣=0,∴t=2,故答案为:210.(5分)已知m∈{﹣1,0,1},n∈{﹣1,1},若随机选取m,n,则直线mx+ny+1=0恰好不经过第二象限的概率是.【解答】解:由mx+ny+1=0得y=,要使直线mx+ny+1=0恰好不经过第二象限,则或者,即或,∴n=1,m=﹣1或n=1,m=0共有2个结果.∵m∈{﹣1,0,1},n∈{﹣1,1},∴m,n的选择共有3×2=6个结果,则根据古典概率的概率公式得所求的概率P=,故答案为:11.(5分)已知f(x)=,则不等式f(x2﹣x+1)<12解集是(﹣1,2).【解答】解:∵f(x)=,∴f(﹣x)=﹣f(x)恒成立,∴函数f(x)为奇函数,再根据二次函数的图象和性质可得:f(x)在(0,+∞)上是增函数,f(0)=0,可得函数f(x)在R上是增函数.令x2+x=12,求得x=3 或x=﹣4(舍去).∴由不等式f(x2﹣x+1)<12,可得x2﹣x+1<3,即(x+1)(x﹣2)<0,解得﹣1<x<2,故答案为:(﹣1,2).12.(5分)在直角坐标系xOy中,已知A(﹣1,0),B(0,1),则满足PA2﹣PB2=4且在圆x2+y2=4上的点P的个数为2.【解答】解:设P(x,y),∵A(﹣1,0),B(0,1),由PA2﹣PB2=4,得(x+1)2+y2﹣x2﹣(y﹣1)2=4.整理得:x+y=2.联立,解得:或.∴P点坐标为(0,2)或(2,0).即满足条件的P点的个数为2.故答案为:2.13.(5分)已知正实数x,y满足xy+2x+y=4,则x+y的最小值为.【解答】解:∵正实数x,y满足xy+2x+y=4,∴(0<x<2).∴x+y=x+==(x+1)+﹣3﹣3=﹣3,当且仅当x=时取等号.∴x+y的最小值为.故答案为:.14.(5分)若(m≠0)对一切x≥4恒成立,则实数m的取值范围是(﹣∞,﹣).【解答】解:等价于(m2x﹣1)(mx+1)<0,x1=,x2=﹣,若(m≠0)对一切x≥4恒成立,则m<0,当﹣1≤m<0时,≥﹣,则<4,解得﹣1≤m<﹣,当m<﹣1时,<﹣,则﹣<4,解得m<﹣1.故答案为:(﹣∞,﹣).二、解答题:本大题共六小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.(14分)在△ABC中,设角A,B,C的对边分别为a,b,c,且acosC+=b.(Ⅰ)求角A的大小;(Ⅱ)若a=,b=4,求边c的大小.【解答】(本题满分为12分)解:(Ⅰ)利用正弦定理化简acosC+c=b,得:sinAcosC+sinC=sinB,…(2分)∵sinB=sin(A+C)=sinAcosC+cosAsinC,…(3分)∴sinAcosC+sinC=sinAcosC+cosAsinC,即sinC=cosAsinC,…(4分)∵sinC≠0,∴cosA=,∵A为三角形内角,∴A=;…(6分)(Ⅱ)∵a=,b=4,cosA=,…(8分)∴由余弦定理得:a2=b2+c2﹣2bccosA,15=16+c2﹣4c,即c2﹣4c+1=0,…(10分)解得:c==2±.…(12分)16.(14分)如图,在四棱锥P﹣ABCD中,四边形ABCD是矩形,平面PCD⊥平面ABCD,M为PC中点.求证:(1)PA∥平面MDB;(2)PD⊥BC.【解答】证明:(1)连接AC,交BD与点O,连接OM,∵M为PC的中点,O为AC的中点,∴MO∥PA,∵MO⊂平面MDB,PA⊄平面MDB,∴PA∥平面MDB.(2)∵平面PCD⊥平面ABCD,平面PCD∩平面ABCD=CD,BC⊂平面ABCD,BC⊥CD,∴BC⊥平面PCD,∵PD⊂平面PCD,∴BC⊥PD.17.(14分)甲、乙两地相距1000km,货车从甲地匀速行驶到乙地,速度不得超过80km/h,已知货车每小时的运输成本(单位:元)由可变成本和固定成本组成,可变成本是速度平方的倍,固定成本为a元.(1)将全程运输成本y(元)表示为速度v(km/h)的函数,并指出这个函数的定义域;(2)为了使全程运输成本最小,货车应以多大的速度行驶?【解答】解:(1)依题意知汽车从甲地匀速行驶到乙地所用时间为,全程运输成本为y=,即y=1000(),定义域为(0,80],(2)依题意知a,v都为正数,故有1000()≥1000,当且仅当,即v=2时,等号成立,①若2≤80,即0<a≤1600时,则当v=2时,时,全程运输成本y最小.②若2>80,即a>1600时,则当v∈(0,80]时,有y′=1000()<0.∴函数在v∈(0,80]上单调递减,也即当v=80时,全程运输成本y最小,综上知,为使全程运输成本y最小,当0<a≤1600时行驶速度应为v=2时千米/时;当a>1600时行驶速度应为v=80千米/时.18.(16分)如图,已知椭圆的右顶点为A(2,0),点P (2e,)在椭圆上(e为椭圆的离心率).(1)求椭圆的方程;(2)若点B,C(C在第一象限)都在椭圆上,满足,且,求实数λ的值.【解答】解:(1)∵椭圆的右顶点为A(2,0),∴a=2,∵点P(2e,)在椭圆上,∴,∵a2=4,,a2=b2+c2,∴b2=1,c2=3,∴椭圆的方程为.(2)设直线OC的斜率为k,则直线OC方程为y=kx,代入椭圆方程,即x2+4y2=4,得(1+4k2)x2=4,∴,∴C(,),又直线AB方程为y=k(x﹣2),代入椭圆方程x2+4y2=4,得(1+4k2)x2﹣16k2x+16k2﹣4=0,∵x A=2,∴x B=,∵=0,∴+=0,∴,∵C 在第一象限,∴k >0,∴k=,∵=(),=(2﹣,0﹣)=(,),由=,得,∴k=,∴.19.(16分)设数列{a n }满足a n +1=2a n +n 2﹣4n +1.(1)若a 1=3,求证:存在f (n )=an 2+bn +c (a ,b ,c 为常数),使数列{a n +f (n )}是等比数列,并求出数列{a n }的通项公式;(2)若a n 是一个等差数列{b n }的前n 项和,求首项a 1的值与数列{b n }的通项公式.【解答】解:(1)∵数列{a n }满足a n +1=2a n +n 2﹣4n +1,设a n +1 +a (n +1)2+b (n +1)+c=2(a n +an 2+bn +c ),即 a n +1=2a n +an 2+(b ﹣2a )n +c ﹣a ﹣b , ∴,即.∵a 1+1﹣2=2,∴存在f (n )=n 2﹣2n ,使数列{a n +f (n )}是等比数列, ∴a n +n 2﹣2n=2×2n ﹣1, ∴a n =2n ﹣n 2+2n .(2)∵a n 是一个等差数列{b n }的前n 项和,数列{a n }满足a n +1=2a n +n 2﹣4n +1, 即 a n +1 +(n +1)2﹣2(n +1)=2(a n +n 2﹣n ), 即a n +1+(n +1)2﹣2(n +1)=2(a n +n 2﹣2n ),∴(a n +n 2﹣2n )=(a 1﹣1)•2n ﹣1,故a n =﹣n 2+2n +(a 1﹣1)•2n ﹣1, ∴b n =.再根据{b n }是等差数列,可得b n 的通项公式是关于n 的一次函数, ∴a 1=1,a n =﹣2n +3.20.(16分)已知a ,b 为常数,a ≠0,函数.(1)若a=2,b=1,求f(x)在(0,+∞)内的极值;(2)①若a>0,b>0,求证:f(x)在区间[1,2]上是增函数;②若f(2)<0,f(﹣2)<e﹣2,且f(x)在区间[1,2]上是增函数,求由所有点(a,b)形成的平面区域的面积.【解答】解:(1)若a=2,b=1,则f(x)=(2+)e x,则f′(x)=(x+1)(2x﹣1),由f′(x)>0,得x>,此时函数单调递增,由f′(x)<0,得0<x<,此时函数单调递减,则当x=时,f(x)取得极小值,f()=4.(2)f′(x)=(ax2+bx﹣b),设g(x)=ax2+bx﹣b,①证明:若a>0,b>0,则二次函数g(x)的图象开口向上,对称轴x=﹣<0,且g(1)=a>0,∴g(x)>0,对一切x∈[1,2]恒成立,又,∴f(x)>0恒成立.即f(x)在区间[1,2]上是增函数;②若f(2)<0,f(﹣2)<e﹣2,则,即,(•),∵f(x)在区间[1,2]上是增函数,∴f′(x)≥0对x∈[1,2]恒成立,即,(••),在(•),(••)的条件下,b<0,且1<≤2,且g()=恒成立,综上求由所有点(a ,b )满足的约束条件为,则不等式组对应的平面区域为△OAB ,其中A (),B (),C (1,0),则形成的平面区域的面积S=S △OAC ﹣S △OBC =.即△OAB 的面积为.赠送—高中数学知识点二次函数(1)一元二次方程20(0)ax bx c a ++=≠根的分布一元二次方程根的分布是二次函数中的重要内容,这部分知识在初中代数中虽有所涉及,但尚不够系统和完整,且解决的方法偏重于二次方程根的判别式和根与系数关系定理(韦达定理)的运用,下面结合二次函数图象的性质,系统地来分析一元二次方程实根的分布.设一元二次方程20(0)ax bx c a ++=≠的两实根为12,x x ,且12x x ≤.令2()f x ax bx c =++,从以下四个方面来分析此类问题:①开口方向:a ②对称轴位置:2bx a=-③判别式:∆ ④端点函数值符号. ①k <x 1≤x 2 ⇔②x 1≤x 2<k ⇔③x1<k <x 2 ⇔ af (k )<0④k 1<x 1≤x 2<k 2 ⇔xy1x 2x 0>a O ∙∙1k2k 0)(1>k f 0)(2>k f ab x 2-=xy1x 2x O∙<a 1k ∙2k 0)(1<k f 0)(2<k f ab x 2-=⑤有且仅有一个根x 1(或x 2)满足k 1<x 1(或x 2)<k 2 ⇔f (k 1)f (k 2)<0,并同时考虑f (k 1)=0或f (k 2)=0这两种情况是否也符合⑥k 1<x 1<k 2≤p 1<x 2<p 2 ⇔ 此结论可直接由⑤推出.(5)二次函数2()(0)f x ax bx c a =++≠在闭区间[,]p q 上的最值设()f x 在区间[,]p q 上的最大值为M ,最小值为m ,令01()2x p q =+. (Ⅰ)当0a >时(开口向上) ①若2b p a -<,则()m f p = ②若2b p q a ≤-≤,则()2b m f a =- ③若2b q a->,则()m f q =①若02b x a -≤,则()M f q = ②02b x a->,则()M f p =(Ⅱ)当0a <时(开口向下) ①若2b p a -<,则()M f p = ②若2b p q a ≤-≤,则()2b M f a =- ③若2b q a->,则()M f q =①若02b x a -≤,则()mf q = ②02b x a->,则()m f p =. xxxx>O-=f (p) f (q)()2b f a-0x x>O -=f(p) f(q)()2b f a-0x xf xfxx<O-=f (p)f(q)()2b f a-x x<O-=f (p)f (q)()2b f a-x。
2017-2018学年苏州市高三上学期期末数学试卷(有答案)

2017-2018学年苏州市高三上学期期末数学试卷(有答案)1.已知复数 $z=a+\dfrac{33}{22}i$,求其模长。
2.已知集合 $A=\{1,2\}$,$B=\{-1,1,4\}$,且 $A\subseteq B$,求正整数 $a$。
3.在平面直角坐标系 $xOy$ 中,已知抛物线 $y^2=-8x$,求其焦点坐标。
4.苏州轨道交通 1 号线每 5 分钟一班,其中列车在车站停留 0.5 分钟。
假设乘客到达站台的时刻是随机的,求该乘客到达站台立即能乘上车的概率。
5.已知 $4=2$,$\log_a x=2a$,求正实数 $x$。
6.XXX是我国南宋时期的数学家,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法。
右边的流程图是秦九韶算法的一个实例。
若输入 $n$,$x$ 的值分别为 $3$,$3$,求输出 $v$ 的值。
7.已知变量 $x,y$ 满足 $x+y\geq 0$,求 $z=2x-3y$ 的最大值。
8.已知等比数列 $\{a_n\}$ 的前 $n$ 项和为 $S_n$,且$S_6=1519$,$a_4-a_2=-8$,求 $a_3$ 的值。
9.鲁班锁是中国传统的智力玩具,起源于中国古代建筑中首创的榫卯结构。
它的外观是如图所示的十字立方体,其上下、左右、前后完全对称,六根等长的正四棱柱体分成三组,经$90^\circ$ 榫卯起来。
若正四棱柱体的高为 $5$,底面正方形的边长为 $1$,现将该鲁班锁放进一个球形内,求该球形的表面积至少为多少(壁的厚度忽略不计,结果保留 $\pi$)。
10.如图,两座建筑物 $AB$,$CD$ 的高度分别是$9\text{ m}$ 和 $15\text{ m}$,从建筑物 $AB$ 的顶部 $A$ 看建筑物 $CD$ 的张角 $\angle CAD=45^\circ$,求这两座建筑物$AB$ 和 $CD$ 底部之间的距离 $BD$。
【江苏省无锡市】2017届高三上学期期末数学试卷-答案

∵ ABCD 为矩形,∴ O 点为中点,
∵ E 为 PC 中点,
∴ OE∥PA ,
∵ OE 平面 PAD , PA 平面 PAD ,
∴ OE∥平面 PAD ,…8 分
同理可得: OF∥平面 PAD ,…10 分
∵ OE OF O ,
∴平面 OEF / / 平面 PAD ,…12 分
∵ EF 平面 OEF ,
∴ EF∥ PAD …14 分
17.解:(1)∵ EM BM , B MEN ,
∴ △BMN≌△EMN ,
∴ BNM MNE ,
∵ AME 2 ,
∴ BNM MNE ,
设 MN x ,
在 △BMN 中, BM xsin ,∴ EM BM xsin ,
∵ r 1 4e 8 0 ,
∴ ex 5 x 4 x 1 ,
从而有
-
1 4
1
m
5 4
2m e1m
,
即当 x 1,1 m , G x1 H x2 恒成立.
21.解:(1)曲线 C 的极坐标方程为 8sin ,即 2 8 sin .
1,
n1
∴ n 2 时, Ti 1 3T2 2T1 4T3 3T2 n 1Tn nTn1 i 1
n 1Tn 2T1 n 1Tn 1.
n1
∴存在关于 n 的整式 g n n 1,使得 Tn 1 Tn g n 1 对一切 n 2 , nN* 都成立. i 1
n
1
2
2n
3n 4
22n 3n
2
0
江苏省高三数学上学期期末联考试题(有答案)-名校版

江苏省苏北四市(徐州、淮安、连云港、宿迁)2017届高三数学上学期期末联考试题一、填空题(本大题共14小题,每小题5分,共70分) 1、已知集合{}{}2,0,2,3A B =-=-,则A B = .2、已知复数z 满足(1)2i z i -=,其中i 为虚数单位,则z 的模为 .3、某次比赛甲得分的茎叶图如图所示,若去掉一个最高分,去掉一个最低分,则剩下4个 分数的方差为 .4、根据如图所示的伪代码,则输出S 的值为 .5、从1,2,3,4,5,6这六个数中一次随机地取2个数,则所取2个数的和能被3整除的概率 为 .6、若抛物线28y x =的焦点恰好是双曲线2221(0)3x y a a -=>的右焦点,则实数a 的值为 .7、已知圆锥的底面直径与高都是2,则该圆锥的侧面积为 .8、若函数()sin()(0)6f x x πωπω=->的最小正周期为15,则1()3f 的值为 .9、已知等比数列{}n a 的前n 项和为n S ,若223323,23S a S a =+=+,则公比q 的值为 .10、已知函数()f x 是定义R 在上的奇函数,当0x >时,()23x f x =-,则不等式()5f x -≤ 的解集为 .11、若实数,x y 满足133(0)2xy x x +=<<,则313x y +-的最小值为 .12、已知非零向量,a b 满足a b a b ==+,则a 与2a b -夹角的余弦值为 .13、已知,A B 是圆221:1C x y +=上的动点,AB =P 是圆222:(3)(4)1C x y -+-= 上的动点,则PA PB +的取值范围为 .14、已知函数32sin ,1()925,1x x f x x x x a x <⎧=⎨-++⎩≥,若函数()f x 的图象与直线y x =有三 个不同的公共点,则实数a 的取值集合为 .二、解答题(本大题共6小题,共90分.解答应写出必要的文字说明、证明 或演算步骤)15、在ABC ∆中,角,,A B C 的对边分别为,,a b c .已知2cos (cos cos )A b C c B a +=. (1)求角A 的值; (2)若3cos 5B =,求sin()BC -的值.16、如图,在四棱锥E ABCD -中,平面EAB ⊥平面ABCD ,四边形ABCD 为矩形,EA EB ⊥,点,M N 分别是,AE CD 的中点.求证:(1)直线MN ∥平面EBC ;(2)直线EA ⊥平面EBC .17、如图,已知,A B 两镇分别位于东西湖岸MN 的A 处和湖中小岛的B 处,点C 在A 的正西方向1km 处,3tan ,44BAN BCN π∠=∠=.现计划铺设一条电缆联通,A B 两镇,有两种铺设方案:①沿线段AB 在水下铺设;②在湖岸MN 上选一点P ,先沿线段AP 在地 下铺设,再沿线段PB 在水下铺设,预算地下、水下的电缆铺设费用分别为2万元∕km 、4万元∕km .(1)求,A B 两镇间的距离;(2)应该如何铺设,使总铺设费用最低?18、如图,在平面直角坐标系xOy中,已知椭圆2222:1(0)x yC a ba b+=>>的离心率为2,且右焦点F到左准线的距离为(1)求椭圆C的标准方程;(2)设A为椭圆C的左顶点,P为椭圆C上位于x轴上方的点,直线PA交y轴于点M,过点F作MF的垂线,交y轴于点N.(ⅰ)当直线的PA斜率为12时,求FMN∆的外接圆的方程;(ⅱ)设直线AN交椭圆C于另一点Q,求APQ∆的面积的最大值.19、已知函数2(),()ln,2Rxf x axg x x ax ae=-=-∈.(1)解关于()Rx x∈的不等式()0f x≤;(2)证明:()()f xg x≥;(3)是否存在常数,a b,使得()()f x ax bg x+≥≥对任意的0x>恒成立?若存在,求出,a b 的值;若不存在,请说明理由.20、已知正项数列{}n a 的前n 项和为n S ,且11,(1)(1)6()n n n a a a a S n +=++=+,*∈N n . (1)求数列{}n a 的通项公式;(2)若对于N n *∀∈ ,都有(31)n S n n +≤成立,求实数a 取值范围;(3)当2a =时,将数列{}n a 中的部分项按原的顺序构成数列{}n b ,且12b a =,证明: 存在无数个满足条件的无穷等比数列{}n b .苏北四市2016-2017学年度高三年级第二次调研测试数学II(附加题)21.[选做题]本题包括A 、B 、C 、D 四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤. A.【选修4-1几何证明选讲】(本小题满分10分)如图,AB 为半圆O 的直径,D 为弧BC 的中点,E 为BC 的中点, 求证:AB ·BC=2AD ·BD .B .【选修4-2矩阵与变换】(本小题满分10分) 已知矩阵A=的一个特征值为2,其对应的一个特征向量为a=,求实数a ,b 的值.C.【选修4-4:坐标系与参数方程】(本小题满分10分)在平面直角坐标系xOy 中,以O 为极点,x 轴的正半轴为极轴建立极坐标系.直线l sin (θ一4π)=m (m ∈R ),圆C 的参数方程为(t 为参数).当圆心C 到直线l 时,求m 的值。
江苏省苏州市2017届高三(上)期末数学试卷(解析版)(2021年整理)

(完整)江苏省苏州市2017届高三(上)期末数学试卷(解析版)(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整)江苏省苏州市2017届高三(上)期末数学试卷(解析版)(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整)江苏省苏州市2017届高三(上)期末数学试卷(解析版)(word版可编辑修改)的全部内容。
2016-2017学年江苏省苏州市高三(上)期末数学试卷一、填空题(共14小题,每小题5分,满分70分)1.若集合A={x|x>1},B={x|x<3},则A∩B= .2.复数z=,其中i是虚数单位,则复数z的虚部是.3.在平面直角坐标系xOy中,双曲线﹣=1的离心率为.4.用分层抽样的方法从某校学生中抽取一个容量为45的样本,其中高一年级抽20人,高三年级抽10人,已知该校高二年级共有学生300人,则该校学生总数是人.5.一架飞机向目标投弹,击毁目标的概率为0.2,目标未受损的概率为0.4,则目标受损但未完全击毁的概率为.6.阅读程序框图,如果输出的函数值在区间内,则输入的实数x的取值范围是.7.已知实数x,y满足,则z=2x﹣y的最大值是.8.设S n是等差数列{a n}的前n项和,若a2=7,S7=﹣7,则a7的值为.9.在平面直角坐标系xOy中,已知过点M(1,1)的直线l与圆(x+1)2+(y﹣2)2=5相切,且与直线ax+y﹣1=0垂直,则实数a= .10.在一个长方体的三条棱长分别为3、8、9,若在该长方体上面钻一个圆柱形的孔后其表面积没有变化,则圆孔的半径为.11.已知正数x,y满足x+y=1,则的最小值为.12.若2tanα=3tan,则tan(α﹣)= .13.已知函数f(x)=若关于x的方程|f(x)|﹣ax﹣5=0恰有三个不同的实数解,则满足条件的所有实数a的取值集合为.14.已知A,B,C是半径为l的圆O上的三点,AB为圆O的直径,P为圆O内一点(含圆周),则的取值范围为.二、解答题(共6小题,满分90分,解答时应写出文字说明、证明过程或演算步骤)15.已知函数f(x)=sin2x﹣cos2x.(1)求f(x)的最小值,并写出取得最小值时的自变量x的集合.(2)设△ABC的内角A,B,C所对的边分别为a,b,c,且c=,f(C)=0,若sinB=2sinA,求a,b的值.16.已知直四棱柱ABCD﹣A1B1C1D1的底面是菱形,F为棱BB1的中点,M为线段AC1的中点.求证:(Ⅰ)直线MF∥平面ABCD;(Ⅱ)平面AFC1⊥平面ACC1A1.17.已知椭圆C:=1(a>b>0)的离心率为,并且过点P(2,﹣1)(1)求椭圆C的方程;(2)设点Q在椭圆C上,且PQ与x轴平行,过p点作两条直线分别交椭圆C于两点A(x1,y1),B(x2,y2),若直线PQ平分∠APB,求证:直线AB的斜率是定值,并求出这个定值.18.某湿地公园内有一条河,现打算建一座桥(如图1)将河两岸的路连接起来,剖面设计图纸(图2)如下,其中,点A,E为x轴上关于原点对称的两点,曲线段BCD是桥的主体,C为桥顶,并且曲线段BCD在图纸上的图形对应函数的解析式为y=(x∈[﹣2,2]),曲线段AB,DE均为开口向上的抛物线段,且A,E分别为两抛物线的顶点.设计时要求:保持两曲线在各衔接处(B,D)的切线的斜率相等.(1)曲线段AB在图纸上对应函数的解析式,并写出定义域;(2)车辆从A经B到C爬坡,定义车辆上桥过程中某点P所需要的爬坡能力为:M=(该点P与桥顶间的水平距离)×(设计图纸上该点P处的切线的斜率)其中M P的单位:米.若该景区可提供三种类型的观光车:①游客踏乘;②蓄电池动力;③内燃机动力,它们的爬坡能力分别为0。
江苏省13市2017届高三上学期考试数学试题分类汇编立体几何Word版含答案(K12教育文档)

江苏省13市2017届高三上学期考试数学试题分类汇编立体几何Word版含答案(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(江苏省13市2017届高三上学期考试数学试题分类汇编立体几何Word版含答案(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为江苏省13市2017届高三上学期考试数学试题分类汇编立体几何Word版含答案(word版可编辑修改)的全部内容。
江苏省13市2017高三上学期考试数学试题分类汇编立体几何一、填空题1、(南京市、盐城市2017届高三第一次模拟)将矩形ABCD绕边AB旋转一周得到一个圆柱,3AB=,2BC=,圆柱上底面圆心为O,EFG∆为下底面圆的一个内接直角三角形,则三棱锥O EFG-体积的最大值是▲ .2、(南通、泰州市2017届高三第一次调研测)如图,在正四棱柱ABCD–A1B1C1D1中,3cmAB=,11cmAA=,则三棱锥D1–A1BD的体积为▲3cm.3、(苏北四市(淮安、宿迁、连云港、徐州)2017届高三上学期期中)将斜边长为4的等腰直角三角形绕其斜边所在直线旋转一周,则所形成的几何体体积是▲ .4、(苏北四市(徐州、淮安、连云港、宿迁)2017届高三上学期期末)已知圆锥的底面直径与高都是2,则该圆锥的侧面积为5、(苏州市2017届高三上学期期末调研)一个长方体的三条棱长分别为983,,,若在该长方体上面钻一个圆柱形的孔后其表面积没有变化,则圆孔的半径为.6、(无锡市2017届高三上学期期末)已知圆锥的侧面展开图为一个圆心角为120,且面积为3π的扇形,则该圆锥的体积等于 .7、(扬州市2017届高三上学期期末)若正四棱锥的底面边长为2(单位:cm),侧面积为8(单位:2cm),则它的体积为▲(单位:3cm)。
2017届高三上学期期末考试试卷 (66)
S ←0For I From 1 To 2015 step 2S ←S + 1(2)I I +End For Print S第4题图2016年第一次全国大联考【江苏版】数学试卷考试时间:理150分钟,文120分钟第Ⅰ卷 必做题部分一、填空题:本大题共14个小题,每小题5分,共计70分,请把答案直接填写在答题卡相....应的位置....上. 1.已知,U R =集合{11}A x x =-<<,2{20}B x x x =-<,则()_______.U A C B =2. 已知复数21iz i-=+,则z 的共轭复数的模为_______. 3. 分别在集合{1234}A =,,,和集合{5678}B =,,,中各取一个 数相乘,则乘积为偶数的概率为_______. 4. 运行如图所示的伪代码,其结果为_______.5. 在平面直角坐标系xOy 中,与双曲线22154x y-=有相同渐近线,且一条准线方程为y =的双曲线的标准方程为_______. 6. 已知存在实数a,使得关于x a ≥恒成立,则a 的最大值为_______.7. 已知()sin())44f x a x x ππ=++-是偶函数,则实数a 的值为_______. 8. 已知正五棱锥底面边长为2,底面正五边形中心到侧面斜高距离为3, 斜高长为4,则此正五棱锥体积为_______.9. 已知函数293()6,3x f x x x x ≥⎧=⎨-+<⎩,,则不等式)43()2(2-<-x f x x f 的解集是_______.10. 在ABC ∆中,3,4AB AC ==,N 是AB 的中点,边AC (含端点)上存在点M ,使得BM CN ⊥,则cos A 的取值范围为_______.11. 设不等式组204020x y x y y ì-+?ïïï+-?íïï-?ïïî表示的平面区域为D ,若指数函数(0,1)x y a a a =>≠的图像上存在区域D 上的点,则a 的取值范围是_______.12. 已知函数2()2ln f x x x a x =++在区间(01),内无极值点,则a 的取值范围是_______. 13. 若函数1()()2,()(3)2x f x g x a x a =-=-+同时满足以下两个条件①,()0x R f x ∀∈<或()0g x <;②(1,1),()()0x f x g x ∃∈-<.则实数a 的取值范围为_______.14.若m b 为数列{2}n 中不超过3*()Am m N ∈的项数,2152=b b b +且310b =,则正整数A 的值为_______.二、解答题:本大题共6小题,计90 分。
江苏省苏州市2017届高三数学 等差数列 含答案 精品
姓名___________________学号___________________一、填空题:1.已知{}n a 为等差数列,n S 为其前n 项和,若16a =,350a a +=,则6=S ______.2.已知{}n a 为等差数列,n S 为其前n 项和,927S =,10=8a ,则100=a ______.3.若n S 为等差数列{}n a 的前n 项和,936S =-,13104S =-,则6a =______.4.设等差数列{}n a 的前n 项和为n S ,若5353a a =,则53S S =______.5.已知等差数列{}n a 的公差0≠d ,且39108a a a a +=-.若0n a =,则n =______.6.设等差数列{}n a 的前n 项和为n S ,12130,0S S ><,当n =______时,n S 取得最大值.7.设n S 是等差数列{}n a 的前n 项和,已知,144,324,3666===-n n S S S 则n =______.8.数列{}n a 满足12a =,21a =,且1111(2)n n n n n n n n a a a a n a a a a -+-+--=≥,则此数列的第10项为______.二、解答题:9.设等差数列{n a }的前n 项和为n S ,已知3a =24,011=S .(1)求n a .(2)求数列{n a }的前n 项和n S .(3)当n 为何值时,n S 最大,并求n S 的最大值.10.已知数列}{n a 的首项为2,前n 项的和为n S ,且142111-=-+n n n S a a (*∈N n ). (1)求2a 的值.(2)设nn n n a a a b -=+1,求数列}{n b 和{}n a 的通项公式.等差数列一、填空题:1.解析:16a =,2d =-,6166562S a d ∴=+⨯= 2.解析:19959()9272a a S a +===,53a =,10515a a d -==,100109098a a d =+=3.解析:19959()9362a a S a +===-,54a =-;11313713()131042a a S a +===-,78a =-57662a a a +∴==-4.解析:由5353a a =,得1a d =,51315105332S a d S a d +==+5.解析:由39108a a a a +=-,得622a d =,6a d =6(6)(5)0n a a n d n d =+-=-=,5n ∴=6.解析:12112671212()()022S a a a a =+=+>,670a a ∴+>,13113713()1302S a a a =+=<, 70a ∴<,60a ∴>,∴当n =6时,n S 取得最大值.7.解析:6180n n S S --=,661()180366()n n n S S S a a --+=+=+,136n a a +=, 1()183242n n n S a a n =+==,18n ∴= 8.解析:111111n n n n a a a a -+-=-,即11211n n n a a a -+=+,1{}na 是等差数列,公差211112d a a =-= 111(1)222n n n a =+-=,2n a n =, 1015a =二、解答题:9.解:(1)3a =24,011=S .∴⎪⎩⎪⎨⎧=⨯+=+0210111124211d a d a ,解得⎩⎨⎧-==8401d a ,∴n a n 848-=. (2)由(1)知,1a =40,n a n 848-=, ∴ n S =1()(40488)22n a a n n n ++-==2444n n -+.(3)由(2)有,n S =2444n n -+=-42112n ⎛⎫- ⎪⎝⎭+121, 故当5=n 或6=n 时,n S 最大,且n S 的最大值为120.10.解:(1)142111-=-+n n n S a a ,当1n =时,解得3142=a . (2)由142111-=-+n n n S a a ,得14211-=-++n n n n n S a a a a ,所以nn n n n a a a a S -=-++11214① 所以21121241n n n n n a a S a a +++++-=-②,由②-①,得n n n n n n n n n a a a a a a a a a ---=+++++++1112121222,因为01≠+n a , 所以n n n n n n a a a a a a ---=++++11222,所以211121=---+++++nn n n n n a a a a a a , 即11121=---++++nn n n n n a a a a a a ,即11=-+n n b b ,所以数列}{n b 是公差为1的等差数列. 因为431211=-=a a a b ,所以数列}{n b 的通项公式为41-=n b n . ∴411-=-+n a a a n n n ,即143414111-+=+-=+n n n a a n n ,即141)1(41-=-++n a n a n n ,104(1)141n n a a n n +-=+--,所以数列}14{-n a n 是等差数列. 由321141=-⨯a ,所以)14(32-=n a n .。
江苏省苏州市2017届高三调研测试数学试题
苏州市2017届高三第一学期期末调研数学试卷一、填空题(本大题共14小题,每小题5分,共70分)1、已知集合{}1>=x x A ,{}3<=x x B ,则集合=B A . 2、已知复数iiz 21-=,其中i 为虚数单位,则复数z 的虚部为 . 3、在平面直角坐标系xOy 中,双曲线16322=-y x 的离心率为 . 4、用分层抽样的方法从某高中校学生中抽取一个容量为45的样本,其中高一年级抽20 人,高三年级抽10人,已知该校高二年级共有学生300人,则该校学生总数为 . 5、一架飞机向目标投弹,击毁目标的概率为20.,目标未受损的概率为40.,则目标受损 但未完全击毁的概率为 .6、阅读下面的流程图,如果输出的函数)(x f 的值在区间],[2141内,那么输入的实数x 的 取值范围是 .7、已知实数y x ,满足⎪⎩⎪⎨⎧≥+≤-≤431y x x x y ,则目标函数y x z -=28、设n S 是等差数列{}n a 的前n 项和,若7772-==S a ,,则7a 9、在平面直角坐标系xOy 中,已知过点),(11M 的直线l 与圆52122=-++)()(y x 相切,且与直线01=-+y ax 垂直,则实数10、一个长方体的三条棱长分别为983,,,若在该长方体上面钻一个圆柱形的孔后其表面 积没有变化,则圆孔的半径为 . 11、已知正数y x ,满足1=+y x ,则1124+++y x 的最小值为 . 12、若832παtantan =,则=-)tan(8πα .13、已知函数⎩⎨⎧>-≤-=05042x e x x x f x ,,)(,若关于x 的方程05=--ax x f )(恰有三个不同的实数解,则满足条件的所有实数a 的取值集合为 个.14、已知C B A ,,是半径为1的圆O 上的三点,AB 为圆O 的直径,P 为圆O 内一点(含圆周),则⋅+⋅+⋅的取值范围为 .二、解答题(本大题共6小题,共90分.解答应写出必要的文字说明、证明 或演算步骤)15、已知函数212232--=x x x f cos sin )(. (1)求函数)(x f 的最小值,并写出取得最小值时的自变量x 的集合 (2)设ABC ∆的内角C B A ,,所对的边分别为c b a ,,,且3=c ,0=)(C f ,若A B sin sin 2=,求b a ,的值.16、如图,已知直四棱柱1111D C B A ABCD -的底面是菱形,F 是1BB 的中点,M 是线 段1AC 的的中点.(1)求证:直线//MF 平面ABCD ;(2)求证:平面⊥1AFC 平面11A ACC .17、已知椭圆)(:012222>>=+b a by a x C 的离心率为23,且过点),(12-P .(1)求椭圆C 的方程;(2)设点Q 在椭圆C 上,且PQ 与x 轴平行,过P 点作两条直线分别交椭圆C 于),(11y x A),(22y x B 两点,若直线PQ 平分APB ∠,求证:直线AB 的斜率是定值,并求出这个定值.18、某湿地公园内有一条河,现打算建一座桥(图1)将河两岸的路连接起来,剖面设计图纸(图2)如下:其中,点E A ,为x 轴上关于原点对称的两点,曲线BCD 是桥的主体,C 为桥顶,且曲线 段BCD 在图纸上的图形对应函数的解析式为],[,22482-∈+=x xy ,曲线段DE AB ,均 为开口向上的抛物线段,且E A ,分别为两抛物线的顶点.设计时要求:保持两曲线在各衔 接处),(D B 的切线的斜率相等.(1)求曲线段AB 在图纸上对应函数的解析式,并写出定义域;(2)车辆从A 经B 到C 爬坡.定义车辆上桥过程中某点P 所需要的爬坡能力为:=P M (该点P 与桥顶间的水平距离)⨯(设计图纸上该点P 处的切线的斜率),其中P M 的单 位:米.若该景区可提供三种类型的观光车:①游客踏乘;②蓄电池动力;③内燃机动力, 它们的爬坡能力分别为80.米,51.米,02.米,又已知图纸上一个单位长度表示实际长度1米,试问三种类型的观光车是否都可以顺利过桥?19、已知数列{}n a 的前n 项和为n S ,且22-=n n a S (*∈N n ).(1)求数列{}n a 的通项公式; (2)若数列{}n b 满足1211212121133221+-+--++-+=+n n n n b b b b a )( ,求数列{}n b 的 通项公式;(3)在(2)的条件下,设n n n b c λ+=2,问是否存在实数λ,使得数列{}n c (*∈N n )是单调递增数列?若存在,求出λ的取值范围;若不存在,请说明你的理由.20、已知函数x k x x f )(ln )(1--=(R ∈k ). (1)当1>x 时,求函数)(x f 的单调区间和极值;(2)若对于任意],[2e e x ∈,都有x xf ln )(4<成立,求实数k 的取值范围; (3)若21x x ≠,且)()(21x f x f =,证明:ke x x 221<.附加题21. 【选做题】在A 、B 、C 、D 四小题中只能选做2题,每小题10分,共20分.解答时应写出必要的文字说明、证明过程或演算步骤. A . 选修4-1:几何证明选讲如图,E 是圆O 内两条弦AB 和CD 的交点,过AD 延长线上一点F 作圆O 的切线FG ,G 为切点,已知EF=FG ,求证:EF ∥CB.(第21-A 题)B . 选修4-2:矩阵与变换 已知矩阵A=2113⎡⎤⎢⎥⎣⎦,B=1101⎡⎤⎢⎥-⎣⎦,求矩阵C ,使得AC=B.C . 选修4-4:坐标系与参数方程在平面直角坐标系xOy 中,直线l的参数方程为1222x y t ⎧=-⎪⎪⎨⎪=+⎪⎩(t 为参数),以坐标原点O 为极点,x 轴正半轴为极轴的极坐标系中,曲线C 的极坐标方程为ρsin 2θ-4cos θ=0,已知直线l 与曲线C 相交于A ,B 两点,求线段AB 的长.D . 选修4-5:不等式选讲已知a ,b ,x ,y 都是正数,且a+b=1,求证:(ax+by )(bx+ay )≥xy.【必做题】第22,23题,每小题10分,共20分.解答时应写出必要的文字说明、证明过程或演算步骤.22.口袋里装有大小相同的卡片八张,其中三张标有数字1,三张标有数字2,两张标有数字3.第一次从口袋里任意抽取一张,放回口袋后第二次再任意抽取一张,记第一次与第二次取到卡片上的数字之和为ξ.(1) ξ为何值时,其发生的概率最大?请说明理由;(2) 求随机变量ξ的数学期望E(ξ).23.在平面直角坐标系xOy中,已知两点M(1,-3),N(5,1),若点C的坐标满足=t+(1-t)(t∈R),且点C的轨迹与抛物线y2=4x交于A,B两点.(1) 求证:OA⊥OB;(2) 在x轴上是否存在一点P(m,0),使得过点P任作一条抛物线的弦,并以该弦为直径的圆都过原点?若存在,求出m的值及圆心的轨迹方程;若不存在,请说明理由.苏州市2017届高三第一学期期末考试答案1.(1,3)2.-12思路分析先化z=a+b i(a ,b ∈R)的形式或设z=a+b i(a ,b ∈R),再去分母.解法1z=(1-i )i 2i ·i=1+i-2=-12-12i,所以z 的虚部是-12.解法2设z=a+b i(a ,b ∈R),则2i(a+b i)=1-i,即-2b+2a i =1-i,所以-2b=1,得b=-12易错警示复数z=a+b i(a ,b ∈R)的虚部是b ,不是b i .3.3思路分析先求出a 2∶b 2∶c 2.由已知,得a 2∶b 2∶c 2=3∶6∶9,得e 2=22=3,所以e=3.4.900思路分析根据分层抽样的特点,建立比例式.设该校学生总数为n ,则300 =45-20-1045,得n=900.5.0.4设“目标受损但未完全击毁”为事件A ,则其对立事件 是“目标未受损或击毁目标”.P (A )=1-P ( )=1-(0.4+0.2)=0.4.解后反思在数学中,“但”与“且”的意义本质上是相同的.6.[-2,-1]流程图表示输出分段函数f (x )=2 ,∈[-2,2],2,∉[-2,2]的值.令f (x )得≤ ≤2,≤2≤12,解得-2≤x ≤-1.7.5思路分析先画出可行域,并解出.可行域是以A (3,1),B (3,2),C (2.5,1.5)为顶点的△ABC 及它的内部.z=2x-y=(2,-1)·(x ,y )≤(2,-1)·(3,1)=5.解后反思利用向量数量积的几何意义——一个向量的模与另一个向量在该向量上的投影的乘积,比平移直线更直观.8.-13思路分析可先求出基本量a 1,d ,再求a 7;也可利用S 7=7a 4先求出a 4.在等差数列{a n }中,S 7=7a 4=-7,所以a 4=-1.又a 2=7,所以公差d=-4,从而a 7=a 4+3d=-1-12=-13.9.12思路分析可用过圆上一点的切线方程求解;也可用垂直条件,设切线方程(x-1)-a (y-1)=0,再令圆心到切线的距离等于半径.因为点M 在圆上,所以切线方程为(1+1)(x+1)+(1-2)(y-2)=5,即2x-y-1=0.由两直线的法向量(2,-1)与(a ,1)垂直,得2a-1=0,即a=12.思想根源以圆(x-a )2+(y-b )2=r 2上一点T (x 0,y 0)为切点的切线方程为(x 0-a )(x-a )+(y 0-b )(y-b )=r 2.10.3思路分析先不考虑在哪个面上钻孔,考察圆柱半径与高的关系,再检验.设圆柱的底面半径为r ,高为h ,该长方体上面钻孔后其表面积少了两个圆柱底面,多了一个圆柱侧面.由题意,得πr 2+πr 2=2πrh ,得r=h.经检验,只有r=3符合要求,此时在8×9的面上打孔.易错警示实际应用问题须检验.11.94解法1令x+2=a ,y +1=b ,则a+b=4(a>2,b>1),4 +1 =14(a+b 4≥14(5+4)=94,当且仅当a=83,b=43,即x=23,y=13时取等号.解法2(幂平均不等式)设a=x+2,b=y+1,则4 +2+1+1=4 +1 =22+12 ≥(1+2)2 +=94.解法3(常数代换)设a=x+2,b=y+1,则4+2+1+1=4 +1 = ++ + 4 =54+ + 4 ≥94,当且仅当a=2b 时取等号.思想根源(权方和不等式)若a ,b ,x ,y ∈(0,+∞),则 2 + 2 ≥( + )2+,当且仅当 =时取等号.12.思路分析可先记t=tan π8,最后再代入化简.解法1记t=tan π8=1-cos π4sin π4=2-1,则tan α=32t.所以tan=32 - 1+32 2= 2+3 2解法2tan =32tan π8-tan π81+32tan 2π8=tan π82+3tan 2π8=sin π8cos π82cos 2π8+3sin 2π8sin π4解后反思有时,“硬做”也是必须的.13.-e ,-5ln5,2思路分析化为定曲线与两条动直线共有三个公共点.关键是两条动直线关于x 轴对称,其交点在x 轴上.方程|f (x )|-ax-5=0⇔f (x )=ax+5或f (x )=-ax-5.所以曲线C :y=f (x )与两条直线l :y=ax+5和m :y=-ax-5共有三个公共点.由曲线的形状可判断直线l 与曲线C 总有两个交点,所以可有情况是:直线m 与曲线C 相切,直线m 与曲线C 相交两点但其中一点是l ,m 的交点-5,0.由m 与C 相切,得当a>0时,y=-ax-5与f (x )图像在x ≤0的一侧相切.设切点为(x 0,y 0),则f'(x 0)=2x 0=-a ,x 0=-2.又切线方程为y-y 0=-a (x-x 0),得y=-ax+ax 0+y 0=-ax+a ·-+ 24-4=-ax- 24-4=-ax-5,得a=2.同理当a<0时,可得a=-e .由题易知a ≠0,从而m 与C 相切时,a=2或a=-e;由点-5,0在C 上,得当a>0时,交点位于f (x )图像在x ≤0的一侧,此时有f =25 2-4=0,a=52;当a<0时,交点位于f (x )图像在x>0的一侧,此时有f e -5-5=0,a=-5ln5,故由交点在C 上得a=52或a=-5ln5.经判断,a 的这四个值均满足要求.解后反思先确定a 的可能值,再检验,较易操作.也可考虑定曲线y=|f (x )|与动直线y=ax+b 的公共点的问题.14.-43,4思路分析固定顶点A ,B 后,就是一个双动点问题,与单个动点问题类似.解法1在平面直角坐标系xOy 中,设A (-1,0),B (1,0),C (cos α,sin α),P (r cos β,r sin β),其中α∈(0,π),r ∈[0,1],β∈R .· + · + · =3r 2-1-2r cos(β-α)∈[3r 2-2r-1,3r 2+2r-1]⊆-43,4,当r=13,β=α时,取得最小值-43;当r=1,β=π+α时,取得最大值4.解法2 · + · + · =( + )2-( - )24+ ·( + )=(2 )2-24+2 ·= 2+2 ·-1.以O 为坐标原点,建立直角坐标系,设P (x 0,y 0),C (cos θ,sin θ),则 2+2 · -1=3 02+3 02-2x 0cos θ-2y 0sin θ-1,其中x 0cos θ+y 0sin θ= 02+ 02sin(θ+φ)∈[- 02+ 02, 02+ 02].令t= 02+ 02∈[0,1],则3t 2-2t-1≤ 2+2 · -1≤3t 2+2t-1,得到 2+2 · -1∈-43,4.解法3 · + · + · =( + )2-( - )24+ ·( + )=(2 )2- 24+2 · = 2+2 ·-1.若知道 · =( - )·( + )=PO 2-OB 2, · + · =( + )· =2 · ,可加快计算速度.实际上,PO 2-OB 2=r 2-1,由向量数量积的定义知2 · =2 ·( - )∈[2r 2-2r ,2r 2+2r ].更进一步, · + · + · =3 2-2 · -1=3 -13 2-43.思想根源设G 是△ABC 的重心,P 是平面ABC 上任意一点,则 · + · + ·=3 2- 2+ 2+ 26.15.思路分析(1)首先把函数化简为f (x )=A sin(ωx+φ)+B 的形式,其中A>0,ω>0.(2)利用正弦、余弦定理,列出关于边a ,b 的方程组.规范解答(1)因为f (x )x-12(1+cos2x )-12(2分)=sin 2 1,(4分)所以函数f (x )的最小值是-2,(5分)此时2x-π6=2k π-π2,k ∈Z,得x=k π-π6,k ∈Z,即x 的取值集合为 = π-π6, ∈Z .(7分)(2)由f (C )=0,得sin 2 1.又C ∈(0,π),所以2C-π6=π2,得C=π3.(9分)由sin B=2sin A 及正弦定理,得b=2a.(11分)由余弦定理c 2=a 2+b 2-2ab cos C ,得a 2+b 2-ab=3.(13分)由=2 , 2+ 2- =3,解得 =1,=2.(14分)16.思路分析(1)要证MF ∥平面ABCD ,只要证MF 与平面ABCD 内的某直线平行.当F 沿 移到B 时,M 恰好移到AC 的中点E.也可以找MF 所在的平面AC 1F 与底面ABCD 的交线.(2)只要先证MF ⊥平面ACC 1A 1,只要证EB ⊥平面ACC 1A 1.规范解答(1)证法1如图1,连结AC ,取AC 的中点E ,连结ME ,EB.因为M ,E 分别是AC 1,AC 的中点,所以ME 12C 1C.(2分)又F 是B 1B 的中点,且B 1B C 1C ,得FB12C 1C ,所以MEFB ,四边形MFBE 是平行四边形,(4分)所以MF ∥EB.因为MF ⊄平面ABCD ,EB ⊂平面ABCD ,所以MF ∥平面ABCD.(7分)图1证法2如图2,延长C 1F ,CB 相交于点G ,连结AG.因为FB12C 1C ,所以F 是GC 1的中点.(2分)又因为M 是AC 1的中点,所以MF ∥AG.(4分)因为MF ⊄平面ABCD ,AG ⊂平面ABCD ,所以MF ∥平面ABCD.(7分)图2(2)如图1,因为底面ABCD 是菱形,得BA=BC ,又E 是AC 的中点,所以EB ⊥AC.因为A 1A ⊥平面ABCD ,EB ⊂平面ABCD ,所以A 1A ⊥EB.(9分)由(1)知,MF ∥EB ,所以MF ⊥AC ,MF ⊥A 1A.(11分)又因为A 1A ∩AC=A ,A 1A ,AC ⊂平面ACC 1A 1,所以MF ⊥平面ACC 1A 1.(13分)因为MF ⊂平面AFC 1,所以平面AFC 1⊥平面ACC 1A 1.(14分)17.思路分析(1)由e 求得a ∶b ∶c.(2)最简单直接的解法是:利用PA ,PB 的斜率互为相反数,直接求出A ,B 的坐标.规范解答(1)由e==得a ∶b ∶c=2∶1∶3,椭圆C 的方程为 24 2+ 22=1.(2分)把P (2,-1)的坐标代入,得b 2=2,所以椭圆C 的方程是 28+ 22=1.(5分)(2)由已知得PA ,PB 的斜率存在,且互为相反数.(6分)设直线PA 的方程为y+1=k (x-2),其中k ≠0.由+1= ( -2),2+4 2=8,消去y ,得x 2+4[kx-(2k+1)]2=8,即(1+4k 2)x 2-8k (2k+1)x+4(2k+1)2-8=0.(8分)因为该方程的两根为2,x A ,所以2x A =4(2 +1)2-81+4 2,即x A =8 2+8 -21+4 2.从而y A =4 2-4 -14 2+1.(10分)把k 换成-k ,得x B =8 2-8 -21+4 2,y B =4 2+4 -14 2+1.(12分)计算,得k AB = --=8-16 =-12,是定值.(14分)解后反思利用直线PA 与椭圆C 已经有一个交点P (2,-1),可使得解答更简单.由+1= ( -2), 2+4 2=8,得+1= ( -2),4( 2-1)=4- 2,当(x ,y )≠(2,-1)时,可得+1= ( -2),4 ( -1)=- -2.解得=8 2+8 -24 2+1,=4 2-4 -14 2+1.以下同解答.下面介绍一个更优雅的解法.由A ,B 在椭圆C :x 2+4y 2=8上,得(x 1+x 2)(x 1-x 2)+4(y 1+y 2)(y 1-y 2)=0,所以k AB = 1- 2 1- 2=-14· 1+21+2.同理k PA =1+1 1-2=-14· 1+21-1,k PB =2+1 2-2=-14· 2+22-1.由已知,得k PA =-k PB ,所以1+1 1-2=-2+1 2-2,且1+2 1-1=-2+2 2-1,即x 1y 2+x 2y 1=2(y 1+y 2)-(x 1+x 2)+4,且x 1y 2+x 2y 1=(x 1+x 2)-2(y 1+y 2)+4.从而可得x 1+x 2=2(y 1+y 2).所以k AB =-14· 1+ 21+2=-12,是定值.18.思路分析(1)首先B (-2,1).设曲线段AB 对应函数的解析式为f (x ),则f (-2)=1且f'(-2)=12.(2)先算出M P 的最大值.规范解答(1)首先B (-2,1),由y'=-16 (4+ 2)2,得曲线段BCD 在点B 处的切线的斜率为12.(2分)设曲线段AB 对应函数的解析式为y=f (x )=a (x-m )2(x ∈[m ,-2]),其中m<-2,a>0.由题意,得 (-2)= (-2- )2=1,'(-2)=2 (-2- )=12,解得=-6,=116.(4分)所以曲线段AB 对应函数的解析式为y=116(x+6)2(x ∈[-6,-2]).(5分)(2)设P (x ,y ),记g (x )=M P =(0-x )+6), ∈[-6,-2],∈[-2,0].(7分)①当x ∈[-6,-2]时,g (x )的最大值为g (-3)=98;(10分)②当x ∈[-2,0]时,g (x )-g (-2)=-( 2-4)2(4+ 2)2≤0,即g (x )≤g (-2)=1,得g (x )的最大值为g (x )max =98.(13分)综上所述,g (x )max =98.(14分)因为0.8<98<1.5<2,所以,游客踏乘的观光车不能过桥,蓄电池动力、内燃机动力观光车能够顺利过桥.(16分)19.思路分析(1)利用a n =1, =1,- -1,≥2,得到a n+1与a n 的关系.(2)与(1)类似,相当于(-1) n 项和为1.当n ≥2时,(-1)n+1 2 +1=1 -1-1.(3)即c n+1-c n >0对n ∈N *恒成立.考虑分离出λ.规范解答(1)a 1=S 1=2.由a n+1=S n+1-S n =(2a n+1-2)-(2a n -2),得a n+1=2a n .(2分)所以数列{a n }是首项为2,公比为2的等比数列,a n =2n .(4分)(2)由1 1= 12+1,得b 1=32.(5分)当n ≥2时,1-1 -1=(-1)n+12 +1,得b n =(-1)n 2 +12.(8分)所以b n =1,1) 2 +12,≥2.(9分)(3)假设数列{c n }是单调增数列,则c n+1-c n =2n +λ(b n+1-b n )>0对n ∈N *恒成立.①当n=1时,由2+0,得λ<8;(11分)②当n ≥2时,b n+1-b n =(-1)n+12 +1+12 +1-(-1)n 2 +12=(-1)n+12 +2+32 +1.若n=2k ,k ∈N *,则λ<12-( -1)+3·2-(2 +1)恒成立,而12-( -1)+3·2-(2 +1)单调递增,当n=2时取最小值3219,得λ<3219;(13分)若n=2k+1,k ∈N *,则λ>-12-( -1)+3·2-(2 +1)恒成立,而-12-( -1)+3·2-(2 +1)单调递减,当n=3时取最大值-12835,得λ>-12835.(15分)综上所述,存在实数λ,且λ的取值范围是-12835(16分)解后反思特别要注意对n=1时的单独处理.20.思路分析(1)只要注意对k 的讨论.(2)分离出k ,转化为k>K (x )恒成立问题.(3)先说明0<x 1<e k <x 2,从而只要证e k <x 2<e 2 1,只要证f (x 1)=f (x 2)转化为关于x 1的不等式对0<x 1<e k 恒成立问题.规范解答(1)f'(x )=ln x-k ,其中x>1.(1分)①若k ≤0,则x>1时,f'(x )>0恒成立,f (x )在(1,+∞)上单调递增,无极值;(2分)②若k>0,则f (x )在(1,e k ]上单调递减,在[e k ,+∞)上单调递增,(4分)有极小值f (e k )=-e k ,无极大值.(5分)(2)问题可转化为k>1x-1对x ∈[e,e 2]恒成立.(7分)设K (x )=1x-1,则K'(x )=42ln x+11=4 2(ln x-1)+1.当x ∈[e,e 2]时,K'(x )≥1>0,所以K (x )在[e,e 2]上单调递增,K (x )max =K (e 2)=1-8e2.(9分)所以实数k 的取值范围是1-8e 2,+∞.(10分)(3)因为f'(x )=ln x-k ,所以f (x )在(0,e k ]上单调递减,在[e k ,+∞)上单调递增.不妨设0<x 1<e k <x 2.要证x 1x 2<e 2k ,只要证x 2<e 21.因为f (x )在[e k ,+∞)上单调递增,所以只要证f (x 1)=f (x 2)即要证(ln x 1-k-1)x 1<(k-ln x 1-1)e 21.(12分)令t=2(k-ln x 1)>0,只要证(t-2)e t +t+2>0.设H (t )=(t-2)e t +t+2,则只要证H (t )>0对t>0恒成立.H'(t )=(t-1)e t +1,H ″(t )=t e t >0对t>0恒成立.所以H'(t )在(0,+∞)上单调递增,H'(t )>H'(0)=0.(14分)所以H (t )在(0,+∞)上单调递增,H (t )>H (0)=0.综上所述,x 1x 2<e 2k .(16分)21.A.规范解答由切割线定理,得FG 2=FD ·FA.(2分)因为EF=FG ,所以EF 2=FD ·FA ,即 =.(5分)又因为∠EFA=∠DFE ,所以△EFA ∽△DFE.所以∠EAF=∠DEF.(8分)因为∠EAF=∠BAD=∠BCD ,所以∠DEF=∠BCD.所以EF ∥CB.(10分)B.规范解答因为AC=B ,所以C=A -1B.(2分)由|A|=2113=6-1=5,得A -13-112.(6分)所以3-112110-1341-3=35-15-3(10分)C.思路分析化曲线C 的极坐标方程为直角坐标方程,可利用直线l 的标准参数方程的几何意义求线段AB 的长.规范解答因为曲线C 经过极点,所以其极坐标方程也为ρ2sin 2θ-4ρcos θ=0,(2分)在平面直角坐标系xOy 中,曲线C 的直角坐标方程为y 2-4x=0.(4分)把直线l 的标准参数方程代入,得t 2+82t=0,解得t 1=0,t 2=-82.(8分)所以AB=|t 2-t 1|=82.(10分)易错警示必须先说明“曲线C 经过极点”,才能在方程ρsin 2θ-4cos θ=0两边同乘ρ,否则新方程表示的曲线可能比曲线C 多一个极点.D.思路分析化x 2+y 2为xy ,显然可用基本不等式x 2+y 2≥2xy.规范解答因为a ,b ,x ,y 都是正数,且a+b=1,所以(ax+by )(bx+ay )=ab (x 2+y 2)+(a 2+b 2)xy ≥ab ·2xy+(a 2+b 2)xy=(a+b )2xy=xy.(9分)当且仅当x=y 时,取等号.(10分)22.思路分析本质上就是要求出ξ的分布,否则怎么说明理由?规范解答(1)设第一次与第二次取到卡片上数字分别为X ,Y.则P (X=1)=P (Y=1)=P (X=2)=P (Y=2)=38,P (X=3)=P (Y=3)=28.随机变量ξ的可能取值为2,3,4,5,6.(2分)P (ξ=2)=P (X=1)P (Y=1)=964,P (ξ=3)=P (X=1)P (Y=2)+P (X=2)P (Y=1)=932,P (ξ=4)=P (X=1)P (Y=3)+P (X=3)P (Y=1)+P (X=2)P (Y=2)=2164,P (ξ=5)=P (X=2)P (Y=3)+P (X=3)P (Y=2)=316,P (ξ=6)=P (X=3)P (Y=3)=116.(7分)所以当ξ=4时,其发生的概率最大.(8分)(2)由(1)可知E (ξ)=2×964+3×1864+4×2164+5×1264+6×464=24064=154.(10分)解后反思利用ξ=X+Y 来计算P (ξ=k ),条理清楚,不易出错.思想根源实际上,因为ξ=X+Y ,所以E (ξ)=E (X )+E (Y )=158+158=154.23.思路分析可直接判断点C 的轨迹是直线MN ,也可设C (x ,y ),得关于(x ,y )的参数方程.(1)只要证 · =x 1x 2+y 1y 2=0.可利用根与系数的关系.(2)设弦为EF ,则 ·=0,可设直线EF 的方程为x-m=λy.规范解答(1)由 =t +(1-t ) ,得 - =t ( - ),即 =t .所以点C 的轨迹就是直线MN ,其轨迹方程为x-y-4=0.(2分)设A (x 1,y 1),B (x 2,y 2).由- -4=0,2=4 ,消去x ,得y 2-4y-16=0,所以y 1y 2=-16.而x 1x 2= 124· 224=16,所以 · =x 1x 2+y 1y 2=0.所以OA ⊥OB.(4分)(2)设经过点P (m ,0)的弦EF 所在的直线方程为x-m=λy.设E (x 1,y 1),F (x 2,y 2),则以EF 为直径的圆经过原点等价于x 1x 2+y 1y 2=0.由- = ,2=4 ,得y 2-4λy-4m=0.当Δ=16λ2+16m>0时,y 1+y 2=4λ,y 1y 2=-4m.从而x 1x 2=12 2216=m 2.所以m 2-4m=0,解得m=0或m=4.(6分)①若m=0,则λ≠0,此时圆心D (x ,y )满足 =2 2,=2 (λ≠0).圆心的轨迹方程为y 2=2x (y ≠0).(8分)②若m=4,则λ∈R,此时圆心D (x ,y )满足=2 2+4, =2 .圆心的轨迹方程为y 2=2(x-4).(10分)易错警示不要轻易舍去m=0的情况.。
2017年高考江苏数学试题及答案(word解析版)(K12教育文档)
2017年高考江苏数学试题及答案(word解析版)(word版可编辑修改) 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2017年高考江苏数学试题及答案(word解析版)(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2017年高考江苏数学试题及答案(word解析版)(word版可编辑修改)的全部内容。
2017年普通高等学校招生全国统一考试(江苏卷)数学I一、填空题:本大题共14小题,每小题5分,共计70分. 请把答案填写在答题卡相应位置.......上.. (1)【2017年江苏,1,5分】已知集合}2{1A =,,23{},B a a =+.若{}1A B =,则实数a 的值为_______. 【答案】1【解析】∵集合}2{1A =,,23{},B a a =+.{}1A B =,∴1a =或231a +=,解得1a =.【点评】本题考查实数值的求法,是基础题,解题时要认真审题,注意交集定义及性质的合理运用. (2)【2017年江苏,2,5分】已知复数()()1i 12i z =-+,其中i 是虚数单位,则z 的模是_______. 【答案】10【解析】复数()()1i 12i 123i 13i z =-+=-+=-+,∴()221310z =-+=.【点评】本题考查了复数的运算法则、模的计算公式,考查了推理能力与计算能力,属于基础题. (3)【2017年江苏,3,5分】某工厂生产甲、乙、丙、丁四种不同型号的产品,产量分别为200,400,300,100件.为检验产品的质量,现用分层抽样的方法从以上所有的产品中抽取60件进行检验,则应从丙种型号的产品中抽取_______件. 【答案】18【解析】产品总数为2004003001001000+++=件,而抽取60辆进行检验,抽样比例为6061000100=,则应从丙种型号的产品中抽取630018100⨯=件. 【点评】本题的考点是分层抽样.分层抽样即要抽样时保证样本的结构和总体的结构保持一致,按照一定的比例,即样本容量和总体容量的比值,在各层中进行抽取. (4)【2017年江苏,4,5分】如图是一个算法流程图:若输入x 的值为116,则输出y 的值是_______. 【答案】2-【解析】初始值116x =,不满足1x ≥,所以41216222log 2log 2y =+=-=-.【点评】本题考查程序框图,模拟程序是解决此类问题的常用方法,注意解题方法的积累,属于基础题.(5)【2017年江苏,5,5分】若1tan 46πα⎛⎫-= ⎪⎝⎭.则tan α=_______.【答案】75【解析】tan tantan 114tan 4tan 161tan tan 4παπααπαα--⎛⎫-=== ⎪+⎝⎭+,∴6tan 6tan 1αα-=+,解得7tan 5α=.【点评】本题考查了两角差的正切公式,属于基础题.(6)【2017年江苏,6,5分】如如图,在圆柱12O O 内有一个球O ,该球与圆柱的上、下底面及母线均相切。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
,
y
16x 4 x2
2
,且
B -2,1
,则曲线在
B
处的切线斜率为
1 2
,
∴
2
a
2
2 2 a
1 1
,∴
a
6
,
1 16
,
2
∴曲线段 AB 在图纸上对应函数的解析式为 y 1 x 62 -6 x 2 ;
16 (2)设 P 为曲线段 AC 上任意一点.
【分析】由集合 A={x|x>1},B={x|x<3},结合集合交集的定义,可得答案.
【解答】解:∵集合 A={x|x>1},B={x|x<3},
∴A∩B={x|1<x<3},
故答案为:{x|1<x<3}
2.2.复数 z 1 i ,其中 i 是虚数单位,则复数 z 的虚部是__ 1 ___.
要证 x1x2
e2k ,只要证 x2
e2k x1
,即证,
∵ f x 在区间 ek , 上单调递增,
∴
f
x2
f
e2k
x1
,
又
f
x1
f
x2 ,即证
f
x1
f
e2k
x1
,
构造函数 h x
f
x
2 2
,∴
y1
y2
k
x1
x2
4k
.
即
y1
y2
k x1
x2 4k
k
16k 1
2 4 4k 2
4k
1
8k 4k
2
, x1
x2
1
16k 4k
2
.
8k
∴直线 AB 的斜率为 kAB
y1 y2 x1 x2
1 4k2 16k
1 . 2
恒成立,令
g
x
x
4 ln
x
x
,则
g'
x
4 ln
x x2
x
4
,
令
t
x
4
ln
x
x
4
,
x
e,
e2
,则
t
x
4 x
1
0
,
∴ t x 在区间 x e,e2 上单调递增,故 t xmin t e e 4 4 e 0 ,故 g x 0 ,
82
(2)证明:由题意,设直线 PA 的方程为 y 1 k x 2 ,
联立
x2 4y2 8
y k x 2
1
,得
1 4k2
x2 8 2k 2 k
x 16k2 16k 4 0 .
∴
2x1
16k 2 16k 1 4k 2
∴数列an 是等比数列,公比为 2,首项为 2.∴ an 2n .
(2)∵
1 2n
1 an
b1 2 1
b2 22
1
b3 23
1
1 n1
bn 2n
1
∴
1 2n1
b1 2 1
b2 22 1
b3 23 1
∴
1 2n
1 2n1
1
17.(1)解:由 c a
3 2
,得
c a
a2 b2 a2
3 4
,即 a2
4b2 ,
∴椭圆 C 的方程可化为 x2 4y2 4b2 .
2 / 18
又椭圆 C 过点 P2,1 ,
∴ 4 4 4b2 ,得 b2 2 ,则 a2 8 . ∴椭圆 C 的方程为 x2 y2 =1;
,
.
证明:(3)∵ f x1 f x2 ,由(1)知,函数 f x 在区间 0,ek 上单调递减,
在区间 ek , 上单调递增,且 f ek1 0 ,
不妨设 x1 x2 ,则 0 x1 ek x2 ek ,
.
20.解:(1)∵ f x ln x k 1 xk R ,
∴ x 0 , f (x) 1 x ln x k 1 ln x k , x
①当 k 0 时,∵ x 1,∴ f x ln x k 0 ,
函数 f x 的单调增区间是 1, ,无单调减区间,无极值;
∴由余弦定理可得: 3 2 a2 b2 2abcos π ,可得: a2 b2 ab 3 ②,…13 分 3 ∴联立①②解得: a 1, b 2 …14 分 16.证明:(Ⅰ)延长 C1F 交 CB 的延长线于点 N ,连接 AN .因为 F 是 BB1 的中点, 所以, F 为 C1N 的中点, B 为 CN 的中点.又 M 是线段 AC1 的中点, 故 MF∥AN . 又 MF 不在平面 ABCD 内, AN 平面 ABCD , ∴ MF∥平面 ABCD . (Ⅱ)连 BD ,由直四棱柱 ABCD A1B1C1D1 , 可知 A1A 平面 ABCD ,又∵ BD 平面 ABCD , ∴ A1A BD . ∵四边形 ABCD 为菱形,∴ AC BD . 又∵ AC A1A A, AC , A1A 平面 ACC1A1 , ∴ BD 平面 ACC1A1 . 在四边形 DANB 中, DA∥BN 且 DA BN ,所以四边形 DANB 为平行四边形, 故 NA∥BD ,∴ NA 平面 ACC1A1 ,又因为 NA 平面 AFC1 , ∴平面 AFC1 ACC1A1 .
江苏省苏州市 2017 届高三上学期期末考试数学试卷 答案
1.x |1 x 3
2. 1 2
3. 3 4.900 5. 0.4
6.
4 3
,
4
7.5 8. 13 9. 1
2 10.3 11. 1
2
12. 5 2 1 49
13.
e,
5 ln 5
,
2,
5 2
②当 k 0 时,令 ln x k 0 ,解得 x ek ,
当1 x ek 时, f x 0 ;当 x ek , f x 0 ,
∴函数 f x 的单调减区间是 1,ek ,单调减区间是 ek , , 在区间 1, 上的极小值为 f ek k k 1ek ek ,无极大值.
2i
2
【考点】复数代数形式的乘除运算.
【分析】直接利用复数代数形式的乘除运算化简得答案.
【解答】解:∵z= =
,
∴复数 z 的虚部是﹣ .
故答案为: .
3.【考点】双曲线的简单性质. 【分析】直接利用双曲线方程求解双曲线的离心率即可.
【解答】解:双曲线 ﹣ =1,可知 a= ,c=3,则双曲线的离心率为: = .
n1
bn 2n 1
,
1 n1
bn 2n 1
∴ bn
1n
1 2n
1
当n
1 时,
b1 3
1 2
,解得 b1
3 2
.∴ bn
3 2
,nLeabharlann 1
1n
1 2n
1, n
. 2
(3) cn 2n bn ,
∴n
3 时, cn
∵ 0.8 9 1.5 2 , 8
∴游客踏乘不能顺利通过该桥;蓄电池动力和内燃机动力能顺利通过该桥.
19.解:(1)由 Sn 2an 2 n N* ,可得 a1 2a1 2 ,解得 a1 2
n 2 时, an Sn Sn1 2an 2 2an1 2 ,化为: an 2an1 .
14.
4 3
,
4
15.解:(1)∵ f x
3 sin 2x cos2 x 1
2
2
3 2
sin
2
x
1
cos 2
2x
1 2
sin
2x
π 6
1
,…4
分
∴当 2x π 2kπ π ,即 x kπ π k Z 时, f x 的最小值为 2 ,…6 分
128 35
.
②当 n 为大于或等于 3 的奇数时,
1
3 22n1
1 2n2
,当且仅当 n 3 时, 32 19
.
当
n
2
时,
c2
c1
22
5 4
2
3 2
0
,即
λ<8.
综上可得:
的取值范围是
128 35
,
32 19
1 4k 2
18.解:(1)由题意 A 为抛物线的顶点,设 Aa,0a 2 ,则可设方程为
