上海高一反三角函数典型例题
反三角函数典型例题

反三角函数典型例题之阳早格格创做例1:正在下列四个式子中,蓄意思的为__________: 解:(4)蓄意思.(1)2)arcsin4π;(3)sin(arcsin 2);(4)arcsin(sin 2).面评:arcsin x ——x [1,1]∈-. 例2:供下列反正弦函数值(1)=解:3π (2)arcsin 0= 解:0(3)1arcsin()2-= 解:6π-(4)arcsin1=解:2π面评:流利影象:0,12±、1±的反正弦值.思索:1sin(arcsin )24π+该怎么样供? 例3:用反正弦函数值的形式表示下列各式中的x(1)sin x =,x [,]22ππ∈-解:x = 变式:x [,]2π∈π?解:x [,]2π∈π时,π-x [0,]2π∈,sin(π-x)=sinx∴π-x =x =π-变式:x [0,]∈π? 解:x =或者x =π-(2)1sin x 4=-,x [,]22ππ∈-解:1x arcsin 4=-变式:1sin x 4=-,3x [,2]2π∈π解:3x [,2]2π∈π时,2π-x [0,]2π∈,sin(2π-x)=-sinx =14 ∴2π-x =arcsin 14,则x =2π-arcsin 14面评:当x [,]22ππ∈-时,x arcsin a =;而当x [,]22ππ∉-,不妨将角转移到区间[,]22ππ-上,再用诱导公式处理对于应角之三角比值即可.训练:(1)sin x =,x [,]22ππ∈- 解:x 3π=(2)sin x =,x [0,]∈π 解:x =x =π-(3)3sin x 5=-,3x [,]22ππ∈ 解:3x arcsin 5=π+例4:供函数y 2arcsin(52x)=-的定义域战值域. 解:由152x 1-≤-≤,则x [2,3]∈,arcsin(52x)[,]22ππ-∈-,则y [,]∈-ππ. 变式:y sin x arcsin x =+ 解:x [1,1]∈-,y [sin1,sin1]22ππ∈--+ 思索:当3x [,]44ππ∈-时,供函数y arcsin(cos x)=的值域.解:当3x [,]44ππ∈-时t cos x [=∈,而y arcsin t =为删函数,则y [,]42ππ∈-. 例5:供下列函数的反函数(1)y sin x =,x [,]2π∈π解:y [0,1]∈,x [,0]2π-π∈-且sin(x )sin x y -π=-=-,则x arcsin(y)-π=-,则x arcsin y =π-,则反函数是1f (x)arcsin x -=π-,x [0,1]∈.(2) y arcsin x =,x [0,1]∈解:y [0,]2π∈,x sin y =,则反函数是1f (x)sin x -=,x [0,]2π∈. [例6] 供下列反三角函数的值:(1)=6π(2)arccos(=34π(二种要领)(3) arccos 0+arctan1=34π(4)arctan(=3π-(5) arcsin (-12)+arccos (-12)=2π (6)5arctan(tan)6π=6π-[例7] 用反三角函数值的形式表示下列各式中的x :(1)1cosx 3=,x [0,]∈π解:1x arccos3=变式:1cosx 3=-,x [,2]∈ππ解:1x 2arccos3=π-(2)tan x 2,x (,)22ππ=-∈-解:x arctan(2)=-变式:3x (,)22ππ∈解:x arctan 2=π+[例8](1) 已知arcsin x arcsin(1x)≥-,供x 的与值范畴.解:由11x x 1-≤-≤≤,得1x 12≤≤.(2) arccos x arccos(1x)>-解:由1x 1x 1-≤<-≤,得10x 2≤<.(3) arctan x 3π> 解:x >(4)arccosx 3π>解:11x 2-≤<[例9供y =arcsinx +arctanx 的值域.解:∵-1≤x ≤1∴-34π≤y ≤34π——波及战函数观念,反正弦、反正切函数单调性[例10] 供下列各式的值:(1)sin(arccos(解:设x arccos(=,则cos x =且x [,]2π∈π,则sin x =(2)tan[arccos(]6π-解:3tan()243ππ-==(3)213cos (arccos )25 解:设3x arccos5=,则3cosx 5=且x [0,]2π∈,则2x 1cosx 4cos 225+==(4)123sin[arctanarcsin ]55-解:设12arctan5α=,3arcsin5β=,则12tan5α=,4sin5β=且,(0,)2παβ∈,则1231245333 sin[arctan arcsin]sin()5513513565-=α-β=⨯-⨯=.思索:若供11arctan arctan23+的值呢?解:1arctan2α=,1arctan2β=,则1tan2α=,1tan3β=且,(0,)2παβ∈,∵tan()1α+β=,且(0,)α+β∈π,∴4πα+β=.。
反三角函数典型例题

精品文档5 5(1) sin x 解:(2) sin x [0,]解: (3) sin x处]解:3•胚或 arcs in 或 x3 .3 arcsin.3 arcsin- 3反三角函数典型例题例2:求下列反正弦函数值1 sin( arcs in)该如何求? 24用反正弦函数值的形式表示下列各式中的变式:x [一,]?2解:x [2,]时,n —x【°,2],sin( n — x) =sinx= £ • n — x = arcsin —3,贝U x = n — arcsin —355解: x = arcsin —3或 x = n — arcsin —35例1:在下列四个式子中,有意义的为解:(4)有意义。
(1) arcs in . 2 ; (2) arcsin _ ; (3) 点评:arcsinx 4 1,1]。
sin( arcs in 2) ; ( 4)arcsin(sin2)。
(1) arcsin -2 (2) arcsin0 解:0(3) arcsin(-)2点评:1熟练记忆:0,-2解:-62,(4) arcs ini1的反正弦值。
思考:(1)sinx £,x [ -,^]解: .43 x = arcs in5变式:x [0,]?⑵ sin x -4变式:si nx2 2 x [—,2 ]2解:.1 arcs in 43解:x [,2 2]时,2-x [0,2],1 sin(2 n — x) = — sinx=— 42 n — x =1 山arcs in ,贝U x = 2 n — arcs in — 点评:当x [ 2,2]时,x arcsina;而当处理对应角之三角比值即可。
[舊],可以将角转化到区间[形]上,再用诱导公式练习:精品文档3x [-,]时,求函数y arcsin(cosx)的值域。
例5:求下列函数的反函数 y arcsinx , x [0,1][例6]求下列反三角函数的值: (1) arccos —⑵ arccos(2)= 3—(两种方法)2 624 3 (3) arccos0 + arcta n1 =⑷arctan( . 3)=43 11 (5) arcs in ( — )+ arccos (— )=-222⑹ arcta n(ta nJ=66[例7]用反三角函数值的形式表示下列各式中的x :11(1) cosx , x[0,]解: x arccos-33变式:cosx- ,x [ ,2 ] 解: x12arccos- 33(2) tanx 2,x(,)2 2解: x arctan( 2) 变式:x (一,一)解: xarcta n22 2[例8] (1)已知arcsinx arcsin(1 x),求x 的取值范围。
上海高一数学下册--09—反三角函数与最简三角方程
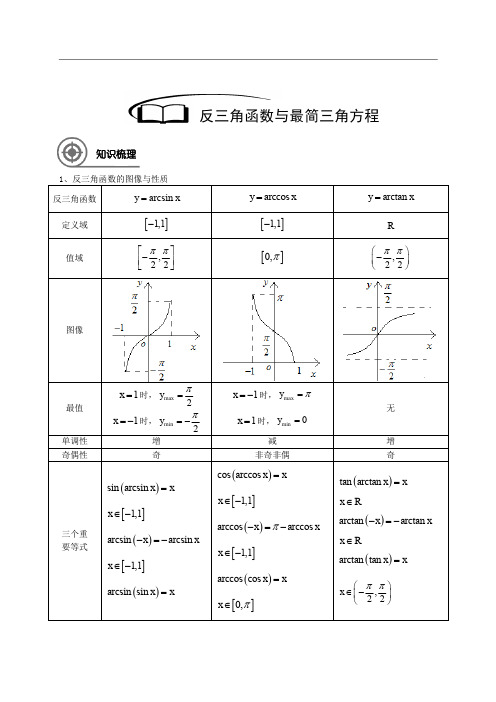
反三角函数与最简三角方程知识梳理2、最简单三角方程的解集:例题解析一、反三角函数的定义【例1】求下列反三角函数的值:(1)arcsin(2-;(2)arcsin1;(3)1arcsin 2(4)arccos2;(5)1arccos()2-; (6)arctan(1)-;(7)arctan 3【难度】★ 【答案】(1)3π-;(2)2π;(3)6π;(4)6π;(5)23π;(6)4π-;(7)6π【例2】已知中,,分别用反正弦函数值、反余弦函数值、反正切函数值表示. 【难度】★ 【答案】415arcsin-π;⎪⎭⎫⎝⎛-41arccos ;15arctan -π;【例3】用反三角函数的形式表示下列角: (1)已知13sin 42x x ππ⎛⎫=- ⎪⎝⎭<<,用反正弦的形式表示x ; (2)已知1cos 042x x π⎛⎫=- ⎪⎝⎭<<,用反余弦的形式表示x ; (3)已知13tan 42x x ππ⎛⎫= ⎪⎝⎭<<,用反正切的形式表示x ; 【难度】★★【答案】(1)1sin4x arc π=+;(2)1cos 4x arc =-;(3)1tan 4x arc π=+ 【解析】此类题目可用两种方法处理:①利用诱导公式转化为反三角函数的运算性质解决;②利用三角函数图像解决,此时应注意原函数与反函数的联系与区别;具体过程略【例4】关于t 的方程()2253172230848t x t x x +++++=有两个不同的实数根,求函数sin y x =的反函数. 【难度】★★【答案】x arcsin y -=π,()sin 4,sin 2x ∈ΔABC 234AB BC CA ===,,B ∠【解析】由()22531723420848x x x ⎛⎫∆=+-⨯++>⎪⎝⎭,得2680x x -+<,解得24x <<函数sin y x =,()2,4x ∈的值域为()sin 4,sin 2 由()sin sin y x x π==-,且,22x πππ⎡⎤-∈-⎢⎥⎣⎦,有arcsin x y π-=, 即arcsin x y π=-将x 与y 互换得到原函数的反函数为:()1arcsin y f x x π-==-,()sin 4,sin 2x ∈【巩固训练】1.求下列反三角函数的值:1)1arcsin 2⎛⎫-⎪⎝⎭2)arcsin 23 3)arccos 21 4)arccos (-23) 5)1arctan 6)arctan (-33)【难度】★ 【答案】(1)6π- ;(2)3π;(3)3π;(4)56π;(5)4π;(6)6π-2.用反正弦函数值表示下列式子中的x : (1)1sin 5x=,(0,)2x π∈; (2)1sin 5x =,(,)2x ππ∈(3)1sin 5x=, x 是第一象限角; (4)1sin 5x =, x R ∈ 【难度】★★ 【答案】(1)1arcsin 5x=;(2)1arcsin 5x π=-;(3)12arcsin 5x k π=+,k Z ∈; (4)12arcsin5x k π=+或12arcsin 5x k ππ=+-,k Z ∈.3.函数3sin 22y x x ππ⎡⎤=∈⎢⎥⎣⎦,,的反函数为 ( )[]A y x x .arcsin =∈-,,11 []B y x x .arcsin =-∈-,,11 []C y x x .arcsin =+∈-π,,11 []D y x x .arcsin =-∈-π,,11【难度】★★ 【答案】D【解析】同上方法,两种皆可.选一种方法作以解释如下:ππ232≤≤x ∴-≤-≤-==ππππ22x x x y ,又sin()sin 由反正先函数的定义,得:arcsin x y π-=,又11y -≤≤,故反函数为:[]arcsin 11y x x π=-∈-,,4.已知1cos 3x=,根据所给范围用反余弦函数值表示x : 1︒x 为锐角 2︒ x 为某三角形内角 3︒ x 为第二象限角 4︒ x R ∈【难度】★★【答案】(1)1arccos 3x =;(2)1arccos 3x =;(3)不存在;(4)12arccos 3x k π=±()k Z ∈5. 1)已知⎪⎭⎫⎝⎛-∈=2,231tan ππx x 且,求x . 2)已知31tan =x 且[]π2,0∈x ,求x 的取值集合. 3)已知1tan 3x =且x R ∈,求x 的取值集合. 【难度】★★【答案】(1)1arctan 3x =;(2)1arctan 3x =或1arctan 3π+; (3)12arctan 3x k π=+或12arctan 3k ππ++()k Z ∈.6.下列命题中,正确命题的个数是( )(1)arcsin y x =的反函数是sin y x = (2)cos ,[,0]y x x π=∈-的反函数是arccos ,[1,1]y x x =-∈-(3)tan ,,23y x x ππ⎛⎫=∈- ⎪⎝⎭的反函数是arctan ,(y x x =∈-∞A .0个B .1个C .2个D . 3个 【难度】★★ 【答案】C二、反三角函数的图像与性质1、反三角函数的图像应用【例5】下列命题中正确的是①函数x y sin =与x y arcsin =互为反函数;②函数x y sin =与x y arcsin =都是增函数; ③函数x y sin =与x y arcsin =都是奇函数;④函数x y sin =与x y arcsin =都是周期函数. 【难度】★ 【答案】③【例6】根据反三角函数的图像比较下列各组数的大小:(1)2arcsin 5与;(2)2arccos 3与2arccos()3-;(3)2arcsin 3与2arccos 3【难度】★【答案】(1)2arcsin5<;(2)2arccos 3<2arccos(3-;(3)2arccos3=Q ,23<,2arcsin 3∴<,22arcsin arccos 33∴<【例7】求解下列不等式中x 的范围: (1)arcsin 1x <;(2)2arccos(21)arccos x x -<; (3)arcsin arccos x x >;(4)()2arccos arccos 0x x -->. 【难度】★★【答案】(1)1sin1x -≤<;(2)112x -≤-<(3)12⎛⎤ ⎥ ⎝⎦;(4)112x -≤<【例8】求下列函数的反函数: (1)arcsin 2y x π=-,[1,1]x ∈-; (2)sin y x =(32x ππ≤≤) (3)2arccos(21)y x =+-; (4)1arctan 32x y = 【难度】★★★【答案】(1)反函数为cos y x =,[0,]x π∈;(2)反函数为arcsin y x π=-,[1,1]x ∈-; (3)反函数为11cos(2)22y x =-+,[2,2]x π∈+;(4)反函数为2tan(3)y x =,(,)66x ππ∈-.【巩固训练】1.若⎥⎦⎤⎝⎛∈653ππ,x arccos ,则x 的取值范围是 . 【难度】★【答案】⎪⎪⎭⎫⎢⎣⎡-2123,2.解不等式:5arccos(2)6x π->. 【难度】★【答案】22⎛⎤+⎥ ⎝⎦【解析】原式即为:arccos(2)arccos(2x ->由arccos y x =为减函数,知12122x x -≤-≤⎧⎪⎨-<⎪⎩解得原不等式的解为:1,22⎡-⎢⎣⎭3.求下列不等式的解集:(1)2arcsin arcsin(1)x x <-;(2)arccos2arccos(1)x x <-;(3)2arctan 2arctan(3)0x x +->.【难度】★★ 【答案】(1)1[1,)2--;(2)11(,]32;(3)(1,3)-2、反三角函数的定义域、值域与最值【例9】写出下列函数的定义域: (1)y = (2)2arcsin()y x x =+ (3)2log arccos 23x y π⎛⎫=- ⎪⎝⎭【难度】★★【答案】(1)[0,1] (2)⎣⎦ (3)[2,1)-【例10】求下列函数的定义域和值域:(1)2arcsin 33x y π=+;(2)y =;(3)arc tan(21)y x =-. 【难度】★★【答案】(1)定义域为[3,3]-,值域为24[,33ππ-;(2)定义域为[1,1)-,值域为)+∞; (3)定义域为R ,值域为(,22ππ-;【例11】函数()21arcsin 2y x x =-的值域是 .【难度】★★ 【答案】⎥⎦⎤⎢⎣⎡-41214arcsin ,π【解析】由22211124411x x x x x ⎧⎛⎫-=--+≤⎪ ⎪⎨⎝⎭⎪-≤-≤⎩⇒2114x x -≤-≤ ⇒()()21111arcsin 1arcsin arcsin 42224x x π-=-≤-≤【例12】求函数xarcsin y 1=的定义域与值域. 【难度】★★【答案】[)+∞,1,⎥⎦⎤ ⎝⎛22,0π 【解析】由⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≤≤-≠01arcsin 1110x x x 得1≥x ,故函数的定义域为[)+∞,1由20,21arcsin 01101ππ≤<∴≤<∴≤<⇒≥y x x x ∴函数的值域为⎥⎦⎤ ⎝⎛22,0π【例13】求函数()21arccos 5arccos ,,12y x x x ⎡⎤=-∈-⎢⎥⎣⎦的最大值和最小值,以及相应的x 的值. 【难度】★★【答案】最大值为0,此时1x =;最小值为241093ππ-,此时12x =-.【例14】函数1arctan arcsin 2y x x =+的值域是 . 【难度】★★【答案】⎥⎦⎤⎢⎣⎡-22ππ, 【解析】函数()1arctan arcsin 2y f x x x ==+在定义域[]1,1-上单调递增, 所以值域为()()1,1,22f f ππ⎡⎤-=-⎡⎤⎣⎦⎢⎥⎣⎦【例15】求函数x x y 2arccos )1arcsin(+-=的值域. 【难度】★★★ 【答案】⎥⎦⎤⎢⎣⎡ππ,6 【解析】先求函数的定义域∴≤≤⇒⎪⎩⎪⎨⎧≤≤-≤≤⇒⎩⎨⎧≤≤-≤-≤-⇒⎪⎩⎪⎨⎧≤≤-,2102121201211111211x x x x x x x 函数的定义域是}⎩⎨⎧≤≤210x x2)1arcsin(6,1121,210ππ≤-≤∴≤-≤∴≤≤x x x 同理:22arccos 0120π≤≤∴≤≤x x∴函数x x y 2arccos )1arcsin(+-=的值域是⎥⎦⎤⎢⎣⎡ππ,6.【巩固训练】1.函数()()arccos arcsin y x a x a =+--(0a >)的定义域D =___________. 【难度】★★【答案】由11110x a x a a -≤+≤⎧⎪-≤-≤⎨⎪>⎩⇔11110a x a a x a a --≤≤-⎧⎪-+≤≤+⎨⎪>⎩。
高中数学反三角函数练习题及讲解

高中数学反三角函数练习题及讲解### 高中数学反三角函数练习题及讲解#### 练习题1. 求值题:计算 \(\sin^{-1}(\frac{1}{2})\) 和 \(\cos^{-1}(\frac{\sqrt{3}}{2})\) 的值。
2. 化简题:将 \(\tan^{-1}\left(\frac{1}{\sqrt{3}}\right) +\sin^{-1}\left(\frac{\sqrt{3}}{2}\right)\) 化简为一个角度。
3. 应用题:在直角三角形ABC中,已知角A的正弦值为\(\frac{3}{5}\),求角A的余弦值。
4. 方程题:解方程 \(\cos^{-1}(x) + \sin^{-1}(x) =\frac{\pi}{4}\),其中 \(x \in [-1,1]\)。
5. 证明题:证明恒等式 \(\tan^{-1}(x) + \cot^{-1}(x) =\frac{\pi}{2}\) 对所有 \(x > 0\) 成立。
6. 综合题:如果 \(\sin(\theta) = \frac{4}{5}\) 且 \(\theta\) 在第一象限,求 \(\cos(\theta)\) 和 \(\tan(\theta)\)。
7. 探索题:探索并证明当 \(x\) 从 0 增加到 1 时,\(\sin^{-1}(x)\) 和 \(x\) 之间的关系。
8. 图形题:在单位圆上,找出 \(\cos^{-1}(\frac{\sqrt{2}}{2})\) 对应的点,并描述该点在坐标系中的位置。
#### 讲解1. 求值题:根据特殊角的三角函数值,我们知道 \(\sin^{-1}(\frac{1}{2}) = 30^\circ\) 或 \(\frac{\pi}{6}\) 弧度,\(\cos^{-1}(\frac{\sqrt{3}}{2}) = 30^\circ\) 或\(\frac{\pi}{6}\) 弧度。
沪教版高中数学高一下册-6.4 反三角函数 -反正弦函数 课件(共14张PPT)
arcsin(x) arcsin x -3 x [1,1].
(4)单调性:是增函数
y
y arcsin x, x [1,1], y [ , ]
2
22
1.5
2 -1
-2
-1
21
0.5
o
-0.5
y sin x, x [ , ], y [1,1] 22
1
2
12
x 3
yx
-1
π 1 -π 2
3π
2 2π
X
- 2π 3π 2
O
ππ
-1
2
*就使得
y
=
sinx,
x
π 2
,π 2
(一一对应)
y 1,1
----这时的正弦函数在上述定义域内就存在反函数.
*感悟: 选择上述区间的科学性、合理性和简便性.
*(1)反正弦函数的定义:
函数 y = 弦函数.
sinx,
x
π 2
,π 2
,y
1,1
的反函数就叫做反正
*记作:
y
arcsinx,x
1,1
,y
π 2
,π 2
.
*(2)当 x 1,1 时,(arcsinx)就表示闭区间
π 2
,π 2
上的一
个唯一确定的角.
〖例题1〗求下列反正弦函数的值.
(1).arcsin 3 ; (2).arcsin0; (3).arcsin( 1 ).
Y
y sinx,x R.
π 1 -π 2
3π
2 2π
X
- 2π 3π 2
O
ππ
-1
反三角函数练习题

反三角函数练习题反三角函数是高中数学中的一个重要概念,它是三角函数的逆运算。
在解决实际问题中,我们经常会遇到需要求解反三角函数的情况。
本文将通过一些具体的练习题来帮助读者更好地掌握反三角函数的应用。
首先,我们来看一个简单的例子。
假设有一个直角三角形,已知斜边的长度为5,对边的长度为3,我们需要求解该直角三角形的一个角的正弦值。
根据三角函数的定义,正弦值等于对边与斜边的比值,即sinθ=对边/斜边。
所以,sinθ=3/5=0.6。
现在我们要求的是角θ的值,即θ=sin^(-1)(0.6)。
这里的sin^(-1)表示反正弦函数,它的作用是求解给定正弦值的角度。
通过计算,我们可以得到θ≈36.87°。
接下来,我们来看一个稍微复杂一些的例子。
假设有一个直角三角形,已知斜边的长度为10,对边的长度为6,我们需要求解该直角三角形的一个角的余弦值。
根据三角函数的定义,余弦值等于邻边与斜边的比值,即cosθ=邻边/斜边。
所以,cosθ=6/10=0.6。
现在我们要求的是角θ的值,即θ=cos^(-1)(0.6)。
这里的cos^(-1)表示反余弦函数,它的作用是求解给定余弦值的角度。
通过计算,我们可以得到θ≈53.13°。
除了求解角度,反三角函数还可以用来求解三角函数的值。
例如,已知一个角的正切值为0.8,我们需要求解该角的正弦值。
根据三角函数的定义,正切值等于对边与邻边的比值,即tanθ=对边/邻边。
所以,tanθ=0.8=对边/邻边。
假设对边为x,邻边为1,根据勾股定理,我们可以得到x^2+1^2=1.64。
解方程得到x≈0.98。
现在我们要求的是角θ的正弦值,即sinθ=对边/斜边。
由于已知斜边的长度为1,我们可以得到sinθ≈0.98/1=0.98。
通过以上的例子,我们可以看到反三角函数在解决实际问题中的重要性。
它不仅可以用来求解角度,还可以用来求解三角函数的值。
在实际应用中,我们经常会遇到需要使用反三角函数的情况,例如在物理学、工程学和计算机图形学等领域。
沪教版高中数学高一下册-6.4 反三角函数 -反正弦函数 课件(共14张PPT)

*(5)反正弦函数的几个常用的条件等式:
(s 1 ( i a ) n r. ) c x , x s i1 , 1 n ;x (a 2r ( ) x c ) - . s air n , x c s 1 , 1 ; inx
( 3a)r. c(ssiin ) n x,x π 2,π 2 .
sinx,
xπ2,π2,y1,1的反函数就叫做反正
*记作: yarc, x s i n 1 , 1 x, y π 2, π 2 .
*(2)当 x1,1时,(arcsinx)就表示闭区间
π 2
,π 2
上的一
个唯一确定的角,其正弦值就等于x.
*(3)反正弦函数 y = arcsinx,在 x1,1上是递增函数; *(4)反正弦函数 y = arcsinx,在 x1,1上是个奇函数.
( 1 a) rc .3 s iπ n ;( 2 a) rc . πs i3 n ;
23
32
(3)a.rcsin12kπ π(k∈Z); 2
(4)a.rcsi(n-π)= -arcsinπ;
3
3
(5 s( ia ) nr .π c 2) sπ 2 i; n (6 s( ia ) nr .c 2 ) s2 i; n 1010
*解法感悟:
反正弦函数的值域为: y = arcsinx
π 2
,π 2
故反正弦函数的值仅能表示在
π 2
,
π 2
上的一个角.
猜想一个恒等式?
反正弦函数y=arcsinx,x∈[-1,1]的图像与性质:
(1)定义域:[-1,1]
(2)值域:
[ , ] 22
(3)奇偶性: 是奇函数,
其图像关于坐标原点对称,
反三角函数及例题

反三角函数及例题
反三角函数是一类特殊的函数,它们的定义域和值域都是实数集,它们的定义域是正弦、余弦和正切函数的值域,而值域是正弦、余弦和正切函数的定义域。
反三角函数包括反正弦函数、反余弦函数和反正切函数,它们的函数图像和正三角函数的函数图像是对称的。
反三角函数的应用非常广泛,它们可以用来解决很多数学问题,比如求解三角形的角度、求解三角形的面积等。
例如,已知三角形的两边长度a和b,求其夹角C的大小,可以用反余弦函数来求解:
C=arccos(a^2+b^2-c^2/2ab)。
另外,反三角函数还可以用来求解微积分中的问题,比如求解曲线的面积、求解曲线的极限等。
例如,已知曲线y=sin(x),求其在区间[0,π]上的面积,可以用反正弦函数来求解:
S=∫0πsin(x)dx=∫0πarcsin(y)dy=π/2。
总之,反三角函数是一类特殊的函数,它们的应用非常广泛,可以用来解决很多数学问题,也可以用来求解微积分中的问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
反三角函数典型例题
例1:在下列四个式子中,有意义的为__________: 解:(4)有意义。
(1)2(2)arcsin 4
π
;(3)sin(arcsin 2);(4)arcsin(sin 2)。
点评:arcsin x ——x [1,1]∈-。
例2:求下列反正弦函数值
(1)3= 解:3π
(2)arcsin0= 解:0 (3)1arcsin()2-= 解:6π- (4)arcsin1= 解:2
π
点评:熟练记忆:0,1
2
±、22±,3,1±的反正弦值。
思考:1sin(arcsin
)24
π
+该如何求?
例3:用反正弦函数值的形式表示下列各式中的x
(1)3sin x ,x [,]22ππ
∈- 解:x =3 变式:x [,]2
π
∈π?
解:x [,]2π
∈π时,π-x [0,]2
π∈,sin(π-x)=sinx 3
∴π-x =3,则x =π-3
变式:x [0,]∈π? 解:x =3或x =π-3
(2)1sin x 4=-,x [,]22ππ∈- 解:1
x arcsin 4
=-
变式:1
sin x 4=-,3x [,2]2π∈π
解:3x [,2]2π∈π时,2π-x [0,]2
π∈,sin(2π-x)=-sinx =1
4
∴2π-x =arcsin 14,则x =2π-arcsin 1
4
点评:当x [,]22ππ
∈-时,x arcsina =;而当x [,]22ππ∉-,可以将角转化到区间[,]22
ππ-上,
再用诱导公式处理对应角之三角比值即可。
练习:
(1)3sin x ,x [,]22ππ
∈- 解:x 3π= (2)3sin x ,x [0,]∈π 解:3x =或3
x =π-(3)3sin x 5=-,3x [,]22ππ∈ 解:3
x arcsin 5
=π+
例4:求函数y 2arcsin(52x)=-的定义域和值域。
解:由152x 1-≤-≤,则x [2,3]∈,arcsin(52x)[,]22ππ-∈-,则y [,]∈-ππ。
变式:y sin x arcsin x =+ 解:x [1,1]∈-,y [sin1,sin1]22
ππ
∈--+
思考:当3x [,]44
ππ
∈-时,求函数y arcsin(cosx)=的值域。
解:当3x [,
]44ππ∈-时2t cos x [2=∈,而y arcsin t =为增函数,则y [,]42
ππ∈-。
例5:求下列函数的反函数 (1) y sin x =,x [,]2
π∈π
解:y [0,1]∈,x [,0]2
π-π∈-且sin(x )sin x y -π=-=-,则x arcsin(y)-π=-,
则x arcsin y =π-,则反函数是1f (x)arcsin x -=π-,x [0,1]∈。
(2) y arcsin x =,x [0,1]∈
解:y [0,]2π∈,x sin y =,则反函数是1f (x)sin x -=,x [0,]2
π∈。
[例6] 求下列反三角函数的值:
(1) 3=6
π
(2) 2arccos()=
34
π
(两种方法) (3) arccos0+arctan1=34π
(4) arctan(3)-=3
π-
(5) arcsin (-12)+arccos (-12
)=2π (6) 5arctan(tan )6π=6π
-
[例7] 用反三角函数值的形式表示下列各式中的x :
(1) 1cos x 3
=,x [0,]∈π 解:1x arccos 3
= 变式:1cos x 3
=-,x [,2]∈ππ
解:1x 2arccos 3
=π- (2) tan x 2,x (,)22
ππ=-∈- 解:x arctan(2)=- 变式:3x (,
)22
ππ
∈ 解:x arctan2=π+
[例8] (1) 已知arcsin x arcsin(1x)≥-,求x 的取值范围。
解:由11x x 1-≤-≤≤,得
1
x 12
≤≤。
(2) arccosx arccos(1x)>-
解:由1x 1x 1-≤<-≤,得10x 2
≤<。
(3) arctan x 3π
>
解:x 3> (4) arccos x 3π> 解:1
1x 2
-≤<
[例9 求y =arcsinx +arctanx 的值域。
解:∵-1≤x ≤1 ∴-
34π≤x ≤34
π ——涉及和函数概念,反正弦、反正切函数单调性
[例10] 求下列各式的值: (1) 2sin(arccos())
解:设2x arccos(=,则2cos x =且x [,]2
π
∈π,则7sin x = (2) 2tan[arccos(]6
π- 解:2
313(31)tan()234313
ππ--+-=
==+- (3) 213
cos (arccos )2
5
解:设3x arccos 5=,则3cos x 5=且x [0,]2π∈,则2x 1cos x 4
cos 225+==
(4) 123
sin[arctan arcsin ]55-
解:设12arctan 5α=,3arcsin 5β=,则12tan 5α=,4sin 5
β=且,(0,)2π
αβ∈,
则1231245333
sin[arctan arcsin ]sin()5513513565-=α-β=⨯-⨯=。
思考:若求11
arctan arctan 23+的值呢?
解:1arc tan 2α=,1arctan 2β=,则1tan 2α=,1tan 3β=且,(0,)2
π
αβ∈,
∵tan()1α+β=,且(0,)α+β∈π,∴4
π
α+β=。
