MOOC慕课 离散数学 电子科技大学 参考答案_作业一
(完整word版)离散数学(第2版,刘爱民)习题解答(1)(1)

附录2 习题答案习题一答案1.1下列各语句中哪些是命题?1) 不是;2) 是;3) 不是;4) 不是;5) 不是;6) 是;7) 是;8) 不是9) 不是;10)是;11)不是;12)是。
1.2 将下列命题符号化。
1) p∧⌝q, p:太阳明亮,q:湿度高;2) q→⌝p, p:明天你看到我,q:我要去深圳。
3) p→q, p:我出校,q:我去图书城;4) q→p , p:你去,q:我去;5) 5.1) p∧q; 5.2) p∧⌝q; 5.3) p∧q; 5.4) p∧⌝q;6) 6.1) p∨q 6.2) ⌝(p ↔q) 6.3) p∧¬q6.4) ¬ (p∧r) 6.5) (p∧q) →r 6.6)¬ (r→ (p∧q))7) p:蓝色和黄色可以调配成绿色;8) ⌝(p↔q), p:李兰现在在宿舍, q:李兰在图书馆里;9) ¬p→¬ q, p:一个人经一事,q:一个人长一智;10) (p∧¬q) →⌝(r↔ s), p:晚上小王做完了做业, q: 晚上小王没有其他事情,r: 晚上小王看电视, s: 晚上小王看电影。
11) ⌝(r↔ s), r:小飞在睡觉, s:小飞在游泳;12) ¬p∧¬q∧r, p:这个星期天我看电视,q: 这个星期天我外出,r:这个星期天我在睡觉。
13) p→q , p:卫星上天了,q:国家强大了;14) p→q, p:今天没有课,q:我呆在图书馆里;15) p→q,p:我去图书城,q:我有时间;16) ¬p→¬q , p:人们辛劳,p: 人们收获1.3 1) 小李家住北大西门外, 他现在坐在公共汽车里看书,没有考虑问题;2) 小李在思考问题, 他没有乘坐公共汽车,也没有看书;3) 小李只要乘坐公共汽车,他就看书或考虑问题;4) 小李乘坐公共汽车,要么看书不考虑问题,要么考虑问题不看书,5) 同4);6) 如果小李家住北大西门外,则他现在没有乘坐公共汽车,没有看书,也没有考虑问题。
慕课 离散数学 电子科技大学 课后习题十 答案

作业参考答案——10-特殊图1.(a)(c)(d)是欧拉图,(a)(b)(c)(d)(e)可以一笔画,(a)(b)(c)(d)(e)(f)(g)是哈密顿图。
2.根据给定条件建立一个无向图G=<V,E>,其中:V={a,b,c,d,e,f,g}E={(u,v)|u,v∈V,且u和v有共同语言}从而图G如下图所示。
abcd e fg将这7个人围圆桌排位,使得每个人都能与他两边的人交谈,就是在图G 中找哈密顿回路,经观察上图可得到两条可能的哈密顿回路,即两种方案:abdfgeca和acbdfgea。
3.证明(法一):根据已知条件,每个结点的度数均为n,则任何两个不相邻的结点v i,v j的度数之和为2n,而图中总共有2n个结点,即deg(v i)+ deg(v j)⩾2n,满足哈密顿图的充分条件,从而图中存在一条哈密顿回路,当然,这就说明图G是连通图。
证明(法二):用反证法,假设G不是连通图,设H是G的一个连通分支,由于图G是简单图且每个结点的度数为n,则子图H与G-H中均至少有n+1个结点。
所以G的结点数大于等于2n+2,这与G中结点数为2n矛盾。
所以假设不成立,从而G是连通图。
4.将n位男士和n位女士分别用结点表示,若某位男士认识某位女士,则在代表他们的结点之间连一条线,得到一个偶图G,假设它的互补结点子集V1、V2分别表示n位男士和n位女士,由题意可知V1中的每个结点度1数至少为2,而V2中的每个结点度数至多为2,从而它满足t条件t=1,因此存在从V1到V2的匹配,故可分配。
5.此平面图具有五个面,如下图所示。
ab c d ef gr1r2r3r4r5•r1,边界为abca,D(r1)=3;•r2,边界为acga,D(r2)=3;•r3,边界为cegc,D(r3)=3;•r4,边界为cdec,D(r4)=3;•r5,边界为abcdefega,D(r5)=8;无限面6.设该连通简单平面图的面数为r,由欧拉公式可得,6−12+r=2,所以r=8,其8个面分别设为r1,r2,r3,r4,r5,r6,r7,r8。
离散数学试题与答案试卷一
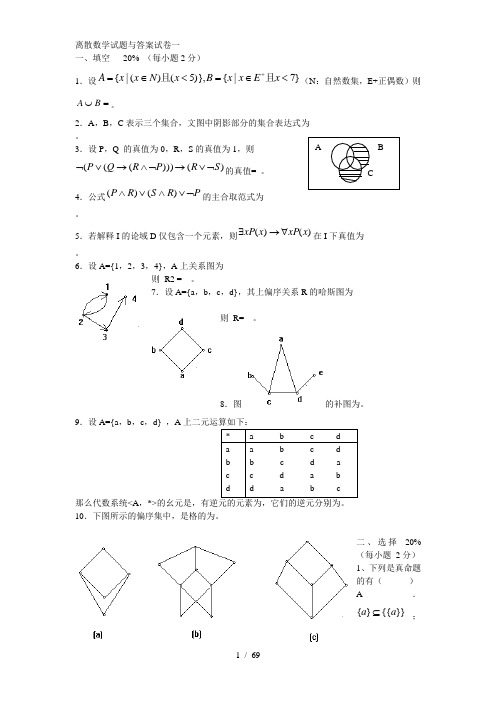
试卷二答案:
填空20%(每小题2分)
1、 ; 2、T 3、 4、R={<2,2>,<2,3>,<2,4>,<2,5>,<2,6>,<3,2>,<3,3>,<3,4>,<3,5>,<3,6>,<4,5>,<4,6>,<5,2>,<5,3>,<5,4>,<5,5>,<5,6>}; 5、R={<1,2>,<1,3>,<2,1>};R={<1,1>,<2,2>,<3,3>} 6、a;否;有7、Klein四元群;循环群8、B 9、 ;图中无奇度结点且连通10、渗釤呛俨匀谔鱉调硯錦鋇絨钞。
前提: 、 结论: ……3分
① P
② P
③ US②
④ T①I
⑤ T③④I
⑥ T①I
⑦ T⑤⑥I
⑧ EG⑦……11分
3、10分
证明:
。
4、8分
证明:设G中两奇数度结点分别为u和v,若u,v不连通,则G至少有两个连通分支G1、G2,使得u和v分别属于G1和G2,于是G1和G2中各含有1个奇数度结点,这与图论基本定理矛盾,因而u,v一定连通。铙誅卧泻噦圣骋贶頂廡缝勵罴。
选择20%(每小题2分)
题目
1
2
3
4
5
6
7
8
9
10Biblioteka 答案B、DD;DD
B
D
A
离散数学习题答案.docx

精品文档离散数学习题答案习题一及答案:( P14-15 )14、将下列命题符号化:( 5)李辛与李末是兄弟解:设 p:李辛与李末是兄弟,则命题符号化的结果是p( 6)王强与刘威都学过法语解:设 p:王强学过法语; q:刘威学过法语;则命题符号化的结果是p q ( 9)只有天下大雨,他才乘班车上班解:设 p:天下大雨; q:他乘班车上班;则命题符号化的结果是q p( 11)下雪路滑,他迟到了解:设 p:下雪; q:路滑; r :他迟到了;则命题符号化的结果是( p q)r15、设 p: 2+3=5.q:大熊猫产在中国 .r:太阳从西方升起 .求下列复合命题的真值:( 4)(p q r )(( p q)r )解: p=1, q=1,r=0 ,(p q r )(110)1,((p q)r )((11)0)(00)1(p q r )(( p q)r ) 1 1119、用真值表判断下列公式的类型:( 2)( p p)q解:列出公式的真值表,如下所示:p q p qp) ( p p)q( p001111011010100101110001由真值表可以看出公式有 3 个成真赋值,故公式是非重言式的可满足式。
20、求下列公式的成真赋值:精品文档( 4)( p q)q解:因为该公式是一个蕴含式,所以首先分析它的成假赋值,成假赋值的条件是:( p q)1p0q0q0所以公式的成真赋值有: 01,10, 11。
习题二及答案:( P38)5、求下列公式的主析取范式,并求成真赋值:( 2)(p q) (q r )解:原式( p q) q r q r( p p) q r( p q r ) ( p q r )m3m7,此即公式的主析取范式,所以成真赋值为011, 111。
6、求下列公式的主合取范式,并求成假赋值:( 2)( p q) ( p r )解:原式( pp r ) ( p q r )( p q r )M 4,此即公式的主合取范式,所以成假赋值为 100。
离散数学形考任务1-7试题及答案完整版

2017年11月上交的离散数学形考任务一本课程的教学内容分为三个单元,其中第三单元的名称是(A ).选择一项:A. 数理逻辑B. 集合论C. 图论D. 谓词逻辑题目2答案已保存满分10.00标记题目题干本课程的教学内容按知识点将各种学习资源和学习环节进行了有机组合,其中第2章关系与函数中的第3个知识点的名称是(D ).选择一项:A. 函数B. 关系的概念及其运算C. 关系的性质与闭包运算D. 几个重要关系题目3答案已保存满分10.00标记题目题干本课程所有教学内容的电视视频讲解集中在VOD点播版块中,VOD点播版块中共有(B)讲.选择一项:A. 18B. 20C. 19D. 17题目4答案已保存满分10.00标记题目题干本课程安排了7次形成性考核作业,第3次形成性考核作业的名称是( C).选择一项:A. 集合恒等式与等价关系的判定B. 图论部分书面作业C. 集合论部分书面作业D. 网上学习问答题目5答案已保存满分10.00标记题目题干课程学习平台左侧第1个版块名称是:(C).选择一项:A. 课程导学B. 课程公告C. 课程信息D. 使用帮助题目6答案已保存满分10.00标记题目题干课程学习平台右侧第5个版块名称是:(D).选择一项:A. 典型例题B. 视频课堂C. VOD点播D. 常见问题题目7答案已保存满分10.00标记题目题干“教学活动资料”版块是课程学习平台右侧的第( A )个版块.选择一项:A. 6B. 7C. 8D. 9题目8答案已保存满分10.00标记题目题干课程学习平台中“课程复习”版块下,放有本课程历年考试试卷的栏目名称是:(D ).选择一项:A. 复习指导B. 视频C. 课件D. 自测请您按照课程导学与章节导学中安排学习进度、学习目标和学习方法设计自己的学习计划,学习计划应该包括:课程性质和目标(参考教学大纲)、学习内容、考核方式,以及自己的学习安排,字数要求在100—500字.完成后在下列文本框中提交.解答:学习计划学习离散数学任务目标:其一是通过学习离散数学,使学生了解和掌握在后续课程中要直接用到的一些数学概念和基本原理,掌握计算机中常用的科学论证方法,为后续课程的学习奠定一个良好的数学基础;其二是在离散数学的学习过程中,培养自学能力、抽象思维能力和逻辑推理能力,解决实际问题的能力,以提高专业理论水平。
国开(中央电大)本科《离散数学(本)》网上形考(任务一至三)试题及答案

国开(中央电大)本科《离散数学(本)》网上形考(任务一至三)试题及答案国开(中央电大)本科《离散数学(本)》网上形考(任务一至三)试题及答案说明:适用于计算机科学与技术本科国开平台网上形考。
形考任务一试题及答案题目为随机,用查找功能(Ctrl+F)搜索题目[题目]若集合A={a,{a},{1,2}},则下列表述正确的是().[答案]{a}A[题目]若集合A={1,2},B={1,2,{1,2}},则下列表述正确的是().[答案]AB,且AB[题目]若集合A={2,a,{a},4},则下列表述正确的是().[答案]{a}A[题目]设集合A={1,2,3},B={3,4,5},C={5,6,7},则A∪B–C=().[答案]{1,2,3,4}[题目]设集合A={a},则A的幂集为().[答案]{,{a}}[题目]设集合A={1,a},则P(A)=().[答案]{,{1},{a},{1,a}}[题目]若集合A的元素个数为10,则其幂集的元素个数为().[答案]1024[题目]设A、B是两个任意集合,则A-B=().[答案]AB[题目]设集合A={2,4,6,8},B={1,3,5,7},A到B 的关系R={<x,y>|y=x+1},则R=().[答案]{<2,3>,<4,5>,<6,7>}[题目]集合A={1,2,3,4,5,6,7,8}上的关系R={<x,y>|x+y=10且x,yA},则R 的性质为().[答案]对称的[题目]集合A={1,2,3,4}上的关系R={<x,y>|x=y且x,yA},则R的性质为().[答案]传递的[题目]如果R1和R2是A上的自反关系,则R1∪R2,R1∩R2,R1-R2中自反关系有()个.[答案]2[题目]设集合A={1,2,3,4}上的二元关系R={<1,1>,<2,2>,<2,3>,<4,4>},S={<1,1>,<2,2>,<2,3>,<3,2>,<4,4>},则S是R的()闭包.[答案]对称[题目]设A={1,2,3,4,5,6,7,8},R是A上的整除关系,B={2,4,6},则集合B的最大元、最小元、上界、下界依次为().[答案]无、2、无、2[题目]设集合A={1,2,3,4,5},偏序关系是A上的整除关系,则偏序集<A,>上的元素5是集合A的().[答案]极大元[题目]设集合A={1,2,3,4,5}上的偏序关系的哈斯图如图所示,若A的子集B={3,4,5},则元素3为B的().[答案]最小上界[题目]设A={a,b,c},B={1,2},作f:A→B,则不同的函数个数为().[答案]8[题目]设A={a,b},B={1,2},C={4,5},从A到B的函数f={<a,1>,<b,2>},从B到C的函数g={<1,5>,<2,4>},则下列表述正确的是().[答案]g°f={<a,5>,<b,4>}[题目]设集合A={1,2,3}上的函数分别为:f={<1,2>,<2,1>,<3,3>},g={<1,3>,<2,2>,<3,2>},h={<1,3>,<2,1>,<3,1>},则h=().[答案]f◦g[题目]设函数f:N→N,f(n)=n+1,下列表述正确的是().[答案]f是单射函数判断题[题目]设集合A={1,2,3},B={2,3,4},C={3,4,5},则A∩(C-B)={1,2,3,5}.()[答案]错[题目]设集合A={1,2,3},B={1,2},则P(A)-P(B)={{3},{1,3},{2,3},{1,2,3}}.()[答案]对[题目]空集的幂集是空集.()[答案]错[题目]设集合A={1,2,3},B={1,2},则A×B={<1,1>,<1,2>,<2,1>,<2,2>,<3,1>,<3,2>}.()[答案]对[题目]设A={1,2},B={a,b,c},则A×B的元素个数为8.()[答案]错[题目]设集合A={0,1,2,3},B={2,3,4,5},R是A到B的二元关系,则R的有序对集合为{<2,2>,<2,3>,<3,2>,<3,3>}.()[答案]对[题目]设集合A={1,2,3,4},B={6,8,12},A到B的二元关系R=那么R-1={<6,3>,<8,4>}.()[答案]对[题目]设集合A={a,b,c,d},A上的二元关系R={<a,b>,<b,a>,<b,c>,<c,d>},则R具有反自反性质.()[答案]对[题目]设集合A={a,b,c,d},A上的二元关系R={<a,a>,<b,b>,<b,c>,<c,d>},若在R中再增加两个元素<c,b>,<d,c>,则新得到的关系就具有反自反性质.()[答案]错[题目]若集合A={1,2,3}上的二元关系R={<1,1>,<1,2>,<3,3>},则R是对称的关系.()[答案]错[题目]若集合A={1,2,3}上的二元关系R={<1,1>,<2,2>,<1,2>},则R是自反的关系.()[答案]错[题目]设A={1,2}上的二元关系为R={<x,y>|xA,yA,x+y=10},则R的自反闭包为{<1,1>,<2,2>}.()[答案]对[题目]设R是集合A上的等价关系,且1,2,3是A中的元素,则R中至少包含<1,1>,<2,2>,<3,3>等元素.()[答案]对[题目]设A={1,2,3},R={<1,1>,<1,2>,<2,1>,<3,3>},则R是等价关系.()[答案]错[题目]如果R1和R2是A上的自反关系,则、R1∪R2、R1∩R2是自反的.()[答案]对[题目]若偏序集<A,R>的哈斯图如图二所示,则集合A的最大元为a,极小元不存在.()[答案]错[题目]设集合A={1,2,3,4},B={2,4,6,8},下列关系f={<1,4>,<2,2,>,<4,6>,<1,8>}可以构成函数f:.()[答案]错[题目]设集合A={1,2,3,4},B={2,4,6,8},下列关系f={<1,8>,<2,6>,<3,4>,<4,2,>}可以构成函数f:.()[答案]对[题目]设A={a,b},B={1,2},C={a,b},从A到B的函数f={<a,1>,<b,2>},从B到C的函数g={<1,b>,<2,a>},则g°f={<1,2>,<2,1>}.()[答案]错[题目]设A={2,3},B={1,2},C={3,4},从A到B的函数f={<2,2>,<3,1>},从B到C的函数g={<1,3>,<2,4>},则Dom(g°f)={2,3}.()[答案]对形考任务二试题及答案题目为随机,用查找功能(Ctrl+F)搜索题目单选题[题目]设图G=<V,E>,v∈V,则下列结论成立的是().[答案][题目]设无向图G的邻接矩阵为,则G的边数为().[答案]5[题目]设无向图G的邻接矩阵为,则G的边数为().[答案]7[题目]已知无向图G的邻接矩阵为,则G有().[答案]5点,7边[题目]如图一所示,以下说法正确的是().[答案]{(d,e)}是边割集[题目]如图二所示,以下说法正确的是().[答案]e是割点[题目]图G如图三所示,以下说法正确的是().[答案]{b,c}是点割集[题目]图G如图四所示,以下说法正确的是().[答案]{(a,d),(b,d)}是边割集[题目]设有向图(a)、(b)、(c)与(d)如图五所示,则下列结论成立的是().[答案](a)是强连通的[题目]设有向图(a)、(b)、(c)与(d)如图六所示,则下列结论成立的是().[答案](d)只是弱连通的[题目]无向图G存在欧拉回路,当且仅当().[答案]G连通且所有结点的度数全为偶数[题目]无向完全图K4是().[答案]汉密尔顿图[题目]若G是一个汉密尔顿图,则G一定是().[答案]连通图[题目]若G是一个欧拉图,则G一定是().[答案]连通图[题目]G是连通平面图,有v个结点,e条边,r个面,则r=().[答案]e-v+2[题目]无向树T有8个结点,则T的边数为().[答案]7[题目]无向简单图G是棵树,当且仅当().[答案]G连通且边数比结点数少1[题目]已知一棵无向树T中有8个顶点,4度、3度、2度的分支点各一个,T的树叶数为().[答案]5[题目]设G是有n个结点,m条边的连通图,必须删去G的()条边,才能确定G的一棵生成树.[答案]m-n+1[题目]以下结论正确的是().[答案]树的每条边都是割边判断题[题目]已知图G中有1个1度结点,2个2度结点,3个3度结点,4个4度结点,则G的边数是15.()[答案]对[题目]设G是一个图,结点集合为V,边集合为E,则.()[答案]对[题目]设图G如图七所示,则图G的点割集是{f}.()[答案]错[题目]若图G=<V,E>,其中V={a,b,c,d},E={(a,b),(a,d),(b,c),(b,d)},则该图中的割边为(b,c).()[答案]对[题目]无向图G存在欧拉回路,当且仅当G连通且结点度数都是偶数.()[答案]对[题目]如果图G是无向图,且其结点度数均为偶数,则图G存在一条欧拉回路.()[答案]错[题目]如图八所示的图G存在一条欧拉回路.()[答案]错[题目]设完全图K有n个结点(n2),m条边,当n为奇数时,Kn中存在欧拉回路.()[答案]对[题目]汉密尔顿图一定是欧拉图.()[答案]错[题目]设G=<V,E>是具有n个结点的简单图,若在G中每一对结点度数之和小于n-1,则在G中存在一条汉密尔顿路.()[答案]错[题目]若图G=<V,E>中具有一条汉密尔顿回路,则对于结点集V的每个非空子集S,在G中删除S中的所有结点得到的连通分支数为W,则S中结点数|S|与W满足的关系式为W|S|.()[答案]对[题目]如图九所示的图G不是欧拉图而是汉密尔顿图.()[答案]对[题目]设G是一个有7个结点16条边的连通图,则G为平面图.()[答案]错[题目]设G是一个连通平面图,且有6个结点11条边,则G有7个面.()[答案]对[题目]设连通平面图G的结点数为5,边数为6,则面数为4.()[答案]错[题目]结点数v与边数e满足e=v的无向连通图就是树.()[答案]错[题目]设图G是有6个结点的连通图,结点的总度数为18,则可从G中删去4条边后使之变成树.()[答案]对[题目]无向图G的结点数比边数多1,则G是树.()[答案]错[题目]设图G是有5个结点的连通图,结点度数总和为10,则可从G中删去6条边后使之变成树.()[答案]错[题目]两个图同构的必要条件是结点数相等;边数相等;度数相同的结点数相等.()[答案]对形考任务三试题及答案题目为随机,用查找功能(Ctrl+F)搜索题目选择题[题目]设P:我将去打球,Q:我有时间.命题“我将去打球,仅当我有时间时”符号化为().[答案]P→Q[题目]设命题公式G:G:┐p→(Q∧R),则使公式G取真值为1的P,Q,R赋值分别是().[答案]1,0,0[题目]命题公式(P∨Q)→R的析取范式是().[答案](┐P∧┐Q)∨R[题目]命题公式(P∨Q)的合取范式是().[答案](P∨Q)[题目]命题公式┐(p→Q)的主析取范式是().[答案]P∧┐Q[题目]命题公式P→Q的主合取范式是().[答案]┐P∨Q[题目]下列等价公式成立的为().[答案]P→(┐Q→P)<=>┐P→(P→Q)[题目]下列等价公式成立的为().[答案]┐P∧P<=>┐Q∧Q[题目]下列公式成立的为().[答案]┐P∧(P∨Q)=>Q[题目]下列公式中()为永真式.[答案]┐A∧┐B↔┐(A∨B)[题目]下列公式()为重言式.[答案]Q→(P∨(P∧Q))↔Q→P[题目]命题公式(P∨Q)→Q为()[答案]可满足式[题目]设A(x):x是书,B(x):x是数学书,则命题“不是所有书都是数学书”可符号化为().[答案][题目]设A(x):x是人,B(x):x是教师,则命题“有人是教师”可符号化为().[答案][题目]设个体域为整数集,则公式的解释可为().[答案]对任一整数x存在整数y满足x+y=0[题目]表达式中的辖域是().[答案][题目]谓词公式(∀x)(A(x)→B(x)∨C(x,y))中的()。
最新电大离散数学形考作业任务0107网考试题及答案

最新电大《离散数学》形考作业任务01-07网考试题及答案100%通过考试说明:《离散数学》形考共有7个任务。
任务3、任务五、任务7是主观题,任务二、任务4、任务6是客观题,任务二、任务4、任务6需在考试中多次抽取试卷,直到显现02任务_0001或02任务_0009、04任务_0001或04任务_0009、06任务_0001或06任务_0009试卷,就能够够依照该套试卷答案答题。
做考题时,利用本文档中的查找工具,把考题中的关键字输到查找工具的查找内容框内,就可迅速查找到该题答案。
本文库还有其他教学考一体化答案,敬请查看。
01任务一、单项选择题(共 8 道试题,共 80 分。
)1. 本课程的教学内容分为三个单元,其中第三单元的名称是().A. 数理逻辑B. 集合论C. 图论D. 谓词逻辑2. 本课程的教学内容按知识点将各类学习资源和学习环节进行了有机组合,其中第2章关系与函数中的第3个知识点的名称是().A. 函数B. 关系的概念及其运算C. 关系的性质与闭包运算D. 几个重要关系3. 本课程所有教学内容的电视视频讲解集中在VOD点播版块中,VOD点播版块中共有()讲.A. 18B. 20C. 19D. 174. 本课程安排了7次形成性考核作业,第3次形成性考核作业的名称是().A. 集合恒等式与等价关系的判定B. 图论部份书面作业C. 集合论部份书面作业D. 网上学习问答5. 课程学习平台左侧第1个版块名称是:().A. 课程导学B. 课程公告C. 课程信息D. 利用帮忙6. 课程学习平台右边第5个版块名称是:().A. 典型例题B. 视频课堂C. VOD点播D. 常见问题7. “教学活动资料”版块是课程学习平台右边的第()个版块.A. 6B. 7C. 8D. 98. 课程学习平台中“课程温习”版块下,放有本课程历年考试试卷的栏目名称是:().A. 温习指导B. 视频C. 课件D. 自测。
国家开放大学《离散数学(本)》形考任务1-3参考答案

14.设 A={1,2,3},R={<1,1>,<1,2>,<2,1>,<3,3>},则 R 是等价关系。
(×)
15.如果 R1 和 R2 是 A 上的自反关系,则 R1-1 、R1 ∪R2 、R1 ∩R2 是自反的。
(√)
16.若偏序集<A,R>的哈斯图如图二所示,则集合 A 的最大元为 a,极小元
1
1 ,则 G 有(
1
0
)。
A.{d}是点割集
B.e 是割点
C.{b,e}是点割集
D.{a,e}是点割集
7.图 G 如图三所示,以下说法正确的是(
)。
A.{b,d}是点割集
B.{b,c}是点割集
C.a 是割点
D.{c}是点割集
8.图 G 如图四所示,以下说法正确的是(
)。
A.{(a,d)}是边割集
为(b,c)。(√)
5.无向图 G 存在欧拉回路,当且仅当 G 连通且结点度数都是偶数。(√)
6.如果图 G 是无向图,且其结点度数均为偶数,则图 G 存在一条欧拉回路。
(×)
7.如图八所示的图 G 存在一条欧拉回路。(×)
8.设完全图 Kn 有 n 个结点(n≥2),m 条边,当 n 为奇数时,Kn 中存在欧拉
5.设 A={1,2},B={a,b,c},则 A×B 的元素个数为 8。(×)
6.设集合 A={0,1,2,3},B={2,3,4,5},R 是 A 到 B 的二元关系,R={(x,y)| x∈A 且
y∈B 且 x,y∈A∩B}则 R 的有序对集合为{<2,2>,<2,3>,<3,2>,<3,3>}。
