缓和曲线长度与超高过渡段长度表
缓和曲线)计算公式

高速公路的线路(缓和曲线)计算公式一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z,y Z为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z,y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:S Z④变坡点高程:H Z⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:。
公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式

公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z,y Z为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z,y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:S Z④变坡点高程:H Z⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x<0时sgn(x)=-1,当x>0时sgn(x)=1,当x=0时sgn(x)=0。
超高缓和段设计长度和过渡方式与适用条件研究

超高缓和段设计长度和过渡方式与适用条件研究1 超高缓和段长度1.1 超高渐变率的选用超高渐变率应控制在一定的数值范围内。
超高渐变率太大,路容不美观,乘客不舒适;太小,排水困难。
我国路线规范针对四车道以下公路规定了不同设计速度时最大超高渐变率。
对六车道和八车道高速公路的超高渐变率没有明确规定,美国AASHO对于多车道路面超高缓和段的长度规定为:三车道公路的超高缓和段长度,为双车道公路长度的1.2倍;四车道公路的超高缓和段长度,为双车道公路长度的1.5倍;六车道公路的超高缓和段长度,为双车道公路长度的2.0倍。
超高缓和段相同时,至旋转轴距离越大,超高渐变率越大;同时路幅扭转的角速度也不同,即旋转路幅越大,超高渐变率的值越大。
出于排水考虑,车道横坡度由-2%(或-1.5%)过渡到2%(或1.5%)的路段超高渐变率p不得小于1/330。
我国未对六车道和八车道高速公路的最小超高渐变率进行规定。
若取相同渐变率,会造成滞水路段长度过长,故设计多车道高速公路,从标准路拱过渡到零坡时,一般取四车道高速公路超高渐变率为1/330时所对应的路面扭转角速度(即超高缓和段长度),反算六车道和八车道的超高渐变率,当超高渐变率大于规范所规定的最大值时,取规范规定的最大值。
例如设计速度为120km/h 的高速公路,六车道从标准路拱过渡至0路段的最小超高渐变率取1/250;八车道的取1/200。
既保证路面排水的通畅性,又保证行车的舒适性。
此外,当超高渐变率大于1/250时,应在外侧路缘折角部分加入缓冲竖曲线,使超高过渡视觉效果连续。
1.2 超高渐变率影响因素:①控制路面外侧边缘的加速度(或路面内侧边缘的降低速度)旋转角度在P相同时,因超高形式不同其值不同。
由试验知,绕中轴旋转时的超高旋转角速度ω取值0.032—0.048(rad/s)时,或绕内边轴旋转时的超高旋转角速度ω取值在0.016—0.024(rad/s)时,司乘人员无不舒适之感。
超高设置与计算说明

超高设置与超高加宽计算说明一、超高设置1、《JTG D20-2006公路路线设计规范》取消了《JTJ 011-94公路路线设计规范》中的“圆曲线半径与超高值”表,各圆曲线半径所设置的超高值应根据设计速度、圆曲线半径、公路条件、自然条件等经计算确定。
路线程序根据《JTG D20-2006公路路线设计规范》送审稿提供的“圆曲线半径与超高值”表编制了圆曲线半径、设计速度等计算超高值的表格模板。
用户可以结合项目情况修改表格模板,该表格模板存储在路线程序安装目录下的“superelevation”文件夹中。
表5 最大超高值10%2、在超高自动计算前,用户可以先进行超高设置,程序中的命令:[数据处理]→[超高分段] →[超高值设置],设置窗体如图1图1 超高值设置3、路线程序根据最大超高值自动选用相应的表,若用户需要修改表格模板可点击“浏览”按钮弹出表格模板,然后修改表格模板。
点击“确定”按钮后,程序就会把用户设置的超高值存入数据库,超高自计算就会以用户设置的超高值进行计算。
若用户不进行超高设置,程序会按程序内默认的超高值进行计算。
4、表格模板格式不能修改,只能修改模板中的数据。
二、超高计算命令:[数据处理]→[超高分段] →[自动计算]图2 超高自动计算1、超高自动计算窗体说明(如图2)1、1 当选中窗体中的“全缓和曲线范围内超高”,程序不考虑渐变率计算的超高缓和长度,默认超高在缓和曲线上完成;反之考虑渐变率计算的超高缓和长度。
1、2 当选中窗体中的“S型曲线YH(HY)全超高”,程序认为S型曲线YH(HY)刚好达到全超高,然后向GQ点推;反之由GQ点向YH(HY)推。
1.3 当选中窗体中的“S型曲线公切点横坡0%”,则公切点超高为0%,若未选中,则公切点为正常路拱。
2、超高自动计算时,线元划分成如下单元进行计算:2、1直线——圆曲线和圆曲线——直线(1)中间没有缓和曲线,超高缓和长度直线和圆曲线上各一半。
道路曲线高程计算公式

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道) 一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:。
公路超高过渡段长度计算表
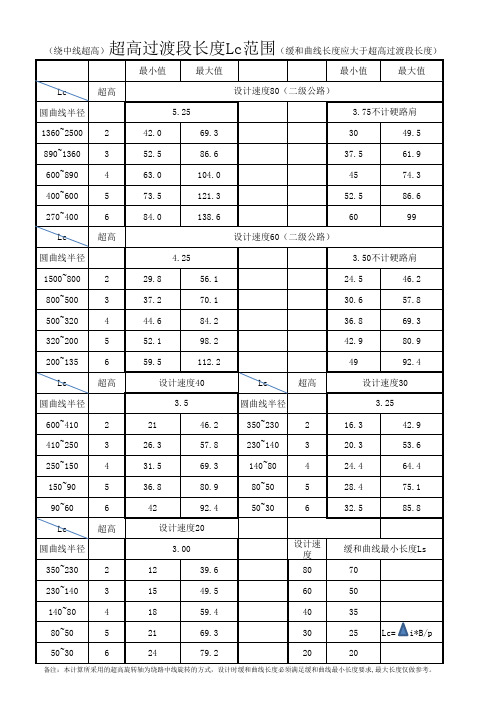
60
50
140~80
4
18
59.4
40
35
80~50
5
21
69.3
30
25
Lc= i*B/p
50~30
6
24
79.2
20
20
备注:本计算所采用的超高旋转轴为绕路中线旋转的方式,设计时缓和曲线长度必须满足缓和曲线最小长度要求,最大长度仅做参考。
超高过渡段长度Lc范围 (计外侧硬路肩)
(缓和曲线长度应大于超高过渡段长度)
152
250.8
Lc
超高
设计速度60(一级公路,0.5m+3.75*2+3) 设计速度60(一级公路,0.5m+3.75*2+1.5)
圆曲线半径
11
绕中分带边缘
11
1500~800
2
77
145.2
1500~800
2
77
145.2
800~500
3
96.3
181.5
800~500
3
96.3
181.5
500~320
Lc
超高
设计速度60(一级公路,0.5m+3.75*2+3) 设计速度60(一级公路,0.5m+3.75*2+1.5)
圆曲线半径
8.5
绕中分带边缘
8.5
1500~800
2
59.5
112.2
1500~800
2
59.5
112.2
800~500
3
74.4
140.3
800~500
3
74.4
140.3
超高计算——精选推荐
1.超高的过渡方式由于本设计的道路等级为高速公路,所以超高的过渡为有中间带道路的超高过渡。
有中间带的道路行车道,在直线路段的横断面均为以中间带为脊向两侧倾斜的路拱。
路面要由双向倾斜的路拱形式过渡到具有超高的单向倾斜的超高形式,外侧逐渐抬高,在抬高过程中,行车道外侧是绕中间带旋转的,若超高横坡度等于路拱横坡,则直至与内侧横坡相等为止。
本设计采用的是绕中央分隔带边缘旋转。
2.超高过渡段长度的确定(1) 超高缓和段的长度按下式计算:p iL c∆=/ B式中:cL——超高缓和段长度(m);β——旋转轴至行车道(设路缘带时为路缘带)外侧边缘的宽度(m);i∆——超高坡度与路拱坡度的代数差,%P ——超高渐变率,即旋转轴线与行车道(设路缘带时为路缘带)外侧边缘线之间的相对坡度;为了行车的舒适,超高过渡段应不小于按上式计算的长度。
但从利于排除路面降水而考虑,横坡度由2%过渡到0%路段的超高渐变率不得小于1/200,即超高不该设置的太长。
一般情况下,在确定缓和曲线长度时,已经考虑了超高过渡段所需的最短长度,故一般取超高过渡段长度L与缓和曲线长度s L相等。
c本设计中,圆曲线半径均小于不设超高的最小圆曲线半径,因此都设置了超高过渡段。
3、资料整理已知本路段在一般地区设计为高速四车道,设计速度为100km/h,R分别为1500m、1600m、转角左为29°46′53.9″,转角右为22°58′40.2″,缓和曲线Ls分别为250 m、220 m,路拱横坡度为2%。
3.1、公路超高渐变值3.2、圆曲线和超高值3.3、各公路等级路基宽度计算其超高过渡段长度。
平曲线半径R =1500m 。
高速公路该公路设计速度100km/h ,由R=1500 m ,s L =250 m 可知超高值为3%,故采用绕中央分隔带边缘旋转,超高渐变率取1/225,旋转轴边缘至行车道边缘(若有路缘带,至路缘带边缘)。
即据规范确定路拱横坡%2=g i ,土路肩坡度为%3=j i ,由此确定缓和段曲线长度:25.146225/1%)2%3(13'=+⨯=∆⨯=PiC B L 取150m缓和曲250=S L >150=C L 取250=S L 时,横坡从路拱坡度(-2%)过渡到超高横坡3%的超高渐变率:3841250%)2%3(131=+⨯=P <3301 又因为不设超高的半径为4000,此点距ZH 点距离为:L=75.934000250150040002=⨯=A 根据此条件确定的超高缓和段长度为:250-93.75=156m ,此时横坡从路拱坡度(-2%)过渡到超高横坡(2%)时的超高渐变率: P= 2401156%)2%3(13=+⨯>3301(2) 计算各桩号处超高值:b j1j2b B1b b 1Bb j2j1b 图3.4 超高计算点位置图图中: B ——行车道宽度;1b ——内侧路缘带; 2b ——外侧路缘带;1j b ——硬路肩宽度; 2j b ——土路肩宽度; g i ——路拱横坡度; j i ——土路肩横坡度;c i ——超高横坡度。
浅析路线设计缓和曲线合理长度取值范围
浅析路线设计缓和曲线合理长度取值范围0 引言缓和曲线是公路平面线形设计中采用的最常用的线形之一。
缓和曲线是在直线和圆曲线之间插入一段曲率半径由+∞逐步渐变为R的回旋线,不仅符合汽车转弯时的行车轨迹,而且使公路的平面线形顺适美观,具有良好的视觉效果和心理作用感。
在缓和曲线设计中,缓和曲线缓和段长度的取值是影响道路平面线形视觉质量的重要因素之一。
如果缓和曲线缓和段长度取值太短,不仅不能起到曲率渐变的作用,而且缓和段与剩余圆曲线的衔接和搭配极不协调,行车视觉效果比较差;如果缓和曲线缓和段长度取值太长,无论从线形组合效果还是弯道超高和加宽设计方面都存在着较大的不足。
因此,合理确定和设计缓和曲线缓和段的长度,是平面缓和曲线线形设计需要解决的重要问题之一。
目前无论是专业参考资料,还是公路线形设计使用的设计软件中,都没有给出合理确定缓和段长度的计算方法,只是按照《公路工程技术标准》(以下简称《标准》)的设计要求,取大于或等于缓和曲线最小缓和段长度即可,而没有考虑不同平曲线半径条件下缓和曲线缓和段长度的合理取值。
缓和段长度对平面线形质量的影响分析在平面缓和曲线设计中,缓和曲线缓和段长度的取值将直接影响到平面线形的视觉质量和行车效果。
道路平面线形由由直线和曲线组合而成,曲线又分为曲率半径为常数的圆曲线和曲率半径为变数的缓和曲线两种。
对于缓和曲线的取值范围,公路相关规范中均只有最小值的界定,而对于最大值,规范并没有明确,本文根据驾驶员反应操作3s行程、离心加速度变化、考虑超高缓和率所需长度、考虑视觉和线形美学所需长度及公路路线设计规范及平纵组合等原则进行最值拟定,为公路设计提供一定的理论价值。
1 缓和曲线的设置设置缓和曲线的目的在于通过曲率的逐渐变化,适应汽车转向操作的行使轨迹及路线的顺畅,缓和行车方向的突变和离心力的突然产生;使离心加速度逐渐变化,不致产生侧向冲击,并缓和超高,作为超高变化的过渡段,来减少行车震荡。
高速公路的一些线路坐标、高程计算公式
高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x<0时sgn(x)=-1,当x>0时sgn(x)=1,当x=0时sgn(x)=0。
超高过渡介绍知识讲解
超高过渡介绍公路超高过渡一、低等级公路超高计算【示例1】山岭重丘区某新建二级公路,设计速度为40km/h,其中一平曲线半径R=150m,缓和曲线Ls=70m,路面宽度为B=7.0m,路肩宽度为0.75m,路拱坡度为iG=2%,路肩坡度iJ=3%,该曲线的主点桩号分别为:ZH=K1+028.665 、HY=K1+098.665 、QZ=K1+131.659 、YH=K1+164.653 、HZ=K1+234.653。
试计算各主点桩以及下列桩号:K1+040、K1+070、K1+180、K1+210处横断面上内外侧和路中线三点的超高值(设计高为路基边缘)。
(1)确定超高缓和段长度根据公路等级、设计速度和平曲线半径查表得圆曲线的超高值iy=5%,新建公路一般采用绕边线旋转,超高渐变率p=1/100,所以超高缓和段长度:Lc=B'△i/p=7×5%/(1/100)=35.0(m)而缓和曲线Ls=70m,先取Lc=Ls=70m,然后检查横坡从路拱坡度(-2%)过渡到超高横坡(2%)时的超高渐变率:p=3.5×[2%-(-2%)]/X0=3.5×[2%-(-2%)]/28=1/200>1/330或p=7×5%/70=1/200>1/330所以取Lc=Ls=70m。
(2)计算临界断面x0X0=iG/ih×Lc=2%/5%×70=28.0m(3)计算各桩号处的超高值超高起点为ZH(HZ)点,分别计算出x值,然后分别代入超高值计算公式(见《道路勘测设计》书)中计算,加宽过渡采用比例过渡,加宽值b=1.0m。
土路肩在超高起点前1m变成与路面相同的横坡,且在整个超高过过渡段保持与相邻行车道相同的横坡。
计算结果见下表。
超高值计算结果表桩号 x 加宽值bx 外侧超高值中线超高值内侧超高值K1+028.665(ZH) 0.000<x0=28 0.000 0.008 0.093 0.008+040 11.335< x0=28 0.162 0.073 0.093 0.004+070 41.335 >x0=28 0.591 0.245 0.126 -0.017+098.665(HY) 1.000 0.410 0.198 -0.065+131.659(QZ) 1.000 0.410 0.198 -0.0651+164.653(YH) 1.000 0.410 0.198 -0.065+180 54.653> x0=28 0.781 0.322 0.159 -0.037+210 24.653< x0=28 0.352 0.149 0.093 0.000+234.653(HZ) 0.000< x0=28 0.000 0.008 0.093 0.008(已知第一段坡度i1,第二段坡度i2,过度段长度l,待求点离第二横坡距离xa=x/l待求点i=(i2-i1)(1-3a2+2a3)+i1)二.超高缓和段长度计算超高缓和段的长度按下式计算:Lc=B'×△i/P式中: Lc——超高缓和段长度(m);B' ——旋转轴至行车道(设路缘带时为路缘带)外侧边缘的宽度(m);△i——旋转轴外侧的超高与路拱坡度的代数差;P ——超高渐变率,其值根据计算行车速度和超高过渡方式从下表中查取。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
132
248
1500~1300
3.0
280
132
248
1300~1220
3.0
260
132
248
1220~1000
4.0
260
158
297
1000~950
4.0
240
158
297
950~850
5.0
220
185
347
850~770
6.0
210
210
396
770~700
6.0
210
210
396
V=100公里/小时,路幅宽33.5米,设超高推荐半径1600~3200米(困难,山区)。不设超高或超高2%~3%的半径2800~5600米(最佳,平原区)。
693
V=80公里/小时,路幅宽24.5米,设超高推荐半径830~2000米(困难,山区)。不设超高或超高2%~3%的半径1600~3200米(最佳,平原区)。
超高渐变段长最小值(m)
超高渐变段长最大值(m)
备注
4000~1900
2.0
320
105
198
采用三次抛物线过渡;绕中央分隔带边缘旋转;最大渐变率1/175,最小渐变率1/330;
B=15.0 m。
1220 m以上不能在全长范围内超高过渡
1900~1710
2.0
300
105
198
1710~1500
3.0
(V=80公里/小时,路幅宽24.5米)
平曲线半径
(m)
超高值
(%)
缓和曲线长
(m)
超高渐变段长最小值(m)
超高渐变段长最大值(m)
备注
2500~3240
2.0
310
63
139
采用三次抛物线过渡;绕中央分隔带边缘旋转;最大渐变率1/150,最小渐变率1/330;
B=12.25 m。
830 m以上不能在全长范围内超高过渡
缓和曲线长度与超高过渡段长度表
(V=120公里/小时,路幅宽34.5米)
平曲线半径(m)
超高值
(%)
缓和曲线长
(m)
超高渐变段长最小值(m)
超高渐变段长最大值(m)
备注
5500~3240
2.0
340
122
201
采用三次抛物线过渡;绕中央分隔带边缘旋转;最大渐变率1/200,最小渐变率1/330;
B=15.25 m。
1620 m以上不能在全长范围内超高过渡
3240~2160
3.0
330
153
251
2160~1620
4.0
320
183
301
1620~1300
5.0
310
214
352
1300~1080
6.0
300
244
402
1080~930
7.0
280
275
452
930~810
8.0
260
305
503
810~720
1240~830
3.0
280
95
208
830~620
4.0
260
126
277
620~500
5.0
260
158
346
500~410
240
189
416
410~350
7.0
220
221
485
350~310
8.0
200
252
555
310~280
9.0
180
284
624
280~250
10.0
160
315
9.0
240
336
553
720~650
10.0
220
366
603
V=120公里/小时,路幅宽35米,设超高推荐半径2600~5200米(困难,山区)。不设超高或超高2%~3%的半径4000~8000米(最佳,平原区)。
(V=100公里/小时,路幅宽33.5米)
平曲线半径
(m)
超高值
(%)
缓和曲线长
(m)
