广东省13市2015届高三上学期期末考试数学理试题分类汇编:复数
2015届高三上学期期末考试数学理试题分类汇编---三角函数(含答案)

2015届高三上学期期末考试数学理试题分类汇编---三角函数(含答案)一、选择、填空题题1、(佛山市2014届高三教学质量检测(一))设函数的最小正周期为,最大值为,则A .,B . ,C .,D ., 答案:C2、(广州市2014届高三1月调研测试).函数(,,)的部分图象如图1所示,则函数对应的解析式为A .B .C .D . 答案:A3、(增城市2014届高三上学期调研)已知,则(A ) (B ) (C ) (D )答案:A4、(省华附、省实、广雅、深中四校2014届高三上学期期末)函数的部分图象如图所示,则AB.C.D.答案:B5、(江门市2014届高三调研考试)在中,,,.答案:sin 2y x x =T A T π=A =T π=2A =2T π=A =2T π=2A =()()sin f x A x ωϕ=+0A >0ω>2πϕ<()y f x =sin 26y x π⎛⎫=+ ⎪⎝⎭sin 26y x π⎛⎫=-⎪⎝⎭cos 26y x π⎛⎫=+ ⎪⎝⎭cos 26y x π⎛⎫=-⎪⎝⎭3177cos ,45124x x πππ⎛⎫+=<< ⎪⎝⎭2sin 22sin 1tan x xx+=-2875-287521100-21100()sin()(0,0)f x A x A ωθω=+>>()f x =π)6x -π)3x -π)3x +π)6x +ABC ∆3=c 045=A =B =a 26、(汕头市2014届高三上学期期末教学质量监测)已知函数①,②,则下列结论正确的是( )A .两个函数的图象均关于点成中心对称B .两个函数的图象均关于直线对称C .两个函数在区间上都是单调递增函数D .可以将函数②的图像向左平移个单位得到函数①的图像答案:C7、(中山市2014届高三上学期期末考试)已知,,则 答案:8、(珠海市2014届高三上学期期末)已知,则 答案: 9、(珠海市2014届高三上学期期末)在△ABC 中,A :B :C =1:2:3,则a :b :c 等于( )A 、1:2:3B 、3:2:1C 、12D 、2 1 答案:C10、(珠海一中等六校2014届高三第三次联考)如果函数的图象关于直线对称,那么a 等于( C ) A.B.-C.1D.-1答案:C 二、解答题1、(佛山市2014届高三教学质量检测(一))在中,角、、的对边分别为、、,且,. (Ⅰ) 求的值;(Ⅱ) 设函数,求的值. 【解析】解法1:(Ⅰ) 因为,所以,……………………………………2分x x y cos sin +=x x y cos sin 22=(,0)4π-4x π=-(,)44ππ-4π20πα<<=+)6cos(πα53=αcos 1cos 3ϕ=-()0ϕπ<<sin 2ϕ=9-sin 2cos 2y x a x =+8x π=-22ABC ∆A B C a b c 2a =B C =cos B ()()sin 2f x x B =+6f π⎛⎫⎪⎝⎭B C =c b =又, 所以, ……………………………3分………………………………………………4分……………………………………………5分 解法2:∵,∴…………………………………2分∵,且,所以 (3)分又 ……………………4分 ∵, ∴.………………………………………5分 (Ⅱ)由(Ⅰ)得,................................................7分 (注:直接得到不扣分) 所以 (8)分 ……………………………10分………………………………11分 . ………………………………………12分 2、(广州市2014届高三1月调研测试)在△中,角,,所对的边分别为,,,且. (1)求的值;(2)若,,求的值.解:(1)在△中,.………………………………………1分所以 …………………………………………………2分a =222cos 2a c b B ac+-=23b ==a =sin A B =B C =A B C ++=πsin 2B B =2sin cos B B B =sin 0B ≠cos B =sin 4B ==sin B =sin 63f B ππ⎛⎫⎛⎫=+⎪ ⎪⎝⎭⎝⎭sin cos cos sin 33B B ππ=+12=+38+=ABC A B C a b c cos 23A C +=cos B 3a =b =c ABC A B C π++=coscos 22A C Bπ+-=.………………………………………………3分 所以 …………………………………………………………5分 .………………………………………………………………7分 (2)因为,,,由余弦定理,……………………………………………9分 得.…………………………………………………………………11分 解得.………………………………………………………………………12分 3、(增城市2014届高三上学期调研) 已知函数(1)当时,求的最大值及相应的x 值; (2)利用函数y=sin的图象经过怎样的变换得到f(x)的图象.解(1) 1分 3分5分∵,∴ 6分 所以当时,即时 7分f(x)所以f(x),相应的x 的值8分(2)函数y=sin的图象向左平移个单位, 9分 把图象上的点横坐标变为原来的倍, 10分 倍, 11分sin23B ==2cos 12sin2BB =-13=3a =b =1cos 3B =2222cos b a c ac B =+-2210c c -+=1c =()()2sin cos sin .f x x x x =-0x π<<()f x x ()()22sin cos sin 2sin cos 2sin f x x x x x x x =-=-sin 2cos 21x x =+-214x π⎛⎫=+- ⎪⎝⎭0x π<<92444x πππ<+<242x ππ+=8x π=118x π=x 4π12最后把图象向下平移1个单位得到y 的图象 12分方法2:把函数y=sin图象上的点横坐标变为原来的倍 9分把函数的图象向左平移个单位, 10分倍,11分最后把图象向下平移1个单位得到y 的图象 12分4、(省华附、省实、广雅、深中四校2014届高三上学期期末)在中,三个内角所对的边分别为 ,. (1) 求; (2) 设求的值. 解: (1) (2)分…………………………………………… 4分………………………………………………………6分(2)(解法一) (7)分214x π⎛⎫=+- ⎪⎝⎭x 12x 8π214x π⎛⎫=+- ⎪⎝⎭ABC ,,A B C ,a ,.bc 222)2b c a bc +-=2B A =tan A ππ(2sin(),1),(sin(),1),44m B n B =-=+-m n ⋅2223()2,b c a bc +-=222cos 2b c a A bc +-∴==0π,A <<sin A ∴==sin tan cos AA A==ππ(2sin(),1),(sin(),1),44m B n B =-=+-ππ2sin()sin()144m n B B ∴⋅=-+-2(cos sin )sin )122B B B B =⨯-+- (9)分 (10)分, (12)分(2)(解法二) (7)分………………………………………………………9分 (10)分, (12)分(2)(解法三), (9)分 (10)分22cos sin 1B B =--22sin .B =-2B A=sin sin 22sin cos B A A A ∴===16.9m n ⋅=-ππ(2sin(),1),(sin(),1),44m B n B =-=+-ππ2sin()sin()144m n B B ∴⋅=-+-πππ2cos ()sin()1244B B ⎡⎤=--+-⎢⎥⎣⎦ππ2cos()sin()144B B =++-πsin(2)12B =+-cos 21B =-22sin .B =-2B A=sin sin 22sin cos B A A A ∴===16.9m n ⋅=-2B A=sin sin 22sin cos B A A A ∴===21cos cos 212sin .3B A A ==-=-π4(2sin(),1)sin ),1)(,1),43m B B B ∴=-=-=- (11)分………………………12分5、(江门市2014届高三调研考试)已知,. ⑴ 求的最小正周期;⑵ 设、,,,求的值. 解:⑴……2分,……4分,的最小正周期……5分⑵因为,,……6分, 所以,……7分,,,……8分,因为,所以,……9分,所以……10分, ……11分,……12分。
广东省13市高三上学期期末考试数学理试卷分类汇编:复数、推理-精品推荐

广东省13市高三上学期期末考试数学理试题分类汇编复数、推理一、复数1、(潮州市2017届高三上学期期末)欧拉公式e i =cos+isin (i 为虚数单位)是由瑞士著名数学家欧拉发明的,它将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,它在复变函数论里占用非常重要的地位,被誉为“数学中的天桥”,根据欧拉公式可知,i e -表示的复数在复平面中位于( )A .第一象限B .第二象限C .第三象限D .第四象限2、(东莞市2017届高三上学期期末)若复数 满足(1+i ) =-2i (i 为虚数单位),z 是 的共轭复数,则z ·=( )A .14B .12C .2D .1 3、(佛山市2017届高三教学质量检测(一))复数满足i i z -=+3)2(,则复数在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限 4、(广州市2017届高三12月模拟)设(1i)(i)x y ++2=,其中,x y 是实数,则2i x y += (A )1 (B )2 (C )3 (D )55、(惠州市2017届高三第三次调研)若复数满足1z i i ⋅=+(i 是虚数单位),则的共轭复数是____________.6、(江门市2017届高三12月调研)是虚数单位,若,则A .1B .C .D .7、(揭阳市2017届高三上学期期末)复数满足(1+i)=i +2,则的虚部为(A )32 (B )12 (C )12- (D )12i -8、(茂名市2017届高三第一次综合测试)设i 为虚数单位,复数(2)1i z i -=+,则的共轭复数z 在复平面中对应的点在( )A .第一象限B .第二象限C .第三象限D .第四象限9、(清远市清城区2017届高三上学期期末)已知复数ii z ++=1)3(2(i 为虚数单位). 则其共轭复数z 在复平面内所对应的点位于( ) A. 第一象限 B. 第二象限 C. 第三象限 D.第四象限10、(汕头市2017届高三上学期期末)设复数i z 21231+=,i z 432+=,其中i 为虚数单位,则=||||220161z z ( ) A .20152 B .20161 C .251 D .51 11、(韶关市2017届高三1月调研)已知复数i t t z )1()1(++-=,t R ∈, z 的最小值是(A) 1 (B) 2 (C) 2 (D) 312、(肇庆市2017届高三第二次模拟)设复数满足()12z i +=,i 为虚数单位,则复数的虚部是(A )1 (B )1- (C )i (D )i -13、(珠海市2017届高三上学期期末)设复数1z =1+2i ,2z =2-i ,i 为虚数单位,则12z z =A .4+3iB .4-3iC .-3iD .3i参考答案1、D2、C3、D4、D5、1i +6、D7、C 8、D 9、A 10、D 11、C 12、B 13、A二、推理1、(佛山市2017届高三教学质量检测(一))所有真约数(除本身之外的正约数)的和等于它本身的正整数叫做完全数(也称为完备数、玩美数),如3216++=;14742128++++=;2481246231168421496++++++++=,此外,它们都可以表示为2的一些连续正整数次幂之和,如21226+=,43222228++=,,按此规律,8128可表示为________2、(揭阳市2017届高三上学期期末)已知(),把数列的各项排成如图所示的三角形数阵,记表示该数阵中第行中从左到右的第个数,则A .67B .69C .73D .753、(清远市清城区2017届高三上学期期末)已知函数)(x f 及)(x g )(D x ∈,若对于任意的D x ∈,存在o x 使得)()(),()(o o x g x g x f x f ≥≥恒成立且)()(o o x g x f =,则称)(),(x g x f 为“兄弟函数”已知函数),()(2R q P q Px x x f ∈++=, x x x x g 1)(2+-=是定义在区间]221,⎢⎣⎡上的“兄弟函数”,那么函数)(x f 在区间]221,⎢⎣⎡上的最大值为4、(韶关市2017届高三1月调研)已知不恒为零的函数()f x 在定义域[0,1]上的图象连续不间断,满足条件(0)(1)0f f ==,且对任意12,[0,1]x x ∈都有12121|()()|||3f x f x x x -≤-,则对下列四个结论:①若(1)()f x f x -=且102x ≤≤时,11()()202f x x x =-,则当112x <≤时,11()(1)()202f x x x =--;②若对[0,1]x ∀∈都有(1)()f x f x -=-,则()y f x =至少有3个零点;③对1[0,1],|()|6x f x ∀∈≤恒成立;④. 对12121,[0,1],|()()|6x x f x f x ∀∈-≤恒成立其中正确的结论个数有(A) 1个(B) 2个 (C) 3 个 (D) 4个参考答案1、 2、A 3、24、【解析】由(1)()f x f x -=得()y f x =图象关于轴12x =, ①正确; (1)()f x f x -=-,111()(1)()222f f f ∴=-=- 1()2f ∴=0,故()y f x =至少有3个零点10,,12. ②正确; 当102x ≤≤时,11|()|||36f x x ≤≤;当112x ≤≤时,则112x -≤ 1111|()||()(1)|(1)3326f x f x f x =-≤-≤⨯=. ③正确, 设1201x x ≤≤≤,当121||2x x -≤时,121211|()()|||36f x f x x x -≤-≤, 当211||2x x ->时,1212|()()||()(0)(1)()|f x f x f x f f f x -=-+- 121211|()(0)||(1)()||0||1|33f x f f f x x x ≤-+-≤-+- 221111111111(1)()33333326x x x =⨯+-=--≤-⨯=. ④正确 选D.。
高考数学 真题分类汇编:专题(15)复数(理科)及答案

专题十五 复数1.【20xx 高考新课标2,理2】若a 为实数且(2)(2)4ai a i i +-=-,则a =( )A .1-B .0C .1D .2【答案】B【解析】由已知得24(4)4a a i i +-=-,所以240,44a a =-=-,解得0a =,故选B .【考点定位】复数的运算.【名师点睛】本题考查复数的运算,要利用复数相等列方程求解,属于基础题.2.【20xx 高考四川,理2】设i 是虚数单位,则复数32i i-( ) (A )-i (B )-3i (C )i. (D )3i【答案】C【解析】32222i i i i i i i i-=--=-+=,选C. 【考点定位】复数的基本运算.【名师点睛】复数的概念及运算也是高考的热点,几乎是每年必考内容,属于容易题.一般来说,掌握复数的基本概念及四则运算即可.3.【20xx 高考广东,理2】若复数()32z i i =- ( i 是虚数单位 ),则z =( )A .32i -B .32i +C .23i +D .23i -【答案】D .【解析】因为()3223z i i i =-=+,所以z =23i -,故选D .【考点定位】复数的基本运算,共轭复数的概念.【名师点睛】本题主要考查复数的乘法运算,共轭复数的概念和运算求解能力,属于容易题;复数的乘法运算应该是简单易解,但学生容易忘记和混淆共轭复数的概念,z a bi =+的共轭复数为z a bi =-.4.【20xx 高考新课标1,理1】设复数z 满足11z z+-=i ,则|z|=( )(A )1 (B (C (D )2【答案】A【解析】由11z i z +=-得,11i z i -+=+=(1)(1)(1)(1)i i i i -+-+-=i ,故|z|=1,故选A. 【考点定位】本题主要考查复数的运算和复数的模等.【名师点睛】本题将方程思想与复数的运算和复数的模结合起来考查,试题设计思路新颖,本题解题思路为利用方程思想和复数的运算法则求出复数z ,再利用复数的模公式求出|z|,本题属于基础题,注意运算的准确性.5.【20xx 高考北京,理1】复数()i 2i -=( )A .12i +B .12i -C .12i -+D .12i --【答案】A考点定位:本题考查复数运算,运用复数的乘法运算方法进行计算,注意21i =-.【名师点睛】本题考查复数的乘法运算,本题属于基础题,数的概念的扩充部分主要知识点有:复数的概念、分类,复数的几何意义、复数的运算,特别是复数的乘法与除法运算,运算时注意21i =-,注意运算的准确性,近几年高考主要考查复数的乘法、除法,求复数的模、复数的虚部、复数在复平面内对应的点的位置等.6.【20xx 高考湖北,理1】 i 为虚数单位,607i 的共轭复数....为( ) A .i B .i - C .1 D .1-【答案】A【解析】i i i i -=⋅=⨯31514607,所以607i 的共轭复数....为i ,选A . 【考点定位】共轭复数.【名师点睛】复数中,i 是虚数单位,24142434111()n n n n i i i i i i i n +++=-==-=-=∈Z ;,,,7.【20xx 高考山东,理2】若复数z 满足1z i i=-,其中i 为虚数为单位,则z =( ) (A )1i - (B )1i + (C )1i -- (D )1i -+【答案】A 【解析】因为1z i i=-,所以,()11z i i i =-=+ ,所以,1z i =- 故选:A. 【考点定位】复数的概念与运算.【名师点睛】本题考查复数的概念和运算,采用复数的乘法和共轭复数的概念进行化简求解. 本题属于基础题,注意运算的准确性.8.【20xx 高考安徽,理1】设i 是虚数单位,则复数21i i-在复平面内所对应的点位于( ) (A )第一象限 (B )第二象限 (C )第三象限 (D )第四象限【答案】B 【解析】由题意22(1)2211(1)(1)2i i i i i i i i +-+===-+--+,其对应的点坐标为(1,1)-,位于第二象限,故选B.【考点定位】1.复数的运算;2.复数的几何意义.【名师点睛】复数的四则运算问题主要是要熟记各种运算法则,尤其是除法运算,要将复数分母实数化(分母乘以自己的共轭复数),这也历年考查的重点;另外,复数z a bi =+在复平面内一一对应的点为(,)Z a b .9.【20xx 高考重庆,理11】设复数a +bi (a ,b ∈R ),则(a +bi )(a -bi )=________.【答案】3【解析】由a +得=,即223a b +=,所以22()()3a bi a bi a b +-=+=.【考点定位】复数的运算.【名师点晴】复数的考查核心是代数形式的四则运算,即使是概念的考查也需要相应的运算支持.本题首先根据复数模的定义得a +,复数相乘可根据平方差公式求得()()a bi a bi +-22()a bi =-22a b =+,也可根据共轭复数的性质得()()a bi a bi +-22a b =+.10.【20xx 高考天津,理9】i 是虚数单位,若复数()()12i a i -+ 是纯虚数,则实数a 的值为 .【答案】2-【解析】()()()12212i a i a a i -+=++-是纯虚数,所以20a +=,即2a =-.【考点定位】复数相关概念与复数的运算.【名师点睛】本题主要考查复数相关概念与复数的运算.先进行复数的乘法运算,再利用纯虚数的概念可求结果,是容易题.11.【20xx 江苏高考,3】设复数z 满足234z i =+(i 是虚数单位),则z 的模为_______.【解析】22|||34|5||5||z i z z =+=⇒=⇒=【考点定位】复数的模【名师点晴】在处理复数相等的问题时,一般将问题中涉及的两个复数均化成一般形式,利用复数相等的充要条件“实部相等,虚部相等”进行求解.本题涉及复数的模,利用复数模的性质求解就比较简便:2211121222||||||||||||.||z z z z z z z z z z ==⋅=,, 12.【20xx 高考湖南,理1】已知()211i i z -=+(i 为虚数单位),则复数z =( ) A.1i + B.1i - C.1i -+ D.1i --【答案】D.【考点定位】复数的计算.【名师点睛】本题主要考查了复数的概念与基本运算,属于容易题,意在考查学生对复数代数形式四则运算的掌握情况,基本思路就是复数的除法运算按“分母实数化”原则,结合复数的乘法进行计算,而复数的乘法则是按多项式的乘法法则进行处理.13.【20xx 高考上海,理2】若复数z 满足31z z i +=+,其中i 为虚数单位,则z = .【答案】1142i +【解析】设(,)z a bi a b R =+∈,则113()1412142a bi a bi i a b z i ++-=+⇒==⇒=+且 【考点定位】复数相等,共轭复数【名师点睛】研究复数问题一般将其设为(,)z a bi a b R =+∈形式,利用复数相等充要条件:实部与实部,虚部与虚部分别对应相等,将复数相等问题转化为实数问题:解对应方程组问题.复数问题实数化转化过程中,需明确概念,如(,)z a bi a b R =+∈的共轭复数为(,)z a bi a b R =-∈,复数加法为实部与实部,虚部与虚部分别对应相加.【20xx 高考上海,理15】设1z ,2C z ∈,则“1z 、2z 中至少有一个数是虚数”是“12z z -是虚数”的( )A .充分非必要条件B .必要非充分条件C .充要条件D .既非充分又非必要条件【答案】B【解析】若1z 、2z 皆是实数,则12z z -一定不是虚数,因此当12z z -是虚数时,则“1z 、2z 中至少有一个数是虚数”成立,即必要性成立;当1z 、2z 中至少有一个数是虚数,12z z -不一定是虚数,如12z z i ==,即充分性不成立,选B.【考点定位】复数概念,充要关系【名师点睛】形如a +b i(a ,b ∈R )的数叫复数,其中a ,b 分别是它的实部和虚部.若b =0,则a +b i 为实数;若b ≠0,则a +b i 为虚数;若a =0且b ≠0,则a +b i 为纯虚数.判断概念必须从其定义出发,不可想当然.。
广东省东莞市2015届高三上学期期末教学质量检查数学理试题 含答案

2014—2015学年度第一学期教学质量检查高三理科数学(A 卷)参考答案BBDA DBAB 9. 24 10. ;623 11. 1- 12.26n n -+ 13. 7个 14.)43,2(π 15. 030(或)6π16.解:(1)因为函数)20,0)(sin(2)(πϕωϕω<<>-=x x f 的最小正周期为π故2,2=∴=ωπωπ…………………………………2分)2sin(2)(ϕ-=∴x x f又6π是它的一个零点,即0)3sin(=-ϕπ …………………………………3分Z k k ∈=-∴,3πϕπ……………………………………4分Z k k ∈-=∴,3ππϕ,因为20πϕ<< ……………………………………5分3,0πϕ==∴k ……………………………………6分所以()f x 的解析式为)32sin(2)(π-=x x f ……………………………………7分(2)由(1))32sin(2)(π-=x x f又因为3)62(,2)1252(=+=+πβπαf f故23sin ,22)2sin(==+βπα ……………………………………9分 22cos =∴α,又]2,0[,πβα∈ 3,4πβπα==∴ ……………………………………10分βαβαβαsin sin cos cos )cos(⋅-⋅=+∴ ……………………………………11分 462232221223sin4sin 3cos 4cos -=⨯-⨯=-=ππππ ……………………………………12分另解:23sin ,22)2sin(==+βπα ……………………………………9分22cos =∴α,又]2,0[,πβα∈21cos ,22sin ==∴βα ……………………………………10分 βαβαβαsin sin cos cos )cos(⋅-⋅=+∴ ……………………………………11分 462232221223sin4sin 3cos 4cos -=⨯-⨯=-=ππππ ……………………………………12分17.解:(1)根据频率分布直方图中的数据,可得1(0.0050.00750.02250.035)100.10.070.0310a -+++⨯==-=,所以 0.03a =. …………………2分 (2)学生成绩在[50,60)内的共有40×0.05=2人,在[60,70)内的共有40×0.225=9人,成绩在[50,70)内的学生共有11人. ……………4分设“从成绩在[50,70)的学生中随机选3名,且他们的成绩都在[60,70)内”为事件A ,则3931128()55C P A C ==.所以选取的3名学生成绩都在[60,70)内的概率为2855. ………6分 (3)依题意,X 的可能取值是1,2,3. ………………7分21293113(1)55C C P X C ===; 122931124(2)55C C P X C ===; 28(3)()55P X P A ===. ……………10分所以X 的分布列为X1 2 3 P355 2455 2855324282712355555511EX =⨯+⨯+⨯=. …………………12分18.解(1)∵,,PC AB PC BC AB BC B ⊥⊥= ………………3分∴PC ABC ⊥平面,………………4分 又∵PC PAC ⊂平面 ………………5分 ∴PAC ABC ⊥平面平面 ………………6分(2)解法一:在平面ABC 内,过C 作CD CB ⊥,建立空间直角坐标系C xyz -(如图)由题意有31,,022A ⎛⎫- ⎪ ⎪⎝⎭,(0,2,0)B 设()()000,0,0P z z >, 则()()000330,1,,,,,0,0,22M z AM z CP z ⎛⎫=-= ⎪ ⎪⎝⎭由直线AM 与直线PC 所成的解为060,得0cos60AM CP AM CP ⋅=⋅⋅,即22000132z z z =+,解得:01z = ………………8分∴3331,,0,,,12222AB AM ⎛⎫⎛⎫=-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,设平面MAB 的一个法向量为111(,,)n x y z =,则111113502233022x y x y z ⎧-+=⎪⎪⎨⎪-++=⎪⎩,取13x =,得33(3,,)55n = …………………………10分平面ABC 的法向量取为()0,0,1m = ……………………………………………………11分设m与n所成的角为θ,则93cos 31m n m nθ⋅==⋅ ………………………………………13分 显然,二面角M AC B --的平面角为锐角, 故二面角M AC B --的平面角余弦值为9331…………………………14分解法二:在平面PCBM 内,过点M 作BC MH ⊥于H , 则显然有PC MH //故ABC MH 面⊥ ………………………………7分过点M 作AB MG ⊥于G ,连接MG ,则MG 在平面ABC 内的摄影为HG 由三垂线定理的逆定理知AB HG ⊥MGH ∠∴为二面角M AB C --的平面角 …………………………10分 因为直线AM 与直线PC 所成的角为︒60,即︒=∠60AMHH G在ACH ∆中,AC=CH=1,︒=∠120ACH ,则AH=3AHM Rt ∆中,23sin ==∠AM AH AMH ,故1,2==MG AM …………11分 在ACB ∆中,由余弦定理7cos 2222=∠⋅⋅-+=ACB BC AC BC AC AB7=∴AB ……………………………………12分1421120sin 21=︒⋅⋅⋅=∴AB BC AC HG 31931692111421cos =+==∠∴MG HG MGH ………………………………13分 故二面角M AC B --的平面角余弦值为9331…………………………14分19.解:(1)设椭圆C 的焦距为2c ,则22232c a a b c ⎧=⎪⎨⎪-=⎩∴222234,3a c c b ==……………………3分∴椭圆C 的方程为:22223314x y c c+= 代入1(3,)2P 得:3c = …………………………5分∴椭圆C 的方程为2214x y += …………………………6分 (2)设[](,),2,2Q x y x ∈-, 则222y x QO+=, ……………7分又:(1,0)A -, 222(1)QA x y =++ ……………8分2222222222221(1)1221QA x y x x y x x y x y x yQOλ-++-++====++++ ……………9分 点),(y x P 满足2214x y +=,∴2214x y =-, …………10分22281133414x xx x λ=+=+++ …………11分当0≤x 时,1≤λ …………12分 当0>x 时,(0,2]x ∈,288114343x x x xλ=+=+++ …………13分 因为4432343x x x x+≥⋅=,所以2313λ≤+,当且仅当233x =时, λ取得最大值2313+.…………14分 (说明:在求最大值部分若用导数求单调区间后再说明最值的,参考上述步骤给分) 20.解(1):()()12323123 4 2=2n n a a a a log log log n log n +⋅⋅⋅⋅=⋅⋅⋅++ ……2分要123n a a a a ⋅⋅⋅⋅为整数,需要()()22log n k k Z +=∈ ∴22k n =- ……3分由于n N +∈, ∴2k ≥,即21222b =-=,32226b =-=,…,122m m b +=- 根据题意,2015<m b ,得2015221<-+m ∴201721<+m ,则9m ≤…………4分∴区间)2015,1(内的所有“穿越数”的和为: ()2310922229421182026+++-⨯=⨯--= …………………………7分证明(2):341123111111112222222m m b b b b +++++=++++---………8分当1m =时,111526b =<成立;当2m =时,121111252636b b +=+=<成立; …………………………10分 当2m ≥时,由1111111122422322232m m m m m+---==≤-⋅-⋅+-⋅,…………………………12分 ∴211112311111111111511232323223262m m m m b b b b ---⎛⎫++++≤++++=+-=- ⎪⋅⋅⋅⎝⎭ …………………………13分 又1102m -> ∴1211156m b b b +++< …………………………14分21.解: 由题有,22,0()ln ,0x x a x f x x x ⎧++<=⎨>⎩ …………………2分(2)由导数的几何意义可知,点A 处的切线斜率为()1f x ',点B 处的切线斜率为()2f x ',故当点A处的切线与点B处的切垂直时,有()()121f x f x ''=-. …………………3分当0x <时,对函数()f x 求导,得()22f x x '=+.因为120x x <<,所以()()1222221x x ++=-, …………………4分 即:121244()5x x x x =-+-222211212121212()4()4()5(2)1x x x x x x x x x x x x -=+-=++++=+++ (6)分当122x x +=-时,1234x x =,此时1231,22x x =-=-,21x x -取得最小值1. ………8分(3)当120x x <<或210x x >>时,()()12f x f x ''≠,故120x x <<. ………9分 当10x <时,函数()f x 的图象在点()()11,x f x 处的切线方程为()()()21111222y x x a x x x -++=+-,即()21122y x x x a =+-+当20x >时,函数()f x 的图象在点()()22,x f x 处的切线方程为()2221ln y x x x x -=-,即221ln 1y x x x =∙+-. ………10分 两切线重合的充要条件是1222112 2 ln 1 x x x x a ⎧=+⎪⎨⎪-=-+⎩①② ………11分由①及120x x <<知,110x -<<. 由①②得,()2211111ln1ln 22122a x x x x =+-=-+-+.设()()21111ln 221(10)h x x x x =-+--<<, ………12分 则()1111201h x x x '=-<+.- 11 - 所以()()1110h x x -<<是减函数.则()()10ln 21h x h >=--,所以ln 21a >--. ………13分 又当1(1,0)x ∈-且趋近于1-时,()1h x 无限增大,所以a 的取值范围是()ln 21,--+∞. 故当函数()f x 的图像在点,A B 处的切线重合时,a 的取值范围是()ln 21,--+∞ ……14分。
广东省四校2015届高三上学期期末联考数学(理科)试题参考答案及评分标准

2 sin( x + ) ≤ 2 ,而 > 2 ,故不存在这样的实数 x ,故 A 错; 4 2 a = 1 时,显然这两直线平行;反过来,若这两直线平行,则 a = ±1 . 因此, a = 1 是这两直线平行的充 x x 分不必要条件,故 B 错;命题“ ∀x > 0 , e > x + 1 ”的否定应该是“ ∃x > 0 , e ≤ x + 1 ” ,故 C 错; 1+ x 1 − x −1 1− x = lg( ) = − lg = − f ( x) ,故 f ( x) 在其 排除 A、B、C ,答案选 D. 事实上, f (− x) = lg 1− x 1+ x 1+ x 定义域 ( −1, 1) 内是奇函数.
从而 S n =
60° ,以 OA、OB 为邻边作菱形 OACB (边长为 1) ,由向量加法的几何意义知, | p |=| OC | = 3 .
12.【解析 解析】 解析 由“直径所对的圆周角为直角”知,使 ∠AMB ≥ 90° 的点 M 落在以 AB 为直径的半圆上或半 圆内,由几何概型知,所求概率为 P ( A) =
1. 【解析 解析】集合 A = { x | 0 < x < 2} , B = { x | x < −1或x > 1} ,则 解析
A ∪ ∁U B = { x | 0 < x < 2} ∪ { x | −1 ≤ x ≤ 1} = { x | −1 ≤ x < 2} ,故选 B.
2i 2i (1 + i ) =− = −i (1 + i ) = 1 − i 对应的点的坐标为 (1, −1) ,故选 A. 1− i 2 1 1 2 1 2 1 3. 【解析 解析】作出可行域是 ∆AOB 及其内部,边界点 A( , ) 、O (0, 0) 、 B ( , ) ,易知当 x = , y = 时, 解析 2 2 3 3 3 3 1 5 z = x + y 取得最大值为 ,故选 C. 2 6
广东省13市2015届高三上学期期末考试数学理试题分类汇编:立体几何
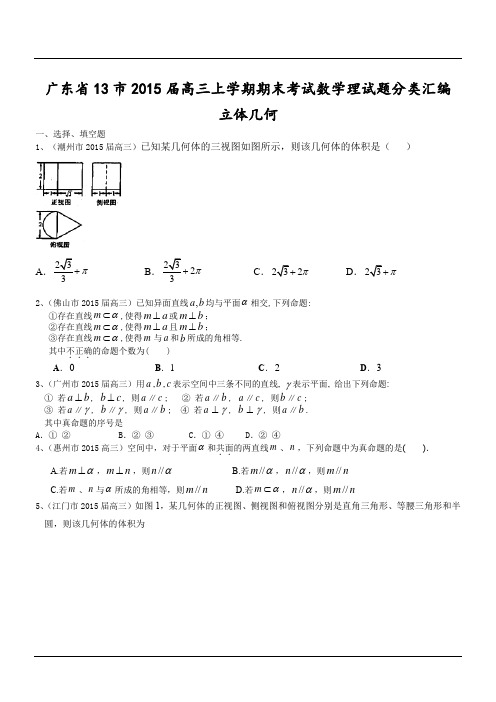
广东省13市2015届高三上学期期末考试数学理试题分类汇编立体几何一、选择、填空题1、(潮州市2015届高三)已知某几何体的三视图如图所示,则该几何体的体积是( )ABC .D . 2、(佛山市2015届高三)已知异面直线,a b 均与平面α相交,下列命题:①存在直线m α⊂,使得m a ⊥或m b ⊥; ②存在直线m α⊂,使得m a ⊥且m b ⊥;③存在直线m α⊂,使得m 与a 和b 所成的角相等. 其中不正确...的命题个数为( ) A .0 B .1 C .2 D .3 3、(广州市2015届高三)用a ,b ,c 表示空间中三条不同的直线, γ表示平面, 给出下列命题: ① 若a b ⊥, b c ⊥, 则a ∥c ; ② 若a ∥b , a ∥c , 则b ∥c ; ③ 若a ∥γ, b ∥γ, 则a ∥b ; ④ 若a ⊥γ, b ⊥γ, 则a ∥b . 其中真命题的序号是A .① ②B .② ③ C.① ④ D .② ④4、(惠州市2015高三)空间中,对于平面和共面..的两直线、,下列命题中为真命题的是( ). A.若,,则 B.若,,则 C.若、与所成的角相等,则 D.若,,则5、(江门市2015届高三)如图1,某几何体的正视图、侧视图和俯视图分别是直角三角形、等腰三角形和半圆,则该几何体的体积为π+2π+2ππαm n m α⊥m n ⊥//n α//m α//n α//m n m n α//m n m α⊂//n α//m nA .4B .8C .π2D .π46、(揭阳市2015届高三)一几何体的三视图如图3示, 则该几何体的体积为________7、(清远市2015届高三)某几何体的三视图如下图所示:其中正视图和侧视图都是上底为3,下底为9,高为4的等腰梯形,则该几何体的全面积为____ 8、(汕头市2015届高三)给出下列命题,其中错误命题的个数为( ) (1)直线a 与平面不平行,则a 与平面内的所有直线都不平行; (2)直线a 与平面不垂直,则a 与平面内的所有直线都不垂直; (3)异面直线a 、b 不垂直,则过a 的任何平面与b 都不垂直; (4)若直线a 和b 共面,直线b 和c 共面,则a 和c 共面A .1 B2 C3 D 4αααα9、(汕尾市2015届高三)已知直线l ⊥平面α,直线m ⊆平面β恒谦网,则下列四个结论:①若//αβ,则l m ⊥ ②若αβ⊥,则//l m③若//l m ,则αβ⊥④若l m ⊥,则//αβ。
广东省13市2015届高三上学期期末考试数学理试题分类汇编:复数

广东省13市2015届高三上学期期末考试数学理试题分类汇编复数一、选择题1、(潮州市2015届高三)复数在复平面内对应的点的坐标为( )A .B .C .D .2、(佛山市2015届高三)复数i 1i 3++等于( ) A .i 21+ B .i 21- C .i 2- D .i 2+3、(广州市2015届高三)已知i 为虚数单位,复数z =()12i i +对应的点位于A .第一象限B .第二象限C .第三象限D .第四象限4、(江门市2015届高三) i 是虚数单位,则=+--)2321)(2123(i i A .1 B .i 2321+- C .i 2321- D .i 2321-- 5、(揭阳市2015届高三)设i 为虚数单位,复数()21z i =+,则z 的共轭复数为A. 2i -B. 2iC. 22i - D .22i +6、(清远市2015届高三)已知a ,b ∈R ,i 是虚数单位,若a +bi 与2-i 互为共轭复数,则(a +bi )2=( )A 、5-4iB 、5+4iC 、3-4iD 、3+4i7、(汕头市2015届高三)我们把复数叫做复数的共轭复数,记作, 若是 虚数单位,,为复数的共轭复数,则( )ABC .D .8、(珠海市2015届高三)若复数z 与23i +互为共轭复数,则复数z 的模||z =A .5 C .7 D . 139、(汕尾市2015届高三)复平面内表示复数(12)i i -的点位于( )A .第一象限B .第二象限C .第三象限 D. 第四象限10、(韶关市2015届高三)已知i 为虚数单位,复数(2i)z i-=在复平面对应点Z 在( ) A .第一象限 B. 第二象限 C .第三象限 D. 第四象限11、(深圳市2015届高三)已知复数z 满足1)1(=+i z (其中i 为虚数单位),则=z ( ) ()()11z i i =+-()1,0()2,0()0,1()0,2bi a -bi a z +=()R b a ∈,z i 1z i =+z z 1z z z ⋅+-=1311A.21i +- B 。
广东省13市2015届高三上学期期末考试数学理试题分类汇编:导数及其应用

广东省13市2015届高三上学期期末考试数学理试题分类汇编导数及其应用一、填空题1、(潮州市2015届高三)曲线323y x x =-+在点1x =处的切线方程为2、(揭阳市2015届高三)函数()1x f x e =-的图象与x 轴相交于点P ,则曲线在P 处的切线方程是3、(深圳市2015届高三)设P 是函数x y ln =图象上的动点,则点P 到直线x y =的距离的最小值为4、(珠海市2015届高三)已知函数()f x 的导函数为()f x ',且满足3()=(2)f x x x f '-⋅,则函数()f x 在点(2,(2)f )处的切线方程为二、解答题1、(潮州市2015届高三)已知函数()ln f x x a x =-,()1ag x x+=-(R a ∈). ()1若1a =,求函数()f x 的极值;()2设函数()()()h x f x g x =-,求函数()h x 的单调区间;()3若在[]1,e ( 2.718e =⋅⋅⋅)上存在一点0x ,使得()()00f x g x <成立,求a 的取值范围.2、(佛山市2015届高三)已知函数()()ln x a f x x-=. (Ⅰ) 若1a =-,证明:函数()f x 是()0,+∞上的减函数;(Ⅱ) 若曲线()y f x =在点()()1,1f 处的切线与直线0x y -=平行,求a 的值; (Ⅲ) 若0x >,证明:()ln 1e 1x x xx +>-(其中e 2.71828=⋅⋅⋅是自然对数的底数).3、(广州市2015届高三)已知函数()2ln af x x x x=--,a ∈R . (1)讨论函数()f x 的单调性;(2)若函数()f x 有两个极值点1x ,2x , 且12x x <, 求a 的取值范围; (3)在(2)的条件下, 证明:()221f x x <-.4、(惠州市2015届高三)已知函数()(0)tf x x x x=+>,过点(1,0)P 作曲线()y f x =的两条切线PM ,PN ,切点分别为M ,N . (1)当2t =时,求函数()f x 的单调递增区间; (2)设()g t MN =,求函数()g t 的表达式;(3)在(2)的条件下,若对任意的正整数n ,在区间642,n n ⎡⎤+⎢⎥⎣⎦内,总存在1m +个数121,,,,,m m a a a a +使得不等式121()()()()m m g a g a g a g a ++++<成立,求m 的最大值.5、(江门市2015届高三)已知函数1)(23-+=ax x x f (R a ∈是常数).⑴设3-=a ,1x x =、2x x =是函数)(x f y =的极值点,试证明曲线)(x f y =关于点) )2( , 2(2121x x f x x M ++对称; ⑵是否存在常数a ,使得] 5 , 1 [-∈∀x ,33|)(|≤x f 恒成立?若存在,求常数a 的值或取值范围;若不存在,请说明理由.(注:曲线)(x f y =关于点M 对称是指,对于曲线)(x f y =上任意一点P ,若点P 关于M 的对称点为Q ,则Q 在曲线)(x f y =上.)6、(揭阳市2015届高三)若实数x 、y 、m 满足||||-≤-x m y m ,则称x 比y 更接近m . (1)若23-x 比1更接近0,求x 的取值范围;(2)对任意两个正数a 、b ,试判断2()2+a b 与222+a b 哪一个更接近ab ?并说明理由; (3)当2≥a 且1≥x 时,证明:ex比+x a 更接近ln x .7、(清远市2015届高三)设函数()ln(1),()ln(1)1xf x a xg x x bx x=-+=+-+. (1)若函数()f x 在0x =处有极值,求函数()f x 的最大值;(2)①若b 是正实数,求使得关于x 的不等式()0g x <在()0,+∞上恒成立的b 取值范围; ②证明:不等式.)*(21ln 112N n n k knk ∈≤-+∑=8、(汕头市2015届高三)已知函数R k k x x k x x x f ∈-+++++=]2)()[(log )(2222,(1)求函数)(x f 的定义域D (用区间表示), (2)当2-<k 时,求函数)(x f 的单调递增区间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广东省13市2015届高三上学期期末考试数学理试题分类汇编
复数
一、选择题
1、(潮州市2015届高三)复数()()11z i i =+-在复平面内对应的点的坐标为( )
A .()1,0
B .()2,0
C .()0,1
D .
()0,2 2、(佛山市2015届高三)复数
i 1i 3++等于( ) A .i 21+
B .i 21-
C .i
2- D .i 2+ 3、(广州市2015届高三)已知i 为虚数单位,复数z =()12i i +对应的点位于
A .第一象限
B .第二象限
C .第三象限
D .第四象限
4、(江门市2015届高三) i 是虚数单位,则=+--)2
321)(2123(i i A .1 B .i 2321+- C .i 2321- D .i 2
321-- 5、(揭阳市2015届高三)设i 为虚数单位,复数()21z i =+,则z 的共轭复数为
A. 2i -
B. 2i
C. 22i - D .22i +
6、(清远市2015届高三)已知a ,b ∈R ,i 是虚数单位,若a +bi 与2-i 互为共轭复数,则(a +bi )2=( )
A 、5-4i
B 、5+4i
C 、3-4i
D 、3+4i
7、(汕头市2015届高三)我们把复数bi a -叫做复数bi a z +=()R b a ∈,的共轭复数,记作z , 若i 是
虚数单位,1z i =+,z 为复数z 的共轭复数,则1z z z ⋅+-=( )
A .21+
B .23+
C .221-
D .221+
8、(珠海市2015届高三)若复数z 与23i +互为共轭复数,则复数z 的模||z =
A .13
B .5
C .7
D . 13
9、(汕尾市2015届高三)复平面内表示复数(12)i i -的点位于( )
A .第一象限
B .第二象限
C .第三象限 D. 第四象限
10、(韶关市2015届高三)已知i 为虚数单位,复数(2i)z i
-=在复平面对应点Z 在( )
A .第一象限 B. 第二象限 C .第三象限 D. 第四象限
11、(深圳市2015届高三)已知复数z 满足1)1(=+i z (其中i 为虚数单位),则=z ( ) A.
21i +- B 。
21i -- C 。
21i + D 。
2
1i - 12、(肇庆市2015届高三)=+-i i 131 A .i 21+
B .i 21+-
C .i 21-
D .i 21--
二、填空题
1、(惠州市2015届高三)已知复数32
z a i =
-⋅ (R a ∈),若i z 23212-=,则实数a 的值为__________
参考答案
一、选择题
1、B
2、C
3、B
4、D
5、A
6、D
7、A 8、A 9、A 10、C 11、D 12、D
二、填空题
1、1
2。
