势垒贯穿与应用解读
量子力学3.4666势垒贯穿

(7)
以上二式说明入射粒子一部分贯穿势垒到 x a 的III区域, 另一部分则被势垒反射回来。
D R 1
表明粒子数守恒
§2.8 势垒贯穿续5
(2)E<U0情形
V ( x)
1 2
2 k2 2 (E U0 )
令 其中
V0
是虚数
k 2 ik 3
1 2
I
II
III
4k12 k32 D 2 (k1 k32 ) 2 sh 2 ak3 4k12 k32
(9)
此结果表明,即使 E U 0,透射系数 D 一般不等于零。 隧道效应 (tunnel effect) 粒子能够穿透比它动 能更高的势垒的现象称为 隧道效应.它是粒子具有 波动性的生动表现。当然, 这种现象只在一定条件下 才比较显著。右图给出了 势垒穿透的波动图象。
代入
k1 k1 ik1a 1 C ik2 a { ( A A ') ( A A ')}e (1 )e 2 2k 2 2 k2
{ A(k1 k2 ) A '(k2 k1 )}eik2 a C (k1 k2 )eik1a
k2 k1 ik2 a ik1a C {A A ' }e e k1 k2
(k1 k2 ) 2 (k2 k1 ) 2 ) ik1a C { } Ae (k1 k2 ) 2 e ik2 a (k2 k1 ) 2 eik2 a
4k1k2 e ik1a C A 2 ik2 a 2 ik2 a (k1 k2 ) e (k2 k1 ) e
(k2 k1 ) (e e ) ik2 a ik1a C {1 } Ae e 2 ik2 a 2 ik2 a (k1 k2 ) e (k2 k1 ) e
S(五章3讲)势垒贯穿

令
k2 ik3
1 2
Ⅰ
Ⅱ
Ⅲ
2 其中 k3 2 (U 0 E )
是实数
在(6)和(7)式中,把 k2换为 ik3, 得:
透射系数:
T
2 4k12 k3 2 , 2 2 2 2 2 (k1 k3 ) sh k3a 4k1 k3
反射系数:
2 2 (k12 k3 ) sh2 k3a R 2 2 2 2 (k1 k3 ) sh2 k3a 4k12k3
宾尼
罗赫尔
鲁斯卡
例1:
U(x)
U0
I 0 II
作业1: 作业2: 作业3:已知核的势能曲线如图,计算α 粒子的透射系数
1.
2.电子通过单一势垒时,透射系数一般很小,但是 在通过双势垒时,却可以出现透射系数为100%的情况,
称为共振隧穿,试研究这种情况并给出共振隧穿发生的条件
附录1:了解纳米与分子电子学
ik1a
可得透射波振幅 C 与入射波振幅 A 间的关系
4k1k 2 e C A 2 ik2 a 2 ik2 a (k1 k 2 ) e (k1 k 2 ) e
(4)
以及反射波振幅A '与入射波振幅A间的关系
2i(k k ) sin ak2 A A 2 ik2 a (k1 k 2 ) e (k1 k 2 ) e
(x a )
由左向右的透射波
因Ⅲ区无由右向左传播 的平面波,故 C 0
定系数:
由 波 函 数 的 连 续 性 条 件
I Aeik1x A eik1x III C eik1x
( x 0) (x a )
(1) (2) (3)
§3-6势垒贯穿、隧道效应Barrierpenetrationthet-解读

(15-39’)
a
De )
在(15-39')中消去C、D、G可得比值: B (k 2 2 ) sh 2a 2ika { } e A 2ikcha (k 2 2 ) sha
而反射系数 2
|B| 4k 2 2 1 R { 1 } | A |2 (k 2 2 ) 2 sh 2a
i ( kx wt )
*由自由粒子的波函数 ( x, t ) e
可得:
(15-3)
i E t i p x 2 2 2 p 2 x
(15-4)
*由(15-1)式,对于自由电子v(x)=0,有
E
p
2
2m
0
乘以即得
p2 2 2 (E ) i 0 或即 2 2m t 2m t
•§3-5 Schoedinger 方程 *Schroedinger方程的建立
(Establishment of the Schroedinger equation)
*Schroedinger方程是量子力学中最主要的一个方 程。但这一方程是Schroedinger “猜”出来的。
*当时de Brogile波的概念刚刚传到瑞士苏黎世,在 Debye的学生Schroedinger 做关于物质波的报告时, Debye评价说,“有了波就应有波的方程”,不久, Schroedinger 就给出了物质波的波动方程。 *“导出” Schroedinger方程的一种方法
势垒贯穿(Barrier penetration) 考察粒子穿越如图(15-6‘)原子的势垒. • 按照经典的观点,当粒子的能量E<V0时, 粒子穿过势垒的概率为零。而当E>V0时, 这一概率为1.
势垒贯穿解读课件

微电子学
微电子学是研究在微米和纳米尺度下电子行为和应用的科学 。在微电子学中,势垒贯穿是一个重要的概念,用于描述电 子通过势垒的传输过程。
在微电子器件中,如晶体管、二极管和集成电路,势垒贯穿 决定了电子的流动和器件的性能。通过优化势垒参数,可以 提高器件的开关速度和降低能耗。
量子计算
量子计算是一种基于量子力学原理的计算方式,具有经典 计算无法比拟的并行性和计算速度。势垒贯穿在量子计算 中扮演着关键角色。
结构设计
通过改变势垒的结构设计,如采用多 级势垒、异质结等结构,实现对电子 传输的更精细调控。
势垒贯穿与其他领域的交叉研究
物理与化学
势垒贯穿涉及到物理和化学等多个学 科领域,交叉研究有助于深入理解势 垒贯穿的机制和拓展其应用范围。
生物医学应用
势垒贯穿技术在生物医学领域如传感 器、诊断和治疗等方面具有潜在的应 用价值,开展交叉研究有助于推动相 关领域的发展。
量子比特是量子计算的基本单元,而势垒贯穿决定了量子 比特的相干性和演化过程。通过控制势垒参数,可以实现 量子比特的逻辑门操作和量子算法的实现。
纳米科技
纳米科技是一门研究在纳米尺度上设计和制备材料、器件和系统的科学。在纳米 科技中,势垒贯穿是一个重要的物理现象,影响纳米器件的性能和稳定性。
在纳米尺度下,材料和系统的性质与宏观尺度有很大的不同,因此需要深入研究 势垒贯穿的机制和规律。通过优化势垒参数,可以提高纳米器件的效率、稳定性 和可靠性。
深入了解实验中如何 观测和验证量子力学 中的现象。
THANKS
感谢观看
确保实验过程中使用的电压和电 流在安全范围内,避免对实验人
员和设备造成伤害。
实验精度要求
在实验过程中,要确保显微镜的焦 距、电压和电流的测量精度,以提 高实验结果的准确性。
势垒贯穿与应用解读

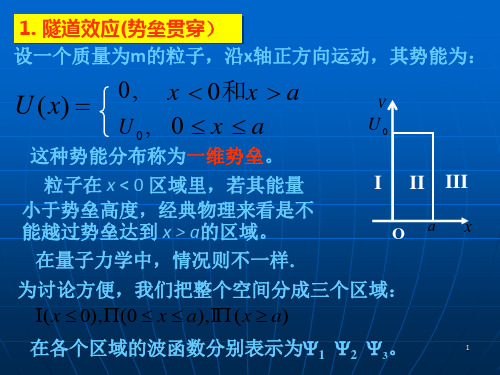
势垒贯穿与应用 势垒贯穿设一个质量为m 的粒子,沿x 轴正方向运动,其势能为: U(x)=0 x<0 和x>a U(x)=U 0 0≤x ≤a这种势能分布称为一维势垒。
粒子在 x < 0 区域里,若其能量小于势垒高度,经典物理来看是不能越过势垒达到 x > a 的区域。
在量子力学中,情况又如果呢?为讨论方便,我们把整个空间分成三个区域: 在各个区域的波函数分别表示为ψ1 ψ2 ψ3三个区间的薛定谔方程简化为:求出解的形式是)(),0(),0(a x a x x ≥I ∏≤≤∏≤I ),()(212122x E dx x d m ϕϕ=- 0≤x ),()()(22202222x E x U dxx d m ϕϕϕ=+- ax ≤≤0),()(232322x E dxx d m ϕϕ=- a x ≥222 mEk =2021)(2 E U m k -=,0)()(12212≤=+x x k dxx d ϕϕa x x k dxx d ≤≤=-0,0)()(221222ϕϕa x x k dxx d ≥=+,0)()(32232ϕϕikxikx e A Ae -'+=ψ1x ik Be 12+=ψikx Ce =ψ3O(1)E>U 0按照经典力学观点,在E>U 0情况下,粒子应畅通无阻地全部通过势垒,而不会在势垒壁上发生反射而在微观粒子的情形,却会发生反射。
(2)E<U 0从解薛定谔方程的结果来看,在势垒内部存在波函数ψ。
即在势垒内部找出粒子的概率不为零,同时,在x>a 区域也存在波函数,所以粒子还可能穿过势垒进入x>a 区域粒子在总能量E 小于势垒高度时仍能贯穿势垒的现象称为隧道效应定义粒子穿过势垒的贯穿系数是:透射波的概率密度与入射波概率密度的比值。
势垒高度U 0越低、势垒宽a 度越小,则粒子穿过势垒的概率就越大。
隧道效应是经典力学所无法解释的由于电子的隧道效应,金属中的电子并不完全局限于表面边界之内,电子密度并不在表面边界处突变为零,而是在表面以外呈指数形式衰减,衰减长度约为1nm只要将原子线度的极细探针以及被研究物质的表面作为两个电极,当样品与针尖的距离非常接近时,它们的表面电子云就可能重叠若在样品与针尖之间加一微小电压U b 电子就会穿过电极间的势垒形成隧道电流。
隧道效应及其应用
8
1981年宾尼希和罗雷尔利用电子扫描隧道显微镜 (STM)给出了晶体表面的三维图象。
钻石中的原子已被看到
利用光学中的受抑全反射理论,研制成功光子 扫描隧道显微镜(PSTM)。1989年提出成象技术。 它可用于不导电样品的观察。
9
Hale Waihona Puke 2a 2 m (U 0 E )
隧道效应是经典力学所无法解释的,因为按经典 力学计算结果,在势垒区,粒子的动能小于零,动 量是虚数。 隧道效应来源于微观粒子的波粒二象性。
由于微观粒子的波动性,微观粒子遵守“不确定关系”, 粒子的坐标x和动量P不可能同时具有确定的值,自然作为坐 标函数的势能和作为动量函数的动能当然也不能同时具有确 定的值。因此,对微观粒子而言,“总能量等于势能和动能 6 之和”这一概念不再具有明确的意义。
2.隧道显微镜STM
Scanning tunneling microscopy 由于电子的隧道效应,金属中的电子并不完全局限于 表面边界之内,电子密度并不在表面边界处突变为零, 而是在表面以外呈指数形式衰减,衰减长度越为1nm。 只要将原子线度的极细探针 以及被研究物质的表面作为 两个电极,当样品与针尖的 距离非常接近时,它们的表 面电子云就可能重叠。 若在样品与针尖之间 加一微小电压U,电子 就会穿过电极间的势 垒形成隧道电流。
2a 2 m (U 0 E )
| 3 (a) |2 | 2 (a) |2 T exp(2k1a) T 2 2 | 1 (0) | | 2 (0) | T exp(2k1 0)
e
2 k1a
e
5
结果表明:势垒高度U0越低、势垒宽a T e 度越小,则粒子穿过势垒的概率就越大。 如果a或m为宏观大小时,T 0 ,粒子实际上将不 能穿过势垒。 隧道效应是一种微观效应。 U 0 E 5eV 时,势垒的宽度约50nm 以上时,贯穿 当 系数会小六个数量级以上。隧道效应在实际上已经 没有意义了。量子概念过渡到经典了。
基于海森堡不确定原理解释势垒贯穿效应

海森堡不确定原理是量子力学中的一个基本原理,它指出无法同时准确确定一个粒子的位置和动量。
这一原理不仅对微观世界有着重要影响,还在解释一些宏观现象中发挥着作用。
其中,基于海森堡不确定原理解释的势垒贯穿效应是一个引人注目的话题。
势垒贯穿效应是指粒子在势垒中以一种不可思议的方式“穿透”了势垒,即使根据经典物理学,这是不可能的。
在经典物理学的观点中,粒子是不能穿透比它的能量高的势垒的,但是根据量子力学的观点,这是可能的。
海森堡不确定原理为我们提供了一种全新的解释方式,帮助我们更好地理解势垒贯穿现象。
让我们简要回顾一下海森堡不确定原理的内容。
海森堡不确定原理指出,我们无法同时准确测定一个粒子的位置和动量,即在某一时刻我们测定粒子的位置时,它的动量就会变得不确定;相反地,如果我们测定它的动量,那么它的位置将变得不确定。
这一原理揭示了微观世界的本质,并对我们理解粒子的运动方式以及与其他粒子的相互作用方式产生了深远的影响。
在量子力学中,粒子并不像经典物理学中的粒子那样具有确定的位置和动量,而是具有一定的概率分布。
也就是说,一个粒子并不一定会出现在一个特定的位置,而是有一定的概率分布,同时具有一定的动量。
这种概率性质使得粒子可以在经典物理学认为不可能通过的势垒中出现的可能性变得非常高。
接下来,让我们着眼于势垒贯穿效应。
在经典物理学中,一个粒子如果能量不够高无法通过势垒,那么它就会被势垒完全阻挡。
然而,根据量子力学的观点,粒子具有一定的概率穿越势垒。
这一现象就是势垒贯穿效应。
海森堡不确定原理解释了这一现象:即使粒子的能量低于势垒的高度,它也有一定概率出现在势垒的另一侧。
从宏观角度来看,势垒贯穿效应在一些重要的领域中有着广泛的应用。
在核聚变反应中,贯穿效应可以帮助核反应进行,从而产生能量。
在半导体器件中,贯穿效应也在电子穿越势垒时起着重要的作用。
海森堡不确定原理为我们解释了一些宏观现象背后微观机制,并且在一定程度上指导了我们的科学研究和技术应用。
势垒贯穿效应的应用

势垒贯穿效应的应用
势垒贯穿效应是一种特殊的物理效应,可以广泛应用于电子学、
半导体工业、光电子学等领域。
它是指当两块不同的半导体接触时,
会形成一层势垒,阻碍电子的流动。
但当外加电压达到某一特定值时,这层势垒会被贯穿,电子开始自由流动。
这种效应可以用于制造二极管、晶体管等电子元件,也可以应用于光电探测器、太阳能电池等领域。
在半导体制造中,势垒贯穿效应可以被用来制造pn结。
pn结是
一种半导体器件,由两块接触的不同半导体组成,其中一块为p型半
导体,另一块为n型半导体。
在接触处形成的势垒使得器件只允许有
一个方向的电流通过,这种器件被广泛应用于电力电子、电子通信等
领域。
势垒贯穿效应也可以被用来制造场效应晶体管(FET),这是一
种非常重要的电子元件,被广泛应用于微电子学、电脑制造等领域。
在光电子学中,势垒贯穿效应可以被用来制造光电探测器。
这种
探测器利用势垒贯穿效应来提高光电子的感受性能,能够将光信号转
换为电信号,被广泛应用于通信、医疗、安全等领域。
最后,势垒贯穿效应也可以被用来制造太阳能电池。
太阳能电池
的工作原理就是利用势垒贯穿效应将光能转换为电能。
当光照射到太
阳能电池上时,会激发电子从势垒中跃出,形成电流。
这种技术已经
被广泛应用于环保、节能等领域,成为未来能源发展的重要方向。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
势垒贯穿与应用 势垒贯穿
设一个质量为m 的粒子,沿x 轴正方向运动,其势能为: U(x)=0 x<0 和x>a U(x)=U 0 0≤x ≤a
这种势能分布称为一维势垒。
粒子在 x < 0 区域里,若其能量小于势垒高度,经典物理来看是不能越过势垒达到 x > a 的区域。
在量子力学中,情况又如果呢?
为讨论方便,我们把整个空间分成三个区域: 在各个区域的波函数分别表示为ψ1 ψ2 ψ3
三个区间的薛定谔方程简化为:
求出解的形式是
)
(),0(),0(a x a x x ≥I ∏≤≤
∏≤I ),()(212
122x E dx x d m ϕϕ=- 0
≤x ),()()(22202222x E x U dx
x d m ϕϕϕ=+- a
x ≤≤0),()(232322x E dx
x d m ϕϕ=- a x ≥222 mE
k =
2
021)(2 E U m k -=
,0)()
(122
12≤=+x x k dx
x d ϕϕa x x k dx
x d ≤≤=-0,0)()(22
12
22ϕϕa x x k dx
x d ≥=+,0)()(32
2
32ϕϕikx
ikx e A Ae -'+=ψ1x ik Be 12+=ψikx Ce =ψ3O
(1)E>U 0
按照经典力学观点,在E>U 0情况下,粒子应畅通无阻地全部通过势垒,而不会在势垒壁上发生反射而在微观粒子的情形,却会发生反射。
(2)E<U 0
从解薛定谔方程的结果来看,在势垒内部存在波函数ψ。
即在势垒内部找出粒子的概率不为零,同时,在x>a 区域也存在波函数,所以粒子还可能穿过势垒进入x>a 区域粒子在总能量E 小于势垒高度时仍能贯穿势垒的现象称为隧道效应定义粒子穿过势垒的贯穿系数是:
透射波的概率密度与入射波概率密度的比值。
势垒高度U 0越低、势垒宽a 度越小,则粒子穿过势垒的概率就越大。
隧道效应是经典力学所无法解释的由于电子的隧道效应,金属中的电子并不完全局限于表面边界之内,电子密度并不在表面边界处突变为零,而是在表面以外呈指数形式衰减,衰减长度约为1nm
只要将原子线度的极细探针以及被研究物质的表面作为两个电极,当样品与针尖的距离非常接近时,它们的表面电子云就可能重叠若在样品与针尖之间加一微小电压U b 电子就会穿过电极间的势垒形成隧道电流。
隧道电流对针尖与样品间的距离十分敏感。
若控制隧道电流不变,则探针在垂直于样品方向上的高度变化就能反映样品表面的起伏。
因为隧道电流对针尖与样品间的距离十分敏感。
若控制针尖高度不变,通过隧道电流的变化可得到表面态密度的起伏利用STM 可以分辨表面上原子的台阶、平台和原子阵列。
可以直接绘出表面的三维图象
使人类第一次能够实时地观测到单个原子在物质表面上的排列状态以及与表面电子行为有关的性质。
在表面科学、材料科学和生命科学等领域中有着重大的意义和广阔的应用前景。
2123|)0(||)(|ϕϕa T =)
02exp()2exp(|)0(||)(|112222k T a k T a --=
=ϕϕ)(22201E U m a
a
k e
e
--
-==
恒星内部能够发生核聚变吗?
太阳的基本参数为
质量:M = 2⨯1033 g , 半径:R = 7⨯1010 cm , 光度:L = 4⨯1033 erg/s 。
据原子核的比结合能曲线知,轻核聚变或重核裂变都会释放能量。
然而,原子核间存在的Coulomb 势垒将阻碍轻核的聚变。
让我们做一简单估计。
质量数为A 原子核的半径为r N = 1.2A 1/3 fm ;在距离小于r N 的区域核力才起作用,而大于r N 时以Coulomb 作用为主。
因此核电荷数为Z 1、Z 2,质量数为A 1、A 2的两个核之间的Coulomb 势垒的高度为
2
1212c 1/31/3N1N2
12
1.2Z Z e Z Z
V r r A A =
++ MeV 。
(5) 然而,两核的热运动动能~ kT ~ 8.6⨯10-11 T MeV ;恒星中心温度只有~107K 。
问题是:对于典型的具有一个太阳质量的恒星,其内部能发生显著的热核聚变反应吗?还以氢燃烧为例,V c ~1MeV>>kT 0~1keV 。
热能大于V c 的粒子所占百分比 ~ exp[-V c /(kT)] ~ e -1000 ~ 5⨯10-435。
每秒
太阳内部氢核发生有效碰撞的次数 ~ Nnv σ ~ 2⨯1063;其中总粒子数N~M /m p ,n = N/(4π3R /3),氢核运动速度v ~ (2kT 0/m p )1/2,碰撞截面σ ~ πr N 2。
如果认为只有能量高于V c 的粒子才能碰撞后聚变,太阳每秒核反应的粒子数目~10-435
<< 。
似乎热核燃烧也不能提供太阳发光。
图1 核Coulomb 势垒
实际上,微观粒子是存在波粒二象性的。
考虑到氢核的波动性,会发生势垒贯穿效应。
研究发现,只要粒子运动动能为Coulomb势垒的ξ倍,即
kT
~ ξV c,ξ∈(10-4, 2⨯10-4),(6)
这类核的燃烧过程就能在恒星内部大规模地出现。
(6)式可以用来定某种核的点火温度。
从这里看到,如果不考虑量子效应,我们甚至不能理会太阳为什么发光。
纳米级隧道效应器件
集成电路问世以来,IC技术一直沿着电路和器件特征尺寸按比例缩小的
办法大踏步前进,特征尺寸越小,电路和器件的性能越好。
正由于此,上世
纪末,Intel公司将集成度和性能都达到空前高水平的奔腾4芯片和PC送到
用户手上。
目前MOSFET的沟道长度已趋近0.1mm(=100nm),按比例缩
小的办法还能继续下去吗?答案是否定的。
早在20年以前,著名的“半导体
器件物理”一书的作者S.M.Sze就预计,传统MOSFET的沟道长度应大于约
70nm。
IBM研究中心的D.J.F.rank盼望能作出沟道长度达20-30nm的MOSFET,但是沟道再短就很困难了。
也就是说20-30nm可能就是器件特征尺寸的物理
极限。
为了减小器件特征尺寸,从而达到整体提升器件性能的目的,人们希望
找到其它的方法来避开上述困难。
在设法抑制短沟道效应的实验中发现,当
特征尺寸逼近物理极限时,基于量子隧道效应的隧道效应器件比传统MOSFET 好。
换言之,双电子层隧道晶体管和共振隧道二极管等隧道效应器件比MOSF ET更适合于纳米电子学。
这是由美国Sandia国家实验室J.Simmons等人首先研究的隧道效应器件。
它由一个绝缘势垒和两个二维量子阱组成,绝缘势垒位于两个量子阱之间。
为使器件正常工作,量子阱和势垒厚度都很小,分别为15nm和12.5nm。
由于势阱厚度很小,势阱可看成是二维的,电子运动被限制在阱平面内。
San
dia的研究者们把Deltt和MOSFET作类比,称上量子阱接触(Top quantum w ell contact)为源(电极)。
下量阱接触(Bottom quantum well contact)为漏(电极)。
器件工作时,由于量子力学隧道效应,电子从上量子阱(Top qua ntum well)隧道穿过势垒层到达下量子阱(Bottom quantum well)。
上量子阱相当于源区,下量子阱相当于漏区,势垒区(Barrier)相当于沟道,上控制栅(Top control gate)相当于MOSFET的栅极;和上控制栅相对应,还有背控制栅(Back control gate),这个栅通常不是必备的(optional)。
从图1可以看到,源漏电极都是平面型的。
为了保证源电极只和上量子阱接触,漏电极只和下量子阱接触,Deltt还有背耗尽栅(Back depletion gate)和上耗尽栅(Top detletion gate)。
由量子力学理论可知:量子阱中的电子能级由阱的尺寸和势垒高度决定,当阱的尺寸很小时,电子能级间隔很大;当由势垒隔开的两个量子阱中的电子能级相同(对准)时,产生电子由一个阱到另一个阱的量子隧穿效应,因为在量子隧穿过程中,电子要遵守能量守恒和动量守恒原理。
一般来讲,在未加外电压(包括源-漏电压和栅压)时,两个量子阱中没有相同的电子能级,因而没有源——漏电流,器件是截止的。
加上外电压时,势阱中电子能级会发生位移,电压增大位移增大,当两个势阱中的电子能级对准时(共振),隧道效应发生,器件导通。
可用较少数量的器件完成相当的功能。
如用两个Deltt串联可组成CMO S电路中需要n型和p型两种MOSFET的静态随机存储器单元。
