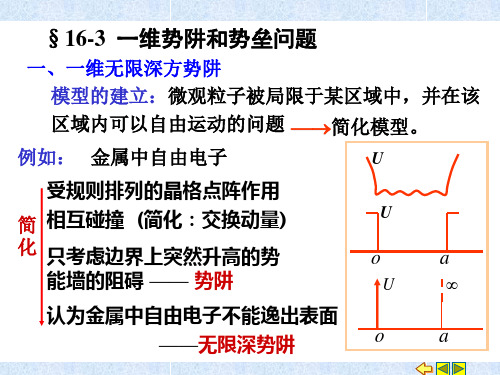
一维方势垒
16-3 一维势阱和势垒问题
]
ψ1 = A1 e + B1 e
ik1x
−ik1x
− ik 2 x
1
( x < 0)
( x > a)
U
通解: 通解
ψ 2 = A2 e
ik 2 x
1
+ B2 e
(0 ≤ x ≤ a )
U0
ψ 3 = A3 eik x + B3 e − ik x
处无反射波： 由 x > a 处无反射波： B 3 = 0 令 A1 = 1（以入射波强度为标准） 以入射波强度为标准） 由波函数的 标准条件得 O 可解得
§16-3 一维势阱和势垒问题
一、一维无限深方势阱 模型的建立：微观粒子被局限于某区域中， 模型的建立：微观粒子被局限于某区域中，并在该 区域内可以自由运动的问题 →简化模型。 →简化模型 简化模型。 例如： 例如： 金属中自由电子 受规则排列的晶格点阵作用 简化：交换动量) 简 相互碰撞 (简化：交换动量) 化 只考虑边界上突然升高的势 能墙的阻碍 —— 势阱 认为金属中自由电子不能逸出表面 ——无限深势阱 无限深势阱
2 2πx p = ∫ |ψ | d x = ∫ sin dx a a 0 0
4 4 2 a a
2a πx 2 πx = ∫ sin d( ) aπ a a 0
4
a
1 πx 1 2 2 2π x = ( − sin ) π a 4 a
a
4
= 9.08 × 10 −2
0
练习： 练习
已知： 已知：
ψ = cx ( L − x )
A A2 ∞ 2 dx = ∫ dx = A arctg x − ∞ = A2π = 1 ∫∞ 1 + ix 1 + x2 − −∞
16-3一维势阱和势垒问题解读
x a
a x
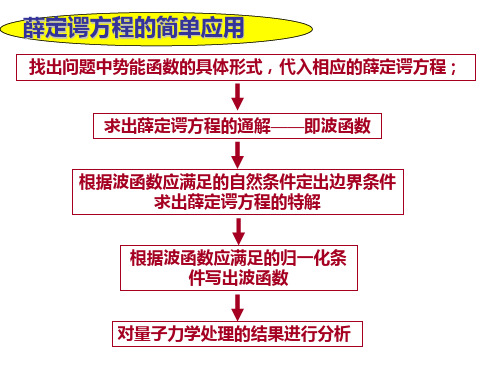
第k激发态(n=k+1)有k个节点。
（2）一维无限深势阱 的粒子位置概率密度 分布
1
2
n 1
0 2 2 n 2 a
2
x
0 无数峰：量子 经典均匀分布 0
a a n 1，x 处，几率最大 0 3 2 b n ，峰数 ，当n 时，
4
U0
II
III
o
a
x
而在微观粒子的情形，却会发生反射。
ቤተ መጻሕፍቲ ባይዱ
（2）E<U0 从解薛定谔方程的结果来看，在 势垒内部存在波函数2。即在势垒内 部找出粒子的概率不为零，同时，在 x>a区域也存在波函数，所以粒子还 I 可能穿过势垒进入x>a区域。
V
V0
II
III
o
a
x
粒子在总能量E小于势垒高度时仍能贯穿势垒的 现象称为隧道效应。
式中 A和α是待定常数，由边界条件和归一化条 件确定。
( x) A sin( kx )
从物理上考虑，粒子不可能透过阱壁，因而按照波 函数的统计诠释，要求在阱壁上和阱外波函数为0。 考虑波函数在阱壁上等于零的情况，即
(0) 0, (a) 0
————边界条件
(0) 0
这说明：并非任何 E值所对应的波函数都能满足一维 无限深方势阱所要求的边界条件，只有当能量取上式 给出的那些分立的值 En（体系的能量本征值）时， 相应的波函数才是物理上有意义的，即本问题中体系 的能量是量子化的，亦即体系的能谱是分立的。
2
2
2 2 2
( x) A sin kx
nx n ( x) A sin( ) a
量子力学课件(6)( 一维方势垒、隧道效应)
探针
空气隙
样品 STM工作示意图
§8 一维方势垒 隧道效应
第二章 薛定谔方程
使人类第一次能够实时地观测到单个原子在物 质表面上的排列状态以及与表面电子行为有关的性 质。在表面科学、材料科学和生命科学等领域中有 着重大的意义和广阔的应用前景。
求出解的形式画于图中。
量子力学结果分析： （1）E>V0情况 在经典力学中，该情况的粒子 可以越过势垒运动到x>a区域，而 在量子力学中有一部分被反弹回去， I 即粒子具有波动性的具体体现。 （2）E<V0情况
V
隧道效应
V0
II
III
o
a
x
在经典力学中，该情况的粒子将完全被势垒挡回， 在x<0的区域内运动；而在量子力学中结果却完全不同 ，此时，虽然粒子被势垒反射回来，但它们仍有粒子穿 透势垒运动到势垒里面去，所以我们将这种量子力学特 有的现象称“隧道效应”。
§8 一维方势垒 隧道效应 X=a处， 2 (a) 3 (a)
第二章 薛定谔方程
可得
于是
d 3 ( x) d 2 ( x) |x a |x a dx dx ik1 k2 ik1a k2a A2 e A3 2k2 ik1 k2 ik1a k2a ' A2 e A3 2k 2 2 2 k1 k2 ik1a ' A1 [ sh(k2 a)]e A3 2ik1k2 2 2 k1 k2 ik1a ' A1 A1 [ch(k2 a) sh(k2 a)]e A3 2ik1k2
§8 一维方势垒 隧道效应
第二章 薛定谔方程
量子力学§3.2一维方势阱
ctg
2V0 a 2
2 2 2
2 2 2V0 a 2 / 2 2 / 4
2 2 2 2 2 即 V0 a ，或 V0 时 2 8 8 a
半壁无限深方势阱存在束缚定态。
为束缚态，相应于第二条
tan 线，第一条线仍存 2 在）。 V0 a 继续增大，则将出现更多激发态。
V0→∞时，结果与无限深势阱的偶宇称态能量一致。
a 2、奇宇称态 2 ( x) ~ sin kx | x | 2 与上类似，由连续条件可得： k cot(ka / 2) cot
a为阱宽，V0为阱深。
V(x)
V0 V0
E
-a/2 0
a/2
势的特点：空间反射对称
x
讨论束缚态，即0 E V0
写出分区定态方程
在阱外(经典禁介区)
d2 2 1 2 (V0 E ) 1 0 2 dx (1)
在阱内(经典允许区)
d 2 E 2 2 2 0 2 dx
阱外
V ( x) ( x 0 x a)
定态薛定谔方程 阱外：
2 d 2 2 dx 2 2 ( x) E 2 ( x)
d ( x ) E ( x ) 1 1 2 dx 2
2 2
阱内：
根据波函数的统计解释 阱外
2 ( x) 0
令
2
2 (V0 E )
2 E k
1 '' k 1 0
(0 x a)
2 '' 2 0
2
x a
一维势垒问题总结
一维势垒中的透射系数利用传递矩阵方法研究了粒子在一维势垒中运动时的粒子的透射系数,主要研究的是在一个方势垒两个方势垒中透射系数，对以上的透射系数的总结，推出了对于任意势垒中透射系数， 并讨论了透射系数、反射系数与势垒宽度的关系.一维方势垒势垒模型在方势垒中，遇到的问题和 值得注意的地方。
在求方势垒波 函数中，首先要知道这是一个什 么样问题，满足什么样的方程， 方程可以写成什么样的形式，在 求解方程中，波函数的形式应该怎样需要怎样的分段，分段的过程中，特别要强调的边界条件问题。
并且验证了概率流密度。
在量子力学中，粒子在势垒附近发生的现象是不一样的，能量E 大于势垒高度0u 的粒子在势垒中有一部分发生反射，而能量小于0u 的粒子也会有部分穿过势垒，这在经典力学中是不会发生的。
下面讨论的是一维散射（即在非束缚态下问题，在无穷远处波函数不趋于零）。
重点讨论的是粒子通过势垒的透射和反射，重点在于求出波函数，这就必须求解薛定谔方程，由于)(x U 是与时间无关的，此处是定态薛定谔方程。
定态薛定谔方程通式：ψψψE U m=+∇-222h 在量子力学里, 必须知道波函数ψ, 因此必须要解薛定谔方程t i U x m ∂∂=+∂∂-ψψψh h 2222一维散射问题是一个非束缚态问题(()U x 与时间无关, 而E 是正的).因此令t Ei ex t x h-=)(),(ψψ由此得到ψψψE U dx d m =+-2222h按照势能()U x 的形式, 方程(2)一般需要分成几个部分求解.将上式改写成如下形式0222=+ψψk dxd⎩⎨⎧><<<=.,0,0;0,)(0a x x a x u x U 先讨论0u E >的情形粒子满足薛定谔方程分解为三个区域：⎪⎪⎪⎩⎪⎪⎪⎨⎧>=-<<=+-<=-a x x E x dx d m a x x E x u x dx d m x x E x dx d m ),()(20),()()(20),()(233222220222211222ψψψψψψψh h h （1） ⎪⎪⎪⎩⎪⎪⎪⎨⎧>=+<<=-+<=+a x x mEx dx d a x x u E x dx d x x mEx dxd ,0)(2)(0,0)()()(0,0)(2)(323222022212122ψψψψψψh h特征方程02=++q pr r 的两个根21,r r方程 0=+'+''qy y p y 的通解两个不相等的实根21r r ≠ x r x r e C e C y 2121+= 两个相等的实根21r r = x r e x C C y 1)(21+= 一对共轭复根βαi r ±=2,1)sin cos (21x C x C e y x ββα+=注： 0=+''qy y 的通解:特征方程02=+q r ,当0<q 时，通解xq xq eC e C y ---+=21，当0>q 时，通解xq ixq ie C e C y -+=21方程（1）的解可以表示为：⎪⎪⎪⎩⎪⎪⎪⎨⎧>+=<<+=<+=-----a x de te x a x ce be x x re ae x x mEi x mE i x u E m i x u E m i x mE i x mE i ,)(0,)(0,)(223)(2)(2222100h h hh hh ψψψ （2）定态波函数321,,ψψψ再分别乘上一个含时间的因子Et i eh-，可以看到式子（2）的三式，第一项是左向右传播的平面波，第二项是由右向左传播的平面波，即入射波和反射波。
52_6半无限深势阱_一维势垒解读
2m 2 (U 0 E )
2
cos(ka) k sin(ka)
cos2 ( ka) 2 U 0 2 1 2 sin ( ka) k E
空气隙
样品
STM工作示意图
16
d变~ 10nm
i 变几十倍，非常灵敏。
竖直分辨本领可达约百分之几 nm； 横向分辨本领与探针、样品材料及绝缘物有关， 在真空中可达0.2nm 技术关键： 1. 消震：多级弹簧，底部铜盘涡流阻尼。 2. 探针尖加工：电化学腐蚀，强电场去污， 针尖只有1~2个原子！ 3. 驱动和到位：利用压电效应的逆效应 —— 电致伸缩，一步一步扫描。 扫描一步0.04nm， 扫描12 ，用0.7s
2 d 2 3 ( x ) E 3 ( x ), 2 2m dx
xa
9
2mE 令： k 2
2
2m(U 0 E ) k 2
2 1
三个区间的薛定谔方程化为
U
d 1 ( x) 2 k 1 ( x ) 0, 2 dx
2
x0
U0
d 2 3 ( x ) 2 k 3 ( x ) 0, 2 dx
2
2mE k 2
2
sin ( ka ) 1或
2
ka
h2 E U0 2 2 8ma 32ma
2 2
( x) Be
x
,
xa
结果说明粒子会出现在x＝a的表层附近
6
§6 一维方势垒 势垒贯穿（隧道效应） U
U ( x ) 0, x 0, x a
一维方势垒
利用在 x 0 和 x a处波函数连续性和波函 数微商连续性条件
A A B B k1A k1A k2B k2B Beik2a Beik2a Ceik1a k2 Beik2a k2Beik2a Ck1eik1a
2.6 一维方势垒
可得出A,C 与 A 关系
A
2i(k12 k22 ) sin k2a (k1 k2 )2 eik2a (k1 k2 )2 eik2a
A 2 A2
(k12
(k12 k22 )2 sin 2 k2a k22 )2 sin 2 k2a 4k12k22
透射系数为：
T
JT JC2 A24k12 k 22 (k12 k22 )2 sin 2 k2a 4k12k22
2.6 一维方势垒
由上两式可见，一般情况下，透射系数T 1 ， 反射系数R 0 ，而这之和为1。这表明，在量 子力学中，即是粒子的能量大于势垒高度，仍 有部分被反射回来。这正是微观粒子具有波动 性的体现。
2.6 一维方势垒
下面分别就来 E U0 与 E U0 来讨论
一、E U0 的情形 此时，(x)满足的薛定谔方程为
d 2l dx2
2m h2
El
0
x 0,
d 2m dx2
2m h2
(E
U0 )m
0
0 xa
d 2r dx2
2m h2
Er
0
xa
2.6 一维方势垒
为方便起见，令 方程可改为：
k12
由第二式可见，一般情况下透射系数T 1 ， 当k2a n的特定情况下，其透射系数T 1 ，
这种情形下的透射现象叫做 共振透射
2.6 一维方势垒
二、E U0 的情形
一一一维维维势势势垒垒垒贯贯贯穿穿穿
(2.88)
(2.89)
在x < 0, x > a的区域, 就是 ψ (x) + k = 0, 在0 ≤ x ≤ a, ψ (x) − β = 0,
�� 2 �� 2
k=
�
2mE �2
(2.90)
β=
�
2m(V0 − E ) . �2
.
(2.106)
2.4. 一维势垒贯穿
37
在以上计算的基础上, 我们来讨论些物理问题. 首先我们看到S 不等于零! 这意味着我们可以在势垒的右边找到粒子! 这一完 全不同于经典力学的结论称为隧 道 效 应 (tunneling effect). 下面作更详细的分析. 在势垒左边, x < 0区域, 我们可以计算几率流密度j . j= 1 ˆψ − ψ p ˆψ ∗ ), (ψ ∗ p 2m (2.107)
2 sinh2 βa V0 4E (V0 −E )
CHAPTER 2. 一维问题
= =
A + B, (A − B )β.
(2.95)
= =
Байду номын сангаас
Seika , ikSeika
(2.96)
= =
β + ik + R(β − ik ) β − ik + R(β + ik ). (2.97)
= =
eika−βa S (β + ik ) eika+βa S (β − ik ).
2 sin2 αa V0 4E (E −V0 )
(2.111) . (2.112)
我们应该可以观察到所谓的共振透射。当αa = nπ , n = 1, 2, 3, · · · , |S |2 = 1. 如果粒子遇到一个势井，V0 < 0, 会怎样？(2.112)仍然适用。唯一要注意的 是：当E → 0, T → 0.
一维势垒问题总结
一维势垒问题总结
一维势垒问题是指在一维空间中存在一个势能障碍的物理问题。
该问题涉及到粒子的运动和势能的影响，有着广泛的应用。
一维势垒问题的主要特点是势能障碍的存在。
这个势能障碍可以是有限高度的，也可以是无限高度的。
有限高度的势能障碍表示粒子可以跨越势垒，而无限高度的势能障碍表示粒子无法穿越势垒。
在求解一维势垒问题时，需要考虑的主要因素包括粒子的动能和势能。
根据量子力学的原理，粒子在势垒两侧会存在反射和透射两种情况。
对于势能障碍的高度低于粒子的能量，粒子可以自由穿越势垒，这称为透射现象。
透射的概率可以通过隧道效应来描述，隧道效应可以用量子力学中的波函数来解释。
对于势能障碍的高度高于粒子的能量，粒子会发生反射现象。
在经典力学中，反射的概率可以通过粒子的入射能量和势垒高度之间的关系来计算。
对于无限高度的势能障碍，粒子无法穿越势垒，只能发生反射现象。
这种情况下，粒子的能量必须超过势能障碍的高度才能透过。
一维势垒问题在物理学和化学领域都有广泛的应用。
例如，它可以用于解释原子核中的核反应、电子在导体中的传输等。
总之，一维势垒问题是涉及势能障碍的物理问题，涉及粒子的运动和势能的影响。
求解该问题需要考虑粒子的动能和势能，以及透射和反射两种现象。
一维势垒问题在科学研究中具有重要的应用价值。
16-3 一维势阱和势垒问题
ψ(x) = Asinkx
nπx ψn(x) = Asin ( ) a
ka = nπ , n = 1,2,3,......
(0< x < a) n =12,3 , ,...
与能量本征值E 与能量本征值 n相对应的本征波函数ψn (x)为：
利用归一化条件
∫
2
ψn(x) dx = ∫ ψn(x) dx =1 0 −∞
ψ2 =0
理由:因为势壁无限高 所以粒子不能穿透势壁 理由 因为势壁无限高,所以粒子不能穿透势壁 故势 因为势壁无限高 所以粒子不能穿透势壁,故势 阱外的 波函数为零
定态薛定谔方程为
d ψ 2µ E + 2 ψ =0 2 dx ℏ
2
E是粒子的总能量，E > 0，令 是粒子的总能量， 是粒子的总能量 ， 定态薛定谔方程变为
ℏ
V
U0
0≤ x≤a
I II III
O a
x
ℏ
d2ψ1(x) 2 + k ψ1(x) = 0, x ≤0 2 dx 三个区间的薛定 2 谔方程简化为： 谔方程简化为： d ψ 2 ( x) − γ 2ψ ( x) = 0, 0≤ x≤a 2 2 dx d 2ψ3 (x) 2 + k ψ3 (x) = 0, x≥a 2 dx
一维无限深方势阱的数学表达形式 ：
U (x ) =
0
(0 < x < a )
∞ ( x ≤ 0 及x ≥ a )
一维无限深方势阱的图形表达形式 ： ∞
U(x)
∞ 粒子只能在宽为 a 的两个无 限高势壁间运动， 限高势壁间运动，这种势称为 一维无限深方势阱。
0
a
x
因为系统的势能与时间无关， 因为系统的势能与时间无关，因此这是一个定 态问题，可以用定态薛定谔方程进行求解。 态问题，可以用定态薛定谔方程进行求解。
一维半导体单量子方势垒中的电子输运
假设 电子 既有左人射 又有 右入射 ， 由于势 垒的存在 ． 在一 ａ ＜ ｚ ， ＞ ｎ
图２
图 ２中， 势垒高度 Ｖ ＝ ５ ０ ｍ ｅ Ｖ 。 对 于不 同的势 垒宽度透 射率随着
入射能量增加的变化 ． 其中虚线代表 ａ ＝ ５ ０ ０ ｎ ｍ， 实线代表 ａ ＝ ｌ Ｏ ０ ０ ｎ ｍ 按照经 典力学观点 ， 若Ｅ ＜ Ｖ ， 则 电子不能进 入势垒 ， 将全部被反 射 回去 。 若Ｅ ＞ Ｖ ， 则 电子将全部穿过势垒。 而从量子力学观点来看 ， 考
由于我们的模型 电子只从势垒的左边入射 ，则实际情况要求 Ｆ ＝ ０ 。 透射几率可从方程 （ ８ ） 获得为
－ Ｉ ｌ
２ 数 值 结 果 和 讨论
１
Ｚ
图 １ 散射势垒结构 考虑 Ｅ ＜ Ｖ 。 的情况 ， 在势垒之外 （ 一 ａ ＜ ｚ ， ｚ ＞ ａ ， 经典允许 区） 和势 垒内 部（ 一 ａ ＜ ｚ ＜ ａ ， 经典禁区 ） ， 定态 Ｓ ｃ ｈ ｒ ｔ ￣ ｄ ｉ ｎ ｇ ｅ ｒ 方程分别为
Ｓ ｃ ｉ ｅ ｎ ｃ ｅ＆ Ｔｅ ｃ ｈ ｎ ｏ ｌ ｏ ｇ ｙ Ｖｉ ｓ ｉ ｏ ｎ
科 技 视 界
一
科技・ 探索・ 争鸣
维半导体单量子方势垒中的电子输运
卢小 琴 （ 浙 江海 洋学 院 数 理 与信 息学 院 ， 浙江 舟山 ３ １ ６ ０ ０ ０ ）
【 摘
要１ 我们研 究 了通过半导体单量子 方势 垒的 电子输运 ， 结果显示 电子能穿透比它动能更 高的势 垒， 发生 了隧道效应 ； 势垒的宽度和 高
【 Ａ ｅ ＋ Ｂ ｅ ～
（ ｚ ） ＝ ｛ Ｃ ｅ ＋
ｌ Ｅｅ ＋
（ ４ ）
一维势阱和势垒问题
1.一维无限深势阱
一维无限深方势阱是金属中自由电子的简化模型
粒子在势阱内受力为零，势能为零。在阱内自由运 动。在阱外势能为无穷大，在阱壁上受极大的斥力, 不能到阱外。
一维无限深方势阱的数学表达形式 ：
0 (0 x a) U (x) (x 0及x a )
无数峰：量子 经典均匀0分布4 2
a
n4
x
0
ax
n时
量子经典
|n | 2 n很大
En
0
a
一维无限深势阱
En n
n(x)
En ( x)
h2 8ma 2
n2
n (x)
2 sin n x
aa
n(x)
2 sin2( n
aa
x)
0
ax
例1: 证明无限深方势阱中，不同能级的粒子波函数 具有正交性：
0 x a;
0,
x 0, x a.
讨论：
① 粒子的能量
En
2k 2
2
22n2
2 a2
,
n 1,2,3,
粒子的最低能量状态称为基态，则一维无限深方势 阱的基态能量为：
E1
22 2a2
0
————零点能
与零点能相对应的，应存在零点运动。这与经典粒
子的运动是相矛盾的。零点能是微观粒子波动性的表 现，因为“静止的波”是没有意义的。
② 图形
一维无限深方势阱中粒子的能级、波函数和几率密度
（2 sin nx , 0 x a;
a a
0,
x 0, x a. 0
除端点外，
一维有限深方势阱和势垒贯穿汇编
从一维无限深方势阱 理解有限深方势阱
k2
2mE
2
V (x)
ka n n 1,2,3,
o
En
2 2
2ma 2
n2
n 1,2,3,
V (x) 0,
V (x) ,
ax
0 xa x 0, x a
E1
2 2
2ma2
1 2
2 2
ma2
,
微观能量尺度可以选取 2 2
ma2
微观动量尺度
ka = n
-a/2 a/2 x
对于参考书p47页说明
a)不在讨论为什么势能对称，波函数也对称了。 b) 公式29和30实质上是利用
c) 估计一下公式32的数值大小？ d)纵轴取决于势阱高度，横轴取决于能量，此处
是势阱内部动能。我们让动能变化，看看什 么时候能冲破势阱束缚。
公式右面=
U0 22
U0
2 2
2
STM样品必须具有一定程度的导电性； 在恒流工作模式下有时对表面某些沟 槽不能准确探测。任何一种技术都有 其局限性。
dx2
V0 2
(x)
E2 (x),
定态薛定谔方程 的解又如何呢？
0 xa
2 2m
d
23 (x)
dx2
E3
( x),
xa
令：
k
2
Байду номын сангаас
2mE 2
k12
2m(V0 2
E)
三个区间的薛定谔方程化为：
V
V0
d
21(
dx2
x)
k
21
(
x)
0,
x0
I
d
量子力学 一维无限深方势阱,线性谐振子,势垒贯穿
(7)
由此得到，
Asin a 0,
B cos a 0
(8)
第二章 波函数和薛定谔方程 2.6、 一维无限深方势阱
A 和 B 不能同时为零，否则 y 处处为零。因此，
A 0, B 0, cos a 0 sin a 0
(9) (10)
由此可求得：
n a , 2
(2n 1) 2 h2 En En1 En ， 8ma 2
a)、 En µ n 2 ，当 n ® ¥时，
DEn 1 n®¥ ~ ¾ ¾¾ ®0 En n
正如对应原理所示大量子数极限下量子理论将逐渐 逼近经典理论。
第二章 波函数和薛定谔方程 2.6、 一维无限深方势阱
b)、 DEn µ
第二章 波函数和薛定谔方程 2.6、 一维无限深方势阱
一维无限深势阱的能量本征函数一维无限深势阱中粒子位置几率密度分布
第二章 波函数和薛定谔方程 2.7、 线性谐振子
2.7.1、谐振子模型
2.7、 线性谐振子 2.7.1、谐振子模型 经典力学中，当质量为 m 的粒子受到弹性力 F kx 作 用，其运动方程为，
考察上式解的渐进行为，当
很大时， 与 相比可
以忽略，方程（4）可以近似表示为：
d 2 2 0 2 d
(5)
第二章 波函数和薛定谔方程 2.7、 线性谐振子
2.7.2、 线性谐振子的能量本征值问题
不难证明，
时， ~ e
2
/2
，
~ e
第二章 波函数和薛定谔方程
第二章 波函数和薛定谔方程
第三部分、一维无限深方势阱，线性谐振子，势垒贯穿
第二章 波函数和薛定谔方程 引言
一维方势垒
(k k )s hk3 a A 2 A, (k1 k ) s hk3a 2ik1k3chk3a
2 1 2 2 3 2 3
2ik1k3e C 2 A, 2 2 (k1 k3 ) s hk3a 2ik1k3chk3a
ik1a
2.6 一维方势垒
反射系数和透射系数为：
2 2 (k12 k3 ) s h 2 k3 a R 2 , 2 2 2 2 2 (k1 k3 ) s h k3 a 4k1 k3 2 4k12 k3 T 2 2 2 2 (k1 k3 ) s h 2 k3 a 4k12 k3
2 2 2 1 2 2 2 2 2 2
A
2
透射系数为：
2 C JT 4k12 k2 T 2 2 2 2 2 2 2 J ( k k ) sin k a 4 k A 般情况下，透射系数 T 1 ， 反射系数R 0 ，而这之和为1。这表明，在量 子力学中，即是粒子的能量大于势垒高度，仍 有部分被反射回来。这正是微观粒子具有波动 性的体现。
由第二式可见，一般情况下透射系数 T 1 ， 当 k2 a n 的特定情况下，其透射系数T 1 ， 这种情形下的透射现象叫做 共振透射
2.6 一维方势垒
二、E U 0 的情形
k2 为虚数。但若令k2 ik3 ，则 此时， 2m 2 k3 2 (U 0 E )
系数关系变为
Be
ik2 a ik2 a ik1a Be Ce ik2 a ik1a k2 B e Ck1e
k2 Be
ik2 a
2.6 一维方势垒
可得出 A, C 与 A 关系
2i (k12 k22 )sin k2 a A A, 2 ik2 a 2 ik2 a (k1 k2 ) e (k1 k2 ) e 4k1k2e C A, 2 ik2 a 2 ik2 a (k1 k2 ) e (k1 k2 ) e
一维对称方势垒量子散射问题及其数值模拟
一维对称方势垒量子散射问题及其数值模拟1. 概述量子力学一直以来都是物理领域中一个备受关注的重要研究课题。
量子力学的发展为科学家们提供了一种全新的研究物质运动规律的方法，尤其是在微观领域的研究中，量子力学的理论和实验数据显示出了其独特的优势和价值。
在量子力学的研究中，量子散射问题是一个重要的课题，可以通过研究了解粒子在势场中的行为及相应的规律性。
在量子散射问题中，一维对称方势垒是较为典型的模型，对其进行深入的研究有助于揭示量子力学规律，提高人们对量子世界的认识。
2. 一维对称方势垒模型一维对称方势垒是量子力学中常见的势场模型之一。
其势垒的形状对称，可通过薛定谔方程进行描述。
具体而言，一维对称方势垒模型的势能函数可表示为：V(x) ={0, x < -aV0, -a <= x <= a0, x > a}其中，V0表示势垒的高度，a表示势垒的宽度。
这个模型对应的薛定谔方程为：[-ħ²/2m * d²ψ(x)/dx² + V(x)ψ(x) = Eψ(x)]其中ħ代表普朗克常数，m代表粒子的质量，E代表粒子的总能量。
3. 量子散射问题的基本理论在量子力学中，散射是指粒子在势场中发生偏折或反射的现象。
量子散射问题是研究粒子在势场中的散射行为并得到相应规律的一个重要课题。
在一维对称方势垒模型中，可以通过求解薛定谔方程来研究粒子在势垒中的散射行为。
根据波函数在势场两侧的表达式，可以得到散射系数、散射振幅等物理量，从而揭示量子散射的特性和规律。
4. 数值模拟方法数值模拟是研究量子散射问题的重要手段之一。
通过数值模拟，可以在一定的精度下求解薛定谔方程，得到粒子在势场中的波函数和相应的物理量。
常见的数值模拟方法包括有限差分法、有限元法、蒙特卡洛方法等。
在一维对称方势垒模型中，可以利用这些数值方法对波函数和散射规律进行模拟计算，得到与理论分析相一致的结果。
5. 数值模拟的具体步骤进行一维对称方势垒模型的数值模拟，通常可分为以下几个步骤：5.1. 网格划分：将计算区域进行网格划分，离散化空间，确保波函数和势能函数在网格点上的计算精度。
高二物理竞赛课件：一维方势垒和隧道效应
Ⅰ区 Ⅱ区 Ⅲ区
d 2Ψ1 ( x) dx2
k12Ψ1 ( x)
0
d2Ψ2 (x) dx2
k22Ψ2
(
x)
0
d 2Ψ3 ( x) dx2
k12Ψ3
(x)
0
0a
k12
2mE 2
k22
2m(U 0 2
E)
k12
2mE 2
三个区域的波函数分别为
Ⅰ区 Ψ1(x) A1eik1x B1eik1x
U0 ⅠⅡ Ⅲ
一维方势垒和隧道效应
一维方势垒 隧道效应
一维方势垒
Ep ( x)
0, x 0, x a Ep(x) Ep0, 0 x a
Ep0
o ax
粒子的能量 E Ep0
d2
dx2
k 2
0
Ep
(x) Asin kx Bcoskx
o ax
波函数的标准条件：单值、有限和连续 .
x 0, 0, B 0
(2)E < U0 , T≠0, 虽然粒子总能量小于势垒高度，入射粒子仍 可能穿过势垒进入 III 区 — 隧道效应
(3) 透射系数T 随势垒宽度a、粒子质量m 和能量差变化， 随着势垒的加宽、加高透射系数减小。
粒子类型 粒子能量 势垒高度 势垒宽度 透射系数
1eV
2eV 5×10-10m 0.024
na
n4
(x) 2 2 sin 2 nπ x
a
a
n 2
16E1
n3
n2 n 1
x0
a x0
9E1
4E1 E1
a
Ep 0
四.隧道效应（势垒贯穿）
势垒 Ⅰ区 U ( x ) = 0 x ≤ 0
第三章一维势垒散射问题
Ⅲ区
2 d 2u Eu 2 2m dx
d 2u 2m E 2 u k32u dx2
2m E k3 k1
2) 解方程
d 2u 2m E 2 u k12u dx2
u1 Aeik1x Beik1x
入射波
反射波
E
Ⅱ区
V 0
V 0
Ⅲ区
x1
x2
x
2 d 2u Eu 2 2m dx
Ⅰ区
d u Eu 2 2m dx
2
2
d 2u 2m E 2 u k12u dx2
k1 2m E
Ⅱ区
d u Vu Eu 2 2m dx
2
2
d 2 u 2m 2 2 (V E )u k2 u dx2
§3.5 量子力学的几个简例
下面我们从能量本征方程，即定态薛定谔方程出发，讨论 几个典型的一维定态问题。这些例子简单，数学处理方便， 定量分析结果明显，揭示出诸多量子化行为，十分有助于理 解量子力学的基本概念，有助于认识量子体系的基本特征， 也为进一步研究复杂问题奠定了基础。
1. 一维无限深势阱 分立谱 2. 一维势垒散射问题 隧道效应
k a 2 ka n n 1,2,3,4,
n取零（n＝0)，给出Ψ≡0 ，无物理意义，n取负值，也给不出 新的波函数，所以n应取1以上的整数。从而给出的能量本征值 (能级)为 k 2mE / 2 2 2 h2 2 En n n n 1,2,3 2 2 2m a 8m a n n n a x ) A sin (x ) 波函数 u ( x) A sin( a 2 a 2 上式说明，只有当能量取上式给出的分立能值时，相应的波函 数或本征态才是可接受的合理解。这就自然地给出了能量量子 化，En是能量本征值,Ψ n是能量本征态函数。另一个常数A由波 函数(几率幅)的归一化条件给出。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
由第二式可见，一般情况下透射系数T 1 ， 当k2a n的特定情况下，其透射系数T 1 ，
这种情形下的透射现象叫做 共振透射
2.6 一维方势垒
二、E U0 的情形
此时，k2 为虚数。但若令k2 ik3 ，则
k32
2m
2
(U0
E)
系数关系变为
A
(k12
(k12 k32 ) s hk3a k32 )2 s hk3a 2ik1k3chk3a
A,
C
2ik1k3eik1a
A,
(k12 k32 )2 s hk3a 2ik1k3chk3a
2.6 一维方势垒
前面讨论了束缚态，这一节我们讨论散射态。
首先讨论一维方势垒问题。
0 U (x) U0
x 0, x a 0<x<a
设能量为E的粒子从势垒的左方向右方运动，
U (x)
E
U0
x
0
a
2.6 一维方势垒
下面分别就来 E U0 与 E U0 来讨论
一、E U0 的情形 此时，(x)满足的薛定谔方程为
反射系数为：
R JR J
A 2 A2
(k12
(k12 k22 )2 sin 2 k2a k22 )2 sin 2 k2a 4k12k22
透射系数为：
T
JT J
C2 A2
4k12 k22 (k12 k22 )2 sin 2 k2a 4k12k22
2.6 一维方势垒
A,
C
4k1k2eik1a (k1 k2 )2 eik2a (k1 k2 )2 eik2a
A,
2.6 一维方势垒
由概率流密度公式可得入射波的概率流密度为：
J
k1 m
A2
透射波的概率流密度为：
JT
k1 m
C2
反射波的概率流密度为：
JR
k1 m
A 2
2.6 一维方势垒
2.6 一维方势垒
反射系数和透射系数为：
R
(k12
(k12 k32 )2 s h2k3a k32 )2 s h2k3a 4k12k32
,
T
(k12
4k12 k32 k32 )2 s h2k3a 4k12k32
由此可见，反射系数R 1和透射系数T 0 ，且 二者之和等于1，这表明，在量子力学中，即使
A A B B k1A k1A k2B k2B Beik2a Beik2a Ceik1a k2 Beik2a k2Beik2a Ck1eik1a
2.6 一维方势垒
可得出A,C 与 A 关系
A
2i(k12 k22 ) sin k2a (k1 k2 )2 eik2a (k1 k2 )2 eik2a
k22m
0
0 xa
d 2r (x) dx2
k12 r
0
xa
2.6 一维方势垒
其解分别为
l (x) Aeik1x Aeik1x , m (x) Beik2x Beik2x , r (x) Ceik1x Ceik1x ,
利用在 x 0 和 x a处波函数连续性和波函 数微商连续性条件
d 2l dx2
2m
2
El
0
x 0,
d 2m dx2
2m
2
(E
U0 )m
0
0 xa
d 2r dx2
2m
2
Er
0
xa
2.6 一பைடு நூலகம்方势垒
为方便起见，令
k12
2mE
2
,
k22
2m
2
(E
U0
)
方程可改为：
d 2l dx2
k12l
0
x 0,
d 2m dx2
2.6 一维方势垒
2、隧道二极管是一种利用隧道效应的半导体器 件，也是隧道效应的重要应用之一。 由于隧道效应而使其伏安特性曲线出现负阳 区，因而隧道二级管具有高频、低噪声的特 点。 隧道二级管是低频放大器、低频噪声振荡器 和超高速开关电路中的重要器件。
粒子的能量小于势垒的高度，粒子仍有一部分 透射过去。
2.6 一维方势垒
这种粒子在其能量 E小于势垒高度 U0时， 仍然会有部分粒子穿过势垒的现象叫
隧道效应，又叫隧穿效应
入射波
U (x)
U0
透射波
0
a
x
2.6 一维方势垒
隧道效应的应用：
1、扫描隧道显微镜（STM）是电子隧道效应的 重要应用之一。 扫描隧道显微镜可以显示表面原子台阶和原 子排布的表面三维图案。 在表面物理、材料科学和生命科学等诸多领 域中，扫描隧道显微镜都能提供十分有价值 的信息。