16-3一维势阱和势垒问题解读
16-3 一维势阱和势垒问题
]
ψ1 = A1 e + B1 e
ik1x
−ik1x
− ik 2 x
1
( x < 0)
( x > a)
U
通解: 通解
ψ 2 = A2 e
ik 2 x
1
+ B2 e
(0 ≤ x ≤ a )
U0
ψ 3 = A3 eik x + B3 e − ik x
处无反射波: 由 x > a 处无反射波: B 3 = 0 令 A1 = 1(以入射波强度为标准) 以入射波强度为标准) 由波函数的 标准条件得 O 可解得
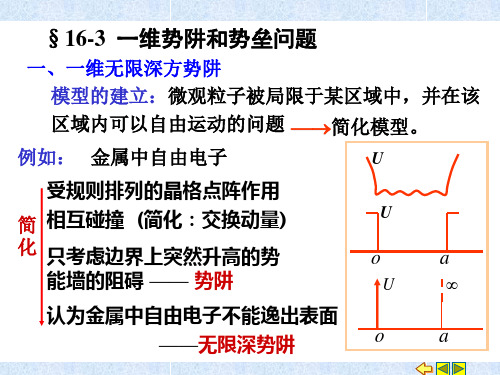
§16-3 一维势阱和势垒问题
一、一维无限深方势阱 模型的建立:微观粒子被局限于某区域中, 模型的建立:微观粒子被局限于某区域中,并在该 区域内可以自由运动的问题 →简化模型。 →简化模型 简化模型。 例如: 例如: 金属中自由电子 受规则排列的晶格点阵作用 简化:交换动量) 简 相互碰撞 (简化:交换动量) 化 只考虑边界上突然升高的势 能墙的阻碍 —— 势阱 认为金属中自由电子不能逸出表面 ——无限深势阱 无限深势阱
2 2πx p = ∫ |ψ | d x = ∫ sin dx a a 0 0
4 4 2 a a
2a πx 2 πx = ∫ sin d( ) aπ a a 0
4
a
1 πx 1 2 2 2π x = ( − sin ) π a 4 a
a
4
= 9.08 × 10 −2
0
练习: 练习
已知: 已知:
ψ = cx ( L − x )
A A2 ∞ 2 dx = ∫ dx = A arctg x − ∞ = A2π = 1 ∫∞ 1 + ix 1 + x2 − −∞
量子力学-第二章-一维势阱

3
时间依赖薛定谔方程
根据能量守恒和时间演化,推导出薛定谔方程。
薛定谔方程的解析解
无限深势阱
假设粒子被限制在一个 无限深的势阱中,无法 逃逸。
波函数的边界条件
在势阱的边界处,波函 数必须满足特定的边界 条件。
波函数的对称性
在势阱中,波函数可能 具有对称或反对称的性 质。
薛定谔方程的数值解
有限差分法
含时薛定谔方程的一维势阱模型
含时薛定谔方程是一维势阱模型中描述粒子动态行为的方 程。该方程包含了时间依赖的势能项,可以描述粒子在时 间演化过程中受到的外部作用力。
含时薛定谔方程的解可以用来研究粒子在一维势阱中的动 态行为,例如粒子在受到激光脉冲作用时的运动轨迹和能 量变化。通过求解含时薛定谔方程,可以深入了解粒子在 一维势阱中的动力学性质。
01
将薛定谔方程转化为差分方程,通过迭代求解。
网格化方法
02
将连续的空间离散化为有限个网格点,对每个网格点上的波函
数进行求解。
量子隧穿效应
03
当势阱深度较小时,粒子有一定的概率隧穿势垒,从势阱中逃
逸。
03
一维势阱中的粒子行为
BIG DATA EMPOWERS TO CREATE A NEW
ERA
粒子在无限深势阱中的行为
时间依赖的一维势阱模型
时间依赖的一维势阱模型描述了粒子在一维空间中受到随时 间变化的势能作用的情况。这种模型可以用来研究粒子在时 间依赖的外部场中的动态行为,例如粒子在激光场中的运动 。
时间依赖的一维势阱模型需要求解含时薛定谔方程,该方程 描述了粒子在时间演化过程中的波函数变化。通过求解含时 薛定谔方程,可以了解粒子在时间依赖的势阱中的动态行为 。
21.7 一维势阱 势垒 隧道效应

STM的发明者 宾尼、罗雷尔和电 子显微镜的发明者 卢斯卡分享了1986 年诺贝尔物理奖。
宾尼
罗雷尔
U0
电子云重叠 U0 U0 E
样 品
d
针 尖
扫描隧道显微镜(STM)装置示意图
用STM得到的神经细胞象
液体中观察原子图象
在电解液中得到的硫酸根离子吸附在铜 单晶表面的STM图象。
“扫描隧道绘画 ” 一氧化碳“分子人”
8 n1 x n2 y n3 z ( x, y, z ) sin sin sin l1l2 l3 l1 l2 l3
三维势阱中粒子的能量:
n12 2 2 n2 2 2 2 n32 2 2 E 2 2 2 2ml1 2ml2 2ml3
处在超晶格的一维量子线和两维量子阱中的电子 就属于一维和两维势阱中的粒子,而处在金属内的电 子可看作三维势阱中的粒子。
i En t
)e
i En t
( px En t )
C 2e
( px En t )
n ( x, t ) 是由两个沿相反方向传播的平面波叠加而
③粒子在阱中的分布 经典力学的结果:均匀分布 P ( x ) 1/ a a a P ( x)dx P ( x) dx P ( x)a 1
(4) 解方程、定常数 在 0<x<a 区域,定态薛定谔方程为
令
d x 2mE 2 x 0 2 dx 2mE 2 k 2 d 2 x 2 k x 0 2 dx
2
比较谐振动方程 特解为
d2x 2 x0 2 dt
( x ) C sin(kx )
2 2 2
量子力学课件(一维势阱)

例1:电子在a 1.0 10 m
2
的势阱中 .
2 h 2 15 E n2 n 3 . 77 10 eV 2 8ma 2 h 15 (近似于连续) E 2n n 7 . 54 10 eV 2 8ma
当 a 0.10nm 时, E n 75.4eV(能量分立)
§7 箱中粒子
( x)
2 nπ sin x a a
第二章 薛定谔方程
一维无限深方势阱中粒子的能级、波函数和概率密度
2
n
n4
2 2 nπ ( x) sin x a a 2 n
16E1
n3 n2
n 1 x0
a2
9 E1
4 E1
a
x0
a2
a
E1
Ep 0
§7 箱中粒子 7.3 箱中粒子的一些性质 1
§7 箱中粒子
第二章 薛定谔方程
求出解的形式画于图中。
量子力学结果分析: (1)E>V0情况 在经典力学中,该情况的粒子 可以越过势垒运动到x>a区域,而 在量子力学中有一部分被反弹回去, I 即粒子具有波动性的具体体现。 (2)E<V0情况
V
隧道效应
V0
II
III
o
a
x
在经典力学中,该情况的粒子将完全被势垒挡回, 在x<0的区域内运动;而在量子力学中结果却完全不同 ,此时,虽然粒子被势垒反射回来,但它们仍有粒子穿 透势垒运动到势垒里面去,所以我们将这种量子力学特 有的现象称“隧道效应”。
所以, B 0;
ka n
n 1,2,3,
n不能取零,否则无意义。
§7 箱中粒子 因为
第二章 薛定谔方程
量子力学中的势阱问题解析

量的可能取值和相应几率 。 ( 2)求上述状态下粒子能量的平均值 。 ( 3)由上述 t =0 时刻的态 , 从能量表象中的 薛定谔方程求出任意时刻 t 的态矢 | Χ ( t)>. 解 ( 1) t = 0 时 刻能 量 表象 中 的 波函 数 |Χ ( t = 0)> 显然未归一化 。 将其乘以归一化常 数 A 后再归一化 , 有
=0 波函数的一级修正为
n Χ ( 1)
( 1) 1) χ 1 ( 2) χ s =χ 1 (
2
χ s
( 0)
( 2)
=χ 1 ( 1) χ 1 ( 2) -2 -2 =
= =
∑′ E
k k ∑′ a 0 ( 0)
n
H′ kn ( 0) k 0) Χ -E k (
2
2μ a H′ kn · π 2( n2 -k 2)
2 2 2 2 2
c1 c2
0
波函数为 Χ mnp = = 1 , 2 , …) 3. 2 势阱的表象问题 例 2 设质量为 μ 的粒子处于宽度为 2a 的 一维无限深势阱中 ( 1) 在能量表象中 , t =0 时粒子处于 |Χ ( t= 0 1 0)>= 1 0 3 3 的状态 , 求在这个状态下粒子能 8 sin nπx sin mπy sin p π z( n ,m , p abc a b c
2 2 n2 π ( n = 1 , 2 , …) 8μ a2
( 3)
3 其他势阱问题 3. 1 三维无限深势阱 例 1 若无限深势阱在 x , y , z 轴上的宽度各
收稿日期 : 2005 - 10 - 16
【大学物理】§3-2薛定谔方程 一维势阱和势垒问题

一、一维无限深方势阱
对于一维无限深方势阱有
一维势阱和势垒问题
∞
∞
U(x)
U
(
x)
0
(0 x a) ( 0 x, x a)
势阱内U(x) = 0,哈密顿算符为
H
2
2
d2 d x2
定态薛定谔方程为
0
a
令
2E
k
薛定谔方程的解为
d 2
d x2
2E
2
0
(x) Asin(kx )
由此解得最大值得位置为
x (2N 1) a 2n
例如
n 1, N 0
最大值位置
x 1a 2
n 2, N 0,1, 最大值位置 x 1 a , 3 a Nhomakorabea44
n 3, N 0,1, 2, 最大值位置 x 1 a , 3 a , 5 a.
6 66
可见,概率密度最大值的数目和量子数n相等。
10
2m dx2
2. 波函数
(
x)
2 sin( n x), 0 x a
aa
0,
x 0或x a
3. 能量
En
n
2
22
2ma 2
n 1,2,3
4. 概率密度
(x) 2 2 sin 2 ( n π x)
a
a
4
讨论
n (x)
2 sin n x
a a
(0 x a)
1.n=0给出的波函数
1
根据 (0,)可以0确定 = 0或m,m =1,2,3,。于是上式改写为
根据 (a) 0,得
(x) Asin kx
ka = n, n = 1,2,3, ···
一维势垒问题总结

一维势垒中的透射系数利用传递矩阵方法研究了粒子在一维势垒中运动时的粒子的透射系数,主要研究的是在一个方势垒两个方势垒中透射系数,对以上的透射系数的总结,推出了对于任意势垒中透射系数, 并讨论了透射系数、反射系数与势垒宽度的关系.一维方势垒势垒模型在方势垒中,遇到的问题和 值得注意的地方。
在求方势垒波 函数中,首先要知道这是一个什 么样问题,满足什么样的方程, 方程可以写成什么样的形式,在 求解方程中,波函数的形式应该怎样需要怎样的分段,分段的过程中,特别要强调的边界条件问题。
并且验证了概率流密度。
在量子力学中,粒子在势垒附近发生的现象是不一样的,能量E 大于势垒高度0u 的粒子在势垒中有一部分发生反射,而能量小于0u 的粒子也会有部分穿过势垒,这在经典力学中是不会发生的。
下面讨论的是一维散射(即在非束缚态下问题,在无穷远处波函数不趋于零)。
重点讨论的是粒子通过势垒的透射和反射,重点在于求出波函数,这就必须求解薛定谔方程,由于)(x U 是与时间无关的,此处是定态薛定谔方程。
定态薛定谔方程通式:ψψψE U m=+∇-222h 在量子力学里, 必须知道波函数ψ, 因此必须要解薛定谔方程t i U x m ∂∂=+∂∂-ψψψh h 2222一维散射问题是一个非束缚态问题(()U x 与时间无关, 而E 是正的).因此令t Ei ex t x h-=)(),(ψψ由此得到ψψψE U dx d m =+-2222h按照势能()U x 的形式, 方程(2)一般需要分成几个部分求解.将上式改写成如下形式0222=+ψψk dxd⎩⎨⎧><<<=.,0,0;0,)(0a x x a x u x U 先讨论0u E >的情形粒子满足薛定谔方程分解为三个区域:⎪⎪⎪⎩⎪⎪⎪⎨⎧>=-<<=+-<=-a x x E x dx d m a x x E x u x dx d m x x E x dx d m ),()(20),()()(20),()(233222220222211222ψψψψψψψh h h (1) ⎪⎪⎪⎩⎪⎪⎪⎨⎧>=+<<=-+<=+a x x mEx dx d a x x u E x dx d x x mEx dxd ,0)(2)(0,0)()()(0,0)(2)(323222022212122ψψψψψψh h特征方程02=++q pr r 的两个根21,r r方程 0=+'+''qy y p y 的通解两个不相等的实根21r r ≠ x r x r e C e C y 2121+= 两个相等的实根21r r = x r e x C C y 1)(21+= 一对共轭复根βαi r ±=2,1)sin cos (21x C x C e y x ββα+=注: 0=+''qy y 的通解:特征方程02=+q r ,当0<q 时,通解xq xq eC e C y ---+=21,当0>q 时,通解xq ixq ie C e C y -+=21方程(1)的解可以表示为:⎪⎪⎪⎩⎪⎪⎪⎨⎧>+=<<+=<+=-----a x de te x a x ce be x x re ae x x mEi x mE i x u E m i x u E m i x mE i x mE i ,)(0,)(0,)(223)(2)(2222100h h hh hh ψψψ (2)定态波函数321,,ψψψ再分别乘上一个含时间的因子Et i eh-,可以看到式子(2)的三式,第一项是左向右传播的平面波,第二项是由右向左传播的平面波,即入射波和反射波。
势阱,势垒及原子结构

本征值
本征函数
4. 讨论解的物理意义
即求| |2,得出粒子在空间的概率分布。
粒子在一维无限深势阱中的波函数
2 n x i Et
Ψ (x) sin e (n 1,2,3,...; 0 x a) aa
Ψ (x) 0
(x 0, x a)
注意:解为驻波形式
5.讨论解的物理意义
强度不等,粒子出现的概率不相同.
Ψ (x,t)
2 n x i Et
sin e
aa
Ψ x,t
|Ψ (x,t) |2 | (x) |2 2 sin2 n x
a
a
x 2
E4 16E1
n=4
n= 4
E3 9E1
E2 4E1
E1
o
n=3 n= 2 n=1
ax o
n= 3
n= 2 n= 1
ax
波长量子化 n 2a n, n 1, 2,3,......
z l0
ml 0
z
l2
ml 0
z
l2 ml 1
x
x
x
电子在核外不是按一定的轨道运动的,量子力学不能断言电 子一定出现在核外某确切位置,而只给出电子在核外各处出现 的概率,其形象描述——“电子云”
1s 2 p(ml 0) 3p(ml 1)
4 f (ml 1) 5 f (ml 1)
——每瞬间氢原子核外电子照片的叠加 电子出现概率大处:雾点密度大
电子出现概率小处:雾点密度小
量子理论与玻尔理论的比较:
玻尔理论:电子只能在一些量子化的轨道上运动, 只有在这些轨道上才能发现电子。 量子理论:电子并不沿轨道运动,在空间任一点都可 能发现电子。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x a
a x
第k激发态(n=k+1)有k个节点。
(2)一维无限深势阱 的粒子位置概率密度 分布
1
2
n 1
0 2 2 n 2 a
2
x
0 无数峰:量子 经典均匀分布 0
a a n 1,x 处,几率最大 0 3 2 b n ,峰数 ,当n 时,
4
U0
II
III
o
a
x
而在微观粒子的情形,却会发生反射。
ቤተ መጻሕፍቲ ባይዱ
(2)E<U0 从解薛定谔方程的结果来看,在 势垒内部存在波函数2。即在势垒内 部找出粒子的概率不为零,同时,在 x>a区域也存在波函数,所以粒子还 I 可能穿过势垒进入x>a区域。
V
V0
II
III
o
a
x
粒子在总能量E小于势垒高度时仍能贯穿势垒的 现象称为隧道效应。
式中 A和α是待定常数,由边界条件和归一化条 件确定。
( x) A sin( kx )
从物理上考虑,粒子不可能透过阱壁,因而按照波 函数的统计诠释,要求在阱壁上和阱外波函数为0。 考虑波函数在阱壁上等于零的情况,即
(0) 0, (a) 0
————边界条件
(0) 0
这说明:并非任何 E值所对应的波函数都能满足一维 无限深方势阱所要求的边界条件,只有当能量取上式 给出的那些分立的值 En(体系的能量本征值)时, 相应的波函数才是物理上有意义的,即本问题中体系 的能量是量子化的,亦即体系的能谱是分立的。
2
2
2 2 2
( x) A sin kx
nx n ( x) A sin( ) a
2 2 U (r ) (r ) E (r ) 2
————定态薛定谔方程 ①列出各区域的定态薛定谔方程
1 2
(0 x a )
( x 0及x a)
势阱内
2
0<x<a
d 1 2E 2 1 0 2 dx
势阱外
m n d
0
即不同能级的波函数是互相正交的。 解: 波函数 m 取其复共轭 m 相乘并积分,得
m ( x ) n ( x )d
a ( 0
2 mπx 2 nπx sin )( sin )dx a a a a
(m n) πx a1 [cos 0 a a
与其它表面分析技术相比,STM所具有的独特优点 是: 1. 具有原子级高分辨率。STM在平行和垂直于样品 表面方向的分辨率分别可达0.1nm和0.01nm,即可分 辨出单个原子。
粒子的最低能量状态称为基态,则一维无限深方势 阱的基态能量为:
E1 2 0 2 a
2 2
————零点能
与零点能相对应的,应存在零点运动。这与经典粒 子的运动是相矛盾的。零点能是微观粒子波动性的表 现,因为“静止的波”是没有意义的。
② 图形 一维无限深方势阱中粒子的能级、波函数和几率密度
隧道电流对针尖与样品间的距离十分敏感。 若控制隧道电流不变,则探针在垂直于样品 方向上的高度变化就能反映样品表面的起伏。
因为隧道电流对针尖与样品间的距离十分敏感。 若控制针尖高度不变,通过隧道电流的变化可 得到表面态密度的分布; 利用STM可以分辨表面上 原子的台阶、平台和原子 探针 阵列。可以直接绘出表面 的三维图象 使人类第一次能够实时地观 空气隙 测到单个原子在物质表面上 的排列状态以及与表面电子 样品 行为有关的性质。在表面科 学、材料科学和生命科学等 STM工作示意图 领域中有着重大的意义和广 阔的应用前景。
隧道效应和扫描隧道显微镜STM Scanning tunneling microscopy 由于电子的隧道效应,金属中的电子并不完全局限于 表面边界之内,电子密度并不在表面边界处突变为零, 而是在表面以外呈指数形式衰减,衰减长度越为1nm。
只要将原子线度的极细探针 以及被研究物质的表面作为 两个电极,当样品与针尖的 距离非常接近时,它们的表 面电子云就可能重叠。 若在样品与针尖之间 加一微小电压Ub电子 就会穿过电极间的势 垒形成隧道电流。
x ≤ 0 ;x ≥a
2 0
理由:因为势壁无限高,所以粒子不能穿透势壁,故势 阱外的 波函数为零
定态薛定谔方程为
d 2 E 2 0 2 dx
2
E是粒子的总能量,E > 0,令 定态薛定谔方程变为
2
k
2 E
d 2 k 0 2 dx
此薛定谔方程的解为
( x) A sin( kx )
1 (0) 2 (0)
2 ( a ) 3 ( a)
d 1 ( x) d 2 ( x ) | x 0 | x 0 dx dx d 3 ( x ) d 2 ( x ) |xa |xa dx dx
求出解的形式画于图中。
讨论:
U
(1)E>U0
按照经典力学观点,在E>U0情况 下,粒子应畅通无阻地全部通过势 垒,而不会在势垒壁上发生反射。 I
(a) 0
2
0, 或m , m 1,2,3,......
A sin kx
波函数改写为: ( x)
ka n , n 1,2,3,......
d 2 0 2 dx
讨论一:n不等于零
d 2 k 0 2 dx
( x) Cx D
(0) 0 (a) 0
R
1
A1
2
B1 A1
定义透射系数: ————粒子穿过势垒的概率 ————穿过势垒的粒子数 / 入射到势垒上的粒 2 2 子数
T
A3 A1
2
A3 A1
R T 1
————概率守恒
反射系数 R 和透射系数 T 的具体值,需要根据波函 数的归一化条件,以及边界条件(波函数及其导数 在全空间连续)来确定。 利用波函数“单值、有限、连续”的标准条件,可 得:
(1)一维无限深势阱的粒子波函数
n ( x)
2 nx sin , a a
0 x a;
x 0, x a.
1
n 1
0, 除端点外,
0
2 n 2
a x a x
0 0
0
基态的波函数(n=1)无节点, 第一激发态(n=2)有一个节点,
3 n 3
4
ka n , n 1,2,3,......
(0 x a ) n 1,2,3,...
与能量本征值En相对应的本征波函数n (x)为:
利用归一化条件
2
a
n ( x) dx n ( x) dx 1
2 2 0
2
a
2 a nx A sin dx A 0 n a 2 a n 2 a A A 1 n 2 2
一维无限深方势阱的数学表达形式 :
U ( x)
0
(0 x a )
( x 0 及x a )
一维无限深方势阱的图形表达形式 : ∞
U(x)
∞ 粒子只能在宽为 a 的两个无 限高势壁间运动,这种势称为 一维无限深方势阱。
0
a
x
因为系统的势能与时间无关,因此这是一个定 态问题,可以用定态薛定谔方程进行求解。
2 d 2 1 ( x) E 1 ( x), x 0 2 2 dx 2 d 2 2 ( x) U 0 2 ( x) E 2 ( x), 2 2 dx 2 d 2 3 ( x) E 3 ( x), x a 2 2 dx 2 E 2 (U 0 E ) 2 2 令: k 2 2
n
0
sin 2tdt
A 2/a
波 函 ( x) 数: n
取 A为正实数
0 x a;
x 0, x a.
2 nx sin , a a
0,
讨论:
2 k 2 22n2 ① 粒子的能量 E n , n 1,2,3, 2 2 2 a
mn
克罗内克符号
mn
二、势垒穿透和隧道效应 有限高的方形势垒 数学形式:
0, U ( x) U 0 ,
图形形式: U
U0
x 0( P区), x a(S区) 0 x a(Q区)
考虑粒子的动能 E小于势垒高 度 U0的情况。( E < U0 )
E
P
Q
S
o
a x
U ( x)
(m n) πx cos ]dx a
1 ( m n)
( m n ) 0
1 cos udu ( m n)
( mn) 0
cos vdv
0
属于不同能级的波函数是正交的。 把波函数的正交性和归一性表示在一起,
m n d
δ mn
mn
1, 0,
2右边的第一项表示穿入势垒的透射波,第二项 表示被“界面(x=a)”反射的反射波。
3右边的第一项表示穿出势垒的透射波, 3的第 二项为零,因为在x>a区域不可能存在反射波(B3=0)。
定义反射系数:
————粒子被势垒反射的概率 ————被势垒反射的粒子数 / 入射到势垒上的 2 2 粒子数 B
方程的通解为:
1 A1e B1e ik1x ik1x 2 A2e B2e ikx ikx 3 A3e B3e
ikx
ikx
三式的右边第一项表示沿x方向传播的平面波, 第二项为沿x负方向传播的平面波。 1右边的第一项表示射向势垒的入射波,第二项 表示被“界面(x=0)”反射的反射波。
