“圆筒体积的测量”的标准不确定度评定
【精品】“圆筒体积的测量”的标准不确定度评定

【精品】“圆筒体积的测量”的标准不确定度评定在工程和科学领域中,测量是一项重要的活动。
在进行测量时,需要评估所得结果的可靠性和准确性。
一个常见的测量任务是测量物体的体积,例如圆筒的体积。
然而,所有测量都存在不确定性,因此需要对测量的不确定度进行评估。
本文将介绍如何评估圆筒体积测量的标准不确定度。
首先需要确定可能产生不确定度的因素。
在圆筒体积测量中,有几个因素可以导致测量结果的不确定度,包括:1. 直径的测量误差:直径的测量可能会存在一定的误差,这将影响到圆筒的体积计算。
3. 圆筒的形状误差:圆筒的圆形、直线和平面的符合度可能也会影响到体积测量。
4. 测量设备的不确定度:使用的测量设备也有一定的不确定度,例如测量直径和高度的卷尺或测量线。
接下来,需要确定每个不确定度因素对测量结果的影响程度。
这可以通过进行实验测量来确定。
在实验中,需要多次测量不同的圆筒,并记录测量结果。
然后,使用这些数据来计算不确定度因素的贡献。
例如,在测量直径时,可能会得到以下三次测量结果:10.2厘米、10.1厘米和10.3厘米。
那么平均值为:(10.2+10.1+10.3)/3=10.2厘米。
标准偏差为:[(10.2-10.2)^2+(10.1-10.2)^2+(10.3-10.2)^2]/(3-1)=0.11厘米。
这个标准偏差给出了直径测量误差的大小,作为估计值的不确定度。
针对所有的不确定度因素的计算,可以使用不确定度传递方法来组合它们。
具体来说,如果有多个不确定度来源,则它们的贡献应该按照它们对最终结果的相对贡献进行加权平均。
这意味着,每个不确定度因素的不确定度应该与其对测量结果的影响成比例。
例如,如果直径测量误差的不确定度为0.1厘米,而高度测量误差的不确定度为0.2厘米,则可以将它们分别乘以它们对圆筒体积的影响系数(即π/4×d²和h)。
这可以得到:直径误差不确定度的贡献=0.1厘米×π/4×d² =0.13×d²高度误差不确定度的贡献=0.2厘米×h然后,将它们平方并相加,然后取平方根,得到圆筒体积测量标准不确定度。
测量不确定度评定程序

文件制修订记录对公司在体系中的测量设备的计量确认过程和测量过程控制的测量不确定度进行评定,使之符合预期的不确定度要求,确保测量结果的正确。
2.0适用范围本程序适用于在进行计量确认过程和测量过程策划或实施测量过程,及在使用测量结果时对测量不确定度进行分析。
有关人员在选用测量设备和测量方法时也可参照本程序。
3.0定义3.1测量不确定度:表征合理地赋予被测量之值的分散性。
3.2标准不确定度:以标准差表示的测量不确定度。
3.3 A类标准不确定度:用对观测列进行统计分析的方法来评定不确定度。
3.4 B类标准不确定度:用不同于对观测列进行统计分析的方法来评定标准不确定度。
4.0职责4.1各单位负责本单位实施的测量过程的测量不确定度评定;4.2质检部负责监督、考核各单位测量不确定度的评定工作。
5.0工作流程5.1测量不确定度评定过程5.1.1过程识别:测量不确定度评定过程的输入是国家法规、规范、统计数据、测量设备的证书(或报告)、测量方法、测量环境条件、测量人员素质等;输出是测量不确定度报告;其活动是对测量不确定度分量的分析、合成及扩展不确定度计算。
5.1.2测量管理体系覆盖的计量确认过程、关键测量过程的测量不确定度评定,在测量管理体系的运行过程中应不断完善。
5.1.3各部门应记录测量不确定度的评价。
确定测量不确定度的记录时,可对类似形式的测量设备给予一个通用的陈述,并同时对每个独立的测量过程所特有的变化给出说明。
5.1.4测量不确定度分析应在测量设备和测量过程的确认有效前完成。
5.1.5根据测量过程的重要程度的不同,测量不确定度的评定可以采用不同的方法进行评定。
对于使用要求较低的测量设备,其测量结果的不确定度可采用简化方法进行评定。
5.1.6测量不确定度评定的基本方法执行《测量不确定度评定与表示》的有效版本。
5.1.6.1确定不确定度的来源,一般从五个方面来分析:➢试验人员的因素;➢测量仪器的因素;➢环境条件的因素;➢试验方法的因素;➢被测量本身的因素。
圆弧检测结果的不确定度评定

MPE:(1. 5 + 2. 8L) μm MPEP:1. 5 μm (2)工件 圆弧半径:R50 mm 公差: ± 0. 50 mm 圆心半角:2° (3)测量参数 圆弧直径及测量不确定度:UR0 圆心位置及测量不确定度:Ux0 、Uy0 2. 1 GUM 方法 2. 1. 1 间接测量圆弧的模型 根据一般圆的方程: x2 + y2 + ax + by + c = 0 将 l( x1ꎬy1 )ꎬm( x2ꎬy2 )ꎬn( x3ꎬy3 ) 代入方程 后ꎬ求得圆心坐标点为: x0 =[(x12 +y12)(y2 -y3) + (x22 + y22)(y3 - y1) + (x32 +y32)(y1 -y2)]/ 2[y1(x3 -x2) +y2(x1 -x3) +y3(x2 -x1)] y0 =[(x12 +y12)(x3 -x2) +(x22 +y22)(x1 -x3) + (x32 +y32)(x2 -x1)]/ 2[y1(x3 -x2) +y2(x1 -x3) +y3(x2 -x1)] 圆弧半径为:
2 圆弧样板测量不确定度评定
本文以 GLOBAL silver Performance 07. 10. 07 为例ꎬ对半径为 50 mm 的工件进行测量ꎬ圆心设 定为(0ꎬ0 ) ꎬ 用 GUM 方法 对 其 进 行 不 确 定 度 评 定ꎮ (1)检测设备的计量特性
收稿日期:2018—02—27
R = (x1 - x0 )2 + (y1 - y0 )2 传递系数 v 和 p 是对圆心坐标 x0、y0 求偏导 求得ꎬ其公式略ꎮ x1 、x2 、x3 、y1 、y2 、y3 具有相同的 测量值不确定度 Uꎬ即 x0 和 y0 的不确定度为 Ux0 和 Uy0 :
15
No. 3 August 2018
测量不确定度评定的方法以及实例

测量不确定度评定的方法以及实例1.标准不确定度方法:U =sqrt(∑(xi-x̅)^2/(n-1))其中,xi表示测量值,x̅表示测量值的平均值,n表示测量次数。
标准不确定度包含随机误差和系统误差等。
例如,对一组长度进行测量,测得的数据为10.2、10.3、10.1、10.2、10.3,计算平均值为10.22,标准差为0.069、则标准不确定度为0.069/√5≈0.031,即U=0.0312.扩展不确定度方法:扩展不确定度是在标准不确定度的基础上,考虑到误差的正态分布,对标准不确定度进行扩展得到的结果,通常以U'表示。
其计算公式如下:U'=kU其中,k表示不确定度的覆盖因子,代表了误差分布的概率密度曲线下的面积,一般取k=2例如,对上述例子中的长度进行测量,标准不确定度为0.031,取k=2,则扩展不确定度为0.031×2=0.062,即U'=0.0623.组合不确定度方法:4.直接测量法:直接测量法是通过多次测量同一物理量,统计测得值的离散程度来评估测量的不确定度。
该方法适用于一些简单的测量,如长度、质量等物理量的测量。
例如,对一些小球的直径进行测量,测得的数据为2.51 cm、2.49 cm、2.52 cm、2.50 cm,计算平均值为2.505 cm,标准差为0.013 cm。
则标准不确定度为0.013/√4≈0.007 cm,即U=0.0075.间接测量法:间接测量法是通过已知物理量之间的数学关系,求解未知物理量的方法来评估测量的不确定度。
该方法适用于一些复杂的测量,如测量速度、加速度等物理量的测量。
例如,测量物体的速度v,则有v=S/t,其中S为位移,t为时间。
若S的不确定度为U_S,t的不确定度为U_t,则根据误差传递法则,计算得到v的不确定度为U_v = sqrt(U_S^2 + (U_t * (∂v/∂t))^2 )。
总之,测量不确定度评定的方法包括标准不确定度方法、扩展不确定度方法、组合不确定度方法、直接测量法和间接测量法。
圆度误差测量结果不确定度的评定

估 计 u 的相对不确 定 度为 1% , 自由度 1 5 】 0 则 =0
52 被测件和光栅尺的热膨胀系数引入的不确定度分 .
量 2
式 中 : 一 被 测 件 的 圆度 误 差 ; 圆度 误 差 测 量 结 y 一
果。
3 灵敏 系数
Cl a = /O1 d:1
被测 件 和 光 栅 尺 的 膨 胀 系 数 差 在 半 宽 为 2× 1 I℃ 的区间 内以等概率 分布 = 06
() 3 三坐标 测量 机重复 性引入 的不确定 度 u 坞
{ /+M=12+ . 2 01 = . ta +/ ; . 01 + . 12 m , ! 2 2 2 3
( 下转第 9 页 ) l
石俊杰 等: 高效液掘 色谱 法铡定小麦粉 中过氧 化苯甲酰
的过氧化苯 甲酰标准 溶液 1 [1, 1 . 方 法处理 , .)L 按 . 1 0【 1 3 进行 加标 回收率测 定 , 果见 表 2 结 。平 均 回收率 为 9 .%, S 80 R D
为 34 .%。
表 1 8份 样 品 精 密 度试 验 结 果 ( n=6 )
表 2 6份 样 品 准确 度试 验 结 果 ( n=6 )
参 考 文 献
[] B 70—2 I. 1G 26 ( '食品添加 剂使用卫生标准 . XI [] 2 中华 人 民共 和 国 国家 标 准 . 品 卫 生检 验 方 法 理 化部 分 . B 食 G/
被测 件和光栅 尺应相 同的温 度 , 由于存 在温 度差 , 但 且 温差 以等概率 落于 一l o , 。 C~1C内 后= o U / 3 .8 3=14 =0 5 ℃
被测 件和光栅 尺 的线 膨胀 系数 a:1 . ×1 ℃ - 15 0 1
测量不确定度评定方法与步骤

测量不确定度评定方法与步骤一、测量不确定度评定资料名称资料名称为:XXXXX 测量结果不确定度评定其中“XXXXX ”表示被测量对象的名称仪器的名称或参数的名称;如:被测量对象为普通压力表,测量方式为检定,则资料名称为:普通压力表检定结果不确定度评定;又如,被测量对象为光谱分析仪,测量方式为校准,则资料名称为:光谱分析仪校准结果不确定度评定;再如,被测量对象为XXX 工件内尺寸,测量方式为直接测量,则资料名称为:XXX 工件内尺寸测量结果不确定度评定; 二、评定步骤1.测量方法与测量数学模型 测量方法当测量是按照相关的规程、规范或标准进行时,测量方法的描述为:依据XXX 规程、规范或标准的规定进行测量;当测量无直接相关的规程、规范或标准作依据,即按相应的测量操作进行测量时,测量方法的描述应简述操作的方法; 测量数学模型1.2.1直接测量数学模型当被测对象的量值即是测量仪器的读数的情况直接绝对测量,测量数学模型为:x y = y 表示被测量值,x 表示测量仪器的读数当被测对象的是求取测量误差的情况直接相对测量,测量数学模型为:s x x e -= e 表示示值误差,x 表示被检定或校准的设备的读数,s x 表示检定或校准所用的测量标准设备的读数;一般检定或校准所用的测量标准设备的读数应在不改变的情况下进行比较测量 1.2.2间接测量数学模型当测量是按照相关的规程、规范或标准进行时,应原式引入规程、规范或标准上给出的被测量的计算公式;当测量无直接相关的规程、规范或标准作依据时,应使用相应的计算公式,如:长方形的面积 b a A ⨯= ; 电流强度 RU i =2.最佳测量值最佳测量值即是将各输入分量的平均值带入测量数学模型后计算并修约得到的结果; 如测量数学模型:),,,(21N x x x f y = 先计算得到各个输入分量的平均值,?=i x带入测量数学模型后计算得到: ?),,,(21==N x x x f y3.方差及灵敏系数方差依据测量数学模型写出方差3.1.1当各输入量之间相互独立即不相关的情况,对任意的测量数学模型,方差形式均为:)()()(222i iC x u x f y u ∑∂∂=)(y u C 表示被测量y 的合成标准不确定度 特别地,当测量数学模型形如N pN ppx x Cx y 2121=时,方差可写成相对合成式:2.2.)]([)(i rel i i rel C x u p y u ∑=3.1.2当各输入量之间相互不独立即不相关的情况,对任意的测量数学模型,方差包含协方差形式为: ),(2)()()(222j i ji i iC x x u x fx f x ux fy u ∂∂∂∂+∂∂=∑∑∑其中:协方差)()(),(),(j i j i j i x u x u x x r x x u = 式中),(j i x x r 为输入量i x 和j x 之间的相关系数,其绝对值小于或等于1 ; 灵敏系数灵敏系数即各偏导数i x f ∂∂ ,一些资料中用字母)(i x C 表示 ,即)(i x C =ix f ∂∂ 应经计算得到具体的结果; 4.标准不确定度分量)(i x u 计算 标准不确定度)(1x u 评定应认为11)(x x f = 为一个简单的直接测量进行评定,主要评定: 测量重复性随即效应引入的不确定度 ns x u =)(11 或 ms x u =)(11测量仪器不准系统效应引入的不确定度 kax u =)(12 该分量合成得到:)()()(122121x u x u x u i +=标准不确定度)(2x u 评定 ┉┉ 仿效)(1x u 的评定,可得到各)(i x u6.合成标准不确定度)(y u C将各标准不确定度分量及其灵敏系数代入方差式,取其正方根即可计算得到; 7.扩展不确定度)(y U一般按简易法进行扩展,)()(y u k y U C ⋅= 2=k注1:扩展不确定度的有效数字不能多于2位,应与测量结果末位对齐;保留1位或2位有效数字时后面的数字除零外应均要进位;注2:各标准不确定度分量的有效数字应多余2位进行保留; 8.结果报告 按绝对量报告报告方式1 )(y U y Y ±= 2=k 或 )(U y Y = 2=k报告方式2 ?=Y ?)(=y U 2=k 按相对量报告报告方式1 )](1[y U y Y rel ±= 2=k 报告方式2 ?=Y ?)(=y U rel 2=k。
计量用圆筒容量测量的不确定度评定

作者简介:赵文海(1985—),男,工程师,主要从事油田QHSE 监督工作。
Evaluation of Measurement Uncertainty of Cylinder VolumeZhao WenhaiShengli Offshore Petroleum Engineering Technology Inspection Co.,Ltd.,Sinopec(Dongying 257000,Shandong,China)Abstract :In order to evaluate the accuracy of measurement results of volume density of fracturing proppant,the uncertainty evaluationmethod of cylinder capacity measurement is established according to JJF1059.1-2012”Evaluation and Expression of Measurement Un⁃certainty ”.Uncertainty is a commonly accepted parameter to evaluate the quality of measurement results,and it is also a measure of re⁃porting.Taking the cylinder with the volume of 100cm 3for the measurement of the volume density of fracturing proppant as an exam⁃ple,it is proved that the established method can accurately obtain the uncertainty of measurement results,and has good practical and popularization value.Key words :cylinder volume;measurement uncertainty;evaluation method赵文海.计量用圆筒容量测量的不确定度评定[J].石油工业技术监督,2020,36(1):47-48,59.Zhao Wenhai.Evaluation of measurement uncertainty of cylinder volume[J].Technology Supervision in Petroleum Industry,2020,36(1):47-48,59.计量用圆筒容量测量的不确定度评定赵文海中国石化胜利海上石油工程技术检验有限公司(山东东营257000)摘要为了评定压裂支撑剂体积密度测量结果的准确性,根据JJF 1059.1—2012《测量不确定度评定与表示》建立了圆筒容量测量不确定度评定方法。
体积和电阻测量不确定度评定实例
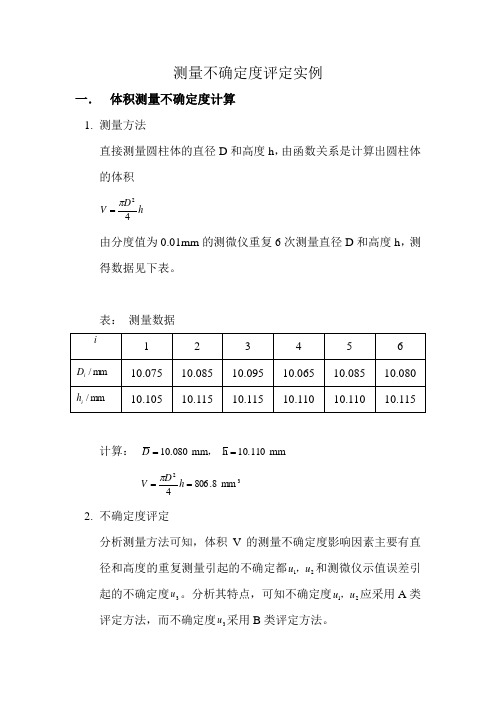
测量不确定度评定实例一. 体积测量不确定度计算1. 测量方法直接测量圆柱体的直径D 和高度h ,由函数关系是计算出圆柱体的体积h D V 42π=由分度值为0.01mm 的测微仪重复6次测量直径D 和高度h ,测得数据见下表。
表: 测量数据i1 2 3 4 5 6 mm /i D 10.075 10.085 10.095 10.065 10.085 10.080 mm /i h10.10510.11510.11510.11010.11010.115计算: mm 0.1110h mm 80.010==,D 32mm 8.8064==h D V π2. 不确定度评定分析测量方法可知,体积V 的测量不确定度影响因素主要有直径和高度的重复测量引起的不确定都21u u ,和测微仪示值误差引起的不确定度3u 。
分析其特点,可知不确定度21u u ,应采用A 类评定方法,而不确定度3u 采用B 类评定方法。
①.直径D 的重复性测量引起的不确定度分量 直径D 的6次测量平均值的标准差: ()mm 0048.0=D s 直径D 误差传递系数:h DD V 2π=∂∂ 直径D 的重复性测量引起的不确定度分量: ()3177.0mm D s DVu =∂∂=②.高度h 的重复性测量引起的不确定度分量 高度h 的6次测量平均值的标准差: ()mm 0026.0=h s 高度h 误差传递系数:42D h V π=∂∂ 高度h 的重复性测量引起的不确定度分量: ()3221.0mm h s hVu =∂∂=③测微仪示值误差引起的不确定度分量由说明书获得测微仪的示值误差范围mm 1.00±,去均匀分布,示值的标准不确定度mm 0058.0301.0==q u 由示值误差引起的直径测量的不确定度 q D u DVu ∂∂=3由示值误差引起的高度测量的不确定度 q h u hV u ∂∂=3 由示值误差引起的体积测量的不确定度分量 ()()323233mm 04.1=+=h D u u u 3. 合成不确定度评定()()()3232221mm 3.1=++=u u u u c 4. 扩展不确定度评定当置信因子3=k 时,体积测量的扩展不确定度为 3mm 9.33.13=⨯==c ku U 5.体积测量结果报告() mm .93.88063±=±=U V V考虑到有效数字的概念,体积测量的结果应为 () mm 48073±=V二. 伏安法电阻测量不确定度计算1. 测量方法:通过测量电阻两端电压和所通过的电流,计算被测电阻。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
“测量圆筒体积〞不确定度评定
1、概述
根据……,在环境温度为20℃下,用
和高度H,各对圆筒的不同位置测量6次,
测量值为:
圆筒不同位置测量结果
2、数学模型
H D
V •=2)2
(π
式中:V —— 圆筒的体积;cm 3。
D —— 圆筒的直径;cm 。
H —— 圆筒的高度。
cm 。
21)2(D H V c π=∂∂=
、 H D
D V c 2
2π=∂∂= 将上表中=D 1.0081cm 、=H 10.0110cm 代入上式计算为:
c 1=0.7982 cm 2, c 2=15.8526 cm 2
3、测量不确定度的来源
测量不确定度主要来源:
①、圆筒高度测量引入标准不确定度; ✧ 游标卡尺的本身不确定度 ✧ 测量人员读数引入标准不确定度 ✧ 圆筒高度不均匀引入标准不确定度 ②、圆筒直径测量引入标准不确定度。
✧ 千分尺本身不确定度;
✧ 测量人员读数引入标准不确定度; ✧ 圆筒直径不均匀引入标准不确定度;
4、标准不确定度分量的评定
1、圆筒高度测量引入标准不确定度〔u 1〕 ①、游标卡尺的本身不确定度〔11u 〕
游标卡尺的本身存在误差引入的标准不确定度根据游标卡尺的说明书〔或技术文件〔如检定规程等〕〕规定其最大允许误差为±0.020mm ,并经过检定且合格。
假设测量值在最大允许误差围的概率分布为均匀分布,即,故其标准不确定度为:
②、测量人员读数引入标准不确定度〔12u 〕
根据游标卡尺分度值0.01mm ,按1/20来估读,那么人员估读产生的测量不确定度为。
③、圆筒高度不均匀引入标准不确定度(13u )
在圆筒的不同位置测量H ,共测量6次,其测量数据见上表,那么标准不确定度)(3H u 为:
cm 000257.06
00063
.0)()(13====n H s H s u
综合上述分析,得圆筒高度测量引入标准不确定度为
cm
0000144.001.03
220/112=⨯=u cm
00115.03
020
.011==u
2
222
132122111000257
.00000144.000115.0++=++=u u u u = 0.001178cm
2、圆筒直径测量引入标准不确定度〔u 2〕 ①、千分尺的本身的标准不确定度)(21u
根据千分尺的说明书〔或技术文件〔如检定规程等〕〕规定其最大允许误差为±0.001cm ,并经过检定且合格。
假设测量值在最大允许误差围的概率分布为均匀分布,即3=k ,故其标准不确定度
)(1H u 为:
cm 000577.03
001
.021==
u ②、测量人员读数引入的标准不确定度)(22u
根据经历估计千分尺读数的分散性不超过最小分度的二分之一,最小分度为0.0005cm ,假设概率分布为均匀分布,那么)(2H u 为:
a = 0.0005 cm /2=0.00025 cm 〔半宽〕
cm 000144.03
cm 00025.022==u
③、圆筒直径的不均匀引入的标准不确定度)(23u
在圆筒的不同位置测量D ,共测量6次,其测量数据见上表,那么标准不确定度)(3D u 为:
cm 000416.06
00102
.0)()(23===
=n D s D s u 综合上述分析,得圆筒高度测量引入标准不确定度为
2
222
232222212000416
.0000144.0000577.0++=++=u u u u = 0.0007258cm 5、合成标准不确定度的计算
根据标准不确定度分量评定结果,按“不确定度传播律〞进展合成得到“相对合成标准不确定度)(c V u 〞。
22222211c )0007258.08526.15()001178.07982.0()()()(⨯+⨯=•+•=u c u c V u
= 0.01154cm 3
标准不确定度分量一览表
6、扩展不确定度确实定
选取包含因子k =2,那么扩展不确定度U 为:
U =k ·u c (V )=2×0.01154cm 3=0.02308cm 3
7、测量结果的最终表示
根据上述计算得到圆筒体积为:
V = 0.8070 cm 3
那么测量结果表示为:
V = (0.807±0.023) cm 3〔 k = 2〕
1、概述
根据……,在环境温度为20℃下,用千分尺直接测量圆筒的直径D 和高度H ,各对圆筒的不同位置测量
6次,测量值为:
圆筒不同位置测量结果
2、数学模型
H D V •=2
)2
(π
式中:V —— 圆筒的体积;cm 3。
D —— 圆筒的直径;cm 。
H —— 圆筒的高度。
cm 。
3、测量不确定度的来源
测量不确定度主要来源: ①、千分尺本身不确定度;
②、测量人员读数引入标准不确定度;
③、圆筒高度不均匀引入标准不确定度; ④、圆筒直径不均匀引入标准不确定度。
4、标准不确定度分量的评定
①、千分尺的本身的标准不确定度1u
根据千分尺的说明书〔或技术文件〔如检定规程等〕〕规定其最大允许误差为±0.001cm ,并经过检定且合格。
假设测量值在最大允许误差围的概率分布为均匀分布,即3=k ,故其标准不确定度
)(1H u 为:
cm 000577.03
001
.0)(1==
H u ②、测量人员读数引入的标准不确定度2u
根据经历估计千分尺读数的分散性不超过最小分度的二分之一,最小分度为0.0005cm ,假设概率分布为均匀分布,那么)(2H u 为:
a = 0.0005 cm /2=0.00025 cm 〔半宽〕
cm 000144.03
cm
00025.0)(2==
H u ③、圆筒高度的不均匀引入的标准不确定度3u
在圆筒的不同位置测量H ,共测量6次,其测量数据见上表,那么标准不确定度)(3H u 为:
cm 000257.06
00063
.0)()()(3===
=n H s H s H u ④、圆筒直径的不均匀引入的标准不确定度4u
在圆筒的不同位置测量D ,共测量6次,其测量数据见上表,那么标准不确定度)(3D u 为:
cm 000416.06
00102
.0)()()(4==
=
=n
D s D s D u
5、合成标准不确定度的计算
测量高度和直径使用同一个千分尺,因此要考虑他们间的相关性。
设千分尺的读数符号为r 表示。
由于H =F (r ) =r 和D =G (r ) =r ,所以H 和D 的协方差为:
)()(),(22r u r u r
G
r F D H S =•∂∂•∂∂=
那么相关项为
)
()()(2),()()(2)()(),()()(22r u D c H c D H S D c H c H u D u D H r D c H c ••=••=•••• 根据标准不确定度分量评定结果,按“不确定度传播律〞进展合成得到“相对合成标准不确定度)(c V u 〞。
)()()(2)()()()(()(2232242c r u D c H c H u H c D u D c V u ••+•+•=
式中传播系数为:
2)2()(D H V H c π=∂∂=
、 H D
D V D c 2
)(π=∂∂= 将上表中=D 1.0081cm 、=H 1.0110cm 代入上式计算为:
=)(H c 0.7982 cm 2, =)(D c 1.6009 cm 2
)()()(2)()()()(()(2232242c r u D c H c H u H c D u D c V u ••+•+•=
2
22)000144.0000577.0(6009.17982.02)000416.06009.1()000257.07982.0(+⨯⨯⨯+⨯+⨯=
= 1.2×10-3cm 3 6、扩展不确定度确实定
选取包含因子k =2,那么扩展不确定度U 为:
U =k ·u c (V )=2×1.5658×10-3cm 3=0.0032cm 3
7、测量结果的最终表示
根据上述计算得到圆筒体积为:
V = 0.8070 cm 3
那么测量结果表示为:
V = (0.8070±0.0032) cm 3〔 k = 2〕。
