采用矩形法求定积分
C语言用六种方法求定积分

C语言用六种方法求定积分C语言中求定积分的方法主要有以下六种:基本公式法、数值积分法、Laplace变换法、微积分概念法、数值积分法和Monte Carlo方法。
下面将详细介绍每种方法的原理和实现。
1.基本公式法:基本公式法是求解定积分的最基本方法,根据不同函数的特点和性质,利用已知的积分公式进行求解。
例如,对于一次函数和常数函数,可以使用基本公式法求解。
2.数值积分法:数值积分法是通过将定积分转化为数值计算问题来求解。
常用的数值积分方法有矩形法、梯形法和辛普森法等。
这些方法基于将求积分区间分割成若干个小区间,然后在每个小区间上近似计算出函数的积分值,再将这些积分值加总得到最终结果。
3. Laplace变换法:Laplace变换法是一种利用Laplace变换求解微分方程的方法,也可以用来求解定积分。
通过将被积函数进行Laplace变换,然后利用Laplace变换公式求解积分,最后再求出反变换得到结果。
4.微积分概念法:微积分概念法是通过将定积分定义为函数曲线下的面积来求解。
具体做法是将被积函数图像与坐标轴围成的面积分为若干个小的矩形、梯形或曲线段以及一个小的区域。
然后根据图形的几何性质进行近似计算,将这些小面积相加得到最终结果。
5.数值积分法:数值积分法也是一种基于数值计算的方法,但与前面提到的数值积分法不同,它通过构造一系列特定形式的插值函数对被积函数进行逼近,然后计算插值函数的积分值来近似求解定积分。
常用的数值积分法有牛顿-科特斯公式和高斯-勒让德公式。
6. Monte Carlo方法:Monte Carlo方法是一种基于统计随机性的数值积分方法,它通过随机抽样来进行数值求解。
具体做法是在被积函数图像下随机抽取一系列点,根据这些随机点的坐标和函数值来估计函数的积分值。
通过对多次随机抽样的结果取平均可以得到定积分的近似值。
以上六种方法都可以用C语言来实现,具体的实现方法可以根据具体问题的特点和要求选择合适的算法和数据结构,然后编写相应的代码实现。
vb程序设计教程ZW9

第9章过程9.1 Sub过程9.1.1建立Sub过程1. 定义Sub过程2VisualBasic程序设计教程(第三版)2. 建立Sub过程图9.1“添加过程”对话框图9.2模块代码窗口9.1.2调用Sub过程1. 用Call语句调用Sub过程2. 把过程名作为一个语句来使用VisualBasic程序设计教程(第三版) 3图9.3时间延迟4VisualBasic程序设计教程(第三版) 9.1.3通用过程与事件过程VisualBasic程序设计教程(第三版) 56VisualBasic程序设计教程(第三版) 9.2 Function过程9.2.1建立Function过程VisualBasic程序设计教程(第三版) 7 9.2.2调用Function过程图9.4输出随机数8VisualBasic程序设计教程(第三版)图9.5求平方根VisualBasic程序设计教程(第三版) 9图9.6 Visual Basic应用程序中的过程9.3参数传送9.3.1形参与实参1. 按位置传送图9.7形参与实参2. 指名传送10VisualBasic程序设计教程(第三版) 9.3.2引用图9.8过程的副作用9.3.3传值9.3.4数组参数的传送图9.9实参数组与形参数组图9.10用梯形法求定积分图9.11求定积分(界面设计)图9.12求定积分(求值结果)9.4可选参数与可变参数9.4.1可选参数9.4.2可变参数9.5对象参数9.5.1窗体参数9.5.2控件参数图9.13控件参数示例图9.14 TypeOf 语句示例图9.15控件移动(界面设计)图9.16控件移动(运行情况)9.6局部内存分配9.7递归图9.17递归调用操作习题9.1编写一个求3个数中最大值Max和最小值Min的过程,然后用这个过程分别求3个数和5个数、7个数中的最大值和最小值。
9.2编写程序,求S=A!+B!+C!,阶乘的计算分别用Sub过程和Function过程两种方法来实现。
矩形法求函数的定积分

用矩形法求函数的定积分(C 语言实现)
在本程序中,先分别定义了 5 个 C 函数 f1、f2、f3、f4、f5,用来代表 5 个不同的函数。然后 定义了一个求定积分的函数 integral。现在介绍矩形法求函数定积分的数学思想。
设函数 在区间[a,b]上连续,在(a,b)上可导,将[a,b]之间的长度等分成 n 份(n 越大计算越精 确)。于是第 块小矩形的面积为 ,
printf("%lf\n",S[j]); } }
运行结果如图所示:
可以发现,计算值与理论值十分接近,当 N 取的足够大时,可以获得十分精确的值,但是运算 次数也会增加,本函数的时间复杂度为 O(n)。
从指针的用法上来讲,本程序使用了“指向函数的指针”。一个函数的函数名,代表了这个函 数的首地址,在主函数中,5 次调用 integral 函数,实现了对 5 个不同的函数求积分。integral 函 数包含了三个参数,前两个参数表示被积函数的上下限。
sum=sum+d*(*fun)(a+i*d);//定积分近似计算公式 }//fun 是指向函数的指针,该指针所指向的函数带有一个 double 型的形参, //同时,该函数的返回值类型为 double return sum; }
2
C 语言在计算中的应用
void main() {
double S[5]; int j; S[0]=integral(0,1,f1);//fun 指向 f1 S[1]=integral(0,1,f2);//fun 指向 f2 S[2]=integral(0,1,f3);//fun 指向 f3 S[3]=integral(0,1,f4);//fun 指向 f4 S[4]=integral(0,1,f5);//fun 指向 f5 printf("输出各个函数的积分值:\n"); for(j=0;j<5;j++) {
C语言使用矩形法求定积分的通用函数
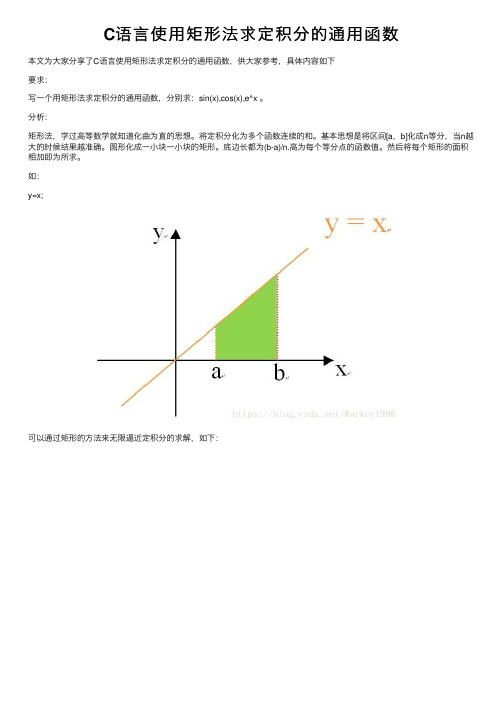
C语⾔使⽤矩形法求定积分的通⽤函数本⽂为⼤家分享了C语⾔使⽤矩形法求定积分的通⽤函数,供⼤家参考,具体内容如下要求:写⼀个⽤矩形法求定积分的通⽤函数,分别求:sin(x),cos(x),e^x 。
分析:矩形法,学过⾼等数学就知道化曲为直的思想。
将定积分化为多个函数连续的和。
基本思想是将区间[a,b]化成n等分,当n越⼤的时候结果越准确。
图形化成⼀⼩块⼀⼩块的矩形。
底边长都为(b-a)/n.⾼为每个等分点的函数值。
然后将每个矩形的⾯积相加即为所求。
如:y=x;可以通过矩形的⽅法来⽆限逼近定积分的求解,如下:因为被分成n等分,就可以认为每⼀等分是⼀个矩形,那么每⼀矩形的⾯积为:每⼀个矩形⾯积为:***Sn=f(x)(b-a)/n 总⾯积为:****S=S1+S2+…+Sn#include <stdio.h>#include <stdlib.h>#include <math.h>//引⼊sin x,cos x,e^x的库//使⽤指向函数的指针变量来复⽤⼀个通⽤函数int main(){int i,j,k,n,m;float res;float (*fun)(float);//定义指向函数的指针变量float integral (float a,float b,float (*fun)(float),int n);//n为将积分区间(b-a)分成n等分,当n的值越⼤的时候结果越精确,数学上的定义是取⽆穷⼤float fsin(float);//sin x函数的声明float fcos(float);//cos x函数的声明float fexp(float);//e^x 函数的声明printf ("请输⼊积分的下限\n");scanf ("%d",&m);printf ("请输⼊积分的上限\n");scanf ("%d",&n);printf("请输⼊你要计算的函数的具体函数\n");printf("1.sin(x) 2.cos(x) 3.e^x\n");scanf ("%d",&i);switch(i){case 1:fun=fsin;//函数地址(⼊⼝)交给指针变量,灵活性强break;case 2:fun=fcos;break;case 3:fun=fexp;}res=(fun)(2.00);//printf("xxxx=%f\n",res);printf ("计算的结果为\n");res=integral(m,n,fun,200000);printf("res=%f",res);return 0;}float fsin(float x){// printf("fsinx=%f\n",x);return sin(x);}float fcos(float x){//printf("fcosx=%f\n",x);return cos(x);}float fexp(float x){//getchar();//printf("fexp=%f\n",x);return exp(x);}float integral(float a,float b,float (*fun)(float),int n){//矩形法计算,定积分转换为连续求和的形式int i=0;float x=a,s=0;float h=(b-a)/n;for (i=1;i<=n;i++){x=x+h;s=s+((*fun)(x)*h);}return s;}结果:以上就是本⽂的全部内容,希望对⼤家的学习有所帮助,也希望⼤家多多⽀持。
数值积分使用数值方法计算定积分

数值积分使用数值方法计算定积分定积分是数学中的重要概念,用于求解曲线下面的面积。
在某些情况下,定积分无法通过解析解来求解,此时可以使用数值方法来进行近似计算。
数值积分是一种广泛应用的技术,本文将介绍数值积分的基本原理以及常见的数值方法。
一、数值积分的基本原理数值积分的基本原理是将曲线下的面积近似为若干个矩形的面积之和。
假设要计算函数f(x)在区间[a, b]上的定积分,首先将[a, b]等分成n个小区间,每个小区间的宽度为Δx=(b-a)/n。
然后,在每个小区间上选择一个代表点xi,计算其对应的函数值f(xi),然后将所有矩形的面积相加,即可得到近似的定积分值。
二、矩形法矩形法是数值积分中最简单的方法之一。
它将每个小区间上的函数值看作是一个常数,然后通过计算矩形的面积来近似定积分的值。
矩形法主要有两种形式:左矩形法和右矩形法。
1. 左矩形法左矩形法使用小区间左端点的函数值来代表整个小区间上的函数值。
即近似矩形的面积为f(xi) * Δx,其中xi为小区间的左端点。
然后将所有矩形的面积相加,得到近似的定积分值。
2. 右矩形法右矩形法与左矩形法相似,仅仅是使用小区间右端点的函数值来代表整个小区间上的函数值。
近似矩形的面积为f(xi + Δx) * Δx,其中xi为小区间的左端点。
同样地,将所有矩形的面积相加,得到近似的定积分值。
三、梯形法梯形法是比矩形法更精确的数值积分方法。
它通过使用每个小区间的两个端点处函数值的平均值来代表整个小区间上的函数值,并计算梯形的面积来近似定积分的值。
梯形法的计算公式为:(f(xi) + f(xi + Δx)) * Δx / 2,其中xi为小区间的左端点。
将所有梯形的面积相加,得到近似的定积分值。
四、辛普森法辛普森法是一种更加高阶的数值积分方法,它使用三个点对应的函数值来逼近曲线。
将每个小区间看作一个二次函数,可以通过拟合这个二次函数来近似定积分的值。
辛普森法的计算公式为:(f(xi) + 4 * f(xi + Δx/2) + f(xi + Δx)) * Δx / 6,其中xi为小区间的左端点。
几种定积分的数值计算方法

f
x C2 a,b,记 M=max xa,b
f
'' x ,则 x1, x2 a
x1
x2 ,有
b
a
f
x dx
ba 2
f
x1
f
x2
b a3
12
M
.
证明: 过 x1, f x1 , x2, f x2 两点的直线方程为
P(x)
f
x1
f
x2
x2
f x1
x1
(
x
x1
)
所以 P(xi ) f (xi ),i 1, 2.令
max
xa ( i 1) h , a ih
f (x) ,i
1.2., n
I~ 与 I 如上,则 I~ 与 I 的误差满足 I I~ O( 1 ) . n
证明:
I I~
b a
f (x)dx b a n
n i 1
f (i )
由命题 1 得,
n i 1
a ih
n
f (x)dx h
将{i }映射到子区间
{a i 1 (b a), a i (b a)} a,b,
n
n
i 1,2,, n
最后,计算 I
的近似值 I~ , I~
ba n
n i 1
f (i ) .
下面用两个命题证明“类矩阵”方法的可行性.
命题 1
设
f (x) C1a,b,记M
max
xa ,b
f
( x)
, x0
几种定积分的数值计算方法
几种定积分的数值计算方法
摘 要:本文归纳了定积分近似计算中的几种常用方法,并着重分析了各种数值方法的计算 思想,结合实例,对其优劣性作了简要说明. 关键词:数值方法;矩形法;梯形法;抛物线法;类矩形;类梯形
定积分的计算与应用

定积分的计算与应用定积分是微积分的重要概念之一,用于计算曲线下的面积、质量、体积等问题。
本文将介绍定积分的计算方法和应用场景。
一、定积分的计算方法定积分的计算基于微积分中的积分运算,可以通过以下方法进行计算:1. 几何解释法:定积分可以视为曲线下的面积,因此可以利用几何图形的面积公式进行计算。
将曲线下的区域分割成无数个小矩形,并求取它们的面积之和,即可得到定积分的近似值。
通过增加小矩形的个数,可以不断提高计算精度。
2. 集合解释法:定积分可以被视为一组数的和,其中这组数是将函数值与对应的间隔长度相乘而得到的。
通过将曲线下的区域分割成若干个小区间,并计算每个小区间内的函数值与对应的间隔长度的乘积,再将这些乘积进行加和,即可得到定积分的近似值。
3. 牛顿-莱布尼茨公式:对于可微函数,可以使用牛顿-莱布尼茨公式进行定积分的计算。
该公式表达了函数的原函数(即不定积分)与定积分之间的关系。
通过求取函数的原函数,并在积分的上下限处进行代入计算,即可得到定积分的准确值。
二、定积分的应用场景定积分在物理学、经济学、工程学等领域都有广泛的应用。
以下将介绍一些常见的应用场景:1. 面积计算:最简单的应用是计算平面图形的面积。
通过确定曲线的方程以及积分的上下限,可以计算出曲线所围成区域的面积。
2. 质量计算:如果将曲线下的区域视为物体的密度分布,则可以利用定积分计算物体的质量。
通过将物体分割成无数个小区域,并计算每个小区域内的密度值与对应的区域面积的乘积,再将这些乘积进行加和,即可得到物体的总质量。
3. 体积计算:类似质量计算,定积分可以被用于计算三维物体的体积。
通过将物体分割成无数个小体积,并计算每个小体积的大小,再将这些体积进行加和,即可得到物体的总体积。
4. 概率计算:在概率论中,定积分可以用于计算随机变量的概率密度函数下的概率。
通过计算概率密度函数在某个区间上的定积分,可以得到该区间内事件发生的概率。
5. 积累量计算:定积分还可以用于计算积累量,例如距离、速度、加速度等。
关于定积分近似计算中矩形法的误差估计

矩形法 =
1 20
&
2.
598 08
&
1
=
0. 129904,
梯形法 = 2. 59808 = 0. 064592, 40
= 抛物线法
5
&
2. 59808 36 0
=
0. 0360844.
这个误差上界有些大.
下面利用文[ 4] 中给出的复合梯形法和复合抛
物线法的误差公式
梯形法 =
(
b - a) 1 2n2
证明 据拉格朗日中值定理, 任给 x ∃ [ a, b] ,
存在 ∃ ( a, b) , 使得
f ( x ) - f ( a) = f ∀( ) ( x - a) .
收稿日期: 2009 - 12 - 07; 修改日期: 2010 - 08 - 31. 基金项目: 西北农林科技大学教学改革项目资助( JY 0902104) . 作者简介: 郑立飞( 1973 - ) , 男, 陕西临潼人, 硕士, 讲师, 主要从事生
xi- 1
#
1 2
Mh2.
由此即知
b
n
% f ( x ) dx - h f ( x i- 1 ) #
a
i= 1
n
%
i= 1
xi
f ( x ) dx - hf ( x i- 1 ) #
x i- 1
n 2
Mh2
=
21nM ( b -
a) 2 .
对于复合右矩形法, 可以同样证明, 其误差估计
与复合左矩形法相同.
从定理 2 可知, 矩形法在使用的时候, 要求有足
够多的分点, 即 n 要足够得大, 否则精度难以保证.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
问题 采用矩形法求定积分⎰
π0sin x y =
▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂ double a; /*积分区间下限*/
double b; /*积分区间上限*/
问题的输出:
double fx; /*积分结果*/
设计 初始算法
初始化积分区间(a ,b )。
如果把积分区间划分为100个格,则h=fabs(a-b)/100;
因为区间划分为100个格,因此循环过程如下:
for(i=0;i<100;i++)
{
fx=f (x+i*h+h/2);
… …
}
▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂
分析 利用矩形法可以求定积分其原理如图(9-1)所示。
求函数f在(a,b )区间的定积分
公式为:
)2/)1(()2/2()2/()2/(()
2/)1(()2/()2/(h h n a f h h a f h h a f h a f h h h n a f h h h a f h h a f s +-++++++++++•=+-+++•+++•+=
图9-1 矩形法求定积分
所需数据与算法如下。
数据要求
问题的输入:
double a;
/*积分区间下限*/ double b;
/*积分区间上限*/
问题的输出:
double fx; /*积分结果*/
设计初始算法
1.初始化积分区间(a,b)。
2.如果把积分区间划分为100个格,则h=fabs(a-b)/100;
3.因为区间划分为100个格,因此循环过程如下:
for(i=0;i<100;i++)
{
fx=f (x+i*h+h/2);
……
}
流程图
实现程序代码如下:
#include "stdio.h"
#include "math.h"
double f (double x)
{
return sin(x);
}
double Jifen(double a,double b)
{
double h;
double fx;
double x;
int i;
double sum=0;
h=fabs(a-b)/100;
x=a;
for(i=0;i<100;i++)
{
fx=f (x+i*h+h/2);
sum=sum+fx;
}
return sum*h;
}
void main()
{
double a;
double b;
double fx;
a=0;
b=3.1415926;
fx=Jifen(a,b);
printf("Ji Fen Y=%f" ,fx);
}
运行结果Ji Fen Y=2.000082
测试如果将积分区间划分为1000个格,则循环条件改为i<1000,得到结果为2.00001。
该测试说明积分区间划分越多,越能够接近正确结果。
