数字信号处理第二章上机作业
《数字信号处理》课后上机题#优选.

subplot(2,2,2);stem(n,sn1,'.')
title('(b)系统1的单位阶跃响应');
xlabel('n');ylabel('s(n)')
%系统2
xn=[1,zeros(1,30)];
%xn=单位脉冲序列,长度N=31
xi=filtic(B2,A2,ys);
实验报告
第一章:时域离散信号和时域离散系统
*16.已知两个系统的差分方程分别为
(1) y(n)=0.6y(n-1)-0.08y(n-2)+x(n)
(2) y(n)=0.7y(n-1)-0.1y(n-2)+2x(n)-x(n-2)
分别求出所描述的系统的单位脉冲响应和单位阶跃响应.
解:(可附程序)
(1)系统差分方程的系数向量为
subplot(2,2,1);stem(n,hn1,'.')
title('(a)系统1的系统单位脉冲响应');
xlabel('n');ylabel('h(n)')
xn=ones(1,30);
%xn=单位阶跃序列,长度N=31
sn1=filter(B1,A1,xn,xi);
%调用filter解差分方程,求系统输出信号sn1
%设差分方程(2)系数向量
%系统1
xn=[1,zeros(1,30)];
ys=0;
%xn=单位脉冲序列,长度N=31
xi=filtic(B1,A1,ys);
%由初始条件计算等效初始条件输入序列xi
hn1=filter(B1,A1,xn,xi);
数字信号处理第2章作业

5、谈谈你对公式2-10的理解,其约束条件是什 么?
❖ 如果连续带通信号的最低频率小于带宽,则不能采 用带通采样。
❖ 允许的带通采样率范围与不允许的带通采样率范围 相互间隔。
2.4带通采样中的频谱倒置
一、什么是频谱倒置
Eq.(2-10) 中m为奇数时发生倒置现象, 如图2-9的b、e。基带(0Hz附近)谱是 原谱正负部分的倒置,即基带正谱部分 是原负谱部分的影像。
❖ 原谱正部分是对称时,谱倒置不会产生问题, 可选择 Eq.(2-10) 中满足避免走样的fs值。
2fc m
6、带通采样频率为什么不宜选在允许带与禁 止带的交界处?有哪两种选取方法?
7、什么情况下会出现频谱倒置?有何简单的 方法使其逆转?
3、离散信号其频谱为什么会周期重复?
答:离散信号是对连续信号的采样,当 以采样频率fs采样时,如果 k 为任意正或 负整数,我们难以区分这是频率为f0 的 正弦曲线的样本还是频率为 f0+kfs 的正弦 曲线样本。这种固有的频率域aliasing现 象导致频谱的周期性重复,重复周期为fs
❖ Any signal energy located above +BHz and below BHz in the original continuous spectrum will always end up in the band of interest after sampling, regardless of the sample rate.
4、实际低通采样时为什么加模拟低通滤波器? P31页。
《数字信号处理》(2-7章)习题解答

第二章习题解答1、求下列序列的z 变换()X z ,并标明收敛域,绘出()X z 的零极点图。
(1) 1()()2nu n (2) 1()()4nu n - (3) (0.5)(1)nu n --- (4) (1)n δ+(5) 1()[()(10)]2nu n u n -- (6) ,01na a <<解:(1) 00.5()0.50.5nn n n zZ u n z z ∞-=⎡⎤==⎣⎦-∑,收敛域为0.5z >,零极点图如题1解图(1)。
(2) ()()014()1414n nn n z Z u n z z ∞-=⎡⎤-=-=⎣⎦+∑,收敛域为14z >,零极点图如题1解图(2)。
(3) ()1(0.5)(1)0.50.5nnn n zZ u n z z --=-∞-⎡⎤---=-=⎣⎦+∑,收敛域为0.5z <,零极点图如题1解图(3)。
(4) [](1Z n z δ+=,收敛域为z <∞,零极点图如题1解图(4)。
(5) 由题可知,101010910109(0.5)[()(10)](0.5)()(0.5)(10)0.50.50.50.50.50.5(0.5)n n nZ u n u n Z u n Z u n z z z z z z z z z z z --⎡⎤⎡⎤⎡⎤--=--⎣⎦⎣⎦⎣⎦⋅=-----==--收敛域为0z >,零极点图如题1解图(5)。
(6) 由于()(1)nn n a a u n a u n -=+--那么,111()(1)()()()nn n Z a Z a u n Z a u n z z z a z a z a a z a z a ----⎡⎤⎡⎤⎡⎤=---⎣⎦⎣⎦⎣⎦=----=-- 收敛域为1a z a <<,零极点图如题1解图(6)。
(1) (2) (3)(4) (5) (6)题1解图2、求下列)(z X 的反变换。
数字信号处理上机作业

数字信号处理上机作业学院:电子工程学院班级:021215组员:实验一:信号、系统及系统响应1、实验目的(1) 熟悉连续信号经理想采样前后的频谱变化关系,加深对时域采样定理的理解。
(2) 熟悉时域离散系统的时域特性。
(3) 利用卷积方法观察分析系统的时域特性。
(4) 掌握序列傅里叶变换的计算机实现方法,利用序列的傅里叶变换对连续信号、离散信号及系统响应进行频域分析。
2、实验原理与方法(1) 时域采样。
(2) LTI系统的输入输出关系。
3、实验内容及步骤(1) 认真复习采样理论、离散信号与系统、线性卷积、序列的傅里叶变换及性质等有关内容,阅读本实验原理与方法。
(2) 编制实验用主程序及相应子程序。
①信号产生子程序,用于产生实验中要用到的下列信号序列:a. xa(t)=A*e^-at *sin(Ω0t)u(t)b. 单位脉冲序列:xb(n)=δ(n)c. 矩形序列: xc(n)=RN(n), N=10②系统单位脉冲响应序列产生子程序。
本实验要用到两种FIR系统。
a. ha(n)=R10(n);b. hb(n)=δ(n)+2.5δ(n-1)+2.5δ(n-2)+δ(n-3)③有限长序列线性卷积子程序用于完成两个给定长度的序列的卷积。
可以直接调用MATLAB语言中的卷积函数conv。
conv 用于两个有限长度序列的卷积,它假定两个序列都从n=0 开始。
调用格式如下:y=conv (x, h)4、实验结果分析①分析采样序列的特性。
a. 取采样频率fs=1 kHz,,即T=1 ms。
b. 改变采样频率,fs=300 Hz,观察|X(e^jω)|的变化,并做记录(打印曲线);进一步降低采样频率,fs=200 Hz,观察频谱混叠是否明显存在,说明原因,并记录(打印)这时的|X(e^j ω)|曲线。
程序代码如下:close all;clear all;clc;A=50;a=50*sqrt(2)*pi;m=50*sqrt(2)*pi;fs1=1000;fs2=300;fs3=200;T1=1/fs1;T2=1/fs2;T3=1/fs3;N=100;x1=A*exp(-a*n*T1).*sin(m*n*T1);x2=A*exp(-a*n*T2).*sin(m*n*T2);x3=A*exp(-a*n*T3).*sin(m*n*T3);w=linspace(-pi,pi,10000);X1=x1*exp(-j*n'*w);X2=x2*exp(-j*n'*w);X3=x3*exp(-j*n'*w);figure(1)subplot(1,3,1)plot(w/pi,abs(X1));xlabel('\omega/π');ylabel('|H(e^j^\omega)|')title('采样频率为1000Hz时的频谱图');subplot(1,3,2)plot(w/pi,abs(X2));xlabel('\omega/π');ylabel('|H(e^j^\omega)|')title('采样频率为300Hz时的频谱图');subplot(1,3,3)plot(w/pi,abs(X3));xlabel('\omega/π');ylabel('|H(e^j^\omega)|')title('采样频率为200Hz时的频谱图');②时域离散信号、系统和系统响应分析。
数字信号处理 第二章习题

1 为因果序列,故收敛域为: z 2
8
(2) (n n0 ) n0 0
解:
X ( z)
n
x(n) z n
n
(n n0 ) z n
X ( z) z
n0
1 n n0 (n n0 ) 0 other
1 n0 z
z 0.5 左边序列 0.5 z 2 双边序列 右边序列 z 2
16
采用围线积分法求解:
3 2 X ( z) 1 1 0.5 z 1 2 z 1 3(1 2 z 1 ) 2(1 0.5 z 1 ) 5 7 z 1 1 1 (1 0.5 z )(1 2 z ) (1 0.5 z 1 )(1 2 z 1 )
z1 1, z2 2
X(z)的收敛域为
左边序列 z 1 1 z 2 双边序列 z 2 右边序列
24
F ( z) X ( z) z
n 1
z ( z 3) ( z 3) n 1 z zn ( z 1)( z 2) ( z 1)( z 2)
z 2
21
当收敛域为: z 2 0.5
1 n n 1 x(n) 3( ) u (n) 2 u (n 1) 2
22
收敛域为: z 2
右边序列
n 0 ,围线c内有2个1阶极点
x(n) Re s[( z 0.5) F ( z), 0.5] Re s[( z 2) F ( z), 2] ( z 0.5) 5z 7 zn ( z 0.5)( z 2) ( z 2)
双边序列
n 0 ,围线c内有1个1阶极点
电子科技大学14秋《数字信号处理》在线作业2答案

14秋《数字信号处理》在线作业2
一,单选题
1. 要处理一个连续时间信号,对其进行采样的频率为6kHz,要无失真的恢复该连续信号,则该连续信号的最高频率可能是()。
A. 12kHz
B. 6kHz
C. 4kHz
D. 3kHz
?
正确答案:D
2. 数字信号的特征是()。
A. 时间连续、幅值量化
B. 时间离散、幅值量化
C. 时间离散、幅值连续
D. 时间连续、幅值连续
?
正确答案:B
3. 对连续时间周期信号的谱分析工具是()。
A. 傅里叶变换
B. 傅里叶级数
C. 离散傅里叶变换
D. 离散傅里叶级数
?
正确答案:B
4. 题目及选项如下图所示
A.
B.
C.
D.
?
正确答案:C
5. 两有限长序列的长度分别是12和15,要利用DFT计算两者的线性卷积,则DFT的点数至少应取()。
A. 15
B. 26
C. 27
D. 28。
(完整word版)数字信号处理第二章习题解答
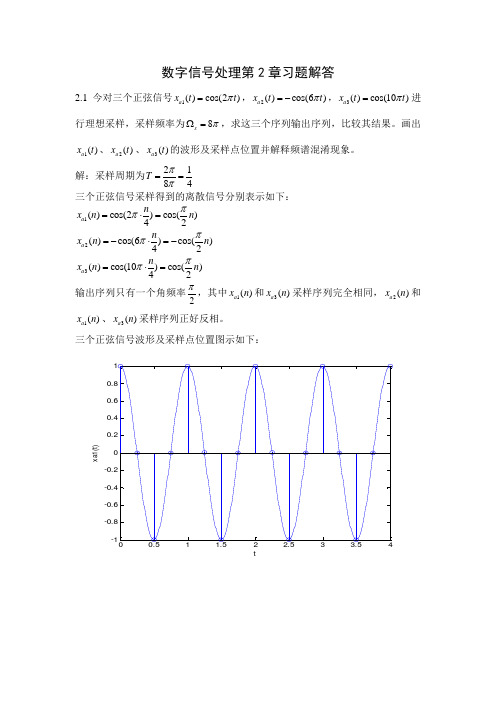
数字信号处理第2章习题解答2.1 今对三个正弦信号1()cos(2)a x t t π=,2()cos(6)a x t t π=-,3()cos(10)a x t t π=进行理想采样,采样频率为8s πΩ=,求这三个序列输出序列,比较其结果。
画出1()a x t 、2()a x t 、3()a x t 的波形及采样点位置并解释频谱混淆现象。
解:采样周期为2184T ππ== 三个正弦信号采样得到的离散信号分别表示如下:1()cos(2)cos()42a n x n n ππ=⋅=2()cos(6)cos()42a n x n n ππ=-⋅=-3()cos(10)cos()42a n x n n ππ=⋅=输出序列只有一个角频率2π,其中1()a x n 和3()a x n 采样序列完全相同,2()a x n 和1()a x n 、3()a x n 采样序列正好反相。
三个正弦信号波形及采样点位置图示如下:tx a 1(t )tx a 2(t )tx a 3(t )三个正弦信号的频率分别为1Hz 、3Hz 和5Hz ,而采样频率为4Hz ,采样频率大于第一个正弦信号频率的两倍,但是小于后两个正弦信号频率的两倍,因而由第一个信号的采样能够正确恢复模拟信号,而后两个信号的采样不能准确原始的模拟信号,产生频谱混叠现象。
2.3 给定一连续带限信号()a x t 其频谱当f B >时,()a X f 。
求以下信号的最低采样频率。
(1)2()a x t (2)(2)a x t (3)()cos(7)a x t Bt π解:设()a x t 的傅里叶变换为()a X j Ω(1)2()a x t 的傅里叶变换为22()[()]Ba a BX j X j d ππωωω-⋅Ω-⎰因为22,22B B B B πωππωπ-≤≤-≤Ω-≤ 所以44B B ππ-≤Ω≤即2()a x t 带限于2B ,最低采样频率为4B 。
数字信号处理第2章答案

=
系统的零点为z=0, 极点为z=0.9, 零点在z平面的原点,
不影响频率特性, 而惟一的极点在实轴的0.9处, 因此滤波 器的通带中心在ω=0处。 毫无疑问, 这是一个低通滤波器。
[例2.4.2]假设x(n)=xr(n)+jxi(n), xr(n)和xj(n)为实序列, X(z)=ZT[x(n)]在单位圆的下半部分为零。 已知
N 1
( z 1)
z
1
2 N 1
z 1 z 1
N
2
[例2.4.4]
时域离散线性非移变系统的系统函数H(z)为
1 ( z a )( z b )
H (z)
,
a 和 b 为常数
第2章
时域离散信号和系统的频域分析
(1) 要求系统稳定, 确定a和b的取值域。
第2章
时域离散信号和系统的频域分析
2.3 分析信号和系统的频率特性
求信号与系统的频域特性要用傅里叶变换。 但分析频 率特性使用Z变换却更方便。 我们已经知道系统函数的极、
零点分布完全决定了系统的频率特性, 因此可以用分析极、
零点分布的方法分析系统的频率特性, 包括定性地画幅频 特性, 估计峰值频率或者谷值频率, 判定滤波器是高通、 低通等滤波特性, 以及设计简单的滤波器(内容在教材第5 章)等。
Re[X(ejω)]=X(ejω) Im[X(ejω)]=0 [例2.4.3] 已知 0≤n≤N N+1≤n≤2N n<0, 2N<n
n x(n) 2 N n 0
求x(n)的Z变换。
第2章
时域离散信号和系统的频域分析
解: 题中x(n)是一个三角序列, 可以看做两个相同的矩
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章上机作业
1、ljdt(A,B)函数定义
function ljdt(A,B)
p=roots(A);
q=roots(B);
p=p';
q=q';
x=max(abs([p q 1]));
x=x+0.1;
y=x;
clf
hold on
axis([-x x -y y])
w=0:pi/300:2*pi;
t=exp(i*w);
plot(t)
axis('square')
plot([-x x],[0 0])
plot([0 0],[-y y])
text(0.1,x,'jIm[z]')
text(y,1/10,'Re[z]')
plot(real(p),imag(p),'x')
plot(ral(q),imag(q),'o')
title('pole-zero diagram for discrete system') hold off
例2.26
a=[3 -1 0 0 0 1];
b=[1 1];
ljdt(a,b)
p=roots(a)
q=roots(b)
pa=abs(p)
程序运行结果如下:
P=
0.7255+0.4633i
0.7255+0.4633i
-0.1861+0.7541i
-0.1861-0.7541i
-0.7455
q=
-1
pa=
0.8608
0.8608
0.7768
0.7768
0.7455
例2.27
b=[0 1 2 1];a=[1 -0.5 -0.005 0.3];
subplot 311
zplane(b,a);xlabel('实部');ylabel('虚部'); num=[0 1 2 1];den=[1 -0.5 -0.005 0.3];
h=impz(num,den);
subplot 312
stem(h);xlabel('k');title('单位脉冲响应'); [H,w]=freqz(num,den);
subplot 313
plot(w/pi,abs(H));
xlabel('频率\omega');
title('频率响应')
例2.28
a=[1,-1];
b=[1];
subplot 321
impz(b,a);
a1=[1,-0.8];
b1=[1];
subplot 322
impz(b1,a1,10);
a2=[1,-2];
b2=[1];
subplot 323
impz(b2,a2,10);
a3=[1,-2*0.8*cos(pi/4),0.8^2];
b3=[1];
subplot 324
impz(b3,a3,20);
a4=[1,-2*0.8*cos(pi/8),1];
b4=[1];
subplot 325
impz(b4,a4,20);
a5=[1,-2*1.2*cos(pi/4),1.2^2];
b5=[1];
subplot 326
impz(b5,a5,20);
例2.29
b=[1,0,-1];a=[1,0,-0.81];
figure(1)
subplot(2,1,1);dimpulse(b,a,50);ylabel('h(n)'); subplot(2,1,2);dstep(b,a,50);ylabel('g(n)'); figure(2)
w=[0:1:500]*pi/500; freqz(b,a,w)
例2.30
b=[1,0,0,0,0,0,0,0,-1];
a0=1;
a1=[1,0,0,0,0,0,0,0,-(0.8)^8];
a2=[1,0,0,0,0,0,0,0,-(0.9)^8];
a3=[1,0,0,0,0,0,0,0,-(0.98)^8];
[H,w]=freqz(b,a0);
[H1,w1]=freqz(b,a1);
[H2,w2]=freqz(b,a2);
[H3,w3]=freqz(b,a3);
subplot(4,2,1);zplane(b,a0);xlabel('实部');ylabel('虚部');title('FIR梳状滤波器零点图')
subplot(4,2,2);zplane(b,a1);xlabel('实部');ylabel('虚部');title('IIR梳状滤波器零点图a=0.8')
subplot(4,2,3);plot(w/pi,abs(H));title('FIR梳状滤波器幅频响应曲线') subplot(4,2,4);plot(w/pi,abs(H1));title('IIR梳状滤波器幅频响应曲线
a=0.8')
subplot(4,2,5);zplane(b,a2);xlabel('实部');ylabel('虚部');title('IIR梳状滤波器零极点图a=0.9')
subplot(4,2,6);zplane(b,a3);xlabel('实部');yalbel('虚部')title('IIR梳状零极点图a=0.98')
a4=[1,0,0,0,0,0,0,0,-(0.9)^8];
a5=[1,0,0,0,0,0,0,0,-(0.98)^8];
[H4,W4]=freqz(b,a4);
[H5,W5]=freqz(b,a5);
subplot(4,2,7);plot(w/pi,abs(H4));title('IIR梳状滤波器频幅响应曲线
a=0.9')
subplot(4,2,8);plot(w/pi,abs(H5));title('IIR梳状滤波器零极点图a=0.98')
例2.31
num=[0.45 0.4 -1];
den=[1 -0.4 -0.45];
x0=[1 2];y0=[0 1];
N=50;
n=[0:N-1]';
x=0.8.^n;
Zi=filtic(num,den,y0,x0);
[y,Zf]=filter(num,den,x,Zi);
plot(n,x,'r-',n,y,'b--');
title('响应');
xlabel('n');ylabel('x(n)-y(n)'); legend('输入x','输入y',1);
grid;
例2.32
num=[18];
den=[18 3 -4 -1];
[r,p,k]=residuez(num,den) 程序运行结果如下:
r =
0.3600
0.2400
0.4000
p =
0.5000
-0.3333
-0.3333
k =
[]
(1)
f=sym('cos(a*k)');
F=ztrans(f)
程序运行结果如下:
F =
(z-cos(a))*z/(z^2-2*z*cos(a)+1) (2)
F=sym('a*z/(z-a)^2');
f=iztrans(F)
程序运行结果如下:
f =
a^n*n
例2.34
(1)
f=sym('a^n')
F=ztrans(f)
程序运行结果如下:
f =
a^n
F =
-z/(a - z)
(2)
f=sym('1');
F=ztrans(f)
程序运行结果如下
F =
z/(z - 1)
b=1;a=poly([0.9 0.9 -0.9]);
[r,p,k]=residuez(b,a)
程序运行结果如下:
r =
0.2500
0.5000
0.2500
p =
0.9000
0.9000
-0.9000
k =
[]
例2.36
x1=[1,2,3];n1=-1:1;
x2=[2,4,3,5];n2=-2:1;
[y,n]=conv_m(x1,n1,x2,n2);
运行结果如下:
y =
2 8 17 2
3 19 15。
