22速率方程与粒子数反转.ppt

合集下载

第讲光增益

W21 B21g()
上下能级间除了自发辐射外，还产生受激吸收和受激
辐射过程。在足够长的时间后，上下能级的粒子数
达到稳定状态。
能级E2粒子数
增加速率：R2 n1B12 g() 减少速率：n22 n2B21g()
相等
能级E1粒子数
增减加少速速率率：：nn122
1
R1 n2B21g( n1B12 g()
能级2粒子数增减加少速速率率：：n22R0 2
相等
能级1粒子数增减加少速速率率：：nn12200 R1
1
相等
平衡时粒子数不变
dn20 dt
R2
n20
2
0
dn10
dt
n20
2
R1
n10
1
0
能级E2上粒子增加速率等于减少速率；
能级E1上粒子增加速率等于减少速率。t A21N2 Nhomakorabeat)dt
0
=
1 N20
t
0
A21N2 (t)dt=
1 N20
t
0
A21 N 20
e A21t dt
=t
0
A21e A21t dt
=
1 A21
结论：能级的平均寿命等于跃迁几率的倒数
跃迁几率越大，粒子在激发态停留的时间越短，即寿命越短。
（2）多能级系统
t时刻，Em能级的粒子数为：
（2）CO2激光器10.6m谱线（小信号增益）
G0 0.005 : 0.01cm-1
二、小信号增益
介质中高能级E2与低能级E1间的跃迁辐射的
线型函数为g(),两能级粒子数密度分别为n2 , n1。强度为I、频率为的准单色光入射到介质上。

速率方程

∆E ≈
τ
• 若跃迁上、下能级的寿命分别为τ2与τ1，则原子发光具有频率不确定量或谱线宽度
∆ν = 1 2πτ 1 + 1 2πτ 2
1 2πτ 2
• 当下能级为基态时，τ1为无穷大，有 ∆ν =
3 晶格振动加宽
• 对于固体激光物质，均匀加宽主要是由晶格热振动引起的，自发辐射和无辐射跃迁造成的谱线加宽是很小的。 • 固体工作物质中，激活离子镶嵌在晶体中，周围的晶格场将影响其能级的位置。由于晶格振动使激活离子处于随时间变化的晶格场中，激活离子的能级所对应的能量在某一范围内变化，因而引起谱线加宽。温度越高，振动越剧烈，谱线越宽。由于晶格振动对于所有激活离子的影响基本相同，所以这种加宽属于均匀加宽。
• 非弹性碰撞：激发态原子和其它原子或器壁碰撞而将自己的内能变为其它原子的动能或给予器壁，而自己回到基态称作无辐射跃迁，同自发辐射过程一样，也会引起激发态寿命的缩短。在晶体中，无辐射跃迁起因于原子和晶格振动相互作用，原子释放的内能转化为声子能量。
• 原子在能级上的有限寿命所引起的均匀加宽也是量子力学测不准原理的直接结果。 • 设原子在能级上的寿命为τ，可理解为原子的时间测不准，原子的能量测不准量∆E为 h
1 爱因斯坦采用唯象法得到光和物质相互作用的关系式
dn21 ( ) sp = A21n2 dt dn21 ( ) st = W21n2 ,W21 = B21 ρν dt dn12 ( ) st = W12 n1 , W12 = B12 ρν dt 3 A21 8π hν = = nν hν , B12 f1 = B21 f 2 3 B21 c
end
授课计划
1. 知识回顾：不考虑原子能级存在不确定度时的知识回顾：受激辐射、受激吸收、自发辐射过程方程。受激辐射、受激吸收、自发辐射过程方程。 2. 考虑了频率增宽之后的自发辐射、受激辐射、考虑了频率增宽之后的自发辐射、受激辐射、吸收方程修正 3.三能级单模速率方程组三能级单模速率方程组 4.四能级单模速率方程组四能级单模速率方程组

2-4 速率方程组理论

d n2 W21 n1 W12 dt (5)
谐振腔的损耗，引起的光子数密度增长率为： d ( 6) dt c 因此，谐振腔内光子数密度变化率方程为：
d n2 W21 n1 W12 dt c
2014年6月10日星期二
(7)
理学院物理系
§2.4速率方程组与粒子数反转
辐射场能量密度与光子数密度关系为：
( ) h
2014年6月10日星期二理学院物理系
§2.4速率方程组与粒子数反转
因此， W12 W21 B 21 h g( , 0 )
B 21 A 21 h m
因此， W12 W21
A 21 g ( , 0 ) m
§2.4速率方程组与粒子数反转
d n4 n1W14 n4 ( S43 A41 S41 ) dt
d n3 A32 n g( , 0 ) n3 ( S 32 A32 ) n4 S43 dt m
(1)
( 2)
d n1 n2 S21 n1 W41 dt
2014年6月10日星期二
(4)
理学院物理系
§2.4速率方程组与粒子数反转
二、四能级系统速率方程组 E4: 抽运能级 E3: 激光上能级 E2: 激光下能级 E1: 基态能级 S21:抽空速率速率方程组：
E4 S43 E3 W14 A41 S41 W32 W23 A S32 32 E2 S21 E1
W21 B21 ( )
爱因斯坦散系数关系：
W12 B12 ( ) A21 / B21 h m
考虑到谱线加宽，定义“单色爱因斯坦散系数”：
A 21 ( ) A21 g( , 0 ) B21 ( ) B21 g( , 0 ) B12 ( ) B12 g( , 0 )

激光原理第二章激光器的工作原理

可以证明，在对称共焦腔内，任意傍轴光线可往返多次
而不横向逸出，而且经两次往返后即可自行闭合。
整个稳定球面腔的模式理论都可以建立在共焦腔振荡理论的基础上，因此，对称共焦腔是最重要和最具有代表性的一种稳定腔。
3.平行平面腔——由两个平面反射镜组成的共轴谐振腔
R1=R2=∞，g1=g2=1， g1 g2=1
图(2-2) 共轴球面腔的稳定图
➢凹凸稳定腔，由一个凹面镜和一个凸面镜组成，对应图中5区和6区。
➢ (g1>1,g2<1; g2>1,g1<1)
➢共焦腔，R1＝R2＝L，因而，g1=0，g2=0，对应图中的坐标原点。(特殊的稳定腔) ➢半共焦腔，由一个平面镜和一个R=2L的凹面镜组成的腔,对应图中E和F点g1=1，g2=1/2
1. 工作物质 2. 激励能源
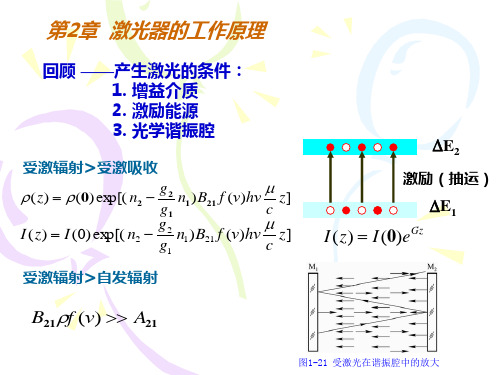
受激辐射>受激吸收
3. 光学谐振腔
受激辐射>自发辐射
是否只要具备激励能源和工作物质就一定可以实现粒子数反转？粒子数反转和什么因素有关？
速率方程方法: 量子理论的一种简化形式
——速率方程理论：把光频电磁场看成量子化的光子，把物质体系描述成具有量子化能级的粒子体系。
(三)临界腔: g1 g2 = 0 , g1 g2= 1
临界腔属于一种极限情况,其稳定性视不同的腔而不同. 在谐振理论研究和实际应用中,临界腔具有非常重要的意义.
1.对称共焦腔——腔中心是两镜公共焦点且：
R1=L
R2=L
R1= R2= R = L=2F F——二镜焦距
F
L
∵ g1 = g2 = 0 ∴ g1 g2 = 0
简化前提: 忽略量子化辐射场的位相特性及光子数的起伏特性
优点: 形式特别简单, 且可给出激光的强度特性，并粗略描述烧孔、兰姆凹陷、多模竞争等效应

激光原理(4)-速率方程

均匀加宽线型函数
∆ν H 2π
2
g H (ν ,ν 0 ) =
∆ν H 2 (ν − ν 0 ) + ( ) 2
1 1 1 ∆ν H = ( + ) = ∆ν N + ∆ν L 2π τ s τ L
一般气体激光器：
NJUPT
非均匀加宽
气体激光器的非均匀加宽往往只有多普勒加宽
gi (ν ,ν 0 ) = g D (ν ,ν 0 ) ∆ν i = ∆ν D
原子和准单色光辐射场的相互作用在频率为 ν 的单色辐射场作用下，受激跃迁（吸收与发射）几率：
W21 = B21 g (ν ,ν 0 ) ρ W12 = B12 g (ν ,ν 0 ) ρ
g (ν ,ν 0 )
ρ = N l hν
发自发辐射线型函数在v处的函数值 N l ——第 l 模式的光子数密度
x( t ) = x e
e
γ ——衰减因子（阻尼系数）
NJUPT
谱线加宽的机理
自然加宽（Natural broadening）
g N (ν ,ν 0 ) =
4 最大值： ν ν= = g (ν 0 ,ν 0 ) 0，
( )2 + 4π 2 (ν − ν 0 )2 2
γ
γ
γ 1 线宽：ν = g N (ν ,ν 0 ) ν 0 ± ， g N (ν ,ν 0 ) = 4π 2
= n2 B21 ∫
+∞ −∞
g (ν ,ν 0 ) ρν dν
NJUPT
原子和准单色光辐射场的相互作用
∆ν ′ ∆ν
在 ∆ν ′ 作不变
g (ν ′,ν )
范围内：近似看

第二章激光器的工作原理(1)

结果，共振腔（又称光学共振腔）是激光器的三个基本组件之一，它的功用是对激光器提供一定的光学反馈能力并对激光振荡模式进行限制；在工作物质和激励条件为给定的条件下，共振腔的选择和具体参量的合理确定是至关重要的，因为它们会直接影响到激光器件的振荡阈值、转换效率、输出发散角以及场图均匀性等项性能指标。
Compressor
靶室及诊断
Target and Measurement
27
附
上光所PW激光系统光路图
10Hz
800nm/l~100nm
Oscillator 10nJ/9-12fs AOPDF
0.5nJ ~2ns
stretcher
Reg.Amp
800nm/4mJ
Nd:glass Pump Laser
dn10 dt
R1 n20 A2
n10 A1
0
23
小信号粒子数反转分布的条件
由
dn20 dt
R2
n20 A2
0
dn10 dt
R1 n20 A2
n10 A1
0
利用爱因斯坦系数和能激寿命之间关系，可以由小信号工作
时的简化速率方程组导出
R2
n20 A2
n20
2
将两式结合可得
R1
n20 A2
n10 A1
✓ (a) 共焦腔：两凹面镜的焦点重合， ✓ (b) 共心腔：两凹面镜的球心重合，距离再远，对称凹面
镜腔也会变得不稳定。（临界腔）
A F
A O
B
M1
M2
(a) 共焦腔
B
M1
M2
(b) 共心腔
6
不稳定腔及其几何光学分析
➢ 距离大于两倍焦距的不稳定平凹腔：A1—A2—B1—B2— C1—逸出

激光器的工作原理ppt课件

定条件可以合并成一个，即： R1=R2=R＞L/2
.
2.平凹稳定腔: 由一个凹面反射镜和一个平面反射镜组成的谐振腔称为平
凹腔。其稳定条件为：R＞L
R
L
证明：∵ R1＞L ,
g1
1
L
;
R1
R2
∞, g2= 1
∴ 0 ＜ 1 1 gR L 1＜ 1 ＜故有 0 ＜ g 1g 2 1
.
3.凹凸稳定腔:
第二部分激光产生的基本原理
2.激光器的基本结构
n w 21 A 21
w 2 1 n1 STE光子集中在几个模式
轴向模
非轴向模
技术思想的重大突破－ F-P 光谐振腔 • 开放式光谐振腔使特定（轴向）模式的增加, 其它（非轴向）模式数
逸出腔外，使轴向模有很高的光子简并度。
• 工作物质, 光学谐振腔, 激励能源是一般激光器的三个基本部分。
图(2-2) 共轴球面腔的稳定图
3.利用稳定条件可将球面腔分类如下:
(1) 稳定腔 (0<g1 g2 <1)
➢双凹稳定腔，由两个凹面镜组成，对应图中 ➢l、2、3和4区.
➢平凹稳定腔，由一个平面镜和一个凹面镜组成，
➢对应图中AC、AD段
图(2-2) 共轴球面腔的稳定图
➢凹凸稳定腔，由一个凹面镜和一个凸面镜组成，对应图中5区和6区。
条件有两种情况.
R1
R2
其一为: R1<L, R2>L
L
此时 g11R L10 g21R L20
所以 g1 g2＜0
.
其二为: R1+R2＜L
可以证明: g1 g2＞1 (证明略)
2.平凹非稳腔稳定条件: R1＜L , R2= ∞

高中化学第2章化学反应的方向、限度与速率 2.2 化学反应的限度课件鲁科版选修4.ppt

5
在1L密闭容器中加入1molN2和3mol H2发生反应
正向反应
N2(g) + 3H2 (g) 逆向反应
2NH3(g)
对于以上反应，请分析：
（1）当反应刚开始时，反应物和生成物的浓度哪个大？反应物浓度最大，生成物浓度为零。
（2）当反应刚开始时，正反应与逆反应哪个
反应速率大？正反应速率最大，逆反应速率为零。
化学反应限度
在一定条件下，化学反应所能进行的最大程度
1
一、可逆反应:
1、定义：在同一条件下, 既能向正反应方
向进行，同时也能向逆反应方向进行的反应。
2、符号：
催化剂
2SO2+O2 △ 2SO3
3、可逆反应的特点
(1)、同一条件同时进行（两同）
2
在某密闭容器中发生反应：2SO2+O2
催化剂
△ 2SO3
随堂练习3
在一定条件下，某容器中充入N2和H2合成 NH3,以下叙述错误的是（ B ） A.开始反应时，正反应速率最大，逆反应速
率为零 B.随着反应的进行，正反应速率逐渐减小，
最后减小为零 C.随着反应的进行逆反应速率逐渐增大，后保持恒定 D.随着反应的进行，正反应速率逐渐减小，
最后与逆反应速率相等且都保持恒定 13
化学平衡的标志
4、在一定温度下,可逆反应A(g)+3B(g)
AC 达到平衡的标志是（
）
A、 C的生成速率与C分解的速率相等
2C(g)
B、单位时间内生成n molA,同时生成3n molB
C、 A、B、C的浓度不再变化
D、 A、B、C的分子数之比为1:3:2
14
化学平衡的标志

第二章-激光的振荡

r= w(z)时，u下降到e-1，光束能量下降到 e-2。 w(z)称为基模的光斑半径。 z=0时，共焦腔中心的光斑半径，也称束 b 腰半径 w
0
z=±b/2时，任一镜面上的光斑半径
b w0 s
2
3)共焦腔模式场分布的函数形式在任一横截面上都相同 w(z)和R波面曲率半径与z有关,共焦腔中
dnl nl g2 A21 ( N2 N1 ) g ( , 0 )nl dt g1 n Rl
考虑了光腔损耗，τRl是光腔第l模的光子寿命
dnl nl nl n0 exp(t / Rl ) dt Rl
2.1.2 四能级系统
1. 四能级系统的工作过程
四能级系统比三能级系统量子效率要高波尔兹曼分布
z
w(z)
R(z)
0 ±b/2
w0 w0s
b
光斑半径和曲率半径确定了共焦腔模式的特征。共焦腔只有一个几何参数b，与b 有关的任一参量( w0 , w0s, w(z)，R) 都可用来表征共焦腔的模式。
4）传播圆法引入：光束参量
w2 ( z ) (b / 2) 2 z 2 b' b/2
1)方型镜共焦腔，z处截面上TEMmn模场分布(Boyd and Gordon)
1 b 2 2 U mn ( x, y, z ) Hm ( x) H n ( y) w( z ) w( z ) w( z ) e
r 2 / w 2 ( z ) i [ k ( z r 2 / 2 R ) ]
dnl g A n ( N 3 3 N 2 ) 32 g ( , 0 )nl l dt g2 n Rl
得到阈值粒子数反转值
2 8 0 Nt 3 c A32 g ( , 0 ) Rl

激光器的工作原理

激光器的工作原理一．光学谐振腔结构与稳定性激光是在光学谐振腔中产生的。

它的主要功能之一是使光在腔内来回反射多次以增长激活介质作用的工作长度，提高腔内的光能密度。

显而易见的是，不垂直于反射镜表面的傍轴光线经过有限次的反射就会投射到平面镜的通光口径之外，而使得激活介质作用的工作长度只得到很有限的增长。

所以，光线能够在谐振腔中反射的次数与其结构密切相关。

能够使腔中任一束傍轴光线经过任意多次往返传播而不逸出腔外的谐振腔能够使激光器稳定地发出激光，这种谐振腔叫做稳定腔，反之称为不稳定腔。

我们讨论光学谐振腔的结构与稳定性的关系。

1.共轴球面谐振腔的稳定性条件光学谐振腔都是由相隔一定距离的两块反射镜组成的。

无论是平面镜还是球面镜，无论是凸面镜还是凹面镜，都可以用“共轴球面”的模型来表示。

因为只要把两个反射镜的球心连线作为光轴，整个系统总是轴对称的，两个反射面可以看成是“共轴球面”。

平面镜是半径为无穷大的球面镜。

如果其中一块是平面镜，可以用通过另一块球面镜球心与平面镜垂直的直线作为光轴。

平行平面腔的光轴则可以是与平面镜垂直的任一直线。

当然两个平面镜不平行不能产生谐振，不在讨论之列。

图（2-1）共轴球面腔结构示意图如图（2-1）所示，共轴球面腔的结构可以用三个参数来表示：两个球面反射镜的曲率半径R1、R2，和腔长即与光轴相交的反射镜面上的两个点之间的距离L。

如果规定凹面镜的曲率半径为正，凸面镜的曲率半径为负，可以证明共轴球面腔的稳定性条件是111021≤⎪⎪⎭⎫ ⎝⎛-⨯⎪⎪⎭⎫ ⎝⎛-≤R L R L （2-1）上式左边成立的条件等价于⎪⎪⎭⎫ ⎝⎛-11R L 和⎪⎪⎭⎫ ⎝⎛-21R L 同时为正或同时为负，这就要求两镜面的曲率半径为正时必须同时大于腔长或同时小于腔长。

如果镜面的曲率半径同时为负，尽管上式左边成立，右边的不等式却不成立。

如果镜面的曲率半径一正一负，则需要具体讨论。

2.共轴球面腔的稳定图及其分类为了直观起见,常用稳定图来表示共轴球面腔的稳定条件。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

ν ν0
ν ν0
2.2.6 均匀增宽型介质粒子数密度反转分布的饱和效应
1.由下式可以看出，当腔内光强I0(即小讯号)时，介质中的粒子数密度反转分布值n最大，其值为n0。当腔内光强的影响不能忽略时，粒子数密度反转分布值 n将随光强的增加而减小，此现象称为粒子数密度反转分布值的饱和效应。

1

0 R ( R R ) n 2 2 1 2 1 1 B f ( ν ) 1 B f ( ν ) 2 21 2 21
2.2.4 小信号工作时的粒子数密度反转分布
0 R ( R R ) n 0 2 2 1 2 1 n R ( R R ) 1. 由式可得： n n n 2 2 1 2 1 2 1 1 B f ( ν ) 1 B f ( ν ) 221 221
dn 2 R n A ( n B n B ) f ( ν ) 2 2 2 2 21 1 12 dt
同理，单位时间内E1能级上增加的粒子数密度为：
d 1n R n A ( n B n B ) f ( ν ) n A 1 2 21 2 21 1 12 1 1 dt
n n n n 0 1 2
以上三式即为在增益介质中同时存在抽运、吸收、自发辐射和受激辐射时各能级上的粒子数密度随时间变化的速率方程组。
图(2-5)）简化的四能级图
2.2.3 稳态工作时的粒子数密度反转分布
1. 在抽运和跃迁达到动平衡时，各能级上粒子数密度并不随时间而改变，即： dn dn dn 0 1 2 0 dt dt dt 假设能级E2、E1的简并度相等，即g1=g2，因此有B12=B21，又认为E2能级向E1 能级的自发跃迁几率远大于E2能级向基态E0的自发跃迁几率，即A2=A21 dn 2 则有： R n A ( n B n B ) f ( ν ) 0 2 2 2 2 21 1 12 dt dn 1 R n A ( n B n B ) f ( ν ) n A 0 1 2 2 2 21 1 12 1 1 dt n 1 将上两式相加可得： ( R R ) n A n ( R R ) 1 2 11 1 1 2 1
2.2.1 三能级系统和四能级系统
1. 实现上下能级之间粒子数反转产生激光的物理过程：三能级和四能级系统
2. 三能级系统：如图(2-4a)，下能级E1是基态能级，上能级E2是亚稳态能级， E3为抽运高能级。其主要特征是激光的下能级为基态，发光过程中下能级的粒子数一直保存有相当的数量。 3. 四能级系统：如图(2-4b)，下能级E1不是基态能级，而是一个激发态能级，在常温下基本上是空的。其激励能量要比三能级系统小得多，产生激光要比三能级系统容易得多。

这就是均匀增宽型介质E2、E1能级之间粒子数反转分布的表达式。它给出能级间粒子数反转分布值与腔内光强、光波的中心频率、介质的饱和光强、激励能源的抽运速率以及介质能级的寿命等参量的关系。
0 n 0 1 I Is n n 2 2 0 I f( ν ) [( ν ν ) ( ν 2 ) ] n 0 1 2 2 Is f( ν ) 0 ( ν ν ) ( 1 I Is)( ν2 ) 0
0
2.2.5 均匀增宽型介质的粒子数密度反转分布
ν 2 且 2 ( ν ) f ( ν ) 1.对于均匀增宽的介质 f 0 2 2 ( ν ν ) ( ν 2 ) ν 0 如果介质中传播的光波频率为 ν 0 ，则有： c ν 2 2 I 其中 I f ( ν ) I B f ( ν ) B I ; s 0 2 21 2 21 2 B 2 c ν c ν I 21 s 如果介质中传播的光波频率 ν ν0 ，则有： 2f ( ν ) 2 f ( ν ) f ( ν ) If ( ν ) I I c c ν 2 νc f ( ν ) 0 f ( ν ) 2 B ( ν ) 2 21 I f B f ( ν ) I 则有： 221 f ( ν ) c ν I ( ν ) 0 sf 0 一般情况下的粒子数密度反转分布可以表示为：图(Biblioteka -4) 三能级系统和四能级系统示意图
2.2.2 速率方程组
1. 图(2-5)为简化的四能级图，n0、n1、n2分别为基态、上能级、下能级的粒子数密度；n为单位体积内增益介质的总粒子数，R1、R2分别是激励能源将基态E0上的粒子抽运到E1、E2能级上的速率；则E2能级在单位时间内增加的粒子数密度为：

R ( R R ) B f ( ν )R ( R R ) B f ( ν ) 2 1 2 1 21 2 2 1 2 1 2 21 n 由上几式可得： 2 A B f ( ν ) 1 B f ( ν ) 2 21 2 21
则激光上下能级粒子数密度反转分布的表达式为： R ( R R ) B f ( ν ) 2 2 1 2 1 2 21 n n n ( R R ) 2 1 1 2 1 1 B f ( ν ) 2 21
它是当分母中的第二项为零时的粒子数密度反转分布值。而分母中的第二项一定是个正值，因此它又是粒子数密度反转分布值可能达到的最大值。显然只有在谐振腔中传播的单色光能密度可能趋近于零，换句话说，参数 n 0对应着谐振腔的单色光能密度为零或者近似为零时的粒子数密度反转分布的大小。参数 n 对应着激光谐振腔尚未发出激光时的状态，通常把这个状态叫作小信号工作状态，而参数 n 0就被称作是小信号工作时的粒子数密度反转分布。