《激光原理》2.2速率方程组与粒子数反转
激光原理 第2章 激光器的工作原理

式中同样采用了 A2 A21 的简化并且假设简并度 g1 g2 即 B21 B12 n 两式相加得到 ( R1 R2 ) n1 A1 1 n1 ( R1 R2 ) 1 n10
1
(第1章)
26
福建师范大学光电学院
低能级粒子数密度代入速率方程组,解得高能级上 粒子数密度为
③
dn0 dn1 dn2 0 dt dt dt
④
0 dn2 dn10 0 0 速率方程组: R2 n2 A2 0 R1 n2 A2 n10 A1 0 dt dt 23
(第1章)
福建
利用爱因斯坦系数和能激寿命之间关系,可以由小 信号工作时的简化速率方程组导出 0 n10 n2 0 0 R1 n2 A2 n10 A1 R2 n2 A2
(第1章)
16
福建师范大学光电学院
2. 半经典理论:用麦克斯韦方程组描述光频电磁场,应 用量子力学理论描述物质原子。1964年,兰姆应用该 理论建立了激光器理论,很好地揭示激光器中大部分的物 理现象,如:强度特性、增益饱和效应、多模耦合与竞争 效应,激光振荡的频率牵引与推斥效应等。其缺点是在于 不能反映与激光场的量子特性有关现象的规律性,数学处 理过于复杂。 3.量子理论:应用量子电动力学的处理方法,对物质原 子系统和光频电磁场都作量子化处理,将两者作为统一的 物理体系加以研究。需严格地确定激光的相干性和噪声以 及线宽极限。
3
(第1章)
福建师范大学光电学院
(1)稳定腔的表达式
光学谐振腔的稳定与否是由谐振腔的几何形状决定的 共轴球面腔结构:两个反射镜的 球心连线为光轴,整个系统总是
R1
O1
O2
R2
半导体激光器中粒子数反转的形成机制_概述及解释说明

半导体激光器中粒子数反转的形成机制概述及解释说明1. 引言1.1 概述半导体激光器是一种关键的光电器件,具有广泛的应用领域,如通信、医疗和制造等。
粒子数反转作为半导体激光器实现放大和产生激光所必需的基本过程之一,在该领域中被广泛研究和应用。
本文将重点讨论半导体激光器中粒子数反转的形成机制。
1.2 文章结构本文按照以下结构进行组织:首先,我们将介绍半导体激光器的基本原理,包括光与物质交互作用、PN结和载流子注入以及积极性反转和自发辐射过程。
接下来,我们将详细分析粒子数反转的原理和机制,包括能带结构对粒子数反转影响的分析、载流子浓度控制与限制因素的讨论以及光吸收和增益特性的解释。
然后,我们将介绍形成粒子数反转所采用的实验方法和技术应用,并探讨加载实验与电流阈值之间存在关系的证明、束缚态材料在半导体激光器中的应用研究进展以及温度对粒子数反转效果的影响研究。
最后,我们将总结文章涵盖的主要观点和论述内容,并展望半导体激光器中粒子数反转机制的未来发展方向和可能的应用领域。
1.3 目的本文旨在提供关于半导体激光器中粒子数反转形成机制的综合概述,并解释说明相关原理和机制。
通过深入探讨这一课题,有助于增进读者对半导体激光器工作原理的理解,以及为相关领域的研究者提供参考和启发。
2. 半导体激光器的基本原理2.1 光与物质交互作用在半导体激光器中,光和物质之间的交互作用是实现粒子数反转的关键。
当光通过半导体材料时,它会与电子和空穴相互作用,从而改变它们的能级分布。
2.2 PN结和载流子注入半导体激光器通常由PN结构组成,其中P区域富集正电荷载流子(空穴),N 区域则富集负电荷载流子(电子)。
通过外部电源施加电压,在PN结附近形成耗尽层。
当正向偏置PN结时,正电压使得正电荷向P区移动,而负电荷向N 区移动。
这个过程被称为载流子注入。
2.3 积极性反转和自发辐射过程在激活载流子注入后,会形成一个积极性反转(population inversion)的状态,即在激发态比基态还要多。
激光原理与应用教案

激光原理与应⽤教案激光原理与应⽤教案⼀. 绪论本节课教学⽬标:让学⽣了解激光的历史,激光形成及发展、理论体系的形成。
让学⽣了解激光科学的分⽀及激光在军事、信息技术、医疗等⽅⾯的应⽤;本节课教学内容:1.激光的概念:激光——利⽤受激辐射的光放⼤。
LASER——Light Amplification by Stimulated Emission of Radiation2.激光的发现:最早在1917年——Einstein⾸次预⾔受激辐射激光,历史上⾸先在微波波段实现量⼦放⼤(1953),1954年——C. H. Townes, I. P. Gorden, H. J. Zeiger 使⽤NH3分⼦射束实现Maser向更短波长进发——ammonia beam maser,1958年——A. L. Schawlow, C. H. Townes, A. M. PoxopoB提出将Maser原理推⼴到光波段——laser,1960年——T. H. Maiman of Bell Lab 红宝⽯⾸次实现laser l=6943? 红光(早期的名称:莱塞、光量⼦振荡器、光激射器受激光,“激光”——钱学森在1963年提出。
61年中国(亚洲)第⼀台激光器诞⽣在长春(长春光机所和光机学院),由王之江院⼠发明。
激光科学技术发展的基础学科——光谱学,物理光学,固体物理,物质结构,⽆线电电⼦学。
推动⼒——⼴阔的应⽤领域:核聚变,加⼯,热处理,通讯,测距,计量,医疗可调谐性和超短脉冲——⾼时间、空间分辨、能量分辨。
3.激光与普通光源的区别?(1)良好的单⾊性。
单⾊性指光源发射的光波长范围很⼩,测距。
(2)良好的⽅向性。
激光的光束⼏乎只沿着⼀个⽅向传输。
测距,通信。
(3)⾼亮度。
激光功率集中在极⼩的空间范围内。
切割,⼿术,军事。
(4)极好的相⼲性。
各列波在很长的时间内存在恒定的相位差。
精确测距。
4.激光的应⽤。
(1)信息科学领域。
激光原理与技术试题答案

2006-2007学年 第1学期 《激光原理与技术》B 卷 试题答案1.填空题(每题4分)[20]激光的相干时间τc 和表征单色性的频谱宽度Δν之间的关系为___1c υτ∆= 一台激光器的单色性为5x10-10,其无源谐振腔的Q 值是_2x109如果某工作物质的某一跃迁波长为100nm 的远紫外光,自发跃迁几率A 10等于105 S -1,该跃迁的受激辐射爱因斯坦系数B 10等于_____6x1010 m 3s -2J -1 设圆形镜共焦腔腔长L=1m ,若振荡阈值以上的增益线宽为80 MHz ,判断可能存在_两_个振荡频率。
对称共焦腔的=+)(21D A _-1_,就稳定性而言,对称共焦腔是___稳定_____腔。
2. 问答题(选做4小题,每小题5分)[20]何谓有源腔和无源腔?如何理解激光线宽极限和频率牵引效应?有源腔:腔内有激活工作物质的谐振腔。
无源腔:腔内没有激活工作物质的谐振腔。
激光线宽极限:无源腔的线宽极限与腔内光子寿命和损耗有关:122'c Rc L δυπτπ∆==;有源腔由于受到自发辐射影响,净损耗不等于零,自发辐射的随机相位造成输出激光的线宽极限2202()t c s t outn h n P πυυυ∆=∆。
频率牵引效应:激光器工作物质的折射率随频率变化造成色散效应,使得振荡模的谐振频率总是偏离无源腔相应的模的频率,并且较后者更靠近激活介质原子跃迁的中心频率。
这种现象称为频率牵引效应。
写出三能级和四能级系统的激光上能级阈值粒子数密度,假设总粒子数密度为n ,阈值反转粒子数密度为n t.三能级系统的上能级阈值粒子数密度22tt n n n +=;四能级系统的上能级阈值粒子数密度2t t n n ≈。
产生多普勒加宽的物理机制是什么?多普勒加宽的物理机制是热运动的原子(分子)对所发出(或吸收)的辐射的多普勒频移。
均匀加宽介质和非均匀加宽介质中的增益饱和有什么不同?分别对形成的激光振荡模式有何影响?均匀加宽介质:随光强的增加增益曲线会展宽。
激光原理2.2
ቤተ መጻሕፍቲ ባይዱ
§ .
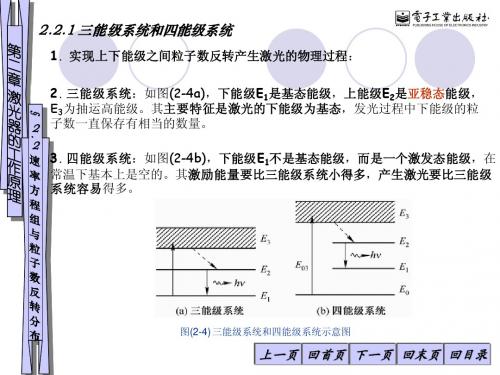
图(2-4) 三能级系统和四能级系统示意图
上一页 回首页 下一页 回末页 回目录
2.2.2 速率方程组
第 图(2-5)为简化的四能级图,n0、n1、n2分别为基态、上能级、下能级的粒子数 二 密度;n为单位体积内增益介质的总粒子数,R1、R2分别是激励能源将基态E0上的 章 粒子抽运到E1、E2能级上的速率;则E2能级在单位时间内增加的粒子数密度为: 激 dn2 光 R2 n2 A2 (n2 B21 n1B12 ) f (ν) 器 2 dt 的 2 工 速 同理,单位时间内E1能级上增加的粒子数密度为 : 作 率 dn1 原 R1 n2 A21 (n2 B21 n1 B12 ) f (ν) n1 A10 理 方 dt
0
§ .
粒子数密度反转分布的最大值 n ,完全取决于激光工作物质的能 级特性和泵浦源向高能级输运粒子的抽运能力。
0
0 显然, n 0 的前提是 n 0 . n0 0 的前提是什么呢?
上一页 回首页 下一页 回末页 回目录
2.2.5 均匀增宽型介质的粒子数密度反转分布
第 ① 若介质中光波的频率为 ν0,则有: 二 cν 2 2 I 章 Is f (ν0 ) I 2 B21 f (ν0 ) 2 B21 I ; 激 2 B21 2 c ν c Is 光 ,则有: 器 2 ② 如果介质中的光波频率 ν ν0 2 f (ν) 2 f (ν ) 的 2 f (ν) I f (ν) I I 工 速 c c ν 2 ν c f (ν0 ) 作 率 原 f (ν) 2 2 B21 I f (ν) 2 B21f (ν) I 理 方 所以:
激光原理第二章 激光器的工作原理
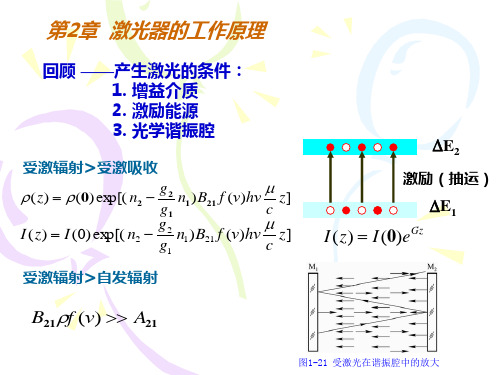
可以证明,在对称共焦腔内,任意傍轴光线可往返多次
而不横向逸出,而且经两次往返后即可自行闭合。
整个稳定球面腔的模式理论都可以建立在共焦腔振荡理 论的基础上,因此,对称共焦腔是最重要和最具有代表性的 一种稳定腔。
3.平行平面腔——由两个平面反射镜组成的共轴谐振腔
R1=R2=∞,g1=g2=1, g1 g2=1
图(2-2) 共轴球面腔的稳定图
➢凹凸稳定腔,由一个凹面镜和一个凸面镜组成,对应图中5区和6区。
➢ (g1>1,g2<1; g2>1,g1<1)
➢共焦腔,R1=R2=L,因而,g1=0,g2=0,对应图中的坐标原点。(特殊的稳定腔) ➢半共焦腔,由一个平面镜和一个R=2L的凹面镜组成的腔,对应图中E和F点g1=1,g2=1/2
1. 工作物质 2. 激励能源
受激辐射>受激吸收
3. 光学谐振腔
受激辐射>自发辐射
是否只要具备激励能源和工作物质就一定可以实 现粒子数反转? 粒子数反转和什么因素有关?
速率方程方法: 量子理论的一种简化形式
——速率方程理论:把光频电磁场看成量子化的光子,把 物质体系描述成具有量子化能级的粒子体系。
(三)临界腔: g1 g2 = 0 , g1 g2= 1
临界腔属于一种极限情况,其稳定性视不同的腔而不同. 在谐振理论研究和实际应用中,临界腔具有非常重要的意义.
1.对称共焦腔——腔中心是两镜公共焦 点且:
R1=L
R2=L
R1= R2= R = L=2F F——二镜焦距
F
L
∵ g1 = g2 = 0 ∴ g1 g2 = 0
简化前提: 忽略量子化辐射场的位相特性及光子数的起伏特 性
优点: 形式特别简单, 且可给出激光的强度特性,并粗略描 述烧孔、兰姆凹陷、多模竞争等效应
激光原理(4)-速率方程
均匀加宽线型函数
∆ν H 2π
2
g H (ν ,ν 0 ) =
∆ν H 2 (ν − ν 0 ) + ( ) 2
1 1 1 ∆ν H = ( + ) = ∆ν N + ∆ν L 2π τ s τ L
一般气体激光器:
NJUPT
非 均 匀 加 宽
气体激光器的非均匀加宽往往只有多普勒加宽
gi (ν ,ν 0 ) = g D (ν ,ν 0 ) ∆ν i = ∆ν D
原子和准单色光辐射场的相互作用 在频率为 ν 的单色辐射场作用下,受激跃迁(吸收与发射)几率:
W21 = B21 g (ν ,ν 0 ) ρ W12 = B12 g (ν ,ν 0 ) ρ
g (ν ,ν 0 )
ρ = N l hν
发自发辐射线型函数 在v处的函数值 N l ——第 l 模式的光子数密度
x( t ) = x e
e
γ ——衰减因子(阻尼系数)
NJUPT
谱线加宽的机理
自然加宽(Natural broadening)
g N (ν ,ν 0 ) =
4 最大值: ν ν= = g (ν 0 ,ν 0 ) 0,
( )2 + 4π 2 (ν − ν 0 )2 2
γ
γ
γ 1 线宽:ν = g N (ν ,ν 0 ) ν 0 ± , g N (ν ,ν 0 ) = 4π 2
= n2 B21 ∫
+∞ −∞
g (ν ,ν 0 ) ρν dν
NJUPT
原子和准单色光辐射场的相互作用
∆ν ′ ∆ν
在 ∆ν ′ 作不变
g (ν ′,ν )
范围内: 近似看
介质在小信号时的粒子数反转分布值 激光原理及应用 [电子教案]电子
介质在小信号时的粒子数反转分布值——激光原理及应用一、教学目标1. 理解介质在小信号时的粒子数反转分布概念。
2. 掌握激光产生的原理及其在小信号时的粒子数反转分布值。
3. 了解激光在现代科技领域中的应用。
二、教学内容1. 介质在小信号时的粒子数反转分布概念介绍。
2. 激光产生的原理及其在小信号时的粒子数反转分布值。
3. 激光的应用领域及实例。
三、教学方法1. 采用讲授法,讲解介质在小信号时的粒子数反转分布概念。
2. 采用案例分析法,分析激光产生的原理及其在小信号时的粒子数反转分布值。
3. 采用实践教学法,介绍激光在现代科技领域中的应用。
四、教学准备1. 教学PPT。
2. 相关教材或参考资料。
3. 投影仪等教学设备。
五、教学过程1. 导入:简要介绍激光的发现及发展历程,引发学生兴趣。
2. 讲解介质在小信号时的粒子数反转分布概念,让学生理解激光产生的基本原理。
3. 分析激光产生的原理及其在小信号时的粒子数反转分布值,引导学生掌握激光产生的条件。
4. 介绍激光在现代科技领域中的应用,如通信、医疗、工业加工等,让学生了解激光技术的广泛应用。
5. 课堂互动:提问学生关于激光原理及应用的问题,检查学生对知识点的掌握情况。
6. 总结:对本节课的主要内容进行归纳总结,强调重点知识点。
7. 作业布置:布置相关练习题,巩固所学知识。
8. 课后反思:教师对本节课的教学效果进行反思,为下一步教学做好准备。
六、教学评估1. 课堂问答:通过提问方式检查学生对激光原理及介质粒子数反转分布的理解程度。
2. 练习题:布置针对性的练习题,让学生课后巩固所学知识。
3. 小组讨论:分组讨论激光应用案例,培养学生的实际应用能力和团队合作精神。
七、教学拓展1. 邀请相关领域的专家或企业人士进行讲座,让学生更直观地了解激光技术在实际生产中的应用。
2. 安排课后参观激光实验室或相关企业,加深学生对激光技术的认识。
3. 组织学生参加激光技术竞赛或项目实践,提高学生的实际操作能力。
激光原理2.2速率方程组与粒子数反转(2014)
激光原理高福斌gaofubin@gaofubin@163com2013.10.201高福斌/342.2 速率方程组与粒子数反转(!可实现粒子数反转的几种量子系统)回顾——实现粒子数反转的两个必要条件:①工作物质粒子有适当的能级结构②有合适的激励能源前瞻——分析方法:速率方程方法以及速率方程的求解步骤速率方程方法: 分析粒子系统能否实现反转的一种方法速率方程:描述各能级粒子数(密度)变化速率高福斌/342的方程组态E 上的粒子抽运到E 、E 能级上的速率;0122.速率方程: 3个能级应有22n 个独立方程(1) E 2能级在单位时间内增1n ρ加的粒子数密度为:dn 图(2-5)简化的四能级图n 2R n A n W n W =−−+R n A n B νn B νd =−−+(2-5a)2221221112()()f f dtρρ()2n ρ1n 2120A A 图(2-5))简化的四能级图n2n ρ1n 图(2-5))简化的四能级图n dn二.小信号粒子数反转的物理条件:1. 激光上能级E 2的寿命要长,使该能级上的粒子不能轻易地通过非受激辐射而离开;2. 激光下能级E 1的寿命要短,使该能级上的粒子很121220)(ττR R R n +−=Δ快地衰减;3. 选择合适的激励能源,使它对介质的E 2能级的抽运速率R 2愈大愈好,2n 而对E 1能级的抽运速率R 1愈小愈好.1n ρ即满足条件12ττ>0n 高福斌/3422足12R R>{图(2-5))简化的四能级图本节研究:反转粒子数密度Δn 的饱和效应(讨论Δn 2n (与各种因素的关系,引出Δn 饱和效应的概念。
)1n ρ。
)图(2-5))简化的四能级图n 由下式可知:()R R R nττ−+ΔnΔ0nΔ20n0IsI0s nΔ0nΔ:0(1)s I f ν+Δ043n Δ由上式可见: 只要I ≠0, 则Δn <Δn0, 仍有饱和效应.20n 012I I νννΔ−=+⋅在处I ≈I s 时s 2202(/2)(/2)3n n n ννΔ+ΔΔ=Δ=Δ222(/2)2(/2)4ννΔ+Δ频率在此范围内的入射光才会引起显著的饱和作用。
半导体激光器粒子数反转的形成机制
半导体激光器粒子数反转的形成机制在半导体激光器中,粒子数反转是实现激光放射的重要机制之一。
粒子数反转是指在激光器中,高能态粒子的数目大于低能态粒子的数目,从而形成了粒子数密度的反转。
本篇文章将介绍半导体激光器粒子数反转的形成机制。
半导体激光器是一种能够通过电流注入来实现放射的半导体器件。
在激光器中,晶体材料通常由两种不同的半导体材料组成,形成p-n 结。
当在这个p-n结中施加适当的电流时,电子从p区域向n区域流动,同时空穴从n区域向p区域流动。
这种电子和空穴的复合过程会导致能量的释放,产生光子。
在激光器中,为了形成激光放射,需要实现粒子数反转。
粒子数反转的实现需要满足以下两个条件:首先,激活态电子(高能态)的数目必须大于基态电子(低能态)的数目;其次,激活态电子在基态电子中的寿命要长,以保持粒子数反转的持续性。
半导体激光器中,粒子数反转的形成主要依赖于能带结构和载流子注入。
在能带结构方面,由于半导体材料的能带结构不一样,会导致不同能态的载流子数目存在差异。
一般来说,在半导体材料的能带结构中,传导带与价带之间存在能隙,而能隙的宽度对应着载流子能态的差别。
通过合适的材料选择和设计,可以实现能隙宽度的调节,进而达到粒子数反转的要求。
在载流子注入方面,电流的注入会引入更多的激活态电子和空穴,但由于材料自身的特性,这些激活态电子和空穴在复合之前会停留在能带之间的碰撞区域。
这种碰撞会促使这些激活态载流子向基态转化,从而实现粒子数反转。
对于半导体激光器来说,这个碰撞区域通常是位于pn结的活性层,也可以是量子阱等特殊结构。
总的来说,半导体激光器粒子数反转的形成机制是通过能带结构和载流子注入相互作用实现的。
粒子数反转的形成是激光器实现激光放射的前提和基础,对于实现高效、稳定的激光器性能有着重要的影响。
通过深入研究粒子数反转的形成机制,可以进一步改进半导体激光器设计和制造工艺,提高激光器的性能和应用范围。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n2W21
n1W12
n1 A10
R1 n2 A21 n2B21f (ν) n1B12f (ν) n1 A10
式中各项的物理过程及物理意义如同以上所述.
总的粒子数为各能级粒子数之和
n0 n1 n2 n
速率方程组
dn2 dt
R2
n2 A21 n2W21 n1W12
R2 n2 A21 n2B21f (ν) n1B12f (ν)
一. 当激光器工作达到稳定时,抽运和跃迁达到动态平衡,各 能级上粒子数密度并不随时间而改变,即:
dn0 dn1 dn2 0 dt dt dt
假设能级E2、E1的简并度相等,即g1=g2,因此有B12=B21,
又认为E2能级向E1能级的自发跃迁几率远大于E2能级向基 态E0的自发跃迁几率,即A2=A21
dn1 dt
R1
n2 A21 n2W21
n1W12
n1 A10
R1 n2 A21 n2B21f (ν) n1B12f (ν) n1 A10
n n0 n1 n2
以上三式即为在增益介质中同时存在抽运、吸收、自发辐 射和受激辐射时各能级上的粒子数密度随时间变化的速率方程 组。
2.2.3 稳态工作时的粒子数密度反转分布
2.2.2 速率方程组
——考虑谱线增宽时的情况
1. 图(2-5)为简化的四能级图,n0、n1、n2分别为基态、上能级、下能级
的粒子数密度;n为单位体积内增益介质的总粒子数,R1、R2分别是激励
能源将基态E0上的粒子抽运到E1、E2能级上的速率;
2.速率方程: 3个能级应有2个独立方程
n2
(1)E2能级在单位时间内增加的粒子数密
即满足条件
2 1
R2 R1
2.2.5 均匀增宽型介质的粒子数密度反转分布
由式
n
n2
n1
R2 2
1
(R1
2B21f
R(ν2))可1 知1
n0
2B21f
(ν)
激光工作物质的光谱线型函数对激光器的工作有很大的影响.具有均匀加宽
谱线和具有非均匀加宽谱线的工作物质的反转密度行为有很大差别,由它们所构成 的激光器的工作特性也有很大不同,因此将分别予以讨论。
一.对于均匀增宽的介质
f
(ν)
ν 2
(ν ν0 )2 (ν
2)2
且f
(ν0 )
2 ν
如果介质中传播的光波频率为 ν0,则有:
它是当分母中的第二项为零时的粒子数密度反转分布值。而分
母中的第二项一定是个正值,因此它又是粒子数密度反转分布
值可能达到的最大值。显然只有在谐振腔中传播的单色光能密
度可能趋近于零(ρ 0即I 0),换句话说,参数 对应n着0 谐振
腔的单色光能密度为零或者近似为零时的粒子数密度反转分布
的大小。
参数n对0 应着激光谐振腔尚未发出激光时的状态,通常把这个
E3 E2
W21
E1
这里对W13的要求很高,由 于这一原因, 除红宝石激光 器采用三能级系统外, 目前 大多数激光器都采用激光 下能级不是基态的四能级 系统.选择工作物质的一条 标准: 粒子有易于实现反转 的能级结构.
若激光下能级不是基态, 则反转条件较易实现 ---- 这正是要 讨论的四能级系统的优点 3. 四能级系统图:
E3
未考虑谱线增宽时的情况
ω32
E2
2.三能级系统速率方程组
(1).速率方程: 3个能级应有2个独立方程
W13 W31 A31 ω31 W12 A21ω21
W21
E1
dn3 dt
W13n1 W31n3
(32
31 A31 )n3
约定: 实线箭头代表辐射跃迁; 虚线箭头代表非辐射跃迁。
∵ W13 ~ W31 但
速率方程的求解步骤:
(1)列出速率方程:
dni dt
( i=1,2,... n)
n是粒子参予光和物质相互作用的能级总数。若粒子有n个 能级, 则可列出n个方程, 其中(n-1)个独立。
(2)求出速率方程的稳定解(数学解): 求出稳态下
( ddnti)各 0能级的粒子数, 或比值
nj ni
dt dt
故由(1)有 代入(2)有
n3
W13 n1 32 A31
n2
W13
( 32 32 A31
)
W12
n1
W21 A21
∵ 32 A31
∴ n2 W13 W12
(3)
n1 W21 A21
当 g1 (如g2红宝石), 则
, 得B12 B21
, 于W是12 W21
n2 W13 W21 n1 A21 W21
n1 n3
故
W13n1 W31n3 W13n1
且 32 31
∵
21 0
∴
dn3 dt
W13n1 (32
A31 )n3
而
dn2 dt
32n3 W12n1 (21 A21 W21 )n2
∴
dn2 dt
32n3
W12n1 ( A21 W21 )n2
三能级系统激光工作物质的典型 例子是红宝石晶体。红宝石在室 温下的一些跃迁几率数据为:
第一项——受激吸收引起的n2的增加率, 取正号
(过程几率与过程始态上粒子数的乘积);
第二项——受激发射引起的n2的减少率, 取负号; 第三项——自发发射引起的n2的减少率, 取负号; 第四项——非辐射跃迁引起的n2的减少率, 取负号。
若设 g1=g2 , 则 W12=W21=W, 速率方程变为
dn2 dt
(3)要实现粒子数反转即 ,
n2 1
应该满足
W13 A21
(4).物理解: 三能级系统粒子数反转(
n1
nn即12 1
)n的物0理条
件是: 必须使从基态E1到E3的抽运速率W13大于从
E2到E1的 自发发射几率A21. 即W13>A21
ω32
W13 W31A 31 ω31 W12 A 21ω21
此处因为考虑到介质的线型函数远比传播着的光能量密度为 的单色 受激辐射光的线宽要宽得多,故应用(1-54)式 W21 B21f (v0 )
和(1-55)式 W12 B12f (v0 )
(2)E1能级在单位时间内增加的粒子数密度为:
n2
n1
n0
图(2-5))简化的四能级图
dn1 dt
E0:基能级/光抽运能级 E1:不是基态能级,而是一个激发态能,是激光下能级, τ10小
而ω10大(迅速弛豫到E0, 抽空E1, 减少n1)在常温下基本上是空的。 E3: 光抽运能级, τ32小而ω32 大(迅速弛豫到E2) E2: 激光上能级/亚稳能级(易积累n2)
(1)用三能级系统速率方程组可 得其数学解:
则有:
dn2 dt
R2
n2 A21 (n2 B21 n1B12 )f (ν) 0
dn1 dt
R1
n2 A21
(n2 B21 n1B12 )f (ν) n1 A1
0
将上两式相加可得:
(R1
R2 )
n1 A1
n1
1
n1
(R1
R2 )1
由上几式可得:
n2
R2
(R1 A2
R2 )1B21f B21f (ν)
ω32≈0.5×107s-l A31≈3×105s-1, A21≈0.3×103s-1, ω21,ω31≈0.
dn3 dt
W13n1 (32
A31 )n3
(1)
dn2 dt
32n3 W12n1 ( A21 W21 )n2
(2)
(2).稳定解(数学解):
当激光器工作达到稳定时,抽运和跃迁达到动平衡,各能级上粒子数密度 并不随时间而改变,即: dn3 dn2 0
W (n1 n2 ) A21n2
21n2
3.稳定解(数学解): 稳态下 dn2, 故 0
dt
n2
W
n1 W A21 21
可见: 对二能级系统, 一般总有 n2 ; n1
仅当激励速率很大时
( W12 )A,21 21
n2 n1
4.结论(物理解): 在光频区, 二能级系统不可能实现粒子数 反转
1.能级图
E2
W12
W21 A21 ω21
约定: 实线箭头代表辐射跃迁; 虚线箭头代表非辐射跃迁。
E1
其中 :W12——受激吸收几率(激励几率)
W12
dn2 n1dt
W21——受激发射几率
W21
dn2 n2 dt
A21——自发发射几率
A21
dn2 n2 dt
ω21——非辐射跃迁几率(热弛豫等, 热弛豫即热运动
n3 W14 exp(h 21 / kT)
n2
( A32
W32 )(1
W14
12
)
(4)
E4
E3
ω43
W14 A41 ω41 W24
A32 W23ω32
W32
E1
E2
ω21
ω12
(2)物理条件: 比较(4)式与三能级系统的(3)即
n2 W13 W21 n1 A21 W21
∵四能级系统中
式中τ2、 τ1分别为上、下能级的寿命
2.2.4 小信号工作时的粒子数密度反转分布
Δn0称作小信号反转粒子数
一.小信号粒子数密度反转分布 n0
密度,它正比于受激辐射上
能级寿命τ2及激发几率R2.
由式
n
n2
n1
R2 2
1
(R1
2B21f
R(ν2))可1 得1:
n0
2B21f
