人教版必修一指数函数
新人教版高中数学必修一4.2.2指数函数的图象与性质

0.99-1
(2) 0.68-0.1,
1.78-0.1
解:(1)由指数函数的性质知,1.2-2<1.20=1,0.99-1>0.990=1, 所以1.2 -2<0.99-1.
(2)由指数函数的性质知,0.68-0.1>0.680=1,1.78-1<1.780=1, 所以0.68-0.1>1.78-1.
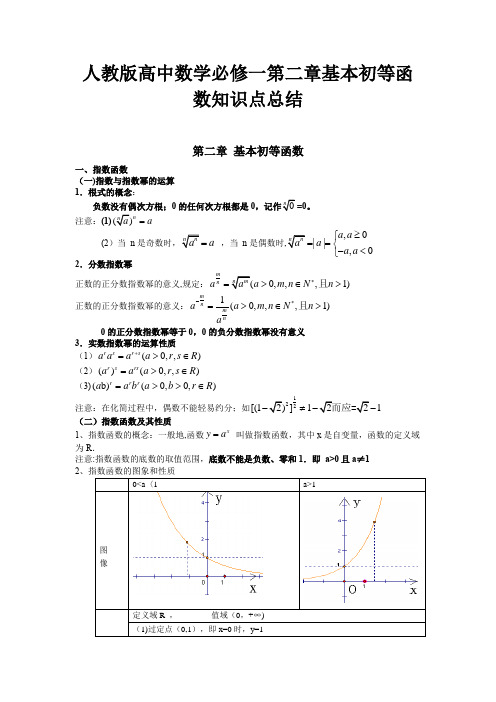
指数函数的图像与性质
a>1
0<a<1
图 像
定义域 值域
过定点 单调性
R (0, +∞)
过定点(0,1),即x=0时,y=1
增函数
减函数
例题1 比较下列各题中两个数的大小: (1) 1.72.5与1.73; (2) 0.8 2 和0.8 3; (3) 1.70.3与0.93.1
解: (1)考查函数,由1.7 >1得函数在实数集上是增函数
列表、描点、连线
x -3 -2 -1 0 1 2
y=2x
1 8
1 4
1 124
2
y y=2x
8
4
2 1
1
-3 -2 -1 02 1 2 3 x
同理画出
y
1 2
x
的图像
x -3 -2 -1
y
1 2
x
8
42
012 1 1/2 1/4
y
y (1)x 2
8
4
2 1
1
∵2.5 < 3 ∴ 1.72.5与1.73 (2) 考查函数,由0<0.8<1得函数在实数集上是减函数
∵ 2 3 ∴ 0.8 2 <0.8 3
人教版高中数学必修一-第二章-基本初等函数知识点总结
人教版高中数学必修一第二章基本初等函数知识点总结第二章 基本初等函数一、指数函数(一)指数与指数幂的运算 1.根式的概念:负数没有偶次方根;0的任何次方根都是0=0。
注意:(1)na =(2)当 n a = ,当 n 是偶数时,0||,0a a a a a ≥⎧==⎨-<⎩2.分数指数幂正数的正分数指数幂的意义,规定:0,,,1)m na a m n N n *=>∈>且正数的正分数指数幂的意义:_1(0,,,1)m nm naa m n N n a*=>∈>且0的正分数指数幂等于0,0的负分数指数幂没有意义 3.实数指数幂的运算性质 (1)(0,,)rsr s a a aa r s R +=>∈(2)()(0,,)r s rsa a a r s R =>∈ (3)(b)(0,0,)rrra ab a b r R =>>∈注意:在化简过程中,偶数不能轻易约分;如122[(1]11≠ (二)指数函数及其性质1、指数函数的概念:一般地,函数xy a = 叫做指数函数,其中x 是自变量,函数的定义域为R .注意:指数函数的底数的取值范围,底数不能是负数、零和1.即 a>0且a ≠1 2a>1注意: 指数增长模型:y=N (1+p)指数型函数: y=ka 3 考点:(1)a b =N, 当b>0时,a,N 在1的同侧;当b 〈0时,a,N 在1的 异侧.(2)指数函数的单调性由底数决定的,底数不明确的时候要进行讨论。
掌握利用单调性比较幂的大小,同底找对应的指数函数,底数不同指数也不同插进1(=a 0)进行传递或者利用(1)的知识。
(3)求指数型函数的定义域可将底数去掉只看指数的式子,值域求法用单调性. (4)分辨不同底的指数函数图象利用a 1=a ,用x=1去截图象得到对应的底数。
(5)指数型函数:y=N (1+p)x 简写:y=ka x 二、对数函数 (一)对数1.对数的概念:一般地,如果x a N = ,那么数x 叫做以a 为底N 的对数,记作:log a x N = ( a - 底数, N — 真数,log a N — 对数式)说明:1。
人教版高中数学必修1第二章知识点汇总 (1)

人教版高中数学必修一第二章知识点汇总第二章 基本初等函数(Ⅰ)〖2.1〗指数函数 【2.1.1】指数与指数幂的运算(1)根式的概念①如果,,,1nx a a R x R n =∈∈>,且n N +∈,那么x 叫做a 的n 次方根.当n 是奇数时,a 的n 次当n 是偶数时,正数a 的正的n 负的n 次方根用符号表示;0的n 次方根是0;负数a 没有n 次方根.①这里n 叫做根指数,a 叫做被开方数.当n 为奇数时,a 为任意实数;当n 为偶数时,0a ≥.①n a =;当n a =;当n (0)|| (0) a a a a a ≥⎧==⎨-<⎩.(2)分数指数幂的概念①正数的正分数指数幂的意义是:0,,,m na a m n N +=>∈且1)n >.0的正分数指数幂等于0.①正数的负分数指数幂的意义是: 1()0,,,mm n n aa m n N a -+==>∈且1)n >.0的负分数指数幂没有意义. 注意口诀:底数取倒数,指数取相反数. (3)分数指数幂的运算性质①(0,,)rsr sa a aa r s R +⋅=>∈ ①()(0,,)r s rs a a a r s R =>∈①()(0,0,)r r rab a b a b r R =>>∈【2.1.2】指数函数及其性质(4)指数函数〖2.2〗对数函数【2.2.1】对数与对数运算(1)对数的定义①若(0,1)xa N a a =>≠且,则x 叫做以a 为底N 的对数,记作log a x N =,其中a 叫做底数,N 叫做真数.①负数和零没有对数.①对数式与指数式的互化:log (0,1,0)xa x N a N a a N =⇔=>≠>.(2)几个重要的对数恒等式log 10a =,log 1a a =,log b a a b =.(3)常用对数与自然对数常用对数:lg N ,即10log N ;自然对数:ln N ,即log e N (其中 2.71828e =…).(4)对数的运算性质 如果0,1,0,0a a M N >≠>>,那么①加法:log log log ()a a a M N MN += ①减法:log log log a a aM M N N-= ①数乘:log log ()na a n M M n R =∈ ①log a N a N =①log log (0,)b n a a nM M b n R b=≠∈ ①换底公式:log log (0,1)log b a b N N b b a =>≠且 【2.2.2】对数函数及其性质(5)对数函数(6)反函数的概念设函数()y f x =的定义域为A ,值域为C ,从式子()y f x =中解出x ,得式子()x y ϕ=.如果对于y 在C 中的任何一个值,通过式子()x y ϕ=,x 在A 中都有唯一确定的值和它对应,那么式子()x y ϕ=表示x 是y 的函数,函数()x y ϕ=叫做函数()y f x =的反函数,记作1()x f y -=,习惯上改写成1()y f x -=.(7)反函数的求法①确定反函数的定义域,即原函数的值域;①从原函数式()y f x =中反解出1()x f y -=;①将1()x f y -=改写成1()y f x -=,并注明反函数的定义域.(8)反函数的性质①原函数()y f x =与反函数1()y f x -=的图象关于直线y x =对称.①函数()y f x =的定义域、值域分别是其反函数1()y f x -=的值域、定义域.①若(,)P a b 在原函数()y f x =的图象上,则'(,)P b a 在反函数1()y f x -=的图象上.①一般地,函数()y f x =要有反函数则它必须为单调函数.〖2.3〗幂函数(1)幂函数的定义一般地,函数y x α=叫做幂函数,其中x 为自变量,α是常数.(3)幂函数的性质①图象分布:幂函数图象分布在第一、二、三象限,第四象限无图象.幂函数是偶函数时,图象分布在第一、二象限(图象关于y 轴对称);是奇函数时,图象分布在第一、三象限(图象关于原点对称);是非奇非偶函数时,图象只分布在第一象限.①过定点:所有的幂函数在(0,)+∞都有定义,并且图象都通过点(1,1).①单调性:如果0α>,则幂函数的图象过原点,并且在[0,)+∞上为增函数.如果0α<,则幂函数的图象在(0,)+∞上为减函数,在第一象限内,图象无限接近x 轴与y 轴.①奇偶性:当α为奇数时,幂函数为奇函数,当α为偶数时,幂函数为偶函数.当qpα=(其中,p q 互质,p 和q Z ∈),若p 为奇数q 为奇数时,则qpy x =是奇函数,若p 为奇数q 为偶数时,则q py x =是偶函数,若p 为偶数q 为奇数时,则q py x =是非奇非偶函数.①图象特征:幂函数,(0,)y x x α=∈+∞,当1α>时,若01x <<,其图象在直线y x =下方,若1x >,其图象在直线y x =上方,当1α<时,若01x <<,其图象在直线y x =上方,若1x >,其图象在直线y x =下方.〖补充知识〗二次函数(1)二次函数解析式的三种形式①一般式:2()(0)f x ax bx c a =++≠①顶点式:2()()(0)f x a x h k a =-+≠①两根式:12()()()(0)f x a x x x x a =--≠(2)求二次函数解析式的方法①已知三个点坐标时,宜用一般式.①已知抛物线的顶点坐标或与对称轴有关或与最大(小)值有关时,常使用顶点式. ①若已知抛物线与x 轴有两个交点,且横线坐标已知时,选用两根式求()f x 更方便.(3)二次函数图象的性质①二次函数2()(0)f x ax bx c a =++≠的图象是一条抛物线,对称轴方程为,2bx a=-顶点坐标是24(,)24b ac b a a--. ①当0a >时,抛物线开口向上,函数在(,]2b a -∞-上递减,在[,)2b a -+∞上递增,当2bx a=-时,2min 4()4ac b f x a -=;当0a <时,抛物线开口向下,函数在(,]2b a -∞-上递增,在[,)2ba -+∞上递减,当2bx a=-时,2max 4()4ac b f x a -=.①二次函数2()(0)f x ax bx c a =++≠当240b ac ∆=->时,图象与x轴有两个交点11221212(,0),(,0),||||||M x M x M M x x a =-=. (4)一元二次方程20(0)ax bx c a ++=≠根的分布一元二次方程根的分布是二次函数中的重要内容,这部分知识在初中代数中虽有所涉及,但尚不够系统和完整,且解决的方法偏重于二次方程根的判别式和根与系数关系定理(韦达定理)的运用,下面结合二次函数图象的性质,系统地来分析一元二次方程实根的分布.设一元二次方程20(0)ax bx c a ++=≠的两实根为12,x x ,且12x x ≤.令2()f x ax bx c =++,从以下四个方面来分析此类问题:①开口方向:a ①对称轴位置:2bx a=- ①判别式:∆ ①端点函数值符号.①k <x 1≤x 2 ⇔①x 1≤x 2<k ⇔①x 1<k <x2 ⇔ af (k )<0①k 1<x 1≤x 2<k 2 ⇔①有且仅有一个根x 1(或x 2)满足k 1<x 1(或x 2)<k 2 ⇔f (k 1)f (k 2)<0,并同时考虑f (k 1)=0或f (k 2)=0这两种情况是否也符合①k 1<x 1<k 2≤p 1<x 2<p 2 ⇔ 此结论可直接由①推出.(5)二次函数2()(0)f x ax bx c a =++≠在闭区间[,]p q 上的最值设()f x 在区间[,]p q 上的最大值为M ,最小值为m ,令01()2x p q =+. (①)当0a >时(开口向上) ①若2b p a -<,则()m f p = ①若2b p q a ≤-≤,则()2b m f a =- ①若2b q a->,则()m f q =①若02b x a -≤,则()M f q = ①02b x a->,则()M f p =(①)当0a <时(开口向下)xxxxx xx①若2b p a -<,则()M f p = ①若2b p q a ≤-≤,则()2b M f a =- ①若2b q a->,则()M f q =①若02b x a -≤,则()m f q = ①02b x a->,则()mf p =.xfxf xfxxx。
人教版数学必修一4.2.2指数函数图像和性质

x
当 x < 0 时0,y > 1; x
定 义 域 :当Rx > 0 时, 0< y < 1。
性
值 域: ( 0,+ ∞ )
恒 过 点: ( 0 , 1 ) ,即 x = 0 时, y = 1 .
质 在 R 上是单调 增函数 在 R 上是单调 减函数
三、深入探究,加深理解
观察图像, 发现图像与底的 关系
其中 x 为自变量,定义域为 R
我 下列函数中,哪些是指数函不 是数?
y 4x y x4 y 4x
y 4x1
二、发现问题,探求新知
• 怎样得到指数函数图像? • 指数函数图像的特点? • 通过图像,你能发现指数函数的哪些
性质?
• 探究并计算并完成以下表格,观察表格, 你发现了什么规律?
n -3 -2 -1 0 1 2 3
(0 a 1)
1 1
0
x
0
1
1
0x
x
y
y ax
(a 1)
1
0
x
y
y ax
(0 a 1)
1
0
x
指数函数
的图像及性质
a>1
0<a<1
图
y
பைடு நூலகம்
y=ax
(a>1)
y=ax
y
(0<a<1)
象 y=1
No (0,1)
(0,1)
y=1
Image 当 x > 0 时,y >01;
当 x < 0 时,0< y < 1。
例
2:(1)解不等式
1 2
x2
4.2.1指数函数的概念PPT课件(人教版)

这说明2001年…
实际问题
例 2(2)在问题 2 中,某生物死亡 10000 年后,它体内碳 14 的含量衰减为原来的百分之几?
这说明…
思考:连续两个半衰期是否就是一个“全衰期”?
例 2 (1)在问题 1 中,如果平均每位游客出游一次可给当地带 来 1000 元门票之外的收入,A 地景区的门票价格为 150 元,比 较这 15 年间 A,B 两地旅游收入变化情况.
1118 113
1244 126
B景区每年旅游人次约为上 一年的1.11倍
年增加量是相邻两年的游客人次 做减法得到的,能否通过对B地 景区每年的游客人次做其他运算 发现游客人次的变化规律呢?
增长率为常数的变化 方式,称为指数增长 .
时间/
A地景区
年
人次/ 万次
年增加量 /万次
2001 600
2002 609 9 2003 620 11 2004 631 11 2005 641 10 2006 650 9 2007 661 11 2008 671 10 2009 681 10 2010 691 10 2011 702 11
1.11x 倍.
设经过 x 年后的游客人次为2001年的 y 倍
探究1:比较两地景区游客人次的变 化情况,你发现怎样的变化规律?
增加量、增长率是 刻画事物变化规律 的两个重要的量.
A地
B地
问题 2 当生物死亡后,它机体内原有的碳 14 含量会按确 定的比率衰减(称为衰减率), 若年衰减率为 p ,你能表 示出死亡生物体内碳 14 含量与死亡年数之间的关系吗?
探究1:比较两地景区游客人次的变化情况, 你发现怎样的变化规律?
A地
B地
线性增长
新人教版高一数学必修一_指数函数_课件

图形
单调性
y (1)x 3
y 3x
.
y 3x 在 (,)
单调递增;
y (1)x在 (,) 3 单调递减;
2.判断下列函数在(−∞,+∞)内的单调性? (1) y 1.1x (2) y 0.3x (3) y 3x (4) y 5 2.718x
(1)增函数; (2)减函数; (3)减函数; (4)增函数.
.m, n的大小. ① 1.5m 1.5n ②
3 4
m
3 4
n
③
2
m
2 n 2
① mn ② mn
③ mn
.
1.本节内容:
指数函数
图像与性质 指数模型
应用
2.需要注意的问题:
(1)指数函数 y ax 的底 a 的取值对函数图像;
及函数单调性的影响; (2)建立指数函数模型的方法.
3.当 a 1 时,函数在定义域
•
R 内是增函数;
y (1)x
2
当 0 a 1 时,函数在定义域
•
•
y 2x
•
R 内是减函数。
•• • •• • • • •
.
指数函数性质 (1)图像都经过点(0,1) (2)函数的定义域是R,值域是 R
(3)当 a 1 , 函数在 R 内是增函数 当 0 a 1, 函数在 R 内是减函数
.
例2.某市2000年国民生产总值20亿元,计划在今 后的10年内,平均每年增长8%,问2010年该市国 民生产总值可达多少亿元(精确到0.01亿元)?
解设: 该市国民生产总值在2000年后的第x年为 y亿元,则: 第1年: y=20+20×8=%20(1+8%=)20×1.08,
人教版高中数学必修一: 2.1《指数函数》(1)(22)

又要钱?借多少?
黄老板,能借点 钱吗?
哦,我每天还的钱是前一 天的2倍是吧,那我需要 很久才能还完你啊?
这样吧,从今天开始在一个 月中,我每天都借你10万元, 而你从今天开始,第一天还 我1元,第二天2元,第三天 4元,第四天8元,.......以后 知道怎么还了吗?
不,你只要还我三十天就 可以了,剩下的就不要了。
∵ 1.2< 5 1 1.2 > 1 5 ∴
3 3
对大 于的 减函 函数 数值 ,反 自而 变小 量
.
练习:比较100.2与1的大小.
课堂练习:用“>”或“<”填空:
(1)0.8
0.1
< 0.80.2
1 m ( 2)若( ) (0.25) n , 则m > n. 4
1 x y =( ) 3
1 x y =( ) 4
y =3
x
y = 4x
1、a > 1 时,底大图陡
0 < a < 1 时,底小图陡
观察图像:你发现了什么?
通过图像,动态图特点,总结指数函数性质
(1)图象都位于 x轴上方 方 (2)图象都过点(0,1) (3) y 2 x 的图象从左到 右上升
1 x (4) y ( 2 )
(口答)判断下列函数是不是指 数函数,为什么?
(1) y ax( a 0且a 1) ( 2) y x
1 3
练习巩固
1 x (3) y ( ) √ 3 x ( 4) y ( 3) (5) y 1
x x
(6) y a ( a 0且a 1) (7 ) y 2 3
(1) 考虑指数函数 y=1.7x, 解:
人教版(2019)高中数学必修一 指数函数的概念 教学课件

=
=
( )
思考:上面几个函数的结构有什么特征?
(1)均为幂的形式;(2)底数是一个正数;(3)自变量都在指数位置;
概念形成
x
y=a
指数函数的概念:一般地,函数
(a>0,且a≠1)叫做指数
函数,其中指数x是自变量,函数的定义域是R.
概念深入
思考1:为什么要规定底数a>0且a≠1?
①若a =0,则当x> 0时,a
求f(0),f(1),f(-3)的值;
课本P114
巩固练习
已知函数() = + ( > , 且 ≠ )经过点
7
(−, ), (, ),则(−)的值为_____________.
题型探究
题型三:指数函数的实际应用
例5.某种储蓄按复利计算利息,若本金为元,每期
利率为,设存期是( ∈ ∗ ),本利和(本金加上利
2
x
x
情景引入
问题2:《庄子》中说:“一尺之棰,日取其半,万世不竭”。
取一根一尺长的木棍,每次截取该木棍剩余部分的
,木棍的剩余长度y与截取次数x有怎样的关系?
截取次数
1
剩余长度
2
3
4
( ) ( ) ( )
=
( )
......
x
......
( )
探究新知
( , ) ∪ ( , +∞)
取值范围是________________.
巩固练习
创新大课堂P75
已知函数() = ( + − ) ∙ 是指数函数,求()
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.指数函数图象问题的处理方法
(1)抓住图象上的特殊点,如指数函数的图象过定点(0,1);
(2)利用图象变换,如函数图象的平移变换(左右平移、上下平
移);
(3)利用函数的奇偶性与单调性.
跟踪 训练
栏栏 目目 链 接接
(2)函数y=af(x)的值域的求法如下:
栏 目
①换元,令t=f(x);
链 接
②求t=f(x)的定义域D;
③求t=f(x)的值域M;
④利用y=at的单调性求y=at,t∈M 的值域.
跟踪 训练
2.求下列函数的定义域和值域:
栏栏 目目 链 接接
跟踪 训练
栏 目 链 接
题型三 指数函数的图象的应用
栏栏 目目
链
接接
跟踪 训练
1.下列函数是指数函数的是( C )
A.y=2x+1 C.y=3-x
B.y=x3 D.y=3·2x
栏栏 目目 链
接接
题型二 求指数函数的定义域与值域 例2 求下列函数的定义域与值域:
栏 目 链 接
栏 目 链 接
点评:函数y=af(x)的定义域、值域 的求法.
(1)函数y=af(x)的定义域与y=f(x)的 定义域相同.
例3 下图是指数函数:
栏 目 链 接
①y=ax(a>0,且a≠1),
②y=bx(b>0,且b≠1),
③y=cx(c>0,且c≠1),
(
④y=dx(d>0,且d≠1)的图象,则a,b,c,d与1的大小关系为 )
栏栏 目目
A.a<b<1<c<d C.b<a<1<c<d
B.b<a<1<d<c D.a<b<1<d<c
栏栏 目目
由图象观察可得c>d>1>a>b.
链
接接
答案:B
点评:1.指数函数的图象随底数变化的规律
(1)无论指数函数的底数a如何变化,指数函数y=ax的图象都与
直线x=1相交于点(1,a).由图象可知:在y轴右侧,图象从下到上
相应的底数.函数的底数与图象间的关系可概括为:在第一象限内,目链接目接
B.y2>y1>y3
C.y1>y2>y3
D.y1>y3>y2
自测 自评
栏 目 链 接
自测 自评
栏栏 目 链接链接
栏栏 目目 链 接接
题型一 指数函数概念的理解和应用
例1
栏 目 链 接
点评:判断一个函数是否为指数函数,只需判定其解析式是否
符合y=ax(a>0且a≠1)这一形式,即底数a为不等于1的正常数,指数 只能是x,且ax的系数为1.
第二章 基本初等函数(Ⅰ) 2.1 指 数 函 数
2.1.3 指数函数及其性质(一)
栏栏 目目 链 接接
1.了解指数函数模型的实际背景,认识数学与现实生活及 其他学科的联系.
2.理解指数函数的概念和意义,能画出具体指数函数的图栏栏
象,探索并理解指数函数的单调性和特殊点.
目目
链
3.在学习的过程中体会研究具体函数及其性质的过程和方接接
式定解义.析因:为形如a>y=0,axx(a是>任0意且一a≠个实1)的数函时数,叫ax 指是数确函定数的,实它数是,一所种以形函 栏目栏目
数的定义域为实数集 R.
链 接接
思考 应用
2.指数函数中,规定底数a大于零且不等于1的理由是什么?
栏栏 目目 链 接接
思考 应用
3.指数函数的图象变化与底数大小的关系是什么?
目目 链 接接
基础 梳理
栏栏 目目 链 接接
基础 梳理
指数函数
栏栏 目目
链
接接
基础 梳理
4.指数函数y=ax(a>0,且a≠1)的图象和性质: (1)图象.
栏栏 目目 链 接接
基础 梳理
栏栏 目目 链 接接
基础 梳理
栏栏 目目 链 接接
思考 应用
1.如何判断指数函数?指数函数的定义域是什么?
法,如具体到一般的过程、数形结合的方法等.
栏栏 目目 链 接接
基础 梳理
1.函数y=ax(a>0,且a≠1)叫做_指__数__函___数__,其中x是自变
量.
因为指数的概念已经扩充到有理数和无理数,所以在底数a>0 栏栏
的前提下,x可以是任意实数,所以指数函数的定义域为
_____R_______.
链 接接
解析:法一:在①②中底数小于1且大于零,在y轴右侧,底数 越小,图象向下越靠近x轴,故有b<a,在③④中底数大于1,在y轴 右边,底数越大图象向上越靠近y轴,故有d<c.
栏栏 目目 链 接接
法二:设直线x=1与①、②、③、④的图象分别交于点A,B,
C,D(如右图),则 其坐标依次为(1,a),(1,b),(1,c),(1,d),
解析:底数越大,函数的图象在
y
轴右侧部分越远离
x
轴,此性
栏栏 目目
质可通过 x=1 的函数值大小去理解.
链 接接
自测 自评
1.指数函数y=f(x)的图象经过点(2,4),那么f(2)·f(4)的值为 ()
A.64 B.256
C.8
D.16
栏栏
目
链接链接
自测 自评
栏栏
目
A.y3>y1>y2
链接链接
