必修一:指数与指数函数
高一数学指数与指数函数试题答案及解析

高一数学指数与指数函数试题答案及解析1.设函数(x)=,则满足的的取值范围是().A.[-1,2]B.[0,2]C.[1,+∞)D.[0,+∞)【答案】D.【解析】当时,,,解得,因此,当时,,解得,因此,综上【考点】分段函数的应用.2.设函数则使得成立的的取值范围是()A.B.C.D.【答案】C【解析】当时,由,可得,即;当时,由,可得,即,综上.故选C【考点】函数的求值.3.已知定义在R上的函数满足,当时,,且.(1)求的值;(2)当时,关于的方程有解,求的取值范围.【答案】(1),(2)【解析】(1)由可知,代入表达式可求得的值.又,可求出的值;(2)由(1)可知方程为,对x进行讨论去绝对值符号,可得,据结合指数函数,二次函数的性质可求得的取值范围.试题解析:解:(1)由已知,可得又由可知 . 5分(2)方程即为在有解.当时,,令,则在单增,当时,,令,则,,综上: . 14分【考点】本题主要考查指数函数,二次函数求值域和分类讨论的数学思想方法.4.函数的图象必经过定点___________.【答案】【解析】∵指数函数过定点,∴函数过定点.【考点】函数图象.5.已知,,且,则与的大小关系_______.【答案】【解析】由,又由,所以,所以由可得,所以,,所以即.【考点】1.分数指数幂的运算;2.对数的运算;3.指数函数的单调性.6.函数在上的最大值比最小值大,则 .【答案】【解析】因为,根据指数函数的性质可知在单调递增,所以最大值为,最小值为,依题意有即,而,所以.【考点】指数函数的图像与性质.7.设,则的大小关系是()A.B.C.D.【答案】B【解析】把看成函数当时的函数值,因为,所以;把看成函数当时的函数值,因为,所以;把看成函数当时的函数值,因为 ,所以 .综上, ,故选B【考点】1、指数函数的性质;2、对数函数的性质.8.若,则__________.【答案】【解析】【考点】指数函数的运算法则9.已知,则的大小关系是.【答案】【解析】因为指数函数在R上单调递减,所以。
人教A版高中数学必修一 《指数函数》指数函数与对数函数PPT(第1课时指数函数的概念、图象及性质)

5.求下列函数的定义域和值域: (1)y=2x-1 4;(2)y=23 -|x|.
解:(1)要使函数有意义,则 x-4≠0,解得 x≠4.
1
所以函数 y=2x-4的定义域为{x|x≠4}. 因为x-1 4≠0,所以 2x-1 4≠1,即函数 y=2x-1 4的值域为{y|y>0,且 y≠1}.
(2)要使函数有意义,则-|x|≥0,解得 x=0. 所以函数 y=23 -|x|的定义域为{x|x=0}. 因为 x=0,所以23 -|x|=230=1,即函数 y=23 -|x|的值域为{y|y= 1}.
本部分内容讲解结束
问题导学 预习教材 P111-P118,并思考以下问题: 1.指数函数的概念是什么? 2.结合指数函数的图象,分别指出指数函数 y=ax(a>1)和 y= ax(0<a<1)的定义域、值域和单调性各是什么?
1.指数函数的概念 一般地,函数 y=__a_x__ (a>0,且 a≠1)叫做指数函数,其中 x 是____自_变__量___.
指数函数的图象
根据函数 f(x)=12x的图象,画出函数 g(x)=12|x|的图象, 并借助图象,写出这个函数的一些重要性质.
【解】
g(x)=12|x
|=12x(x≥0),其图象如图. 2x(x<0),
由图象可知,函数 g(x)的定义域为 R,值域是(0,1], 图象关于 y 轴对称,单调递增区间是(-∞,0], 单调递减区间是(0,+∞).
■名师点拨 指数函数解析式的 3 个特征
(1)底数 a 为大于 0 且不等于 1 的常数. (2)自变量 x 的位置在指数上,且 x 的系数是 1. (3)ax 的系数是 1.
高一数学必修一第二章基本初等函数知识点总结
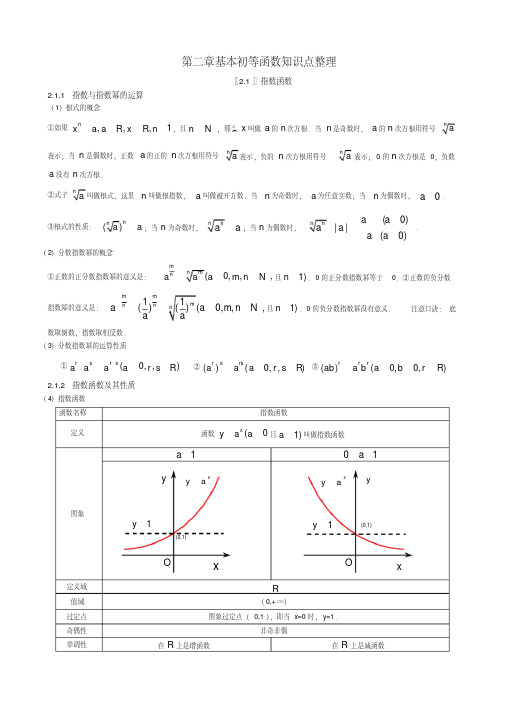
在 R 上是减函数
函数值的 变化情况
a 变化对
图象的影 响
y>1(x > 0), y=1(x=0), 0 < y<1(x < 0)
y> 1(x < 0), y=1(x=0), 0 < y< 1(x > 0)
在第一象限内, a 越大图象越高,越靠近 y 轴; 在第一象限内, a 越小图象越高,越靠近 y 轴; 在第二象限内, a 越大图象越低,越靠近 x 轴. 在第二象限内, a 越小图象越低,越靠近 x 轴.
y
f ( x) 中反解出 x
1
f ( y) ;
③将 x f 1( y ) 改写成 y f 1 ( x) ,并注明反函数的定义域.
( 8)反函数的性质
①原函数 y
f (x) 与反函数 y
1
f ( x) 的图象关于直线 y
x 对称.
②函数 y f ( x) 的定义域、值域分别是其反函数 y f 1 (x ) 的值域、定义域. ③若 P(a,b) 在原函数 y f (x ) 的图象上,则 P' (b, a) 在反函数 y f 1(x ) 的图象上.
③根式的性质: (n a )n a ;当 n 为奇数时, n an
a ;当 n 为偶数时, n an | a |
a (a 0)
.
a (a 0)
( 2)分数指数幂的概念
m
①正数的正分数指数幂的意义是: a n n a m (a 0, m, n N , 且 n 1) . 0 的正分数指数幂等于 0.②正数的负分数
设一元二次方程 ax 2 bx c 0( a 0) 的两实根为 x1, x2 ,且 x1 x2 .令 f ( x) ax 2 bx c ,从以下四个方
面来分析此类问题:①开口方向: a ②对称轴位置: x
人教B版高中数学必修一课件-3.1 指数与指数函数

y y=(1/3)x
y=3x
1
o -3 -2 -1 1 2 3
x
y
y
1 3
指数函数
y 的图像a及x性质
y ax (a 1)
定义域 值域 单调性
过定点
函数值变 化情况
R
(0,+(∞0,)+∞) 在R上是增函数
(0,1)
x > 0时,y > 1 x < 0时,0< y <1
R
R
(0,1)
(0,+∞) 在R上是减函数
(0,1)
x > 0时,0< y <1 x < 0时,y > 1
x
y
1 2
x
y 3x
y 2x
1
0
1
x
1. 定义域: R ; 2. 值 域: ( 0 , +∞) ; 3. 过 点: ( 0 , 1) ; 4. 单调性: 在 R 上是增函数; 5. 函数值的变化情况:
当 x > 0时, y > 1. 当 x < 0时, 0< y <1.
y
·(0,1)
0
x
函数
数,其中x是自变量,函数的定义域是__. R
2020/12/22
y 1 ax
自变量仅有这一种形 式
系数为1
底数为正数且不为1
探究2 指数函数的图象与性质 用描点法作出下列两组函数的图象,
人教A版数学必修第一册期末复习:指数与指数函数课件

B.2xy
C.4x2y
D.-2x2y
因为x<0,y<0,
所以
4
16 8 4
=
1
16 8 4 4
= 16
1
4
8
=2x2|y|
=-2x2y.
1
4
4
1
4
3.已知当x>0时,函数f(x)=(3a-2)x的值总大于1,则实数a的
取值范围是( C )
A.
2
,1
3
C.(1,+∞)
B.(-∞,1)
n
a
叫做根式,这里____叫做根指数,______叫做被开方数.
②a的n次方根的表示:
xn=a⇒
x=
,当n为奇数且n∈N* , n>1时
x= ± ,当n为偶数且n∈N* 时
(2)根式的性质
①( )n=a(n∈N*,且n>1).
a,n为奇数
②
=
a,a≥0
|a| =
-a,a<0
D. 0,
2
3
✓ 根据指数函数性质知3a-2>1,解得a>1.
4.(易错题)若函数f(x)=ax(a>0,且a≠1)的图象经过点P 2,
则f(-1)=________.
2
1
=a2
2
a=
2
2
f(x)=
f(-1)=
2
2
2
2
−1
= 2
1
2
,
2
5.(易错题)已知函数f(x)=ax(a>0,a≠1)在[1,2]上的最大值比最小值大 ,
高中数学必修一 指数运算性质及指数函数

第8课时 指数运算性质及指数函数知识点一 分数指数幂 给定正实数a ,对于任意给定的整数m ,n (m ,n 互素),存在唯一的正实数b ,使得b n =a m,我们把b 叫作a 的mn次幂,记作b =mn a .指数运算性质 一般地,在研究实数指数幂的运算性质时,约定底数为大于零的实数.当a >0,b >0时,有: (1)a m ·a n = ;(2)(a m )n = ;(3)(ab )n = ,其中m ,n ∈R . 例1 计算下列各式(式中字母都是正数).(1)10.5233277(0.027)21259-⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭;2)211511336622(2)(6)(3)a b a b a b ÷--;2152.530.064-0⎡⎤-π.⎢⎥⎣⎦() 知识点二 指数函数一般地,函数 叫作指数函数,其中x 是自变量,函数的定义域是R .注意①底数是大于0且不等于1的常数;②指数函数的自变量必须位于指数的位置上;③a x 的系数必须为1;④指数函数等号右边不会是多项式,如y =2x +1不是指数函数. 知识点三 指数函数的图像和性质例2 (1)下列函数中是指数函数的是________.(填序号) ①y =2·(2)x ;②y =2x -1;③y =⎝⎛⎭⎫π2x;④y =13x-;⑤y =13x . (2)若函数y =(a 2-3a +3)·a x 是指数函数,则实数a =________. (3)若函数y =(2a -3)x 是指数函数,则实数a 的取值范围是________. 例3 (1)函数y =a x -1a(a >0,且a ≠1)的图像可能是( )(2)函数f (x )=1+a x -2(a >0,且a ≠1)恒过定点________.(3)已知函数y =3x 的图像,怎样变换得到y =⎝⎛⎭⎫13x +1+2的图像?并画出相应图像.跟踪训练3 (1)已知函数f (x )=4+a x +1(a >0,且a ≠1)的图像经过定点P ,则点P 的坐标是( ) A.(-1,5) B.(-1,4) C.(0,4) D.(4,0) 例4 比较下列各题中两个值的大小. (1)1.7-2.5,1.7-3;(2)1.70.3,1.50.3;(3)1.70.3,0.83.1.跟踪训练4 比较下列各题中的两个值的大小.(1)0.8-0.1,1.250.2;(2)⎝⎛⎭⎫1π-π,1;(3)0.2-3,(-3)0.2.例5 (1)不等式4x <42-3x的解集是________.(2)解关于x 的不等式:a 2x +1≤a x -5(a >0,且a ≠1).例6 判断f (x )=2213x x⎛⎫ ⎪⎝⎭-的单调性,并求其值域.反思感悟研究y =a f (x )型单调区间时,要注意a >1还是0<a <1.当a >1时,y =a f (x )与f (x )的单调性相同.当0<a <1时,y =a f (x )与f (x )的单调性相反.跟踪训练6 求函数y =223x x a +-的单调区间.课后作业1.化简238的值为( ) A.2 B.4 C.6 D.82.下列根式与分数指数幂的互化正确的是( ) A.-x =12()x -(x >0) B.1263=y y (y <0) C.33441=xx ⎛⎫⎪⎝⎭-(x >0) D.133=x x -(x ≠0) 3.式子a 2a ·3a 2(a >0)经过计算可得到( ) A.a B.1a6 C.5a 6 D.6a 5 4.计算124-⎝⎛⎭⎫12-1=________.5.下列各函数中,是指数函数的是( ) A.y =(-3)x B.y =-3x C.y =3x -1D.y =⎝⎛⎭⎫13x6.若函数y =(2a -1)x (x 是自变量)是指数函数,则a 的取值范围是( ) A.a >0,且a ≠1 B.a ≥0,且a ≠1 C.a >12,且a ≠1 D.a ≥127.函数f (x )=a x -b的图像如图所示,其中a ,b 均为常数,则下列结论正确的是( )A.a >1,b <0B.a >1,b >0C.0<a <1,b >0D.0<a <1,b <08.函数y =a x -3+3(a >0,且a ≠1)的图像恒过定点_________________________________. 9.函数f (x )=1-2x +1x +3的定义域为________. 10.下列各式中成立的是( )A.⎝⎛⎭⎫m n 7=177n m B.12(-3)4=3-3 C.4x 3+y 3=34()x y + D.39=3311.下列大小关系正确的是( )A.0.43<30.4<π0B.0.43<π0<30.4C.30.4<0.43<π0D.π0<30.4<0.43 12.方程42x -1=16的解是( )A.x =-32B.x =32 C.x =1 D.x =213.函数f (x )=2112x ⎛⎫⎪⎝⎭-的递增区间为( )A.(-∞,0]B.[0,+∞)C.(-1,+∞)D.(-∞,-1) 14.函数y =⎝⎛⎭⎫12x,y =2x ,y =3x的图像(如图)分别是________.(用序号作答)15.设0<a <1,则关于x 的不等式22232223x x x x aa -++->的解集为________.16.已知a =0.80.7,b =0.80.9,c =1.20.8,则a ,b ,c 的大小关系是( ) A.a >b >c B.b >a >c C.c >b >a D.c >a >b 17.已知函数f (x )=3x -⎝⎛⎭⎫13x ,则f (x )( ) A.是奇函数,且在R 上是增函数 B.是偶函数,且在R 上是增函数 C.是奇函数,且在R 上是减函数 D.是偶函数,且在R 上是减函数18.计算:⎝⎛⎭⎫2590.5-⎝⎛⎭⎫27813--⎝⎛⎭⎫-780+160.25=__________________________________.19.已知函数f (x )=2|x -a |(a 为常数),若f (x )在区间[1,+∞)上是增函数,则a 的取值范围是________. 20.已知函数f (x )=4x -14x +1.(1)解不等式f (x )<13;(2)求函数f (x )的值域.能力提升 已知定义在R 上的函数f (x )=a +14x +1是奇函数.(1)求a 的值;(2)判断f (x )的单调性(不需要写出理由);(3)若对任意的t ∈R ,不等式f (t 2-2t )+f (2t 2-k )<0恒成立,求实数k 的取值范围.。
北师大版高中数学课件必修第1册第三章 指数运算与指数函数

2.
3.1 指数函数的概念+ 3.2 指数函数的图象和性质
刷基础
3.[江苏镇江 2021 高一期中]已知指数函数 f(x)的图象过点(-2,4),则 f(6)=( B )
3
1
4
A.
B.
C.
4
64
3
1 D.
12
解析
1
设
f(x)=ax(a>0
且
a≠1),∴f(-2)=a-2=4,解得
1 a= ,∴f(6)=
3.1 指数函数的概念+ 3.2 指数函数的图象和性质
刷基础
6.[宁夏大学附属中学 2021 高一期中]已知 f(x)=ka-x(k,a 为常数,a>0 且 a≠1)的图象过点 A(0,1),B(- 3,8). (1)求 f(x)的解析式;
f(x)-1
(2)若函数 g(x)=
,试判断 g(x)的奇偶性并给出证明.
10
解析
103x-2y=103x=(10x)3=33=27,故选 C. 102y (10y)2 42 16
§2 指数幂的运算性质
刷能力
5.已知 ab=-5,则 a
A.2 5 C.-2 5
解析
b - +b
a
a - 的值是( B )
b
B.0
D.±2 5
由题意知 ab<0,a 故选 B.
b - +b
a
a - =a
2
6=
1
.故选
B.
2
64
3.1 指数函数的概念+ 3.2 指数函数的图象和性质
刷基础
4.[福建福州第三中学 2021 高一期中]以下关于函数 f(x)=2x 的说法正确的是( D ) A.f(mn)=f(m)f(n) B.f(mn)=f(m)+f(n) C.f(m+n)=f(m)+f(n) D.f(m)f(n)=f(m+n)
新课标人教版必修一指数函数及其性质课件(共17张PPT)

2 x 1 5的最大值为_______
a 2x a 2 例4:设函数f(x)= 为奇函数. x 2 1
求: (1)实数a的值; (2)用定义法判断f(x)在其定义域上的单调性.
课堂总结:
1:根式的概念与相关的结论
2:指数幂运算的推广:
整数
有理数
实数
3:指数的运算性质: 求值与化简(整体思想)
高中数学必修1同步辅导课程——指数函数及其性质
牢记底的限制;
a>0且 a 1
熟悉单调分类; a 1单增;0 a 1单减; 弄清值域变化; 掌握草图画法。 一撇一捺
高中数学必修1同步辅导课程——指数函数及其性质
典型题例:
例1:比较下列各题中两个值的大小: (1) 0.8 -0 . 1 < 0.8 -0 . 2
1 x 2 8 2 x (1) ( ) 3 3 解:原不等式可化为
3
x 2 8
3
2 x
∵ 函数 y=3x 在R上是增函数 ∴ - x2 + 8 > - 2x
解之得:- 4 < x < 2
∴ 原不等式的解集是(- 4, 2)
高中数学必修1同步辅导课程——指数函数及其性质
(2) a
x 2 2 x
解:原不等式可化为
1 x2 ( ) (a 0且a 1) a
a
x2 2x
a
x2
(1)若a>1,则原不等式等价于 x2 - 2x >- x2 ∵原不等式ห้องสมุดไป่ตู้解集为(-∞ ,0)∪(1,+∞ ) (2)若0<a<1,则原不等式等价于 x2 - 2x < -x2 ∴原不等式的解集为(0,1 )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
指数与指数函数
级级: 姓名: 学号: 得分:
一、选择题(每题5分,共40分)
1.(369a )4(639a )4等于( )
(A )a 16 (B )a 8 (C )a 4 (D )a 2
2.下列函数中,定义域为R 的是( )
(A )y=5x -21 (B )y=(3
1)1-x (C )y=1)2
1
(-x (D )y=x 21- 3.已知0<a<1,b<-1,则函数y=a x
+b 的图像必定不经过( )
(A)第一象限 (B)第二象限
(C)第三象限 (D)第四象限
4.函数f (x )=a x -b 的图像如图,其中a ,b 为常数,则下列结论正确的是( )
A .a >1,b <0
B .a >1,b >0
C .0<a <1,b >0
D .0<a <1,b <0 5.设5.1344.029.01)2
1(,8,4-===y y y ,则( ) A .3y >1y >2y
B .2y >1y >3y
C .1y >2y >3y
D .1y >3y >2y 6.若函数1-+=b a y x (10≠>a a 且)的图象经过二、三、四象限,则一定有
A.10<<a 且0>b
B.1>a 且0>b
C.10<<a 且0<b
D.1>a 且0<b 7.在下列图象中,二次函数c bx ax y ++=2与函数x a
b
y )(=的图象可能是( )
8.指数函数(1)x a y =,(2)x b y =,(3)x c y =,(4)x
d y =的图象如下,则d c b a ,,,与1大小关系是
y
A.a <b <1<c <d
B.b <a <1<d <c
C.1<a <b <c <d
D.a <b <1<d <c
二、填空题(每题5分,共30分)
10.已知函数()14x f x a
-=+的图像恒过定点P ,则点P 的坐标是___________ 11.方程96370x x -⋅-=的解是_________
12.指数函数x a x f )1()(2-=是减函数,则实数a 的取值范围是 . 13.函数221x x y a a =+-(0>a 且1≠a )在区间]1,1[-上的最大值为14,a 的值是
14.计算:412121325.0320625.0])32.0()02.0()008.0()9
45()833[(÷⨯÷+---_______________ 15.若()10x f x =,则()3f =————————
三、解答题(16/17/19题各5分,18题15分,共30分)
16.设关于x 的方程02
41=--+b x x 有实数解,求实数b 的取值范围。
),1[+∞-
17.设0<a<1,解关于x 的不等式a
1322+-x x >a 522-+x x .
18.已知2()()1
x x a f x a a a -=-- (0>a 且1≠a ). (1)判断)(x f 的奇偶性;(2)讨论)(x f 的单调性;(3)当]1,1[-∈x 时,b x f ≥)(恒成立,求b 的取值范围。
19.若函数4323x x
y =-+的值域为[]1,7,试确定x 的取值范围。
