数字信号处理之DCT变换公式
DCT算法的相关知识与原理

DCT算法的相关知识与原理DCT(Discrete Cosine Transform,离散余弦变换)是一种基于频域的信号处理技术,广泛应用于图像和音频压缩、数据压缩和信号处理等领域。
其主要原理是将时域的一段信号变换为频域的一组余弦系数,通过保留部分重要系数来减少信号的冗余信息,从而实现信号的压缩和重建。
正变换的具体步骤如下:1.将时域信号分为若干个相同大小的块,并在每个块的边缘上添加一个边界。
2.对每个块进行离散余弦变换,并计算出对应的余弦系数矩阵。
3.对余弦系数矩阵进行量化处理,将其舍入为整数值。
量化矩阵是用于将高频部分的系数舍弃,从而减少冗余信息的重要步骤。
4.保留部分重要的系数,舍弃剩余的系数。
常用的方法是选择一个适当的阈值来判断系数的重要性,将小于阈值的系数置为零。
5.将量化后的系数按照其中一种编码方式进行编码,以便存储和传输。
常用的编码方式包括霍夫曼编码和算术编码等。
逆变换则是正变换的逆过程,用于将频域信号恢复为时域信号。
1.将编码后的系数解码,恢复为量化前的系数。
2.逆量化步骤是将量化后的系数乘以量化矩阵,以恢复出原始大小的系数矩阵。
3.对逆量化后的系数矩阵进行离散余弦逆变换,得到逆变换后的时域信号。
4.去掉边界,得到最终的还原信号。
DCT算法主要应用在图像和音频压缩中。
在图像压缩中,通常将图像分为若干个8x8的图像块,并对每个块进行DCT变换。
由于图像的高频成分较低频成分所占比例较小,因此可以通过量化和舍弃高频系数来减少数据量。
在音频压缩中,也可以将音频信号分帧处理,并使用DCT变换将时域信号转换为频域系数,之后再通过量化和编码来减少数据量。
总之,DCT算法通过将时域信号转换为频域系数,并舍弃冗余信息来实现信号的压缩。
其核心思想是通过保留重要的低频成分来表示原始信号,在不失真的情况下减少信号的体积,并在需要时进行解码和还原。
DCT算法在图像和音频压缩领域有着广泛的应用,是实现高效数据压缩和传输的重要技术。
DCT--离散余弦变换

K. R. Rao and P. Yip, 离散余弦变换 : 算法、优点和应用 (Discrete Cosine Transform: Algorithms, Advantages, Applications) (Academic Press, Boston, 1990).
A. V. Oppenheim, R. W. Schafer, and J. R. Buck, 时间离散信号处理 (Discrete-Time Signal Processing), second edition (Prentice-Hall, New Jersey, 1999).
mhtml:file://C:\Documents%20and%20Settings\Administrator\桌面\FAT3... 2010-10-22
Hale Waihona Puke 反变换DCT-I的反变换是把DCT-I乘以系数
。 DCT-IV的反变换是把DCT-IV乘以系数 。
DCT-II的反变换是把DCT-III乘以系数 ,反之亦然。
离散余弦变换
维基百科,自由的百科全书
离散余弦变换(DCT for Discrete Cosine Transform)是与傅里叶变换相关的一 种变换,它类似于离散傅里叶变换 (DFT for Discrete Fourier Transform),但 是只使用实数。离散余弦变换相当于 一个长度大概是它两倍的离散傅里叶 变换,这个离散傅里叶变换是对一个 实偶函数进行的(因为一个实偶函数的 傅里叶变换仍然是一个实偶函数),在 有些变形里面需要将输入或者输出的 位置移动半个单位(DCT有8种标准类 型,其中4种是常见的)。
和离散傅里叶变换类似,变化前面的归一化系数仅仅是常规而已,改变这个系数并不改变变
DCT变换
DCT变换的全称是离散余弦变换(Discrete Cosine Transform),离散余弦变换相当于一个长度大概是它两倍的离散傅里叶变换,这个离散傅里叶变换是对一个实偶函数进行的。
通过数字信号处理的学习我们知道实函数的傅立叶变换获得的频谱大多是复数,而偶函数的傅立叶变换结果是实函数。
以此为基础,使信号函数成为偶函数,去掉频谱函数的虚部,是余弦变换的特点之一。
要实现DCT有多种方法,一种可以采用DSP处理器,但这是牺牲了速度换来设计的灵活;一种是采用ASIC技术,这使得速度较快但灵活性又不好;还有一种就是用FPGA(可编程逻辑器件),利用这项技术既能加快速度又能带来设计的灵活性。
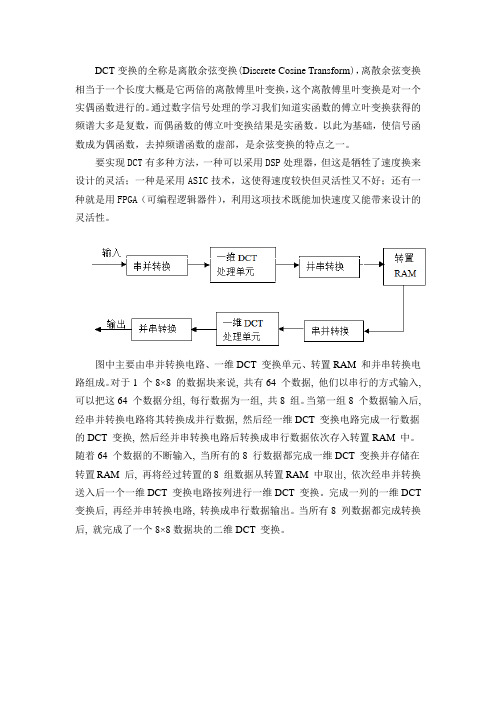
图中主要由串并转换电路、一维DCT 变换单元、转置RAM 和并串转换电路组成。
对于1 个8×8 的数据块来说, 共有64 个数据, 他们以串行的方式输入, 可以把这64 个数据分组, 每行数据为一组, 共8 组。
当第一组8 个数据输入后, 经串并转换电路将其转换成并行数据, 然后经一维DCT 变换电路完成一行数据的DCT 变换, 然后经并串转换电路后转换成串行数据依次存入转置RAM 中。
随着64 个数据的不断输入, 当所有的8 行数据都完成一维DCT 变换并存储在转置RAM 后, 再将经过转置的8 组数据从转置RAM 中取出, 依次经串并转换送入后一个一维DCT 变换电路按列进行一维DCT 变换。
完成一列的一维DCT 变换后, 再经并串转换电路, 转换成串行数据输出。
当所有8 列数据都完成转换后, 就完成了一个8×8数据块的二维DCT 变换。
离散余弦变换(DCT)

离散余弦变换(DCT)DCT变换、DCT反变换、分块DCT变换⼀、引⾔DCT变换的全称是离散余弦变换(Discrete Cosine Transform),主要⽤于将数据或图像的压缩,能够将空域的信号转换到频域上,具有良好的去相关性的性能。
DCT变换本⾝是⽆损的,但是在图像编码等领域给接下来的量化、哈弗曼编码等创造了很好的条件,同时,由于DCT变换时对称的,所以,我们可以在量化编码后利⽤DCT反变换,在接收端恢复原始的图像信息。
DCT变换在当前的图像分析已经压缩领域有着极为⼴⼤的⽤途,我们常见的JPEG静态图像编码以及MJPEG、MPEG动态编码等标准中都使⽤了DCT变换。
⼆、⼀维DCT变换⼀维DCT变换时⼆维DCT变换的基础,所以我们先来讨论下⼀维DCT变换。
⼀维DCT变换共有8种形式,其中最常⽤的是第⼆种形式,由于其运算简单、适⽤范围⼴。
我们在这⾥只讨论这种形式,其表达式如下:其中,f(i)为原始的信号,F(u)是DCT变换后的系数,N为原始信号的点数,c(u)可以认为是⼀个补偿系数,可以使DCT变换矩阵为正交矩阵。
三、⼆维DCT变换⼆维DCT变换其实是在⼀维DCT变换的基础上在做了⼀次DCT变换,其公式如下:由公式我们可以看出,上⾯只讨论了⼆维图像数据为⽅阵的情况,在实际应⽤中,如果不是⽅阵的数据⼀般都是补齐之后再做变换的,重构之后可以去掉补齐的部分,得到原始的图像信息,这个尝试⼀下,应该⽐较容易理解。
另外,由于DCT变换⾼度的对称性,在使⽤Matlab进⾏相关的运算时,我们可以使⽤更简单的矩阵处理⽅式:接下来利⽤Matlab对这个过程进⾏仿真处理:1clear;2clc;3 X=round(rand(4)*100) %产⽣随机矩阵4 A=zeros(4);5for i=0:36for j=0:37if i==08 a=sqrt(1/4);9else10 a=sqrt(2/4);11 end12 A(i+1,j+1)=a*cos(pi*(j+0.5)*i/4);13 end14end15 Y=A*X*A' %DCT变换16 YY=dct2(X) %Matlab⾃带的dct变换运⾏结果为:1 X =23 42 66 68 664 92 4 76 175 79 85 74 716 96 93 39 3789 Y =1011 242.7500 48.4317 -9.7500 23.505212 -12.6428 -54.0659 7.4278 22.795013 -6.2500 10.7158 -19.7500 -38.804614 40.6852 -38.7050 -11.4653 -45.9341151617 YY =1819 242.7500 48.4317 -9.7500 23.505220 -12.6428 -54.0659 7.4278 22.795021 -6.2500 10.7158 -19.7500 -38.804622 40.6852 -38.7050 -11.4653 -45.9341由上⾯的结果我们可以看出,我们采⽤的公式的⽅法和Matlab⾃带的dct变化⽅法结果是⼀致的,所以验证了我们⽅法的正确性。
简单描述离散余弦变换dct基本原理

简单描述离散余弦变换dct基本原理
离散余弦变换(Discrete Cosine Transform,DCT)是一种常用的信号处理方法,它将时序信号或图像转换为频域信号或图像,常见于视频压缩、音频压缩、图像压缩等领域。
DCT 可以将一个长度为N 的实数序列转换为另一个长度为N 的实数序列,这个过程类似于傅里叶变换,但是更适用于实数信号的处理。
DCT 的基本原理是将原始信号表示为余弦函数的线性组合,通过将原始信号转换为一组余弦基函数来实现。
离散余弦变换使用的基函数是从正余弦函数中选取出来的一组奇偶性相同的余弦函数,它们的频率依次递增,形成一个正交基。
这组基函数的选择使得信号的变换能够更好地适应实际情况,因为大多数实际信号都是以相对于它们的平均值为中心的,这与余弦函数的性质非常相似。
DCT 变换的过程可以通过矩阵乘法来实现,这个矩阵称为变换矩阵。
由于DCT 变换的基函数是正交的,所以变换矩阵是一个正交矩阵,它的逆矩阵等于其转置矩阵,因此,DCT 变换是可逆的,可以通过对变换后的频域信号进行逆变换,恢复原始信号。
总之,离散余弦变换在时域和频域之间建立了一种转换关系,它通过将原始信号表示为一组余弦基函数的线性组合来实现。
离散余弦变换是一种常用的信号处理方法,在压缩领域、音频领域、图像领域等方面都有广泛的应用。
dct 变换 原理

dct 变换原理DCT变换原理DCT(Discrete Cosine Transform,离散余弦变换)是一种常用的信号处理技术,广泛应用于图像、音频和视频等领域。
它通过将输入信号分解为一系列余弦函数的加权和来表示,同时保留了原始信号的主要特征。
本文将介绍DCT变换的原理及其应用。
一、DCT变换的原理DCT变换的基本思想是将输入的离散信号分解为一系列具有不同频率的余弦函数的加权和。
DCT变换可以将信号从时域转换到频域,通过分析不同频率分量的能量分布,可以提取信号的主要特征。
DCT 变换的公式如下:X(k) = 2/N * Σ[n=0 to N-1] x(n) * cos(π/N * (n + 0.5) * k)其中,x(n)表示输入信号的离散采样值,N表示采样点数,X(k)表示变换后的频域系数,k表示频域的索引。
DCT变换可以分为一维和二维变换。
一维DCT变换用于处理一维信号,如音频;而二维DCT变换用于处理二维信号,如图像。
二、DCT变换的应用DCT变换在图像、音频和视频等领域有广泛的应用。
以下分别介绍其在这些领域的应用。
1. 图像压缩DCT变换在图像压缩中起到了重要作用。
在JPEG图像压缩中,图像先被分成8x8的图像块,然后对每个图像块进行DCT变换,将图像从时域转换到频域。
通过保留主要的频域系数,可以实现对图像的高效压缩。
2. 音频压缩DCT变换在音频压缩中也有广泛应用。
在MP3音频压缩中,音频信号被分成一系列短时窗口,然后对每个窗口的音频信号进行DCT变换。
通过量化和编码DCT系数,可以实现对音频信号的高比特率压缩。
3. 视频压缩DCT变换在视频压缩中也发挥着重要作用。
在H.264视频编码中,视频帧被分成一系列宏块,然后对每个宏块的亮度和色度分量进行DCT变换。
通过压缩和编码DCT系数,可以实现对视频的高效压缩。
除了压缩应用外,DCT变换还可以用于信号去噪、特征提取、模式识别等领域。
例如,在图像去噪中,通过DCT变换将图像从时域转换到频域,然后滤除高频噪声,最后再通过逆DCT变换将图像恢复到时域。
javadct_DCT(离散余弦变换)算法原理和源码

javadct_DCT(离散余弦变换)算法原理和源码离散余弦变换(Discrete Cosine Transform,简称DCT)是一种常用的信号处理技术,广泛应用于图像和音频压缩领域。
DCT将输入的离散信号转换为一组系数,这些系数代表了信号的频域特征。
在压缩领域中,DCT可将信号从时域转换为频域,通过舍弃一些高频系数实现信号的压缩。
DCT算法的原理基于傅里叶变换(Fourier Transform)的思想,将时域信号转换为频域信号。
然而,与傅里叶变换相比,DCT更适合处理实数信号,因为它只使用实数运算,而不需要复数运算。
DCT算法的一般步骤如下:1.将输入的离散信号分为若干个块,每个块包含N个采样点。
2.对每个块进行预处理,例如减去均值。
3.对每个块进行DCT变换。
4.根据需要舍弃一些高频系数。
5.对经过舍弃的系数进行逆DCT变换,恢复原始信号。
下面是一个简单的离散余弦变换的Python实现:```pythonimport numpy as npdef dct_transform(signal):N = len(signal)dct_coef = np.zeros(N)for k in range(N):sum = 0for n in range(N):sum += signal[n] * np.cos((np.pi/N)*(n+0.5)*k)dct_coef[k] = sumreturn dct_coefdef idct_transform(dct_coef):N = len(dct_coef)signal = np.zeros(N)for n in range(N):sum = 0for k in range(N):sum += dct_coef[k] * np.cos((np.pi/N)*(n+0.5)*k)signal[n] = sum / Nreturn signal```以上是一个简单的DCT变换和逆变换的实现,其中`dct_transform`函数接受输入信号并返回DCT系数,`idct_transform`函数接受DCT系数并返回恢复的原始信号。
Chen快速DCT实现

Chen的快速DCT算法一、原始DCT变换原理1、一维DCT变换定义对于离散函数f(j),j=0,1…,N-1,(N=2m,m≥2)一维离散余弦变换(1-D DCT)定义为:F(k)=2c(k)N ∑f(j)cos[(2j+1)kπ2N]N−1j=0;K=0,1,…,N-1其逆变换公式(1-D IDCT)为:f(j)=∑F(k)cos[(2j+1)kπ2N ]N−1k=0; (1)j=0,1,…,N-1其中:c(k)=√2 当k=01 ,当k≠0通过直接计算,当N=8时,利用公式(4-1)进行DCT变化需要64次乘法和56次加法运算。
2、二维DCT变换定义一维离散余弦变换的定义可推广到二维的情形,对于离散函数f(i,j),i=0,1,…,N-1;j=0,1,…,M-1, 二维离散余弦变换(2-D DCT)定义为:F(u,v)=√MN∑f(i,j)M−1j=0cos[(2i+1)uπ2N]N−1i=0cos[(2j+1)vπ2N]; (2)u=0,1,…N-1;v=0,1,…,M-1,其中:c(u),c(v)=√2 当u,v=01 ,其他取N=M=8时,利用公式(4-3)进行直接计算需要4096次乘法和3584次加法,通常利用DCT的可分解的性质,先进行8行一维DCT变换,在进行8列一维DCT变换,可将计算量减少为直接计算的1/4,需要1024次乘法和896次加法。
二、Chen的快速DCT原理离散余弦变换(DCT for Discrete Cosine Transform)是与傅立叶变换相关的一种变换,它类似于离散傅立叶变换(DFT for Discrete Fourier Transform),但是只使用实数。
离散余弦变换相当于一个长度大概是它两倍的离散傅立叶变换,这个离散傅立叶变换是对一个实偶函数进行的(因为一个实偶函数的傅立叶变换仍然是一个实偶函数),在有些变形里面需要将输入或者输出的位置移动半个单位(DCT有8种标准类型,其中4种是常见的)。
