高斯白噪声地matlab实现
MATLAB仿真实现LMS和RLS算法
MATLAB 仿真实现LMS 和RLS 算法题目：序列x(n)有AR （2）模型产生：)()2()1()(21n w n x a n x a n x +-+-=，w(n)是均值为0、方差为1的高斯白噪声序列。
.7.0,4.121-==a a 用LMS 算法和RLS 算法来估计模型参数21,a a 。
按照课本第三章63页的要求，仿真实现LMS 算法和RLS 算法，比较两种算法的权值收敛速度，并对比不同u 值对LMS 算法以及λ值对RLS 算法的影响。
解答：1 数据模型（1）高斯白噪声用用randn 函数产生均值为0、方差为1的标准正态分布随机矩阵来实现。
随后的产生的信号用题目中的AR （2)模型产生，激励源是之前产生的高斯白噪声。
（2）信号点数这里取为2000，用2000个信号来估计滤波器系数。
（3）分别取3个不同的u 、λ值来分析对不同算法对收敛效果的影响。
其中u=[0.001,0.003,0.006]，lam=[1,0.98,0.94]。
2 算法模型2.1自适应算法的基本原理自适应算法的基本信号关系如下图所示：图 1 自适应滤波器框图输入信号x(n)通过参数可调的数字滤波器后产生输出信号y(n)，将其与参考信号d(n)进行比较，形成误差信号e(n)。
e(n)通过某种自适应算法对滤波器参数进行调整，最终是e(n)的均方值最小。
当误差信号e(n)的均方误差达到最小的时候，可以证明信号y(n)是信号d(n)的最佳估计。
2.2 LMS 算法简介LMS 算法采用平方误差最小的原则代替最小均方误差最小的原则，信号基本关系如下：1()()()()()()(1)()2()()(0,1,2,....1)N i i i y n w n x n i e n d n y n w n w n e n x n i i N μ-=-=-+=+-=-∑ 写成矩阵型式为：()()()()()()(1)()2()()T y n W n X n e n d n y n W n W n e n X n μ==-+=+ 式中，W(n) 为n 时刻自适应滤波器的权矢量，011()[(),(),....()]TN W n w n w n w n -=，N 为自适应滤波器的阶数；X( n) 为n 时刻自适应滤波器的参考输入矢量，由最近N 个信号采样值构成，()[(),(1),....(1)]TX n x n x n x n N =--+；d ( n) 是期望的输出值；e ( n) 为自适应滤波器的输出误差调节信号(简称失调信号) ；μ是控制自适应速度与稳定性的增益常数，又叫收敛因子或步长因子。
matlab 正弦波 高斯白噪声 均匀白噪声 功率谱密度 自相关函数(word文档良心出品)
现代通信原理作业一姓名：张英伟学号：133320085208036 班级：13级理工部3班利用matlab完成：●产生正弦波信号、均匀白噪声以及高斯白噪声并分别将两种噪声叠加到正弦波信号上，绘出波形。
●分别求取均匀白噪声序列和高斯白噪声序列的自相关及功率谱密度，绘出波形。
一、白噪声区别及产生方法1、定义：均匀白噪声：噪声的幅度分布服从均匀分布，功率谱密度在整个频域内均匀分布的噪声。
高斯白噪声：噪声的幅度分布服从正态分布，功率谱密度在整个频域内均匀分布的噪声。
2、matlab仿真函数：rand函数默认产生是区间在[0,1]的随机数，这里需要利用公式：z2=a+(b-(a))*rand(m,n)............（公式1）randn函数默认产生均值是0、方差是1的随机序列，所以可以用其来产生均值为0、方差为1的正态分布白噪声，即N(0，12)。
利用公式：z1=a+b*randn(1,n).................（公式2）可以产生均值为a，方差为b2 高斯白噪声，即N(a，b2)。
二、自相关函数与功率谱密度之间的关系1、功率谱密度：每单位频率波携带的功率，这被称为信号的功率谱密度。
2、自相关函数：描述随机信号X(t)在任意两个不同时刻t1，t2的取值之间的相关程度。
3、维纳-辛钦定理：由于平均值不为零的信号不是平方可积的，所以在这种情况下就没有傅里叶变换。
幸运的是维纳-辛钦定理提供了一个简单的替换方法，如果信号可以看作是平稳随机过程，那么功率谱密度就是信号自相关函数的傅里叶变换。
4、平稳随机过程：是在固定时间和位置的概率分布与所有时间和位置的概率分布相同的随机过程。
（就是指得仅一个随机过程，中途没有变成另外一个统计特性的随机过程）二、源代码及仿真结果1、正弦波x=(0:0.01:2); %采样频率100Hzy1=sin(10*pi*x); %产生频率5Hz的sin函数plot(x,y1,'b');2、高斯白噪声+正弦波z1=0.1*randn(1,201); %产生方差N（0，0.12）高斯白噪声（b=0.01/0.1/1）plot(x,z1,'b');y2=y1+z1; %叠加高斯白噪声的正弦波plot(x,y2,'b');3、均匀白噪声+正弦波z2=-.3+.6*rand(1,201); %产生-0.3到0.3的均匀白噪声plot(x,z2,'b');y3=y1+z2; %叠加均匀白噪声的正弦波plot(x,y3,'b');4、高斯白噪声序列自相关函数及功率谱密度z1=0.1*randn(1,201); %产生方差N（0，0.12）高斯白噪声[r1,lags]=xcorr(z1); %自相关函数的估计plot(lags,r1);f1=fft(r1);f2=fftshift(f1); %频谱校正l1=(0:length(f2)-1)*200/length(f2)-100; %功率谱密度x轴y4=abs(f2);plot(l1,y4);5、均匀白噪声序列自相关函数及功率谱密度z2=-.3+.6*rand(1,201); %产生-0.3到0.3的均匀白噪声[r2,lags]=xcorr(z2); %自相关函数的估计plot(lags,r2);f3=fft(r2);f4=fftshift(f3); %频谱校正l2=(0:length(f4)-1)*200/length(f4)-100; %功率谱密度x轴y5=abs(f4);plot(l2,y5);。
产生高斯白噪声和有色噪声的MATLAB程序
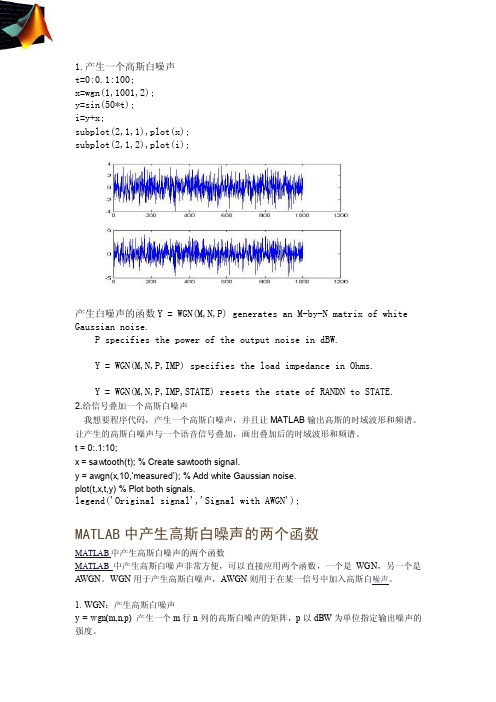
1.产生一个高斯白噪声t=0:0.1:100;x=wgn(1,1001,2);y=sin(50*t);i=y+x;subplot(2,1,1),plot(x);subplot(2,1,2),plot(i);产生白噪声的函数Y = WGN(M,N,P) generates an M-by-N matrix of white Gaussian noise.P specifies the power of the output noise in dBW.Y = WGN(M,N,P,IMP) specifies the load impedance in Ohms.Y = WGN(M,N,P,IMP,STATE) resets the state of RANDN to STATE.2.给信号叠加一个高斯白噪声我想要程序代码，产生一个高斯白噪声，并且让MATLAB输出高斯的时域波形和频谱。
让产生的高斯白噪声与一个语音信号叠加，画出叠加后的时域波形和频谱。
t = 0:.1:10;x = sawtooth(t); % Create sawtooth signal.y = awgn(x,10,'measured'); % Add white Gaussian noise.plot(t,x,t,y) % Plot both signals.legend('Original signal','Signal with AWGN');MATLAB中产生高斯白噪声的两个函数MATLAB中产生高斯白噪声的两个函数MATLAB中产生高斯白噪声非常方便，可以直接应用两个函数，一个是WGN，另一个是A WGN。
WGN用于产生高斯白噪声，AWGN则用于在某一信号中加入高斯白噪声。
1. WGN：产生高斯白噪声y = wgn(m,n,p) 产生一个m行n列的高斯白噪声的矩阵，p以dBW为单位指定输出噪声的强度。
基于MATLAB的高斯白噪声信道分析报告
基于MATLAB的⾼斯⽩噪声信道分析报告基于matlab⾼斯⽩噪声信道分析系统的设计××（陕西理⼯学院物理与电信⼯程学院通信⼯程专业1202班，陕西汉中 723003）指导教师：吴燕[摘要] MATLAB 是⼀种⽤于算法开发、数据可视化、数据分析以及数值计算的⾼级技术计算语⾔和交互式环境。
本⽂在matlab的环境下构建了BFSK在⾼斯⽩噪声信道中传输的系统模型，通过simulink程序仿真，研究系统的误码率与信道质量的关系，找到在⾼斯⽩噪声信道上传输的最⼤信噪⽐及所需发射功率和调制频率，从⽽得出该系统在⾼斯⽩噪声信道中的最佳传输性能。
[关键词] MATLAB；⾼斯⽩噪声；信道分析；simulink仿真Design and production of the Gauss white noise channel analysis system based on MATLAB××(Grade 2012,Class 2,Major of Communication Engineering,School of Physics and Telecommunication Engineering of Shaanxi University of Technology,Hanzhong 723003,Shaanxi)Tutor: Wu YanAbstract: MATLAB is a high-level technical computing language and interactive environment for the development of algorithms, data visualization, data analysis and numerical calculation. This article in the matlab environment build BFSK in AWGN channel model simulation,by running simulation the program on the system of quality of error rate and channel relationships,found in AWGN channel transport of maximum signal-to-noise ratio and the desired transmitter power.Key words:MA TLAB; Gauss white noise; channel analysis; Simulink simulation⽬录1.绪论 .................................... 错误！未定义书签。
matlab模拟地震波信号代码
地震是地球表面因地下岩石断裂而引起的振动现象，其产生的地震波信号对于地震学和工程领域具有重要意义。
通过模拟地震波信号，可以更好地了解地震的特性和规律，有助于预测地震的发生以及减轻地震带来的损失。
MATLAB作为一种强大的计算软件，具有丰富的信号处理工具包，可以用来模拟地震波信号，为地震研究和工程应用提供支持。
二、MATLAB模拟地震波信号的基本原理1. 地震波信号的生成地震波信号是由地壳中的地震源产生，并向四周传播所形成的振动信号。
地震波信号通常包括P波、S波和地表波等成分，具有复杂的波形特征。
2. MATLAB的信号处理工具MATLAB提供了丰富的信号处理工具，包括信号生成、滤波、傅里叶变换等功能。
利用这些工具，可以对地震波信号进行模拟和分析，从而更好地理解地震现象。
三、MATLAB模拟地震波信号的代码实现在MATLAB中，可以编写代码来实现地震波信号的模拟。
以下是一段简单的MATLAB代码示例，用于生成地震波信号的模拟：定义地震波信号的参数Fs = 1000; 采样频率t = 0:1/Fs:1; 时间范围f = 5; 地震波信号的频率生成地震波信号x = sin(2*pi*f*t); 此处以正弦波作为简单示例绘制地震波信号plot(t,x);xlabel('时间(s)');ylabel('振幅');title('地震波信号模拟');```以上代码示例中，首先定义了地震波信号的采样频率、时间范围和频率等参数，然后利用MATLAB的信号生成函数生成了一个简单的正弦波地震波信号，并使用plot函数绘制了该信号的波形图像。
四、MATLAB模拟地震波信号的应用1. 地震学研究利用MATLAB模拟地震波信号，可以更好地研究地震波信号的特性和传播规律，有助于深入理解地震的机制和地球的内部结构，为地震学的研究提供支持。
2. 地震工程应用地震波信号的模拟对于地震工程具有重要意义，可以用于评估建筑物和结构在地震作用下的响应情况，为建筑物的抗震设计和地震灾害预防提供重要参考。
matlab高斯函数信号
Matlab高斯函数信号引言高斯函数是数学中常见的一种连续函数，它在很多领域有广泛的应用。
在信号处理中，高斯函数信号常被用来模拟各种现象，如声音、光线等。
Matlab作为一种强大的数学软件，提供了丰富的工具和函数库来生成和处理高斯函数信号。
本文将介绍如何使用Matlab来生成和处理高斯函数信号。
生成高斯函数信号为了生成高斯函数信号，我们首先需要了解高斯函数的数学表达式。
高斯函数的一般形式为：其中，是高斯函数的均值，是高斯函数的标准差。
在Matlab中，我们可以使用normpdf函数来生成高斯函数信号。
下面是一个示例：% 生成高斯函数信号x = -10:0.1:10; % x轴范围mu = 0; % 均值sigma = 1; % 标准差y = normpdf(x, mu, sigma); % 使用normpdf函数生成高斯函数信号% 绘制高斯函数信号plot(x, y);title('高斯函数信号');xlabel('x');ylabel('y');以上代码将生成一个以0为均值、1为标准差的高斯函数信号，并将其绘制出来。
高斯函数信号的特点高斯函数信号具有以下几个重要的特点：对称性高斯函数信号关于均值点是对称的，即高斯函数在处取得最大值，并且在均值的两侧按对称分布。
单峰性高斯函数信号只有一个峰值，峰值对应于均值点。
一阶矩和二阶矩高斯函数信号的均值和方差分别等于高斯函数的均值和方差。
这两个参数描述了高斯函数信号的位置和形状。
高斯函数信号的应用高斯函数信号在信号处理领域有广泛的应用。
下面介绍几个常见的应用场景：窗函数在信号处理中，窗函数是一种用来分析和处理有限时间信号的方法。
高斯函数信号常被用作窗函数，因为它具有良好的抗尖峰和滚降特性。
模糊滤波在图像处理中，模糊滤波是一种常用的图像处理技术。
高斯函数信号常被用来生成模糊核，通过与原始图像进行卷积操作，可以实现图像的模糊效果。
qpsk、bpsk蒙特卡洛仿真matlab代码
qpsk、bpsk的蒙特卡洛仿真是一种用于测试和验证通信系统性能的重要工具。
通过模拟大量的随机输入数据，并对系统进行多次仿真运算，可以对系统的性能进行全面评估，包括误码率、信噪比要求等。
在matlab中，我们可以通过编写相应的仿真代码来实现qpsk、bpsk 的蒙特卡洛仿真。
下面将分别介绍qpsk和bpsk的蒙特卡洛仿真matlab代码。
一、qpsk的蒙特卡洛仿真matlab代码1. 生成随机的qpsk调制信号我们需要生成一组随机的qpsk调制信号，可以使用randi函数生成随机整数序列，然后将其映射到qpsk符号点上。
2. 添加高斯白噪声在信号传输过程中，会受到各种干扰，其中最主要的干扰之一就是高斯白噪声。
我们可以使用randn函数生成高斯白噪声序列，然后与调制信号相加，模拟信号在传输过程中受到的噪声干扰。
3. 解调和判决接收端需要进行解调和判决操作，将接收到的信号重新映射到qpsk符号点上，并判断接收到的符号与发送的符号是否一致，从而判断是否发生误码。
4. 统计误码率通过多次仿真运算，记录错误判决的次数，从而可以计算出系统的误码率。
二、bpsk的蒙特卡洛仿真matlab代码1. 生成随机的bpsk调制信号与qpsk相似，我们需要先生成一组随机的bpsk调制信号，然后模拟信号传输过程中的噪声干扰。
2. 添加高斯白噪声同样使用randn函数生成高斯白噪声序列，与bpsk调制信号相加。
3. 解调和判决接收端对接收到的信号进行解调和判决，判断接收到的符号是否与发送的符号一致。
4. 统计误码率通过多次仿真运算，记录错误判决的次数，计算系统的误码率。
需要注意的是，在编写matlab代码时，要考虑到信号的长度、仿真次数、信噪比的范围等参数的选择，以及仿真结果的统计分析和可视化呈现。
qpsk、bpsk的蒙特卡洛仿真matlab代码可以通过以上步骤实现。
通过对系统性能进行全面评估，可以帮助工程师优化通信系统设计，提高系统的可靠性和稳定性。
噪声方差软解调matlab -回复
噪声方差软解调matlab -回复噪声方差软解调是一种常见的信号处理技术，广泛应用于通信、雷达、图像处理等领域。
在这篇文章中，我们将详细介绍噪声方差软解调的原理和实现方法，并使用MATLAB进行演示和实践。
一、噪声方差软解调原理在通信系统中，信号的传输过程中会受到各种噪声的干扰，这些噪声将导致信号的失真和误判。
噪声方差软解调是一种基于噪声方差估计的信号解调方法，通过对接收信号进行合适的滤波和处理，可以有效地减小噪声的影响，提高信号的恢复质量。
噪声方差软解调的原理可以简单地概括为以下几个步骤：1. 接收信号采样：从信道中接收到的模拟信号首先需要进行采样，将连续的模拟信号转换为离散的数字信号。
采样过程中，要根据信号的带宽和采样频率进行适当的选择，以避免信号信息的失真。
2. 解调器设计：根据所要解调的信号类型和性质，设计相应的解调器。
解调器可以是模拟电路或数字电路，其功能是将接收到的信号转换为原始信号。
对于噪声方差软解调而言，解调器通常包括滤波和信号处理等部分。
3. 滤波处理：在接收信号中，噪声是不可避免的。
为了减小噪声对信号的干扰，需要对接收信号进行滤波处理。
滤波的基本原理是利用滤波器抑制噪声频率分量，从而增强信号的有效部分。
噪声方差软解调中常用的滤波器有FIR滤波器和IIR滤波器等。
4. 噪声方差估计：在滤波处理后，噪声仍然存在。
为了更好地进行信号解调，需要对噪声进行估计和量化。
噪声方差估计是通过一定的统计方法来对噪声进行建模和估计，从而获取噪声的统计特性和参数。
5. 软解调：基于噪声方差估计的结果，进行软解调操作。
软解调通常采用最大似然估计（Maximum Likelihood Estimation,MLE）或最小均方误差（Minimum Mean Square Error,MMSE）等方法，以降低噪声对信号恢复的影响。
软解调可以通过调整解调器的参数来实现。
二、MATLAB实现噪声方差软解调在MATLAB中，可以使用一系列信号处理工具箱和函数来实现噪声方差软解调。
(word完整版)高斯白噪声的matlab实现
通信系统建模与仿真实验一、高斯白噪声的matlab 实现要求：样本点：100 1000标准差：0.2 2 10均值： 0 0.2白噪声如果噪声的功率谱密度在所有的频率上均为一常数，即)/(),(,)(0Hz W f n f P n +∞<<-∞=式中：0n 为常数，责成该噪声为白噪声，用)(t n 表示。
高斯白噪声的matlab实现1．样本点为1000、均值为0、标准差为0.2时，高斯白噪声分布为下图所示：程序如下所示：% White background noisclear allf = 1:1:1000;for i = 1:length(f)K = (0.2) * randn(1,1) - 0;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i));endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft));plot(ti,realx2)程序如下所示：% White background noisclear allf = 1:1:1000;for i = 1:length(f)K = (2) * randn(1,1) - 0;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i)); endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft)); plot(ti,realx2)程序如下所示：% White background noisclear allf = 1:1:1000;for i = 1:length(f)K = (10) * randn(1,1) - 0;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i)); endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft)); plot(ti,realx2)程序如下所示：% White background noisclear allf = 1:1:1000;for i = 1:length(f)K = (0.2) * randn(1,1) - 10;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i)); endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft)); plot(ti,realx2)程序如下所示：% White background noisclear allf = 1:1:1000;for i = 1:length(f)K = (2) * randn(1,1) - 10;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i)); endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft)); plot(ti,realx2)程序如下所示：% White background noisclear allf = 1:1:1000;for i = 1:length(f)K = (10) * randn(1,1) - 10;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i)); endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft)); plot(ti,realx2)程序如下所示：% White background noisclear allf = 1:1:100;for i = 1:length(f)K = (0.2) * randn(1,1) - 0;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i)); endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft)); plot(ti,realx2)程序如下所示：% White background noisclear allf = 1:1:100;for i = 1:length(f)K = (2) * randn(1,1) - 0;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i)); endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft)); plot(ti,realx2)程序如下所示：% White background noisclear allf = 1:1:100;for i = 1:length(f)K = (10) * randn(1,1) - 0;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i)); endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft)); plot(ti,realx2)程序如下所示：% White background noisclear allf = 1:1:100;for i = 1:length(f)K = (0.2) * randn(1,1) - 10;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i)); endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft)); plot(ti,realx2)程序如下所示：% White background noisclear allf = 1:1:100;for i = 1:length(f)K = (2) * randn(1,1) - 10;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i)); endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft)); plot(ti,realx2)程序如下所示：% White background noisclear allf = 1:1:100;for i = 1:length(f)K = (10) * randn(1,1) - 10;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i)); endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft)); plot(ti,realx2)。
matlab傅里叶变换滤除高斯白噪声
文章主题：matlab中使用傅里叶变换滤除高斯白噪声在这篇文章中，我将会从简单到复杂，由浅入深地探讨如何利用matlab中的傅里叶变换来滤除高斯白噪声。
我将会介绍基本的概念和原理，并给出具体的代码实现。
通过本文的阅读，你将能够全面、深刻理解如何运用傅里叶变换来处理高斯白噪声。
1. 傅里叶变换让我们简单了解一下傅里叶变换的基本原理。
傅里叶变换可以将一个信号从时域转换到频域，从而可以分析信号的频率成分。
在matlab中，我们可以利用fft函数来进行傅里叶变换的计算。
在处理高斯白噪声时，傅里叶变换可以帮助我们更好地理解信号的频谱特性。
2. 高斯白噪声接下来，让我们来了解一下高斯白噪声的特点。
高斯白噪声是一种在任意时刻具有相互独立、均值为零、方差为常数的随机信号。
在实际的信号处理中，由于各种原因，会产生一些背景噪声，其中就包括高斯白噪声。
如何滤除高斯白噪声成为了信号处理中的一个重要问题。
3. matlab中的傅里叶变换滤波在matlab中，我们可以利用傅里叶变换来对信号进行滤波处理，从而滤除信号中的高斯白噪声。
我们需要对信号进行傅里叶变换，然后利用滤波器来消除噪声成分，最后再进行逆变换将信号从频域转换回时域。
在此过程中，我们需要注意滤波器的选取，以及如何控制滤波器的参数来获得理想的滤波效果。
4. 代码实现让我们通过一个具体的例子来演示如何在matlab中利用傅里叶变换来滤除高斯白噪声。
我们需要生成一段包含高斯白噪声的信号，并对其进行傅里叶变换。
我们将设计一个滤波器，利用其频率特性来滤除噪声成分。
我们再将滤波后的信号进行逆变换，从而得到滤除高斯白噪声后的信号。
在代码中，我们将会逐步介绍每个步骤的具体实现。
5. 总结与展望通过本文的阅读，你应该能够全面、深刻地了解如何在matlab中利用傅里叶变换来滤除高斯白噪声。
我们从傅里叶变换的基本原理入手，介绍了高斯白噪声的特点，然后详细讨论了在matlab中的滤波实现。
加性高斯白噪声AWGN
加性⾼斯⽩噪声AWGN
加性⾼斯⽩噪声 AWGN(Additive White Gaussian Noise) 是最基本的噪声与⼲扰模型。
加性噪声：叠加在信号上的⼀种噪声，通常记为n(t)，⽽且⽆论有⽆信号，噪声n(t)都是始终存在的。
因此通常称它为加性噪声或者加性⼲扰。
⽩噪声：噪声的功率谱密度在所有的频率上均为⼀常数，则称这样的噪声为⽩噪声。
如果⽩噪声取值的概率分布服从⾼斯分布，则称这样的噪声为⾼斯⽩噪声。
Matlab中实现加性⾼斯⽩噪声：
y = awgn(x,SNR)
在信号x中加⼊⾼斯⽩噪声。
信噪⽐SNR以dB为单位。
x的强度假定为0dBW。
如果x是复数，就加⼊复噪声。
y = awgn(x,SNR,SIGPOWER)
如果SIGPOWER是数值，则其代表以dBW为单位的信号强度；如果SIGPOWER为'measured'，则函数将在加⼊噪声之前测定信号强度。
y = awgn(x,SNR,SIGPOWER,STATE)
重置RANDN的状态。
y = awgn(…,POWERTYPE)
指定SNR和SIGPOWER的单位。
POWERTYPE可以是'dB'或'linear'。
如果POWERTYPE是'dB'，那么SNR以dB为单位，⽽SIGPOWER以dBW为单位。
如果POWERTYPE是'linear'，那么SNR作为⽐值来度量，⽽SIGPOWER以⽡特为单位。
白噪声(matlab)
均匀分布的白噪声信号u(n),画出其波形，并检验其分布情况%-----------------------------------------------------------------% To test rand.m and to generate the white noise signal u(n)% with uniform distribution% 产生均匀分布的随机白噪信号,并观察数据分布的直方图%-----------------------------------------------------------------clear;N=50000;u=rand(1,N);u_mean=mean(u)power_u=var(u)subplot(211)plot(u(1:100));grid on;ylabel('u(n)')xlabel('n')subplot(212)hist(u,50);grid on;ylabel('histogram of u(n)')思考：如何产生一均匀分布、均值为0，功率为0.01的白噪声信号u(n)提示：u （n ）~[a ，b]上均匀分布，E （u ）= (a+b)/2, 12/)()(2a b u -=σ% to generate the white noise signal u(n) with uniform distribution% and power p;% 产生均匀分布的白噪信号，使均值为0，功率为p%-----------------------------------------------------------------clear;p=0.01;N=50000;u=rand(1,N);u=u-mean(u);a=sqrt(12*p);u1=u*a;power_u1=dot(u1,u1)/Nsubplot(211)plot(u1(1:200));grid on;ylabel('u(n)')xlabel('n')example2: 产生零均值功率0.1且服从高斯分布的白噪声%-----------------------------------------------------------------% to test randn.m and to generate the white noise signal u(n)% with Gaussian distribution and power p% 产生高斯分布的白噪信号，使功率为p，并观察数据分布的直方图%-----------------------------------------------------------------clear;p=0.1;N=500000;u=randn(1,N);a=sqrt(p)u=u*a;power_u=var(u)subplot(211)plot(u(1:200));grid on;ylabel('u(n)');xlabel('n')subplot(212)hist(u,50);grid on;ylabel('histogram of u(n)');example3: sinc信号%-----------------------------------------------------------------% to generate the sinc function.% 产生一sinc 函数；%-----------------------------------------------------------------clear;n=200;stept=4*pi/n;t=-2*pi:stept:2*pi;y=sinc(t);plot(t,y,t,zeros(size(t)));ylabel('sinc(t)');xlabel('t=-2*pi~2*pi');grid on;example4: chirp信号%-----------------------------------------------------------------% to test chirp.m and to generate the chirp signal x(t)% 产生一chirp 信号；% chirp(T0,F0,T1,F1):% T0: 信号的开始时间；F0:信号在T0时的瞬时频率，单位为Hz；% T1: 信号的结束时间；F1:信号在T1时的瞬时频率，单位为Hz；%-----------------------------------------------------------------clear;t=0:0.001:1;x=chirp(t,0,1,125);plot(t,x);ylabel('x(t)')xlabel('t')%-------------------------------------------------------------------------% to test specgram.m ：估计信号谱图（SFFT）%specgram（x，Nfft，Fs，window，Noverlap）%x-信号；Fs抽样频率（2），Nfft做FFT长度（256）, window窗函数（Hanning）%Noverlap：估计功率谱时每一段叠合长度（0）%-------------------------------------------------------------------------clear;t=0:0.001:1.024-.001;N=1024;% 得到两个Chirp 信号，并相加；y1=chirp(t,0,1,350);y2=chirp(t,350,1,0);y=y1+y2;subplot(211);plot(t,y1);ylabel(' Chirp signal y1')% 求两个Chirp 信号和的短时傅里叶变换；[S,F,T]=specgram(y,127,1,hanning(127),126);subplot(212);surf(T/1000,F,abs(S).^2)view(-80,30);shading flat;colormap(cool);xlabel('Time')ylabel('Frequency')zlabel('spectrogram')还有diric信号（周期SINC）gauspuls(高斯信号)pulstran(脉冲串信号)tripuls三角波脉冲信号example5:线性卷积%-----------------------------------------------------------------% to test conv.m% 计算两个序列的线性卷积；%-----------------------------------------------------------------clear;N=5;M=6;L=N+M-1;x=[1,2,3,4,5];h=[6,2,3,6,4,2];y=conv(x,h);nx=0:N-1;nh=0:M-1;ny=0:L-1;subplot(231);stem(nx,x,'.k');xlabel('n');ylabel('x(n)');grid on;subplot(232);stem(nh,h,'.k');xlabel('n');ylabel('h(n)');grid on;subplot(233);stem(ny,y,'.k');xlabel('n');ylabel('y(n)');grid on;思考：设信号x(n)由正弦信号加均值为0白噪声所组成，正弦信号幅度为1，白噪声方差为1 SNR = 10LG(PS/PU) = -3dB,试分析信号；%-----------------------------------------------------------------% to test xcorr.m% 求两个序列的互相关函数，或一个序列的自相关函数；%-----------------------------------------------------------------clear;N=500;p1=1;p2=0.1;f=1/8;Mlag=50;u=randn(1,N);n=[0:N-1];s=sin(2*pi*f*n);% 混有高斯白噪的正弦信号的自相关u1=u*sqrt(p1);x1=u1(1:N)+s;rx1=xcorr(x1,Mlag,'biased');subplot(221);plot(x1(1:Mlag));xlabel('n');ylabel('x1(n)');grid on;subplot(223);plot((-Mlag:Mlag),rx1);grid on;xlabel('m');ylabel('rx1(m)');% 高斯白噪功率由原来的p1减少为p2，再观察混合信号的自相关u2=u*sqrt(p2);x2=u2(1:N)+s;rx2=xcorr(x2,Mlag,'biased');subplot(222);plot(x2(1:Mlag));xlabel('n');ylabel('x2(n)');grid on;subplot(224);plot((-Mlag:Mlag),rx2);grid on;xlabel('m');ylabel('rx2(m)');用乘同余法产生(见光盘FLch2bzsheg2.m)①编程如下：A=6; x0=1; M=255; f=2; N=100；%初始化；x0=1; M=255;for k=1: N %乘同余法递推100次；x2=A*x0; %分别用x2和x0表示x i+1和x i-1；x1=mod (x2,M); %取x2存储器的数除以M的余数放x1（x i）中；v1=x1/256; %将x1存储器中的数除以256得到小于1的随机数放v1中；）减去0.5再乘以存储器f中的系数，存放在v(:,k)=(v1-0.5 )*f; %将v1中的数（i矩阵存储器v的第k列中，v(:,k)表示行不变、列随递推循环次数变化；x0=x1; % x i-1= x i；v0=v1;end %递推100次结束；v2=v %该语句后无‘；’，实现矩阵存储器v中随机数放在v2中，且可直接显示在MATLAB的window中；k1=k;%grapher %以下是绘图程序；k=1:k1;plot(k,v,k,v,'r');xlabel('k'), ylabel('v');tktle(' (-1,+1)均匀分布的白噪声')②程序运行结果如图2.6所示。
变分模态分解心电信号降噪matlab代码
变分模态分解（VMD）是一种用于信号处理的先进技术，它可以有效地对心电信号进行降噪和分解。
在本文中，我将探讨VMD在心电信号处理中的应用，并共享一些关于VMD在MATLAB中的代码实现。
VMD是一种基于优化的信号分解方法，它通过将信号分解为多个本征模态函数（IMF）来处理非线性和非平稳信号。
VMD的主要思想是将信号分解为多个模态成分，每个成分都具有不同的频率和幅值。
通过对每个模态成分进行处理，可以更好地理解和处理复杂的信号。
在MATLAB中，可以使用VMD工具箱来实现心电信号的降噪和分解。
下面是VMD在MATLAB中的代码示例：```matlab% 输入心电信号数据fs = 1000; % 采样频率t = (0:1/fs:1-1/fs); % 时间范围f1 = 50; % 心电信号的频率成分f2 = 120; % 噪声的频率成分x = 1.5*sin(2*pi*10*t) + 2*sin(2*pi*15*t) + 0.5*sin(2*pi*40*t) + 0.2*sin(2*pi*120*t); % 生成心电信号x = x + 2*randn(size(t)); % 添加高斯白噪声% 使用VMD对心电信号进行分解alpha = 2000; % 控制VMD的收敛速度tau = 0; % VMD的频率-模态混合参数K = 3; % VMD的模态数tol = 1e-5; % VMD的收敛容限maxit = 100; % VMD的最大迭代次数[u, u_hat, omega] = VMD(x, alpha, K, tau, tol, maxit);% 对VMD分解后的模态成分进行处理figure;for k=1:Ksubplot(K,1,k);plot(t, u(k,:));title(['VMD分解模态成分', num2str(k)]);end```在上面的代码中，首先生成了一个包含心电信号和高斯白噪声的示例数据。
matlab滤波器设计命令
matlab滤波器设计命令Matlab滤波器设计命令滤波器是数字信号处理中常用的工具，用于去除信号中的噪声、频率干扰或其他不需要的成分。
Matlab提供了一系列有用的滤波器设计命令，使用户能够轻松设计并应用各种类型的滤波器。
在本文中，我们将详细介绍Matlab中常用的滤波器设计命令，包括滤波器设计函数、滤波器类型和设计过程。
I. Matlab中常用的滤波器设计函数在Matlab中，有几种函数可用于设计滤波器，其中最常用的函数是`designfilt`函数和`fir1`函数。
1. designfilt函数`designfilt`函数是Matlab中最灵活和功能强大的滤波器设计函数之一，可用于设计各种类型的IIR和FIR滤波器。
它的基本语法如下：`filt = designfilt(FilterType, 'PropertyName', PropertyValue, ...)`其中，`FilterType`代表滤波器类型，包括低通滤波器(Lowpass)、高通滤波器(Highpass)、带通滤波器(Bandpass)、带阻滤波器(Bandstop)等。
`PropertyName`和`PropertyValue`是可选的参数，用于设置滤波器的各种属性，如阶数(Order)、截止频率(CutoffFrequency)、通带和阻带的最大衰减(MaximumAttenuation)等。
下面是一个使用`designfilt`函数设计低通滤波器的例子：Fs = 1000; 采样频率Fpass = 20; 通带截止频率Fstop = 30; 阻带截止频率designfilt('lowpassiir', 'FilterOrder', 4, 'PassbandFrequency', Fpass, 'StopbandFrequency', Fstop, 'SampleRate', Fs)该命令将设计一个4阶的低通IIR滤波器，其通带截止频率为20Hz，阻带截止频率为30Hz，采样频率为1000Hz。
matlab好用的带通滤波算法
matlab好用的带通滤波算法"使用MATLAB实现的带通滤波算法"MATLAB是一种强大的数学软件工具，可以用于信号处理、图像处理和滤波等应用。
带通滤波是一种常见的信号处理技术，可以用于去除噪声、提取特定频率的信号等。
在MATLAB中，有许多内置的函数和工具箱，可以方便地实现带通滤波算法。
带通滤波是一种频域滤波技术，通过选择一个频率范围内的信号进行滤波处理。
在MATLAB中，可以使用fft函数将信号转换到频域，然后使用带通滤波器设计函数（如butter、cheby1、ellip等）设计带通滤波器，最后使用ifft函数将信号转换回时域。
下面是一个简单的例子，演示了如何使用MATLAB实现带通滤波算法：matlab.% 生成一个频率为50Hz的正弦信号。
fs = 1000; % 采样频率为1000Hz.t = 0:1/fs:1-1/fs; % 1秒钟的时间。
f1 = 50; % 信号频率为50Hz.x = sin(2pif1t); % 生成正弦信号。
% 添加高斯白噪声。
noise = 0.5randn(size(t)); % 生成高斯白噪声。
x_noisy = x + noise; % 添加噪声。
% 设计带通滤波器。
f_low = 40; % 低通截止频率为40Hz.f_high = 60; % 高通截止频率为60Hz.order = 4; % 滤波器阶数。
[b, a] = butter(order, [f_low/(fs/2), f_high/(fs/2)],'bandpass'); % 设计带通滤波器。
% 应用滤波器。
x_filtered = filtfilt(b, a, x_noisy); % 应用带通滤波器。
% 绘制结果。
figure;subplot(3,1,1);plot(t, x);title('原始信号');subplot(3,1,2);plot(t, x_noisy);title('添加噪声后的信号');subplot(3,1,3);plot(t, x_filtered);title('经过带通滤波后的信号');在这个例子中，我们首先生成了一个频率为50Hz的正弦信号，并添加了高斯白噪声。
MATLAB中的信号噪声分析与处理方法
MATLAB中的信号噪声分析与处理方法一、引言信号噪声是在实际工程应用中普遍存在的问题，噪声会对信号的质量和准确性产生不良影响。
因此，对信号噪声进行分析和处理是非常重要的。
MATLAB作为一款强大的科学计算软件，提供了丰富的信号处理工具和算法，可以方便地进行信号噪声分析与处理。
本文将介绍一些常用的MATLAB工具和方法，帮助读者更好地处理信号噪声。
二、信号噪声分析在进行信号噪声分析之前，首先需要了解噪声的特性和类型。
常见的噪声类型有白噪声、高斯噪声、脉冲噪声等。
其中，白噪声是一种功率谱密度恒定的噪声，常用于模拟信号分析。
高斯噪声则符合正态分布特性，常用于数字信号处理。
脉冲噪声则表现为突然出现的噪声干扰。
对于信号噪声的分析，可以使用MATLAB中的频谱分析工具来实现。
例如，可以利用MATLAB中的fft函数对信号进行频谱分析，得到信号的功率谱密度。
通过观察功率谱密度图，可以清楚地看到信号的频域特性和噪声的功率分布情况。
此外，MATLAB还提供了丰富的统计工具，可以计算信号的均值、方差等统计参数，帮助进一步分析信号的噪声特性。
三、信号噪声处理1. 滤波方法滤波是一种常用的信号噪声处理方法，其目的是通过选择合适的滤波器对信号进行处理，抑制或消除噪声。
在MATLAB中，可以利用fir1、butter等函数来设计和应用滤波器。
滤波器可以分为低通滤波器、高通滤波器、带通滤波器和带阻滤波器等不同类型。
根据信号噪声的特点和需求，选择合适的滤波器类型是十分重要的。
例如，如果信号中的噪声主要集中在高频段，可以选择高通滤波器进行去噪处理。
2. 去噪算法除了滤波方法外，还有其他一些去噪算法可以应用于信号噪声处理。
例如，小波去噪算法是一种常用的信号去噪方法。
该算法通过对信号进行小波分解，并利用小波系数的特性进行噪声抑制。
MATLAB提供了丰富的小波变换函数和去噪函数，可以方便地进行信号去噪处理。
另外，独立分量分析（ICA）是一种基于统计的信号盲源分离方法，也可以用于信号噪声的降维和去噪。
matlab-正弦波-高斯白噪声-均匀白噪声-功率谱密度-自相关函数
现代通信原理作业一利用matlab完成：●产生正弦波信号、均匀白噪声以及高斯白噪声并分别将两种噪声叠加到正弦波信号上，绘出波形。
●分别求取均匀白噪声序列和高斯白噪声序列的自相关及功率谱密度，绘出波形。
一、白噪声区别及产生方法1、定义：均匀白噪声：噪声的幅度分布服从均匀分布，功率谱密度在整个频域内均匀分布的噪声。
高斯白噪声：噪声的幅度分布服从正态分布，功率谱密度在整个频域内均匀分布的噪声。
2、matlab仿真函数：rand函数默认产生是区间在[0,1]的随机数，这里需要利用公式：z2=a+(b-(a))*rand(m,n)............（公式1）randn函数默认产生均值是0、方差是1的随机序列，所以可以用其来产生均值为0、方差为1的正态分布白噪声，即N(0，12)。
利用公式：z1=a+b*randn(1,n).................（公式2）可以产生均值为a，方差为b2 高斯白噪声，即N(a，b2)。
二、自相关函数与功率谱密度之间的关系1、功率谱密度：每单位频率波携带的功率，这被称为信号的功率谱密度。
2、自相关函数：描述随机信号X(t)在任意两个不同时刻t1，t2的取值之间的相关程度。
3、维纳-辛钦定理：由于平均值不为零的信号不是平方可积的，所以在这种情况下就没有傅里叶变换。
幸运的是维纳-辛钦定理提供了一个简单的替换方法，如果信号可以看作是平稳随机过程，那么功率谱密度就是信号自相关函数的傅里叶变换。
4、平稳随机过程：是在固定时间和位置的概率分布与所有时间和位置的概率分布相同的随机过程。
（就是指得仅一个随机过程，中途没有变成另外一个统计特性的随机过程）二、源代码及仿真结果1、正弦波x=(0:0.01:2); %采样频率100Hzy1=sin(10*pi*x); %产生频率5Hz的sin函数plot(x,y1,'b');2、高斯白噪声+正弦波z1=0.1*randn(1,201); %产生方差N（0，0.12）高斯白噪声（b=0.01/0.1/1）plot(x,z1,'b');y2=y1+z1; %叠加高斯白噪声的正弦波plot(x,y2,'b');3、均匀白噪声+正弦波z2=-.3+.6*rand(1,201); %产生-0.3到0.3的均匀白噪声plot(x,z2,'b');y3=y1+z2; %叠加均匀白噪声的正弦波plot(x,y3,'b');4、高斯白噪声序列自相关函数及功率谱密度z1=0.1*randn(1,201); %产生方差N（0，0.12）高斯白噪声[r1,lags]=xcorr(z1); %自相关函数的估计plot(lags,r1);f1=fft(r1);f2=fftshift(f1); %频谱校正l1=(0:length(f2)-1)*200/length(f2)-100; %功率谱密度x轴y4=abs(f2);plot(l1,y4);5、均匀白噪声序列自相关函数及功率谱密度z2=-.3+.6*rand(1,201); %产生-0.3到0.3的均匀白噪声[r2,lags]=xcorr(z2); %自相关函数的估计plot(lags,r2);f3=fft(r2);f4=fftshift(f3); %频谱校正l2=(0:length(f4)-1)*200/length(f4)-100; %功率谱密度x轴y5=abs(f4);plot(l2,y5);。
matlab 白噪声的时间积分
Matlab中白噪声的时间积分在Matlab中，对白噪声进行时间积分是一个常见且重要的过程。
白噪声是一种频谱特性非常均匀的噪声信号，其功率谱密度在所有频率上都是恒定的。
在实际应用中，我们经常需要对白噪声进行时间积分，以得到随机游走过程或布朗运动过程，这在金融工程、信号处理等领域具有重要意义。
对于Matlab用户来说，如何进行白噪声的时间积分是一个常见问题。
在Matlab中，可以通过以下步骤实现这一过程。
1. 生成白噪声信号我们需要生成一个白噪声信号。
在Matlab中，可以使用awgn函数生成均值为0、方差为1的高斯白噪声信号，具体代码如下：```matlabN = 1000; % 信号长度white_noise = randn(1, N); % 生成白噪声信号```2. 对白噪声进行时间积分接下来，我们需要对生成的白噪声进行时间积分。
在Matlab中，可以使用cumsum函数对信号进行累积和运算，实现时间积分的过程，具体代码如下：```matlabintegrated_noise = cumsum(white_noise); % 对白噪声进行时间积分```3. 绘制结果并分析我们可以将生成的白噪声信号和对其进行时间积分后的信号进行绘图，以便更直观地观察时间积分的效果。
还可以对结果进行进一步分析，比如计算信号的均值、方差等统计特性，以及观察信号的频谱特性等。
个人观点和理解对于白噪声的时间积分，在Matlab中的实现过程相对简单，但在实际应用中具有重要意义。
通过对白噪声进行时间积分，可以得到随机游走过程或布朗运动过程，这对于模拟金融资产价格、分析信号处理中的随机干扰等问题具有重要意义。
掌握在Matlab中实现白噪声的时间积分是非常有益的。
总结本文通过介绍在Matlab中对白噪声进行时间积分的方法，以及对结果进行分析的过程，希望读者能够对这一问题有所了解。
在实际应用中，对白噪声进行时间积分是一个常见且重要的过程，通过本文的介绍，希望读者能够掌握这一技能，并在实际工程中加以应用。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
通信系统建模与仿真实验一、高斯白噪声的matlab 实现要求：样本点：100 1000标准差：0.2 2 10均值： 0 0.2白噪声如果噪声的功率谱密度在所有的频率上均为一常数，即)/(),(,)(0Hz W f n f P n +∞<<-∞=式中：0n 为常数，责成该噪声为白噪声，用)(t n 表示。
高斯白噪声的matlab 实现1．样本点为1000、均值为0、标准差为0.2时，高斯白噪声分布为下图所示：程序如下所示：% White background noisclear allf = 1:1:1000;for i = 1:length(f)K = (0.2) * randn(1,1) - 0;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i));endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft));plot(ti,realx2)2．样本点为1000、均值为0、标准差为2时，高斯白噪声分布为下图所示：程序如下所示：% White background noisclear allf = 1:1:1000;for i = 1:length(f)K = (2) * randn(1,1) - 0;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i));endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft));plot(ti,realx2)3．样本点为1000、均值为0、标准差为10时，高斯白噪声分布为下图所示：程序如下所示：% White background noisclear allf = 1:1:1000;for i = 1:length(f)K = (10) * randn(1,1) - 0;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i));endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft));plot(ti,realx2)4．样本点为1000、均值为10、标准差为0.2时，高斯白噪声分布为下图所示：程序如下所示：% White background noisclear allf = 1:1:1000;for i = 1:length(f)K = (0.2) * randn(1,1) - 10;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i));endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft));plot(ti,realx2)5．样本点为1000、均值为10、标准差为2时，高斯白噪声分布为下图所示：程序如下所示：% White background noisclear allf = 1:1:1000;for i = 1:length(f)K = (2) * randn(1,1) - 10;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i));endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft));plot(ti,realx2)6．样本点为1000、均值为10、标准差为10时，高斯白噪声分布为下图所示：程序如下所示：% White background noisclear allf = 1:1:1000;for i = 1:length(f)K = (10) * randn(1,1) - 10;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i));endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft));plot(ti,realx2)7．样本点为100、均值为0、标准差为0.2时，高斯白噪声分布为下图所示：程序如下所示：% White background noisclear allf = 1:1:100;for i = 1:length(f)K = (0.2) * randn(1,1) - 0;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i));endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft));plot(ti,realx2)8．样本点为100、均值为0、标准差为2时，高斯白噪声分布为下图所示：程序如下所示：% White background noisclear allf = 1:1:100;for i = 1:length(f)K = (2) * randn(1,1) - 0;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i));endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft));plot(ti,realx2)9.样本点为100、均值为0、标准差为10时，高斯白噪声分布为下图所示：程序如下所示：% White background noisclear allf = 1:1:100;for i = 1:length(f)K = (10) * randn(1,1) - 0;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i));endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft));plot(ti,realx2)10. 样本点为100、均值为10、标准差为0.2时，高斯白噪声分布为下图所示：程序如下所示：% White background noisclear allf = 1:1:100;for i = 1:length(f)K = (0.2) * randn(1,1) - 10;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i));endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft));plot(ti,realx2)11. 样本点为100、均值为10、标准差为10时，高斯白噪声分布为下图所示：程序如下所示：% White background noisclear allf = 1:1:100;for i = 1:length(f)K = (2) * randn(1,1) - 10;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i));endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft));plot(ti,realx2)12.样本点为100、均值为0、标准差为10时，高斯白噪声分布为下图所示：程序如下所示：% White background noisclear allf = 1:1:100;for i = 1:length(f)K = (10) * randn(1,1) - 10;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i)); endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft));plot(ti,realx2)。