河北省容城中学2014-2015学年高二11月月考数学(理)试题
河北省容城中学高二11月月考数学文试题 Word版无答案
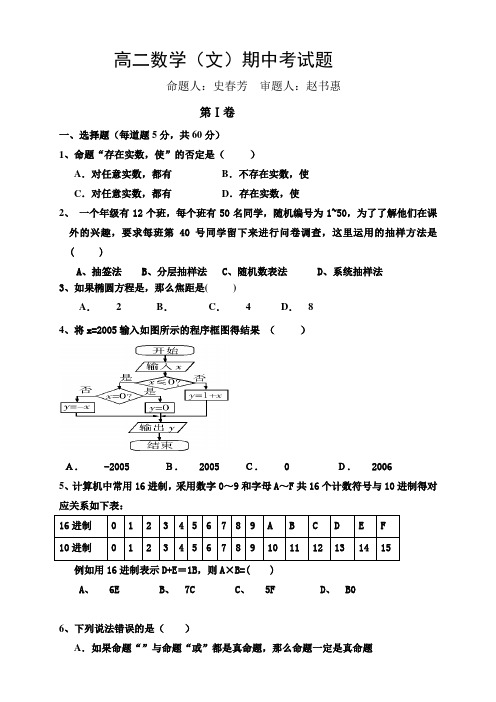
高二数学(文)期中考试题命题人:史春芳审题人:赵书惠第Ⅰ卷一、选择题(每道题5分,共60分)1、命题“存在实数,使”的否定是()A.对任意实数,都有B.不存在实数,使C.对任意实数,都有D.存在实数,使2、一个年级有12个班,每个班有50名同学,随机编号为1~50,为了了解他们在课外的兴趣,要求每班第40号同学留下来进行问卷调查,这里运用的抽样方法是( )A、抽签法B、分层抽样法C、随机数表法D、系统抽样法3、如果椭圆方程是,那么焦距是()A.2B.C.4D.84、将x=2005输入如图所示的程序框图得结果()A. -2005 B. 2005 C. 0 D. 20065、计算机中常用16进制,采用数字0~9和字母A~F共16个计数符号与10进制得对应关系如下表:例如用16进制表示D+E=1B,则A×B=( )A、 6EB、 7CC、 5FD、 B06、下列说法错误的是()A.如果命题“”与命题“或”都是真命题,那么命题一定是真命题B .命题“若,则”的逆否命题是:“若,则”C .命题:存在,使,则:对任意的D .特称命题“存在,使”是真命题7、一个质地均匀的正四面体玩具的四个面上分别标有1,2,3,4这四个数字.若连续两次抛掷这个玩具,则两次向下的面上的数字之积为偶数的概率是( )A 、B 、 34C 、D 、 588、命题“(2x+1)(x-3)<0”的一个必要不充分条件是( )A. B. C.D.9、已知两点,且是与的等差中项,则动点的轨迹方程是( ) A . B . C . D .10、200辆汽车通过某一段公路时的时速频率分布图如图所示, 则时速在分汽车大约有多少辆?( )A 、 30B 、 40C 、 50D 、 60 11、已知椭圆C 的短轴长为6,离心率为45,则椭圆C的焦点F 到长轴的一个端点的距离为( )A .9B .1C .1或9D .以上都不对12、已知为椭圆上的一个点, ,分别为圆和圆上的点,则的最小值为 ( )A . 5B . 7C . 13D . 15 第Ⅱ卷 二、填空题(每小题5分,共20分)13、利用计算机产生0~1之间的均匀随机数a ,则事件“3a -1>0”发生的概率为__________.14、将某选手的9个得分去掉1个最高分,去掉1个最低分,7个剩余分数的平均分为91,现场作的9个分数的茎叶图后来有1个数据模糊,无法辨认,在图中以x 表示:则7个剩余分数的方差为__________。
高二数学试题(含答案)

A C
B1E BC1
B
又 EF BC1 ,所以 BC1 平面 B1EF ,即 B1F BC1 ,
所以 B1FE 就是平面 A1BC1 与平面 B1BC1 所成的锐二面角的平面角。…………8 分
在 B1EF 中, B1EF 90 0 , B1E
2 2
,
B1 F
1
2 3
,
sin B1FE
从某校随机抽取 100 名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到
组号
分组
频数
数据分组及频数分布和频率分布直方图
1 2 3 4 5 6 7 8 9 合计
[0,2) [2,4) [4,6) [6,8) [8,10) [10,12) [12,14) [14,16) [16,18) 100
河北容城中学 2014~2015 学年度题(共 12 小题,每题 5 分,共 60 分)只有一个答案符合题目要求,多选、不选或错 选均不得分. 1. 一个人打靶时连续射击两次,事件“至少有一次中靶”的互斥事件是
A. 至多有一次中靶 B. 两次都中靶 C. 只有一次中靶 D. 两次都不中靶
④连接四面体 ABCD 每组对棱中点的线段互垂直平分 ⑤从四面体 ABCD 每个顶点出发的三条棱的长可作为一个三角形的三边长 16. 已知正方体 ABCD A1B1C1D1 中,E 、F 分别为 BB1、CC1 的中点,那么异面直线 AE 与
D1F 所成角的余弦值为____________.
三.解答题(本大题共 6 个小题,共 70 分). 17. (本小题满分 10 分)
B1
2
(2)设向量 n (x, y, z) 且 n 平面 A1BC1
于是 n A1B 且 n A1C1 ,即 n A1B 0 且 n A1C1 0 ,
河北省容城中学2014-2015学年高二11月月考化学试卷 Word版含答案.pdf

高二年级11月月考化学试题 命题人 胡欣阁 审题人 阴增彬 考试时间:90分钟; 总分:100分。
可能用到的相对原子质量:H-l C-40 N-14 O-16 S-32 Al-27 Cl-35.5 Cu-64 Ag-108 Pb-207 C-12 第I卷(选择题,每小题2分,共60分) 1.国际巴黎车展示上,世界各大汽车商纷纷推出环保动力小汽车,使用的新型环保电池为? (? ) 氢氧燃料电池 B锌锰电池 C镍镉电池 D铅蓄电池.0mol/L,经过20s后,它的浓度变成了0.2mol/L,在这20s内它的反应速率为 ( )A、0.04B、0.04mol / (L.s)C、0.08mol / (L.s)D、0.04mol / L 3.将纯水加热至较高温度,下列叙述正确的是A?、 水的离子积变大、pH变小、呈酸性B?、 水的离了积不变、pH不变、呈中性 C? 水的离子积变小、pH变大、呈碱性D?、 水的离子积变大、pH变小、呈中性 ).汽车的启动电源常用铅蓄电池,放电时的电池反应如下:PbO2 + Pb + 2H2SO4=2PbSO4↓+ 2H2O,根据此反应判断下列叙述中正确是? ? (? ) ?A.PbO2是电池的负极 ?B.负极的电极反应式为:Pb + SO - 2e -=PbSO4↓ C.PbO2得电子,被氧化 D.电池放电时,溶液酸性增强 、下列说法正确的是 A.钢铁发生电化腐蚀的正极反应式:Fe-2e-===Fe2+ B.氢氧燃料电池的负极反应式:O2 +2H2O +4e-===4OH- C.粗铜精炼时,与电源正极相连的是纯铜 D.用惰性电极电解饱和食盐水时,阳极的电极反应式为:2Cl-2e-===Cl2.①②③ B.②③④⑤C.②③④⑤⑥D.①②③④⑤⑥ 9.一种新型燃料电池,以铂板为电极插入KOH溶液中,分别向两极通乙烷和氧气,电极反应为C2H6 + 18OH-=2CO + 12H2O + 14e-; 14H2O + 7O2 + 28e-=28 OH-,有关推断错误的是 ( ) A.通氧气的电极为正极 B.在电解质溶液中CO向正极移动 C.放电一段时间后,KOH的物质的量浓度将下降 D.参加反应的氧气和乙烷的物质的量之比为7:2 10.一定条件下,在体积为10 L的密闭容器中,1 mol X和1 mol Y进行反应: 2X(g)+Y(g)Z(g),经60 s达到平衡,生成0.3 mol Z,下列说法正确的是( ) A.以X浓度变化表示的反应速率为0.001 mol/(L·s) B.将容器体积变为20 L,Z的平衡浓度变为原来的1/2 C.若升高温度Y的转化率减小,则正反应为吸热反应 D.达到平衡时,X与Y 的浓度相等 11.25℃时,水的电离达到平衡:H2OH++OH-;ΔH>0,下列叙述正确的是A、 向水中加稀氨水,平衡逆向移动,c(OH)降低 B 向水中加入少量固体硫酸氢钠,c(H+)增大,Kw不变 C 向水中加入少量固体CH3COONa,平衡逆向移动,c(H+)降低 D 将水加热,Kw增大,pH不变在25、101 kPa下,1 g甲醇燃烧生成CO2和液态水时放热22.68 kJ,下列热化学方程式正确的是(? ) A.CH3OH(l)+O2(g)===CO2(g)+2H2O(l);ΔH=+725.8 kJ/mol B.2CH3OH(l)+3O2(g)===2CO2(g)+4H2O(l);ΔH=-1452 kJ/mol C.2CH3OH(l)+3O2(g)===2CO2(g)+4H2O(l);ΔH=-725.8 kJ/mol D.2CH3OH(l)+3O2(g)===2CO2(g)+4H2O(l);ΔH=+1452 kJ/mol 13.在0.1mol/L的CH3COOH溶液中,要促进醋酸电离,且氢离子浓度增大,应采取的措施是( )A. 升温B. 降温C. 加入NaOH溶液D. 加入稀HCl 14.在同温同压下,下列各组热化学方程式中Q2 > Q1的是( ) A、2H2(g)+O2(g)=2H2O(g) ΔH==- Q1 2H2(g)+O2(g)=2H2O(l) ΔH==- Q2 B、S(g)+O2(g)=SO2(g) ΔH==- Q1 S(s)+O2(g)=SO2(g) ΔH==- Q2 C、C(s)+O2(g)=CO2(g) ΔH==- Q1 C(s)+1/2O2(g)=CO(g) ΔH==- Q2 D、H2(g)+Cl2(g)=2HCl(g) ΔH==- Q1 1/2H2(g)+1/2Cl2(g)=HCl(g) ΔH==- Q2 15. 以下现象与电化腐蚀无关的是? A? 黄铜(铜锌合金)制作的铜锣不易产生铜绿(铜锈) B? 生铁比软铁芯(几乎是纯铁)容易生锈? C? 质器件附有铜质配件,在接触处易生铁锈D? 银质奖牌久置后表面变暗 .用铂电极电解下列溶液时,阴极和阳极上的主要产物分别为H2和O2的是( )A、稀NaOH溶液? ?B、HCl溶液C、CuSO4溶液?D、AgNO3溶液.某原电池总反应离子方程式为.2Fe3++Fe=3Fe2+ ,不能实现该反应的原电池是( ) A.正极为Cu,负极为Fe,电解质溶液为FeCl3 溶液 B.正极为C,负极为Fe,电解质溶液为Fe(NO3)3 溶液 C.正极为Ag,负极为Fe,电解质溶液为Fe2(SO4)3 溶液 D.正极为Ag,负极为Fe,电解质溶液为CuSO4溶液NH4Cl与Ba(OH)2.8H2OA.(1) (2) (6)B.(1) (2) (4) (6)C.(2) (6)D.(2) (4) (6) 19.已知:H2(g)+F2(g)===2HF(g) H=-270kJ,下列说法正确的是A.1个氢气分子与1个氟气分子反应生成2个氟化氢分子放出270kJ B.1mol氢气与1mol氟气反应生成2mol液态氟化氢放出的热量小于270kJ C.相同条件下,1mol氢气与1mol氟气的能量总和大于2mol氟化氢气体的量 D.2氟化氢气体分解成1的氢气和1的氟气270kJ热量H>0已知:298K时,2SO2(g) + O2(g) 2SO3(g);H=—Q1KJ/mol,在相同温度下,向密闭容器中通入2molSO2和1molO2,达到平衡时放出热量Q2KJ,则下列关系式正确的是 () A. 无法比较 B.Q1<Q2 C.Q1=Q2 D.Q1>Q2 可逆反应N2+3H22NH3的正、逆反应速率可用各反应物或生成物浓度的变化来表示。
河北省容城中学2014-2015学年高二下学期第一次月考数学(理)试题 Word版含答案

1.用三段论推理:“指数函数x a y =是增函数,因为x y )21(=是指数函数,所以x y )21(=是增函数”,你认为这个推理( ) A .大前提错误 B 小前提错误C .推理形式错误D .是正确的2.若'0()3f x =-,则000()(3)limh f x h f x h h→+--=( )A .3-B .6-C .9-D .12-3.定积分⎠⎜⎛01(2x +e x )d x 的值为( ) A .e +2 B .e +1 C .e D .e -14.函数xxy ln =的最大值为( ) A .1-e B .e C .2e D .310 5.数列2,5,11,20,,47,x …中的x 等于( ) A .28 B .32 C .33 D .276.直线y =4x 与曲线y =x 3在第一象限内围成的封闭图形的面积为( )A. 2 2B. 4 2C. 2D. 4 7. 曲线y =x e x -1在点(1,1)处切线的斜率等于( )A .2eB .eC .2D .18. 设曲线y =ax -ln(x +1)在点(0,0)处的切线方程为y =2x ,则a =( )A .0B .1C .2D .39.已知32()32f x x x x a =-++,若()f x 在R 上的极值点分别为,m n ,则m n +的值为( )A .2 B .3 C .4 D .610.函数)(x f 的定义域为开区间),(b a ,导函数)(x f '在),(b a 内的图象如图所示,则函数)(x f 在开区间),(b a 内有极小值点( )A .1个B .2个C .3个D .4个 11.设△ABC 的三边长分别为,,,c b a △ABC 的面积为S ,内切圆半径为r ,则cb a Sr ++=2.类比这个结论可知:四面体ABC P -的四个面的面积分别为,1S ,2S ,3S ,4S 内切球的半径为r ,四面体ABC P -的体积为V ,则r=( )A.VS 1+S 2+S 3+S 4 B.2V S 1+S 2+S 3+S 4C.3V S 1+S 2+S 3+S 4D.4VS 1+S 2+S 3+S 412.对于R 上可导的任意函数()f x ,若满足'(1)()0x f x -≥,则必有( )A . (0)(2)2(1)f f f +< B. (0)(2)2(1)f f f +≤ C. (0)(2)2(1)f f f +≥ D. (0)(2)2(1)f f f +>二、填空题.( 本题共4个小题,每小题5分,满分20分)13. 220sin 2xdx π=⎰14. 若函数x a x x f sin 2cos )(+=在区间)2,6(ππ是减函数,则a 的取值范围是_15.)(131211)(+∈+⋅⋅⋅+++=N n nn f ,经计算的27)32(,3)16(,25)8(,2)4(,23)2(>>>>=f f f f f , 推测当2≥n 时,有__________________________.16.如图14,在边长为e(e 为自然对数的底数)的正方形中随机撒一粒黄豆,则它落到阴影部分的概率为________.三、解答题:17.(10分)已知函数32()39f x x x x a =-+++ (1)求函数()y f x =的单调递减区间(2)函数()y f x =在区间[]2,2-上的最大值是20,求它在该区间上的最小值18.(12分)已知函数23bx ax y +=,当1x =时,有极大值3; (1)求,a b 的值;(2)求函数y 的极小值。
河北省保定市容城中学2014-2015学年高二数学下学期第二次月考试题 理

河北省保定市容城中学2014-2015学年高二数学下学期第二次月考试题 理第I 卷(选择题)一、选择题(每题5分)1.在复平面内,复数32i 1i --对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限2.用三段论推理:“任何实数的平方大于0,因为a 是实数,所以02>a ”,你认为这个推理( )A .大前提错误B .小前提错误C .推理形式错误D .是正确的 3.命题“x ∀∈R ,xe -x +1≥0”的否定是( ) A .x ∀∈R ,lnx +x +1<0 B .x ∃∈R ,xe -x +1<0 C .x ∀∈R ,xe -x +1>0 D .x ∃∈R ,x e -x +1≥04.设随机变量X 服从正态分布N (3,4),若P (X <2a+3)=P (X >a ﹣2),则a 的值为( ). A . B .3 C .5 D .5.已知盒中装有3个红球、2个白球、5个黑球,它们大小形状完全相同,现需一个红球,甲每次从中任取一个不放回,在他第一次拿到白球的条件下,第二次拿到红球的概率( ). A . B . C . D .6.某人上班途中要经过三个有红绿灯的路口,设遇到红灯的事件相互独立,且概率都是0.3,则此人上班途中遇到红灯的次数的期望为( ).A .0.3B .0.33C .0.9D .0.7 7.设(x ﹣)6的展开式中x3的系数为a ,二项式系数为b ,则的值为( ).A .B .C .16D .48.甲,乙,丙,丁四位同学各自对A ,B 两变量的线性相关试验,并用回归分析方法分别求得相关系数r 如表: 甲 乙 丙 丁 r0.820.780.690.85则这四位同学的试验结果能体现出A ,B 两变量有更强的线性相关性的是( ). A .甲 B .乙 C .丙 D .丁9.用数学归纳法证明12+22+…+(n ﹣1)2+n2+(n ﹣1)2+…+22+12═时,由n=k的假设到证明n=k+1时,等式左边应添加的式子是()A.(k+1)2+2k2B.(k+1)2+k2C.(k+1)2D.10.某城市有3个演习点同时进行消防演习,现将4个消防队分配到这3个演习点,若每个演习点至少安排1个消防队,则不同的分配方案种数为().A.12 B.36 C.72 D.10811.函数f(x)=(x2﹣2x)ex(e为自然数的底数)的图象大致是().12.已知函数2(0)()(0)x xf xx x⎧≥⎪=⎨-<⎪⎩则1x=是()2f x=成立的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件13.已知()24f x x x=++-的最小值为n,则2()nxx-的展开式中常数项为()A.20 B.160 C.-160 D.-20[来源:学&科&网]14.若函数1()e(0,)axf x a bb=->>0的图象在0x=处的切线与圆221x y+=相切,则a b+的最大值是()A.4B.22C.2D.2二、填空题(每题5分)15.若(x+m)9=a0+a1(x+1)+a2(x+1)2+…+a9(x+1)9,且a0﹣a1+a2﹣a3+…+a8﹣a9=39,则实数m的值为.16.已知函数f(x)=x3+ax2﹣a(a∈R),若存在x0,使f(x)在x=x0处取得极值,且f (x0)=0,则a的值为.17.22sin2xdxπ=⎰.18.计算12323n n n n n C C C nC +++⋅⋅⋅+,可以采用以下方法:构造等式:0122n nn n n n C C x C x C x +++⋅⋅⋅+()1nx =+,两边对x 求导,得()112321231n n n n n n n C C x C x nC x n x --+++⋅⋅⋅+=+,在上式中令1x =,得1231232n n n n n n C C C nC n -+++⋅⋅⋅+=⋅.类比上述计算方法,计算12223223n n n n n C C C n C +++⋅⋅⋅+= .三、解答题(19题10分,20题12分,21、22题各14分)19.在平面直角坐标系中,以原点为极点,x 轴为极轴建立极坐标系,曲线1C 的方程为sin x y θθ⎧=⎪⎨=⎪⎩(θ为参数),曲线2C 的极坐标方程为2:cos sin 1C ρθρθ+=,若曲线1C 与2C 相交于A 、B 两点.(1)求||AB 的值;(2)求点(1,2)M -到A 、B 两点的距离之积.20.某次考试中,从甲、乙两个班各随机抽取10名学生的成绩进行统计分析,学生成绩的茎叶图如图所示,成绩不小于90分为及格.(1)从每班抽取的学生中各随机抽取一人,求至少有一人及格的概率(2)从甲班10人中随机抽取一人,乙班10人中随机抽取两人,三人中及格人数记为X ,求X 的分布列和期望.21.设数列{an}满足a1=3,an+1=an2﹣2nan+2,n∈N*.(1)求出a2,a3,a4的值,并猜想数列{an}的通项公式(不需证明);(2)记Sn为数列{an}的前n项和,试求使得2n>Sn成立的最小正整数n,并给出证明.22.已知函数f(x)=alnx﹣ax﹣3(a<0).(1)求函数f (x )的单调区间;(2)若函数y=f (x )的图象在点(2,f (2))处的切线的倾斜角为45°,对于任意的t ∈[0,1],函数g (x )=x3+x2[f ′(x )+m]在区间(t ,2)上总不是单调函数,其中f ′(x )为f (x )的导函数,求实数m 的取值范围. 参考答案 1.A 【解析】试题分析:ii i 21123+=--,对应的点()2,1,因此是第一象限。
河北省保定市满城中学2014-2015学年高二10月月考数学(理)试题(无答案)

一、 选择题(本大题共12个小题,每小题5分,共60分)二、1. 某商场有四类食品,其中粮食类、植物油类、动物性食品类及果蔬类分别有40种、10种、30种、20种,现从中抽取一个容量为20的样本进行食品安全检测,若采用分层抽样的方法抽取样本,则抽取的植物油类与果蔬类食品种数之和是( ) A.4 B.5 C.6 D.72.命题p :若a ·b <0,则a 与b 的夹角为钝角.命题q :定义域为R 的函数f (x )在(-∞,0)及(0,+∞)上都是增函数,则f (x )在(-∞,+∞)上是增函数.下列说法正确的是( )A.“p 或q”是真命题B.“p 且q”是假命题C.“p ⌝”是假命题D.“q ⌝”是假命题3.已知p : “a=”,q :“直线x+y=0与圆x 2+(y-a )2=1相切”,则p 是q的( )A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件4.执行如图所示的程序框图,输入m=828,n=345,则输出的实数m 的值是A.68B.69C. 138D. 1395.与圆222212:26260,:4240C x y x y C x y x y ++--=+-++=都相切的直线有( )A 、1条B 、2条C 、3条D 、4条6. 下列判断正确的是( )A.命题“负数的平方是正数”不是全称命题7882466792B.命题“任意的x ∈N ,x 3>x 2”的否定是“存在x 0∈N ,”C.“a=1”是“函数f(x)=cos 2ax-sin 2ax 的最小正周期是π”的必要不充分条件D.“b=0”是“函数f(x)=ax 2+bx+c 是偶函数”的充要条件 7.已知F 1,F 2是椭圆=1的两焦点,过点F 2的直线交椭圆于A ,B 两点.在△AF 1B 中,若有两边之和是10,则第三边的长度为( ) A.6 B.5 C.4 D.3 8.若右面的程序框图输出的S 是126,则①应为()A.n ≤5?B.n ≤6?C.n ≤7?D.n ≤8?9.为了了解某地区10 000名高三男生的身体发育情况,抽查了该地区100名年龄为17~18岁的高三男生体重(kg),得到频率分布直方图如图.根据图示,请你估计该地区高三男生中体重在[56.5,64.5] kg 的学生人数是()A.40B.400C.4 000D.4 400 10. 已知条件p:x ≤1,条件q:1x <1,则q 是⌝p 的成立的( ) A .充分不必要条件 B.必要不充分条件 C. 充要条件 D. 非充分非必要条件11.已知直线m x y l +=:与曲线21x y -=有两个公共点,则实数m 的取值范围是( )A .(-2,2)B .(-1,1)C .D .]22[,- 12.已知A={1,2,3},B={x ∈R |x 2-ax+b=0,a ∈A ,b ∈A },则A ∩B=B 的概率是( )A. B. C. D.1二、填空题(本在题共4小题,每小题5分,共20分.) 13.如图是2013年元旦歌咏比赛,七位评委为某班打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的方差为_ _.14. 把“二进制”数)2(1011001化为“五进制”数是15. 已知动点(,)P x y4=,则点P 的轨迹的方程是_________. 16. 在区域M=内随机撒一把黄豆,落在区域N=内的概率是 .三、解答题(本大题共6小题,70分.)17. (10分)(1)写出命题05末位数字是的多位数是“的倍数”的否命题,并判断其真假;(2)写出命题“所有的偶数都能被2整除”的否定,并判断其真假. 18. (12分)已知下面两个命题: 命题:p R x ∈∃,使012=+-ax x ; 命题:q R x ∈∀,都有012>+-ax ax若“p ⌝”为真命题,“q p ∨”也是真命题,求实数a 的取值范围.19、(12分)已知过点)2,1(P 的直线l 和圆622=+y x 交于B A ,两点.(1)若点P 恰好为线段AB 的中点,求直线l 的方程; (2)若52=AB ,求直线l 的方程.20. (12分)某大型养鸡场在本年度的第x 月的盈利y (万元)与x 的对应值如下表:注:∑∑==Λ--=ni i nii i xn x yx n y x b 1221(1)依据这些数据求出x ,y 之间的回归直线方程ˆˆˆybx a =+; (2)依据此回归直线方程预测第五个月大约能盈利多少万元.21. (12分)有两枚大小相同、质地均匀的正四面体玩具,每个玩具的各个面上分别写着数字1,2,3,5. 同时投掷这两枚玩具一次,记m 为两个朝上的面上的数字之和.(要求列出基本事件) (1)求事件“m 不小于6”的概率;(2)“m 为奇数”的概率和“m 为偶数”的概率是不是相等?证明你作出的结论.。
河北省容城中学2014-2015学年高二11月月考数学理试题 Word版含答案

河北容城中学高二年级2014年11月份月考数学(理)试题命题人 段美英 审题人 段飞华一、选择题(每小题5分,共60分)1.已知椭圆2214x y +=,则椭圆的焦距长为( )(A). 1 (B). 2 (C). (D). 232. 一个年级有12个班,每个班有50名同学,随机编号为1-50,为了了解他们在课外的兴趣,要求每班第40号同学留下来进行问卷调查,这里运用的抽样方法是( )(A ) 抽签法 (B)系统抽样法 (C)随机数表法 (D)分层抽样法 3.若命题“p ∨q ”为真,“﹁p ”为真,则( ) (A) p 真q 真 (B) p 假q 假 (C)p 真q 假 (D)p 假q 真4.从区间()0,1内任取一个实数,则这个数小于56的概率是( )(A )35 (B) 45 (C)56 (D)16255.已知椭圆C 1、C 2的离心率分别为e 1、e 2,若椭圆C 1比C 2更圆,则e 1与e 2的大小关系正确的是 ( )(A )e 1<e 2 (B) e 1=e 2 (C) e 1>e 2 (D) e 1、e 2大小不确定 6.计算机中常用16进制,采用数字0~9和字母A ~F 共16个计数符号与10进制得对应关系如下表:例如用16进制表示D+E =1B ,则A×B=( )(A ) 6E (B) 7C (C)5F (D) B07.某产品分为甲、乙、丙三级,其中乙、丙两级均属次品,若生产中出现乙级品的概率为0.03,出现丙级品的概率为0.01,则对产品抽查一次抽得正品的概率是( )(A)0.99 (B)0.98 (C)0.97 (D)0.968.将x=2005输入如图所示的程序框图得结果 ( )(A )-2005 (B) 2005 (C) 0(D) 20069.已知|x|≤2,|y|≤2,点P 的坐标为(x ,y),则当x ,y ∈Z 时,P 满足(x -2)2+(y -2)2≤4的概率为( )(A)225 (B) 425 (C) 625 (D) 82510.已知椭圆22143x y +=的长轴的左、右端点分别为A 、B ,在椭圆上有一个异于点A 、B 的动点P ,若直线PA 的斜率k PA =12,则直线PB 的斜率k PB 为( )(A)32 (B) -32 (C)34 (D) -3411.下列说法正确的是( )(A )“1>a ”是“)1,0(log )(≠>=a a x x f a 在),0(+∞上为增函数”的充要条件 (B )命题“R x ∈∃使得0322<++x x ”的否定是:“032,2>++∈∀x x R x ” (C )“1-=x ”是“0322=++x x ”的必要不充分条件 (D ) 命题:p “2cos sin ,≤+∈∀x x R x ”,则p ⌝是真命题12.已知椭圆2222:1(0)x y C a b a b+=>>的左焦点为F,C 与过原点的直线相交于A,B 两点,连接AF,BF. 若AB 10=,BF 8=,4cos ABF 5∠=,则C 的离心率为 ( )(A ) (B) (C) (D)二、填空题(每题5分,共20分)13.如图阴影部分是圆O 的内接正方形,随机撒314粒黄豆,则预测黄豆落在正方形内的约_____粒.14.已知x,y 的取值如下表所示,若y 与x 线性相关,且0.95,y x a a ∧=+=则15. 表示椭圆,则k 的取值范围为___________16.已知2214x y +=,1F ,2F 分别为其左右焦点,P 为椭圆上一点,则12F PF ∠的取值范围是 三、解答题:(共70分)17. (10分)求椭圆9x 2+25y 2=900的长轴和短轴的长、离心率、焦点和顶点的坐标. .18. (12分)为了对某课题进行研究,用分层抽样方法从三所高校A 、B 、C 的相关人员中,抽取若干人组成研究小组,有关数据如下表(单位:人)(1)求x 、y ;(2)若从高校B 、C 抽取的人中选2人作专题发言,求这二人来自高校C 的概率。
河北省容城中学14—15学年高二升级考试数学(理)(附答案)

高二年级升级考试数学试题(理科)(考试时间:120分钟 分值:150分)一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1、集合{}{}202,0A x x B x x x A B =≤≤=->⋂=,则 ( )A.RB. ()()012-∞⋃,,C.∅D. (]12,2、已知复数1z i =-,则21z z =- ( ) A.2 B.-2 C.2i D.-2i3、若0<a ,01<<-b ,那么下列不等式中正确的是 ( ) A. 2ab ab a << B. ab a ab <<2C.ab ab a <<2D .a ab ab <<24、给定函数①12yx = ②12log (1)y x =+ ③1y x =- ④12x y +=,其中在区间()0,1上单调递减的函数序号是 ( ) A .①② B .②③ C .③④ D .①④5、类比平面内“垂直于同一条直线的两条直线互相平行”的性质,可得出空间内的下列结论: ( ) ①垂直于同一个平面的两条直线互相平行; ②垂直于同一条直线的两条直线互相平行; ③垂直于同一个平面的两个平面互相平行; ④垂直于同一条直线的两个平面互相平行; A.①②B.②③C.③④D.①④6、一个几何体的俯视图是半径为l 的圆,其主视图和侧视图如图所示,则该几何体的表面积为 ( )A .3πB .4πC .5πD .7π7、如图是一个算法的流程图.若输入x 的值为2,则输出y 的值是( ) A .0 B .1-C .2-D .3-8、已知53)4cos(=-x π,那么sin 2x = ( ) A. 2518 B. 2524±C. 257-D . 2579、在等差数列{}n a 中,912162a a =+,则数列{}n a 的前11项和S 11等于( ) A.132B.66C.48D .2410、已知函数()()21cos ,4f x x x f x '=+是函数()f x 的导函数,则()f x '的图象大致是( )11、已知,x y 满足约束条件133x x y ay x ≥⎧⎪+≤⎨⎪≥-⎩,若2z x y =+的最小值为1,则实数a 的值是( )A.4B.12C.1D.2 12、已知函数()0()210x e a x f x a R x x ⎧+≤=∈⎨->⎩,若函数()f x 在R 上有两个零点,则a 的取值范围是 ( ) A .(),1-∞- B .(),0-∞ C .()1,0- D .[)1,0-二、填空题(每题5分,满分20分,将答案填在答题纸上)13、某校对全校1600名男女学生的视力状况进行调查,现用分层抽样的方法抽取一个容量是200的样本,已知女生比男生少抽10人,则该校的女生人数是 人. 14、已知21k π-=⎰,直线1y kx =+交圆22:1P xy +=于,A B 两点,则AB = .15、已知向量()1,2=,()1,0-=.若()⊥+λ,则实数λ= .16、设函数222(1)()log (1)x x f x x x ⎧+≤=⎨>⎩,则((0))f f =三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17、(本小题满分10分)在ABC ∆中,角A ,B ,C 的对边分别是a ,b ,c ,已知5c =,23B π=,ABC ∆的面积是(1)求b 的值; (2)求cos 2A 的值.18、(本小题满分12分)已知函数21()cos cos2222xxxf x ωωω=-(0)ω>的最小正周期为π.(1)求ω的值及函数()f x 的最大值和最小值; (2)求函数()f x 的单调递增区间.19、(本小题满分12分)如图,在四棱锥P -ABCD 中,底面ABCD 是菱形,∠DAB =45°,PD ⊥平面ABCD ,PD =AD =1,点E 为AB 上一点,且k ABAE=,点F 为PD 中点. (1)若21=k ,求证:直线AF //平面PEC ; (2)是否存在一个常数k ,使得平面PED ⊥平面P AB ,若存在,求出k 的值;若不存在,说明理由,20、(本小题满分12分)观察下列等式:1=1 2+3+4=9 3+4+5+6+7=25 4+5+6+7+8+9+10=49……照以上式子规律.......: (1)写出第5个等式,并猜想第n 个等式; (n ∈N *) (2)用数学归纳法证明上述所猜想的第n 个等式成立. (n ∈N *)21、(本小题满分12分)已知数列{}n a 前n 项和n S 满足:21n n S a +=(1)求数列{}n a 的通项公式;(2)设()()11211n n n n a b a a ++=++,数列{}n b 的前n 项和为n T ,求证:14n T <.22、(本小题满分12分)已知函数1()ln ,()(0)af x x a xg x a x+=-=->. (1)若1a =,求函数()f x 的极值;(2)设函数()()()h x f x g x =-,求函数()h x 的单调区间;(3)若存在0[1,]x e ∈,使得00()()f x g x <成立,求a 的取值范围.高二年级升级考试数学参考答案(理科) (考试时间: 120分钟 分值:150分)一、1、D2、A3、C4、B5、D6、C7、C8、 C9、A 10、A 11、D 12、D二、13、760 14、17178 15、5 16、1三、17、解:(1)因为ABC ∆,5c =,23B π=,所以1sin 2ac B =4 即1522a ⋅⋅=4所以 3.a = …………… 3分 由余弦定理2222cos b a c ac B =+-,得22259253cos49.3b π=+-⨯⨯⨯= 所以7.b = …………………… 5分(2)由正弦定理.sin sin a b A B =所以3sin 7214A =⨯= …………… 8分所以2271cos 212sin 12.1498A A ⎛=-=-⨯= ⎝⎭……………… 10分18、解析:(1)21()coscos2222xxxf x ωωω=-21sin 232cos 1-++=x x ωω x x ωωc o s 21s i n 23+=)6s i n (πω+=x . ……… 3分 因为πωπ==2T ,0>ω,所以2=ω. 5分因为)62sin()(π+=x x f ,R x ∈,所以1)62sin(1≤+≤-πx .所以函数()f x 的最大值为1,最小值为-1. ……8分 (2)令226222πππππ+≤+≤-k x k )(Z k ∈,得322322ππππ+≤≤-k x k )(Z k ∈,所以63ππππ+≤≤-k x k )(Z k ∈.所以函数()f x 的单调递增区间为3[ππ-k ,]6ππ+k )(Z k ∈.……………………12分19、解:(1)证明:作FM ∥CD 交PC 于M . ∵点F 为PD 中点,∴CD FM 21=. ∵21=k ,∴FM AB AE ==21,又FM ∥CD ∥AB ∴AEMF 为平行四边形,∴AF ∥EM ,∵AF PEC EM PEC ⊄⊂平面,平面,∴直线AF //平面PEC . ……………6分(2)存在常数22=k ,使得平面PED ⊥平面P AB .…………8分 ∵k AB AE =,1AB =,22=k,∴AE =, 又∵∠DAB =45°,∴AB ⊥DE . 又∵PD ⊥平面ABCD ,∴PD ⊥AB . 又∵PD DE D ⋂=,∴AB ⊥平面PDE ,∵PAB AB 平面⊂,∴平面PED ⊥平面P AB . …………………12分 20、解:(1)第5个等式为: 5+6+7+8+9+10+11+12+13=92 (2)分第n 个等式为:2)12()23()2()1(-=-++++++n n n n n ,*n N ∈ (5)分(2)①当1n =时,等式左边=1,等式右边=(2-1)2=1,所以等式成立. (6)分②假设n k=*()k N ∈时,等式成立,即),1()12()23()2()1(2*∈≥-=-++++++N k k k k k k k那么,当1n k =+时,2222]1)1(2[)12(81448)12()13(3)13()23()2()1()13()3()2()1(]2)1(3[]2)1[(]1)1[()1(-+=+=++-=+-=-+++-+-++++++=++++++++=-++++++++++k k k k k kk k k k k k k k k k k k k k k k k 即1n k =+时等式成立.……………… 11分根据(1)和(2),可知对任何*n N ∈,等式都成立.……… 12分 21、22、解:(1)()ln f x x a x =-的定义域为(0,)+∞. ………1分 当1a =时,1()x f x x-'=. ………2分 由()0f x '=,解得1x =.当01x <<时,()0,()f x f x '<单调递减; 当1x >时,()0,()f x f x '>单调递增;所以当1x =时,函数()f x 取得极小值,极小值为(1)1ln11f =-=; ……..4分 (2)1()()()ln ah x f x g x x a x x+=-=-+,其定义域为(0,)+∞. 又222(1)(1)[(1)]()x ax a x x a h x x x--++-+'==. …………..6分 由0a >可得10a +>,在(0,1)x a ∈+上()0h x '<,在(1,)x a ∈++∞上()0h x '>, 所以()h x 的递减区间为(0,1)a +;递增区间为(1,)a ++∞. ……..……7分 (3)若在[1,]e 上存在一点0x ,使得00()()f x g x <成立,即在[1,]e 上存在一点0x ,使得0()0h x <.即()h x 在[1,]e 上的最小值小于零. …8分 ①当1a e +≥,即1a e ≥-时,由(II )可知()h x 在[1,]e 上单调递减. 故()h x 在[1,]e 上的最小值为()h e ,由1()0a h e e a e +=+-<,可得211e a e +>-. ………9分 因为2111e e e +>--.所以211e a e +>-; ………10分 ②当11a e <+<,即01a e <<-时,由(II )可知()h x 在(1,1)+a 上单调递减,在(1,)a e +上单调递增.()h x 在[1,]e 上最小值为(1)2ln(1)h a +a a a +=-+. ………11分因为0ln(1)1a <+<,所以0ln(1)a a a <+<.2ln(1)2+a a a ∴-+>,即(1)2h a +>不满足题意,舍去.综上所述:a ∈21(,)1e e ++∞-. ………12分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河北省容城中学2014-2015学年高二11月月考数学(理)试题 一、选择题(每小题5分,共60分)
1.已知椭圆2
214
x y +=,则椭圆的焦距长为( )
(A). 1 (B). 2 (C)(D). 23
2. 一个年级有12个班,每个班有50名同学,随机编号为1-50,为了了解他们在课外的兴趣,要求每班第40号同学留下来进行问卷调查,这里运用的抽样方法是( ) (A ) 抽签法 (B)系统抽样法 (C)随机数表法 (D)分层抽样法
3.若命题“p ∨q ”为真,“﹁p ”为真,则( ) (A) p 真q 真 (B) p 假q 假 (C)p 真q 假 (D)p 假q 真
4.从区间()0,1内任取一个实数,则这个数小于5
6的概率是( )
(A )35 (B) 45 (C)
5
6 (D)
16
25
5.已知椭圆C 1、C 2的离心率分别为e 1、e 2,若椭圆C 1比C 2更圆,则e 1与e 2的大小关系正确的
是 ( )
(A )e 1<e 2 (B) e 1=e 2 (C) e 1>e 2 (D) e 1、e 2大小不确定
6.计算机中常用16进制,采用数字0~9和字母A ~F 共16个计数符号与10进制得对应关系如下表:
例如用16进制表示D+E =1B ,则A×B=( )
(A ) 6E (B) 7C (C)5F (D) B0
7.某产品分为甲、乙、丙三级,其中乙、丙两级均属次品,若生产中出现乙级品的概率为0.03,出现丙级品的概率为0.01,则对产品抽查一次抽得正品的概率是( ) (A)0.99 (B)0.98 (C)0.97 (D)0.96
8.将x=2005输入如图所示的程序框图得结果 ( )
(A )-2005 (B) 2005 (C) 0
(D) 2006
9.已知|x|≤2,|y|≤2,点P 的坐标为(x ,y),则当x ,y ∈Z 时,P 满足(x -2)2+(y -2)2≤4的概率为( )
(A)
225 (B) 425 (C) 625 (D) 8
25
10.已知椭圆22
143
x y +=的长轴的左、右端点分别为A 、B ,在椭圆上有一个异于点A 、B 的动
点P ,若直线PA 的斜率k PA =1
2
,则直线PB 的斜率k PB 为
( )
(A)
32 (B) -
32 (C)
34 (D) -
34
11.下列说法正确的是( )
(A )“1>a ”是“)1,0(log )(≠>=a a x x f a 在),0(+∞上为增函数”的充要条件 (B )命题“R x ∈∃使得0322<++x x ”的否定是:“032,2>++∈∀x x R x ” (C )“1-=x ”是“0322=++x x ”的必要不充分条件 (D ) 命题:p “2cos sin ,≤+∈∀x x R x ”,则p ⌝是真命题
12.已知椭圆22
22:1(0)x y C a b a b
+=>>的左焦点为F,C 与过原点的直线相交于A,B 两点,连接AF,BF.
若AB 10=,BF 8=,4
cos ABF 5
∠=
,则C 的离心率为 ( )
(A ) (B) (C) (D)
二、填空题(每题5分,共20分)
13.如图阴影部分是圆O 的内接正方形,随机撒314粒黄豆,则预测黄豆落在正方形内的约_____粒.
14.已知x,y 的取值如下表所示,若y 与x 线性相关,且0.95,y x a a ∧
=+=则
15. 表示椭圆,则k 的取值范围为___________
16.已知2
214
x y +=,1F ,2F 分别为其左右焦点,P 为椭圆上一点,则12F PF ∠的取值范围是
三、解答题:(共70分)
17. (10分)求椭圆9x 2+25y 2=900的长轴和短轴的长、离心率、焦点和顶点的坐标. .
18. (12分)为了对某课题进行研究,用分层抽样方法从三所高校A 、B 、C 的相关人员中,抽取若干人组成研究小组,有关数据如下表(单位:人)
(1)求x 、y ;
(2)若从高校B 、C 抽取的人中选2人作专题发言,求这二人来自高校C 的概率。
19.(12分)已知动点P 与平面上两定点(1,0),(1,0)A B -连线的斜率的积为定值2-. (1)试求动点P 的轨迹方程C.
(2)设直线:1l y x =+与曲线C 交于M 、N 两点,求|MN|
20.(12分)已知p :函数2()()1f x m m x =--的图象在R 上递减;q :曲线()2231y x m x =+-+与x 轴交于不同两点,如果p 或q 为真,p 且q 为假,求m 的取值范围.
21.(12分)设函数()f x =的定义域为D. (1)a ∈{1,2,3,4},b ∈{1,2,3},求使D=R 的概率; (2)a ∈[0,4],b ∈[0,3],求使D=R 的概率.
22.(12分)已知直线:220l mx y m -+=(m R ∈)和椭圆22
22:1(0)x y C a b a b +=>>, 椭圆C 的离
心率为
2
2
,连接椭圆的四个顶点形成四边形的面积为.
(Ⅰ)求椭圆C 的方程;
(Ⅱ)设直线l 与椭圆C 交于A ,B 两点,若以线段AB 为直径的圆过原点,求实数m 的值.
数学(理))答案
17解:椭圆的长轴和短轴分别为2a=20和2b=12,离心率e=4
5,两个焦点分别为F 1(-8,0)和
F 2(8,0),四个顶点坐标分别为A 1(-10,0),A 2(10,0),B 1(0, -6),B 2(0, 6).
7P .
12
=
19
解:1)
2
2
1.
2y x +=(
1x ≠±)
(2)
12|||MN x x =-==
20解:由p 知,01m <<;
由q 知,0∆>,即12m <
或52
m >. 又因为p 或q 为真,p 且q 为假,所以p 与q 一真一假.
011522m m <<⎧⎪∴⎨≤≤⎪⎩ 或01
1522
m m m m ≤≥⎧⎪⎨<>⎪⎩或或 所以m ∈
[
1
2,1) ∪(-∞,0] ∪(
5
2,+∞)
21. 解:(1)(a ,b )的所有可能共12种,满足条件的有9种,所以概率P=
3
4.(6分)
(2)∵a ∈[0,4],b ∈[0,3], ∴所有的点(a ,b )构成的区域的面积为12. 而D=R ,有4(a-1)2
-4b 2
≤0, 即|a-1|≤|b |.满足|a-1|≤|b |的 点(a ,b )构成的区域(如左图所示)
的面积为7. 故所求概率7P .12
=
由题意,得
0OA OB ⋅=,即12120x x y y += ∴ 1212(
)()022
m m
x x x m x m +++=, 即222
1212(1)()042m m x x x x m ++++= ∴ 2222222
222(1)0421122m m m m m m m --+⋅+⋅+=++
解得m =,满足0∆>,∴
m =。
