6.2二次型的标准形
合集下载
6_2 配方法化二次型为标准形
《线性代数》 返回
②将x1, x2,…, xn正交化标准 化为h1, h2,…, hn，令 P=(h1, h2,…, hn), 仍有 P -1AP= 正交必无关 , 即有 P TAP= 因为PT=P -1.
下页 结束
返回 下页 下页 结束
作业：
P128页 习题四 8， 9
《线性代数》
返回
下页
结束
现将X=PY代入二次型，得
f ( X ) X T AX
X PY
( PY )T A( PY ) Y T ( PT AP)Y ,
d1 0 0 y1 0 d 0 y2 2 T yn Y Y , 0 0 d y n n
2
(1)就是相应的满秩线性变换，其中的 满秩方阵 P 为
《线性代数》 返回 下页 下页
P 0 0
1 0
结束
2 3 1
例2 用配方法化下列二次型为标准型．
f ( x1 , x2 , x3 ) x1 x2 x2 x3
解：f 中不含变量的平方项，但f 中含乘积项x1x2，为使f 出现平 方项可作下列变换：
上式右端除第一外，已不再含x1 ，继续对x２配方得： 4 2 y1 x1 x2 x3 f 2( x1 x2 x3 ) 2 3( x2 x2 x3 ) 3 x3 3 2 2 2 5 2 令 y2 x2 x3 2 3 2( x1 x2 x3 ) 3( x2 x3 ) x3 3 3 x3 y3
第 6章
二次型
一、二次型与二次型的化简 *二、配方法化二次型为标准形 *三、合同变换法化二次型为标准形 四、正交变换化二次型为标准形 五、惯性定律与正定二次型
②将x1, x2,…, xn正交化标准 化为h1, h2,…, hn，令 P=(h1, h2,…, hn), 仍有 P -1AP= 正交必无关 , 即有 P TAP= 因为PT=P -1.
下页 结束
返回 下页 下页 结束
作业：
P128页 习题四 8， 9
《线性代数》
返回
下页
结束
现将X=PY代入二次型，得
f ( X ) X T AX
X PY
( PY )T A( PY ) Y T ( PT AP)Y ,
d1 0 0 y1 0 d 0 y2 2 T yn Y Y , 0 0 d y n n
2
(1)就是相应的满秩线性变换，其中的 满秩方阵 P 为
《线性代数》 返回 下页 下页
P 0 0
1 0
结束
2 3 1
例2 用配方法化下列二次型为标准型．
f ( x1 , x2 , x3 ) x1 x2 x2 x3
解：f 中不含变量的平方项，但f 中含乘积项x1x2，为使f 出现平 方项可作下列变换：
上式右端除第一外，已不再含x1 ，继续对x２配方得： 4 2 y1 x1 x2 x3 f 2( x1 x2 x3 ) 2 3( x2 x2 x3 ) 3 x3 3 2 2 2 5 2 令 y2 x2 x3 2 3 2( x1 x2 x3 ) 3( x2 x3 ) x3 3 3 x3 y3
第 6章
二次型
一、二次型与二次型的化简 *二、配方法化二次型为标准形 *三、合同变换法化二次型为标准形 四、正交变换化二次型为标准形 五、惯性定律与正定二次型
§6.2 二次型化为标准型的三种方法
因此可以找到一个非退化线性替换化为二 次型为标准形.
定理 对任意对称阵A,存在可逆阵C使得CTAC 为对角阵. 即任何对称矩阵合同于一个对角阵.
上述定理的证明实绩上给出了一种化二次 型为标准型的方法：配方法.
拉格朗日配方法的步骤
1. 若二次型含有 xi 的平方项，则先把含有 xi 的乘积项集中，然后配方，再对其余的变量同 样进行，直到都配成平方项为止，经过非退化线 性变换，就得到标准形 .
2a23x2x3 ... 2a2nx2xn ...... 2an1,n xn1xn
令
x1 y1
x
2 x3
y1 y 2 y3
...
xn y n
它是非退化线性的替换,代入后
f (x1, x2,..., xn ) 2a12y1(y1 y2) 2a13y1y3 ... 2a1ny1yn
1 1 01 0 1
C
C1C2
1
1
0
0
1
2
0 0 1 0 0 1
1 1 3 1 1 1.
0 0 1
C 2 0.
正交变换法
由实对称矩阵的理论，对任意n阶实对称阵
A, 存在正交矩阵Q使得
step3．将特征向量正交化
取 1 1,2 2, 3
得正交向量组
3
( 3 ( 2
,2 ,2
) )
2
,
1 (1 2,1,1)T , 2 (2,1,0)T ,
3 (2 5,4 5,1)T .
step4．将正交向量组单位化，得正交矩阵P
定理 对任意对称阵A,存在可逆阵C使得CTAC 为对角阵. 即任何对称矩阵合同于一个对角阵.
上述定理的证明实绩上给出了一种化二次 型为标准型的方法：配方法.
拉格朗日配方法的步骤
1. 若二次型含有 xi 的平方项，则先把含有 xi 的乘积项集中，然后配方，再对其余的变量同 样进行，直到都配成平方项为止，经过非退化线 性变换，就得到标准形 .
2a23x2x3 ... 2a2nx2xn ...... 2an1,n xn1xn
令
x1 y1
x
2 x3
y1 y 2 y3
...
xn y n
它是非退化线性的替换,代入后
f (x1, x2,..., xn ) 2a12y1(y1 y2) 2a13y1y3 ... 2a1ny1yn
1 1 01 0 1
C
C1C2
1
1
0
0
1
2
0 0 1 0 0 1
1 1 3 1 1 1.
0 0 1
C 2 0.
正交变换法
由实对称矩阵的理论，对任意n阶实对称阵
A, 存在正交矩阵Q使得
step3．将特征向量正交化
取 1 1,2 2, 3
得正交向量组
3
( 3 ( 2
,2 ,2
) )
2
,
1 (1 2,1,1)T , 2 (2,1,0)T ,
3 (2 5,4 5,1)T .
step4．将正交向量组单位化，得正交矩阵P
6.2 二次型的标准型
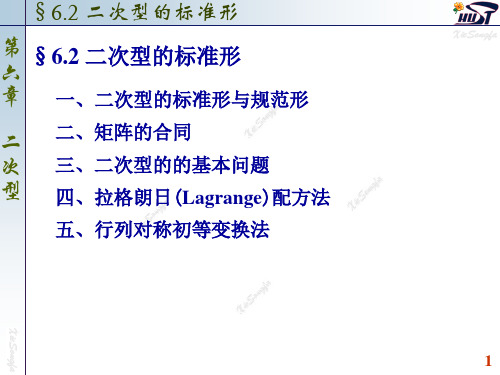
y1 = x1 + x2 + x3 , 令 y2 = x 2 + 2 x 3 , y = x3 , 3
X = CY
x1 = y1 − y2 + y3 , 即 x 2 = y2 − 2 y3 , x = y3 , 3
1 −1 1 其中 C = 0 1 − 2 . 0 0 1
其中，r 为 A 的秩， 其中， 的秩， di ≠ 0 . 证明 (略) 6
第 六 章 二 次 型
§6.2 二次型的标准形
三、二次型的的基本问题
问题一 二次型能否经过非退化线性变换一定化为标准形? 二次型能否经过非退化线性变换一定化为标准形 化为标准形 问题二 如何化二次型为标准形 如何化二次型为标准形? 常见的方法 针对二次型 拉格朗日(Lagrange)配方法。 拉格朗日( )配方法。 针对二次型所对应的对称阵 针对二次型所对应的对称阵 二次型所对应的 行列对称初等变换法； 行列对称初等变换法； 正交变换法。 正交变换法。
(3) 将 h(Z) 化为规范型
2 2 2 h( Z ) = z1 − z 2 + 16 z 3 ,
z1 = w1 , w1 = z1 , w2 = 4 z3， 即 z2 = w3 , 令 z = (1 / 4)w , w = z , 3 2 3 2
代入得 h(Z )
A B= I
64748 64 4 4 4 7 8 T Pm L P2T P1T A P1 P2 L Pm
行变换 列变换
Λ . I P1 P2 L Pm P 14 4 2 3
列变换
17
第 六 章 二 次 型
§6.2 二次型的标准形
线性代数 6-2标准形规范形
2 2 2 λ y + λ y + + λ y ⋯ X＝QY 化为标准形 1 1 2 2 n n ,其中
λ1 , λ2 ,⋯, λn为A的全部特征值, Q的列向量为对应
于 λ1 , λ2 ,⋯, λn 的标准正交 特征向量 . 标准正交特征向量 特征向量.
机动 目录 上页 下页 返回 结束
. 求正交阵Q, 使Q-1AQ为对角形 为对角形. T ⎛ 1 1 1⎞ λ = 3 α = (1,1,1) 1 1 ⎜ ⎟ T T A = ⎜ 1 1 1⎟ λ = λ = 0 α = ( − 1,1,0) α = ( − 1,0,1) , 2 3 2 3 ⎜ 1 1 1⎟ 1 1 ⎞ ⎛ 1 ⎝ ⎠ − −
机动
目录
上页
下页
返回
结束
, 在解析几何中 在解析几何中, 中心与坐标原点重合的有心二次曲线
f = ax 2 + 2bxy + cy 2
选择适当角度 θ,逆时针旋转 坐标轴
{
x = x′ cosθ − y = x′ cosθ +
y′ sinθ y′ sinθ
f = a′x′ 2 + c′y′ 2
(标准方程 ) 标准方程)
−5 5 = − 5 − 5 T 5 T 5 × 10 = α α f (α ) = α T Aα ≤ α α= ×10 = 5 5 2 2 2 2
故 m = −5 5, M = 5 5
机动 目录 上页 下页 返回 结束
二、配方法
定理2 数域F上的任意一个二次型均可经过可逆线性 替换化为标准形. . 证明略。后面以例说明 证明略。后面以例说明. : 用“矩阵合同”概念表述定理 概念表述定理: 3 数域F上任一对称矩阵都与一个对角阵合同 . 定理 定理3 上任一对称矩阵都与一个对角阵合同.
λ1 , λ2 ,⋯, λn为A的全部特征值, Q的列向量为对应
于 λ1 , λ2 ,⋯, λn 的标准正交 特征向量 . 标准正交特征向量 特征向量.
机动 目录 上页 下页 返回 结束
. 求正交阵Q, 使Q-1AQ为对角形 为对角形. T ⎛ 1 1 1⎞ λ = 3 α = (1,1,1) 1 1 ⎜ ⎟ T T A = ⎜ 1 1 1⎟ λ = λ = 0 α = ( − 1,1,0) α = ( − 1,0,1) , 2 3 2 3 ⎜ 1 1 1⎟ 1 1 ⎞ ⎛ 1 ⎝ ⎠ − −
机动
目录
上页
下页
返回
结束
, 在解析几何中 在解析几何中, 中心与坐标原点重合的有心二次曲线
f = ax 2 + 2bxy + cy 2
选择适当角度 θ,逆时针旋转 坐标轴
{
x = x′ cosθ − y = x′ cosθ +
y′ sinθ y′ sinθ
f = a′x′ 2 + c′y′ 2
(标准方程 ) 标准方程)
−5 5 = − 5 − 5 T 5 T 5 × 10 = α α f (α ) = α T Aα ≤ α α= ×10 = 5 5 2 2 2 2
故 m = −5 5, M = 5 5
机动 目录 上页 下页 返回 结束
二、配方法
定理2 数域F上的任意一个二次型均可经过可逆线性 替换化为标准形. . 证明略。后面以例说明 证明略。后面以例说明. : 用“矩阵合同”概念表述定理 概念表述定理: 3 数域F上任一对称矩阵都与一个对角阵合同 . 定理 定理3 上任一对称矩阵都与一个对角阵合同.
第六节 二次型的标准形和规范形
一个实二次型，既可以通过正交变换化为标准 形，也可以通过拉格朗日配方法化为标准形，显然， 其标准形一般来说是不唯一的。
但是，标准形中所含有的项数是确定的，项数 等于二次型的秩．
f k1 y12 k2 y22 kr yr2 , (ki 0)
实际上，不仅标准形中的非零系数的个数是确 定的，其中正的系数个数和负的系数个数也被原二 次型所确定，这就是下面的“惯性定理”。
A
1 1 1
1 1 1 1
1 1 1 1
1 1
1 11
0 0 0
1 0 0 0
1 0 0 0
1
0 0 0
,
1
1
1
2
1 0 0
,
3
0 1 0
,
4
0 0 1
,
18
1
1
1
2
1 0 0
,
3
0 1 0
,
4
0 0 1
,
正交化，
1 1 1
正交化，
3
2 0 1
4 5
2 1 0
1 5
2 4 5
,
再单位化，合在一起，即得所求正交变换的矩阵
1 3 2 5 2 45
P 2 3 1 5 4 45
2 3
0
5 45
14
于是所求正交变换为 X PY , 标准形为 f 9 y12 18y22 18y32 .
2 1
3 1 1 1
1 3 ,
3E
A
1 1 1
3 1 1
1 3 1
1
13
17
3E
A
3 1 1
1 E3A 1
1 1 3
但是，标准形中所含有的项数是确定的，项数 等于二次型的秩．
f k1 y12 k2 y22 kr yr2 , (ki 0)
实际上，不仅标准形中的非零系数的个数是确 定的，其中正的系数个数和负的系数个数也被原二 次型所确定，这就是下面的“惯性定理”。
A
1 1 1
1 1 1 1
1 1 1 1
1 1
1 11
0 0 0
1 0 0 0
1 0 0 0
1
0 0 0
,
1
1
1
2
1 0 0
,
3
0 1 0
,
4
0 0 1
,
18
1
1
1
2
1 0 0
,
3
0 1 0
,
4
0 0 1
,
正交化，
1 1 1
正交化，
3
2 0 1
4 5
2 1 0
1 5
2 4 5
,
再单位化，合在一起，即得所求正交变换的矩阵
1 3 2 5 2 45
P 2 3 1 5 4 45
2 3
0
5 45
14
于是所求正交变换为 X PY , 标准形为 f 9 y12 18y22 18y32 .
2 1
3 1 1 1
1 3 ,
3E
A
1 1 1
3 1 1
1 3 1
1
13
17
3E
A
3 1 1
1 E3A 1
1 1 3
线性代数第六章第二节二次型化为标准型的三种方法
用正交变换化二次型为标准形，其特点是保 持几何形状不变．
问题：有没有其它方法，也可以把二次型化为标 准形？
问题的回答是肯定的。下面介绍一种行之有 效的方法——拉格朗日配方法．
用正交变换能够化实二次型为标准型，这种方法是根据实 对称矩阵的性质，求出二次型 的特征值和规范正交的特征向量， 条件要求较强，当研究一般数域P上的二次型(包括实二次型) 的标准型时，可以用拉格朗日配方法，这种方法不用解矩阵特征 值问题，只需反复利用以下两个初等公式
零多项式，故 可化为标准型.
含有平方项，这归结为情形1，
推论1 任意n阶对称矩阵A都与对角形矩阵合同. 证明 由定理4，存在非退化线性变换X=CY，使得
右端标准型的矩阵为
新旧变量二次型的矩阵A与B满足CTAC=B，即A与对角形矩阵 B合同.
3 初等变换法 根据实对称矩阵及合同变换的特征得到.
只作列 变换
C为所 求
思考
1、化二次型为标准形的正交变换是否 唯一？
2、二次型的标准形是否唯一？
3、二次型的平方和和标准形主要区别 是什么？
4、在实数域里考虑，正交变换法和配
平方法没有改变二次型的那些特征？
思考题解答
1、正交变换不唯一；
2、标准形不计顺序的话是唯一的；
3、标准形的系数为其特征值，而平方 和的系数则不是特征值，可以任意变 动.
时,解方程组
得基础解系
当
时,解方程组
得基础解系
将特征向量正交化、单位化
再对α1,β2, β3单位化,得
写出正交变换的矩阵
由
构成正交矩阵
则二次型经正交变换x=Ty化为标准形
显然,f =1表示的二次曲面为单叶双曲面. 注意：化f为标准形的正交变换不唯一.
问题：有没有其它方法，也可以把二次型化为标 准形？
问题的回答是肯定的。下面介绍一种行之有 效的方法——拉格朗日配方法．
用正交变换能够化实二次型为标准型，这种方法是根据实 对称矩阵的性质，求出二次型 的特征值和规范正交的特征向量， 条件要求较强，当研究一般数域P上的二次型(包括实二次型) 的标准型时，可以用拉格朗日配方法，这种方法不用解矩阵特征 值问题，只需反复利用以下两个初等公式
零多项式，故 可化为标准型.
含有平方项，这归结为情形1，
推论1 任意n阶对称矩阵A都与对角形矩阵合同. 证明 由定理4，存在非退化线性变换X=CY，使得
右端标准型的矩阵为
新旧变量二次型的矩阵A与B满足CTAC=B，即A与对角形矩阵 B合同.
3 初等变换法 根据实对称矩阵及合同变换的特征得到.
只作列 变换
C为所 求
思考
1、化二次型为标准形的正交变换是否 唯一？
2、二次型的标准形是否唯一？
3、二次型的平方和和标准形主要区别 是什么？
4、在实数域里考虑，正交变换法和配
平方法没有改变二次型的那些特征？
思考题解答
1、正交变换不唯一；
2、标准形不计顺序的话是唯一的；
3、标准形的系数为其特征值，而平方 和的系数则不是特征值，可以任意变 动.
时,解方程组
得基础解系
当
时,解方程组
得基础解系
将特征向量正交化、单位化
再对α1,β2, β3单位化,得
写出正交变换的矩阵
由
构成正交矩阵
则二次型经正交变换x=Ty化为标准形
显然,f =1表示的二次曲面为单叶双曲面. 注意：化f为标准形的正交变换不唯一.
二次型的标准形
以 1 与2 正交，只需单位化得 p1
1 1
1 2
(1，1，0)T
，
p2
2 2
(0 ，0 ，1)T ．
②
当 3 0 时，由 Ax 0 得基础解系为 3 (1，1，0)T ，直接单位化得
p3
3 3
1 (1，1，0)T ． 2
1.1 用正交变换化二次型为标准形
1
2
（4）令
P
(
p1
，p2
，p3
应用线性代数
二次型的标准形
若二次型 f (x1 ，x2 ， ，xn ) 经过可逆线性变换 x Cy 可化为只含平方项的形式 f b1 y12 b2 y22 bn yn2 ， 则称上式为二次型 f (x1 ，x2 ， ，xn ) 的标准形， B diag(b1 ，b2 ， ，bn ) 为标准形矩阵．
T
，1
，再将
2
，3
单位化得
p2
2 2
(
2 5
，1 5
，0)T
，
p3
3 3
( 2 ， 4 ， 5 )T ． 35 35 35
1
3
（4）令
P
(
p1
，p2
，p3
)
2 3
2
3
2 5
1 5
0
2 35
4 35 5
，
x
x1 x2 x3
，
y
y1 y2 y3
，则正交变换
解
二次型
f
( x1
，x2
，x3 ) 不含平方项，令
x1 x2
y1 y1
y2 ，
y2
，即
x1 x2
1
线性代数知识点归纳
线性代数知识点归纳线性代数是一门研究向量、向量空间、线性变换以及有限维线性方程组的数学分支。
它广泛应用于各个领域，如物理、计算机科学、工程学等。
线性代数的核心概念和工具包括行列式、矩阵、向量组以及线性方程组等。
下面将详细介绍线性代数的相关知识点。
一、行列式1.1 行列式的概念：行列式是一个函数，它从n×n阶方阵到实数（或复数）的映射。
行列式记作|A|，其中A是一个n×n的方阵。
1.2 逆序数：在n×n阶方阵A中，将行列式中元素a_ij与a_ji互换，所得到的新的行列式称为原行列式的逆序数。
1.3 余子式：在n×n阶方阵A中，将第i行第j列的元素a_ij删去，剩下的(n-1)×(n-1)阶方阵的行列式称为原行列式的余子式，记作M_ij。
1.4 代数余子式：在n×n阶方阵A中，将第i行第j列的元素a_ij替换为它的相反数，然后计算得到的新的行列式，称为原行列式的代数余子式，记作A_ij。
1.5 行列式的性质：行列式具有以下性质：（1）交换行列式中任意两个元素的位置，行列式的值变号。
（2）行列式中某一行（列）的元素乘以常数k，行列式的值也乘以k。
（3）行列式中某一行（列）的元素与另一行（列）的元素相加，行列式的值不变。
（4）行列式某一行（列）的元素与另一行（列）的元素相减，行列式的值变号。
1.6 行列式的计算方法：行列式的计算方法有：降阶法、按行（列）展开法、克拉默法则等。
二、矩阵2.1 矩阵的概念：矩阵是一个由数组元素构成的矩形阵列，矩阵中的元素称为矩阵的项。
矩阵记作A，其中A是一个m×n的矩阵，A_ij表示矩阵A中第i行第j列的元素。
2.2 矩阵的线性运算：矩阵的线性运算包括加法、减法、数乘等。
2.3 矩阵的乘法：两个矩阵A和B的乘法，记作A×B，要求A是一个m×n的矩阵，B是一个n×p的矩阵。
矩阵的乘法满足交换律、结合律和分配律。
第6章 二次型及其标准形
T
3）对每个基础解系进行Schmidt正交化、再单位化：
1 4 2 1 1 1 1 2 , 2 45 2 , 3 3 1 , 5 5 2 0
1 5 4 45 4令Q 1 , 2 , 3 2 5 2 45 0 5 45 并且QT AQ Q 1 AQ diag 5,5,4
x
~ x
x2 y2 1 4 20 见图所示.
定义1： 含有n个变量 x1 , x2 ,, xn 的二次齐次多项式
f ( x1 , x2 , , xn ) a11 x12 2a12 x1 x2 2a13 x1 x3 2a1 n x1 xn
2 a22 x2 2a23 x2 x3 2a2 n x2 xn
化为标准形。 解
1 1 1 0 0 1 1 1 求二次型的矩阵 A , 的特征值 1 1 0 1 1 1 1 0
1 1 1
1 1 1 1
1 1 1 E A 1 1 1 1 1 1
1 1 1 ( 1) 1 1 1 i 2,3,4 1 1 1
例如：二次型 f ( x1 , x2 , x3 ) x1 3 x3 4 x1 x2 x2 x3
2 2
0 x1 1 -2 ( x1 , x2 , x3 ) -2 0 1/2 x2 0 1/2 -3 x 3
5)写出正交变换 X=QY，则可得标准型
2 f 5 y12 5 y2 4 y32
2 3 1 3 , 则Q是正交矩阵。 2 3
注：正交变换化为标准形的优点： 在几何中，可以保持曲线 （曲面）的几何形状不变。
第六章 二次型及其标准形
定理6.1 (Cauchy-Schwarz不等式)
即
这由
的判别式
易知.
性质6.2（向量长度的性质）
(1)非负性 当
时，
；当
时，
(2)齐次性
(3)三角不等式 (三角不等式用Cauchy-Schwarz不等式易证)
定义6.3（单位向量） 当
时，称 x 为 n 维单位向量.
向量
是与 同方向长度是1的向量，称为对 单位化.
(3) A是正交矩阵，则
；
(4) P是正交矩阵，则
，
即正交变换保持向量的长度不变。
6.2 实对称矩阵对角化
定理6.3 实对称矩阵的特征值必为实数. 从而特征向量可取到实的. (证明自学)
定理6.4 证明
对称矩阵不同特征值对应的特征向量必正交.
定理6.5 设A是一个n阶实对称矩阵，则必存在一个n 阶
两边分别与
内积
定义6.8（正交矩阵） 若n阶方阵A满足ATA=E，则称A为正交矩阵.
等价定义 A 是正交矩阵
AAT=E A-1=AT A 的列组是规范正交组 A 的行组是规范正交组
证 (只证第一条)
性质6.4 (1) A是正交矩阵，则A-1和A*都是正交矩阵；
(2) A，B都是正交矩阵，则AB也是正交矩阵；
其中r 为f 的秩，p为正惯性指数，r－p为负惯性指数。
为可逆线性变换。 为正交变换。
矩阵的合同： 定理 设A为对称矩阵，且A与B合同，则
证明
注：合同仍然是一种等价关系 矩阵合同的性质：(1) 反身性 (2) 对称性 (3) 传递性
二. 化二次型为标准形
目标：
1. 正交变换法（重点） 2. 配方法
问题转化为：
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 (1 2,1,1)T .
将2 3 18代入A E x 0,得基础解系
2 (2,1,0)T , 3 (2,0,1)T .
3．将特征向量正交化
取 1 1, 2 2, 3 3
得正交向量组
2 ,3 2 , 2
2
,
1 (1 2,1,1)T , 2 (2,1,0)T , 3 (2 5,4 5,1)T .
• 此变换亦可写成向量的形式： y Ax
x1
y1
a11 a12 a1n
•
其中
xxx n 2,
yyy m 2,
Aaa m 211
a22 am2
a2n a mn
• 此处：A 称为线性变换的系数矩阵，或简 称为线性变换的矩阵.
• •
定 恒 A当义 等为6变.n3换阶，可当即逆A；为矩uyrn阵阶时rx单，位y 阵时Ax ，y 称为A 可x 称逆为性
• 例6.6 求 f 2x1x2 2x1x3 6x2x3 的负惯性指数。
• 解：f可化为如下的标准形
。
因为其中正系数有两个:2、26z，12 所2z2以2 正6z32惯性
指数为2；负系数有一个：-2，所以负惯性
指数为1.
• 定义6.7 非零平方项的系数为１或－１的 二次型称为规范形.
• 例如：f x12 x22 ， f x12 x22 x32
为二次型的标准形.
2/21
对于二次型，我们讨论的主要问题是：寻求 可逆的线性变换，将二次型化为标准形．
设 x1 c11 y1 c12 y2 c1n yn ,
x2
c21 y1 c22 y2
c2n
yn
,
xn cn1 y1 cn2 y2 cnn yn
记C (cij),则上述可逆线性变换可 记作
即B为对称矩阵.
B CT AC , RB RAC RA,
又 A CT 1 BC 1 , RA R BC 1 RB.
RA RB.
9/21
定的矩理阵6.2变为经可C T逆A线C性, 即变换f xyT
Cy (C T
A,C二)次y 型
f
xT Ax
且二次型 f 的秩不变.
说明 1. 二次型经可逆变换x Cy后,其秩不变, 但 f
八、小结
1. 实二次型的化简问题，在理论和实际中 经常遇到，通过在二次型和对称矩阵之间建立一 一对应的关系，将二次型的化简转化为将对称矩 阵化为对角矩阵，而这是已经解决了的问题，请 同学们注意这种研究问题的思想方法．
2. 实二次型的化简，并不局限于使用正交 矩阵，根据二次型本身的特点，可以找到某种运 算更快的可逆变换．
• 定义6.2 设变量能用变量线性表示为
•
y1 a11x1 a12x2 a1n xn ,
y2 a21x1 a22x2 a2n xn ,
ym am1x1 am2x2 amnxn ,
• 其中 aij 为常数，则称上式为从 x1,x2,,xn 到 y1,y2,,ym的线性变换.
• 定理 6.6 任意一个实二次型一定可以经过 可逆变换化为规范形，且规范形是唯一确定 的。 即任意一个实对称矩阵都可以合同于 一个形如
•
1
O
1
1
O
1
0
O
0
• 的对角阵，其中１的个数就是对应实二次型 的正惯性指数，－１的个数就是对应实二次
型的负惯性指数，它们的和就是对应实二次 型的秩
6.2.2. 用正交变换化二次型为标准形
由于对任意的实对称矩阵A,总有正交矩阵P, 使P1AP ,即 PT AP .把此结论应用于二次 型, 有下述结论：
11/21
n
定理6.4 任给二次型 f aij xi xj aij a ji ,总有 i, j1
正交变换x Py,使 f 化为标准形
• 及 f k 1 y 1 2 k 2 y 2 2 k r y r 2 ( k i 0 , i 1 , 2 , , r )
• 则 1,2,,r中正数的个数与 k1,k2,,kr
中正数的个数相等.
• 定义6.6 标准形中正系数的个数称为二次 型的正惯性指数，负系数的个数称为二次 型的负惯性指数.
的矩阵由A变为B C T AC; 2. 要使二次型f经可逆变换 x Cy变成标准形,
就是要使yT CT ACy
k1 y12
k2
y
2 2
kn
y
2 n
k1
( y1, y2 , , yn)
k2
y1
y2
,
kn yn
也就是要使CT AC成为对角矩阵.
10/21
a ij a ij
6.2.1 线性变换与矩阵的合同
21/21
x1 1 3 x2 2 3 x3 2 3
2 5 15
0
2 45 y1 4 45 y2 , 5 45 y3
且有 f 9 y12 18 y22 18 y32 .
16/21
6.2.4 惯性定理与二次型的规范型
• 定理6.5（惯性定理）设实二次型 f xTAx
• 的 及秩x 为P rz ，若,使有f 两 个1 z 1 2 实 的2 z 2 2 可 逆 线r z r 2 性变( i 换 0 , x i 1 , 2 C , y , r )
• 定义6.5 设A、B均为n阶实对称矩阵，如果
• 存在n阶可逆矩阵C，使得 CT AC B ，
• 则称矩阵A与B合同. 从A到B的变换称为合 同变换，C称为合同变换矩阵.
• 注﹡
• (1)合同的矩阵秩相等，但行列式不一定相 等.
• (2) 两方阵相似不一定合同，合同也不一定 相似.
• (3) 两实对称矩阵相似必合同，合同必等价.
2 4 5 0 1 1
0 11
• 由此可知，A的特征值为1,1,6。既然特征值 均为正数，那么根据上述的推论可知f为正 定二次型。
• 例6.8 判别二次型 f x12 3x22 9x32 2x1x2 4x1x3 是正定的，还是负定的？
• 解:
1
A
1
1 3
2
0
2 0 9
a11 1 0
若 y Ax 是可逆线性变换，则
xA1y
• 也是可逆线性变换，称为 yAx的逆变
换.
• 定义6.4 设 xr (x1, x2, L , xn )T yr ( y1, y2 , L , yn )T • C (cij )nn 为阶可逆矩阵，则可逆线性变换 • xr Cyr ( | C | 0 ) 称为可逆变换.
14/21
4．将正交向量组单位化，得正交矩阵 P
令
i
i i
,
i 1,2,3,
1 3
2 5
2 45
得 1 2 3, 2 1 5 , 3 4 45 .
2 3
0
5
45
所以
1 3
P 2 3
2
3
2 5 150ຫໍສະໝຸດ 2 45 4 45 .
5
45
15/21
于是所求正交变换为
f 1 y12 2 y22 n yn2 ,
其中1, 2 , , n是 f 的矩阵A aij 的特征值.
用正交变换化二次型为标准形的具体步骤
1. 将二次型表成矩阵形式f xT Ax,求出A;
2. 求出A的所有特征值1,2 , ,n;
3. 求出对应于特征值的特征向量1 ,2 , ,n;
x Cy
8/21
将其代入 f xT Ax,有
f xT Ax CyT ACy yT CT AC y.
定理6.1 任给可逆矩阵C,令B CT AC,如果A为对称
矩阵,则B也为对称矩阵,且R B R A.
证明 A为对称矩阵,即有A AT ,于是
BT C T AC T C T AT C C T AC B,
4. 将特征向量1 , 2 , ,n正交化,单位化,得
1 ,2 , ,n ,记C 1 ,2 , ,n ;
5. 作正交变换x Cy,则得f的标准形
f
1 y12
n
y
2 n
.
12/21
例2 将二次型
f 17 x12 14x22 14x32 4 x1 x2 4 x1 x3 8 x2 x3 通过正交变换 x Py,化成标准形.
• •
的正定性. 解1：二次型的矩阵为：A
2 2
2 2 5 4,
2
4
5
• 而A的各阶主子式
2 2 2
220,
22 60
2
5 4 100,
25
2 4 5
• 所以为A正定矩阵，从而f为正定二次型.
• 解2：我们先来计算A的特征值。
2 2 2 2 2 2
2 2 2
2 5 4 2 5 4 (1 ) 2 5 4 12 ( 6)
1 1 20
1 3
1 1 2 1 3 0 6 0 2 0 9
• 故f为负定二次型．
• 例6.9* 证明：若A，B均为n阶正定矩阵， 则A+B也是正定矩阵.
• 证：由于A，B均为阶实对称矩阵，所以 A所+以B也对是任n意阶实对x 称，矩有0阵.因Ax T ，A ，x B 是0 正x 定TB .x 的从，0 而 x T ( A B ) x x T A x x T B x .0 故是A+B正 定矩阵.
• 推论：n元实二次型为正定的充分必要条件 是：n阶实对称矩阵的n个特征值全为正数.
• 定义6.10
a11 a12
设有n阶方阵
A
a21 an1
a22 an2
a1n
a2n ann
,
• 位于左上角的各阶子式
a11,
a11 a12, a21 a22