(完整)初中数学几个常用模型资料
初中数学模型归纳大全

初中数学模型归纳大全初中数学模型归纳大全近年来,初中数学的课程安排越来越注重将数学的思维方法和现实生活相结合,让学生在数学学习中掌握丰富的实际应用技能。
其中一个重要的教学方式就是数学建模。
初中数学模型归纳大全,决是一篇非常有用的参考资料。
这篇文章将会对初中数学中的各种数学模型进行归纳介绍,供初中生及学科教师们参考学习。
模型一:生活中的数学模型物质交换、能量转化、社会相互作用、周期变化等生活中的各种现象都可以用数学模型来描述和研究,例如:1.物质平衡模型:糖果换水果的比例;汽油和尾气的关系。
2.周期变化模型:季节变换图;一天的时间变换图。
3.变化速率模型:打车计价器;电费计算表。
模型二:图形化数学模型在初中数学中,一些图形化的数学模型可以帮助学生更好地理解和掌握一些抽象的数学概念。
以下是几种常见的图形化数学模型:1.函数图像模型:介绍函数图像的概念,如y=x^2、y=|x|等等。
2.平面几何模型:为学生介绍平面几何中的各种概念,如直线、角度和三角形等等。
3.三维几何模型:三维几何不仅可以帮助学生更好地理解三维空间的概念,同时还可以培养学生的空间想象力和建模能力。
模型三:奥数模型奥数一直以来都是中国教育中的一大特色,在初中数学中也有一些与奥数相关的数学模型,例如:1.排列组合模型:介绍排列组合的概念,如A(4,2)、C(4,2)等等。
2.数学归纳模型:帮助学生更好地掌握数学归纳的思路,如猴子吃桃、阶乘问题等等。
3.数形结合模型:利用具体的图形问题结合数学解法,例如数轴上的问题、目测问题等等。
模型四:工程数学模型在工程领域中,数学模型的运用是不可或缺的。
初中数学中也有一些与工程相关的数学模型,例如:1.自然增长模型:介绍自然增长的概念,如人口增长、金融投资等等。
2.传热模型:帮助学生了解传热的基本原理,如热力学等等。
3.循环流动模型:帮助学生了解循环流动的规律和应用,例如水循环、风循环等等。
总结初中数学模型的归纳总结可以为学生提供更多的实践题材,培养学生发掘问题并解决问题的能力,更重要的是,可以加深学生对数学知识的理解和应用。
七年级数学几何模型大全

七年级数学几何模型大全七年级的小伙伴们,今天咱们来唠唠七年级数学里那些超有趣的几何模型。
一、角平分线模型1. 双角平分线模型- 想象一下,有一个角,然后从这个角的顶点引出两条角平分线。
比如说∠AOB,OC平分∠AOB,OD平分∠AOC。
这里面就有很多好玩的关系哦。
- 如果设∠AOB = 2α,那么∠AOC=α,∠AOD = α/2。
这里面的关键就是根据角平分线的定义,把角之间的关系找出来。
就像分蛋糕一样,角平分线就是把角这个“大蛋糕”分成相等的“小蛋糕”。
- 而且还有个重要的结论呢,如果两个角平分线所夹的角是β,那么β = 1/2∠AOB或者β = 1/2 (∠AOB - ∠COD),这就看具体的图形情况啦。
2. 邻补角角平分线模型- 当有两个邻补角的时候,它们的角平分线可是很特别的。
比如说∠AOC和∠BOC是邻补角,OE平分∠AOC,OF平分∠BOC。
- 因为∠AOC+∠BOC = 180°,又因为OE和OF是角平分线,所以∠EOC+∠FOC=1/2(∠AOC + ∠BOC)=90°。
这就像两个小伙伴,把相邻的两块“角蛋糕”各自分一半,然后这两半加起来正好是个直角呢。
二、平行线模型1. “Z”字形模型(内错角模型)- 当有两条平行线被第三条直线所截的时候,就会出现像“Z”字一样的图形。
比如说直线a∥b,直线c与a、b相交。
- 这里面的内错角是相等的哦。
就好像在两条平行的铁轨(a和b)上,有一根枕木(c)横过来,形成的内错角就像在铁轨两边对称的位置,它们的大小是一样的。
- 如果∠1和∠2是内错角,那么∠1 = ∠2。
这个结论在证明角相等或者计算角的度数的时候可太有用啦。
2. “F”字形模型(同位角模型)- 还是两条平行线被第三条直线所截,不过这个时候是同位角的关系。
就像“F”字的形状。
- 同位角也是相等的呢。
比如说∠3和∠4是同位角,只要a∥b,那么∠3 = ∠4。
可以想象成在平行的道路(a和b)上,同样位置的标记(∠3和∠4),它们的角度肯定是一样的呀。
七八九年级23种数学模型

七八九年级23种数学模型
整理一些合集类的初中/会考/中考学习资料,方便同学们使用。
如果觉得还不错的话,记得三连哦!
总结了初中数学常考的23种模型,掌握这些模型做题速度将大大加快,这份资料适合初中各个年级
三线八角
拐角模型
等积变换模型
八字模型
飞镖模型
内内角平分模型
内外角平分模型
外外角平分模型
平行平分出等腰模型
等面积模型
倍长中线模型
角分线构造全等模型
三垂模型
手拉手模型
半角模型
将军饮马模型
费马点模型
中位线模型
斜边中线模型
平移构造全等
对称构造全等
射影定理模型
相似八大模型
二次函数中等积变换模型
二次函数中线段最值模型
二次函数中面积最值模型
二次函数中等腰三角形存在性模型二次函数中直角三角形存在性模型二次函数中平行四边形存在性模型。
初中数学必背几何模型
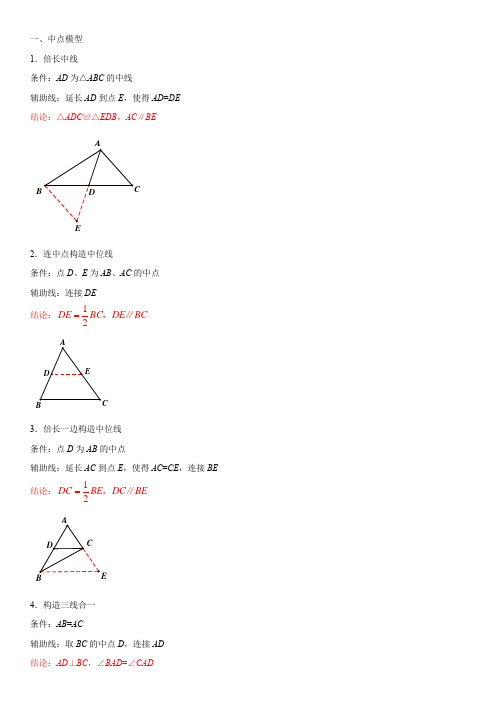
一、中点模型1.倍长中线条件:AD 为△ABC 的中线辅助线:延长AD 到点E ,使得AD =DE结论:△ADC ≌△EDB ,AC ∥BE2.连中点构造中位线条件:点D 、E 为AB 、AC 的中点辅助线:连接DE 结论:12DE BC DE BC =,∥3.倍长一边构造中位线条件:点D 为AB 的中点辅助线:延长AC 到点E ,使得AC =CE ,连接BE 结论:12DC BE DC BE =,∥4.构造三线合一条件:AB =AC辅助线:取BC 的中点D ,连接AD结论:AD ⊥BC ,∠BAD =∠CADB5.构造斜边中线条件:∠ABC =90°辅助线:取AC 的中点D ,连接BD 结论:12BD AC AD CD ===二、角平分线模型6.往角两边作垂线条件:AD 平分∠BAC辅助线:过点D 作AB 、AC 的垂线,垂足分别为E 、F结论:△ADE ≌△ADF7.在角的两边截取等长线段条件:AD 平分∠BAC辅助线:在AB 、AC 上取点E 、F ,满足AE =AF ,连接DE 、DF 结论:△ADE ≌△ADF8.过角平分线上一点作垂线条件:AD 平分∠BAC辅助线:过点D 作EF ⊥AD ,交AB 、AC 于点E 、FD CBB CCC结论:△ADE ≌△ADF三、双角平分线模型9.内内模型条件:BD 、CD 平分∠ABC 、∠ACB 结论:1902D A ∠=︒+∠10.内外模型条件:BD 、CD 平分∠ABC 、∠ACE 结论:12D A ∠=∠11.外外模型条件:BD 、CD 平分∠CBE 、∠BCF 结论:1902D A ∠=︒-∠四、平行线模型12.猪蹄模型CA BCC ED条件:AB ∥CD辅助线:过点E 作EF ∥AB结论:∠B +∠D =∠BED13.铅笔头模型条件:AB ∥CD辅助线:过点E 作EF ∥AB结论:∠B +∠D +∠BED =360°14.鸟头模型条件:AB ∥CD辅助线:过点E 作EF ∥AB结论:∠D +∠BED =∠B15.平行线+角平分线模型条件:AB ∥CD ,CE 平分∠ACD结论:AC =AE五、等积模型16.等底等高条件:AD ∥BCFAFBC结论:ABC DBC S S =,ADB ADC S S =17.等高模型条件:B 、C 、D 共线结论:::ABD ADC S S BD CD =18.等底模型条件:AE 、DE 为△ABC 、△DBC 边BC 上的高结论:::ABC DBC S S AE DE =六、对称半角模型19.对称半角模型-含45°角的三角形条件:∠BAC =45°,AD ⊥BC辅助线:作点D 关于AB 的对称点E ,关于AC 的对称点F , 连接AE 、AF 、BE 、CF 、EF结论:△AEF 是等腰直角三角形20.对称半角模型-含30°角的三角形B CB C DED条件:∠BAC =30°,AD ⊥BC辅助线:作点D 关于AB 的对称点E ,关于AC 的对称点F , 连接AE 、AF 、BE 、CF 、EF结论:△AEF 是等边三角形七、旋转半角模型21.旋转半角模型-等腰直角三角形条件:AB =AC ,∠BAC =90°,∠MAN =45°辅助线:将△ABM 绕点A 逆时针旋转90°,得到△ACM ' 结论:ANM ANM '≌,222BM CN MN +=22.旋转半角模型-等边三角形条件:△ABC 是等边三角形,BD =CD ,∠BDC =120°, ∠MDN =60°辅助线:将△BDM 绕点D 顺时针旋转120°,得到△DCM ' 结论:NDM NDM '≌,BM CN MN +=23.旋转半角模型-正方形条件:正方形ABCD ,∠MAN =45°,FEAM'M CAB辅助线:将△ABM 绕点A 逆时针旋转90°,得到△ADM ' 结论:NAM NAM '≌,BM DN MN +=八、自旋转模型24.自旋转模型-等边三角形条件:△ABC 是等边三角形,点P 为其内任意一点辅助线:将△BAP 绕点B 顺时针旋转60°,得到△BCP ' 结论:△BPP '是等边三角形25.自旋转模型-等腰直角三角形条件:△ABC 中,∠BAC =90°,AB =AC ,点P 为△ABC 内任 意一点辅助线:将△BAP 绕点A 逆时针旋转90°,得到△ACP ' 结论:△APP '是等腰直角三角形26.自旋转模型-等腰三角形条件:△ABC 中,AB =AC ,点P 为△ABC 内任意一点,∠BAC =α 辅助线:将△BAP 绕点A 逆时针旋转α,得到△ACP ' 结论:△APP '是等腰三角形M'DNCBAB九、手拉手模型29.手拉手模型-等边三角形条件:△ABC和△CDE都是等边三角形结论:△ACE≌△BCD27.手拉手模型-等腰直角三角形条件:△ABC和△CDE都是等腰直角三角形结论:△ACE≌△BCD,AE⊥BDEE28.手拉手模型-等腰三角形条件:△ABC 和△CDE 都是等腰三角形,CA =CB , CD =CE ,且∠ACB =∠DCE结论:△ACE ≌△BCD30.手拉手模型-正方形条件:四边形ABCD 和AEFH 都是正方形结论:△ABE ≌△ADH ,BE ⊥DH十、最短路程模型31.直线同侧两线段之和最小(将军饮马)条件:点A 、B 在直线l 同侧,点P 为l 上一点辅助线:作点A 关于直线l 的对称点A ',连接A 'B 结论:点P 为A 'B 和l 交点时,AP +BP 最小C32.直线异侧两线段之差最小条件:点A 、B 在直线l 异侧,点P 为l 上一点辅助线:作线段AB 的垂直平分线m结论:点P 为m 和l 交点时,|AP -BP |最小33.直线同侧两线段之差最小条件:点A 、B 在直线l 同侧,点P 为l 上一点辅助线:作线段AB 的垂直平分线m结论:点P 为m 和l 交点时,|AP -BP |最小34.过桥模型(将军饮马)条件:A 、B 为定点,l 1∥l 2,MN 为定长线段且MN ⊥l 1 辅助线:将点A 向上平移MN 的长度得到A ',连接A 'B 结论:点N 为A 'B 与l 1交点时,AM +MN +BN 最小35.四边形周长最小(将军饮马)条件:A 、B 为定点,M 、N 为角两边上的动点辅助线:作点A 、B 关于角两边的对称点A '、B ',连接 lAlAll 1l 2A'B'结论:M、N为A'B'与角两边交点时,四边形ABMN的周长最小B'36.三角形周长最小(将军饮马)条件:A为定点,B、C为角两边上的动点辅助线:作点A关于角两边的对称点A'、A",连接A'A"结论:B、C为A'A"与角两边交点时,△ABC的周长最小37.旋转类最短路程模型条件:线段OA=a,OB=b(a>b),OB绕点O在平面内旋转结论:点B与点N重合时,AB最小;点B与点M重合时,AB最大十一、基本相似模型38.A字型条件:BC∥DE结论:△ABC∽△ADE条件:∠ABC =∠ADE结论:△ABC ∽△ADE39.8字型条件:AB ∥CD结论:△AOB ∽△DOC条件:∠BAO =∠DCO结论:△AOB ∽△COD40.母子型条件:△ABC 中,∠ACB =90°,CD ⊥AB结论:△ABC ∽△ACD ∽△CBD41.一线三等角模型条件:∠B =∠D =∠ACE结论:△ABC ∽△CDECBCC A42.手拉手相似模型条件:△ABC ∽△ADE结论:△ACE ∽△ABD十二、对角互补模型43.对角互补模型-90°全等型条件:∠AOB =∠DCE =90°,OC 平分∠AOB辅助线:过点C 作CM ⊥AO ,CN ⊥BO ,垂足分别为M 、N 结论:△CDM ≌△CEN ,CD =CE ,OD +OEOC ,212OECD S OC 四边形CB ACE AB D CDD44.对角互补模型-120°全等型条件:∠AOB =120°,∠DCE =60°,OC 平分∠AOB辅助线:过点C 作CM ⊥AO ,CN ⊥BO ,垂足分别为M 、N 结论:△CDM ≌△CEN ,CD =CE ,OD +OE =OC ,24OECD S =四边形45.对角互补模型-任意角全等型条件:∠AOB =2α,∠DCE =180°-2α,OC 平分∠AOB辅助线:过点C 作CM ⊥AO ,CN ⊥BO ,垂足分别为M 、N 结论:△CDM ≌△CEN ,CD =CE ,2cos OD OE OC α+=⋅, 2sin cos OEC OCD S S OC αα+=⋅46.邻边相等的对角互补模型条件:四边形ABCD 中,AB =AD ,∠ABC +∠ADC =180°D BAN E OB辅助线:延长CD 到E ,使得DE =BC ,连接AE结论:△ABC ≌△ADE ,CA 平分∠BCD十三、隐圆模型47.动点定长模型条件:AB =AC =AP ,点P 为动点结论:点B 、C 、P 三点共圆,点A 为圆心,AB 为半径48.直角圆周角模型条件:点C 为动点,∠ACB =90°结论:点A 、B 、C 三点共圆,线段AB 的中点为圆心,线段 AB 为直径49.定弦定长模型条件:点P 为动点,固定线段AB 所对的动角∠APB 为定值 结论:点A 、B 、P 三点共圆,线段AB 和BP 的中垂线的交点 为圆心BA50.四点共圆模型①条件:点A 、C 为动点,∠BAD +∠BCD =180°结论:点A 、B 、C 、D 四点共圆,线段AB 和BC 的中垂线的 交点为圆心当∠BAD =∠BCD =90°,BD 为直径51.四点共圆模型②条件:线段AB 为固定长度,点D 为动点,∠C =∠D结论:点A 、B 、C 、D 四点共圆,线段AB 和BC 的中垂线的 交点为圆心CCA当∠C=∠D=90°,AB为直径。
(完整版)初中常用数学模型
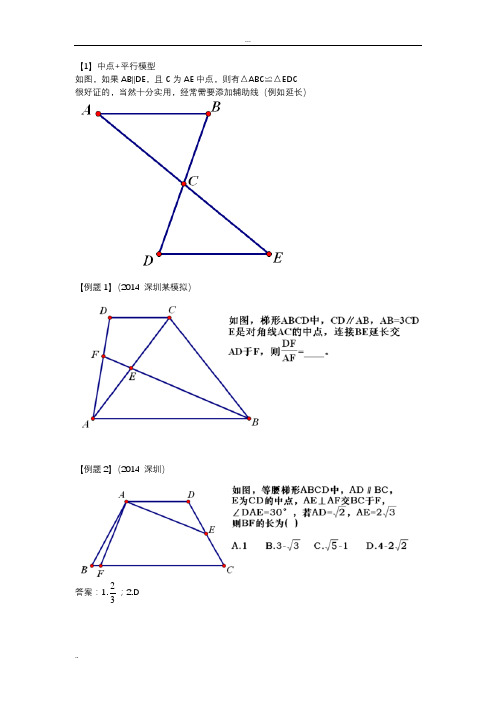
如图,如果AB ‖DE ,且C 为AE 中点,则有△ABC ≌△EDC 很好证的,当然十分实用,经常需要添加辅助线(例如延长)【例题1】(2014 深圳某模拟)【例题2】(2014 深圳)答案:1.32;2.D如图,若∠B=∠C=∠DEF=α(0<α≤90)则一定有△BDE与△CEF相似。
十分好证(外角和什么一大堆),并且也很实用。
经常在矩形里出题。
【例题1】(2009 太原)【例题2】(2006 河南)【例题3】(原创)答案:1. 2或3-24或25 2.(5453-,) 【3】巧造旋转模型在某些几何题中,往往有一些奇怪的结论,此时可以通过几何三大变换之一【旋转】求解。
巧造旋转往往要有一定的等量关系和特殊角度,如下题:通过观察可得∠ABC=∠C=45°,AB=AC 。
我们可以将△ACD 绕A 顺时针旋转90°得到△ABE ,使得AC 与AB 重合。
那么就有EB ⊥BC ,而在RT △AED 中,DE ²=2AD ²(等腰直角三角形) 所以BE ²+BD ²=DE ²,即BD ²+CD ²=2AD ²是不是赶脚很难想到?要学会判断,这种感觉是要练出来的! 【例题1】(2014 武汉)【例题2】【例题3】(2014 菏泽改编)答案:1.41 2.9 3.(1.)2,(2.)直角三角形,旋转后证全等,证明略【4】等腰模型这是一个很基础的模型——什么样的结构会生成等腰三角形首先:平行+角平分线,如图,若AD‖BE,BC平分∠ABE,则AB=AC,很好证的,导角即可。
其次:垂直+角平分这个不难理解,因为等腰三角形三线合一。
这种模型很常用,常常需要做辅助线(延长之类)【例题1】(原创)AB‖CD【例题2】(原创)【例题3】(改编)1.112.33.延长CD交AB于M,利用中位线,证明略【5】倍长中线法常考,选填大证明都可能会用。
初二数学几何基本模型

初二数学几何基本模型
1. 平面几何中的四边形模型:四边形是由四条线段组成的平面图形。
常见的四边形有正方形、长方形、菱形和梯形等。
2. 立体几何中的长方体模型:长方体是由六个矩形面组成的立体图形。
它有八个顶点、十二个棱和六个面。
3. 平面几何中的圆模型:圆是一个没有边界的平面图形,由半径相等的无限多的点组成,其中心是圆的中心。
圆的特性包括直径、半径和圆周等。
4. 立体几何中的球模型:球是一个没有边界的立体图形,由无限多的点组成。
球的特性包括直径、半径和表面积等。
5. 平面几何中的三角形模型:三角形是由三条线段组成的平面图形。
常见的三角形有等边三角形、等腰三角形和直角三角形等。
6. 立体几何中的棱柱模型:棱柱是由两个平行多边形底面和连接底面对应顶点的多个侧面组成的立体图形。
7. 平面几何中的直线模型:直线是由无数个连续点组成的,它没有起点和终点。
注意:以上只是一些数学几何基本模型的简要介绍,并不全面详尽。
建议学生根据教材或老师的要求进一步学习和理解。
初中几何46种模型大全

初中几何46种模型大全篇一:初中几何46种模型大全引言几何是初中数学的重要分支,其知识点涵盖了平面几何、立体几何、向量等多个方面。
在学习几何时,掌握各种几何模型是非常重要的,这些模型可以帮助我们理解和解决几何问题,提高解题能力。
本文将介绍初中几何中的46种常见的模型,包括它们的名称、定义、性质和应用。
正文1. 正方形模型正方形模型是几何中最基本的模型之一,它是一种边长相等的矩形。
正方形模型的定义如下:在一个平面直角坐标系中,任意两条直角边的平方和等于斜边的平方。
正方形模型的性质有:- 正方形的四条边相等;- 正方形的对角线相等;- 正方形的面积等于其边长的平方。
2. 长方形模型长方形模型是有两个相等的长和两个不相等的宽的英雄。
长方形模型的定义如下:在一个平面直角坐标系中,任意两条直角边的平方和小于斜边的平方。
长方形模型的性质有:- 长方形的两条对角线相等;- 长方形的宽比长大,长比宽大;- 长方形的长和宽相等。
3. 平行线模型平行线模型是相互平行的直线。
平行线模型的定义如下:- 两直线平行,当且仅当它们的对应角相等且且它们的方向相同。
平行线模型的性质有:- 平行线之间有且仅有一个交点;- 平行线上的点的横坐标相等;- 平行线的方向相同。
4. 菱形模型菱形模型是具有四个相等的直角边的矩形。
菱形模型的定义如下:在一个平面直角坐标系中,任意两条直角边的平方和等于斜边的平方,且任意两条边的长度小于第三条边的长度。
菱形模型的性质有:- 菱形的四条边相等;- 菱形的对角线相等;- 菱形的面积等于其四条边长度的平方和。
5. 等腰三角形模型等腰三角形模型是有一个相等的腰部的两个三角形。
等腰三角形模型的定义如下:- 在一个平面直角坐标系中,任意两条直角边的平方和等于斜边的平方。
等腰三角形模型的性质有:- 等腰三角形的两条直角边相等;- 等腰三角形的底角相等;- 等腰三角形的顶角平分线相等。
6. 等边三角形模型等边三角形模型是具有三个相等的边长的三角形。
中考数学九大几何模型标准版

初中数学九大几何模型、手拉手模型 - 旋转型全等条件】:△ OAB 和△ OCD 均为等边三角形;条件】:△ OAB 和△ OCD 均为等腰直角三角形;结论】:①△ OAC ≌△ OBD ;②∠ AEB=90°;③ OE 平分∠ AEDD EAED 1)等边三角形D结论】:①△ OAC ≌△ OBD ;②∠ AEB=60°;③ OE 平分∠、模型二:手拉手模型 -- 旋转型相似(1)一般情况 【条件】:CD ∥AB , 将△ OCD 旋转至右图的位置 O OD EA A结论】:①右图中△ OCD ∽△ OAB →→→△ OAC ∽△ OBD ;②延长 AC 交 BD 于点 E ,必有∠ BEC=∠ BOA2)特殊情况 条件】:CD ∥ AB ,∠ AOB=90°将△ OCD 旋转至右图的位置 A 结论】:①右图中△ OCD ∽△ OAB →→→△ OAC ∽△ OBD ; ②延长 AC 交 BD 于点 E ,必有∠ BEC=∠ BOA ; ③ A BD C O O C D O O A B tan ∠OCD ;④BD ⊥AC ; ⑤连接 AD 、BC ,必有 AD 2 BC 2 AB 2三、模型三、对角互补模型1)全等型 -90 ° 条件】:①∠ AOB=∠ DCE=90°;② OC 平分∠ AOB结论】:① CD=CE ;② OD+OE= 2 OC ;③ S △DCE CD ;⑥S△BCD证明提示: ①作垂直,如图 2,证明△ CDM ≌△ CEN ②过点 C 作 CF ⊥ OC , 如图 3,证明△ ODC ≌△ FEC ※当∠ DCE 的一边交 AO 的延长线于 D 时(如图 4): S△OCDS以上三个结论:① CD=CE ;② OE-OD= 2 OC ; ③ S △ OCE S △ OCD2)全等型 -120 °条件】:①∠ AOB=2∠ DCE=120°;② OC 平分∠ AOB32 结论】:① CD=CE ;② OD+OE=O ;C ③ S △DCES △OCDS △OCEOC 2 4证明提示:①可参考“全等型 -90 °”证法一;②如右下图:在 OB 上取一点 F ,使 OF=OC ,证明△ OCF 为等边三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
方形纸板上,能否裁剪制作一个这种模型(侧面和底面要完整,不能拼凑)( C )
(A)一个也不能做 (B)能做一个 (C)可做二个 (D)可做二个以上
4、(2004 河北 T7)在正方形铁皮上剪下个圆形和扇形,使之恰好围成如图所示的圆锥模型.设圆的半径
为 r,扇形的半径为 R,则圆半径与扇形半径之间的关系是(D
(1)选择:两船相遇之处 E 点(
)。
A、在线段 AB 上 B、在线段 BC 上 C、可以在线段 AB 上,也可以在线段 BC 上
(2)求货轮从出发到两船相遇共航行了多少海里?(结果保留根号)。
A
D
C
B
⒒将一把三角尺放在边长为 1 的正方形 ABCD 上,并使它的直角顶点 P 在对角线 AC 上滑动,
A
A
A
M
M
M
P
P
C
C
O
DB
O
DB
O
B
图甲
图乙
图丙
⑩如图,客轮沿折线 A-B-C 从 A 出发经 B 再到 C 匀速航行,货轮从 AC 的中点 D 出发沿某
一方向匀速直线航行,将一批物品送达客轮。两船同时起航,并同时到达折线 A-B-C 的某
点 E 处,已知 AB=BC=200 海里,∠ABC=90°,客轮速度是货轮速度的 2 倍。
图②
E M
C
F N
E M
C F
N
A
GD
HB A
GD
HB
图③
图④
第 24 题图
⑥一副三角板由一个等腰直角三角形和一个含 300 的直角三角形组成,利用这副三角板构成 一个含有 150 角的方法较多,请你画出其中两种不同构成的示意图,并在图上标出必要的标注, 不写作法. ⑦将一副三角尺如图摆放一起,连接 AD, 则∠ADB 的余切值为 .
四边形 ABCD 是正方形
B
C
AC 垂直平分 BD, ODC OCD 450
PB=PD, 4 900
1 2
图 (1)
PB PD
3 4 900
1 3
2 3
PDQ 2 ODC 2 450
PQD 3 OCD 3 450
PDQ PQD
PD PQ
PB PQ
∴ PEB PFQ
------4 分
设 PM=x,BM=1-x, QC=1-x-x=1-2x
S SPBC S PCQ
∴PB=PQ
1 BC PM 1 CQ PF
2
2
1 1 x 1 (2x 1)x
2
2
x2
-----------8 分
③有可能成为等腰三角形,求出 x 值-------11 分
(1) 将一副三角板如图叠放,则左右阴影部分面积 S1 : S2 之比等于________
(2) 将一副三角板如图放置,则上下两块三角板面积 A1 : A2 之比等于________
⑤(2006 年武汉市 T24.10 分)已知:将一副三角板(Rt△ABC 和 Rt△DEF)如图①摆放, 点 E、A、D、B 在一条直线上,且 D 是 AB 的中点。将 Rt△DEF 绕点 D 顺时针方向旋 转角α(0°<α<90°),在旋转过程中,直线 DE、AC 相交于点 M,直线 DF、BC 相 交于点 N,分别过点 M、N 作直线 AB 的垂线,垂足为 G、H。
CQ=PC= 2 x, BQ 2 BC 2 CQ 2 1 ( 2 x)2 由(1)证得,PB=PQ,
PB2 ( 2 BQ)2 1 1 ( 2 x)2
2
2
PB2 BO2 OP2
A
1 1 ( 2 x)2 ( 2 )2 (x 2 )2
2
2
2
由 x 1
…………….3 分
(2)操作:将三角板绕点 P 旋转到图 2 情形时,三角板的两边分别交 BA 的延长线、边 AC
于点 E、F.
① 探究1:△BPE 与△CFP 还相似吗?(只需写出结论)
② 探究2:连结 EF,△BPE 与△PFE 是否相似?请说明理由;
③ 设 EF=m,△EPF 的面积为 S,试用 m 的代数式表示 S.
1( 2
2 x)(
2 x)
E C
y 1 x2 1(1 x 2 ) 2
………………………………………………4 分
(3)可能
当 P 与 A 重合时,Q 与 D 重合,有 PQ=QC,X=0
当 PC=CQ 时,且 Q 在 DC 的延长线上时,(图形 3),连接 BD 交 AC 于点 O,连接 BQ,则
直角的另一边始终经过点 B,另一边与射线 DC 相交于点 Q。设 A、P 两点间的距离为 x,
(1)当点 Q 在 CD 上时,线段 PQ、PB 之间有怎样的大小关系?试证明你观察到的结论。
(2)当点 Q 在 CD 上时,求四边形 PBCQ 的面积 y 与 x 的函数解析式,并求出 X 的取值范围;
3 ②在图乙中,点 G 是 CD 与 OP 的交点,且 PG= 2 PD,求△POD 与△PDG 的面积之比.
(2)将三角板的直角顶点 P 在射线 OM 上移动,一直角边与边 OB 交于点 D,OD=1,另一直 角边与直线 OA,直线 OB 分别交于点 C,E,使以 P,D,E 为顶点的三角形与△OCD 相似,在 图丙中作出图形,试求 OP 的长.
……………………………..4 分
(2)连接 BD 交 AC 于点 O,作 QE AC 于点 E(如图 2)
A
D
P
PB PQ, PBO QPE, POB QEP 900
O
Q
POB QEP
QE OP OA AP 2 x
2
B
SPBCQ
S PBC
S PCQ
1 2
PC(BO QE)
)A、2r=R B、9 r R C、3r R 4
D、 4r R
模型 2、角平分线+平行=等腰三角形
如图, ABC 中 BD、CD 平分∠ABC、∠ACB,过 D 作直线平行于 BC,
交 AB、AC 于 E、F,当∠A 的位置及大小变化时,线段 EF 和 BE+CF 的
大小关系( B ).
(A)EF>BE+CF
(3)当点 P 在线段 AC 上滑动时,三角形 PCQ 是否能为等腰三角形?如果可能,指出所有可
能使三角形 PCQ 成为等腰三角形的点 Q 的位置,并求出相应
的 X 的值;如果不能说明理由(以下三个图的形状,大小相 A
P
同,以供操与解题时备用)
3
解:(1)PQ=PB
4O
D 1
Q
证明:连接 BD 交 AC 于点 O,连接 PD,如图(1)
(B)EF=BE+CF
(C)EF<BE+CF
(D)不能确定
模型 3、一副三角板
①在△ABC 中,a=1,b= 3 ,∠A=300,则∠B=___60___度。
②两个全等的含 300, 600 角的三角板 ADE 和三角板 ABC 如图所示放置,E,A,C 三点在一条 直线上,连结 BD,取 BD 的中点 M,连结 ME,MC.试判断△EMC 的形状,并说明理由.(等 腰直角三角形)
在 Rt△BPH 中, PH BP sin PBH = 2 3
∴S= 3m
……………… 8 分
B
模型 4 知二求四
H AE
F G
P
C
(2)
在上图中隐含有以下重要性质: ⑴两对相等的锐角;∠A= ∠BCD ,∠B= ∠ACD ⑵三对相似三角形:⊿ACD∽⊿ CBD∽⊿ABC, AC2=AD·AB BC2=BD·AB CD2=BD·AD ⑶边之比的推广
⑧如图, ABC中, ACB 90 , B 30 , AC 1,过点 C 作 CD1 AB 于 D1 ,
过 D1 作 D1D2 BC 于 D2 ,过 D2 作 D2 D3 AB 于 D3 ,这样继续作下去,……,线段
Dn Dn1 能等于( n 为正整数)
3 n (A) 2
(B)Βιβλιοθήκη 3 2n1(C)
3 2
n
(D)
3 2
n 1
C D2 D4 D6
A
⑨已知∠AOB=90°,OM 是∠AOB 的平分线,按以下要求解答问题:
D1 D3 D5
(第⑧题图)
B
(1)将三角板的直角顶点 P 在射线 OM 上移动,两直角边分别与边 OA,OB 交于点 C,D..
①在图甲中,证明:PC=PD;
--------5 分
13.(12 分)用两个全等的等边三角形△ABC 和△ACD 拼成菱形 ABCD.把一个含 60°角的三 角尺与这个菱形叠合,使三角尺的 60°角的顶点与点 A 重合,两边分别与 AB,AC 重合.将 三角尺绕点 A 按逆时针方向旋转. (1)当三角尺的两边分别与菱形的两边 BC,CD 相交于点 E,F 时,(如图 13—1),通过观 察或测量 BE,CF 的长度,你能得出什么结论?并证明你的结论; (2)当三角尺的两边分别与菱形的两边 BC,CD 的延长线相交于点 E,F 时(如图 13—2),
(1)当 α=30°时(如图②),求证:AG=DH; (2)当 α=60°时(如图③),(1)中的结论是否成立?请写出你的结论,并说明理由; (3)当 0°<α<90°时,(1)中的结论是否成立?请写出你的结论,并根据图④说明理由。
EA
F
45°
D
图①
C
60°
B
E M
AG
第 24 题图
F C (N)
D HB
12.如图,操作:将一把三角尺放在边长为 1 的正方形 ABCD 上,并使 B 它的直角顶点 P 在对角线 AC 上滑动,直角的一边始终经过点 B,另一 边与边 DC 或射线 DC 相交于点 Q。 当点 Q 在边 CD 上时,线段 PQ 与线段 PB 之间有怎样的大小关系?试证 明你观察得到的结论; ② 当点 Q 在边 CD 运动上时,设四边形 PBCQ 的面积为 S 时,试用含有 x 的代数式表示 S: ③ 当点 P 在线段 AC 上滑动时,△PCQ 是否可能成为等腰三角形?如果 可能,指出所有能使△PCQ 成为等腰三角形的点 Q 的位置,并求出相应 的 x 的值;如果不可能,试说明理由。
