七年级数学下册培优新帮手专题13位置确定试题(新版)新人教版【含解析】
部编数学七年级下册 坐标与规律变化专项提升训练【拔尖特训】2023培优(解析版)【人教版】含答案

【拔尖特训】2022-2023学年七年级数学下册尖子生培优必刷题【人教版】专题7.4坐标与规律变化专项提升训练班级:___________________ 姓名:_________________ 得分:_______________一.选择题(共10小题)1.(2021秋•宜兴市校级月考)一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→…],且每秒跳动一个单位,那么第25秒时跳蚤所在位置的坐标是( )A.(4,O)B.(5,0)C.(0,5)D.(5,5)【分析】由题目中所给的跳蚤运动的特点找出规律,即可解答.【解答】解:由图可得,(0,1)表示1=12秒后跳蚤所在位置;(0,2)表示8=(2+1)2﹣1秒后跳蚤所在位置;(0,3)表示9=32秒后跳蚤所在位置;(0,4)表示24=(4+1)2﹣1秒后跳蚤所在位置;…则(0,5)表示第25秒时跳蚤所在位置的坐标.故选:C.2.(2022秋•李沧区期末)如图,在平面直角坐标系中,A1(1,﹣2),A2(2,0),A3(3,2),A4(4,0),…根据这个规律,点A2023的坐标是( )A.(2022,0)B.(2023,0)C.(2023,2)D.(2023,﹣2)【分析】由图形得出点的横坐标依次是1、2、3、4、…、n,纵坐标依次是﹣2、0、2、0、﹣2、0、2、…,四个一循环,继而求得答案.【解答】解:观察图形可知,点的横坐标依次是1、2、3、4、…、n,纵坐标依次是﹣2、0、2、0、﹣2、0、2、…,四个一循环,2023÷4=505……3,所以点A2023坐标是(2023,2).故选:C.3.(2021秋•海州区期末)如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向不断地移动,每移动一个单位,得到点A1(0,1)、A2(1,1)、A3(1,0)、A4(2,0)…,那么点A2022的坐标为( )A.(1011,0)B.(1011,1)C.(2022,0)D.(2022,1)【分析】观察图形结合点的坐标的变化,可得出点A4n+2(n为自然数)的坐标为(2n+1,1),依此规律即可得出结论.【解答】解:∵点A1(0,1)、A2(1,1)、A3(1,0)、A4(2,0)、A5(2,1)、A6(3,1)、A7(3,0)、A8(4,0)、A9(4,1)、…,∴点A4n+2(n为自然数)的坐标为(2n+1,1),∴点A2022的坐标为(1011,1).故选:B.4.(2022秋•宜都市期中)如图所示,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向不断移动,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…,那么点A2016的坐标为( )A.(1007,0)B.(1008,0)C.(1007,1)D.(1008,1)【分析】根据图形分别求出n=1、2、3时对应的点的坐标,然后根据变化规律写出即可.【解答】解:由图可知,n=1时,4×1=4,点A4(2,0),n=2时,4×2=8,点A8(4,0),n=3时,4×3=12,点A12(6,0),所以,点A4n(2n,0).∴点A2016的坐标为(1008,0),故选:B.5.(2022春•高坪区校级月考)一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→……],且每秒跳动一个单位,那么第2022秒时跳蚤所在位置的坐标是( )A.(5,44)B.(2,44)C.(4,45)D.(5,45)【分析】由题目中所给的跳蚤运动的特点找出规律,即可解答.【解答】解:由图可得,(0,1)表示1=12秒后跳蚤所在位置;(0,2)表示8=(2+1)2﹣1秒后跳蚤所在位置;(0,3)表示9=32秒后跳蚤所在位置;(0,4)表示24=(4+1)2﹣1秒后跳蚤所在位置;…,∴(0,44)表示(44+1)2﹣1=2024秒后跳蚤所在位置,则(2,44)表示第2022秒后跳蚤所在位置.故选:B.6.(2022春•渝中区校级月考)如图,在平面直角坐标系中,A(2,2),B(﹣2,2),C(﹣2,﹣4),D (2,﹣4),把一条长为4044个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A→B→C→D→A⋯的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( )A.(2,2)B.(0,2)C.(﹣2,0)D.(﹣2,2)【分析】先求出四边形ABCD的周长为20,得到4044÷20的余数为4,由此即可解决问题.【解答】解:∵A(2,2),B(﹣2,2),C(﹣2,﹣4),D(2,﹣4),∴AB=2﹣(﹣2)=4,BC=2﹣(﹣4)=6,CD=2﹣(﹣2)=4,DA=2﹣(﹣4)=6,∴绕四边形ABCD一周的细线长度为4+6+4+6=20,4044÷20=202…4,∴细线另一端在绕四边形第203圈的第4个单位长度的位置,即细线另一端所在位置的点在点B的位置,坐标为(﹣2,2).故选:D.7.(2021秋•九江期末)如图,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙都从点A(2,0)同时出发,沿长方形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2022次相遇点的坐标是( )A.(2,0)B.(﹣1,1)C.(﹣2,0)D.(﹣1,﹣1)【分析】根据两个物体运动速度和矩形周长,得到两个物体的相遇时间间隔,进而得到两个点相遇的位置规律.【解答】解:由已知,矩形周长为12,∵甲、乙速度分别为1单位/秒,2单位/秒,则两个物体每次相遇时间间隔为=4秒,则两个物体相遇点依次为(﹣1,1)、(﹣1,﹣1)、(2,0),∵2022=3×673…3,∴第2022次两个物体相遇位置为(2,0),故选:A.8.(2022秋•隆安县期中)如图,在直角坐标系中,已知点A(﹣3,0),B(0,4),对△OAB连续作旋转变换,依次得到三角形①,②,③,④,…,则三角形⑩的直角顶点的坐标为( )A.(40,0)B.(36,0)C.(41,0)D.(39,0)【分析】根据旋转的性质观察△OAB连续作旋转变换,得到△OAB每三次旋转后回到原来的状态,并且每三次向前移动了3+4+5=12个单位,于是判断三角形⑩和三角形①的状态一样,然后可计算出它的直角顶点的横坐标,从而得到三角形⑩的直角顶点的坐标.【解答】解:∵对△OAB连续作如图所示的旋转变换,∴△OAB每三次旋转后回到原来的状态,并且每三次向前移动了3+4+5=12个单位,而10=3×3+1,∴三角形⑩和三角形①的状态一样,则三角形⑩与三角形⑨的直角顶点相同,∴三角形⑩的直角顶点的横坐标为3×12=36,纵坐标为0.三角形⑩的直角顶点的坐标为:(36,0).故选:B.9.(2021秋•兖州区期末)如图,小球起始时位于(3,0)处,沿所示的方向击球,小球运动的轨迹如图所示、如果小球起始时位于(1,0)处,仍按原来方向击球,小球第一次碰到球桌边时,小球的位置是(0,1),那么小球第2022次碰到球桌边时,小球的位置是( )A.(1,0)B.(5,4)C.(7,0)D.(8,1)【分析】根据题意,可以画出相应的图形,然后即可发现点所在位置的变化特点,即可得到小球第2022次碰到球桌边时,小球的位置.【解答】解:点(1,0)第一次碰撞后的点的坐标为(0,1),第二次碰撞后的点的坐标为(3,4),第三次碰撞后的点的坐标为(7,0),第四次碰撞后的点的坐标为(8,1),第五次碰撞后的点的坐标为(5,4),第六次碰撞后的点的坐标为(1,0),…,∵2022÷6=337,∴小球第2022次碰到球桌边时,小球的位置是(1,0),故选:A.10.(2022秋•二七区校级期中)如图,在平面直角坐标系中,A(﹣1,1),B(﹣1,﹣2),C(3,﹣2),D(3,1),一只瓢虫从点A出发以2个单位长度/秒的速度沿A→B→C→D→A循环爬行,问第2020秒瓢虫在( )处.A.(3,1)B.(﹣1,﹣1)C.(1,﹣2)D.(3,﹣1)【分析】分别求出瓢虫第1秒、第2秒、第3秒、第4秒、第5秒、第6秒、第7秒、第8秒、第9秒所在的位置坐标,根据其周期性,再求第2020秒瓢虫所在位置坐标即可.【解答】解:根据题意可得,第1秒瓢虫所在位置坐标为:(﹣1,﹣1),第2秒瓢虫所在位置坐标为:(0,﹣2),第3秒瓢虫所在位置坐标为:(2,﹣2),第4秒瓢虫所在位置坐标为:(3,﹣1),第5秒瓢虫所在位置坐标为:(3,1),第6秒瓢虫所在位置坐标为:(1,1),第7秒瓢虫所在位置坐标为:(﹣1,1),第8秒瓢虫所在位置坐标为:(﹣1,﹣1),第9秒瓢虫所在位置坐标为:(0,﹣2),……,瓢虫所在位置坐标具有周期性,2020÷7=288……4,∴第2020秒瓢虫在(3,﹣1)处.故选:D.二.填空题(共6小题)11.(2022秋•埇桥区期中)如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0),(2,0),(2,1),(1,1),(1,2),(2,2),…,根据这个规律,第25个点的坐标为 (5,0) ,第2022个点的坐标为 (45,3) .【分析】观察图形可知,以最外边的矩形边长上的点为准,点的总个数等于x轴上右下角的点的横坐标的平方,并且右下角的点的横坐标是奇数时最后以横坐标为该数,纵坐标为0结束,当右下角的点横坐标是偶数时,以横坐标为1,纵坐标为右下角横坐标的偶数减1的点结束,根据此规律解答即可.【解答】解:根据图形,以最外边的矩形边长上的点为准,点的总个数等于x轴上右下角的点的横坐标的平方,例如:右下角的点的横坐标为1,共有1个,1=12,右下角的点的横坐标为2时,共有4个,4=22,右下角的点的横坐标为3时,共有9个,9=32,右下角的点的横坐标为4时,共有16个,16=42,…,右下角的点的横坐标为n时,共有n2个,①∵52=25,5是奇数,∴第25个点是(5,0),②∵452=2025,45是奇数,∴第2025个点是(45,0),即第2022个点是(45,3)故答案为(5,0),(45,3).12.(2022•兴义市校级模拟)在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图所示.则点A2022的坐标是 (1011,1) .【分析】观察图形,找到点的坐标变化规律,每移动4个点为一个循环,利用规律求解即可.【解答】解:观察发现:每移动4个点为一个循环,2022÷4=505……2,由图可知A2(1,1),A6(3,1),A10(5,1),......,根据规律可知A的下标为2、6、10、......,即第n个数可以用4n+1表示,点的横坐标依次为1、3、5、......,∴点列A2、A6、A10、......的第n个点为A4n+2(2n+1,1),当4n+2=2022时,n=505,∴A2022(1011,1),故答案为(1011,1).13.(2022•嘉峪关一模)如图,平面直角坐标系xOy内,动点P按图中箭头所示方向依次运动,第1次从点(0,1)运动到点(1,0),第二次运动到点(2,﹣2),第3次运动到点(3,0),……按这样的运动规律,动点P第2022次运动到的点的坐标是 (2000,﹣2) .【分析】根据图形分析点P的运动规律:第n次运动到的点的横坐标为n,纵坐标每四次为一个循环,即可得到答案.【解答】解:∵第1次运动到点(1,0),第二次运动到点(2,﹣2),第3次运动到点(3,0),…,∴第n次运动到的点的横坐标为n,纵坐标每四次一个循环,从第一次运动到的纵坐标开始,分别为0、﹣2、0、1、…,∵2022÷4=505⋯2,∴动点P第2022次运动到的点的坐标是(2022,﹣2),故答案为:(2022,﹣2).14.(2022秋•诸城市校级月考)如图,弹性小球从点P(0,1)出发,沿所示方向运动,每当小球碰到正方形OABC的边时反弹,反弹的反射角等于入射角(反射前后的线与边的夹角相等),当小球第1次碰到正方形的边时的点为P1(2,0),第2次碰到正方形的边时的点为P2,….,第n次碰到正方形的边时的点为P n,则点P2022的坐标为 (0,1) .【分析】按照反弹规律依次画图即可.【解答】解:如图:根据反射角等于入射角画图,可知小球从P2反射后到P3(0,3),再反射到P4(2,4),再反射到P5(4,3),再反射到P点(0,1)之后,再循环反射,每6次一循环,2022÷6=337,即点P2022的坐标是(0,1).故答案为:(0,1).15.(2022秋•涡阳县校级月考)如图,一动点在第一象限内及x轴,y轴上运动,第一分钟,它从原点运动到(1,0),第二分钟,从(1,0)运动到(1,1),而后它接着按图中箭头所示在与x轴,y轴平行的方向来回运动,每分钟运动1个单位长度.第30分钟,动点所在的位置的坐标是 (5,5) .【分析】根据移动次数与点的坐标的所呈现的规律进行计算即可.【解答】解:根据移动的方向,距离所呈现的规律可得,当移动到点(1,0)时,对应的移动次数为1次,当移动到点(2,0)时,对应的移动次数为4+2×2=8次,当移动到点(3,0)时,对应的移动次数为8+1=9次,当移动到点(4,0)时,对应的移动次数为9+3×2+1+4×2=24次,当移动到点(5,0)时,对应的移动次数为24+1=25次,所以移动30次,所对应的点的坐标为(5,5),故答案为:(5,5).16.(2021秋•肥城市期末)如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),第4次接着运动到点(4,0),…,按这样的运动规律,经过第2022次运动后,动点P的坐标是 (2022,0) .【分析】分析点P的运动规律,找到循环次数即可.【解答】解:分析图象可以发现,点P的运动每4次位置循环一次.每循环一次向右移动四个单位.∴2022=4×505+2,当第505循环结束时,点P位置在(2020,0),在此基础之上运动二次到(2022,0)故答案为:(2022,0).三.解答题(共7小题)17.(2022春•新乐市校级月考)在平面直角坐标系中,一只蚂蚁从A(﹣2,0)处出发,按向上、向右、向下、向右的方向依次不断移动,每次移动距离为1个单位长度,其行走路线如图所示:(1)在图中补出y轴,并写出点A1,A5,A9的坐标;的坐标(n为正整数);(2)写出点A4n﹣3(3)蚂蚁从点A2021到点A2022的移动方向是 向右 (填“向上”“向右”或“向下”).【分析】(1)根据点的坐标变化即可补出y轴,并写出各点的坐标;的坐标(n为正整数);(2)根据(1)发现规律即可写出点A4n﹣3(3)根据(2)发现的规律,每四个点一个循环,进而可得蜗牛从点A2021到点A2022的移动方向.【解答】解:(1)补出y轴如图,根据点的坐标变化可知:A1(﹣2,1),A5(0,1),A9(2,1);(2)根据(1)发现:的纵坐标(n为正整数)为1,横坐标为2n﹣4,点A4n﹣3的坐标(n为正整数)为(2n﹣4,1);点A4n﹣3(3)因为每四个点一个循环,所以2021÷4=505…1.所以蜗牛从点A2021到点A2022的移动方向是向右.18.(2022秋•无为市月考)在平面直角坐标系中,一个动点A从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次只移动1个单位长度,其行走路线如图所示.(1)填写下列各点的坐标:A4 (2,0) ,A6 (3,1) ,A12 (6,0) ,A14 (7,1) .(2)按此规律移动,n为正整数,则点A4n的坐标为 (2n,0) ,点A4n+2的坐标为 (2n+1,1) .(3)动点A从点A2022到点A2023的移动方向是 向下 .(填“向上”、“向右”或“向下”)【分析】(1)根据点的坐标变化即可填写各点的坐标;(2)根据(1)发现规律即可写出点A4n的坐标(n为正整数);(3)根据(2)发现的规律,每四个点一个循环,进而可得蜗牛从点A2020到点A2021的移动方向.【解答】解:(1)根据点的坐标变化可知:各点的坐标为:A4(2,0),A6(3,1),A12(6,0),A14(7,1);故答案为:(2,0),(3,1),(6,0),(7,1);(2)根据(1)发现:点A4n的坐标(n为正整数)为(2n,0);点A4n+2的坐标为(2n+1,1);故答案为:(2n,0),(2n+1,1);(3)因为每四个点一个循环,所以2023÷4=505…3.所以从点A2022到点A2023的移动方向是向下.故答案为:向下.19.(2022•安徽模拟)在平面直角坐标系中,点A1从原点O出发,沿x轴正方向按折线不断向前运动,其移动路线如图所示.这时点A1,A2,A3,A4的坐标分别为A1(0,0),A2(0,1),A3(1,1),A4(1,0),…按照这个规律解决下列问题:(1)写出点A5,A6,A7,A8的坐标;(2)点A100和点A2022的位置分别在 x轴上 , x轴下方 .(填x轴上方、x轴下方或x轴上)【分析】(1)根据图象可得点A5,A6,A7,A8的坐标;(2)根据图象可得移动6次图象完成一个循环,从而可得出点A100和点A2022的坐标.【解答】解:(1)根据题意可知,A1(0,0),A2(0,1),A3(1,1),A4(1,0),A5(1,﹣1),A6(2,﹣1),A7(2,0),A8(2,1);(2)根据图象可得移动6次图象完成一个循环,∵100÷6=16……4,2022÷6=337,则点A100的纵坐标是0,点A2022的纵坐标是﹣1,∴点A100在x轴上,A2022在x轴下方.故答案为:x轴上,x轴下方.20.(2022春•西城区校级期中)在平面直角坐标系中,﹣蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位.其行走路线如图所示.(1)填写下列各点的坐标:A4( 2 , 0 ),A8( 4 , 0 );(2)写出点A4n的坐标(n是正整数)A4n( 2n , 0 );(3)求出A2022的坐标.【分析】根据题意可直接找出点的坐标规律,A4n(2n,0),A4n+1(2n,1),A4n+2(2n+1,1),A4n+3(2n+1,0),根据规律直接求出A4(2,0),A8(4,0),A4n(2n,0)A2022(1012,1).【解答】解:观察图形可知,A1(0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,1),A6(3,1),...,A4n(2n,0),A4n+1(2n,1),A4n+2(2n+1,1),A4n+3(2n+1,0),(1)根据题意,可直接读出A4(2,0),A8(4,0),故答案为:2,0,4,0;(2)根据点的坐标规律可知,A4n(2n,0),故答案为:2n,0;(3)∵2022=4×505+2,∴A2022(1011,1).21.(2022•马鞍山一模)如图,某小区绿化区的护栏是由两种大小不等的正方形间隔排列组成,将护栏的图案放在平面直角坐标系中.已知小正方形的边长为1,A1的坐标为(2,2),A2的坐标为(5,2).(1)A3的坐标为 (8,2) ,A n的坐标为 (3n﹣1,2) 用含n的代数式表示;(2)若护栏长为2020,则需要小正方形 674 个,大正方形 673 个.【分析】(1)根据已知条件与图形可知,大正方形的对角线长为2,由此可得规律:A1,A2,A3,…,A n各点的纵坐标均为2,横坐标依次大3,由此便可得结果;(2)先求出一个小正方形与一个大正方形所构成的护栏长度,再计算2020米包含多少这样的长度,进而便可求出结果.【解答】解:(1)∵A1的坐标为(2,2)、A2的坐标为(5,2),∴A1,A2,A3,…,A n各点的纵坐标均为2,∵小正方形的边长为1,∴A1,A2,A3,…,A n各点的横坐标依次大3,∴A3(5+3,2),A n(2+,2),即A3(8,2),A n(3n﹣1,2),故答案为(8,2);(3n﹣1,2);(2)∵2020÷3=673…1,∴需要小正方形674个,大正方形673个.22.(2021秋•长丰县期末)如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2、4、6、8、…,顶点依次用A1、A2、A3、A4、…表示.(1)请直接写出A5、A6、A7、A8的坐标;(2)根据规律,求出A2022的坐标.【分析】(1)看图观察即可直接写出答案;(2)根据正方形的性质找出部分A n点的坐标,根据坐标的变化找出变化规律“A4n+1(﹣n﹣1,﹣n﹣1),A4n+2(﹣n﹣1,n+1),A4n+3(n+1,n+1),A4n+4(n+1,﹣n﹣1)(n为自然数)”,依此即可得出结论.【解答】解:(1)A5(﹣2,﹣2),A6(﹣2,2),A7(2,2),A8(2,﹣2);(2)观察发现:A1(﹣1,﹣1),A2(﹣1,1),A3(1,1),A4(1,﹣1),A5(﹣2,﹣2),A6(﹣2,2),A7(2,2),A8(2,﹣2),A9(﹣3,﹣3),…,∴A4n+1(﹣n﹣1,﹣n﹣1),A4n+2(﹣n﹣1,n+1),A4n+3(n+1,n+1),A4n+4(n+1,﹣n﹣1)(n为自然数),∵2022=505×4+2,∴A2022(﹣506,506).23.(2021秋•万秀区月考)在平面直角坐标系xOy中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫做点P的“伴随点”.已知点A1的“伴随点”为A2,点A2的“伴随点”为A3,点A3的“伴随点”为A4,…,这样依次得到点A1,A2,A3,…,A n.(1)若点A1(3,1),则点A3的坐标为 (﹣3,1) ,点A2022的坐标为 (0,4) ;(2)若点A1(a,b),对于任意的正整数n,若点A n均在x轴的上方,则a,b应满足什么条件?【分析】(1)根据点A1的坐标结合伴随点的定义,即可找到点A2,A3,A4,A5的坐标,进而得出坐标的变化规律:每4个点为一个循环组依次循环,按照此规律即可得出答案;(2)根据点A1的坐标为(a,b)和伴随点的定义,即可求得点A2,A3,A4,A5,A6,……的坐标,总结得出规律,再根据“对于任意的正整数n,点A n均在x轴上方”列出不等式组求解即可.【解答】解:(1)∵点A1的坐标为(3,1),∴点A2的坐标为(0,4),点A3的坐标为(﹣3,1),点A4的坐标为(0,﹣2),点A5的坐标为(3,1),点A6的坐标为(0,4),……,依此类推,每4个点为一个循环组依次循环,∵2022÷4=505……2,∴点A2022的坐标与点A2的坐标相同,为(0,4).故答案为:(﹣3,1),(0,4).(2)∵点A1的坐标为(a,b),∴点A2的坐标为(﹣b+1,a+1),点A3的坐标为(﹣a,﹣b+2),点A4的坐标为(b﹣1,﹣a+1),点A5的坐标为(a,b),点A6的坐标为(﹣b+1,a+1),……,∴点A n的坐标四次一循环.∵对于任意的正整数n,点A n均在x轴上方,∴,解得:﹣1<a<1且0<b<2.。
七年级数学下学期期末培优强化训练13 新人教版

数学培优强化训练(十三)1、2003年10月15日9时10分,我国神舟五号载人飞船准确进入预定轨道.16日5时59分,返回舱与推进舱分离,返回地面.其间飞船绕地球共飞行了14圈,飞行的路程约60万千米,则神舟五号飞船绕地球平均每圈约飞行 (用科学记数法表示保留三个有效数字) ( ) (A )4.28×104千米 (B )4.29×104千米(C )4.28×105千米(D )4.29×105千米2、钟表8时30分时,时针与分针所成的角的度数为 ( )(A )30°(B )60°(C )75°(D )90°3、如图4,在一个正方体的两个面上画了两条对角线AB ,AC , 那么这两条对角线的夹角等于 ( ) (A )600(B )750(C )900(D )13504、若两条平行直线被第三条直线所截得的8个角中有一个角的度数已知,则 ( ) (A )只能求出其余3个角的度数 (B )只能求出其余5个角的度数 (C )只能求出其余6个角的度数 (D )只能求出其余7个角的度数5、如图,有一个无盖的正方体纸盒,下底面标有字母“M”,沿图中粗线将其剪开展成平面图形,想一想,这个平面图形是 ( )(A )(B )(C ) (D )6、如图5,在直角三角形ABC 中,∠ACB=90º,以BC 所在直线为轴旋转一周所得到的几何体是 .图5图67、如图6,∠AOB =600,OD 、OE 分别平分∠BOC 、∠AOC ,那么∠EOD = 0.BAC无盖MMMM图4BAC O AECD B8、每一个多边形都可以按图甲的方法分割成若干个三角形.(图甲) (图乙)根据图甲的方法,图乙中的七边形能分割成 个三角形,那么n 边形能分割成 个三角形.9、有这样一道题: “计算)3()2()232(323323223y y x x y xy x xy y x x -+-++----的值,其中1,21-==y x ”。
人教版七年级数学下册 7.2.1用坐标表示地理位置 培优训练(包含答案)

人教版七年级数学下册7.2.1《用坐标表示地理位置》培优训练一、选择题(共10小题,3*10=30)1.如图是李明家附近区域的平面示意图,如果宠物店所在位置的坐标为(2,-4),儿童公园所在位置的坐标为(0,-3),则学校所在的位置是( )A.(4,-3) B.(4,3)C.(5,-1) D.(2,1)2.在方格纸上有A、B两点,若以B点为原点建立直角坐标系,则A点坐标为(2,5),若以A点为原点建立直角坐标系,则B点坐标为()A.(-2,-5)B.(-2,5)C.(2,-5)D.(2,5)3. 如图是杭州西湖的部分示意图,如以过“曲院风荷”、“中国印学博物馆”的直线为x轴,以这两景点连线的中垂线为y轴,建立直角坐标系(每个小正方形的边长表示1个单位长度),则“苏堤春晓”的坐标是()A.(-7,2) B.(2,-7)C.(-2,-7) D.(-7,-2)4. 如图表示点A的位置,正确的是()A.距离O点3 km的地方B.在O点东偏北40°的方向上C.在O点北偏东40°方向,距O点3 km的地方D.在O点北偏东50°方向,距O点3 km的地方5.如图是株洲市的行政区域平面地图,下列说法明显错误的是( )A.炎陵位于株洲市区南偏东约35°的方向上B.醴陵位于攸县的北偏东约17°的方向上C.株洲县位于茶陵的南偏东约30°的方向上D.株洲市区位于攸县的北偏西约21°的方向上6. 如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(-3,2),(b,m),(c,m),则点E的坐标是()A.(2,-3) B.(2,3)C.(3,2) D.(3,-2)7.点A的位置如图所示,则关于点A的位置下列说法中正确的是()A.距点O 4 km处B.北偏东40°方向上4 km处C.在点O北偏东50°方向上4 km处D.在点O北偏东40°方向上4 km处8.如图是A,B,C,D四位同学的家所在位置,若以A同学家的位置为坐标原点建立平面直角坐标系,那么C同学家的位置的坐标为(1,5),则B,D两同学家的坐标分别为( )A.(2,3),(3,2) B.(3,2),(2,3)C.(2,3),(-3,2) D.(3,2),(-2,3)9.如图所示,若在象棋盘上建立平面直角坐标系,使“将”位于点(1,-2),“象”位于点(3,-2),则“炮”位于点( )A.(1,3) B.(-2,0)C.(-1,2) D.(-2,2)10.“健步走”越来越受到人们的喜爱.某个“健步走”小组将自己的活动场地定在奥林匹克公园,所走路线为:森林公园——玲珑塔——国家体育场——水立方.如图,在奥林匹克公园设计图上设玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),那么水立方的坐标为()A.(-2,-4)B.(-1,-4)C.(-2,4) D.(-4,-1)二.填空题(共8小题,3*8=24)11. 如图,已知A(-2,1),B(-6,0),若白棋A飞挂后,黑棋C尖顶,黑棋C的坐标为(______,_______).12.某镇三个厂址的地理位置如下:汽车配件厂在饲料厂的正南1 000 m,酒厂在汽车配件厂的正西800 m处,若酒厂的坐标是(-800,-1 000),则选取的坐标原点是________.13. 如图,若以解放公园为原点建立平面直角坐标系,则博物馆的坐标为______________.14.如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标分别为A(-2,1)和B(-2,-3),那么第一架轰炸机C的平面坐标是___________.15.如图,图书馆相对于大门的位置是_________________,操场相对于大门的位置是___________________,车站相对于大门的位置是______________.16.如图,小明从点O出发,先向西走40米,再向南走30米到达点M,如果点M的位置用(-40,-30)表示,那么(10,20)表示的位置是______________.17.某飞行监控中心发现某飞机从某个飞机场起飞后沿正南方向飞行100千米,然后向正西方向飞行300千米,又测得该机场的位置位于监控中心的西100千米,北300千米的地方,若以监控中心为坐标原点,以正东、正北方向为x轴、y轴的正方向,请指出该飞机现在的位置____________.(用坐标表示)18.如图是益阳市行政区域图,图中益阳市区所在地用坐标表示为(1,0),安化县城所在地用坐标表示为(-3,-1),那么南县县城所在地用坐标表示为.三.解答题(共6小题,46分)19.(6分) 如图是某市的部分简图,如果少年宫的坐标为(-3, 1),宾馆的坐标为(2, 2),请建立适当的平面直角坐标系,并分别写出其余四个地方的坐标.20.(6分) 如图,这是某市部分简图(图中小正方形的边长代表1 km长).以火车站为坐标原点建立平面直角坐标系.(1)在图中画出平面直角坐标系;(2)分别写出各地的坐标.21.(8分)如图标出了李明家附近的一些地方.(1)根据图中所建立的平面直角坐标系,写出学校、邮局的坐标;(2)某星期日早晨,李明从家里出发,沿着(-2,-1),(-1,-2),(1,-2),(2,-1),(1,-1),(1,3),(-1,0),(0,-1)的路线转了一下,写出他路上经过的地方;22.(8分)如图,长方形ABCD的长与宽分别是6和3,建立适当的直角坐标系,并写出各个顶点的坐标.23.(8分) 如图,一艘客轮在灯塔A的北偏东30°方向上的B处遇险,向相距45海里的码头C发出求救信号.(1)你能准确描述客轮B相对于灯塔A的位置吗?为什么?(2)若客轮B与灯塔A相距60海里,你能用方向和距离描述客轮B相对于灯塔A的位置吗?(3)如何用方向和距离描述客轮B相对于码头C的位置?反过来,如何用方向和距离描述码头C相对于客轮B的位置?24.(10分) 如图所示标明了小刚家附近的一些地方.(1)写出学校和公园的坐标;(2)某星期日早晨,小刚从家里出发,沿(1,-2),(-1,0),(-2,-1),(-2,2),(1,2),(0,1)的路线转了一下,又回到家里,写出他路上经过的地方;(3)连接他在(2)中路过的地点,你能说出它像什么吗?参考答案1-5BABDC 6-10CDDBA11. -1,112. 饲料厂13.(2,2)14. (2,-1)15. 北偏东56°,3 km;北偏西34°,6 km;正南,4 km16.点B17. (-400,200)18. (2,4)19. 解:如图,依题意得原点在客运站的位置,建立如图所示的坐标系,∴超市、客运站、医院、体育馆的坐标分别为(2,-3)、(0,0)、(-2,-2)、(-4,3).20. 解:(1)如图所示:.(2)火车站(0,0),医院(-2,-2),文化宫(-3,1),体育场(-4,3),宾馆(2,2),市场(4,3),超市(2,-3).21. 解:(1)学校(1,3),邮局(0,-1)(2)李明家→商店→公园→汽车站→水果店→学校→游乐场→邮局22. 解:以点B为原点,BC所在直线为x轴,AB所在直线为y轴建立直角坐标系,则A(0,3),B(0,0),C(6,0),D(6,3).23. 解:(1)不能,因为表示平面内的点一般需要两个数据,只有一个数据无法确定物体的位置(2)能,客轮B在灯塔A的北偏东30°,相距60海里处(3)客轮B在码头C的北偏西45°,相距45海里处;码头C在客轮B的南偏东45°,相距45海里处24. 解:(1)学校(-2,-2),公园(1,2).(2)小刚经过的地方分别是小刚家→副食店→汽车站→二姨家→娱乐中心→公园→文具店→小刚家.(3)如图,像一个箭头.。
人教七年级下册数学期末解答题培优试卷(含答案)

人教七年级下册数学期末解答题培优试卷(含答案)一、解答题1.如图,用两个面积为2200cm的小正方形拼成一个大的正方形.(1)则大正方形的边长是;(2)若沿着大正方形边的方向裁出一个长方形,能否使裁出的长方形纸片的长宽之比为4:3,且面积为2360cm?2.如图,用两个面积为28cm的小正方形纸片剪拼成一个大的正方形.(1)大正方形的边长是________cm;(2)请你探究是否能将此大正方形纸片沿着边的方向裁出一个面积为214cm的长方形纸片,使它的长宽之比为2:1,若能,求出这个长方形纸片的长和宽,若不能,请说明理由.3.如图所示的正方形纸板是由两张大小相同的长方形纸板拼接而成的,已知一个长方形纸板的面积为162平方厘米,求正方形纸板的边长.4.如图,这是由8个同样大小的立方体组成的魔方,体积为64.(1)求出这个魔方的棱长;(2)图中阴影部分是一个正方形ABCD,求出阴影部分的边长.5.如图,用两个边长为3.(1)求大正方形的边长?(2)若沿此大正方形边的方向出一个长方形,能否使裁出的长方形的长宽之比为3:2,且面积为480cm2?二、解答题6.已知直线AB//CD,点P、Q分别在AB、CD上,如图所示,射线PB按逆时针方向以每秒12°的速度旋转至PA便立即回转,并不断往返旋转;射线QC按逆时针方向每秒3°旋转至QD停止,此时射线PB也停止旋转.(1)若射线PB、QC同时开始旋转,当旋转时间10秒时,PB'与QC'的位置关系为;(2)若射线QC先转15秒,射线PB才开始转动,当射线PB旋转的时间为多少秒时,PB′//QC′.7.如图1,已知直线CD∥EF,点A,B分别在直线CD与EF上.P为两平行线间一点.(1)若∠DAP=40°,∠FBP=70°,则∠APB=(2)猜想∠DAP,∠FBP,∠APB之间有什么关系?并说明理由;(3)利用(2)的结论解答:①如图2,AP1,BP1分别平分∠DAP,∠FBP,请你写出∠P与∠P1的数量关系,并说明理由;②如图3,AP2,BP2分别平分∠CAP,∠EBP,若∠APB=β,求∠AP2B.(用含β的代数式表示)8.如图1,AB//CD,点E、F分别在AB、CD上,点O在直线AB、CD之间,且∠=︒.100EOF(1)求BEO OFD ∠+∠的值;(2)如图2,直线MN 分别交BEO ∠、OFC ∠的角平分线于点M 、N ,直接写出EMN FNM ∠-∠的值;(3)如图3,EG 在AEO ∠内,AEG m OEG ∠=∠;FH 在DFO ∠内,DFH m OFH ∠=∠,直线MN 分别交EG 、FH 分别于点M 、N ,且50FMN ENM ∠-∠=︒,直接写出m 的值.9.如图1,把一块含30°的直角三角板ABC 的BC 边放置于长方形直尺DEFG 的EF 边上. (1)根据图1填空:∠1= °,∠2= °; (2)现把三角板绕B 点逆时针旋转n °.①如图2,当n =25°,且点C 恰好落在DG 边上时,求∠1、∠2的度数;②当0°<n <180°时,是否会存在三角板某一边所在的直线与直尺(有四条边)某一边所在的直线垂直?如果存在,请直接写出所有n 的值和对应的那两条垂线;如果不存在,请说明理由.10.点A ,C ,E 在直线l 上,点B 不在直线l 上,把线段AB 沿直线l 向右平移得到线段CD .(1)如图1,若点E 在线段AC 上,求证:∠B +∠D =∠BED ;(2)若点E 不在线段AC 上,试猜想并证明∠B ,∠D ,∠BED 之间的等量关系; (3)在(1)的条件下,如图2所示,过点B 作PB //ED ,在直线BP ,ED 之间有点M ,使得∠ABE =∠EBM ,∠CDE =∠EDM ,同时点F 使得∠ABE =n ∠EBF ,∠CDE =n ∠EDF ,其中n ≥1,设∠BMD =m ,利用(1)中的结论求∠BFD 的度数(用含m ,n 的代数式表示).三、解答题11.问题情境(1)如图1,已知//, 125155AB CD PBA PCD ︒︒∠=∠=,,求BPC ∠的度数.佩佩同学的思路:过点P 作//PN AB ,进而//PN CD ,由平行线的性质来求BPC ∠,求得BPC ∠︒;问题迁移(2)图2,图3均是由一块三角板和一把直尺拼成的图形,三角板的两直角边与直尺的两边重合90,//,ACB DF CG AB ︒∠=与FD 相交于点E ,有一动点P 在边BC 上运动,连接, PE PA ,记,PED PAC αβ∠=∠∠=∠.①如图2,当点P 在,C D 两点之间运动时,请直接写出APE ∠与,αβ∠∠之间的数量关系;②如图3,当点P 在,B D 两点之间运动时,APE ∠与,αβ∠∠之间有何数量关系?请判断并说明理由.12.已知AB ∥CD ,点M 在直线AB 上,点N 、Q 在直线CD 上,点P 在直线AB 、CD 之间,∠AMP =∠PQN =α,PQ 平分∠MPN .(1)如图①,求∠MPQ 的度数(用含α的式子表示);(2)如图②,过点Q 作QE ∥PN 交PM 的延长线于点E ,过E 作EF 平分∠PEQ 交PQ 于点F .请你判断EF 与PQ 的位置关系,并说明理由;(3)如图③,在(2)的条件下,连接EN ,若NE 平分∠PNQ ,请你判断∠NEF 与∠AMP 的数量关系,并说明理由.13.如图1,O 为直线AB 上一点,过点O 作射线,30OC AOC ︒∠=,将一直角三角板(30M ︒∠=)的直角顶点放在点O 处,一边ON 在射线OA 上,另一边OM 与OC 都在直线AB 的上方,将图1中的三角板绕点O 以每秒3°的速度沿顺时针方向旋转一周.(1)几秒后ON 与OC 重合?(2)如图2,经过t 秒后,//MN AB ,求此时t 的值.(3)若三角板在转动的同时,射线OC 也绕O 点以每秒6°的速度沿顺时针方向旋转一周,那么经过多长时间OC 与OM 重合?请画图并说明理由.(4)在(3)的条件下,求经过多长时间OC 平分MOB ∠?请画图并说明理由. 14.如图所示,已知//AM BN ,点P 是射线AM 上一动点(与点A 不重合),BC 、BD 分别平分ABP ∠和PBN ∠,分别交射线AM 于点C 、D ,且60CBD ∠=︒ (1)求A ∠的度数.(2)当点P 运动时,APB ∠与ADB ∠之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律. (3)当点P 运动到使ACB ABD =∠∠时,求ABC ∠的度数.15.如图1,D 是△ABC 延长线上的一点,CE //AB . (1)求证:∠ACD =∠A+∠B ;(2)如图2,过点A 作BC 的平行线交CE 于点H ,CF 平分∠ECD ,FA 平分∠HAD ,若∠BAD =70°,求∠F 的度数.(3)如图3,AH //BD ,G 为CD 上一点,Q 为AC 上一点,GR 平分∠QGD 交AH 于R ,QN 平分∠AQG 交AH 于N ,QM //GR ,猜想∠MQN 与∠ACB 的关系,说明理由.四、解答题16.如图,直线//AB CD ,E 、F 是AB 、CD 上的两点,直线l 与AB 、CD 分别交于点G 、H ,点P 是直线l 上的一个动点(不与点G 、H 重合),连接PE 、PF .(1)当点P 与点E 、F 在一直线上时,GEP EGP ∠=∠,60FHP ∠=︒,则PFD ∠=_____.(2)若点P 与点E 、F 不在一直线上,试探索AEP ∠、EPF ∠、CFP ∠之间的关系,并证明你的结论.17.己知:如图①,直线MN ⊥直线PQ ,垂足为O ,点A 在射线OP 上,点B 在射线OQ 上(A 、B 不与O 点重合),点C 在射线ON 上且2OC =,过点C 作直线//l PQ .点D 在点C 的左边且3CD =(1)直接写出的BCD ∆面积 ;(2)如图②,若AC BC ⊥,作CBA ∠的平分线交OC 于E ,交AC 于F ,试说明CEF CFE ∠=∠;(3)如图③,若ADC DAC ∠=∠,点B 在射线OQ 上运动,ACB ∠的平分线交DA 的延长线于点H ,在点B 运动过程中HABC∠∠的值是否变化?若不变,求出其值;若变化,求出变化范围. 18.如果三角形的两个内角α与β满足290αβ+=︒,那么我们称这样的三角形是“准互余三角形”.(1)如图1,在Rt ABC 中,90ACB ∠=︒,BD 是ABC 的角平分线,求证:ABD △是“准互余三角形”;(2)关于“准互余三角形”,有下列说法:①在ABC 中,若100A ∠=︒,70B ∠=︒,10C ∠=︒,则ABC 是“准互余三角形”; ②若ABC 是“准互余三角形”,90C ∠>︒,60A ∠=︒,则20B ∠=︒; ③“准互余三角形”一定是钝角三角形.其中正确的结论是___________(填写所有正确说法的序号);(3)如图2,B ,C 为直线l 上两点,点A 在直线l 外,且50ABC ∠=︒.若P 是直线l 上一点,且ABP △是“准互余三角形”,请直接写出APB ∠的度数.19.如图,//MN GH ,点A 、B 分别在直线MN 、GH 上,点O 在直线MN 、GH 之间,若116NAO ∠=︒,144OBH ∠=︒.(1)AOB ∠= ︒;(2)如图2,点C 、D 是NAO ∠、GBO ∠角平分线上的两点,且35CDB ∠=︒,求ACD ∠ 的度数;(3)如图3,点F 是平面上的一点,连结FA 、FB ,E 是射线FA 上的一点,若MAE ∠=n OAE ∠,HBF n OBF ∠=∠,且60AFB ∠=︒,求n 的值.20.已知,//AB CD ,点E 为射线FG 上一点.(1)如图1,写出EAF ∠、AED ∠、EDG ∠之间的数量关系并证明; (2)如图2,当点E 在FG 延长线上时,求证:EAF AED EDG ∠=∠+∠;(3)如图3,AI 平分BAE ∠,DI 交AI 于点I ,交AE 于点K ,且EDI ∠:2:1CDI ∠=,20AED ∠=︒,30I ∠=︒,求EKD ∠的度数.【参考答案】一、解答题1.(1);(2)无法裁出这样的长方形. 【分析】(1)先计算两个小正方形的面积之和,在根据算术平方根的定义,即可求解; (2)设长方形长为cm ,宽为cm ,根据题意列出方程,解方程比较4x 与20的大小 解析:(1)20;(2)无法裁出这样的长方形. 【分析】(1)先计算两个小正方形的面积之和,在根据算术平方根的定义,即可求解;(2)设长方形长为4x cm ,宽为3x cm ,根据题意列出方程,解方程比较4x 与20的大小即可. 【详解】解:(1)由题意得,大正方形的面积为200+200=400cm 2, ∴400=20cm ;()2根据题意设长方形长为4x cm ,宽为3x cm ,由题:43360x x ⋅= 则230x =0x30x ∴=∴长为>43020∴无法裁出这样的长方形.【点睛】本题考查了算术平方根,根据题意列出算式(方程)是解决此题的关键.2.(1)4;(2)不能,理由见解析.【分析】(1)根据已知正方形的面积求出大正方形的边长即可;(2)先设未知数根据面积=14(cm2)列方程,求出长方形的边长,将长方形的长与正方形边长比较大小再解析:(1)4;(2)不能,理由见解析.【分析】(1)根据已知正方形的面积求出大正方形的边长即可;(2)先设未知数根据面积=14(cm2)列方程,求出长方形的边长,将长方形的长与正方形边长比较大小再判断即可.【详解】解:(1)两个正方形面积之和为:2×8=16(cm2),∴拼成的大正方形的面积=16(cm2),∴大正方形的边长是4cm;故答案为:4;(2)设长方形纸片的长为2xcm,宽为xcm,则2x•x=14,解得:x=2x,∴不存在长宽之比为2:1且面积为214cm的长方形纸片.【点睛】本题考查了算术平方根,能够根据题意列出算式是解此题的关键.3.正方形纸板的边长是18厘米【分析】根据正方形的面积公式进行解答.【详解】解:设小长方形的宽为x厘米,则小长方形的长为厘米,即得正方形纸板的边长是厘米,根据题意得:,∴,取正值,可得,解析:正方形纸板的边长是18厘米【分析】根据正方形的面积公式进行解答. 【详解】解:设小长方形的宽为x 厘米,则小长方形的长为2x 厘米,即得正方形纸板的边长是2x 厘米,根据题意得:2162x x ⋅=,∴281x =,取正值9x =,可得218x =, ∴答:正方形纸板的边长是18厘米. 【点评】本题考查了算术平方根的实际应用,解题的关键是熟悉正方形的面积公式.4.(1)棱长为4;(2)边长为:(或) 【分析】(1)由立方体的体积为棱长的立方可以得到答案;(2)用勾股定理直接计算得到答案. 【详解】解:(1)设正方体的棱长为,则,所以,即正方体的棱长为4.解析:(1)棱长为4;(2 【分析】(1)由立方体的体积为棱长的立方可以得到答案;(2)用勾股定理直接计算得到答案. 【详解】解:(1)设正方体的棱长为x ,则364x =,所以4x =,即正方体的棱长为4.(2)因为正方体的棱长为4,所以AB= 【点睛】本题考查的是立方根与算术平方根的理解与计算,由实际的情境去理解问题本身就是求一个数的立方根与算术平方根是关键.5.(1)大正方形的边长是;(2)不能 【分析】(1)根据已知正方形的面积求出大正方形的面积,即可求出边长; (2)先求出长方形的边长,再判断即可. 【详解】(1)大正方形的边长是 (2)设长方形纸解析:(1)大正方形的边长是2)不能 【分析】(1)根据已知正方形的面积求出大正方形的面积,即可求出边长; (2)先求出长方形的边长,再判断即可.【详解】(1)大正方形的边长是106(2)设长方形纸片的长为3xcm,宽为2xcm,则3x•2x=480,解得:x=80因为380106,所以沿此大正方形边的方向剪出一个长方形,不能使剪出的长方形纸片的长宽之比为2:3,且面积为480cm2.【点睛】本题考查算术平方根,解题的关键是能根据题意列出算式.二、解答题6.(1)PB′⊥QC′;(2)当射线PB旋转的时间为5秒或25秒或45秒时,PB′∥QC′【分析】(1)求出旋转10秒时,∠BPB′和∠CQC′的度数,设PB′与QC′交于O,过O作OE∥AB,根解析:(1)PB′⊥QC′;(2)当射线PB旋转的时间为5秒或25秒或45秒时,PB′∥QC′【分析】(1)求出旋转10秒时,∠BPB′和∠CQC′的度数,设PB′与QC′交于O,过O作OE∥AB,根据平行线的性质求得∠POE和∠QOE的度数,进而得结论;(2)分三种情况:①当0<t≤15时,②当15<t≤30时,③当30<t<45时,根据平行线的性质,得出角的关系,列出t的方程便可求得旋转时间.【详解】解:(1)如图1,当旋转时间30秒时,由已知得∠BPB′=10°×12=120°,∠CQC′=3°×10=30°,过O作OE∥AB,∵AB∥CD,∴AB∥OE∥CD,∴∠POE=180°﹣∠BPB′=60°,∠QOE=∠CQC′=30°,∴∠POQ=90°,∴PB′⊥QC′,故答案为:PB′⊥QC′;(2)①当0<t≤15时,如图,则∠BPB′=12t°,∠CQC′=45°+3t°,∵AB∥CD,PB′∥QC′,∴∠BPB′=∠PEC=∠CQC′,即12t=45+3t,解得,t=5;②当15<t≤30时,如图,则∠APB′=12t﹣180°,∠CQC'=3t+45°,∵AB∥CD,PB′∥QC′,∴∠BPB′=∠BEQ=∠CQC′,即12t﹣180=45+3t,解得,t=25;③当30<t≤45时,如图,则∠BPB′=12t﹣360°,∠CQC′=3t+45°,∵AB∥CD,PB′∥QC′,∴∠BPB′=∠BEQ=∠CQC′,即12t﹣360=45+3t,解得,t=45;综上,当射线PB旋转的时间为5秒或25秒或45秒时,PB′∥QC′.【点睛】本题主要考查了平行线的性质,第(1)题关键是作平行线,第(2)题关键是分情况讨论,运用方程思想解决几何问题.7.(1)110°;(2)猜想:∠APB=∠DAP+∠FBP,理由见解析;(3)①∠P=2∠P1,理由见解析;②∠AP2B=.【分析】(1)过P作PM∥CD,根据两直线平行,内错角相等可得∠APM=解析:(1)110°;(2)猜想:∠APB=∠DAP+∠FBP,理由见解析;(3)①∠P=2∠P1,理由见解析;②∠AP2B=1 1802β︒-.【分析】(1)过P作PM∥CD,根据两直线平行,内错角相等可得∠APM=∠DAP,再根据平行公理求出CD∥EF然后根据两直线平行,内错角相等可得∠MPB=∠FBP,最后根据∠APM+∠MPB=∠DAP+∠FBP等量代换即可得证;(2)结论:∠APB=∠DAP+∠FBP.(3)①根据(2)的规律和角平分线定义解答;②根据①的规律可得∠APB=∠DAP+∠FBP,∠AP2B=∠CAP2+∠EBP2,然后根据角平分线的定义和平角等于180°列式整理即可得解.【详解】(1)证明:过P作PM∥CD,∴∠APM=∠DAP.(两直线平行,内错角相等),∵CD∥EF(已知),∴PM∥CD(平行于同一条直线的两条直线互相平行),∴∠MPB=∠FBP.(两直线平行,内错角相等),∴∠APM+∠MPB=∠DAP+∠FBP.(等式性质)即∠APB=∠DAP+∠FBP=40°+70°=110°.(2)结论:∠APB=∠DAP+∠FBP.理由:见(1)中证明.(3)①结论:∠P=2∠P1;理由:由(2)可知:∠P=∠DAP+∠FBP,∠P1=∠DAP1+∠FBP1,∵∠DAP=2∠DAP1,∠FBP=2∠FBP1,∴∠P=2∠P1.②由①得∠APB =∠DAP +∠FBP ,∠AP 2B =∠CAP 2+∠EBP 2,∵AP 2、BP 2分别平分∠CAP 、∠EBP ,∴∠CAP 2=12∠CAP ,∠EBP 2=12∠EBP ,∴∠AP 2B =12∠CAP +12∠EBP , = 12(180°-∠DAP )+ 12(180°-∠FBP ),=180°- 12(∠DAP +∠FBP ),=180°- 12∠APB ,=180°- 12β.【点睛】本题考查了平行线的性质,角平分线的定义,熟记性质与概念是解题的关键,此类题目,难点在于过拐点作平行线. 8.(1) ;(2)的值为40°;(3).【分析】(1)过点O 作OG ∥AB ,可得AB ∥OG ∥CD ,利用平行线的性质可求解; (2)过点M 作MK ∥AB ,过点N 作NH ∥CD ,由角平分线的定义可设∠BEM解析:(1)260BEO DFO ∠+∠=︒ ;(2)EMN FNM ∠-∠的值为40°;(3)53. 【分析】(1)过点O 作OG ∥AB ,可得AB ∥OG ∥CD ,利用平行线的性质可求解;(2)过点M 作MK ∥A B ,过点N 作NH ∥CD ,由角平分线的定义可设∠BEM =∠OEM =x ,∠CFN =∠OFN =y ,由∠BEO +∠DFO =260°可求x -y =40°,进而求解;(3)设直线FK 与EG 交于点H ,FK 与AB 交于点K ,根据平行线的性质即三角形外角的性质及50FMN ENM ∠-∠=︒,可得50KFD AEG ∠-∠=︒,结合260AEG n OEG DFK n OFK BEO DFO ∠=∠=∠∠+∠=︒,,,可得11180100AEG AEG KFD KFD n n∠+∠+︒-∠-∠=︒, 即可得关于n 的方程,计算可求解n 值.【详解】证明:过点O 作OG ∥AB ,∵AB ∥CD ,∴AB ∥OG ∥CD ,∴180180BEO EOG DFO FOG ∠+∠=︒∠+∠=︒,,∴360BEO EOG DFO FOG ∠+∠+∠+∠=︒,即360BEO EOF DFO ∠+∠+∠=︒,∵∠EOF =100°,∴∠260BEO DFO +∠=︒;(2)解:过点M 作MK ∥AB ,过点N 作NH ∥CD ,∵EM 平分∠BEO ,FN 平分∠CFO ,设BEM OEM x CFN OFN y ∠=∠=∠=∠=,,∵260BEO DFO ∠+∠=︒∴21802260BEO DFO x y ∠+∠=+︒-=︒,∴x -y =40°,∵MK ∥AB ,NH ∥CD ,AB ∥CD ,∴AB ∥MK ∥NH ∥CD ,∴EMK BEM x HNF CFN y KMN HNM ∠=∠=∠=∠=∠=∠,,,∴EMN FNM EMK KMN HNM HNF ∠+∠=∠+∠-∠+∠()x KMN HNM y =+∠-∠-=x -y=40°,故EMN FNM ∠-∠的值为40°;(3)如图,设直线FK 与EG 交于点H ,FK 与AB 交于点K ,∵AB ∥CD ,∴AKF KFD ∠=∠,∵AKF EHK HEK EHK AEG ∠=∠+∠=∠+∠,∴KFD EHK AEG ∠=∠+∠,∵50EHK NMF ENM ∠=∠-∠=︒,∴50KFD AEG ∠=︒+∠,即50KFD AEG ∠-∠=︒,∵AEG n OEG ∠=∠,FK 在∠DFO 内,DFK n OFK ∠=∠. ∴1180180CFO DFK OFK KFD KFD n∠=︒-∠-∠=︒-∠-∠ , 1AEO AEG OEG AEG AEG n∠=∠+∠=∠+∠, ∵260BEO DFO ∠+∠=︒,∴100AEO CFO ∠+∠=︒, ∴11180100AEG AEG KFD KFD n n∠+∠+︒-∠-∠=︒, 即(180)1KFD AEG n ⎛⎫ ⎪⎝∠⎭+-∠︒=, ∴115080n ⎛⎫ ⎪⨯⎭︒︒⎝+=, 解得53n = .经检验,符合题意, 故答案为:53. 【点睛】本题主要考查平行线的性质,角平分线的定义,灵活运用平行线的性质是解题的关键. 9.(1)120,90;(2)①∠1=120°-n°,∠2=90°+n°;②见解析【分析】(1)根据邻补角的定义和平行线的性质解答;(2)①根据邻补角的定义求出∠ABE,再根据两直线平行,同位角相解析:(1)120,90;(2)①∠1=120°-n°,∠2=90°+n°;②见解析【分析】(1)根据邻补角的定义和平行线的性质解答;(2)①根据邻补角的定义求出∠ABE,再根据两直线平行,同位角相等可得∠1=∠ABE,根据两直线平行,同旁内角互补求出∠BCG,然后根据周角等于360°计算即可得到∠2;②结合图形,分A B、B C、AC三条边与直尺垂直讨论求解.【详解】解:(1)∠1=180°-60°=120°,∠2=90°;故答案为:120,90;(2)①如图2,∵∠ABC=60°,∴∠ABE=180°-60°-n°=120°-n°,∵DG∥EF,∴∠1=∠ABE=120°-n°,∠BCG=180°-∠CBF=180°-n°,∵∠ACB+∠BCG+∠2=360°,∴∠2=360°-∠ACB-∠BCG=360°-90°-(180°-n°)=90°+n°;②当n=30°时,∵∠ABC=60°,∴∠ABF=30°+60°=90°,AB⊥DG(EF);当n=90°时,∠C=∠CBF=90°,∴BC⊥DG(EF),AC⊥DE(GF);当n=120°时,∴AB⊥DE(GF).【点睛】本题考查了平行线角的计算,垂线的定义,主要利用了平行线的性质,直角三角形的性质,读懂题目信息并准确识图是解题的关键.10.(1)见解析;(2)当点E在CA的延长线上时,∠BED=∠D-∠B;当点E 在AC的延长线上时,∠BED=∠BET-∠DET=∠B-∠D;(3)【分析】(1)如图1中,过点E作ET∥AB.利用平行解析:(1)见解析;(2)当点E在CA的延长线上时,∠BED=∠D-∠B;当点E在AC的延长线上时,∠BED=∠BET-∠DET=∠B-∠D;(3)()12m nn-【分析】(1)如图1中,过点E作ET∥A B.利用平行线的性质解决问题.(2)分两种情形:如图2-1中,当点E在CA的延长线上时,如图2-2中,当点E在AC的延长线上时,构造平行线,利用平行线的性质求解即可.(3)利用(1)中结论,可得∠BMD=∠ABM+∠CDM,∠BFD=∠ABF+∠CDF,由此解决问题即可.【详解】解:(1)证明:如图1中,过点E作ET∥A B.由平移可得AB∥CD,∵AB∥ET,AB∥CD,∴ET∥CD∥AB,∴∠B=∠BET,∠TED=∠D,∴∠BED=∠BET+∠DET=∠B+∠D.(2)如图2-1中,当点E在CA的延长线上时,过点E作ET∥A B.∵AB∥ET,AB∥CD,∴ET∥CD∥AB,∴∠B=∠BET,∠TED=∠D,∴∠BED=∠DET-∠BET=∠D-∠B.如图2-2中,当点E在AC的延长线上时,过点E作ET∥A B.∵AB∥ET,AB∥CD,∴ET∥CD∥AB,∴∠B=∠BET,∠TED=∠D,∴∠BED=∠BET-∠DET=∠B-∠D.(3)如图,设∠ABE=∠EBM=x,∠CDE=∠EDM=y,∵AB ∥CD ,∴∠BMD =∠ABM +∠CDM ,∴m =2x +2y ,∴x +y =12m ,∵∠BFD =∠ABF +∠CDF ,∠ABE =n ∠EBF ,∠CDE =n ∠EDF ,∴∠BFD =()111n n n x y x y n n n ---+=+=112n m n -⨯=()12m n n -. 【点睛】本题属于几何变换综合题,考查了平行线的性质,角平分线的定义等知识,解题的关键是学会条件常用辅助线,构造平行线解决问题,属于中考常考题型. 三、解答题11.(1)80;(2)①;②【分析】(1)过点P 作PG ∥AB ,则PG ∥CD ,由平行线的性质可得∠BPC 的度数; (2)①过点P 作FD 的平行线,依据平行线的性质可得∠APE 与∠α,∠β之间的数量关系;解析:(1)80;(2)①APE αβ∠=∠+∠;②APE βα∠=∠-∠【分析】(1)过点P 作PG ∥AB ,则PG ∥CD ,由平行线的性质可得∠BPC 的度数;(2)①过点P 作FD 的平行线,依据平行线的性质可得∠APE 与∠α,∠β之间的数量关系;②过P 作PQ ∥DF ,依据平行线的性质可得∠β=∠QPA ,∠α=∠QPE ,即可得到∠APE =∠APQ -∠EPQ =∠β-∠α.【详解】解:(1)过点P 作PG ∥AB ,则PG ∥CD ,由平行线的性质可得∠B +∠BPG =180°,∠C +∠CPG =180°,又∵∠PBA =125°,∠PCD =155°,∴∠BPC =360°-125°-155°=80°,故答案为:80;(2)①如图2,过点P 作FD 的平行线PQ ,则DF∥PQ∥AC,∴∠α=∠EPQ,∠β=∠APQ,∴∠APE=∠EPQ+∠APQ=∠α+∠β,∠APE与∠α,∠β之间的数量关系为∠APE=∠α+∠β;②如图3,∠APE与∠α,∠β之间的数量关系为∠APE=∠β-∠α;理由:过P作PQ∥DF,∵DF∥CG,∴PQ∥CG,∴∠β=∠QPA,∠α=∠QPE,∴∠APE=∠APQ-∠EPQ=∠β-∠α.【点睛】本题主要考查了平行线的性质,解决问题的关键是过拐点作平行线,利用平行线的性质得出结论.12.(1)2α;(2)EF⊥PQ,见解析;(3)∠NEF=∠AMP,见解析【分析】1)如图①,过点P作PR∥AB,可得AB∥CD∥PR,进而可得结论;(2)根据已知条件可得2∠EPQ+2∠PEF=∠AMP,见解析解析:(1)2α;(2)EF⊥PQ,见解析;(3)∠NEF=12【分析】1)如图①,过点P作PR∥AB,可得AB∥CD∥PR,进而可得结论;(2)根据已知条件可得2∠EPQ+2∠PEF=180°,进而可得EF与PQ的位置关系;(3)结合(2)和已知条件可得∠QNE=∠QEN,根据三角形内角和定理可得∠QNE=12(180°﹣3α),可得∠NEF=180°﹣∠QEF﹣∠NQE﹣∠QNE,进而可(180°﹣∠NQE)=12得结论.【详解】解:(1)如图①,过点P作PR∥AB,∵AB∥CD,∴AB∥CD∥PR,∴∠AMP=∠MPR=α,∠PQN=∠RPQ=α,∴∠MPQ=∠MPR+∠RPQ=2α;(2)如图②,EF⊥PQ,理由如下:∵PQ平分∠MPN.∴∠MPQ=∠NPQ=2α,∵QE∥PN,∴∠EQP=∠NPQ=2α,∴∠EPQ=∠EQP=2α,∵EF平分∠PEQ,∴∠PEQ=2∠PEF=2∠QEF,∵∠EPQ+∠EQP+∠PEQ=180°,∴2∠EPQ+2∠PEF=180°,∴∠EPQ+∠PEF=90°,∴∠PFE=180°﹣90°=90°,∴EF⊥PQ;∠AMP,理由如下:(3)如图③,∠NEF=12由(2)可知:∠EQP=2α,∠EFQ=90°,∴∠QEF=90°﹣2α,∵∠PQN=α,∴∠NQE=∠PQN+∠EQP=3α,∵NE平分∠PNQ,∴∠PNE=∠QNE,∵QE∥PN,∴∠QEN=∠PNE,∴∠QNE=∠QEN,∵∠NQE=3α,∴∠QNE=12(180°﹣∠NQE)=12(180°﹣3α),∴∠NEF=180°﹣∠QEF﹣∠NQE﹣∠QNE=180°﹣(90°﹣2α)﹣3α﹣12(180°﹣3α)=180°﹣90°+2α﹣3α﹣90°+3 2α=12α=12∠AMP.∴∠NEF=12∠AMP.【点睛】本题考查了平行线的性质,角平分线的性质,熟悉相关性质是解题的关键.13.(1)10秒;(2)20秒;(3)20秒,画图见解析;(4)秒,画图见解析【分析】(1)用角的度数除以转动速度即可得;(2)求出∠AON=60°,结合旋转速度可得时间t;(3)设∠AON=3解析:(1)10秒;(2)20秒;(3)20秒,画图见解析;(4)703秒,画图见解析【分析】(1)用角的度数除以转动速度即可得;(2)求出∠AON=60°,结合旋转速度可得时间t;(3)设∠AON=3t,则∠AOC=30°+6t,由题意列出方程,解方程即可;(4)根据转动速度关系和OC平分∠MOB,由题意列出方程,解方程即可.【详解】解:(1)∵30÷3=10,∴10秒后ON与OC重合;(2)∵MN∥AB∴∠BOM=∠M=30°,∵∠AON+∠BOM=90°,∴∠AON=60°,∴t=60÷3=20∴经过t秒后,MN∥AB,t=20秒.(3)如图3所示:∵∠AON+∠BOM=90°,∠BOC=∠BOM,∵三角板绕点O以每秒3°的速度,射线OC也绕O点以每秒6°的速度旋转,设∠AON=3t,则∠AOC=30°+6t,∵OC与OM重合,∵∠AOC+∠BOC=180°,可得:(30°+6t)+(90°-3t)=180°,解得:t=20秒;即经过20秒时间OC与OM重合;(4)如图4所示:∵∠AON+∠BOM=90°,∠BOC=∠COM,∵三角板绕点O以每秒3°的速度,射线OC也绕O点以每秒6°的速度旋转,设∠AON=3t,∠AOC=30°+6t,∵∠BOM+∠AON=90°,∴∠BOC=∠COM=12∠BOM=12(90°-3t),由题意得:180°-(30°+6t)=12( 90°-3t),解得:t=703秒,即经过703秒OC 平分∠MOB . 【点睛】 此题考查了平行线的判定与性质,角的计算以及方程的应用,关键是应该认真审题并仔细观察图形,找到各个量之间的关系求出角的度数是解题的关键.14.(1);(2)不变化,,理由见解析;(3)【分析】(1)结合题意,根据角平分线的性质,得;再根据平行线的性质计算,即可得到答案;(2)根据平行线的性质,得,;结合角平分线性质,得,即可完成求解 解析:(1)60A ∠=;(2)不变化,2APB ADB ∠=∠,理由见解析;(3)30ABC ∠=【分析】(1)结合题意,根据角平分线的性质,得ABN ∠;再根据平行线的性质计算,即可得到答案;(2)根据平行线的性质,得APB PBN ∠=∠,ADB DBN ∠=∠;结合角平分线性质,得2APB ADB ∠=∠,即可完成求解;(3)根据平行线的性质,得ACB CBN ∠=∠;结合ACB ABD =∠∠,推导得ABC DBN ∠=∠;再结合(1)的结论计算,即可得到答案.【详解】(1)∵BC ,BD 分别评分ABP ∠和PBN ∠, ∴1122CBP ABP DBP PBN ∠=∠∠=∠,, ∴2ABN CBD ∠=∠又∵60CBD ∠=,∴120ABN ∠=∵//AM BN ,∴180A ABN ∠+∠=∴60A ∠=;(2)∵//AM BN ,∴APB PBN ∠=∠,ADB DBN ∠=∠又∵BD 平分PBN ∠∴2PBN DBN ∠=∠,∴2APB ADB ∠=∠;∴APB ∠与ADB ∠之间的数量关系保持不变;(3)∵//AD BN ,∴ACB CBN ∠=∠又∵ACB ABD =∠∠,∴CBN ABD ∠=∠,∵ABC CBN ABD DBN ∠+∠=∠+∠∴ABC DBN ∠=∠由(1)可得60CBD ∠=,120ABN ∠= ∴()112060302ABC ∠=⨯-=. 【点睛】本题考查了角平分线、平行线的知识;解题的关键是熟练掌握角平分线、平行线的性质,从而完成求解.15.(1)证明见解析;(2)∠F=55°;(3)∠MQN =∠ACB ;理由见解析.【分析】(1)首先根据平行线的性质得出∠ACE =∠A ,∠ECD =∠B ,然后通过等量代换即可得出答案;(2)首先根据角解析:(1)证明见解析;(2)∠F=55°;(3)∠MQN =12∠ACB ;理由见解析.【分析】(1)首先根据平行线的性质得出∠ACE =∠A ,∠ECD =∠B ,然后通过等量代换即可得出答案;(2)首先根据角平分线的定义得出∠FCD =12∠ECD ,∠HAF =12∠HAD ,进而得出∠F =12(∠HAD+∠ECD ),然后根据平行线的性质得出∠HAD+∠ECD 的度数,进而可得出答案;(3)根据平行线的性质及角平分线的定义得出12QGR QGD ∠=∠,12NQG AQG ∠=∠,180MQG QGR ∠+∠=︒ ,再通过等量代换即可得出∠MQN =12∠ACB . 【详解】解:(1)∵CE //AB ,∴∠ACE =∠A ,∠ECD =∠B ,∵∠ACD =∠ACE+∠ECD ,∴∠ACD =∠A+∠B ;(2)∵CF 平分∠ECD ,FA 平分∠HAD ,∴∠FCD =12∠ECD ,∠HAF =12∠HAD ,∴∠F =12∠HAD+12∠ECD =12(∠HAD+∠ECD ),∵CH //AB ,∴∠ECD =∠B ,∵AH //BC ,∴∠B+∠HAB =180°,∵∠BAD =70°, 110B HAD ∴∠+∠=︒,∴∠F =12(∠B+∠HAD )=55°;(3)∠MQN =12∠ACB ,理由如下: GR 平分QGD ∠,12QGR QGD ∴∠=∠. GN 平分AQG ∠,12NQG AQG ∴∠=∠. //QM GR ,180MQG QGR ∴∠+∠=︒ .∴∠MQN =∠MQG ﹣∠NQG=180°﹣∠QGR ﹣∠NQG=180°﹣12(∠AQG+∠QGD )=180°﹣12(180°﹣∠CQG+180°﹣∠QGC ) =12(∠CQG+∠QGC ) =12∠ACB .【点睛】本题主要考查平行线的性质和角平分线的定义,掌握平行线的性质和角平分线的定义是解题的关键. 四、解答题16.(1)120°;(2)∠EPF =∠AEP+∠CFP 或∠AEP=∠EPF+∠CFP ,证明见详解.【分析】(1)根据题意,当点与点、在一直线上时,作出图形,由AB ∥CD ,∠FHP=60°,可以推出解析:(1)120°;(2)∠EPF =∠AEP+∠CFP 或∠AEP=∠EPF+∠CFP ,证明见详解.【分析】(1)根据题意,当点P 与点E 、F 在一直线上时,作出图形,由AB ∥CD ,∠FHP=60°,可以推出GEP EGP ∠=∠=60°,计算∠PFD 即可;(2)根据点P 是动点,分三种情况讨论:①当点P 在AB 与CD 之间时;②当点P 在AB 上方时;③当点P 在CD 下方时,分别求出∠AEP 、∠EPF 、∠CFP 之间的关系即可.【详解】(1)当点P 与点E 、F 在一直线上时,作图如下,∵AB ∥CD ,∠FHP=60°,GEP EGP ∠=∠,∴GEP EGP ∠=∠=∠FHP=60°,∴∠EFD=180°-∠GEP=180°-60°=120°,∴∠PFD=120°,故答案为:120°;(2)满足关系式为∠EPF =∠AEP+∠CFP或∠AEP=∠EPF+∠CFP.证明:根据点P是动点,分三种情况讨论:①当点P在AB与CD之间时,过点P作PQ∥AB,如下图,∵AB∥CD,∴PQ∥AB∥CD,∴∠AEP=∠EPQ,∠CFP=∠FPQ,∴∠EPF=∠EPQ+∠FPQ=∠AEP+∠CFP,即∠EPF =∠AEP+∠CFP;②当点P在AB上方时,如下图所示,∵∠AEP=∠EPF+∠EQP,∵AB∥CD,∴∠CFP=∠EQP,∴∠AEP=∠EPF+∠CFP;③当点P在CD下方时,∵AB∥CD,∴∠AEP=∠EQF,∴∠EQF=∠EPF+∠CFP,∴∠AEP=∠EPF+∠CFP ,综上所述,∠AEP 、∠EPF 、∠CFP 之间满足的关系式为:∠EPF =∠AEP+∠CFP 或∠AEP=∠EPF+∠CFP ,故答案为:∠EPF =∠AEP+∠CFP 或∠AEP=∠EPF+∠CFP .【点睛】本题考查了平行线的性质,外角的性质,掌握平行线的性质是解题的关键,注意分情况讨论问题.17.(1)3; (2)见解析; (3)见解析【详解】分析:(1)因为△BCD 的高为OC ,所以S △BCD=CD•OC ,(2)利用∠CFE+∠CBF=90°,∠OBE+∠OEB=90°,求出∠CEF=∠解析:(1)3; (2)见解析; (3)见解析【详解】分析:(1)因为△BCD 的高为OC ,所以S △BCD =12CD •OC ,(2)利用∠CFE +∠CBF =90°,∠OBE +∠OEB =90°,求出∠CEF =∠CFE .(3)由∠ABC +∠ACB =2∠DAC ,∠H +∠HCA =∠DAC ,∠ACB =2∠HCA ,求出∠ABC =2∠H ,即可得答案.详解:(1)S △BCD =12CD •OC =12×3×2=3. (2)如图②,∵AC ⊥BC ,∴∠BCF =90°,∴∠CFE +∠CBF =90°.∵直线MN ⊥直线PQ ,∴∠BOC =∠OBE +∠OEB =90°.∵BF 是∠CBA 的平分线,∴∠CBF =∠OBE .∵∠CEF =∠OBE ,∴∠CFE +∠CBF =∠CEF +∠OBE ,∴∠CEF =∠CFE .(3)如图③,∵直线l ∥PQ ,∴∠ADC =∠PAD .∵∠ADC =∠DAC∴∠CAP =2∠DAC .∵∠ABC +∠ACB =∠CAP ,∴∠ABC +∠ACB =2∠DAC .∵∠H +∠HCA =∠DAC ,∴∠ABC +∠ACB =2∠H +2∠HCA ∵CH 是,∠ACB 的平分线,∴∠ACB =2∠HCA ,∴∠ABC =2∠H ,∴H ABC ∠∠=12.点睛:本题主要考查垂线,角平分线和三角形面积,解题的关键是找准相等的角求解. 18.(1)见解析;(2)①③;(3)∠APB 的度数是10°或20°或40°或110°【分析】(1)由和是的角平分线,证明即可;(2)根据“准互余三角形”的定义逐个判断即可;(3)根据“准互余三角解析:(1)见解析;(2)①③;(3)∠APB 的度数是10°或20°或40°或110°【分析】(1)由90ABC A ∠+∠=︒和BD 是ABC 的角平分线,证明290ABD A ∠+∠=︒即可; (2)根据“准互余三角形”的定义逐个判断即可;(3)根据“准互余三角形”的定义,分类讨论:①2∠A +∠ABC =90°;②∠A +2∠APB =90°;③2∠APB +∠ABC =90°;④2∠A +∠APB =90°,由三角形内角和定理和外角的性质结合“准互余三角形”的定义,即可求出答案.【详解】(1)证明:∵在Rt ABC 中,90ACB ∠=︒,∴90ABC A ∠+∠=︒,∵BD 是ABC ∠的角平分线,∴2ABC ABD ∠=∠,∴290ABD A ∠+∠=︒,∴ABD △是“准互余三角形”;(2)①∵70,10B C ∠=︒∠=︒,∴290B C ∠+∠=︒,∴ABC 是“准互余三角形”,故①正确;②∵60A ∠=︒, 20B ∠=︒,∴210090A B ∠+∠=︒≠︒,∴ABC 不是“准互余三角形”,故②错误;③设三角形的三个内角分别为,,αβγ,且αβγ<<,∵三角形是“准互余三角形”,∴290αβ+=︒或290αβ+=︒,∴90αβ+<︒,∴180()90γαβ=︒-+>︒,∴“准互余三角形”一定是钝角三角形,故③正确;综上所述,①③正确,故答案为:①③;(3)∠APB 的度数是10°或20°或40°或110°;如图①,当2∠A +∠ABC =90°时,△ABP 是“准直角三角形”,∵∠ABC =50°,∴∠A =20°,∴∠APB =110°;如图②,当∠A +2∠APB =90°时,△ABP 是“准直角三角形”,∵∠ABC =50°,∴∠A +∠APB =50°,∴∠APB =40°;如图③,当2∠APB +∠ABC =90°时,△ABP 是“准直角三角形”,∵∠ABC =50°,∴∠APB =20°;如图④,当2∠A +∠APB =90°时,△ABP 是“准直角三角形”,∵∠ABC =50°,∴∠A +∠APB =50°,所以∠A =40°,所以∠APB =10°;综上,∠APB 的度数是10°或20°或40°或110°时,ABP △是“准互余三角形”.【点睛】本题是三角形综合题,考查了三角形内角和定理,三角形的外角的性质,解题关键是理解题意,根据三角形内角和定理和三角形的外角的性质,结合新定义进行求解. 19.(1)100;(2)75°;(3)n=3.【分析】(1)如图:过O 作OP//MN ,由MN//OP//GH 得∠NAO+∠POA=180°,∠POB+∠OBH=180°,即∠NAO+∠AOB+∠OB解析:(1)100;(2)75°;(3)n =3.【分析】(1)如图:过O 作OP //MN ,由MN //OP //GH 得∠NAO +∠POA =180°,∠POB +∠OBH =180°,即∠NAO +∠AOB +∠OBH =360°,即可求出∠AOB ;(2)如图:分别延长AC 、CD 交GH 于点E 、F ,先根据角平分线求得58NAC ∠=︒,再根据平行线的性质得到58CEF ∠=︒;进一步求得18DBF ∠=︒,17DFB ∠=︒,然后根据三角形外角的性质解答即可;(3)设BF 交MN 于K ,由∠NAO =116°,得∠MAO =64°,故∠MAE =641n n ︒⨯+,同理∠OBH =144°,∠HBF =n ∠OBF ,得∠FBH =1441n n ︒⨯+,从而=n BKA FBH n ∠∠=⨯︒+1441,又∠FKN =∠F +∠FAK ,得144606411n n n n ︒︒︒⨯=+⨯++,即可求n . 【详解】解:(1)如图:过O 作OP //MN ,∵MN //GHl∴MN //OP //GH∴∠NAO +∠POA =180°,∠POB +∠OBH =180°∴∠NAO +∠AOB +∠OBH =360°∵∠NAO =116°,∠OBH =144°∴∠AOB =360°-116°-144°=100°;。
部编数学七年级下册 三元一次方程组专项提升训练(重难点培优)2023培优(解析版)【人教版】含答案

2022-2023学年七年级数学下册尖子生培优题典【人教版】专题8.4三元一次方程组专项提升训练(重难点培优)班级:___________________ 姓名:_________________ 得分:_______________注意事项:本试卷满分120分,试题共24题,其中选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.(2022•南京模拟)解方程组2x−y +3z =13x +y−7z =25x−y +3z =3,如果要使运算简便,那么消元时最好应( )A .先消去x B .先消去y C .先消去z D .先消常数项【分析】观察发现,未知数y 的系数具有相同,或互为相反数,从而可确定先消去y .【解答】解:观察未知数x ,y ,z 的系数特点发现:未知数y 的系数要么相等,要么互为相反数,所以要使运算简便,那么消元时最好应先消去y ,故选:B .2.(2022春•岚山区期末)已知方程组x +y =2y +z =−1z +x =3,则x +y +z 的值是( )A .1B .2C .3D .4【分析】把三个方程相加,即可得出x +y +z 的值.【解答】解:x +y =2①y +z =−1②z +x =3③,①+②+③,得2x +2y +2z =4,即2(x +y +z )=4,解得x +y +z =2.故选:B .3.(2022春•巴东县期末)已知x =3y y +4z =0,且y ≠0,则x z 的值为( )A .34B .−34C .﹣12D .12【分析】由②得出y =﹣4z ③,把③代入①得出x =3×(﹣4z ),求出x =﹣12z ,再等式两边都除以z 即可.【解答】解:x=3y①y+4z=0②,由②,得y=﹣4z③,把③代入①,得x=3×(﹣4z),即x=﹣12z,等式两边都除以z得:xz=−12,故选:C.4.(2022春•黄冈期末)已知x,y,z满足4x+3y+z=72x−3y−13z=−1,则2x+y﹣z的值为( )A.2B.3C.4D.5【分析】按照解三元一次方程组的步骤先求出x=1+2z,y=1﹣3z,然后代入式子中进行计算即可解答.【解答】解:4x+3y+z=7①2x−3y−13z=−1②,①+②得:6x﹣12z=6,x﹣2z=1,x=1+2z,把x=1+2z代入①中得:4(1+2z)+3y+z=7,4+8z+3y+z=7,9z+3y=3,y=1﹣3z,把x=1+2z,y=1﹣3z代入2x+y﹣z中得:2(1+2z)+1﹣3z﹣z=2+4z+1﹣3z﹣z=3,故选:B.5.(2022春•南安市期末)若方程组x−by+4z=1x−2by+3z=3的解是x=ay=1z=c,则a+b+6c的值是( )A.﹣3B.0C.3D.6【分析】把x,y与z代入方程组,将c看作已知数表示出a与b,代入原式计算即可求出值.【解答】解:把x=ay=1z=c代入方程组得:a−b+4c=1①a−2b+3c=3②,①﹣②得:b+c=﹣2,即b=﹣2﹣c,①×2﹣②得:a+5c=﹣1,即a=﹣5c﹣1,则原式=﹣5c﹣1﹣2﹣c+6c=﹣3.故选:A.6.(2022春•青龙县期中)已知方程组x+y=3y+z=−6z+x=9,则x+y+z的值是( )A.3B.4C.5D.6【分析】把三个方程相加,进行计算即可解答.【解答】解:x+y=3①y+z=−6②z+x=9③,①+②+③得:2x+2y+2z=3+(﹣6)+9,∴x+y+z=3,故选:A.7.(2022春•滨州期末)有甲、乙、丙三种文具,若购买甲1件,乙2件比购买丙1件,多花9元;若购甲2件,丙8件比购买乙1件多花18元.现在购买甲、乙、丙各一件文具,则共需费用( )A.7元B.8元C.9元D.10元【分析】设甲文具的单价为x元,乙文具的单价为y元,丙文具的单价为z元,根据“若购买甲1件,乙2件比购买丙1件,多花9元;若购甲2件,丙8件比购买乙1件多花18元”,即可得出关于x,y,z 的三元一次方程组,利用(3×①+②)÷5,即可求出购买甲、乙、丙各一件文具所需的费用.【解答】解:设甲文具的单价为x元,乙文具的单价为y元,丙文具的单价为z元,依题意,得:x+2y−z=9①2x+8z−y=18②,∴(3×①+②)÷5,得:x+y+z=9.故选:C.8.(2022春•如东县期中)三个二元一次方程3x﹣y=7,2x+3y=1,y=kx﹣9有公共解,则k的值是( )A.3B.−163C.﹣2D.4【分析】利用方程3x﹣y=7和2x+3y=1组成方程组,求出x、y,再代入y=kx﹣9求出k值.【解答】解:3x−y=7①2x+3y=1②,把①式两边乘3,得9x﹣3y=21③,②+①得11x=22,得x=2,把x=2代入①得6﹣y=7,解得y=﹣1,将x=2y=−1代入y=kx﹣9得2k﹣9=﹣1,解得k=4.故选:D.9.(2021秋•肥西县月考)如图,边长为x的两个正方形靠边各放置两个边长为a,b的长方形,然后分别以a+x,b+x构造两个大正方形,根据图中的数据,可求得x的值是( )A.80cm B.75cm C.70cm D.65cm【分析】根据两个图形分别可得a+x=b+90,b+x=a+60,联立方程组求解即可.【解答】解:由题意得:a+x=b+90①b+x=a+60②,①+②得:a+b+2x=a+b+150,解得:x=75,故选:B.10.(2022春•绍兴期末)若关于x、y的二元一次方程组ax−by=−2cx+dy=4的解为x=3y=2,则方程组ax−by+2a+b=−2cx+dy−d=4−2c的解为( )A.x=1y=2B.x=1y=3C.x=2y=2D.x=2y=3【分析】先将所求的方程组化简为a(x +2)−b(y−1)=2c(x +2)+d(y−1)=4,再结合已知方程组的解可得x +2=3y−1=2,求解即可.【解答】解:化简方程组ax−by +2a +b =−2cx +dy−d =4−2c 为方程组a(x +2)−b(y−1)=2c(x +2)+d(y−1)=4,∵二元一次方程组ax−by =−2cx +dy =4的解为x =3y =2,∴x +2=3y−1=2,解得x =1y =3,故选:B .二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上11.(2022春•开福区校级期中)已知x +y =5y +z =−2z +x =3,则x +y +z = 0 .【分析】三式相加再两边同时除以2即可得答案.【解答】解:将三个方程相加得:2(x +y +z )=0,∴x +y +z =0.12.(2022春•洪雅县期末)三元一次方程组x +y =5y +z =9z +x =8=2=3=6 .【分析】将方程组三个方程相加求出x +y +z 的值,进而将每一个方程代入即可求出x ,y ,z 的值.【解答】解:x +y =5①y +z =9②z +x =8③,①+②+③得:2(x +y +z )=22,即x +y +z =11④,将①代入④得:z =6,将②代入④得:x =2,将③代入④得:y =3,则方程组的解为x =2y =3z =6.故答案为:x =2y =3z =613.(2021春•饶平县校级期末)已知关于x ,y 的方程组为3x +5y =m−4x +2y =m ,若x +y =﹣1,则m = ﹣3 .【分析】将上述两式相减,整理得,2x+3y=﹣4,由x+y=﹣1,得x=﹣1﹣y,再将其代入2x+3y=﹣4,求得x和y的值,然后将x和y的值代x+2y=m,即可求得m的值.【解答】解:3x+5y=m−4 x+2y=m将上述两式相减,整理得2x+3y=﹣4,①由x+y=﹣1,得x=﹣1﹣y,②将②代入①得y=﹣2,把y=﹣2代入②得x=1,将x=1,y=﹣2代入x+2y=m得m=﹣3.故答案为﹣3.14.(2021春•高新区期末)如果方程组x=4ax+by=5的解与方程组y=3bx+ay=2的解相同,则a+b= 1 .【分析】两个方程组的解相同,意思是这两个方程组中的x都等于4,y都等于3,即x=4y=3是方程组ax+by=5bx+ay=2的解,根据方程组的解的定义,即可求出a+b的值.【解答】解:依题意,知x=4y=3是方程组ax+by=5bx+ay=2的解,∴4a+3b=5①3b+4a=2②①+②,得7a+7b=7,方程两边都除以7,得a+b=1.15.(2021春•南陵县期末)已知:a3=b5=c7,且3a+2b﹣4c=9,则a+b+c的值等于 ﹣15 .【分析】先设比例系数为k,代入3a+2b﹣4c=9,转化为关于k的一元一次方程解答.【解答】解:设a3=b5=c7=k,则a=3k,b=5k,c=7k,代入3a+2b﹣4c=9,得9k+10k﹣28k=9,解得:k=﹣1,∴a=﹣3,b=﹣5,c=﹣7,于是a+b+c=﹣3﹣5﹣7=﹣15.故本题答案为:﹣15.16.(2020春•淮阳区期末)有A、B、C三种商品,如果购5件A、2件B、3件C共需513元,购3件A、6件B、5件C共需375元,那么购A、B、C各一件共需 111 元.【分析】设A、B和C商品的单价分别为x,y和z元,则根据“购5件A、2件B、3件C共需513元,购3件A、6件B、5件C共需375元”列出方程组,然后求解x+y+z即可.【解答】解:设A、B和C商品的单价分别为x,y和z元,根据题意可列方程5x+2y+3z=513①3x+6y+5z=375②,由①+②得,8x+8y+8z=888,化简得x+y+z=111.答:购A、B、C各一件共需111元17.(2020春•水磨沟区校级期中)“六一”儿童节将至,“孩子王”儿童商店推出甲、乙、丙三种特价玩具,若购甲3件,乙2件,丙1件需400元:购甲1件,乙2件,丙3件需440元,则购买甲、乙、丙三种玩具各一件需 210 元.【分析】设甲玩具的单价为x元,乙玩具的单价为y元,丙玩具的单价为z元,根据“购甲3件,乙2件,丙1件需400元:购甲1件,乙2件,丙3件需440元”,即可得出关于x,y,z的三元一次方程组,再利用(①+②)÷4,即可求出结论.【解答】解:设甲玩具的单价为x元,乙玩具的单价为y元,丙玩具的单价为z元,依题意,得:3x+2y+z=400①x+2y+3z=440②,(①+②)÷4,得:x+y+z=210.故答案为:210.18.(2019春•利川市期末)小丽在3张同样的卡片上各写了一个正整数,从中随机抽取2张,并将它们上面的数字相加.重复这样做,每次所得的和都是5,6,7中的一个数,并且这3个数都能抽取到.那么,小丽在这3张卡片上写的数字分别是 2,3,4 .【分析】三张卡片上的数分别用a,b,c表示,随机抽取2张,每次所得的和都是5,6,7中的一个数,则a+b=5,a+c=6,b+c=7.解之可得.【解答】解:令三张卡片上的数分别用a,b,c表示,依题意得,a+b=5a+c=6b+c=7,把这三个方程相加得a+b+c=9,可解得a=2,b=3,c=4,答:小丽在这3张卡片上写的数字分别是:2,3,4.三、解答题(本大题共6小题,共66分.解答时应写出文字说明、证明过程或演算步骤)19.(2019春•金山区期末)解方程组:x−z=−5 x+y=7z−y=8.【分析】①+③得出x﹣y=3④,由④和②组成二元一次方程组x−y=3x+y=7,求出x、y的值,把x=5代入①求出z即可.【解答】解:x−z=−5①x+y=7②z−y=8③①+③得:x﹣y=3④,由④和②组成方程组x−y=3x+y=7,解得:x=5 y=2,把x=5代入①得:5﹣z=﹣5,解得:z=10,所以原方程组的解为x=5y=2z=10.20.(2021春•浦东新区校级期末)解方程组3x+2y+z=4 2x−y=−72x+3y−z=1.【分析】先将三元一次方程组通过加减消元法转化为二元一次方程组,再通过加减消元法转化为一元一次方程,从而可以解答本题.【解答】解:3x+2y+z=4①2x−y=−7②2x+3y−z=1③,①+③,得5x+5y=5④,②×5+④,得15x=﹣30,解得x=﹣2,将x=﹣2代入②,得y=3,将x=﹣2,y=3代入①,得z=4.故原方程组的解是x=−2 y=3z=4.21.(2020春•涪城区校级期末)在等式y=ax2+bx+c中,当x=1时,y=2;当x=﹣1时,y=20;当x=3 2与x=13时,y的值相等,求a,b,c的值.【分析】根据题意列出关于a,b,c的方程组,求出方程组的解即可得到a,b,c的值.【解答】解:在等式y=ax2+bx+c中,当x=1时,y=2;当x=﹣1时,y=20;当x=32与x=13时,y的值相等,b+c=2①+c=20②a+32b+c=19a+13b+c③,解得:a=5411,b=﹣9,c=6711.22.(2009秋•越城区期末)已知关于x,y的二元一次方程组2x+y=6m3x−2y=2m的解满足二元一次方程x3−y5=4,求m的值.【分析】理解清楚题意,运用三元一次方程组的知识,把x,y用m表示出来,代入方程x3−y5=4求出m 的值.【解答】解:由题意得三元一次方程组:+y=6m=2m−y5=4化简得2x+y=6m①3x−2y=2m②5x−3y=60③①+②﹣③得:2y=8m﹣60,y=4m﹣30 ④,②×2﹣①×3得:7y=14m,y=2m⑤,由④⑤得:4m﹣30=2m,2m=30,∴m=15.23.买2匹马、3头牛或4只羊,价钱分别都不满10000文(古时货币单位).如果买2匹马加上1头牛,或者买3头牛加上1只羊,或者买4只羊加上1匹马,那么各自的价钱正好都是10000文.求马、牛、羊的单价.【分析】直接利用买2匹马加上1头牛,或者买3头牛加上1只羊,或者买4只羊加上1匹马,各自的价钱正好都是10000文,得出等式组成方程组求出答案.【解答】解:设1匹马的价格为x文,1头牛的价格为y文,1只羊的价格为z文,根据题意可得:2x+y=100003y+z=100004z+x=10000,解得:x=3600 y=2800 z=1600,答:1匹马的价格为3600文,1头牛的价格为2800文,1只羊的价格为1600文.24.(2022春•绍兴期末)2022年北京冬奥会取得了圆满成功,巧妙蕴含中华文化的冬奥场馆,是北京冬奥会上一道特有的风景.某校40名同学要去参观A、B、C三个冬奥场馆,每一位同学只能选择一个场馆参观.已知购买2张A场馆门票加1张B场馆的门票共需要110元,购买3张A场馆门票和2张B场馆门票共需要180元.(1)求A场馆和B场馆门票的单价;(2)已知C场馆门票每张售价15元,且参观当天有优惠活动:每购买1张A场馆门票就赠送1张C场馆门票.①若购买A场馆门票赠送的C场馆门票刚好够参观C场馆的同学使用,此次购买门票所需总金额为1140元,则购买A场馆门票 3 张;②若参观C场馆的同学除了使用掉赠送的门票外,还需另外购买部分门票,且最终购买三种门票共花费了1035元,求所有满足条件的购买方案.【分析】(1)设A场馆门票的单价为x元,B场馆门票的单价为y元,根据“购买2张A场馆门票和1张B场馆门票共需要110元,购买3张A场馆门票和2张B场馆门票共需要180元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;(2)①设购买A场馆门票a张,则购买B场馆门票(40﹣2a)张,根据此次购买门票所需总金额为1140元,列方程即可;②设购买A场馆门票m张,C场馆门票n张,则购买B场馆门票(40﹣2m﹣n),利用购买门票所需总金额=门票单价×购买数量,即可得出关于m,n的二元一次方程,结合m,n均为正整数,即可得出m,n的值,再结合到A场馆参观的人数要少于到B场馆参观的人数,即可得出各购买方案.【解答】解:(1)设A场馆门票的单价为x元,B场馆门票的单价为y元,依题意得:2x+y=1103x+2y=180,解得:x=40 y=30.答:A场馆门票的单价为40元,B场馆门票的单价为30元.(2)①设购买A场馆门票a张,则购买B场馆门票(40﹣2a)张,40a+30(40﹣2a)=1140,解得a=3,故答案为:3.②设购买A场馆门票m张,C场馆门票n张,则购买B场馆门票(40﹣2m﹣n),依题意得:40m+30(40﹣2m﹣n)+15n=1035,∴n=11−43 m.又∵m,n均为正整数,∴m=3n=7或m=6n=3.当m=3,n=7时,40﹣2m﹣n=40﹣2×3﹣7=27,当m=6,n=3时,40﹣2m﹣n=40﹣2×6﹣3=25,∴共有2种购买方案,方案1:购买3张A场馆门票,27张B场馆门票,7张C场馆门票;方案2:购买6张A场馆门票,25张B场馆门票,3张C场馆门票.。
七年级数学下学期培优试题 新人教版-新人教版初中七年级全册数学试题

七年级数学培优试题填空题(共25题,满分100)1、有一只手表每小时比准确时间慢3分钟, 若在清晨4:30与准确时间对准, 则当天上午手表指示的时间是10:50, 准确时间应该是。
2、将正方形纸片由下往上对折,再由左向右对折,称为完成一次操作(见下图).按上边规则完成五次操作以后,剪去所得小正方形的左下角. 问:当展开这X正方形纸片后,一共有个小孔3、已知关于x的整系数的二次三项式ax2+bx+c,当x分别取1,3,6,8时,某同学算得这个二次三项式的值分别为1,5,25,50,经过验算,只有一个结果是错误的,这个错误的结果是。
4、下表记录了某次钓鱼比赛中,钓到n条鱼的选手数:n 0 1 2 3 …13 14 15 钓到n条鱼的人数9 5 7 23 … 5 2 1 已知:(1)冠军钓到了15条鱼; (2)钓到3条或更多条鱼的所有选手平均钓到6条鱼; (3)钓到12条或更少鱼的所有选手平均钓到5条鱼;则参加钓鱼比赛的所有选手共钓到条鱼。
5、如图,在一个正方体的两个面上画了两条对角线AB,AC,那么这两条对角线的夹角等于度。
6、一个木制的立方体,棱长为n(n是大于2的整数),表面涂上黑色,用刀片平行于立方体的各面,将它切成3n个棱长为1的小立方体,若恰有一个面涂黑色的小立方体的个数等于没有一个面涂黑色的小立方体的个数,则n= .7、把8X不同的扑克牌交替的分发成左右两叠:左一X,右一X,左一X,右一X,……;然后把左边一叠放在右边一叠上面,称为一次操作。
重复进行这个过程,为了使扑克牌恢复到最初的次序,至少要进行操作的次数是。
8、一台大型计算机中排列着500个外形相同的同一种元件,其中有一只元件已损坏,为了找出这一元件,检验员将这些元件按1-500的顺序编号,第一次先从中取出单数序号的元件,发现其中没有坏元件,他将剩下的元件在原来的位置上又按1-250编号。
(原来的2号变成1号,原来的4号变成2号…)又从中取出单数序号的元件进行检查,仍没有发现…如此下去,检查到最后一个元件,才是坏元件。
人教版七年级数学下册培优资料教师版
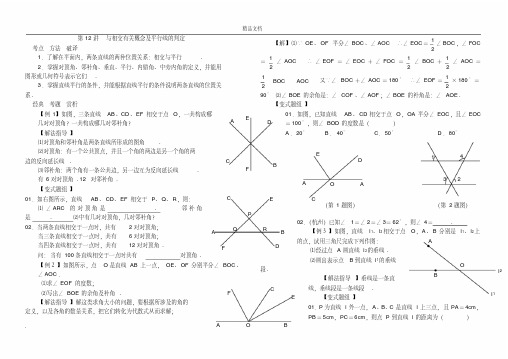
点在同一直线上, 设 Sn 表示过这几个点中的任意两个点所作的所有直
线的条数, 显然:S2= 1,S3= 3,S4=
【 例7 】如图⑴, 平面内有六条两两不平行的直线, 试证: 在所有的交角中,
01.如图,∠ EAC =∠ ADB = 90° . 下列说法正确的是(
②∠ 1=∠ 7,③∠ 2+∠ 3= 180°,④∠ 4=∠ 7,其中能判断 a∥ b 的条件的
序号是
.
E
2 C
使 AD ∥ BC. F
A B
D 第 14 题图
B D B F D
E C
.
精品文档
06.平面上三条直线相互间的交点的个数是(
)
A. 3 B. 1 或 3
C. 1 或 2 或 3
D .不一定是 1,2,3
A
Q
R
B
【 例3 】如图,直线 l 1、 l2 相交于点 O,A 、 B 分别是 l 1、 l2 上
当三条直线相交于一点时,共有 当四条直线相交于一点时,共有
6 对对顶角; 12 对对顶角 .
的点,试用三角尺完成下列作图:
A
F
D
⑴经过点 A 画直线 l 2 的垂线 .
问: 当有 100 条直线相交于一点时共有
C.不大于 4cm
D.不小于 6cm
02 如图,一辆汽车在直线形的公路 AB 上由 A 向 B 行驶, M 、 N 为位于公路两
侧的村庄;
⑴求∠ AOC 的度数; ⑵试说明 OD 与 AB 的位置关系 .
⑴设汽车行驶到路 AB 上点 P 的位置时距离村庄 M 最近 .行驶到 AB 上点 Q 的位置时, 距离村庄 N 最近, 请在图中的公路上分别画出点 P、Q 的位置 .
人教版七年级数学下册常考点微专题提分精练 专题13 点到坐标轴的距离(原卷版+解析)

微课:为学困生“助跑”【摘要】微课是一种新型学习方式,对于学困生有着重要的作用。
本文首先介绍了微课的定义和学困生现状,然后探讨了微课如何助跑学困生以及其优势和特点。
文章还分析了微课在教育领域的发展趋势,以及如何提高学习效率。
分享了一些微课在帮助学困生方面的实践经验。
通过对微课对学困生的意义和影响进行总结,表明微课为学困生提供了更多学习机会和发展空间。
未来微课将带来更多发展机遇,学校也应该更好地利用微课帮助学困生。
微课的发展将不仅改变学习方式,也将为学困生提供更多学习支持和帮助。
【关键词】微课, 学困生, 教育, 学习效率, 实践经验, 意义, 影响, 发展机遇, 学校利用。
1. 引言1.1 微课的定义和作用微课是一种基于互联网和多媒体技术的教学方式,通过短小精悍的视频课程,为学生提供个性化、灵活的学习方式。
微课的作用主要体现在以下几个方面:一是能够提供学习资源的快速获取和分享,学生可以随时随地通过手机或电脑学习知识。
二是可以激发学生的学习兴趣,因为微课通常采用生动有趣的方式呈现知识,让学习变得更加生动和轻松。
三是能够帮助学生复习和巩固知识,通过反复观看微课视频,学生可以更好地理解和记忆知识点。
四是可以提高学生的学习效率,微课通常是按照知识点划分的,学生可以选择需要学习的知识点进行学习,避免浪费时间和精力。
微课在提高学习效率、激发学习兴趣和辅助复习方面发挥着重要作用,对于学困生的学习帮助也有着积极的意义。
1.2 学困生的现状学困生指的是在学习方面遇到困难、表现较差的学生。
随着教育竞争的加剧和学习压力的增加,学困生的数量逐渐增多。
根据统计数据显示,目前学困生已经成为一个不容忽视的群体。
他们可能因为学习能力不足、学习方法不当、家庭环境不利等原因导致学习成绩偏低,甚至出现严重的学习困难。
对于学困生来说,他们需要更多的关爱和帮助,以提高学习成绩和学习兴趣。
2. 正文2.1 微课如何助跑学困生通过合理利用微课的优势和特点,结合学校和教师的教学实践和教育改革,可以更好地帮助学困生解决学习困难和提高学习能力,促进学校和教育事业的发展,实现教育公平和提升教育质量的目标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
13 位置确定——平面直角坐标系阅读与思考在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系.从而坐标平面上的点与有序数对(x,y)之间建立了一一对应关系.利用平面直角坐标系是确定位置的有效方法之一,解与此相关的问题需注意:(1)理解点的坐标意义;(2)熟悉象限内的点、坐标轴上的点、对称轴的坐标特征;(3)善于促成坐标与线段的转化.例题与求解a =______________.【例1】(1)已知点A(2a+3b,-2)和B(8,3a+2b)关于x轴对称,那么b(四川省中考试题) (2)在平面直角坐标系中,若点M(1,3)和点N(x,3)之间的距离为5,则x的值是____________.(辽宁省沈阳市中考试题) 解题思路:对于(1)纵坐标互为相反数,对于(2),M,N在平行于x轴的直线上787.【例2】如图的象棋盘中,“卒”从A点到B点,最短路径共有 ( )A.14条 B.15条C.20条 D.35条(全国初中数学竞赛预赛试题) 解题思路:以点A为起点,逐渐地寻找到达每一个点的不同走法的种数,找到不同走法的规律.例2题图 例3题图 【例3】 如图,已知OABC 是一个长方形,其中顶点A ,B 的坐标分别为(0,a )和(9,a ),点E 在AB 上,且AB AE 31=,点F 在OC 上,且OC OF 31=.点G 在OA 上,且使△GEC 的面积为20,△GFB 的面积为16,试求a 的值.(“创新杯”竞赛试题)解题思路:把三角形的面积用a 表示,列出等式进而求出a 的值.【例4】 如图,在平面直角坐标系中,四边形各顶点的坐标分别为:A (0,0),B (7,0),C (9,5),D (2,7) .(1)在坐标系中,画出此四边形.(2)求此四边形的面积.(3)在坐标轴上,你能否找一个点P ,使50=∆PBC S ?若能,求出P 点坐标;若不能说明理由.解题思路:对于(2),过C ,D 两点分别向x 轴,y 轴引垂线,由坐标得到相关线段.对于(3),由于P 点位置不确定,故需分类讨论.【例5】如果将电P 绕顶点M 旋转1800后与点Q 重合,那么称点P 与点Q 关于电M 对称,定点M 叫作对称中心,此时,点M 是线段PQ 的中点,如图,在平面直角坐标系中,△ABO 的顶点A ,B ,O 的坐标分别为(1,0),(0,1),(0,0),点1P ,2P ,3P ,…中相邻两点都关于△ABO 的一个顶点对称,点1P 与点2P 关于点A 对称,点2P 与点3P 关于点B 对称,点3P 与点4P 关于点O 对称,点4P 与点5P 关于点A 对称,点5P 与点6P 关于点B 对称,点6P 与点7P 关于点O 对称,…对称中心分别是A ,B ,C ,A ,B ,C ,…且这些对称中心依次循环,已知1P 的坐标是(1,1).试写出点2P ,7P ,100P 的坐标.(江苏省南京市中考试题)解题思路:在操作的基础上,探寻点的坐标变化规律.【例6】如图①,在平面直角坐标系中,点A 、B 的坐标分别为(-1,0),(3,0),现同时将点A ,B 分别向上平移2个单位.再向右平移1个单位,分别得到点A ,B 的对应点C ,D ,连接AC ,BD .(1)求点C ,D 的坐标及四边形ABDC 的面积ABDC S 四边形.(2)在y 轴上是否存在一点P ,连接PA ,PB ,使ABD C PAB S S 四边形=∆,若存在这样一点,求出点P 的坐标,若不存在,试说明理由.(3)如图②,点P 是线段BD 上的一个动点,连接PC ,PO .当点P 在BD 上移动时(不与B ,D 重合),CPOBOPDCP ∠∠+∠的值是否变化?若不变,求其值.解题思路:(1)由平移知C (0,2),D (4,2) .另求出四边形面积.(2)设OP =h ,用h 表示出ABDC PAB S S 四边形=∆可求出h 的值.若为整数,则是y 轴上的点,若不是,则说明该点不存在.图②图①能力训练A 级1. 如图,△AOB 绕点O 逆时针旋转900,得到''OB A ∆,若点A 的坐标为(a ,b ),则点'A 的坐标为______.(吉林省中考试题)x2. △ABC 的坐标系中的位置如图所示,若'''C B A 与△ABC 关于y 轴对称,则点A 的对应点'A 的坐标为______.(山东省青岛市中考试题)x3.线段CD 是由线段AB 平移得到的,点A (-1,4)的对应点为C (4,7),则点B (-4,-1)的对应点D 的坐标是____________.(内蒙古包头市中考试题)4.如图,在平面直角坐标系中,有若干个整数点.其顺序按图中“→”方向排列,如(1,0),(2,0),(3,2),(3,1),(3,0),…,根据这个规律探究可得,第100个点的坐标为____________.(四川省德阳市中考试题)5.若点A (-2,n )在x 轴上,则点B (n -1,n +1)在( ).A. 第一象限B. 第二象限C. 第三象限D.第四象限(江西省南昌市中考试题)6.若点M (a +2,3-2a )在y 轴上,则点M 的坐标是 ( ).A. (-2,7)B. (0,3)C. (0,7)D. (7,0)(重庆市中考试题)7.如图,若平行四边形的顶点A ,B ,D 的坐标分别是(0,0),(5,0),(2,3),则顶点C 的坐标是( ).A. (3,7)B. (5,3)C. (7,3)D. (8,2)(江苏省南京市中考试题)x8.如果点P(m ,1-2m)在第四象限,那么m 的取值范围是( ).A. 210<<m B. 021<<-m C.0<m D .21>m(陕西省中考试题)9.如图,已知A (8,2),B (2,2),E ,F 在AB 上且∠EOA =∠EAO ,OF 平分∠BOE . (1)求∠FOA .(2)若将A 点向右平移,在平移过程中∠OAB : ∠OEB 的值是否发生变化?请说明理由.x10.如图,智能机器猫从平面上的O 点出发,按下列规律走:由O 向东走12cm 到1A ,再由1A 向北走24cm 到2A ,由2A 向西走36cm 到3A ,由3A 向南走18cm 到4A ,由4A 向东走60cm 到5A ,…,问:智能机器猫到达6A 点与O 点的距离是多少?(“华罗庚金杯”数学竞赛试题)x11.中国象棋棋盘中蕴含这平面直角坐标系,如右图是中国象棋棋盘的一半,棋子“马”走的规律是沿“日”形的对角线走.例如:图中“马”所在的位置可以直接走到点A ,B 处.(1)如果“帅”位于点(0,0),“相”位于点(4,2),则“马”所在的点的坐标为 ,点C 的坐标为 ,点D 的坐标为 .(2)若“马”的位置在C 点,为了达到D 点,请按“马”走的规律,在图中画出一种你认为合理的行走路线,并用坐标表示.(浙江省舟山市中考试题)B 级1.点A (-3,2)关于原点的对称点为B ,点B 关于x 轴的对称点为C ,则点C 的坐标为______.(广西壮族自治区竞赛试题)2.在平面直角坐标系中,已知A (3,-3),点P 是y 轴上一点,则使△AOP 为等腰三角形的点P 共有______个.(内蒙古自治区包头市中考试题)3.如图,在直角坐标系中,已知点A (-3,0),B (0,4),且AB =5,对△OAB 连续作旋转变换,依次得到三角形①,②,③,④,…,则三角形⑩的直角顶点的坐标为______.(浙江省嘉兴市中考试题)x4.若关于x ,y 的方程组⎩⎨⎧=-=+93323my x y mx 的解为坐标的点(x ,y )在第二象限,则符合条件的实数m 的范围是( ).A. 91>m B. 2-<m C.912<<-m D .921<<-m (四川省竞赛试题)5.在平面直角坐标系中, 对于平面内任一点(a ,b ),若规定以下三种变换: ①),(),(b a b a f -=.如)3,1()3,1(-=f ; ②),(),(a b b a g =.如)1,3()3,1(=g ; ③),(),(b a b a h --=.如)3,1()3,1(--=h .按照以上变换由:)2,3()2,3()]3,2([=-=-f g f ,那么)]3,5([-h f 等于( ).A .(-5,-3)B . (5,3)C . (5,-3)D .(-5,3)(山东省济南市中考试题)6.设平面直角坐标系的轴以1cm 作为长度单位,△PQR 的顶点坐标为P (0,3),Q (4,0),R (k ,5),其中40<<k ,若该三角形的面积为8cm 2,则k 的值是( ).A .1B . 38C . 2D .413 E .21 (澳洲数学竞赛试题)7.如图,四边形ABCO 各个顶点的坐标分别为(-2,8),(-11,6),(-14,0),(0,0) . (1)求这个四边形的面积.(2)若把原来四边形ABCO 各个顶点纵坐标保持不变,横坐标增大a ,则所得的四边形面积又是多少?x8.如图,平面直角坐标系中A (-2,0),B (2,-2),线段AB 交轴于点C . (1)求点C 的坐标.(2)若D (6,0),动点P 从D 点开始在x 轴上以每秒3个单位向左运动,同时,动点Q 从C 点开始在y 轴上以每秒1个单位向下运动.问:经过多少秒钟,AO Q APC S S ∆∆=?x9.某校数学课外小组,在坐标纸上为学校的一块空地设计植树方案如下:第K 棵树种植在),(k k y x P 处,其中1,111==y x ,当2≥k 时,⎪⎩⎪⎨⎧---+=----+=--]52[]51[])52[]51([5111k k y y k k x x k k k k][a 表示非负实数a 的整数部分,例如0]2.0[,2]6.2[==,按此方案,求第2009棵树种植点的坐标.(浙江省杭州市中考试题)10.如图①,在平面直角坐标系中,点A 的坐标为(-1,0),现将点A 向上平移2个单位,再向右平移1个单位,得到点A 的对应点B ,点C 的坐标为(3,2) .(1)判断BC 与x 轴的位置关系,并求出△ABC 的面积ABC S ∆. (2)在y 轴上是否存在一点P ,连接PA ,PC ,使ABC PBC S S ∆∆=21,若存在这样的点,求出点P 的坐标,若不存在,试说明理由.(3)如图②所示,点D 是线段AC 上的一个动点,过D 作DE ⊥AC 交x 轴于点E ,过E 点作∠DEF =∠DEA 交AC 于F 点,试求出∠ACB 与∠1之间的数量关系,并证明你的结论.图①图②C13 位置确定 ——平面直角坐标系例1 (1)2 提示:由题意知238322a b a b +=⎧⎨+=⎩,解得24a b =-⎧⎨=⎩,故a +b =(-2)+4=2.(2)6或-4 提示:由题意知|1-x |=5,解得 x =6或-4.例2 D 提示:如右图,从点A 出发,每次向上或向右走一步,到达每一点的最短路径条数如图中所标数字,如:到达点P ,Q 的最短路径条数分别为2和3,以此类推,到达点B 的最短路径条数为35条.例 3 如图:设G 点坐标为(0,b ),b >0,因为S长方形OABC-S ΔGEC =S ΔOGC +S ΔAGE +S ΔBEC ,所以9a -20=11193()6222b a b a +-+ ,解得32023b a =-.同理,由S 长方形OABC-S ΔGFB =S ΔABG +S ΔOGF +S ΔBFC ,得1119169()36222a a b b a -=-++ ,解得3a =32-6b .把32023b a =-代入上式中,得3a =72-9a ,解得a =6例4 (1)略 (2)S 四边形ABCD =44 (3)①当点P 在x 轴上,设P (x ,0).∴PB =|x -7|,∴1|7|5=502PBC S x =⨯-⨯ .∴x =27或-13.∴P 1(27,0),P 2(-13,0).②当P 点在y 轴上,延长CB 交y 轴于E 点,过点C 作CF ⊥y 轴于F .设E (0,y E ),C F E 11S =5-)9,7()22E BOE E y S y ∴=⨯⨯- (,1(79)52S +⨯梯形CFOB=.又CFE S =BOE CFOB S S ∴+ 梯形,解得352E y =-.35(0,)2E ∴-,设P (0,y ),当P 点在E 点上方时,PE =y +352,∴PBC PEC PEB S S S =- ,解得652y =;当P 点在E 点下方时,PE =352y --,∴P B C P E C P E BS S S =- ,解得1352y =-.综上:P 1(27,0),P 2(-13,0),P 3(0,652),P 4(0,1352-)满足题意. 例5 点P 7与点P 1重合,6个点构成一个循环,P 2(1,-1),P 7(1,1).∵100=6×16+4,∴点P 100与点P 4坐标相同,为(1,-3).例6 (1)由平移知C (0,2),D (4,2).S 四边形ABCD =4×2=8.(2)∵S ΔPAB =S四边形ABDC=8,设OP =h ,则182PAB S AB h == .又AB =4,∵AB =4,1482h ∴⨯⨯=,解得h =4.故点P 的坐标为(0,4)或(0,-4).(3)∵CD ∥AB ,∴∠OPC =∠DCP +∠POB ,DCP BOPCPO∠+∠∴∠的值为1.A 级1.(-b ,a ) 2.(4,2) 3.(1,2) 4.(14,8) 提示:第一列1个点,第二列2个点,……,前13列一共(113)13912+⨯=个点,第100个点位于第14列第9个点,坐标为(14,8). 5.B 6.C 7.C 8.D 9.(1)∠FOA =22.50. (2)会变化.A 点向右平移,∠OEB 不会发生变化,但∠OAB 会变化.10.依规律第6次由A 5向北走72cm 到A 6,OP =12-36+60=36cm ,PA 6=24-48+72=48cm ,OA 62=OP 2+PA 62=362+482=602,得OA 6=60cm ,即A 6与O 点的距离为60cm .11.(1)(-3,0) (1,3) (3,1) (2)略 B 级1.(3,2) 提示:由题意知,点B 坐标为(3,-2),点B 关于x 轴的对称点C 的坐标为(3,2). 2.4 3.(36,0)提示:图形摆放形状每3个一循环,第10个图形与第1个图形摆放形状相同,横坐标为(4+5+3)×3=36.4.B 5.B 6.B 7.两个四边形面积都为808.(1)由面积公式可知:C (0,-1). (2)设经过t 秒后,APC ADQ S S = .∴PA =|8-3t |,则1|83|12APC S t =⨯-⨯ ,OQ =1+t ,则11(1) 2.|83|22AOQ S t t =⨯+⨯∴⨯-×1=1+t ,解之得65t =或10. 9.根据题意知,当k=6 ,11,16,21,…时,12155k k --⎡⎤⎡⎤-=⎢⎥⎢⎥⎣⎦⎣⎦,当k(k ≥2)取其他值时,12055k k --⎡⎤⎡⎤-=⎢⎥⎢⎥⎣⎦⎣⎦;所示横坐标x k 值有如下规律:x 1=1,x 2 =x l +1=2,x 3=x 2+1=3,x 4=x 3 +1=4,x 5=x 4+15;x 6=x 5+1-5=1;x 7=x 6+1=2;x 8=x 7+1=3;x 9=x 8+1=4;x 10=x 9+1=5;x 11=x 10+1-5=1;x 12=x 11+1=3;x 13=x 12 +1=3;x 14= x 13 +1=4;x 15= x 14 +1=5;…因为2 009÷5=401×5+4,所以x 2 009 =x 4 =4. 对于纵坐标有如下规律: y 2 =y 3 =y 4 =y 5=y 1=1,y 6=y 5+1=2 y 7 = y 8=y 9= y 10=y 6=2,y 11=y 10 +1=3;y l2 = y l3=y14 =y15=y11=3,y16=y15 +1=4;y17= y l8=y l9 = y20= y16 =4, y21=y20 +1=5; ...所以y5(n-1)+1=n(n≥1,n为整数).令5(n-l)d+l= 2 009,解得34025n=,又因为n是整数,所以y2009= 402.即第2 009棵树种植点的坐标为(4,402).10.(1)∵B(0,2),C(3,2),∴BC∥x轴,又∵BC=3,∴1132322ABCS BC OB===.(2)1323221PBC ABCS S===.∴1322BC PB=,即13322PB=,∴PB=1.又∵B点坐标为(0,2),∵P点坐标为(0,1)或(0,3).(3)∠1=2∠ACB,理由如下:∵∠ACB+∠AED=∠CAE+∠AED= 90°,两边同时乘以2得:2∠ACB+ 2∠AED= 180°.又∵∠1+2∠AED= 180°,∴∠1= 2∠ACB.。
