16-5圆幂定理.讲义教师版
(完整)圆幂定理讲义(带答案)

(完整)圆幂定理讲义(带答案)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整)圆幂定理讲义(带答案))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整)圆幂定理讲义(带答案)的全部内容。
1 / 29圆幂定理STEP 1:进门考理念:1。
检测垂径定理的基本知识点与题型。
2。
垂径定理典型例题的回顾检测。
3. 分析学生圆部分的薄弱环节.(1)例题复习。
1.(2015•夏津县一模)一副量角器与一块含30°锐角的三角板如图所示放置,三角板的直角顶点C落在量角器的直径MN上,顶点A,B恰好都落在量角器的圆弧上,且AB∥MN.若AB=8cm,则量角器的直径MN=cm.【考点】M3:垂径定理的应用;KQ:勾股定理;T7:解直角三角形.【分析】作CD⊥AB于点D,取圆心O,连接OA,作OE⊥AB于点E,首先求得CD的长,即OE的长,在直角△A OE中,利用勾股定理求得半径OA的长,则MN即可求解.【解答】解:作CD⊥AB于点D,取圆心O,连接OA,作OE⊥AB于点E.在直角△ABC中,∠A=30°,则BC=AB=4cm,在直角△BCD中,∠B=90°﹣∠A=60°,∴CD=BC•sinB=4×=2(cm), ∴OE=CD=2,在△AOE中,AE=AB=4cm,则OA===2(cm),则MN=2OA=4(cm).故答案是:4.2 / 29【点评】本题考查了垂径定理的应用,在半径或直径、弦长以及弦心距之间的计算中,常用的方法是转化为解直角三角形.3 / 292.(2017•阿坝州)如图将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为()A.2cm B.cm C.2cm D.2cm【考点】M2:垂径定理;PB:翻折变换(折叠问题).【分析】通过作辅助线,过点O作OD⊥AB交AB于点D,根据折叠的性质可知OA=2OD,根据勾股定理可将AD的长求出,通过垂径定理可求出AB的长.【解答】解:过点O作OD⊥AB交AB于点D,连接OA,∵OA=2OD=2cm,∴AD===(cm),∵OD⊥AB,∴AB=2AD=2cm.故选:D.【点评】本题考查了垂径定理和勾股定理的运用,正确应用勾股定理是解题关键.3.(2014•泸州)如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被⊙P截得的弦AB的长为,则a的值是()4 / 295 / 29A .4B .C .D .【考点】M2:垂径定理;F8:一次函数图象上点的坐标特征;KQ:勾股定理.【专题】11 :计算题;16 :压轴题.【分析】PC⊥x 轴于C ,交AB 于D ,作PE⊥AB 于E ,连结PB ,由于OC=3,PC=a ,易得D 点坐标为(3,3),则△OCD 为等腰直角三角形,△PED 也为等腰直角三角形.由PE⊥AB ,根据垂径定理得AE=BE=AB=2,在Rt△PBE 中,利用勾股定理可计算出PE=1,则PD=PE=,所以a=3+. 【解答】解:作PC⊥x 轴于C,交AB 于D ,作PE⊥AB 于E ,连结PB ,如图,∵⊙P 的圆心坐标是(3,a ), ∴OC=3,PC=a ,把x=3代入y=x 得y=3, ∴D 点坐标为(3,3), ∴CD=3,∴△OCD 为等腰直角三角形, ∴△PED 也为等腰直角三角形,∵PE⊥AB, ∴AE=BE=AB=×4=2, 在Rt△PBE 中,PB=3, ∴PE=, ∴PD=PE=, ∴a=3+. 故选:B .【点评】本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理和等腰直角三角形的性质.4.(2013•内江)在平面直角坐标系xOy中,以原点O为圆心的圆过点A (13,0),直线y=kx﹣3k+4与⊙O交于B、C两点,则弦BC的长的最小值为.【考点】FI:一次函数综合题.【专题】16 :压轴题.【分析】根据直线y=kx﹣3k+4必过点D(3,4),求出最短的弦CB是过点D且与该圆直径垂直的弦,再求出OD的长,再根据以原点O为圆心的圆过点A(13,0),求出OB的长,再利用勾股定理求出BD,即可得出答案.【解答】解:∵直线y=kx﹣3k+4=k(x﹣3)+4, ∴k(x﹣3)=y﹣4,∵k有无数个值, ∴x﹣3=0,y﹣4=0,解得x=3,y=4,∴直线必过点D(3,4),∴最短的弦CB是过点D且与该圆直径垂直的弦,∵点D的坐标是(3,4), ∴OD=5,∵以原点O为圆心的圆过点A(13,0),∴圆的半径为13,∴OB=13,∴BD=12,∴BC的长的最小值为24; 故答案为:24.【点评】此题考查了一次函数的综合,用到的知识点是垂径定理、勾股定理、圆的有关性质,关键是求出BC最短时的位置.STEP 2:新课讲解6 / 297 / 291、熟练掌握圆幂定理的基本概念。
最新北师大版九年级下册数学 第3章 圆 第5节 切线定理与圆幂定理 讲义

1
5. 如图 4, PA 切⊙ O 于 A, AB PO, P 300, AB 6, 则⊙ O 的半径为__________.
A
E D
D O
C
B
O
图3
A C
图4
B
E
图5
图6
【典型例题】
例 1.①如图 5, CD 是⊙O 的直径, AE 切⊙O 于点 B, DC 的延长线交 AB 于点 A, A 200 ,则
的长为____________. A
B A
OM C
O
C
B
图 13
图
A
D
O
F
B
C
E 图 14
例 2.①12如图 15,从圆 O 外一点 P 引圆的切线 PA 和 PB ,切点分别是 A 和 B ,如果 APB 700 , 那么这
两条切线所夹 AB 的度数是( )
A. 1100
B.70
C.55
D.35
DBE =_______. ②如图 6, ABC 是圆内接三角形, BC 是圆的直径, B 350 , MN 是过 A 点的切线,那么
C =________; CAM =________; BAM =________. ③如图 7, ABC 内接于⊙O, AB AC, BOC 1000 , MN 是过 B 点而垂直 OB 的直线,
半径长为_________.
3. RTABC 的斜边 AB 5, 直角边 AC 3, 若 AB 与⊙ C 相切,则⊙ C 的半径是__________.
4.如图 3,已知半圆的圆心在 RTABC 的斜边上,且半圆分别切 AB, AC 于 D, E, AB 3cm, AC 4cm ,
五大圆幂定理证明

五大圆幂定理证明五大圆幂定理是指:1. 圆内接正多边形的边数是多边形周长与直径之比的平方。
2. 圆外切正多边形的边数是多边形周长与直径之比的平方。
3. 任意一个正n边形的内切圆半径等于半径与n之和的1/n。
4. 任意一个正n边形的外接圆半径等于半径的n倍。
5. 任意一个正n边形的周长等于n倍的外接圆周长。
下面给出五大圆幂定理的证明:1. 周长与直径之比的平方设正n边形的周长为P,直径为d,则n个边的长度之和为2P/n。
因为每个边上的弧长等于周长除以360度,所以每个边的长度为(2P/n)/360度。
因为正n边形的每个内角都相等,所以内角和为(180度/n) * n,即180度。
因此,每个边所对的圆心角为180度除以n,即36度。
又因为圆周角的大小与圆心角的大小成正比,所以每个圆周所对的圆心角为36度,即每个圆周的长度为2πr,其中r为圆的半径。
因此,每个边的长度等于2πr * (2/360) * n,即πr/3。
因此,直径d等于πr/3,周长P等于3πr,所以正n边形的边数n等于周长P除以直径d的平方,即n=3P/d²。
2. 外切正多边形的边数是周长与直径之比的平方证明同上,只是将周长P替换为周长与直径之比的平方P/d²。
3. 内切圆半径等于半径与n之和的1/n设正n边形的边长为a,内接圆的半径为r,则内接圆的周长为2πr,因为内接圆与正n边形相切,所以内接圆的周长等于正n边形的周长除以n,即2πr=P/n。
因此,πr=P/n,即r=P/nπ。
又因为内接圆的半径等于边长a与半径r之差的一半,即r=a-(a/2r)=a*(1-1/n),所以a=2r/n。
因此,内切圆半径等于半径与n之和的1/n,即r=P/2nπ/(n-1)。
4. 外接圆半径等于半径的n倍设正n边形的边长为a,外接圆的半径为R,则外接圆的周长为2πR,因为外接圆与正n边形相切,所以外接圆的周长等于正n边形的周长除以n,即2πR=P/n。
圆幂定理ppt课件

D
A P
图1 O
D
A P
B
图2 O
B D 图3
B
P
O A
C PA·PB=PC·PD……(1) 证明:连接AD、BC. ∴△APD∽△CPB.
C PA·PB=PC·PD……(2)
C PA·PB=PC·PD……(3)
则由圆周角定理的推论可得:∠A=∠C.
综上所述,不论AB 、 CD具有什 么样的位置,都有结论(1)成立!
∴PA = PB ,∠OPA=∠OPB
OP垂直平分AB
切线长定理为证明线段相等,角相等,弧相等,垂直关系提供 了理论依据。必须掌握并能灵活应用。
2.圆的外切四边形的两组对边的和相等 4
例.如图所示PA、PB分别切圆O于A、B, 并与圆O的切线分别相交于C、D, 已知 PA=7cm, (1)求△PCD的周长. (2) 如果∠P=70°, 求∠COD的度数
得到.
P
BDO
C
课堂小结
Company Logo
1、这节课我们学习了割线定理、切割线定理、切线长定理,它们统称圆幂定理。
2、要注意圆中的比例线段的结论的特点及实际中的用。 3、圆中的比例线段在实际应用中也非常重要,注意与
代数、几何等知识的联系及应用
20
11
C
P O
A
图3
B 点P从圆内移动到圆外
D
C
D
图5
P
O
B A
PA∙PB=PC∙PD 证明:连接AC、AD,同样可以证明
PA∙PB=PC∙PD
使割线PA绕P点运动到切 线的位置,是否还有 PA∙PB=PC∙PD?
△PAD∽△PCA, 所以PA:PC=PD:PA, 即PA2=PC•PD仍成立.
高中数学-圆幂定理(教师版)

补充内容:圆幂定理一、圆幂定理及其逆定理:(1)割线定理:设过圆O 外一点P 的两直线分别与圆O 交于点B A ,和D C ,,则PD PC PB P A ⋅=⋅,反之PD PC PB P A ⋅=⋅,则D C B A ,,,四点共圆(2)相交弦定理:圆O 的两条弦CD AB ,相交于点P ,则PD PC PB P A ⋅=⋅,反之过点P 的两直线上四点D C B A ,,,满足PD PC PB P A ⋅=⋅,则D C B A ,,,四点共圆(3)切割线定理:设直线P A 与圆切于点T ,过点P 的直线交圆于C B ,两点,则PBP A PT ⋅=2证明:(1)连接BC AD ,,由圆的性质D B ∠=∠,所以P AD ∆∽PCB ∆所以⇒=PBPDPC P A PD PC PB P A ⋅=⋅(2)连接BC AD ,,则C A ∠=∠,B D ∠=∠,所以P AD ∆∽PCB ∆所以⇒=PBPDPC P A PD PC PB P A ⋅=⋅(3)连接TB TA ,,则PBT PTA ∠=∠,所以PTA ∆∽PBT ∆所以⇒=PTP APB PT PB P A PT ⋅=2二、圆幂定理的应用例1.“圆幂定理”是平面几何中关于圆的一个重要定理,它包含三个结论,其中一个是相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等,如图,已知圆O 的半径为2,点P 是圆O 内的定点,且2=OP ,弦BD AC ,均过点P ,则下列说法正确的是A.0)(=⋅+DB OB ODB.PC P A ⋅为定值C.OC OA ⋅的取值范围为]0,2[-D.当BD AC ⊥时,CD AB ⋅为定值解析:连接OP OD OC OB OA ,,,,,直线OP 交圆O 于F E ,,设BD 的中点S ,则BD OS ⊥02)(=⋅=⋅+DB OS DB OB OD ,A 正确;由相交弦定理得PF PE PC P A PC P A ⋅-=⋅-=⋅242)()(22-=-=-=+⋅--=R OP OP R OP R ,B 正确;取AC 的中点M ,则OCOA ⋅42)4(4122222-=--=-=OM OM OM AC OM ,又OPOM ≤≤0即]2,0[∈OM ,所以OC OA ⋅]0,4[-∈,所以C 错误;当BD AC ⊥时,)()(PC PD P A PB CD AB -⋅-=⋅4)4(222-=--=⋅-=⋅-⋅-=⋅+⋅=OP PF PE PC P A PD PB PC P A PD PB ,D 正确例2.在平面直角坐标系xOy 中,设直线2+-=x y 与圆)0(222>=+r r y x 交于B A ,两点,O 为坐标原点,若圆上一点C 满足OB OA OC 4345+=,则=r ()A.22 B.5C.3D.10r ===,设θ2=∠AOB ,则将OB OA OC 4345+=平方得θ2cos 3092516163016916252222222r r r r OB OA OB OA OC ++=⇒⋅++=432cos -=⇒θ55cos 531cos 22=⇒-=-⇒θθ,所以圆心到直线2+-=x y 的距离为θcos 22r =10552==⇒=⇒r r ,故选D例3.在平面直角坐标系xOy 中,圆O :322=+y x ,),2(m T ,若圆O 上存在以M 为中点的弦AB ,且MT AB 2=,则实数m 的取值范围是()A.]0,2[- B.]2,0( C.]2,2[- D.)2,2(-解法1:设),(y x M ,连OM ,由垂径定理知AB OM ⊥⇒32222=+=+MT OM MB OM 42)2()1(3)()2(2222222m m y x m y x y x -=-++⇒=-+-++⇒,所以点M 在以)2,1(m D -为圆心,222m -为半径的圆上,又点M 为圆O 的弦AB 的中点,所以点M 在圆O 内,所以两圆内含,所以223)2()1(222m m --<+-0)1(22>+⇔m ,只需022>-m 解得22<<-m ,即实数m 的取值范围是]2,2[-,故选C解法2:因为M 为弦AB 的中点,且MT AB 2=,所以090=∠ATB ,过点T 作圆的切线TF TE ,,F E ,为切点,则只需090≥∠ETF 即可,所以045≥∠OTE ,所以OTE∠sin 6223≤⇒≥=OT OT ,所以642≤+m ,解得22≤≤-m ,故选C例4.在平面直角坐标系xOy 中,直线kx y =与圆C :5)36()27(22=-+-y x 交于B A ,,则=⋅OB OA 解析:过点O 作圆C 的切线OT ,T 为切点,则由切割线定理得20205362722222=-+=-==⋅R OC OT OB OA 例5.在平面直角坐标系xOy 中,已知点)1,0(P 在圆C :01422222=+-+-++m m y mx y x 内,若存在过点P 的直线交圆C 于B A ,两点,且PBC ∆的面积是P AC ∆的面积的2倍,则实数m 的取值范围为解析:圆C :m y m x 4)1()(22=-++,圆心)1,(m -,半径为m r 2=,所以0>m 点P 在圆C 内40014212<<⇒<+-+-⇒m m m设AB 的中点为D ,t AP 2=,则t PD =,圆心到直线AB 的距离为d ,由PBC ∆的面积是P AC ∆的面积的2倍可知P A PB 2=,所以⎪⎩⎪⎨⎧=+=+⇐⎪⎩⎪⎨⎧=+=+mt d mt d r P A CD CP PD CD 492222222222222849d m m =-⇒,因为220m d <≤,所以494849022<≤⇒<-≤m m m m 当94=m 时,C B A P ,,,四点共线,不能构成三角形,所以m 的取值范围为)4,94(例6.在平面直角坐标系xOy 中,圆C :3)()2(22=-++m y x ,若圆C 存在以G 为中点的弦AB ,且GO AB 2=,则实数m 的取值范围是解析:类例3,]2,2[-例7.已知椭圆E 的中心为坐标原点O ,焦点在x 轴上,离心率为23,21,F F 分别为椭圆E 的左右焦点,点P 在椭圆E 上,以线段21F F 为直径的圆经过点P ,线段P F 1与y 轴交于点B ,且611=⋅B F P F (1)求椭圆E 的方程(2)设动直线l 与椭圆E 交于N M ,两点,且0=⋅ON OM ,求证:动直线l 与圆5422=+y x 相切解析:(1)设椭圆E :)0(12222>>=+b a b y a x ,c F F 221=,因为211F PF O BF ∠=∠,2211π=∠=∠PF F BOF ,所以BO F 1∆∽P F F 21∆,所以P F O F F F B F 11211=21111F F O F B F P F ⋅=⋅⇒3622=⇒==c c ,所以1,2233==⇒==b a a e ,所以椭圆E :1422=+y x (2)设OM 的倾斜角为θ,则)sin ,cos (θθOM OM M ,))90sin(),90cos((00±±θθON ON M ,又点N M ,在椭圆上,所以⎪⎪⎩⎪⎪⎨⎧=+=+⇒⎪⎩⎪⎨⎧=±+±=+22222202202222224cos 4sin 4sin 4cos 1)90(sin 4)90(cos 4sin 4cos ON OM ON ON OM OM θθθθθθθθ两式相加得4511541442222=+⇒=+=+ONOMONOM,设原点到直线MN 的距为d 由5421212222222=+=⇒=+=∆ONOM ON OM d ON OM d ON OM S OMN所以动直线l 与圆5422=+y x 相切。
圆幂定理
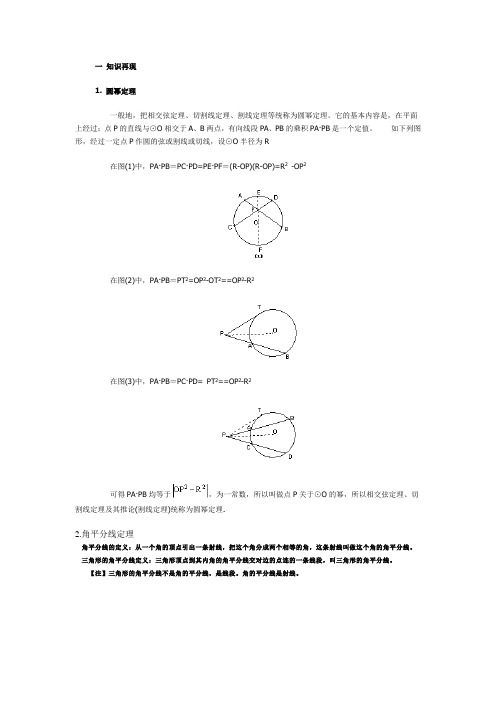
一知识再现1. 圆幂定理一般地,把相交弦定理、切割线定理、割线定理等统称为圆幂定理。
它的基本内容是,在平面上经过;点P的直线与⊙O相交于A、B两点,有向线段PA、PB的乘积PA·PB是一个定值。
如下列图形,经过一定点P作圆的弦或割线或切线,设⊙O半径为R在图(1)中,PA·PB=PC·PD=PE·PF=(R-OP)(R-OP)=R2-OP2在图(2)中,PA·PB=PT2=OP2-OT2==OP2-R2在图(3)中,PA·PB=PC·PD= PT2==OP2-R2可得PA·PB均等于,为一常数,所以叫做点P关于⊙O的幂,所以相交弦定理、切割线定理及其推论(割线定理)统称为圆幂定理.2.角平分线定理角平分线的定义:从一个角的顶点引出一条射线,把这个角分成两个相等的角,这条射线叫做这个角的角平分线。
三角形的角平分线定义:三角形顶点到其内角的角平分线交对边的点连的一条线段,叫三角形的角平分线。
【注】三角形的角平分线不是角的平分线,是线段。
角的平分线是射线。
■拓展:三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等!(即内心)。
■定理1:在角平分线上的任意一点到这个角的两边距离相等。
■逆定理:在一个角的内部(包括顶角),且到这个角的两边距离相等的点在这个角的角平分线上。
■定理2:三角形一个角的平分线分对边所成的两条线段与这个角的两邻边对应成比例,如:在△ABC 中,BD 平分∠ABC ,则AD :DC=AB :BC 3.平行线分线段定理定理 三条平行线截两条直线,所得的对应线段成比例.二 例题讲解例1如图4AB 是⊙O 的弦,P 是AB 上一点,AB = 10cm ,P A : PB = 2 : 3,OP = 5cm ,则⊙O 的半径等于 .解析:设⊙O 的半径为R .∵AB = 10cm ,P A : PB = 2 : 3,∴PA = 4 cm ,PB = 6 cm . 由相交弦定理,得P A ·PB = PC ·PD = R 2-OP 2,即4×6 = R 2-52. 所以,R = 7. 故⊙O 的半径等于7 cm . 例2.如图5,已知P AC 为⊙O 的割线,连接PO 交⊙O 于B ,PB = 2,OP = 7,P A= AC ,则P A 的长为( )A .7B .23C .14D .32解析:延长PO 交⊙O 于D .∵PB = 2,OP = 7,∴OB = 5,即PC = 12. 由切割线定理的推论,得 P A ·AC = PB ·PC . ∵P A = AC ,∴2 P A 2 = 2×12. 所以,P A = 23.故应选B .一、“四心”分类讨论1、外心三解形三条垂直平分线的交点叫做三角形的外心,即外接圆圆心。
圆幂定理

圆幂定理是平面几何中的一个定理。
所以圆内的点的幂为负数,圆外的点的幂为正数,圆上的点的幂为零。
圆幂定理是一个总结性的定理,是对相交弦定理、切割线定理及割线定理(切割线定理推论)以及它们推论的统一与归纳。
根据两条与圆有相交关系的线的位置不同,有以下定理:相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等。
切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
割线定理:从圆外一点P引两条割线与圆分别交于A、B;C、D,则有PA·PB=PC·PD从上述定理可以看出,两条线的位置从内到外,都有着相似的结论。
经过总结和归纳,便得出了圆幂定理。
基本定义定义:一点P对半径R的圆O的幂定义如下:圆幂a=OP²-R²符号:圆内的点的幂为负数,圆外的点的幂为正数,圆上的点的幂为零。
定理内容过任意不在圆上的一点P引两条直线L1、L2,L1与圆交于A、B(可重合,即切线),L2与圆交于C、D(可重合,即切线),则有PA×PB=PC×PD 。
考虑经过P点与圆心O的直线,设PO交⊙O于M、N,R 为圆的半径,则有PA×PB=PC×PD=PM×PN=(OP+R)│OP-R│=│OP²-R²│定理证明图Ⅰ:相交弦定理。
如图,AB、CD为圆O的两条任意弦。
相交于点P,连接AD、BC,由于∠B与∠D同为弧AC 所对的圆周角,因此由圆周角定理知:∠B=∠D,同理∠A=∠C,所以△PAD∽△PCB。
所以有:PA/PC=PD/PB,即:PA×PB=PC×PD 。
图Ⅱ:割线定理。
如图,连接AD、BC。
可知∠B=∠D,又因为∠P为公共角,所以有△PAD∽△PCB,同上证得PA×PB=PC×PD。
图Ⅲ:切割线定理。
如图,连接AC、AD。
∠PAC为切线PA与弦AC组成的弦切角,因此有∠PAC=∠D,又因为∠P为公共角,所以有△PAC∽△PDA ,易证PA²=PC×PD。
圆幂定理讲义(带答案解析)

【点评】 本题考查了垂径定理的应用,在半径或直径、弦长以及弦心距之间的计算中, 常用 的方法是转化为解直角三角形.圆幂定理STEP 1: 进门考理念: 1. 检测垂径定理的基本知识点与题型2. 垂径定理典型例题的回顾检测。
3. 分析学生圆部分的薄弱环节。
1)例题复习1. (2015?夏津县一模)一副量角器与一块含 30°锐角的三角板如图所示放置,三角板的直角顶点 C 落在量角器的直径 MN 上,顶点 A ,B 恰好都落在量角 器的圆弧上,且 AB ∥MN .若 AB=8cm ,则量角器的直径 MN= cm . 【考点】 M3:垂径定理的应用; KQ :勾股定理; T7:解直角三角形. 【分析】 作 CD ⊥ AB 于点 D ,取圆心 O ,连接 OA ,作 OE ⊥AB 于点 E ,首先求得 CD 的长,即 OE 的长,在直角△ AOE 中,利用勾股定理求得半径 OA 的长,则 MN 即可求解. 解答】 解:作 CD ⊥AB 于点 D ,取圆心 O ,连接 OA ,作 OE ⊥ AB 于点 E .在直角△ ABC 中,∠ A=30°,则 BC= AB=4cm , 在直角△ BCD 中,∠ B=90°﹣∠ A=60°, =2 (cm ), ∴ OE=CD=2 , 在△ AOE 中, AE= AB=4cm , ∴CD=BC?sinB=×4 则 OA= = =2 ( cm ), 则 MN=2OA=4 ( cm ). 故答案是: 4 .2. (2017?阿坝州)如图将半径为 2cm 的圆形纸片折叠后,圆弧恰好经过【考点】 M2:垂径定理; PB :翻折变换(折叠问题).【分析】 通过作辅助线, 过点 O 作 OD ⊥AB 交 AB 于点 D ,根据折叠的性质可知 OA=2O ,D 根据 勾股定理可将 AD 的长求出,通过垂径定理可求出 AB 的长. 【解答】 解:过点 O 作 OD ⊥ AB 交 AB 于点 D ,连接 OA , ∵OA=2OD=2c ,m ∴ AD== = ( cm ),点评】 本题考查了垂径定理和勾股定理的运用,正确应用勾股定理是解题关键.3. (2014?泸州)如图,在平面直角坐标系中,⊙ P 的圆心坐标是( 3,a ) a >3),半径为 3,函数 y=x 的图象被⊙ P 截得的弦 AB 的长为 ,则 a的值A .4考点】 M2:垂径定理; F8:一次函数图象上点的坐标特征; KQ :勾股定理.cmD .2 cm故选: D .cm.专题】11 :计算题;16 :压轴题.【分析】 PC ⊥x 轴于 C ,交 AB 于 D ,作 PE ⊥AB 于 E ,连结 PB ,由于 OC=3,PC=a ,易得D 点 坐标为( 3, 3),则△ OCD 为等腰直角三角形,△ PED 也为等腰直角三角形.由 PE ⊥ AB ,根 据垂径定理得 AE=BE= AB=2 ,在 Rt △PBE 中,利用勾股定理可计算出 PE=1,则 PD= PE=,所以 a=3+ .【解答】 解:作 PC ⊥x 轴于 C ,交 AB 于 D ,作 PE ⊥ AB 于 E ,连结 PB ,如图, ∵⊙ P 的圆心坐标是( 3, a ), ∴OC=3,PC=a ,把 x=3 代入 y=x 得 y=3, ∴ D 点坐标为( 3,3), ∴CD=3, ∴△ OCD 为等腰直角三角形, ∴△ PED 也为等腰直角三角形, ∵PE ⊥ AB , ∴PE=, ∴PD= PE= , ∴ a=3+ . 故选: B .4. (2013?内江)在平面直角坐标系 xOy 中,以原点 O 为圆心的圆过点 A 13,0),直线 y=kx ﹣3k+4与⊙O 交于 B 、C 两点,则弦 BC 的长的最小值为【分析】 根据直线 y=kx ﹣3k+4 必过点 D (3,4),求出最短的弦 CB 是过点 D 且与该圆直径 垂直的弦,再求出 OD 的长,再根据以原点 O 为圆心的圆过点 A (13,0),求出 OB 的长, 再利用勾股定理求出 BD ,即可得出答案.∴ AE=BE= AB在 Rt △ PBE 中, PB=3,考查了勾股定理和等腰直角三角形的性质.并且平分弦所对的两条弧.也【解答】解:∵直线y=kx ﹣3k+4=k (x﹣3)+4,∴k(x﹣3)=y﹣4,∵k 有无数个值,∴x﹣3=0,y ﹣4=0,解得x=3,y=4,∴直线必过点D(3,4),∴最短的弦CB是过点 D 且与该圆直径垂直的弦,∵点 D 的坐标是(3,4),∴OD=5,∵以原点O为圆心的圆过点A(13,0),∴圆的半径为13,∴OB=13,∴ BD=12,∴ BC 的长的最小值为24;故答案为:24.【点评】此题考查了一次函数的综合,用到的知识点是垂径定理、勾股定理、圆的有关性质,关键是求出BC最短时的位置.STEP 2: 新课讲解1、熟练掌握圆幂定理的基本概念。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基本要求
略高要求
较高要求
圆幂定理
会在相应的图中确定圆幂定理的条件和结论
能用圆幂定理解决有关问题
板块一 相交弦定理
相交弦定理:圆内的两条相交弦被交点分成的两条线段长的乘积相等.
如图,弦 和 交于 内一点 ,则 .
相交弦定理的推论:如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项.
∵ ,由射影定理得 ,∴ ,
在 中, ,
∴ .
由割线定理得 ,
∴ .
【答案】
【例10】如图,同心圆 , 交小圆于 两点,求证: .
【考点】切割线定理
【题型】解答
【难度】3星
【关键词】
【解析】解法一:过 分别作小圆的切线 , 为切点,
连结 .
则 ,
∵ ,∴ ,
∵ 是小圆的切线,
∴ ,
∴ .
解法二:过 作割线交小圆于 ,过 作割线交小圆于 .
【例3】如图, 的两条弦 交于点 ,已知 ,则 的长为________.
【考点】相交弦定理
【题型】填空
【难度】2星
【关键词】
【解析】省略
【答案】
【例4】如图,圆的半径是 , 两点在圆上,点 在圆内, , , 求点 到圆心的距离.
【考点】相交弦定理
【题型】解答
【难度】4星
【关键词】
【解析】连结 ,则线段 的长就是所求点 到圆心的距离.
连结 ,延长 交 于 ,过 点作 于 ,延长 交 于 .
设 ,由相交弦定理可得 ,
则 ,
∵ ,∴ ,
,
在 中, ,∴ ,
即 ,解得 ,
∴ ,
.
【答案】
【例5】如图,正方形 内接于 ,点 在劣弧 上,连结 交 于点 .若 ,则 的值为___________.
【考点】相交弦定理,勾股定理
【题型】填空
【难度】4星
【例1】如下左图,在 中,弦 与 相交于点 ,已知 ,那么 .
【考点】相交弦定理
【题型】填空
【难度】2星
【关键词】
【解析】省略
【答案】
【例2】如下中图,在 中,弦 与半径 相交于点 ,且 ,若 ,则 的长为()
A. B. C. D.
【考点】相交弦定理
【题型】选择
【难度】2星
【关键词】
【解析】省略
【答案】D
由割线定理得 ,
∵ ,
∴ ,
∴ .
【答案】见解析
1.如下右图,在 中, 为弦 上一点, , 交 于 ,那么()
A. B.
C. D.
【考点】相交弦定理
【题型】选择
【难度】2星
【关键词】
【解析】省略
【答案】B
2.如图, 是 的直径,弦 ,垂足为 , 是 延长线上的点,连结 交 于 ,如果 ,且 ,那么 的长是.
【考点】切割线定理
【题型】填空
【难度】3星
【关键词】
【解析】省略
【答案】 .
A. B. C. D.
【考点】切割线定理
【题型】选择
【难度】3星
【关键词】
【解析】省略
【答案】B.
【例9】如图, 是半圆 的直径, 于点 , .已知点 在 的延长线上, 与半圆交于 ,且 ,则 的长为_____________.
【考点】切割关键词】
【解析】连结 ,
∵ 是 的直径,∴ ,
【解析】⑴ 过圆心 ,且 分别切 于点
∴ 于点 , 于点 ,
∴ 与 重合, 与 重合.
∵ ,
∴ .
⑵连接
∵ 于点 ,且 ,
∴ ,∴ ,
∵ ,
∴ , ,
∴ ,
在 中, ,
同理 ,
∴ .
⑶猜想 .
证明:过点 作直径交 于点 ,连结 ,
∴
∵ ,∴ 且
∴ ,∴ ,
∴ ,
同理 ,∴ .
则
∴ .
过点 做直径交 于点 ,
则有阅读材料可知 ,
∴ .
【答案】见解析
板块二、切割线定理
如图,在 中, 是 的切线, 是 的割线,则题意中满足
【例7】如图, 是半圆的切线,且 ,过 的切线交 与 ,若 ,则 半径为, __________.
【考点】切割线定理
【题型】填空
【难度】3星
【关键词】
【解析】省略
【答案】 ; .
【例8】如图,过点 作 的两条割线分别交 于点 和点 ,已知 ,则 的长是()
⑴ 若 恰经过圆心 ,请你在图3中画出符合题意的图形,并计算 的值;
⑵若 ,请你在图4中画出符合题意的图形,并计算 的值;
⑶若 是过点 的任一弦(图2),请你结合⑴⑵的结论,猜想 的值,并给出证明.
【考点】相交弦定理,切线的性质及判定,相似三角形的性质及判定
【题型】解答
【难度】4星
【关键词】2009年,东城一模
【关键词】
【解析】连结 ,设 半径为 , ,则 .
在 中,根据相交弦定理得 ,
即 ,∴ ,
由勾股定理得 ,
即 ,解得 .
∴ .
【答案】
【例6】(09东城一模)请阅读下列材料:
圆内的两条相交弦被交点分成的两条线段长的积相等.如图1,若弦 交于点 ,则 .
请你根据以上材料,解决下列问题.
已知 的半径为 , 是 内一点,且 ,过点 任作一弦 ,过 两点分别作 的切线 和 ,作 于点 , 于点 .(如图2)
