材料力学剪切实用计算上交
合集下载
材料力学剪切与联接件的实用计算教案
单击此处添加副标题
第八章 剪切 与连接件的实 用计算
演讲人姓名
目录
CONTENT
01 本章主要内容 单击此处添加正文
03 搭接铆接（单 剪 ） 单击此处添加正文
05 铆钉群连接 单击此处添加正文
02 强度计算的实 用 计算 方 法 单击此处添加正文
04 对接铆接（双 剪 ） 单击此处添加正文
06 其它连接 单击此处添加正文
1、剪切破坏：沿m-m截面剪断；
2、挤压破坏：连接孔因挤压产生塑性变形，连接产生松动； 3、拉断破坏；板在开孔削弱截面被拉断。
§8-1 概述
三、三种破坏失效形式
F
F
1、剪切破坏：2、挤压破坏：3、拉断破坏；
四、实用计算方法
连接件本身尺寸较小，其受力和变形情 F
F
b
况很复杂，要精确地分析计算其内力和应
一、工程实际中的连接与联接件
§8-1 概述 连接件：在构件连接处起连接作用的部件， 如铆钉、螺栓键块等 1、螺栓连接；2、铆钉连接；3、销轴连 接；4、键块连接； 5、焊接连接；6、榫齿连接；7、胶接连 接等 螺栓连接
铆钉连接
焊接连接
榫齿连接
键块连接
销轴接
胶结连 接
§8-1 概述
一、工程实际中的连接与联接件
例题1 重新布置铆钉位置
1-1截面两个削弱孔， 2-2截面一个削弱孔 哪一种布置方式更好？ 剪切、挤压情况相同。 比较拉伸情况 更好
FN
F
d b
2
3F
F
21
FN
F
1
F
3F
§8-2 铆接强度计算 三、铆钉群连接的计算
一、搭接铆接
F d
二、对接铆接
第八章 剪切 与连接件的实 用计算
演讲人姓名
目录
CONTENT
01 本章主要内容 单击此处添加正文
03 搭接铆接（单 剪 ） 单击此处添加正文
05 铆钉群连接 单击此处添加正文
02 强度计算的实 用 计算 方 法 单击此处添加正文
04 对接铆接（双 剪 ） 单击此处添加正文
06 其它连接 单击此处添加正文
1、剪切破坏：沿m-m截面剪断；
2、挤压破坏：连接孔因挤压产生塑性变形，连接产生松动； 3、拉断破坏；板在开孔削弱截面被拉断。
§8-1 概述
三、三种破坏失效形式
F
F
1、剪切破坏：2、挤压破坏：3、拉断破坏；
四、实用计算方法
连接件本身尺寸较小，其受力和变形情 F
F
b
况很复杂，要精确地分析计算其内力和应
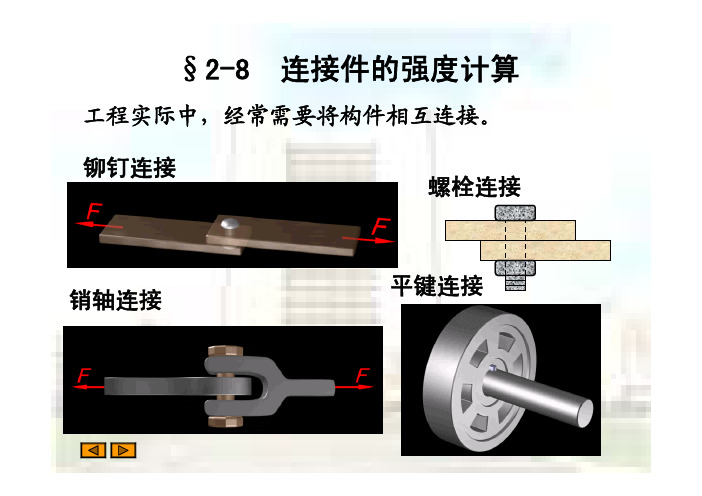
一、工程实际中的连接与联接件
§8-1 概述 连接件：在构件连接处起连接作用的部件， 如铆钉、螺栓键块等 1、螺栓连接；2、铆钉连接；3、销轴连 接；4、键块连接； 5、焊接连接；6、榫齿连接；7、胶接连 接等 螺栓连接
铆钉连接
焊接连接
榫齿连接
键块连接
销轴接
胶结连 接
§8-1 概述
一、工程实际中的连接与联接件
例题1 重新布置铆钉位置
1-1截面两个削弱孔， 2-2截面一个削弱孔 哪一种布置方式更好？ 剪切、挤压情况相同。 比较拉伸情况 更好
FN
F
d b
2
3F
F
21
FN
F
1
F
3F
§8-2 铆接强度计算 三、铆钉群连接的计算
一、搭接铆接
F d
二、对接铆接
材料力学答案-剪切的实用计算
习 题3-1 夹剪的尺寸如图示，销子C 的直径d ＝0.5 cm ，作用力F=200 N ，在剪直径与用子直径相同的铜丝A 时，若a ＝2cm ，b ＝15cm ．试求铜丝与销子横截面上的平均剪应力τ。
解:QA F b F a ⨯=⨯ 2001515002QA Fb F N a ==⨯= 22444150076.390.510QAA F MPa d τππ-⨯===⨯⨯ ()QC F a b F a +=⨯()200(215)17002QC F a b F N a ++=== MPa C 58.86105.01700442=⨯⨯⨯=-πτ 3-2 图示摇臂，试确定其轴销B 的直径d 。
已知用材料的许用应力[τj ]=100Mpa,[σbs ]=240Mpa 。
解:0=∑B Mcos450.6500.4F ⋅⨯=⨯47.14F KN =37.27B F KN =[]242B F d πττ=≤ []3262237.2710 1.541010010B F d m πτπ-⨯⨯===⨯⨯⨯＝15.4mm 验算挤压应力[]32237.27102421.5410110B bs bs bs F MPa A σσ--⨯===≈⨯⨯⨯ 3-3 图示直径为 d 的拉杆，其端头的直径为D ，高度为h ，试建立 D 、h 与d 的合理比值（从强度考虑）。
已知：[σ]＝120 MPa ，[τj ]＝90 MPa ，[σbs ]＝240 MPa ．解:[]310030.14-⨯==P Pd σπ []jy p d D σππ=-2244310261.1-⨯=P D[]310717.12-⨯==P d P h τπ ∴67.1:22.1:1::=h D d 3－4 两根矩形截面木杆，用两块钢板连接在一起，受轴向载荷P ＝45kN 作用。
已知截面宽度 b ＝25 cm ，沿材的顺纹方向，许用拉应力[σ]＝6MPa ，许用挤压应力[σjy ]＝10 MPa ，许用剪应力[τj ]＝1MPa ，试确定接头的尺寸δ、l 和 h 。
材料力学2—剪切
Q τ = ≤ [τ ] A
2.3、挤压的实用计算 在外力作用下，连接件和被连接的构件之间， 必将在接触面上相互压紧，这种现象称为挤压。 在外力作用下，剪切构件除可能被剪断外，还 可能发生挤压破坏。挤压破坏的特点是：构件互相 接触的表面上，因承受了较大的压力作用，使接触 处的局部区域发生显著的塑性变形或被压碎。这种 作用在接触面上的压力称为挤压力；在接触处产生 的变形称为挤压变形。
例 2.5 m3挖掘机减速器的一轴上装一齿轮，齿轮与轴通过平 键连接，已知键所受的力为F＝12.1 kN。平键的尺寸为：b＝ 28 mm，h＝16 mm，l2＝70 mm，圆头半径R＝14 mm。键的 许用切应力[τ]=87 MPa，轮毂的许用挤压应力取[σbs]＝100 MPa，试校核键连接的强度。
解：(1) 校核剪切强度 销轴的受力如图所示，a-a和b-b两截面 皆为剪切面，这种情况称为双剪。 利用截面法以假想的截面沿a-a和b-b将 销轴截开，由所取研究对象的平衡条件 可知，销轴剪切面上的剪力为
F 188 Q= = = 94 KN 2 2
剪切面面积为
A=
πd2
4
=
π × 92
4
= 63.6 cm 2 = 63.6 ×10−4 m 2
h Abs = ⋅ l p 2 1.6 = (7.0 − 2 ×1.4) 2 = 3.36 cm 2 = 3.36 ×10−4 m 2
故轮毂的工作挤压应力为
12100 P σ bs = = = 36 × 106bs 3.36 × 10−4
2.1 工程实际中的剪切问题 再看连接轴与轮的键(图a)。作用于轮和轴上的 传动力偶和阻抗力偶大小相等，方向相反，键的受 力情况如图b所示。作用于键的左右两个侧面上的 力，意图使键的上、下两部分沿n－n截面发生相对 错动。
材料力学第五章剪切和挤压的实用计算
> A[s]:=Pi*d*delta:
> d:=25e-3: tao[u]:=300e6: delta:=10e-3:
> ineq:=evalf(ineq,4);
ineq := 235600.F
答：需要 235.6kN 的冲剪力。
#清零。 #剪切强度条件 #剪切面积。 #已知条件。 #冲孔所需要冲剪力的数值。
图5-2连接轴与轮的键的工程实例
（1）作用于构件某一截面两侧的外力，大小相等，方向相反，作用线相距很近且垂 直于轴线。
（2）处于两个平行外力之间的截面，发生相对错动变形。 把有错动变形趋势的截面为剪切面，剪切面上的内力与截面相切，称为剪力， 用 FS 表示。
图5-3钢杆剪切实例
5.2剪切的实用计算
式中 bs 为材料的许用挤压应力，一般 bs 1.7 ~ 2 。
(a)
(b) (c)
图5-4圆孔及铆钉挤压应力的分布
当连接件与被连接件的接触面为平面时，如键连接，此时挤压面的面积 就是连接与被连接件的接触面积。
对于像销钉一类的连接件，它们的承压面实际上是半个圆柱面。在实用
> SOL1:=solve({eq1},{Fs}): > Fbs:=F: > tau:=Fs/A[s]: > tau:=subs(SOL1,tau): > sigma[bs]:=F/A[bs]: > A[s]:=Pi/4*d^2: > A[bs]:=delta1*d: > delta1:=1.5*delta: > d:=20e-3: delta:=8e-3: F:=15e3: > tau:=evalf(tau,4);
计算中通常是用半个圆柱面在垂直于总挤压作用线平面上的投影作为挤压 面的计算面积。这样得到的挤压应力更接近于挤压应力的最大值，因而可 以使设计更趋于安全。
材料力学：第三章 剪切
F 挤压面上应力分布也是复杂的
F
实用计算中，名义挤压应力公式
bs
Fbs Abs
Fbs
Fbs
Abs d
——挤压面的计算面积
挤压强度条件：
bs
Fbs Abs
bs
挤压强度条件同样可解三类问题 bs 常由实验方法确定
例: 已知： =2 mm，b =15 mm，d =4 mm，[ =100 MPa， [] bs =300 MPa，[ ]=160 MPa。 试求：[F]
第三章 剪 切
一. 剪切的概念和实例 二. 剪切的实用计算 三. 挤压的实用计算
一. 剪切的概念和实例 工程实际中用到各种各样的连接，如： 铆钉
销轴
平键 榫连接
(剪切)受力特点： 作用在构件两侧面上的外力合力大小相 等、方向相反且作用线相距很近。
变形特点： 构件沿两力作用线之间的某一截面产生相 对错动或错动趋势。
F F
剪切面上的内力 Fs （用截面法求）
实用计算中假设切应力在剪切
F
m m
面（m-m截面）上是均匀分布的 F
名义切应力计算公式：
F
m
m
FS
FS m
m
F
Fs
A
剪切强度条件：
Fs
A
——名义许用切应力
由实验方法确定
剪切强度条件同样可解三类问题
三. 挤压的实用计算
挤压力不是内力，而是外力
解： 1、剪切强度
4F πd 2
[
]
F πd 2[ ] 1.257 kN
4
2、挤压强度
bs
F
d
[ ]bs
F d[ ]bs 2.40KN
3、钢板拉伸强度 F
材料力学 第三章 剪切
根据平衡条件可得
F0 =F =70kN
钢板危险截面拉伸应力为
0
F0 A0
=
70103 N 252106 m2
277.78MPa>275MPa
277.78 275 100% 1.01% 故螺栓满足强度条件
275
明德行远 交通天下
材料力学
例题3-2 某接头部分销钉如图所示，F=110 kN，试求销钉的切应力和挤压应力。
明德行远 交通天下
材料力学
单面剪切
双面剪切
明德行远 交通天下
复杂双面剪切
材料力学
二、剪切的工程实例
铆钉或高强螺栓连接
销轴连接
明德行远 交通天下
铆钉连接
榫连接
材料力学
§3-2 剪切的实用计算
一、连接处破坏三种形式 ①剪切破坏
以铆钉为例：
沿铆钉的剪切面剪断，如沿m–
m面剪断 。
②挤压破坏
铆钉与钢板在相互接触面上因
明德行远 交通天下
材料力学
解：先分析螺栓的剪切面积和挤压面积
剪切面积为 挤压面积为
A
d2
3.14 30 mm2
=
706.5mm2
4
4
Abs dh=3018mm2 540mm2
根据平衡条件可得
挤压力为
FS=F =70kN
FbS =F =70kN
明德行远 交通天下
材料力学
螺栓截面切应力为
FS A
材料力学
第三章 剪切
明德行远 交通天下
材料力学
主要内容
• §3-1 剪切的概念和工程实例 • §3-2 剪切的实用计算 • §3-3 挤压的实用计算
明德行远 交通天下
材料力学第2章 连接部分的计算
b
d
3.铆钉的剪切强度
a
Fs 4F 2F 2 2 A 2 πd πd 2 50 10 3 2 π 0.017 110 10 6 110 MPa [ ]
4.板和铆钉的挤压强度 Fbs F 50 103 bs Abs 2d 2 0.017 0.01
40 10 3 4 2 ba 50 10 m bs 8 10 6 FS P 2. 顺纹剪切强度条件为 A bl P
ba
b 11.4 10 2 m 114 mm l 35.1 10 2 m 351mm a 4.4 10 2 m 44 mm
bs 2
为充分利用材料，切 应力和挤压应力应满足
Fbs F bs Abs dh
4F 8h F 2 2 d d dh
b
d
a
图示接头，受轴向力F 作 用。已知F=50kN，b=150mm， δ=10mm，d=17mm，a=80mm， [σ]=160MPa，[τ]=120MPa， [σbs]=320MPa，铆钉和板的材 料相同，试校核其强度。
例: t=2mm,b=15mm,d=4mm， []= 100MPa, [bs]= 300MPa, []= 160MPa，计算许用载荷[F]。
F
b
F
F
t
F
F 3-3 2－2 F t 1－1
b
F
F
解：一、破坏形式分析 1.剪断(沿1-1截面) 2.拉断(沿2-2截面) 3.“剪豁” (剪出缺口 3-3截面) 4.挤压破坏
d 2
F td 2.4kN
材料力学-第三章-剪切实用计算(上交)
FQ A
材料力学
剪切实用计算
剪切强度条件：
FQ A
[ ]
名义许用剪应力
可解决三类问题： 1、选择截面尺寸; 2、确定最大许可载荷， 3、强度校核。
材料力学
在假定的前提下进行 实物或模型实验，确 定许用应力。
[例3.1 ] 图示装置常用来确定胶接处的抗剪强度，如已知 破坏时的荷载为10kN，试求胶接处的极限剪（切）应力。 F F
F / 2n [ j ] 1 A d 2 4
2F n 3 . 98 2 d [ j ]
FQ
（2）铆钉的挤压计算
jy
Fb F /n [ A jy t1 d
]
jy
]
F n t1 d [
材料力学
3 . 72
jy
剪切实用计算
因此取 n=4. I F/n F/n F/n F F/n
R
R0
t
1 t R0 10 为薄壁圆筒
材料力学
材料力学
（1）
C D A B C D
A B
横截面上存在剪应力
材料力学
纯剪切的概念
（2）其他变形现象：圆周线之间的距离保持不变，仍为圆形， 绕轴线产生相对转动。 横截面上不存在正应力，且横截面上的剪应力的 方向是沿着圆周的切线方向，并设沿壁厚方向是 均匀分布的。 T
h d F d
剪切面
h
解
FN 4 F A d 2 F Q F AQ dh
当 ， 分别达到 [] ， [] 时， 材料的利用最合理
材料力学
F 4F 0 .6 2 得 d : h 2 .4 dh d
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Abs
hl 2
h——平键高度
l——平键长度
F h
b F
l
材料力学
剪切实用计算
2、柱面接触（如铆钉）：挤压面面积为实际的承压面积在其直径 平面上的投影。 挤压强度条件：
bs
Fb A bs
[ bs ]
F F
Abs d
d——铆钉或销钉直径， ——接触柱面的长度
材料力学
剪切实用计算
*挤压强度条件：
材料力学
（1）
A
B
C
A
C
DB
D
横截面上存在剪应力
材料力学
纯剪切的概念
（2）其他变形现象：圆周线之间的距离保持不变，仍为圆形， 绕轴线产生相对转动。 横截面上不存在正应力，且横截面上的剪应力的 方向是沿着圆周的切线方向，并设沿壁厚方向是 均匀分布的。
T
材料力学
薄壁圆筒横截面 上的剪应力分布
材料力学
受力也相等。
材料力学
F/n
F/n
F
F/n F/n
当各铆钉的材料与直径均相同，且外力作用线在
铆钉群剪切面上的投影，通过铆钉群剪切面形心时，
通常即认为各铆钉剪切面上的剪力相等
若有n个铆钉，则每一个铆钉受力
F/n
F/2n F/2n
材料力学
剪切实用计算
F/2n
F/n
FQ
F/2n
（1）铆钉剪切计算
F/2n
）。
F 剪床剪钢板
单剪：有一个剪切面的杆件。
材料力学
F
剪切面
双剪：有两个剪切面的杆件.
销轴连接
F
F
材料力学
剪切面
剪切是复杂的情况，这里仅介绍工程上的实用计算方法
剪切面上的内力 用截面法——FQ
材料力学
FQ F p
双剪
F
材料力学
F
FQ F / 2 FQ F / 2
剪切实用计算
求应力（剪应力）： *实用计算方法：根据构件破坏的可能性，以直接试验 为基础，以较为近似的名义应力公式进行构件的强度计 算。
材料力学
纯剪切的概念
三、纯剪切的概念
纯剪切——若单元体各个面上只承受剪应力而没有正应力。 单元体——是指围绕受力物体内一点截取一边长为无限小的
正立方体，以表示几何上的一点。
材料力学
纯剪切的变形规律与材料在剪切下的力学性质，通过薄壁圆筒 的纯扭转进行研究。
R R0
材料力学
t
t
1 10
R0
为薄壁圆筒
bs
Fb A bs
[ bs ]
塑性材料：
名义许用挤压应 力，由试验测定。
脆性材料：
材料力学
bs 1.5 2.5 bs 0.9 1.5
剪切实用计算
例题3-3 两矩形截面木杆，用两块钢板连接如图示。已知拉杆的 截面宽度 b=25cm，沿顺纹方向承受拉力F=50KN，木材的顺纹许 用剪应力为 [ j ] 1MPa , 顺纹许用挤压应力为 [ jy ] 10 MPa 。试求
例题3-4 厚度为t1 12 mm 的主钢板用两块厚度为 t2 6cm 的同样 材料的盖板对接如图示。已知铆钉直径为d=2cm，钢板的许用拉应 力 [F] 160 MPa ，钢板和铆钉许用剪应力和许用挤压应力相b同，分F 别为 [ j ] 100 MPa ， [ jy ] 280 MPa 。若F=250KN，试求 （1）每边所需的铆钉个数n；
名义剪应力：假设剪应力在整个剪切面上均匀分布。
FQ
A
材料力学
剪切实用计算
剪切强度条件： FQ [ ] A
名义许用剪应力
可解决三类问题： 1、选择截面尺寸; 2、确定最大许可载荷， 3、强度校核。
材料力学
在假定的前提下进行 实物或模型实验，确 定许用应力。
[例3.1 ] 图示装置常用来确定胶接处的抗剪强度，如已知 破坏时的荷载为10kN，试求胶接处的极限剪（切）应力。
4F
d 2
当 ， 分 别 达 到 [] ， [] 时 ，
FQ
F
材料的利用最合理
AQ dh
F 0.6 4F 得 d : h 2.4
材料力学 dh
d 2
二、挤压概念及其实用计算 挤压：连接件和被连接件在接触面上相互压紧的现象。
挤压力不是内力，而是外力
F
F
挤压面
挤压破坏实例
压溃(塑性变形)
剪切实用计算
2-2 图(a)所示铆接件，板件的受力情况如图（ｂ）所示． 已知：P＝7 kN，t＝0.15cm，b1＝0.4cm，b2=0.5cm， b3=0.6cml。试绘板件的轴力图，并计算板内的最大拉应力。
外力通过铆钉组的形心， 且各铆钉直径相同，则 每个铆钉的受力也相等。
材料力学
剪切实用计算
接头处所需的尺寸L和 。
F
b
F
材料力学
LL
剪切实用计算
解：剪切面如图所示。剪
F/2
切面面积为：
F
A Lb
剪切面
由剪切强度条件：
F/2
Fs F / 2 [ ]
A Lb
由挤压强度条件：
L
F
2b[ j ]
100 mm
材料力学
jy
Fb A jy
F /2
b
[
jy
]
F 2b[ jy ]
10 mm
（2）若铆钉按图(b)排列，所需板宽b为多少？
F
F
材料力学
剪切实用计算
F
F
图(a)
F
F
材料力学
图(b)
剪切实用计算
解： 可能造成的破坏：
（1）因铆钉被剪断而使铆接被破坏；
（2）铆钉和板在钉孔之间相互挤压过大，而使铆接被 破坏；
（3）因板有钉孔，在截面被削弱处被拉断。
可采用假设的计算方法：
1.不考虑弯曲的影响； 2.外力通过铆钉组的形心，且各铆钉直径相同，则每个铆钉的
FQ A
F / 2n
1 d 2
[ j ]
4
（2）铆钉的挤压计算
n 2F
d 2 [ j ]
jy
Fb A jy
F /n t1d
[ jy ]
3 .98
材料力学
n F
t1d [ jy ]
3 .72
剪切实用计算
因此取 n=4.
I
F/n
F/n
F/n F/n
I
F/2
材料力学
（3）主板拉断的校核。 危险截面为I-I截面。
第三章 剪切实用计算
一、剪切概念及其实用计算
材料力学
例: 连接件：铆钉、销钉、 螺栓、键等。
材料力学
当前无法显示此图像。
铆钉 铆钉
螺栓
材料力学
销钉
搭接
F
m
m
F
*受力特征：
剪切面
作用在构件两侧面上的外力合力大小相等、方向相反且作用 线相距很近。
*变形特征：
杆件沿两力之间的截面发生错动，
直至破坏（小矩形
材料力★学挤压计算对联接件与被联接件都需进行
*挤压实用计算方法：
假设挤压应力在整个挤压面上均匀分布。
bs
Fb A bs
*注意挤压面面积的计算
1、挤压面为平面，计算挤压面就是该面,例如平键
F
键:连接轴和轴上的传动件（如齿轮、皮带轮等）,使轴
和传动件不发生相对转动，以传递扭矩。 Me
材料力学
平面接触（如平键）：挤压面面积等于实际的承压面积。
F
t
F
主板的强度条件为（忽略 应力集中的影响）：
max
F (b 2 d )t1
[ ]
b F 2d
[ ]t1
0 .17 m 17 cm
连接件失效
剪切构件破坏
被连接件由于钉孔削弱截面而拉断
沿剪切面被剪断 剪切强度条件
接触面受挤压造成连接松动， 构件压溃、孔被“豁开”
挤压强度条件
拉、压强度条件
F F
10mm
① ②③
胶缝
①
FQ
FQ
解：
FQ
F 2
5kN
A 0.03 0.01 3104 m2
材料力学
FQ A
5 103 3104
16.7 106 Pa
16.7MPa
[例3.2] 如图螺钉穿过一个端部固接的圆盘，已知：[]=0.6[]，
求其d:h的合理比值。
h d
d h
剪切面
F
解
FN A
*薄壁圆筒纵截面上的剪应力
dy
dz dx
材料力学
纯剪切的概念
*剪切虎克定律
A C
c
B
D
D
单位：Mpa、Gpa. 且
实验证明：当剪应力不超过
材料的比例极限
时，剪
p
应力 与剪应变 成正比。
即
G
其中G是材料的剪切弹性模量。
材料力学
G
E
2 (1 )