距离变换图和骨架图生成算法
计算机地图制图复习题

1.计算机地图制图的优越性:(1)数字地图易于贮存,并保证了贮存中的不变形性,从而提高了地图的使用精度;(2)数字地图易于校正、编辑和更新,增加地图的适应性、实用性和用户的广泛性;(3)用绘图机绘图不仅减轻了制图人员的劳动强度,而且减少了制图人员的主观随意性而产生的偏差,为地图制图进一步标准化、规范化铺平了道路;(4)提高了成图速度,缩短了成图周期,改进了制图和制印工艺。
(5)增加了地图品种,拓宽了服务领域。
(6)数字地图的容量大,它只受计算机存贮器的限制,可以包含比一般模拟地图多得多的地理信息2. 计算机地图制图:计算机地图制图是以传统的地图制图原理为基础,以计算机及其外围设备为工具,采用数据库技术和图形数字处理方法,实现地图信息的获取、变换、传输、识别、存贮、处理、显示和绘图的应用科学。
3. 计算机地图制图涉及的主要理论:地图学:坐标系、投影、综合等计算机图形学:坐标变换、图形生成、图形显示、图形裁剪等数字图像处理:图像的采样、重采样、裁剪等数据库技术:空间数据的存储、管理等4. 计算机地图制图的过程可分为哪几个阶段? 每个阶段的主要任务是什么?计算机制图的方法包括以下三个阶段:即数据获取、数据处理和图形输出。
数据获取阶段的任务:全站仪和GPS数据采集;扫描数字化;遥感图像处理;数字摄影测量;图板数字化图形处理;统计资料;地图资料;数据处理阶段:数据预处理;投影变换;制图综合;图形编辑;数字地图接边;图形输出阶段:地形图;专题地图;分析评价图;统计图表辑;其他地图;5. 用来表示地图图形的数据形式有矢量形式的数据和栅格形式的数据,简称矢量数据和栅格数据6. 计算机制图系统的组成1)输入设备2)中心系统硬件3)输出设备7. 举例说明计算机制图系统中常用的输入、输出设备有那些?输入设备:键盘和鼠标;操纵杆和跟踪;数字化仪;扫描仪;三维激光扫描-CYRAX;三维激光扫描ILRIS-3D输出设备:显示器种类;点阵式和矢量式输出设备8. 主要应用软件是ARC/INFO、Geostar、GeoMedia、GenaMap、 MapInfo、AutoDesk Map、ArcView、MapObjects等9.在计算机科学中,数据压缩是指用资格筛选法,信息量法或其他统计方法,把大量的原始数据或由存贮器取出来的数据转换为有用的、有条理的,精炼而简单的信息的过程,又称数据简化或数据综合。
基于距离场的骨架细化算法

基于距离场骨架的细化算法摘要:骨架是现在物体识别的一种有效手段,保存和处理对象的拓扑信息,是图像分析的重要研究之一。
传统的距离场和基于图像求取的骨架难以保证连通,而细化所得的骨架受噪声影响较大,不能保证结果的准确性,但是细化在骨架识别中起到举重若轻的作用。
本文提出一种优良的骨架细化和骨架提取算法,将经典的距离变换和细化相结合,使骨架在原有识别的基础上更加的精确。
关键词:骨架提取;细化算法;距离场。
1引言骨架(Skeleton)是一种中轴变换用来描述物体的拓扑结构的主要手段之一,首先由Blum提出,它是一种线条状的几何体,线条位于物体的几何中心,有着和原物体相同的拓扑结构,在保持原物体的形状信息的同时,尽量减少了原物体的冗余信息。
骨架有着广泛的应用比如形状描述、文字识别、工程图处理、图像重建、压缩编码和红外图像识别等。
骨架的提取算法主要分为两类:一类是基于细化的算法,另一类是基于距离场的方法。
细化算法是采用迭代的手段不断的剥除目标的边界点,并且保留边界上满足骨架特性的点,直到没有多余的边界可以剥除,剩下的就是骨架。
这个方法在连续域是正确的,但由于图像是离散点,在向内推进过程中无法按照图像的收缩方向进行。
提取的骨架是连续的,但骨架的定位不确定,这两种细化算法在距离场中都对距离场中的脊线有所偏离。
距离场的脊就是骨架线,由于脊的判断方法不准确,有时候很难鉴定一个点是否为距离场的脊,所有得到的点往往是一些离散点,一般的做法是找出距离场中的最大值按照一定的拓扑结构连接起来就构成了原图的骨架如图(1),此方法的结果是准确的但是不连续。
(1)2 基于细化的骨架提取图像的细化是对一个二值图像进行收缩的过程,按照原来的形状让其等比列变小,在连线域上即使收缩到很小的程度还是保持着原来的的形状。
根据细化过程的特点,便有人提出各种算法进行提取骨架,比如“烧草”算法,它的核心思想是,将目标内的所有点看做一个草原,同时从边界点火,再向目标内部蔓延,在蔓延的过程中,燃烧点重合的地方即为骨架点。
三维骨架细化算法

三维骨架细化算法
三维骨架细化算法是一种用于图像处理和计算机视觉中的算法,其目的是从三维体数据中提取出它的骨架结构。
该算法主要包括以下几步:灰度化、二值化、分割、细化、分支点剪枝等。
在细化过程中,通过对像素进行二值化操作,将其转化为0和1两个值,再通过特定的算法将其细化为一个像素宽度的线条,从而提取出其骨架结构。
在分支点剪枝中,通过对骨架中的分支点进行剪枝,使其更符合实际的结构形态。
三维骨架细化算法在医学影像处理、机器人控制和模型建立等领域有着广泛的应用。
- 1 -。
骨架线算法-概述说明以及解释

骨架线算法-概述说明以及解释1.引言1.1 概述概述:骨架线算法(Skeletonization algorithm)是一种用于提取物体或图像形状中主要特征的计算方法。
它通过将图像或物体的边界区域简化为其主要骨架,从而实现对形状的抽象和表示。
骨架线算法在图像处理、模式识别、计算机视觉等领域具有广泛的应用。
骨架线算法的主要思想是通过去除图像中的冗余信息,保留物体或形状的主要结构和特征。
这种算法可以有效地减少数据量,简化图像表示,同时保持重要的拓扑关系和形状特征。
通过提取物体的骨架线,我们可以得到物体的主轴或中心线,从而更好地理解和分析对象的形态、结构和特征。
骨架线算法的原理通常基于图像的连通性和几何形状的局部特征。
常见的骨架线算法包括细化算法、距离变换算法、分水岭算法等。
这些算法可以根据不同的需求和应用场景选择合适的方法进行骨架线提取。
骨架线算法在许多领域都有广泛的应用。
在医学影像中,骨架线算法可以用于血管或神经的提取和分析,有助于辅助诊断和手术规划。
在图像识别和模式分类中,骨架线算法可以用于特征提取和形状匹配,提高图像的分类准确率。
此外,骨架线算法还在工程设计、地质勘探、数字艺术等方面具有重要的应用价值。
本文将介绍骨架线算法的定义、原理和应用。
通过对骨架线算法的深入讨论,我们可以更好地理解和应用这一算法,为相关领域的研究和应用提供指导和参考。
文章结构部分的内容可以按照如下方式撰写:1.2 文章结构本文按照以下结构进行组织和阐述:1. 引言在引言部分,我们将对骨架线算法进行一个概述,介绍其背景和基本概念。
我们将讨论骨架线算法在图像处理领域中的重要性和应用前景。
2. 正文正文部分主要分为三个部分进行论述。
2.1 骨架线算法的定义首先,我们将详细介绍骨架线算法的定义,并解释其核心思想和基本原理。
我们将探讨骨架线算法的起源以及它与其他相关算法的关系。
2.2 骨架线算法的原理在本部分,我们将深入讨论骨架线算法的原理。
第七讲 二值图像处理与形状分析重点

二值图像的连接性和距离
像素的连接
对于二值图像中具有相同值的两个像素A和B,所有和A、B 具有相同值的像素系列p0(=A),p1,p2,…,pn-1,pn(=B)存在,并 且pi-1和pi互为4-/8-邻接,那么像素A和B叫做4-/8-连接,以 上的像素序列叫4-/8-路径。如图8.1.3。
二值图像的连接性和距离
8.2 二值图像连接成分的变形 操作
二值图像连接成分的变形操作
1、连接成分的标记
为区分二值图像中的连接成分,求得连接成分个数,对属于 同一个1像素连接成分的所有像素分配相同的编号,对不同 的连接成分分配不同的编号的操作,叫做连接成分的标记。
对图像进行TV光栅扫描,发现没有分配标号的1像素,对这个像素分 配还没有使用的标号,对位于这个像素8-邻域内的1像素也赋予同一 标号,然后对位于其8-邻域内的1像素也赋予同一标号。
1 0 B 1 1
二值图像连接成分的变形操作
2.4、开运算
先腐蚀后膨胀的运算称为开运算。它一般的作用是消除细小物体。 在纤点处分离物体和平滑物体边界时又不明显改变其面积
A B (A
B) B
2.5、闭运算
先膨胀后腐蚀的运算称为闭运算。它一般的作用是填充物体内细小 空洞,连接相邻物体,在不明显改变其面积的情况下平滑物体
膨胀运算的一个例子
0 0 A 0 0 0 1 1 0 0 0 0 1 0 0 1 0 1 0 1 0 0 0 1 1 0 0 0 0 0 0
1 0 B 1 1
二值图像连接成分的变形操作
2.3、收缩/腐蚀
腐蚀的运算符为⊙,A用B来腐蚀记作A⊙B
骨架线算法

骨架线算法全文共四篇示例,供读者参考第一篇示例:骨架线算法是一种用于提取对象骨架的计算机视觉算法。
在图像处理领域中,骨架线通常指物体的中轴线或中心线,是表示物体形状和结构的重要特征。
骨架线算法可以帮助识别物体的形状、轮廓和结构信息,对于数字化建模、医学图像处理、工程设计等领域有着广泛的应用。
骨架线算法的基本思想是从对象的边缘逐渐收缩,直到最终形成对象的中心线。
这个过程通常包括三个步骤:边缘提取、骨架化和细化。
通过图像处理技术提取出对象的边缘信息;然后,利用数学形态学等方法对边缘进行骨架化处理,得到初步的骨架;通过迭代细化算法对初步骨架进行进一步处理,获得更加精细的骨架线。
骨架线算法的主要优点包括:可以提取出对象的主要轮廓和结构信息,对于形状分析和识别具有较高的准确性和稳定性;可以减少图像数据的复杂度,节省存储和传输空间,便于后续处理和分析;骨架线还可以用于对象的比较和匹配,帮助识别不同对象之间的相似性和差异性。
在实际应用中,骨架线算法广泛应用于医学影像分析、工业检测、自动驾驶等领域。
在医学影像领域,骨架线算法可以帮助医生快速准确地识别病变部位、量化分析组织结构,辅助诊断和治疗。
在工业领域,骨架线算法可以用于产品设计、质量控制、零部件匹配等方面,提高生产效率和品质。
在自动驾驶领域,骨架线算法可以帮助车辆感知周围环境、规划路径,实现智能驾驶。
值得注意的是,骨架线算法虽然在图像处理领域有着广泛的应用,但也存在一些挑战和限制。
算法的鲁棒性和稳定性仍然需要进一步改进,对图像噪声、变形、遮挡等情况的处理效果有待提高;骨架线算法对于不规则形状和复杂结构的物体提取效果可能不理想,需要针对性优化和改进算法。
骨架线算法是一种有效的图像处理技术,可以帮助提取对象的骨架信息,对于形状分析、识别和匹配等领域有着广泛的应用前景。
随着人工智能、深度学习等技术的不断发展和应用,相信骨架线算法还会有更多的创新和突破,为图像处理领域带来更多的发展机会和挑战。
中轴变换与骨架提取
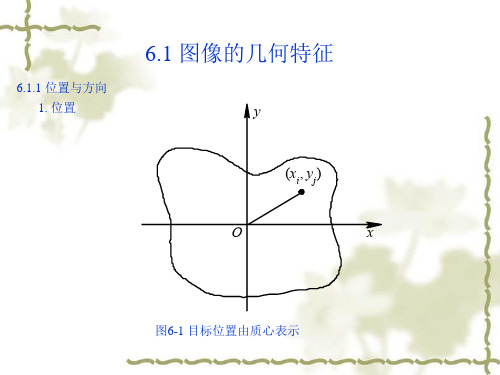
计算MER的一种方法是,将目标的边界以每次3°左右的增量在60°范围内旋转。 每旋转一次记录一次其坐标系方向上的外接矩形边界点的最大和最小x、y值。旋转 到某一个角度后,外接矩形的面积达到最小。取面积最小的外接矩形的参数为主轴 意义下的长度和宽度,如图6-4(b)所示。此外,主轴可以通过矩(Moments)的计算 得到,也可以用求目标的最佳拟合直线的方法求出。
A
1 2
(
xdy
Hale Waihona Puke ydx)(6-8)
其中,积分沿着该闭合曲线进行。将其离散化,式(6-8)变为
A
1 2
Nb
[xi ( yi1
i 1
yi )
yi ( xi1
xi )]
1 2
Nb
[ xi yi1
i 1
xi1 yi ]
(6-6)
式中,Nb为边界点的数目。
6.1.4
当目标的边界已知时,用其外接矩形的尺寸来刻画它的基本形状是最简单的方法, 如图6-4(a)所示。求目标在坐标系方向上的外接矩形, 只需计算目标边界点的最大和 最小坐标值,就可得到目标的水平和垂直跨度。但是,对任意朝向的目标, 水平和垂 直并非是我们感兴趣的方向。这时,就有必要确定目标的主轴, 然后计算反映目标形 状特征的主轴方向上的长度和与之垂直方向上的宽度,这样的外接矩形是目标的最小 外接矩形(Minimum Enclosing Rectangle, MER)。
设屏幕左上角为坐标原点,起始点坐标为(x0, y0),第k段链码终端的y坐标为
k
yk y0 yi
(6-5)
i 1
式中
1
εi=1, 2, 3
yi 0
εi=0,4 εi=5, 6, 7
图像细化算法 2

图像细化算法一、细化算法简介图像细化(Image Thinning),一般指二值图像的骨架化(Image keletonization)的一种操作运算。
所谓的细化就是经过一层层的剥离,从原来的图中去掉一些点,但仍要保持原来的形状,直到得到图像的骨架。
骨架,可以理解为图象的中轴。
好的细化算法一定要满足:∙收敛性;∙保证细化后细线的连通性∙保持原图的基本形状∙减少笔画相交处的畸变∙细化结果是原图像的中心线∙细化的快速性和迭代次数少依据是否使用迭代运算可以分为两类:(1)非迭代算法一次即产生骨架,如基于距离变换的方法。
游程长度编码细化等。
(2)迭代算法即重复删除图像边缘满足一定条件的像素,最终得到单像素宽带骨架。
迭代方法依据其检查像素的方法又可以再分成①串行算法是否删除像素在每次迭代的执行中是固定顺序的,它不仅取决于前次迭代的结果,也取决于本次迭代中已处理过像素点分布情况.②并行算法像素点删除与否与像素值图像中的顺序无关,仅取决于前次迭代的结果二、本文所用算法我所采用的是Zhang并行快速细化算法,它的原理也很简单:我们对一副二值图像进行骨架提取,就是删除不需要的轮廓点,只保留其骨架点。
假设一个像素点,我们定义该点为p1,则它的八邻域点p2->p9位置如下图所示,该算法考虑p1点邻域的实际情况,以便决定是否删除p1点。
假设我们处理的为二值图像,背景为黑色,值为0,要细化的前景物体像素值为1。
算法的描述如下。
首先复制源图像到目地图像,然后建立一个临时图像,接着执行下面操作:1. 把目地图像复制给临时图像,对临时图像进行一次扫描,对于不为0的点,如果满足以下四个条件,则在目地图像中删除该点(就是设置该像素为0),这里p2,…,p9是对应位置的像素灰度值(其为1或者0)。
a. 2<= p2+p3+p4+p5+p6+p7+p8+p9<=6大于等于2会保证p1点不是端点或孤立点,因为删除端点和孤立点是不合理的,小于等于6保证p1点是一个边界点,而不是一个内部点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
只要图中a、b、c 的取值满足1< b/a < 2, 1<c/b < 2, 那么 它就是欧几里德距离的一个在栅格空间中的整数近似值。
6.8 距离变换图和骨架图生成算法
1、距离变换图算法
(3)基于栅格图像间的运算
6.8 距离变换图和骨架图生成算法
1、距离变换图算法
(2)基于“欧几里德距离”公式的距离变换图算法
在二维平面上定义两点,那么他们之间的欧氏距离表示为 :
在二值图像中,1代表目标点,0代表背景;在灰度图像中,栅格的灰度值 表示该栅格点到最近目标点的距离值。这样一张M×N的图像可以表示为 一个二维数组A[M][N],其中A[i][j]=1对应的栅格表示目标点,A[i][j]=0对应 的栅格表示背景点。设B={(x,y)|A[i][j]=1}为目标点集合,则欧氏距离变换 就是对A中所有的栅格点求:
6.8 距离变换图和骨架图生成算法
2、骨架图算法
基于距离变换的骨架图生成算法
6.8 距离变换图和骨架图生成算法
3、距离变换图和骨架图的应用
距离变换图常用于地图制图、地理空间的各种量度 (如面积、密度、坡度、坡向等)及空间分析(如缓冲 区分析、Voronoi分析、DEM分析等)等方面。
其中
从而得到二值图像A的欧氏距离变换图。
欧氏距离变换1
欧氏距离变换2
加权欧氏距离变换
6.8 距离变换图和骨架图生成算法
1、距离变换图算法
(2)基于“欧几里德距离”公式的距离变换图算 法
栅格空间中的“欧几里德距离”距离变(i, j , m, n) (m i ) 2 (n j ) 2
获取距离变换图的算法
基于栅格图像间的运算获取距离变换图算法的基本方法是:反 复对原图进行“减细”和将减细结果与中间结果作算术“叠加”两种基 本运算。其终止条件是:“若对原图再减细,则将成为全零矩阵” 。
6.8 距离变换图和骨架图生成算法
2、骨架图算法
骨架图就是从距离变换图中提取出具有相对 最大灰度值的那些像元所组成的图像。 骨架图算法是一种简洁、直观的目标表示 方法,它综合利用了目标的外部轮廓和内部区 域信息,在描述目标形状方面具有传统表示方 法不可比拟的优势,且骨架图“山脊线”的连 接关系保留了空间拓扑结构的完整,从而极大 地扩展了骨架图算法的应用领域。
距离变换图和骨架图生成算法
6.8 距离变换图和骨架图生成算法
1、距离变换图算法
距离变换图算法是一种针对栅格图像的特 殊变换,是把二值图像变换为灰度图像,其中 每个像素的灰度值等于它到栅格地图上相邻物 体的最近距离。
6.8 距离变换图和骨架图生成算法
1、距离变换图算法
(1)基本思想
是把离散分布在空间中的目标根据一定的 距离定义方式生成距离图, 其中每一点的距离 值是到所有空间目标距离中最小的一个。 对于距离的量度是通过四方向距离(又称 “城市块距离”或“出租车距离”)的运算来 实现的,即只允许沿四个主方向而不允许沿对 角方向进行跨栅格的最小路段的计数。因此, 每个路段为一个像元边长。
(1)保留原物体的拓扑。 (2)骨架点的位置精确,要靠近物体的中心。 (3)骨架的连通性。 (4)获得骨架的半径值。 (5)骨架能表达物体在人类视觉中的重要部分。
6.8 距离变换图和骨架图生成算法
2、骨架图算法
骨架图算法实现的途径主要有两条,其一是基 于灰度图像的骨架图算法,其二是直接从灰度图像 提取目标骨架的算法。 其中,基于灰度图像的骨架图算法主要有3类: (1) 从距离变换中提取骨架,即通过计算灰度图像 的距离变换,从距离变换图中检测并连接骨架点得 到目标的骨架,其缺点是难以设计恰当的邻域条件, 需要较多的后处理。
6.8 距离变换图和骨架图生成算法
2、骨架图算法
(2) 采用边界模型提取骨架,即采用离散边 界模型在逼近真实形状的同时提取骨架,可 得到在噪声环境下稳健的骨架。但是,运用 该方法时因构造离散边界模型比较困难,提 取出的骨架有时可能是不连通的。
6.8 距离变换图和骨架图生成算法
2、骨架图算法
(3) 基于区域标记的方法。其典型代表是Liu等人 (2000)提出的基于Arcelli的“非脊点下降”算子 的骨架提取算法。该算法通过并行地对图像中的所 有非脊点进行下降,将图像分别标记为骨架点和背 景点,可以获得单像素宽的、与原始图像同伦的骨 架。但该算法有时不能提取一些规则目标的完整骨 架,而且算法对边界噪声比较敏感(陈晓飞等, 2003)。
6.8 距离变换图和骨架图生成算法
2、骨架图算法
自1967年Blum提出中轴的概念以来,骨架已经成为表示和识别 物体的重要手段之一,骨架组合了目标的轮廓喝中药区域信息,反 映了目标的重要视觉线索,因而,寄语骨架的目标表示和识别技术 成为牧师识别和计算机视觉的重要研究内容。
为了准确的对物体进行识别,要求骨架要求具有如下性质:
