径向分布函数、角度分布函数电子云图形的绘制
径向分布函数

2.2.3 径向部分和角度部分的对画图1. 径向部分的对画图结尾部分增加如下内容:需要指出,常有人将4πr 2ψ2作为径向分布函数的定义,“理由”是:ψ2代表概率密度,4πr 2代表球面积,二者相乘即为半径为r 的球面上的概率。
但这种说法至少是片面的,甚至是错误的。
事实上,以上说法只对s 电子云才成立,因为它们是与方向无关的球对称形,Y 00=(4π)-1/2,|Y 00|2=(4π)-1,R 2( r )=ψ2/|Y 00|2=4πψ2,从而D ( r )= r 2R 2( r )才可以进一步写成D ( r )=4πr 2ψ2。
可见,D ( r )= r 2R 2( r )对于任何原子轨道的电子云都是适用的,而D ( r )= 4πr 2ψ2只适用于s 电子云,用于其它电子云都是错误的。
电子云在空间的分布并没有一个明确的边界,所以,衡量轨道的大小取决于如何定义轨道的半径。
文献中常见到两种定义:(1) 轨道最可几半径,即径向分布函数D (r )最大值对应的半径r max 。
在这个半径上,单位厚度球壳内电子出现的几率最大。
以单电子原子的1s 轨道为例:0000000321003222210303322222330003230020()24()d ()4d 422d d 421010Zr a Zr a Zr Zr Zr a a a Zr a Zr a Z R r e a Z D r r R r e a D r Z Z Z r e re r e r a r a a Z Zr re a a Zr re a −−−−−−−⎛⎞=⎜⎟⎝⎠==⎡⎤⎡⎤==−⎢⎥⎢⎥⎣⎦⎣⎦⎛⎞=−=⎜⎟⎝⎠⎛⎞−=⎜⎟⎝⎠此式为0,只有三种可能:(i )r = 0,但这导致D (r )=0, 故应舍去;(ii )020Zr a e −=,这也导致R 10=0, D (r )=0,应舍去;(iii )0010,a Zr r a Z−==,这就是类氢离子基态的r 的最可几半径,对于氢原子基态1s ,最可几半径就是Bohr 半径。
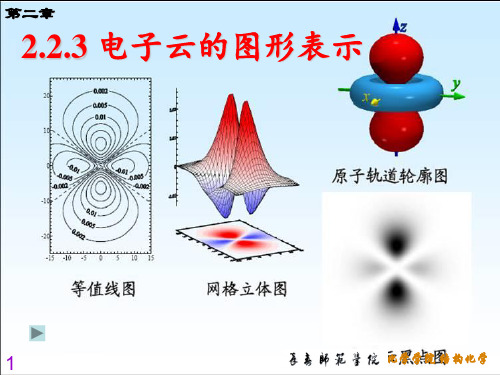
11-2-4电子云的角度分布图

p 电子云的角度分布图 m = 0,±1 以2p z为例(m 0)
Y () 3 cos 4π
z
Y 2 () 3 cos2
4π
z
z
y
y
y
x
Y2 2pz
x
Y2 2p x
x
Y2 2py
波函数角度与电子云的角度分布图的区别
1) 角度波函数 Yl,m 只与量子数 l,m 有关而与主量子数 n 无关。对于 l,m 相同而 n 不同的状态,波函数和 电子云的角度分布图都分别是相同的。例如,1s、2s、 3s 或者 2px、3px、4px的角度分布图相同,如此类推。
z
z
z
+
y
-
-
y +
-+ y
x
Y2p z
z
x
Y2p x
z
x
Y2p y
z
y
y
y
x
Y2 2pz
x
Y2 2p x
x
Y2 2py
虚线部分 pz 轨道的角度分布图
实线部分 pz 电子云的角度分布图
实线部分 虚线部分
原子轨道角度分பைடு நூலகம்图 电子云的角度分布图
2) 由于 Y(pz) 值有正负值,故它的图上对应位置分别标 注了正负号,该符号可用于判断共价键的方向性。 而Y2(pz) 值都是正值,故它的图形无正负号之分。
3) 由于Y2(pz) 值小于对应的 Y(pz) 值,所以电子云的角 度分布图比波函数的角度分布图“瘦”些。
波函数角度与电子云的角度分布图的区别
波函数角度与电子云的角度分布图的区别虚线部分轨道的角度分布图实线部分电子云的角度分布图实线部分原子轨道角度分布图虚线部分电子云的角度分布图
§1-6 波函数和电子云的图形表示-结构化学课件

Yl ,m , 的图形在空间有五个伸展方向。 l 2时,
§1-6
波函数和电子云的图形表示
2
2.电子云角度分布图 Y ,
(1)由于Yl ,m , 总小于1,电子云的角度分布图形与原子 轨道的角度分布图形类似,只是变得“狭窄”一些。
§1-6
波函数和电子云的图形表示
作图方法主要包括: 函数-对变量画图 等值面(线)图 界面图 网格图 黑点图
§1-6
波函数和电子云的图形表示
一、径向部分图形 1. 径向函数图 Rn,l r ① 物理意义:
它是反映在任意给定的角度方向上(即一定的θ 和φ ), 波函数随r变化的情况。 ② 径向波函数满足归一化的条件。
(2)恒为正值。
§1-6
波函数和电子云的图形表示
三、 —r, 2—r 这两种图形一般只用来表示S态的分布,因为S态的波函数只 与r有关,而与θ ,φ 无关。ns这一特点使它分布具有球体 对称性,即离核为 r 的球面上各点波函数 的数值相同,几 率密度2的数值也相同.
§1-6
波函数和电子云的图形表示
§1-6
完全图形有:
波函数和电子云的图形表示
波函数图
电子云图 r , , 部分图形有: 径向函数图 R r 径向密度函数图 径向分布函数图
r , ,
2
R2 r
r 2 R2 r 即 D r
2
波函数角度分布图 Y ,
电子云角度分布图 Y ,
●
3 p又比3d近。 如3s比3 p的第一个峰离核近,
即所谓的轨道的钻穿效应。
●
在核附近D(r)为0,1s态D(r)极大值在r=a0处
6.2.5 电子云的角度分布图

电子云(electron cloud)
电子在核外空间出现的概率密度大小 大的地方,电子出现的概率密度大
氢原子1s电子云
以小黑点的疏密程度表示电子在核外空间各点 的概率密度,所得图像形象化描述为电子云
电子云的空间图形
电子云 电子在核外空间概率密度的形象化描述 作图 电子云的空间图形
角度分布图 反映了电子在核外空间各个方向 上出现的概率密度的分布规律
s 电子云的角度分布图
H原子的1s轨道
Y (θ, φ) 1 Y 2 ( , φ) 1
4π
4π
z
y
x
球形对称分布
p电子云的角度分布图
H原子的 2 pz (m 0)
Y(θ φ) 3 cos θ 4π
Y 2(θ φ) 3 cos2 θ 4π
z
z
z
y
y
y
x
Y2 2pz
x
Y2 2p x
x
Y2 2py
波函数和电子云的图形表示结构化学课件

§1-6 波函数和电子云的图形表示
③ 图:1-7.6(a)
④径向节面数:n l 1
§1-6 波函数和电子云的图形表示
2.
径向密度函数图
R2 n,l
r
~
r
(1) 物理意义:在距核r处电子出现的径向几率密度。
(2) 图:1-7.6(b)
(3) 特点:n s 态的电子在核附近有相当大的几率密度,其
余各态的电子在核附近的几率密度为零。
3.径向分布函数 D r ~ r
前面R2(r)描述的是几率密度随r的分布情况,要真正了解 电子的分布情况,要关心电子分布的几率---电子在半径为r处 ,厚度为dr的球壳内电子出现的几率。
2n,l,m(r,,) 电子在(r, , )处出现的几率密度
dr2sindrdd 三维空间中的微体积元
2n,l,m(r,,)d 电子在微体积元d中出现的几率
角度分布图Yl,m ,与 n 无关,所以只要l , m 相同,图形形
状就相似。如:2px,3px,4px ,但 npx,npy,npz 图形方
重要意义。但是 , 2 是关于 r , , 的函数,作图需要四 维空间,比较困难。因此,我们把 分离为径向部分和角
度部分。
§1-6 波函数和电子云的图形表示
原子轨道和电子云有多种图形,为了搞清这些图形是怎么画 出来的,相互之间是什么关系,应当区分两个问题: 1. 作图对象
2. 作图方法 作图对象主要包括: (1) 复函数还是实函数? (2) 波函数(即轨道)还是电子云? (3) 完全图形还是部分图形?
例:p z 定函数: Y 1,0 1,0 02 6cos2 1 4 3 cos
p z 的 Yl,m , 是 cos 的函数(和 无关),故其轨道是关
结构化学课件
4
化学学院 结构化学
第二章
5
化学学院 结构化学
第二章 C. 径向分布函数 2R2n,l(r)~r图 径向分布函数r 图
6
化学学院 结构化学
第二章
球极坐标与笛卡儿坐标的关系
7
化学学院 结构化学
第二章
☆1s态:核附近D为0;r=a0时,D极大。表 1s态 核附近D 极大。 明在r 附近,厚度为dr的球壳夹层内 明在r=a0附近,厚度为dr的球壳夹层内 找到电子的几率要比任何其它地方同样厚 度的球壳夹层内找到电子的几率大。 度的球壳夹层内找到电子的几率大。 ☆每一 n 和 l 确定的状态,有n-l个极大值 确定的状态, 值为0的点。 和n-l-1个D值为0的点。 ☆n相同时:l越大,主峰离核越近;l越小, 相同时: 越大,主峰离核越近; 越小, 峰数越多,最内层的峰离核越近; 峰数越多,最内层的峰离核越近; l相同时:n越大,主峰离核越远;说明n小 相同时: 越大,主峰离核越远;说明n 的轨道靠内层,能量低; 的轨道靠内层,能量低; 电子有波性,除在主峰范围活动外, ☆电子有波性,除在主峰范围活动外,主量 子数大的有一部分会钻到近核的内层。 子数大的有一部分会钻到近核的内层。
25
化学学院 结构化学
10
第二章
11
化学学院 结构化学
第二章
12
化学学院 结构化学
第二章
13
化学学院 结构化学
第二章
14
化学学院 结构化学
第二章 (3) 空间分布 )
ψ −r 和 ψ2 −r图 ★ s态的 态的
Z 3 − a0 1 −r ψ1s = 3 e ⇒ψ1s = e πa π 0
3 1 Z ψ 2s = 2πa3 4 0 1/ 2 r − Zr − 2a0 1 1 2 2 − e ⇒ψ 2s = (2 − r)e a0 4 2π Zr
波函数和电子云的图形表示

§1-8 波函数和电子云的图形表示一.氢原子基态的各种图示:电子行踪不定地按一定几率在原子核附近空间各处出现.二. 径向分布函数和径向分布图1. 定义式:D(r)=r2R2(r)只考虑某一角度上径向的分布是无意义的,所以须将角度部分积分掉. 即:2. 物理意义:D(r)——指在半径r处单位厚度壳层(dr=1)内找到电子的几率D(r)dr——在半径为r和r+dr的两个球壳夹层内找到电子的几率。
表明:在r=a 0处即玻尔半径球面上发现电子的几率最大.4. 问题:氢原子基态径向分布图与Ψ1s 2 ~ r 图比较二者是否矛盾?5. 径向分布图的特点:极大值: 共(n-l )个极小值: 即节面(球面) 共( n-l -1)个.6. 钻穿效应:l 越小,第一个峰钻得越深 ——惰电子对效应如:n=4, l=0, 1, 2, 3.示例:无关与φθcos c Y z p =1232221021222311801501351209060453000000000----Yθ讨论化学键时,轨道重迭时波的迭加必须考虑位相的正负号.同理:可得其它轨道,其中px 、py与pz的形状相同,只是极三个p轨道构成了l=1时彼此正交归一的波函数集合.对于d-轨道(l=2)角度分布, 共有(2l+1)=5种, 5个d轨道构成l=2时彼此正交归一的波函数集合.2). 图形的特点:节面数=角量子数l : 令Y=0四. 空间分布图及特点五. 练习试回答下列问题:θπcos )6()1(8120302303a r p e a r a H z--=ψ原子的已知1). 原子轨道能;轨道角动量和轨道磁矩. 2). 列出计算电子离核平均距离的公式.3). 轨道角动量M 和Z 轴的夹角是多少?角向分布极大值的位置在何处?4). 总节面、角节面和径向节面的个数、位置和形状怎样? 5). 画出径向分布和空间分布示意4). 总节面数:n-1=3-1=2角节面数:l=1 位于XOY 平面 径向节面数:n-l -1=3-1-1=15). 3p z 轨道的角度、径向和空间分布示意图:.0)]([)(22极小值处,形状为球面位于==drr R r d drr dD。
31 径向分布函数、角度分布函数 电子云图形的绘制

实验三十一 径向分布函数、角度分布函数电子云图形的绘制1.目的要求(1) 绘制波函数及其各种分布以及电子云的图像,观察各种函数的分布情况。
(2) 了解计算机绘图方法。
2.基本原理(1) 程序原理:本程序可绘制类氢原子的径向分布函数,角度分布函数及原子轨道、杂化轨道和分子轨道等电子几率密度图,绘制过程中的各函数形式列于下列各表中。
式中,n 为主量子数, =0.0529nm ,为波尔半径, Z 是有效核电荷,由Slater 规则计算得到的周期表中前四个周期元素的有效核电荷列于表Ⅱ-24-1中,下面简要叙述对各类图形的处理方案。
①径向分布函数图:径向分布函数D(r)=r 2R 2(r)反映了电子的几率随半径r 的分布情况, D(r)dr 代表半径r 到r+dr 两个球壳夹层内找到电子的几率。
其中R(r)为类氢原子的径向函数,本程序所采用的径向函数R(r)分别列于表Ⅱ-24-2中。
②角度分布函数图:波函数 的角度部分 以及角度分布函数表示同一球面不同方向上 或的相对大小,本程序所采用的角度函数分别列于表Ⅱ-24-3中。
322232,),(,,,,sp d sp yz xz z z z Y Y f f f p p 角度分布图是画的X-Z 平面的截面图,其余角度分布图都是画的X-Y 平面的截面图。
角度分布函数图中,凡轨道形状相同,而仅方向不同者,则仅绘出一个图形作为代表。
③等电子几率密度图:2),,(φθψr 称为电子几率密度函数,它描述在该轨道中的电子在三维空间的分布情况,为了在平面上表示出这种分布往往采用某一切面上的等值面图,程序按指定的轨道在该切面上逐点计算2ψ的值,及找出2maxψ的最大值,求出相对几率密度2max 2/ψψ=P ,该值在X-Y 平面上是位置坐标(x,y)的函数(对于23z d 轨道是在X-Z 平面),绘图时不是将取值相同的点连成曲线,而是打印一系列符号表示相对几率密度的分布区域。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
径向分布函数、角度分布函数电子云图形的绘制1.目的要求(1) 绘制波函数及其各种分布以及电子云的图像,观察各种函数的分布情况。
(2) 了解计算机绘图方法。
2.基本原理(1) 程序原理:本程序可绘制类氢原子的径向分布函数,角度分布函数及原子轨道、杂化轨道和分子轨道等电子几率密度图,绘制过程中的各函数形式列于下列各表中。
式中 ,n 为主量子数, =0.0529nm ,为波尔半径, Z 是有效核电荷,由Slater 规则计算得到的周期表中前四个周期元素的有效核电荷列于表Ⅱ-24-1中,下面简要叙述对各类图形的处理方案。
①径向分布函数图:径向分布函数D(r)=r 2R 2(r)反映了电子的几率随半径r 的分布情况, D(r)dr 代表半径r 到r+dr 两个球壳夹层内找到电子的几率。
其中R(r)为类氢原子的径向函数,本程序所采用的径向函数R(r)分别列于表Ⅱ-24-2中。
②角度分布函数图:波函数的角度部分 以及角度分布函数 表示同一球面不同方向上 或 的相对大小,本程序所采用的角度函数分别列于表Ⅱ-24-3中。
322232,),(,,,,sp d sp yz xz z zz Y Y f f f p p 角度分布图是画的X-Z 平面的截面图,其余角度分布图都是画的X-Y 平面的截面图。
角度分布函数图中,凡轨道形状相同,而仅方向不同者,则仅绘出一个图形作为代表。
2naZr=ρ0a ),,(φθψr nlm ),(φθψlm ),(2φθψlm ),,(φθψr nlm ),,(2φθψr nlm ),(φθψlm③等电子几率密度图:2),,(φθψr 称为电子几率密度函数,它描述在该轨道中的电子在三维空间的分布情况,为了在平面上表示出这种分布往往采用某一切面上的等值面图,程序按指定的轨道在该切面上逐点计算2ψ的值,及找出2maxψ的最大值,求出相对几率密度2max2/ψψ=P,该值在X-Y 平面上是位置坐标(x,y)的函数(对于23z d 轨道是在X-Z 平面),绘图时不是将取值相同的点连成曲线,而是打印一系列符号表示相对几率密度的分布区域。
当P <0.01时为空白,0.01≤P <0.02时用“:”,0.02≤P <0.1时用“/”,0.1≤P <0.25时用“O ”,0.25≤P <0.5时用“&”和P >0.5时用“#”符号表示。
根据这些符号可以粗略看出几率密度的分布情况。
在X-Y 平面内,坐标变化范围为 -2.4≤x ≤2.4(步长=0.08) -1.42≤y ≤1.42(步长=0.133) 所有距离的长度单位都是10-10m 。
原子轨道使用的波函数如表Ⅱ-24-4所示。
对23224,4,4,3xz z zzf f dd 和轨道采用X-Z 平面做截面,所有其它原子轨道都画在X-Y 平面上,程序使用原子轨道的四重轴对称性,首先计算第三象限内,即-2.4≤x ≤0,-1.42≤y ≤0的Ψ值,随后被2m ax2/ψψ=P代替,在其它三个象限内的相应值由对称性得到,用P(x,y)代表电子在坐标(x ,y)点的几率密度,则: P(-x,-y)=P(-x,y)=P(x,-y)=P(x,y)表Ⅱ-24-1 Slater轨道中的Z*参量值杂化轨道采用的杂化方式如表Ⅱ-24-5所示,程序中应用了以X轴为对称轴的二重轴对称性,在X-Y平面上画出杂化轨道等电子几率密度图。
分子轨道采用如表Ⅱ-24-6所示的原子轨道的线性组合,取双原子-A、B 的两个原子核在Y轴上,及以Y轴为分子轴,其坐标分别为-R A B/2,R A B/2,若Z A=Z B,则分子轨道具有四重轴对称性,否则仅有以Y轴为对称轴的二重轴对称性。
表19-2类氢原子的径向波函数)(rRnl表19-3波函数角度部分),(φθlm Yπ41=Sφθπcos sin 43=xpφθπsin sin 43=ypθπcos 43=zp)1cos 3(16522-=θπz dφθθπcos cos sin 415=xzd φθθπsin cos sin 415=yz dφθπ2sin sin 4152=xydφθπ2cos sin 1615222=-y x d)cos 3cos 5(16733θθπ-=z fφθθπcos )1cos5(sin 322122-=xz f φθθπsin )1cos 5(sin 322122-=yzfφθθπ2cos cos sin161052)(22=-y x z f φθθπ2sin cos sin 161052=xyzfφθπ3cos sin 32353)3(22=-y x y f φθπ3sin sin 32353)3(22=-y x x f()θπcos 3181+=sp Y⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-++=15231cos 52cos 1615232θθπsp d Y表19-4类氢原子波函数),,(φθψr nlm2231)(1ρπψ-=ea ZS2232)(241ρπψ-=ea Z S2)66()(31812233ρρρπψ-+-=ea Z S3234)123624()(19210ρρρρπψ--+-=ea Z Sφθρπψρcos sin )(2412232-=ea ZxP φθρπψρsin sin )(2412232-=ea Z yPθρπψρcos )(2412232-=e a Z zPφθρρπψρcos sin )4()(21812233--=ea Z xP φθρρρπψρcos sin )1020()(564122324-+-=e a Z xP)1cos 3()(63612223232-=-θρπψρea Z o zd φθρπψρ2cos sin)(236122232322-=-ea Z o yx dφθρπψρ2sin sin)(2361222323-=ea Z oxyd )1cos 3()6()(384122322324--=-θρρπψρea Z o zd φθρρπψρ2cos sin )6()(31281223223224---=ea Zo yx d φθρρπψρ2sin sin)6()(312812232234--=ea Z o xyd )cos 3cos 5()(538413232334θθρπψρ-=-ea Z o zf φθθρπψρcos )1cos5(sin )(3012812232324-=-ea Z o xzfφθρπψρ3cos sin)(2384132323)22(4--=ea Z o yx x fφθθρπψρ2cos cos sin )(3128122323)22(4--=ea Zoyx z f表19-5杂化轨道)(2122xp sspψψψ+=)2(31222xp sspψψψ+=)(2122223zp yp xp sspψψψψψ+++=xp yx d sdsp422342212121ψψψψ++=-234223432121212161dzxp yx d sspdψψψψψ-++=-表19-6分子轨道成键轨道 反键轨道Bs A s s 111ψψσ+= Bs A s s11*1ψψσ-=Bs A s s 222ψψσ+= Bs A s s22*2ψψσ-= yBp yA p y p 222ψψσ-= yBp yA p yp 22*2ψψσ+=xB p xA p x p 222ψψπ+= xB p xA p x p 22*2ψψπ-= yBp A s y p s 2121ψψσ+= yB p A s y p s 21*21ψψσ-= yBp A s y p s 2222ψψσ+= yBp A s yp s 22*21ψψσ-=(2)程序功能:该程序可绘制下列三类图形:①1s 至4s ,2p 至4p ,3d 至4d, 4f 轨道的径向函数、径向密度函数、径向分布函数图形。
②所有s 、p 、d 、f 轨道和sp 、d2sp3杂化轨道的角度函数和角度分布函数图形。
③1s 至4s ,2x p 至4x p 、23zd 、223yx d-、xyd 3、24zd 、224yxd-、xyd 4、34zf 、24xzf、)22(4y x x f-、)22(4y x z f-原子轨道;sp 、2sp 、3sp 、2dsp 、32sp d 杂化轨道;s s 11±,s s 22±,xx p p 22±,yy p p 22±,y p s 21±,y p s 22±分子轨道中电子的几率密度等值面图。
(3)使用方法本程序采用Turbo BASIC 语言编程,并已编译成可执行文件,适用于486系列微机,VGA 彩色显示器。
本软件的运行环境为MS -DOS3.30或更高版本。
3 仪器试剂486微型计算机1台(配VGA 彩色显示器) MS-DOS3.30或更高版本 4 实验步骤(1) 打开稳压电源开关,待电压稳定后,打开显示器、打印机和主机开关,启动程序。
(2) 选择适当参数,绘制径向分布,角度分布和原子轨道、杂化轨道、分子轨道等电子几率密度图各1个。
(3) 关掉主机和附件开关,切断电源。
5 数据处理记录所绘图形,观察各类函数的极大值、界面位置和数目以及分布情况。
6 注意事项在绘制径向分布函数和等电子几率密度图时只有选择合适的参数,才能观察到大小适当完整的图形。
7 思考题(1) 在绘制径向分布函数、等电子几率密度图时为什么要选用有效核电荷?(2) 讨论有效核电荷大小对电子云及其各种分布的影响。
