氢原子的径向概率密度
合集下载
氢原子

电子相对核的运动方程
2 2 U E 2 2 2 2 x y z
(4)
我们感兴趣的是描述氢原子的内部状态的方程(4), 它描述一个质量为 的粒子在势能为 U e s2 r 的力场 中的运动。这是一个电子相对于核运动的波函数 r 所满足的方程,相对运动能量 E 就是电子的能级。这 与上节电子在库仑场中运动的内容一致,按照上节的 讨论 e n 1, 2 , 3, E 能量本征值 (5) 2 n
6
3.4 氢原子(续6)
(2)基态能
E1
es
4
2 2
1 3 .6
es
2
2 4
电子伏
1 3 .6 eV
基态氢原子电离的能量:E (3)氢原子谱线 系统由高能级 E n 低 能级 E n 时,辐射一个 光子,其频率
v E nE h
n
E1
电离能
1 1 R c 2 2 n n
电子相对核的坐标
质心坐标
X
Y
折合质量
x x1 x 2 y y1 y 2 z z z 1 2
势能
U ( x, y, z) ze s
m 1 x1 m 2 x 2 m1 m 2
m 1 y1 m 2 y 2 m1 m 2
m1m 2 m1 m 2
z
P-态电子
Y1 0
2
z
W10
y
x
Z
Y1 1
2
z
W 1, 1
y
x
16
3.4 氢原子(续16)
14.10量子物理之氢原子的电子云图和概率密度等值面图

对于4d态电子,当m = 0时, 概率密度分为上下双峰,上下 还有两包,左右还有四双包。 彩色电子云图分上下左右八片, 上下的中间两片比较鲜艳。 概率密度的等值面是六个曲面,上下 四个是封闭曲面,中间两个是环面。
对于4d态电子,当m = ±1时,概 率密度分为对称的四峰和四包。 彩色电子云图分为四角对称的八片。 概率密度的等值面是 上下四个分立的环面。
对于4f态电子,当m =±2时,概率 密度分为上下左右四峰和左右两包。 彩色电子云图分上下左右 六片,上下四片比较鲜艳。 概率密度的等值面是三个曲面,上下 两个是封闭曲面,中间一个是环面。
对于4f态电子,当m = ±2时, 概率密度分为对称的四峰,与m = ±1的3d态电子类似。 彩色电子云图分为四角对称的四片。 概率密度的等值面是上下两个分 立的环面,其形状与3d态(m = ±1)电子的概率密度形状相似。
MATLAB可视化 大学物理学
第十四章结束 湖南大学物电院 子,当磁量子数m = 0时,概 率密度曲面形成上下双峰,峰顶比较圆。 上下两片电子云是双峰的投影, 等值线分别围绕着两个峰。 概率密度的等值面是两个分立的闭合曲 面,由此可知:上下两片电子云是分立。
对于2p态电子,当m = ±1时,概 率密度曲面分为左右双峰。 在彩色电子云图中,左右 两片电子云是双峰的投影。 概率密度的等值面是中间空心的环面, 左右两片电子云是绕z轴联成一体的。
对于4p态电子,当m = 0时,概率密度 除了上下双峰之外,还有四个波包, 比m = 0的3p态电子多两个波包。 彩色电子云图分为上下六片,相 邻的波峰和波包是分开的,等值 线分别围绕着各自的波峰和波包。 概率密度的等值面是上 下六个分立的闭合曲面。
对于4p态电子,当m = ±1时,概 率密度分为左右双峰和四个波包, 比m = ±1的4p态电子多一对波包。 彩色电子云图分为左右对称的六片。 概率密度的等值面是三个 空心的环面,环面层层相 套,三个环面是相似的。
大学物理学电子教案 氢原子的量子理论简介

可容纳的电子数为
n1
Nn22l12n2
21
l0
01 sp
2 d
3 f
4 g
5 h
6 i
Nn
1K 2
2
2L 2 6
8
3 M 2 6 10
18
4 N 2 6 10 14
32
5 O 2 6 10 14 18
50
6 P 2 6 10 14 18 22
72
7 Q 2 6 10 14 18 22 26 98
例题:试确定基态氦原子中电子的量子数。
2、角动量量子化及角量子数
求解氢原子波函数的经度方程,可得氢原子中电子的角动量 是量子化的
L ll 1 h ll 1 l 0 ,1 ,2 , ,n 1 2
其中l 叫做轨道角动量量子数或角量子数。
讨论:
•波耳理论的L=nh/2,最小值为h/2;而量子力学得出角
动量的最小值为0。实验证明,量子力学得结论是正确的;
Rnl2r2d r n 2lrdr| n0 |2
径向概率密度为:
pnl
(r)
2 nl
(r)
1s 2s 3s
| n1 |2
2p
| n2 |2
4s r
3p
4p
r
3d 4d
r
15
19-10 多电子原子中的电子分布
一、电子自旋 自旋磁量子数
1、斯特恩-盖拉赫实验
银原子通过狭缝,经 过不均匀磁场后,打
在照相底板上。s 态
23
小结
• 氢原子的量子理论简介 • 氢原子的定态薛定谔方程 • 三个量子数 • 氢原子在基态时的径向波函数和电子的分布概率
• 多电子原子中的电子分布 • 电子自旋 自旋磁量子数 • 四个量子数 • 多电子原子中的电子分布
§3-3氢原子量子理论电子的概率分布

§3-3 氢原子理论
电子的概率分布
一、电子概率的径向分布
d体积元内的概率应表示为
nlm
nlm
d
Rnl (r)Ylm ( ,) 2 r 2 sindrdd
Rnl (r) 2 r 2dr Ylm ( ,) 2 sindd
在半径为r到r+dr的球壳内发现电子的概率为
wnl (r)dr
π 0
2π 0
(r)]
0
(r为最概然半径 )
可以证明,对于n-l-1 = 0 , n 1, 2,
这与玻尔理论中各能级所对应的圆形轨道半径公
式完全一致 。
二、电子概率的角度分布
立体角d = sin d d内发现电子的概率为
wlm (,)d
0
Rnl
(r)Ylm (,)
2 r 2dr sin
d
d
Ylm (,) 2 sin d d = Ylm (,) 2 d
式中wlm (, )是电子出现在相应立体角内的概率
密度,称为电子概率的角度分布函数。
3
在上式中,由于
Ylm(,) 2 Nl2m[Plm (cos)]2 e-im eim Nl2m[Plm (cos)]2
与无关,所以角度分 布函数wlm(,)是以z轴
Rnl (r)
2 r 2dr Ylm ( ,)
2
s in d d
Rn2l (r )r 2dr
式中wnl (r) Rn2l (r)r2 是电子出现在相应球壳内的概
率密度,称为电子概率的径向分布函数。
1
一些低量子数的径向概率分布曲线
2
对分布函数的一阶导数等于零求得
d dr
wnl
(r)
d dr
电子的概率分布
一、电子概率的径向分布
d体积元内的概率应表示为
nlm
nlm
d
Rnl (r)Ylm ( ,) 2 r 2 sindrdd
Rnl (r) 2 r 2dr Ylm ( ,) 2 sindd
在半径为r到r+dr的球壳内发现电子的概率为
wnl (r)dr
π 0
2π 0
(r)]
0
(r为最概然半径 )
可以证明,对于n-l-1 = 0 , n 1, 2,
这与玻尔理论中各能级所对应的圆形轨道半径公
式完全一致 。
二、电子概率的角度分布
立体角d = sin d d内发现电子的概率为
wlm (,)d
0
Rnl
(r)Ylm (,)
2 r 2dr sin
d
d
Ylm (,) 2 sin d d = Ylm (,) 2 d
式中wlm (, )是电子出现在相应立体角内的概率
密度,称为电子概率的角度分布函数。
3
在上式中,由于
Ylm(,) 2 Nl2m[Plm (cos)]2 e-im eim Nl2m[Plm (cos)]2
与无关,所以角度分 布函数wlm(,)是以z轴
Rnl (r)
2 r 2dr Ylm ( ,)
2
s in d d
Rn2l (r )r 2dr
式中wnl (r) Rn2l (r)r2 是电子出现在相应球壳内的概
率密度,称为电子概率的径向分布函数。
1
一些低量子数的径向概率分布曲线
2
对分布函数的一阶导数等于零求得
d dr
wnl
(r)
d dr
物理-氢原子和类氢原子

r
驻波
计算表明径向波函数
的节点数
通常把节点数为零(
)的“态”,称为
圆轨道,例如:1s, 2p, 3d, …,它们极大值的位
置:
,其中 是第一玻尔轨道半径。
§2. 量子力学对(类)氢原子的描述
➢电子的几率密度随角度的变化
电子在 附近的立体角 内的几率:
Y0,0 ( ,)
1
4
Y2,0 ( ,)
1 (3 cos2 1) 4
Y1,0 ( ,)
1 cos 4
Y2,1 ( ,)
1 sin cos ei 4
Y1,1 ( ,)
1
4
sin ei
Y2,2 ( ,)
1 sin2 ei2 4
§2. 量子力学对(类)氢原子的描述
粒子概率分布随角度的变化|Ylm|2,与φ角无关
Y00 2
Y10 2
实验数据和理论结果之差异可以通过考虑原子核的质量得
到消除。即把电子质量m用约化质量 = mM/(m+M)替代。
对类氢离子(He+, Li++, Be+++等),结果都适用。 只需把核电荷+e换为+Ze(Z为核所带正电荷数)。
§2. 量子力学对(类)氢原子的描述
2)氢原子的几个光谱线系
赖曼(Lyman,1914)系:
Y11 2
Y20 2
Y21 2
Y22 2
Y30 2
Y31 2
Y32 2
Y33 2
§2. 量子力学对(类)氢原子的描述
概率密度: 2 Rnl (r)Ylm ( ,) 2 Rnl2 (r) Ylm ( ,) 2 “电子(几率)云”图象
径向分布函数图
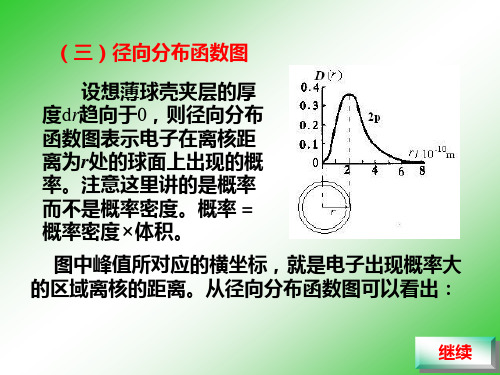
n 越小,主峰离核越近;n 越大,主峰离核越
远;好象电子处于某一电子层中。
继续
(三)径向分布函数图
4. 主量子数n 相同,角量子数l 不同时,ns比np
多一个离核较近的峰,np比<nf,说明l不同,
“钻穿”到核附近的能力不同。钻穿能力的顺序
(三)径向分布函数图
2. 径向分布函数图中的峰值有(n-l)个。 例如:1s有1个峰;2s有2个峰; 3s有3个峰;
2p有1个峰;3p有2个峰;3d有1个峰等等。 峰所在位置就是电子出现概率大的位置。 继续
(三)径向分布函数图
3. 角量子数 l 相同,主量子数 n 不同时,主 峰离核的距离不同。
是ns>np>nd>nf。
继续
(三)径向分布函数图 例如:4s的第一个峰竟钻穿到3d的主峰内去了。
3d和4s轨道的径向分布图
这说明玻尔理论中假设的固定轨道是不存在的, 外层电子也可以在内层出现,这正是反映了电子的 波动性。
返回
(三)径向分布函数图
设想薄球壳夹层的厚 度dr趋向于0,则径向分布 函数图表示电子在离核距 离为r处的球面上出现的概 率。注意这里讲的是概率 而不是概率密度。概率 = 概率密度×体积。
图中峰值所对应的横坐标,就是电子出现概率大 的区域离核的距离。从径向分布函数图可以看出:
继续
(三)径向分布函数图
1. 在基态氢原子 中,电子出现概率的 极大值在r=a0(玻尔半 径,a0 =52.9pm)的球 面上,从量子力学的 观点来理解,玻尔半 径就是电子出现概率 最大的球壳离核的距 离。
p14_10氢原子的电子云图和概率密度等值面图1

根据氢原子的薛定谔方程的解,求概率密度。 (1)为什么说用点的疏密表示的概率密度称为电子云图? (2)氢原子的概率密度曲面是什么形状?彩色电子云图是 如何分布的?通过氢原子最大概率密度的百分之一的等 值曲面,说明概率密度的三维形状。
氢原子中的电子在体积元dV之中出现的概率为
wnlmdV = |ψnlm|2dV = |Rnl|2|Θlm|2|Φm|2dV, 由于|Φm(φ)|2 = 1/2π,所以电子出 现在原子核周围的概率密度为
w n lm (r ,,) |R n l(r )|22 1 π | lm ()|2 r 1 2w n l(r )w lm ()
wlm(θ) = |Θlm(θ)|2/2π是角向概率密度, wnl = |Rnl(r)r|2是径向概率密度。
当主量子数和角量子数确定之后,径向概率密度就
20确21/7定/1 了,磁量子数不同,概率密度的分布就不同。
7
2021/7/1
8
2021/7/1
9
2021/7/1
10
2021/7/1
11
2021/7/1
12
*{范例14.10} 氢原子的电子云图和概率密度等值面图
根据氢原子的薛定谔方程的解,求概率密度。 (1)为什么说用点的疏密表示的概率密度称为电子云图? (2)氢原子的概率密度曲面是什么形状?彩色电子云图是 如何分布的?通过氢原子最大概率密度的百分之一的等 值曲面,说明概率密度的三维形状。
*{范例14.10} 氢原子的电子云图和概率密度等值面图
根据氢原子的薛定谔方程的解,求概率密度。 (1)为什么说用点的疏密表示的概率密度称为电子云图? (2)氢原子的概率密度曲面是什么形状?彩色电子云图是 如何分布的?通过氢原子最大概率密度的百分之一的等 值曲面,说明概率密度的三维形状。
氢原子中的电子在体积元dV之中出现的概率为
wnlmdV = |ψnlm|2dV = |Rnl|2|Θlm|2|Φm|2dV, 由于|Φm(φ)|2 = 1/2π,所以电子出 现在原子核周围的概率密度为
w n lm (r ,,) |R n l(r )|22 1 π | lm ()|2 r 1 2w n l(r )w lm ()
wlm(θ) = |Θlm(θ)|2/2π是角向概率密度, wnl = |Rnl(r)r|2是径向概率密度。
当主量子数和角量子数确定之后,径向概率密度就
20确21/7定/1 了,磁量子数不同,概率密度的分布就不同。
7
2021/7/1
8
2021/7/1
9
2021/7/1
10
2021/7/1
11
2021/7/1
12
*{范例14.10} 氢原子的电子云图和概率密度等值面图
根据氢原子的薛定谔方程的解,求概率密度。 (1)为什么说用点的疏密表示的概率密度称为电子云图? (2)氢原子的概率密度曲面是什么形状?彩色电子云图是 如何分布的?通过氢原子最大概率密度的百分之一的等 值曲面,说明概率密度的三维形状。
*{范例14.10} 氢原子的电子云图和概率密度等值面图
根据氢原子的薛定谔方程的解,求概率密度。 (1)为什么说用点的疏密表示的概率密度称为电子云图? (2)氢原子的概率密度曲面是什么形状?彩色电子云图是 如何分布的?通过氢原子最大概率密度的百分之一的等 值曲面,说明概率密度的三维形状。
5第3章概念2-氢原子、守恒量
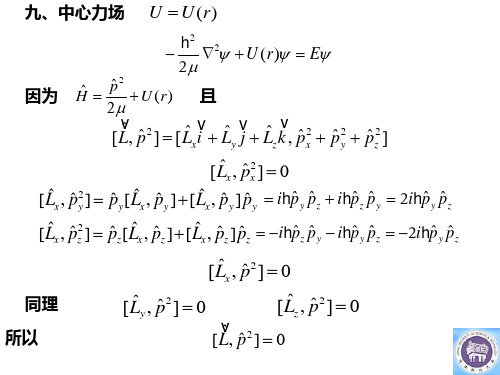
ˆ 1 ∂F 1 * ˆ ˆ ˆˆ = − ∫ψ HFψ dx + ∫ψ * FHψ dx ∂t ih ih ˆ ˆ ∂F 1 ˆ ˆ ∂F 1 * ˆ ˆ + [F , H ] = + ∫ψ [ F , H ]ψ dx = ∂t ih ∂t ih
即
ˆ d F ∂F 1 ˆ ˆ = + [F , H ] dt ∂t ih
ˆ ˆ [ Lx , p 2 ] = 0
同理 所以
ˆ ˆ [ Ly , p 2 ] = 0
ˆ ˆ [ Lz , p 2 ] = 0
v 2 ˆ ˆ [ L, p ] = 0
v ˆ ϕ 因为 L 仅与θ 、 有关
因此 同理
且 U = U (r )
v ˆ 所以 [ L,U ] = 0
v ˆ ˆ [ L, H ] = 0 ˆ ˆ [L , H ] = 0
θ 有关, 无关, 而Ylm中关于 ϕ 的部分仅为 e imϕ ,则wlm (θ , ϕ ) 仅与 有关,而与ϕ无关, 即关于 ϕ 是对称的,所以角向概率分布绕z轴具有旋转对称性。 是对称的,所以角向概率分布绕 轴具有旋转对称性。 轴具有旋转对称性
如: l = 1, m = 0 5.电流分布和磁矩 电流密度矢量 v v ih * * J e = qJ = q (ψ nlm∇ψ nlm −ψ nlm∇ψ nlm ) 2µ
[
]
3.径向概率分布 2 2 wnlm dτ = ψ dτ = Rnl 2 (r ) Ylm (θ , ϕ ) r 2 sin θ drdθ dϕ
2 2 * dW ( r ) = Rnl r 2 dr ∫∫ YlmYlm sin θ dθ dϕ = Rnl r 2 dr
径向概率密度
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
xi
氢原子中的电子出现 在r到dr之间的概率为 wnldr = |Rnl|2r2dr
径向概率 密度为
wnl
(r)
|
Rnl (r)r
|2
M
2 nl
[exp(
Z na0
2Z r)(
na0
r)l
L2nll1 (
2Z na0
r)r]2.
当氢原子主量子数n为1时,角量子数l 只能取0,径向概率密度wnl随距离的增 加先增后减,其峰值出现在r = a0处。
*{范例14.9} 氢原子的角向概率密度和径向概率密度
(2)当氢原子主量子数n一定时,各种角量子数 的径向概率密度随距离分布的规律是什么?
[解析](2)氢原子薛定谔方 程的径向分布函数为
Rnl
(r)
M nl
exp(
Z na0
2Z r)(
na0
r)l
L2l 1 nl
(
2Z na0
r)
Z为原子序数(氢原子Z = 1),a0是第一玻 尔半径, Mnl是归一化常数(以区别Nlm)
最高峰还要高一些。
当n = 4时,曲 线族如图所示。
当n = 5时,曲 线族如图所示。
当n = 6时,曲 线族如图所示。
当n = 7时,曲 线族如图所示。
比较这些图可知:
对于主量子数n来 说,角量子数l可取 0,1,...,n – 1, 共n个值,每条曲 线有n - l个峰。当l = n – 1时,峰值出 现在r = n2a0处,这 个峰比其他曲线的
M
nl
( 2Z )3 (n l 1)! na0 2n[(n l)!]3
设 x 2Z r,
na0
L2l 1 nl
(
x)
是缔合(连带)拉盖尔多项式。
下标n + l表示拉盖尔多项式阶数,即n + l阶拉盖尔多项 式Ln+l(x);上标2l + 1表示对Ln + l(x)求2l + 1阶导数。
(1)k[(n (k !)2 (n l
l)!]2 k)!
xk
对于幂函数y = xk, y(n) k(k 1)...(k n 1)xkn k ! xkn
其n阶导数为
(k n)!
因此缔合拉盖
尔多项式为
L2l 1 nl
(
x)
d 2l 1 dx 2l 1
Lnl
*{范例14.9} 氢原子的角向概率密度和径向概率密度
(2)当氢原子主量子数n一定时,各种角量子数 的径向概率密度随距离分布的规律是什么?
n阶拉盖尔
多项式为
Ln
(
x)
k
n 0
(பைடு நூலகம்1)k (n!)2 (k !)2 (n k)!
x
k
n多+项l 式阶为拉盖尔Lnl
(
x)
nl k 0
当主量子数n为2时,如果l为 0,径向概率密度有两个峰, 两峰之间有一个节点;如果l 为1,径向概率密度只有一 个峰,峰值出现在r = 4a0处。
当主量子数n为3时,如果l为 0,曲线有3个峰,随着距离
增加,一个峰比一个峰高, 曲线共有2个节点;如果l为1, 曲线有2个峰,1个节点;如 果l为2,曲线只有1个峰,峰 值出现在r = 9a0处。
(x)
nl (1)k [(n+l)!]2 xk2l1 k2l1 k !(n l k )! (k 2l 1)!
设k - 2l – 1 = i,即k = i + 2l + 1,可得
L2l 1 nl
(
x)
nl 1 i0
(n
(1)i+1[(n+l)!]2 l 1 i)!(2l+1+i)!i!
