径向分布函数
径向分布函数

实验一 径向分布函数、角度分布函数电子云图形的绘制一、实验目的1.绘制波函数及其各种分布以及电子云的图像,观察各种函数的分布情况。
2.了解电脑绘图方法。
二、实验原理1.程序原理:本程序可绘制类氢原子的径向分布函数,角度分布函数及原子轨道、杂化轨道和分子轨道等电子几率密度图,绘制过程中的各函数形式列于以下各表中。
式中,n 为主量子数, =0.0529nm ,为波尔半径, Z 是有效核电荷,由Slater 规则计算得到的周期表中前四个周期元素的有效核电荷列于表中,下面简要表达对各类图形的处理方案。
①径向分布函数图:径向分布函数D(r)=r 2R 2(r)反映了电子的几率随半径r 的分布情况, D(r)dr 代表半径r 到r+dr 两个球壳夹层内找到电子的几率。
其中R(r)为类氢原子的径向函数,本程序所采用的径向函数R(r)分别列于表2-2中。
②角度分布函数图:的角度部分 以及角度分布函数 表示同一球面不同方向上 或 的相对大小,本程序所采用的角度函数分别列于表3-3中。
02na Zr=ρ0a ),,(φθψr nlm ),(φθψlm ),(2φθψlm ),,(φθψr nlm ),,(2φθψr nlm ),(φθψlm322232,),(,,,,sp d sp yz xz z z z Y Y f f f p p 角度分布图是画的X-Z 平面的截面图,其余角度分布图都是画的X-Y 平面的截面图。
角度分布函数图中,凡轨道形状相同,而仅方向不同者,则仅绘出一个图形作为代表。
③等电子几率密度图:2),,(φθψr 称为电子几率密度函数,它描述在该轨道中的电子在三维空间的分布情况,为了在平面上表示出这种分布往往采用某一切面上的等值面图,程序按指定的轨道在该切面上逐点计算2ψ的值,及找出2max ψ的最大值,求出相对几率密度2max 2/ψψ=P ,该值在X-Y 平面上是位置坐标(x,y)的函数(对于23z d 轨道是在X-Z 平面),绘图时不是将取值相同的点连成曲线,而是打印一系列符号表示相对几率密度的分布区域。
径向分布函数..

三、径向分布函数法中心分子第一层:第一配位圈 第二层:第二配位圈 . . .短程有序,远程无序1、 基本概念,基本定义首先定义一个新的函数---n 重相关函数 为当系统的位能E N = 0 ,则系统内分子是独立的,由分布函数公式可得到:g(r)r因此对于分子相互独立的系统,,对于分子间有相互作用的系统,相当于对分子独立性的校正,亦即表示了分子的相关性,因而称之为相关函数。
相关函数中,最重要的是二重相关函数g(2),它可由X射线衍射实验和计算机分子模拟的机器实验结果获得,由式子可知表示如下上式即二重相关函数与位形积分的关系。
对于由球星对称分子构成的液体,仅取决于分子1和2的距离,即可写成g(r),所以就有故上式中的分子相对函数g(r)就是分子的径向分布函数。
因,即第一个分子是任意分布的。
由于液体分子间存在相互作用,第二个分子不可能任意分布,而构成相对于中心分子的局部密度,相应的二重分布函数为将上式代入到中得到所以径向分布函数g(r)的物理意义可解释为:在一个中心分子周围距离为r处,分子的局部密度相对于本体密度的比值。
从径向分布函数g(r)可以计算液体的配位数:实际上N为中心分子周围分子的总数,而为距中心分子r处在r + dr壳层内的分子数目。
若将上式积分到第一配位圈的距离L处,即可得到配位数N(L)为N(L)实际上也是围绕中心分子,半径为r=L的球体内的分子数。
如图已知:r1,r2…rN 代表坐标系原点,指向分子1,2,… N 的向量,体系分子1,分子2分别出现在r1处的体系元 的几率为:称双重标明分布函数;:泛指(任意分子分布在r1, r2处的概率):双重分布函数()()()NkT r r u N kT q u K KNTr id d de d d d e Q N N ττττττϕϕϕ............121/...21/1⎰⎰⎰⎰=-*===2τd ()()()KN kT r r r u d d d d e d d r r P N ϕττττττ213/,...,21212]......[,21⎰⎰-=()()()KN kTr r u d d e r r P N ϕττ⎰⎰-=......,3/...2121()()21212,ττd d r r P()()212,r r ρ()()()()()()()2122212212,,1,r r PNr r P N N r r ≈-=ρxy所以: (几率归一化性质)N 重分布函数:(n 重标明分布函数)(n 重分布函数)数密度径向分布函数定义由式子得到,与一指定分子相距r 处,分子局部密度与平均数密度之比;的定义:()()()()()221212212121,1,NN N d d r r d d r r P V≈-==⎰⎰⎰⎰ττρττ()()()KN n r r r u N n d d e r r r P N ϕττ⎰⎰+-=.........,1,...,2121()()()()()()n n n n r r P n N N M r r ,...1...1,...11+--=ρ()()V r P 111=()()11111==⎰⎰V d d r P ττ()()V Nr n =1ρzr 1xr 2d τ1 d τ2yr 12 ()()ρρr r g =()()()()()()()1221212..,21r g P P r r r r =ρ()12r g ()()()()r g V N r g V N V N r (2)12122⎪⎭⎫ ⎝⎛=⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛=ρ所以:最简单的: 2、热力学的计算(用径向分布函数计算)由正则系统配分函数为 从而得到系统的能量为E式中第一项为体系的平均动能,第二项为体系的平均位能。
径向分布函数图
n 越小,主峰离核越近;n 越大,主峰离核越
远;好象电子处于某一电子层中。
继续
(三)径向分布函数图
4. 主量子数n 相同,角量子数l 不同时,ns比np
多一个离核较近的峰,np比<nf,说明l不同,
“钻穿”到核附近的能力不同。钻穿能力的顺序
(三)径向分布函数图
2. 径向分布函数图中的峰值有(n-l)个。 例如:1s有1个峰;2s有2个峰; 3s有3个峰;
2p有1个峰;3p有2个峰;3d有1个峰等等。 峰所在位置就是电子出现概率大的位置。 继续
(三)径向分布函数图
3. 角量子数 l 相同,主量子数 n 不同时,主 峰离核的距离不同。
是ns>np>nd>nf。
继续
(三)径向分布函数图 例如:4s的第一个峰竟钻穿到3d的主峰内去了。
3d和4s轨道的径向分布图
这说明玻尔理论中假设的固定轨道是不存在的, 外层电子也可以在内层出现,这正是反映了电子的 波动性。
返回
(三)径向分布函数图
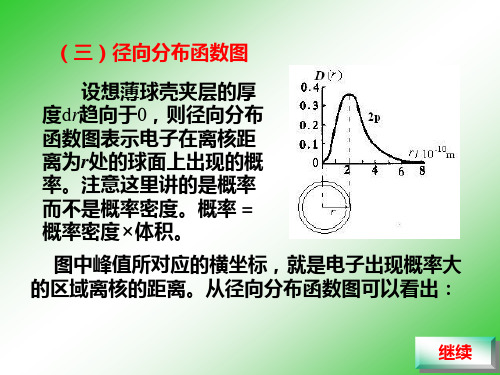
设想薄球壳夹层的厚 度dr趋向于0,则径向分布 函数图表示电子在离核距 离为r处的球面上出现的概 率。注意这里讲的是概率 而不是概率密度。概率 = 概率密度×体积。
图中峰值所对应的横坐标,就是电子出现概率大 的区域离核的距离。从径向分布函数图可以看出:
继续
(三)径向分布函数图
1. 在基态氢原子 中,电子出现概率的 极大值在r=a0(玻尔半 径,a0 =52.9pm)的球 面上,从量子力学的 观点来理解,玻尔半 径就是电子出现概率 最大的球壳离核的距 离。
径向分布函数(rdf)

径向分布函数(rdf)径向分布函数(RDF)是材料科学和化学领域中一个常用的工具,用于描述原子或分子之间的空间分布,从而揭示出材料的结构特征和反应行为。
下面将从RDF的定义、计算方法和应用场景三个方面对其进行介绍。
一、RDF的定义RDF是指一组函数,用于描述原子或分子在一定距离范围上的密度分布情况。
通俗地讲,RDF可以表达离某一个特定原子(或分子)一定距离处,其他原子(或分子)的分布密度情况,从而展示出材料的结构。
二、RDF的计算方法RDF的计算与材料类型、原子(或分子)种类、距离范围等因素有关,但是其基本思路都是一样的。
这里,我们以分子为例进行介绍。
1.选取一个分子作为参考分子,计算出该分子中所有原子之间的距离。
2.设定一定间距,比如说0.01安培(angstrom),然后将距离范围分为多个小区间,每个区间长度为0.01安培。
3.统计所有分子中,在每个小区间内,距离参考分子一定距离处的原子(或分子)的个数,并归一化,以便比较不同系统间的RDF。
4.对于一个分子的RDF,可以通过归一化的个数除以总数的形式计算得出。
三、RDF的应用场景RDF在材料和化学领域中具有广泛的应用价值,主要体现在以下两个方面:1.材料的结构研究。
通过计算材料中不同原子(或分子)的RDF,可以获得材料内部的结构特征。
比如说,晶体中原子之间的距离分布情况,液体中分子之间的相互作用特征等等。
2.反应过程的模拟。
在模拟化学反应的过程中,RDF可以帮助我们更加清晰地了解反应物与产物之间的相互作用情况。
通过计算反应前后不同分子的RDF,我们可以判断反应是否发生,以及判断反应机理。
综上所述,RDF作为一种常见的研究手段,对于材料和化学领域的研究都具有重要价值。
python计算径向分布函数的代码

python计算径向分布函数的代码Python是一种功能强大的编程语言,拥有广泛的应用领域。
其中一个重要的应用领域是科学计算和数据分析。
在这篇文章中,我们将探讨如何使用Python计算径向分布函数(Radial Distribution Function,简称RDF)。
径向分布函数是描述分子或原子之间距离分布的函数。
它可以用于研究固体的结构、液体的密度分布以及气体的分子运动等。
径向分布函数的计算方法相对简单,但对于大量的原子或分子数据,手动计算是不现实的。
因此,使用Python编写计算径向分布函数的代码是非常有必要的。
我们需要明确计算径向分布函数的原理。
给定一组原子的坐标,径向分布函数描述了不同距离范围内的原子对数密度。
具体来说,径向分布函数表示了每个距离范围内原子对数密度的变化情况。
通过计算不同距离范围内的原子对数密度,并将其归一化,我们可以得到径向分布函数。
在Python中,我们可以使用numpy和matplotlib等库来计算和绘制径向分布函数。
首先,我们需要将原子的坐标数据导入到Python中。
可以使用pandas库来读取和处理数据文件,以便我们能够方便地进行后续的计算和分析。
接下来,我们需要计算不同距离范围内的原子对数密度。
可以使用numpy库中的函数来计算两个原子之间的距离,并将其分为不同的距离范围。
然后,我们可以使用numpy的histogram函数来计算每个距离范围内的原子对数密度。
一旦我们计算出了不同距离范围内的原子对数密度,我们可以对其进行归一化。
通过除以总原子数和体积元素,我们可以得到每个距离范围内的归一化原子对数密度。
我们可以使用matplotlib库来绘制径向分布函数的图形。
通过将距离范围作为x轴,归一化原子对数密度作为y轴,我们可以得到一个描述原子之间距离分布的曲线图。
在实际的应用中,我们可能会遇到一些问题。
例如,如何选择合适的距离范围和间隔,以便得到准确的径向分布函数。
【转帖】径向分布函数程序与简单说明(小木虫)

【转帖】径向分布函数程序与简单说明(⼩⽊⾍)径向分布函数g(r)代表了球壳内的平均数密度为离中⼼分⼦距离为r,体积为的球壳内的瞬时分⼦数。
具体参见李如⽣,《平衡和⾮平衡统计⼒学》科学出版社:1995CODE:SUBROUTINE GR(NSWITCH)IMPLICIT DOUBLE PRECISION(A-H,O-Z)PARAMETER(NM=40000,PI=3.141592653589793D0,NHIS=100)COMMON/LCS/X0(3,-2:2*NM),X(3,-2:2*NM,5),XIN(3,-2:2*NM),XX0(3,−2:2∗NM),XX(3,−2:2∗NM,5),XXIN(3,−2:2∗NM)COMMON/MOLEC/LPBC(3),MOLSP,MOLSA,NBX,NBY,NBZ,NPLA,LPBCSM,NC,NN,MCCOMMON/WALLS/HI(3,3 YIJ*(G22*YIJ+G23D*ZIJ)+G33*ZIJ*ZIJRRR=SQRT(RSQ)RRR=RRR/H(1,1)C====================================================================C 以上⽤数组G和H的结果与下同C RRR=SQRT(XIJ**2+YIJ**2+ZIJ**2)C G11=H(1,1)**2C====================================================================IF(RRR.LT.HALF)THENIG=INT(RRR/DELR)GG(IG)=GG(IG)+2ENDIFENDDOENDDOELSE IF(NSWITCH.EQ.2)THENDO I=1,NHISR(I)=DELR*(I+0.5D0)ENDDODO I=1,NHISVB=(4.D0/3.D0)*PI*(((I+1)**3-I**3)*(DELR**3))GNID=VB*DEN_IDEALGG(I)=GG(I)/(NGR*MOLSP*GNID)ENDDOOPEN(UNIT=31,FILE="GR.DAT")DO I=1,NHISWRITE(31,*)R(I),GG(I)ENDDOCLOSE(31)ENDIFRETURNEND这样的代码看着不够明了。
对关联函数和径向分布函数的理解

对关联函数和径向分布函数的理解关联函数和径向分布函数是统计物理学中常用的概念和工具,用于描述和分析粒子之间的关联和分布特性。
它们在研究各种复杂物理系统的性质和行为时都起到了重要作用。
首先,我们来了解一下关联函数是什么。
关联函数描述了系统中不同位置或不同粒子之间的关联程度。
它是一个用来度量两个粒子之间的关联性的函数。
关联函数可以是一个简单的数值,也可以是一个复杂的函数,取决于系统的特性和所关注的问题。
在统计物理学中,最常用的关联函数是两点关联函数,也称为自关联函数或格林函数。
两点关联函数表示了系统中两个粒子之间的关联程度。
它可以用来描述物理量在空间和时间上的分布,从而揭示粒子之间的相互作用和集体行为。
在具体计算关联函数时,常会用到径向分布函数。
径向分布函数描述了粒子在系统中的空间分布特性。
它是一个关于距离的函数,表示在特定条件下粒子在不同半径上的分布密度。
径向分布函数可以帮助我们理解粒子之间的位置关系和相互作用方式。
接下来,我们将逐步回答相关问题,从数学定义到实际应用。
首先,我们来看一下关联函数的数学定义和基本性质。
关联函数的数学定义如下:设A和B是两个物理量,其期望值分别为⟨A⟨和⟨B⟨,关联函数Corr(A,B)定义为:Corr(A,B) = ⟨(A-⟨A⟨)(B-⟨B⟨)⟨其中⟨⋯⟨表示统计平均。
关联函数的几个基本性质如下:1. 对称性:Corr(A,B) = Corr(B,A)2. 线性性:Corr(A,B+C) = Corr(A,B) + Corr(A,C)3. 正定性:Corr(A,A) ≥0,等号成立当且仅当A为常数以上这些性质使得关联函数成为了一种非常有用的统计物理学工具。
通过计算和分析关联函数,我们可以揭示系统中不同物理量之间的相互作用和关联性。
这对于理解和解释复杂系统的行为非常重要。
接下来,我们来了解一下径向分布函数的定义和性质。
径向分布函数g(r)的定义如下:g(r) = (1/Vρ)⟨Σδ( r'-r - r′)⟨其中V是系统的体积,ρ是粒子的密度,δ是狄拉克函数,r'是其他粒子的位置。
python径向分布函数

Python径向分布函数一、概述径向分布函数(Radial Distribution Function,简称RDF)是用来描述粒子在空间中的分布情况的一种函数。
在物理、化学和材料科学等领域中,径向分布函数是一种常用的工具,可以用来研究原子、分子或离子之间的相互作用、结构和动力学等问题。
在Python中,我们可以使用不同的方法和库来计算和绘制径向分布函数。
本文将介绍如何用Python编写径向分布函数的代码,并给出一些实例来帮助读者更好地理解和应用径向分布函数。
二、计算径向分布函数的方法计算径向分布函数的方法有很多种,其中比较常用的方法有直接计算法、快速傅里叶变换法和分子动力学模拟法等。
下面将分别介绍这三种方法的原理和应用。
2.1 直接计算法直接计算法是最简单和直接的方法,它基于统计学原理,通过计算在一定距离范围内的粒子对的数量来估计径向分布函数。
具体步骤如下:1.将空间划分为一系列的小体积元,通常是立方体或球体。
2.对于每个小体积元,计算其中粒子对的数量。
3.根据粒子对的数量和小体积元的体积,计算径向分布函数的值。
直接计算法的优点是简单易懂,计算速度比较快。
但是它也有一些局限性,比如需要将空间离散化,对于连续分布的粒子系统不适用。
2.2 快速傅里叶变换法快速傅里叶变换法(Fast Fourier Transform,简称FFT)是一种基于傅里叶变换的计算径向分布函数的方法。
它的基本思想是将径向分布函数转化为频率域上的信号,然后利用快速傅里叶变换算法进行计算。
具体步骤如下:1.将粒子的坐标数据转化为径向距离数据。
2.对径向距离数据进行快速傅里叶变换,得到频域上的信号。
3.根据频域上的信号,计算径向分布函数的值。
快速傅里叶变换法的优点是计算速度非常快,尤其适用于大规模的粒子系统。
但是它也有一些限制,比如需要将粒子的坐标数据转化为径向距离数据,对于非球对称的粒子系统不适用。
2.3 分子动力学模拟法分子动力学模拟法是一种基于分子动力学模拟的计算径向分布函数的方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一 径向分布函数、角度分布函数电子云图形的绘制一、实验目的1.绘制波函数及其各种分布以及电子云的图像,观察各种函数的分布情况。
2.了解计算机绘图方法。
二、实验原理1.程序原理:本程序可绘制类氢原子的径向分布函数,角度分布函数及原子轨道、杂化轨道和分子轨道等电子几率密度图,绘制过程中的各函数形式列于下列各表中。
式中 ,n 为主量子数,=0.0529nm ,为波尔半径, Z 是有效核电荷,由Slater 规则计算得到的周期表中前四个周期元素的有效核电荷列于表1.1中,下面简要叙述对各类图形的处理方案。
①径向分布函数图:径向分布函数D(r)=r 2R 2(r)反映了电子的几率随半径r 的分布情况, D(r)dr 代表半径r 到r+dr 两个球壳夹层内找到电子的几率。
其中R(r)为类氢原子的径向函数,本程序所采用的径向函数R(r)分别列于表2-2中。
②角度分布函数图:的角度部分 以及角度分布函数 表示同一球面不同方向上 或 的相对大小,本程序所采用的角度函数分别列于表3-3中。
02na Zr=ρ0a ),,(φθψr nlm ),(φθψlm ),(2φθψlm ),,(φθψr nlm ),,(2φθψr nlm ),(φθψlm322232,),(,,,,spd sp yzxzzzz YY fffpp 角度分布图是画的X-Z 平面的截面图,其余角度分布图都是画的X-Y 平面的截面图。
角度分布函数图中,凡轨道形状相同,而仅方向不同者,则仅绘出一个图形作为代表。
③等电子几率密度图:2),,(φθψr 称为电子几率密度函数,它描述在该轨道中的电子在三维空间的分布情况,为了在平面上表示出这种分布往往采用某一切面上的等值面图,程序按指定的轨道在该切面上逐点计算2ψ的值,及找出2maxψ的最大值,求出相对几率密度2max2/ψψ=P ,该值在X-Y 平面上是位置坐标(x,y)的函数(对于23z d 轨道是在X-Z 平面),绘图时不是将取值相同的点连成曲线,而是打印一系列符号表示相对几率密度的分布区域。
当P <0.01时为空白, 0.01≤P <0.02时用“:”,0.02≤P <0.1时用“/”,0.1≤P <0.25时用“O ”,0.25≤P <0.5时用“&”和P >0.5时用“#”符号表示。
根据这些符号可以粗略看出几率密度的分布情况。
在X-Y 平面内,坐标变化范围为 -2.4≤x ≤2.4(步长=0.08) -1.42≤y ≤1.42(步长=0.133)所有距离的长度单位都是10-10m 。
原子轨道使用的波函数如表1-4所示。
对23224,4,4,3xzzzzffdd 和轨道采用X-Z 平面做截面,所有其它原子轨道都画在X-Y 平面上,程序使用原子轨道的四重轴对称性,首先计算第三象限内,即-2.4≤x ≤0,-1.42≤y ≤0的Ψ值,随后被2max2/ψψ=P代替,在其它三个象限内的相应值由对称性得到,用P(x,y)代表电子在坐标(x ,y)点的几率密度,则:P(-x,-y)=P(-x,y)=P(x,-y)=P(x,y)表1-1 Slater轨道中的Z*参量值杂化轨道采用的杂化方式如表1-5所示,程序中应用了以X 轴为对称轴的二重轴对称性,在X-Y 平面上画出杂化轨道等电子几率密度图。
分子轨道采用如表1-6所示的原子轨道的线性组合,取双原子-A 、B 的两个原子核在Y 轴上,及以Y 轴为分子轴,其坐标分别为-R AB /2,R AB /2,若Z A =Z B ,则分子轨道具有四重轴对称性,否则仅有以Y 轴为对称轴的二重轴对称性。
表1-2 类氢原子的径向波函数)(r R nl表1-3 波函数角度部分),(φθlm Yπ41=Sφθπcos sin 43=xpφθπsin sin 43=y pθπcos 43=zp)1cos 3(16522-=θπzdφθθπcos cos sin 415=xzd φθθπs i n c o s s i n 415=yzdφθπ2sin sin4152=xydφθπ2cos sin1615222=-yx d)cos 3cos5(16733θθπ-=zfφθθπcos )1cos5(sin 322122-=xzfφθθπs i n )1c o s 5(s i n 322122-=yzfφθθπ2cos cos sin161052)(22=-y x z fφθθπ2s i n c o s s i n 161052=xyzfφθπ3cos sin32353)3(22=-y x y fφθπ3sin sin32353)3(22=-y x x f()θπcos 3181+=sp Y⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-++=15231cos 52cos 1615232θθπspd Y表1-4 类氢原子波函数),,(φθψr nlm20231)(1ρπψ-=ea Z S2232)(241ρπψ-=ea ZS2)66()(31812233ρρρπψ-+-=ea Z S232234)123624()(1921ρρρρπψ--+-=ea Z Sφθρπψρcos sin )(2412232-=ea Z xPφθρπψρsin sin )(24122302-=ea Z yPθρπψρcos )(2412232-=e a Z zPφθρρπψρcos sin )4()(21812233--=ea Z xPφθρρρπψρcos sin )1020()(5641223024-+-=ea Z xP)1cos3()(63612223232-=-θρπψρea Z o zdφθρπψρ2cos sin)(236122232322-=-ea Z o yxdφθρπψρ2sin sin)(2361222323-=ea Z oxyd )1cos3()6()(384122322324--=-θρρπψρea Z o zd φθρρπψρ2cos sin)6()(31281223223224---=ea Z oyxdφθρρπψρ2sin sin)6()(312812232234--=ea Z oxyd )cos 3cos5()(538413232334θθρπψρ-=-ea Z ozfφθθρπψρcos )1cos5(sin )(3012812232324-=-ea Z o xzfφθρπψρ3cos sin)(2384132323)22(4--=ea Z oyxx fφθθρπψρ2cos cos sin)(3128122323)22(4--=ea Z oyxz f表1-5杂化轨道)(2122xp sspψψψ+=)2(31222xp sspψψψ+=)(2122223zp yp xp sspψψψψψ+++=xp yxdsdsp422342212121ψψψψ++=-234223432121212161dzxp yxdsspdψψψψψ-++=-表1-6分子轨道成键轨道 反键轨道Bs As s 111ψψσ+=BsAs s 11*1ψψσ-=Bs As s222ψψσ+= Bs As s22*2ψψσ-= yB p yAp yp 222ψψσ-= yBp yAp y p 22*2ψψσ+= xBp xAp xp 222ψψπ+= xBp xAp xp 22*2ψψπ-= yBp As yps 2121ψψσ+= yBp As y ps 21*21ψψσ-= yBp A s y p s 2222ψψσ+=yBp A s yps 22*21ψψσ-=2.程序功能:该程序可绘制下列三类图形:①1s 至4s ,2p 至4p ,3d 至4d, 4f 轨道的径向函数、径向密度函数、径向分布函数图形。
②所有s 、p 、d 、f 轨道和sp 、d2sp3杂化轨道的角度函数和角度分布函数图形。
③1s 至4s ,2x p 至4x p 、23z d 、223yx d-、xyd 3、24zd 、224yxd-、xyd 4、34zf 、24xzf、)22(4yxx f-、)22(4yxz f-原子轨道;sp 、2sp 、3sp 、2dsp 、32sp d 杂化轨道;s s 11±,s s 22±,xxp p 22±,yypp 22±,yps 21±,y p s 22±分子轨道中电子的几率密度等值面图。
3.使用方法本程序采用Turbo BASIC 语言编程,并已编译成可执行文件,适用于486系列微机,VGA 彩色显示器。
本软件的运行环境为MS -DOS3.30或更高版本。
三、实验所需的仪器计算机MS-DOS3.30或更高版本 四、实验步骤1.打开稳压电源开关,待电压稳定后,打开显示器、打印机和主机开关,启动程序。
2.选择适当参数,绘制径向分布,角度分布和原子轨道、杂化轨道、分子轨道等电子几率密度图各1个。
3.关掉主机和附件开关,切断电源。
五、数据处理记录所绘图形,观察各类函数的极大值、界面位置和数目以及分布情况。
六、注意事项在绘制径向分布函数和等电子几率密度图时只有选择合适的参数,才能观察到大小适当完整的图形。
七、结果与讨论1.在绘制径向分布函数、等电子几率密度图时为什么要选用有效核电荷?2.讨论有效核电荷大小对电子云及其各种分布的影响。
