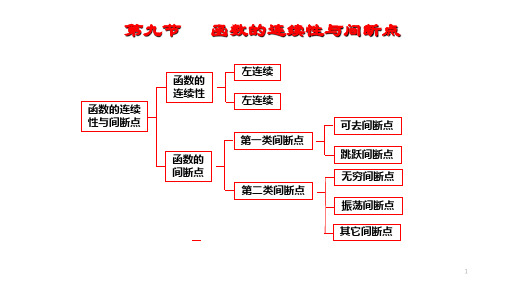
函数的连续性与间断性
合集下载
连续性间断点,连续函数的运算
无穷间断点 左右极限至少有一 第二类间断点 振荡间断点 个不存在
思考与练习
讨论函数
f
(x)
x2
x2 1 3x
2
间断点的类型.
答案: x = 1 是第一类可去间断点 ,
x = 2 是第二类无穷间断点 .
备用题 确定函数 f (x)
1 间断点的类型. x
1 e1x
解: 间断点 x 0, x 1
证: x ( , )
y sin(x x) sin x
2
sin
x 2
cos(
x
x 2
)
y
2
sin
x
2
cos(
x
x
2
)
2
x
2
1
x
x 0
0
即 lim y 0
x0
这说明 y sin x 在 ( , )内连续 .
同样可证: 函数 y cos x 在( , )内连续 .
二、 函数的间断点
y
y f (x)
y x
0 x0 x0 x x
y
y f (x)
y
x
0 x0 x0 x x
2. 连续的定义
定义 1：设 f (x) 在U (x0 , )内有定义，若
lim y
x0
lim [
x0
f
( x0
x)
f
(x0 )]
0,
则称 f (x) 在 x0 点连续，x0 称为 f (x)的连续点.
设 x x x0 ,
y
y f (x)
y f ( x) f ( x0 ),
y
x 0 就是 x x0,
x
函数的连续与间断
f(x)=f(x0 )］，则称函数y=f(x)在点x0处左(或右)连续.
设函数y=f(x)在区间［a,b］内有定义，如果有limx→b－
f(x)=f(b)，那么我们就称函数y=f(x)
b左连续；如果
limx→a+f(x)=f(a)，那么我们就称函数y=f(x)在左端点a右连续.
一、 函数的连续性
定义19
y=f(x)
x0连续.
在定义16中，若令x=x0+Δx, 即Δx=x－x0，则当Δx→0时，也就
是当x→x0时.又因为Δy=f(x0+Δx)－f(x0)=f(x)－f(x0)，因而
limΔx→0Δy=0
limΔx→0［f(x)－f(x0)］=0，即limx→x0f(x)=f(x0).
因此，函数y=f(x)在点x0处连续的定义又可叙述如下.
A=x2，当自变量x有一个改变 量Δx时，相应函数的增量为ΔA.
ΔA=f(x+Δx)－f(x)=(x+Δx)2－x2=2x•Δx+(Δx)2.
一、 函数的连续性
2. 函数的连续性概念
定义16
设函数y=f(x)在点x0的某个邻域内有定义，如果当Δx趋向于零时，
函数相对应的增量Δy也趋向于零，即limΔx→0Δy=0成立，则称函数
一、 函数的连续性
定义17
设函数y=f(x)在点x0的某个邻域内有定义，如果有limx→x0f(x)=f(x0) 成立，则称函数y=f(x)在点x0处连续，且称x0为函数y=f(x)的连续点.
(1)函数y=f(x)在点x0有定义.
(2)limx→x0f(x)
.
(3)极限值等于该点的函数值f(x0) .
图 2-12
函数的连续性与间断点
。
.
O
x
10
例3 函数
x − 1, y = f ( x) = 0, x + 1,
x → −0 x → +0 x → −0
x < 0, x = 0, x > 0.
y
lim f ( x ) = lim ( x − 1) = −1
。
１
lim f ( x ) = lim ( x + 1) = +1
18
1 − x 2n ⋅ x 的连续性，若有间断点 例7 讨论函数 f ( x ) = lim 的连续性， 2n n→∞ 1 + x
判断其类型。 判断其类型。 解 Q lim x 2 n
n→∞
0, = 1, ∞,
1, x <1 2n 1− x x = 1, lim = 0, 2n n →∞ 1 + x − 1, x >1
x → +0
O。
－１
•
x
x 不存在。 所以 lim f ( x )不存在。 = 0 称为 x→0
跳跃间断点。 该函数的跳跃间断点 该函数的跳跃间断点。
11
例4 正切函数 y = tan x 在 x =
π
处没有定义， 处没有定义，
2 π 的间断点。 所以 x = 是函数 y = tan x 的间断点。 2
∆y = sin( x + ∆x ) − sin x = 2 sin
∆x Q cos x + ≤1 2 ∆x ∴ ∆y = sin( x + ∆x ) − sin x ≤ 2 sin . 2 又因为当α ≠ 0 时， sinα < α
函数的连续性和间断点
函数的连续性一、函数连续的定义如果函数f(x)在点x0的邻域内有定义，如果limx→x0f(x)=f(x0)，那么称函数f(x)在点x0连续。
如果函数f(x)在点x0的邻域内有定义，如果limx→x0−f(x)=f(x0)，那么称函数f(x)在点x0左连续。
如果函数f(x)在点x0的邻域内有定义，如果limx→x0+f(x)=f(x0)，那么称函数f(x)在点x0右连续。
如果limx→x0+f(x)=limx→x0−f(x)=f(x0)，则函数f(x)在点x0连续。
如果函数f(x)在点x0连续，则limx→x0+f(x)=limx→x0−f(x)=f(x0)。
二、函数的间断点：函数f(x)在点x0的某去心邻域内有定义，如果函数f(x)有下列三种情形之一，则称x0是函数f(x)的间断点。
（1）.在x0处无定义；（2）.在x0处有定义，但limx→x0f(x)在x0处的极限不存在；（3）.在x0处有定义，而且limx→x0f(x)在x0处的极限也存在，但limx→x0f(x)≠f(x0)；间断点可分为两类，即第一类间断点和第二类间断点。
如果函数的左极限和右极限都存在，则称为第一类间断点。
如果左右极限至少有一个不存在，则称为第二类间断点。
如果左右极限都存在且相等，则该间断点称为可去间断点，可去间断点很显然是第一类间断点。
如果函数在x0处的极限值为∞，则点x0称为无穷间断点。
至于震荡间断点和跳跃间断点，可以很容易根据函数图像的特征加以判别。
历年真题1、函数f (x )=|x |x −1x (x+1)ln |x |的可去间断点的个数为(A )0 (B )1 (C )2 (D )3(2013，数三，4分)【解析】函数f (x )=|x |x −1x (x+1)ln |x |在x =−1,0,1处没定义，lim x→−1f (x )=lim x→−1|x |x −1x (x +1)ln |x |=lim x→−1e xln |x |−1x (x +1)ln |x |=lim x→−1xln |x |x (x +1)ln |x |=limx→−11(x +1)=∞lim x→0f (x )=lim x→0|x |x −1x (x +1)ln |x |=lim x→0e xln |x |−1x (x +1)ln |x |=lim x→0xln |x |x (x +1)ln |x |=limx→01(x +1)=1lim x→1f (x )=lim x→1|x |x −1x (x +1)ln |x |=lim x→1e xln |x |−1x (x +1)ln |x |=lim x→1xln |x |x (x +1)ln |x |=limx→11(x +1)=12所以x =0和x =1为可去间断点。
函数连续性定义和间断点
例3：设
,讨论在x=0处的连续性
解:
则称 为函数 的跳跃间断点
如果 在 点存在左、右极限，但
例4：
2.跳跃间断点
解
跳跃间断点与可去间断点统称为第一类间断 的第二类间断点
函数 在 点的左、右极限至少有一个不存在，
例5：
处的连续性
在
讨论函数
解
例6
例7 解
所以
性质5：（反函数的连续性） 连续且严格单调递增（递减）的反函数必是连续 且严格单调递增（递减）的函数.
初等函数的连续性
定理2：一切初等函数在其定义区间内都是连续的.
例如,
定理1：基本初等函数在定义域内是连续的.
故
01
为跳跃间断点.
02
解: 间断点 备用题 确定函数 间断点的类型. 为无穷间断点;
介值定理 .
02
最值定理 ;
例3. 设函数
03
零点定理 ;
提示:
1．当
时，
较
等价无穷小量 (B) 同阶无穷小量 (C) 低阶无穷小量 (D) 高阶无穷小量
是 （ ）
课堂测验
下列各式中正确的是 （ ）
3
C
2
B
4
D
A
3．无穷小量是（ ） A 比零稍大一点的一个数 B 一个很小很小的数 C 以零为极限的一个变量 D 数零
间断的演示
第一类间断点
第二类间断点
可去间断点 跳跃间断点
无穷间断点 震荡间断点
间断的演示
第一类间断点
第二类间断点
可去间断点 无定义、值太高、值太低 跳跃间断点
无穷间断点 震荡间断点
间断的演示
●
●
,讨论在x=0处的连续性
解:
则称 为函数 的跳跃间断点
如果 在 点存在左、右极限，但
例4：
2.跳跃间断点
解
跳跃间断点与可去间断点统称为第一类间断 的第二类间断点
函数 在 点的左、右极限至少有一个不存在，
例5：
处的连续性
在
讨论函数
解
例6
例7 解
所以
性质5：（反函数的连续性） 连续且严格单调递增（递减）的反函数必是连续 且严格单调递增（递减）的函数.
初等函数的连续性
定理2：一切初等函数在其定义区间内都是连续的.
例如,
定理1：基本初等函数在定义域内是连续的.
故
01
为跳跃间断点.
02
解: 间断点 备用题 确定函数 间断点的类型. 为无穷间断点;
介值定理 .
02
最值定理 ;
例3. 设函数
03
零点定理 ;
提示:
1．当
时，
较
等价无穷小量 (B) 同阶无穷小量 (C) 低阶无穷小量 (D) 高阶无穷小量
是 （ ）
课堂测验
下列各式中正确的是 （ ）
3
C
2
B
4
D
A
3．无穷小量是（ ） A 比零稍大一点的一个数 B 一个很小很小的数 C 以零为极限的一个变量 D 数零
间断的演示
第一类间断点
第二类间断点
可去间断点 跳跃间断点
无穷间断点 震荡间断点
间断的演示
第一类间断点
第二类间断点
可去间断点 无定义、值太高、值太低 跳跃间断点
无穷间断点 震荡间断点
间断的演示
●
●
函数的连续性与间断点
x x0
第 一 章 函 数 与 极 限
第 八 节 函 数 的 连 续 性 与 间 断 点
( 3) 虽然在 x x0 有定义 , 且 lim f ( x ) 存在,
x x0
但 lim f ( x ) f ( x0 );
x x0
则 f ( x ) 在 x0 不连续, x0 称为 f ( x ) 的不连续点(间断点).
高 等 数 学
思考与练习
3. 确定函数 f ( x )
第 一 章 函 数 与 极 限
1 1 e
x 1 x
的间断点的类型 .
解
间断点为 x 0 , x 1.
第 八 节 函 数 的 连 续 性 与 间 断 点
因为 lim f ( x ) , 所以 x 0 为无穷间断点 ; x 0
高 等 数 学
一、 函数的连续性
例1
第 一 章 函 数 与 极 限
1 x sin , 试证函数 f ( x ) x 0,
x 0, x 0,
在 x 0处
连续.
证
第 八 节 函 数 的 连 续 性 与 间 断 点
1 因为 lim x sin 0, x 0 x
又 f (0) 0,
由定义2知
lim f ( x ) f (0),
x 0
函数 f ( x ) 在 x 0 处连续.
上一张
下一张
返 回
高 等 数 学
一、 函数的连续性
例2 证明函数 y sinx在 (,)内每一点连续 . 证
第 一 章 函 数 与 极 限
任取 x ( ,),
y sin( x x ) sin x 2 sin
第 一 章 函 数 与 极 限
第 八 节 函 数 的 连 续 性 与 间 断 点
( 3) 虽然在 x x0 有定义 , 且 lim f ( x ) 存在,
x x0
但 lim f ( x ) f ( x0 );
x x0
则 f ( x ) 在 x0 不连续, x0 称为 f ( x ) 的不连续点(间断点).
高 等 数 学
思考与练习
3. 确定函数 f ( x )
第 一 章 函 数 与 极 限
1 1 e
x 1 x
的间断点的类型 .
解
间断点为 x 0 , x 1.
第 八 节 函 数 的 连 续 性 与 间 断 点
因为 lim f ( x ) , 所以 x 0 为无穷间断点 ; x 0
高 等 数 学
一、 函数的连续性
例1
第 一 章 函 数 与 极 限
1 x sin , 试证函数 f ( x ) x 0,
x 0, x 0,
在 x 0处
连续.
证
第 八 节 函 数 的 连 续 性 与 间 断 点
1 因为 lim x sin 0, x 0 x
又 f (0) 0,
由定义2知
lim f ( x ) f (0),
x 0
函数 f ( x ) 在 x 0 处连续.
上一张
下一张
返 回
高 等 数 学
一、 函数的连续性
例2 证明函数 y sinx在 (,)内每一点连续 . 证
第 一 章 函 数 与 极 限
任取 x ( ,),
y sin( x x ) sin x 2 sin
1-6-函数的连续性与间断点
由连续函数定义可知，基本初等函数在其各自定义域
内连续，有理分式函数在其定义域内连续.
例 3 讨论函数
f
(
x)
x2 1,
10 x 1,
arccos x π, 1 x 1
在其定义域内的连续性.
解 显然在(10, 1) (1,1]内，函数 f (x) 连续.
f (1 ) lim x2 1 0， x1
定义 1 设函数y f (x) 在U (x0 ) 内有定义，如果当自变
量 的 增 量 x x x0 趋 于 零 时 ， 对 应 的 函 数 增 量
y
f (x0
x)
f
(
x0
)
也趋于零，
即
lim
x0
0 ，则称函数
y f (x)在点x0 连续.
在定义 1 中，设 x x0 x ，且x 0 ，即x x0 ， 又因为
增量为
y (x0 x)3 x03 3x03x 3x0x2 x3
又
lim
x0
y
lim (3
x0
x0
2
x
3x0x2
x3 )
0
所以 y x3在点x0 连续，这是对定义 1 给出的证明.
如果函数 f (x) 在点 x0 的左极限 f (x0 ) 存在且等于
该点函数值 f (x0 )，即 f (x0 ) f (x0 )，则称 f (x)在点 x0左 连续.
图1-30
lim f (x) lim f (x2 1) 1, lim f (x) lim f (x 1) 1,
x0
x0
x0
x0
即 f (0 ) f (0 ) .所以lim f (x) 不存在,因此 x 0 为 f (x) 的
高等数学 第1章 第九节 函数的连续性与间断点
有定义，但 lim f ( x)不存在；
0
x x0
x （3） 虽在
0 有定义，且
lim f ( x)存在，但
x x0
x x 则函数 f ( x)在点 0不连续， 而点 0 称为函数
或间断点。
若函数 f ( x)
lim
x x0
f (x)
f ( x0 );
f ( x) 的不连续点
5
函数间断点的几种常见类型：
0,
1,
x 1 x 1, x 1
x,
f
(
x
)
0,
x,
x,
x x
1 1
0, x,
x 1
0,
x,
x 1 x 1 1 x 1 x 1 x 1
14
f 1 0 lim x 1 f 1 x10
f 1 0 lim x 1 f 1 x10
函数在 x 1处既不左连续，也不右连续。 x 1是跳跃间断点。
x
3
证明：函数
y sin x 是连续函数。
证： 设 x (,),
x x 当 有增量
时，则
y sin( x x) sin x 2sin x cos(x x )
cos x x 1
2
2
2
y sin( x x) sin x 2 sin x .
2
又因为当 0 时， sin
f 1 0 lim 3 x 2 x10
则
x 1是跳跃间断点，属于第一类间断点。
所以 x 0
13
例7 讨论函数 判断其类型。
1 x2n
f ( x) lim
x 的连续性，若有间断点
n 1 x 2n
0,
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
lim x21lim (x1)2. x 1x1 x 1
如果补充分定义：令x=1时y=2， 则所给函数在x=1成为连续. 所以x=1称为该函数的可去间断点.
y
2 1
o1 x
例6 函数
x,x1 y f(x)12,x1
1
y
这 li里 fm (x ) lix m 1 ,
x 1
x 1
但f(1)1,所以 2
连续函数的图形是一条连续而不间断的曲线.
例2
证 函 明 y s 数 x i在 n ( 区 , ) 内 间 .连
证 任x 取 (, ) ,
y six n x )( sx i n 2si n xcoxs(x)
2
2
因为 coxs(x)1, 从而 y2sinx.
2
2
对任,意 当 的 0时 , 有 si n,
3. 间断点的分类
设 x0是函 f(x数 )的间断点
(1).如 果 左 极 限 f(x０ )及 右 极 限 f(x０ )都 存 在 , 那 么 x0称 为f (x)的第一类间断点;
(2)如 . x0 果 不f(是 x)的第一,那 类x0 么 称 间为 断点
f (x)的第二类间断点.
在第一类间断右 点极 中限 左相 、等者称为
x
例4
函数 ysin 1在x0处没有 . 定义
x
1
Sin
x
1
当 x 0 时 ,函数 1 与 值 1 之 在 间0.5
-0.4 -0.2
变动无,所 限以 多 x点 0 次 称
-0.5
x
0.2
0.4
-1
为函s数 in1的振荡间.断点 x
例5 函y数 x21在x点 1没定 ,所 义 以函数
x1 x1为不.但 连这 续里
函数的连续性与间断性
一、函数的连续性
1.函数的增量
U 设函 f(x)数 在 U(x0,)内有 , 定 x义 (x0,),
xxx0, 称为自x 变 0的量 增 . 在 量点 y f ( x ) f ( x 0 ) f ( x 0 x ) f ( x 0 ) ,称f ( 为 x ) 相
连续点.
lixm 0f(x0x)f(x0)
""定义 : 0,0,使x当 x0时 , 恒f有 (x)f(x0).
例1
试证函 f(x)数 xsin1x, x0, 在x0
0, x0,
处连. 续
证 因为 lim xsin 10,
x0
x
又 f(0)0, lim f(x)f(0), x 0
由定义知
函f数 (x)在 x0处连 . 续
故y2si nxx, 所 当 x 以 0 时 , y 0 . 2
即 函y 数 six 对 n x 任 (,意 )都 是 . 连续
二、函数的间断点
1.定义
设函 f(x 数 )在x 点 0的某去心邻,在 域此 内前 有
下,如果函f(数 x)有下列三种情:形之一
(1)在xx0没有;定义
(2 )虽 x 在 x 0 有,但 定 x l ix 0m f义 (x )不;存在 ( 3 ) 虽 x x 0 有 在 , 且 x l x 0 f i ( 定 x ) 存 m , 但 x l x 0 f i ( 义 x ) 在 m f ( x 0 )
去间断,不 点相等者称为跳点 跃.无间穷断 间断点
和振荡间断点是第二类
间断点 .
应于 x的增. 量
y
yf(x)
y
yf(x)
y y
x
x
0 x 0 x0 x x 0 x 0 x0 x x
2.连续的定义
定义 1 设函数 f ( x)在U (x0, )内有定义,如果
lim y 0
x 0
或
lim[
x 0
f
( x0
x)
f ( x0 )] 0,
那么就称函数 f ( x)在点 x0连续, x0称为 f ( x)的
1
2o 1 x
lim f(x)f(1).
x 1
因此，点x=1是函数f(x)的间断点.但如果改变函
数f(x)在x=1处的定义：令f(1)=1，则f(x)在x=1
成为连续.所以x=1也称为该函数的可去间断点.
例７
函数
f (x)
0x,1,
这,当 里 x 0 时 , x1,
limf(x)lim (x1)1,
x0
x0
limf(x)lim (x1)1.
x0
x0
x 0,
x0, y x 0.
yx1
1
o1 x
故 lif 极 ( m x ) 不 限 ,所 存 x 0 以 是 在 f ( x ) 点 的 函 x 0
断.因 点 yf(x)的图 x0 形 处在 产生 ,称 x 跳 0 跃
为函数 f(x)的跳跃间断 . 点
3.单侧连续
若f(函 x )在 (a ,x 数 0 ] 内有 ,且 f(x 0 定 0 ) f(x 义 0 ), 则 f(x ) 称 在 x 0 处 点左 ; 连续
若f(函 x )在 [x 0 ,b 数 ) 内有 ,且 f(x 0 定 0 ) f(x 义 0 ), 则 f(x ) 称 在 x 0 处 点右 . 连续
则 函f数 (x)在x点 0为不(或 连间 续 ), 断 而x点 0称为f(函 x)的数 不连 (或续 间)点 .断点
2.间断点举例
例3
正切函y数 tanx在x处没有定 , 义 2
所以x点 是函t数 anx的间断点.因
2
limtanx,
x
称x 为函数tan2x
y
2
的无穷间断. 点
2
o 2
3 2
定理 函数 f(x)在x0处连 续 是函f(数 x)在x0
处既左连续 . 又右连续
4.连续函数与连续区间
在开区间（a,b者说函数在该区间内连 续.
如果函数在(a开 ,b)内 区连 间 , 续 并且在左端 xa处右连 , 在 续右端 x点 b处左连 , 则 续称 函数 f(x)在闭区 [a,b间 ]上连. 续