一元一次方程概念、等式基本性质、解法专项习题-一对一
一元一次方程知识点总结和例题讲解

一元一次方程知识点及题型一、方程的有关概念1. 方程:含有未知数的等式就叫做方程.2. 一元一次方程:只含有一个未知数(元)x ,未知数x 的指数都是1(次),这样的方程叫做一元一次方程. 3.方程的解:使方程中等号左右两边相等的未知数的值,叫做方程的解.注:⑴ 方程的解和解方程是不同的概念,方程的解实质上是求得的结果,它是一个数值(或几个数值),而解方程的含义是指求出方程的解或判断方程无解的过程. ⑵ 方程的解的检验方法,首先把未知数的值分别代入方程的左、右两边计算它们的值,其次比较两边的值是否相等从而得出结论. 二、等式的性质三、移项法则:把等式一边的某项变号后移到另一边,叫做移项. 四、去括号法则 五、解方程的一般步骤1. 去分母(方程两边同乘各分母的最小公倍数)2. 去括号(按去括号法则和分配律)3. 移项(把含有未知数的项移到方程一边,其他项都移到方程的另一边,移项要变号)4. 合并(把方程化成ax = b (a≠0)形式)5. 系数化为1(在方程两边都除以未知数的系数a ,得到方程的解x=ba ).六.列一元一次方程解应用题的一般步骤(1)审题:弄清题意.(2)找出等量关系:找出能够表示本题含义的相等关系.(3)设出未知数,列出方程:设出未知数后,表示出有关的含字母的式子,•然后利用已找出的等量关系列出方程.(4)解方程:解所列的方程,求出未知数的值.(5)检验,写答案:检验所求出的未知数的值是否是方程的解,•是否符合实际,写出答案 【基础与提高】 一.选择题1.下列各式中,是方程的个数为( )(1)﹣4﹣3=﹣7;(2)3x ﹣5=2x+1;(3)2x+6;(4)x ﹣y=v ;(4)a+b >3;(5)a 2+a ﹣6=0. A . 1个B . 2个C . 3个D . 4个2.下列说法正确的是( ) A . 如果ac=bc ,那么a=b B . 如果,那么a=bC .如果a=b ,那么D . 如果,那么x=﹣2y3.若关于x 的方程mx m ﹣2﹣m+3=0是一元一次方程,则这个方程的解是( ) A .x =0 B .x =3 C . x =﹣3D .x =24.方程(m+1)x|m|+1=0是关于x的一元一次方程,则m()A.m=±1 B.m=1 C.m=﹣1 D.m≠﹣15.若关于x的方程nx n﹣1+n﹣4=0是一元一次方程,则这个方程的解是()A.x=﹣1 B.x=1 C.x=﹣4 D.x=46.已知x=3是关于x的方程x+m=2x﹣1的解,则(m+1)2的值是()A.1B.9C.0D.47.已知x=﹣6是方程2x﹣6=ax的解,则代数式的值是()A.4B.3C.2D.18.设P=2x﹣1,Q=4﹣3x,则5P﹣6Q=7时,x的值应为()A.B.C.D.﹣9.服装店同时销售两种商品,销售价都是100元,结果一种赔了20%,另一种赚了20%,那么在这次销售中,该服装店()A.总体上是赚了B.总体上是赔了C.总体上不赔不赚D.没法判断是赚了还是赔了10.如图是一个长方形试管架,在a cm长的木条上钻了4个圆孔,每个孔的直径为2cm,则x等于()A.cm B.cm C.cm D.cm11.关于x的方程(k﹣3)x﹣1=0的解是x=﹣1,那么k的值是()A.k≠3 B.k=﹣2 C.k=﹣4 D.k=212.江苏卫视《一站到底》栏目中,有一期的题目如图,两个天平都保持平衡,则三个球体的重量等于()个正方体的重量.A.2B.3C.4D.513.已知方程2x+k=5的解为正整数,则k所能取的正整数值为()A.1B.1或3 C.3D.2或314.小芳同学解关于x的一元一次方程﹣时,发现有个数模糊看不清楚,聪明的小芳翻看了书后的答案,知道这个方程的解是3.于是她很快补上了这个数.她补的这个数是()A.B.3C.8D.915.若代数式3x﹣7和6x+13互为相反数,则x的值为()A.B.C.D.16.按下面的程序计算,若开始输入的值x为正数,最后输出的结果为656,则满足条件的x的不同值最多有()A.2个B.3个C.4个D.5个二.填空题17.一件衣服先按成本提高50%标价,再以8折(标价的80%)出售,结果获利28元.若设这件衣服的成本是x元,根据题意,可得到的方程是_________.18.图1是边长为30cm的正方形纸板,裁掉阴影部分后将其折叠成如图2所示的长方体盒子,已知该长方体的宽是高的2倍,则它的体积是_________cm3.19.已知与的值相等时,x=_________.20.若x=﹣1是关于x方程ax+b=1的根,则代数式(a﹣b)2011的值是_________.21.某人用24000元买进甲、乙两种股票,在甲股票升值15%,乙股票下跌10%时卖出,共获利1350元,则此人买甲股票的钱比买乙股票的钱多_________元.22如果要由等式m﹙a+1﹚=x﹙a+1﹚得到m=x,需要满足的条件是_________.23.关于x的方程(a﹣1)x2+x+a2﹣4=0是一元一次方程,则方程的解为_________.24.关于x的方程(m+2)x=6解为自然数,当m为整数时,则m的值为_________.25.已知m+n=2008(m﹣n),则=_________.三计算题解方程:(1)3(x﹣1)﹣2(2x+1)=12;(2)(3).(4)﹣=.(5).(6)(7).(8)﹣=3.(9)(10)四.解答题1.若x=2是方程ax-1=3的解,求a的值2.方程x+2=5与方程ax-3=9的解相等 求a 的值3.为何值时,关于的方程4231x m x -=-的解是23x x m =-的解的2倍?4.已知,2x =是方程12()23m x x --=的解,求代数式2(62)m m -+的值.5.一家商店将某种服装按进价提高40%后标价,又以8折优惠卖出,结果每件仍获利15元,这种服装每件的进价是多少?6.一批货物,甲把原价降低10元卖出,用售价的10%做积累,乙把原价降低20元,用售价的20%做积累,若两种积累一样多,则这批货物的原售价是多少?7.某商店开张,为了吸引顾客,所有商品一律按八折优惠出售,已知某种皮鞋进价60元一双,八折出售后商家获利润率为40%,问这种皮鞋标价是多少元?优惠价是多少元?8.某蔬菜公司收购到某种蔬菜140吨,准备加工上市销售.该公司的加工能力是:每天可以精加工6吨或粗加工16吨,现计划用15天完成加工任务,该公司应安排几天精加工,几天粗加工?9.今年“六•一”儿童节,张红用8.8元钱购买了甲、乙两种礼物,甲礼物每件1.2元,乙礼物每件0.8元,其中甲礼物比乙礼物少1件,问甲、乙两种礼物各买了多少件?10.小明和小东两人练习跑步,都从甲地出发跑到乙地,小明每分钟跑250米,小东每分钟跑200米,小明让小东先出发3分钟之后再出发,结果两人同时到达乙地,求甲、乙两地之间的路程是多少米?11.某船从A地顺流而下到达B地,然后逆流返回,到达A、B两地之间的C地,一共航行了7小时,已知此船在静水中的速度为8千米/时,水流速度为2千米/时。
一元一次方程高频考点+经典题型演练

一元一次方程高频考点+经典题型演练一、方程的有关概念1. 方程:含有未知数的等式就叫做方程。
2. 一元一次方程:只含有一个未知数(元)x,未知数x的指数都是1(次),这样的方程叫做一元一次方程。
例如:1700+50x=1800,2(x+1.5x)=5等都是一元一次方程。
3.方程的解:使方程中等号左右两边相等的未知数的值,叫做方程的解。
注:⑴方程的解和解方程是不同的概念,方程的解实质上是求得的结果,它是一个数值(或几个数值),而解方程的含义是指求出方程的解或判断方程无解的过程。
⑵方程的解的检验方法,首先把未知数的值分别代入方程的左、右两边计算它们的值,其次比较两边的值是否相等从而得出结论。
二、等式的性质等式的性质(1):等式两边都加上(或减去)同个数(或式子),结果仍相等.用式子形式表示为:如果a=b,那么a±c=b±c等式的性质(2):等式两边乘同一个数,或除以同一个不为0的数,结果仍相等,用式子形式表示为:如果a=b,那么ac=bc;如果a=b(c≠0),那么a/c=b/c三、移项法则把等式一边的某项变号后移到另一边,叫做移项。
四、去括号法则1. 括号外的因数是正数,去括号后各项的符号与原括号内相应各项的符号相同。
2. 括号外的因数是负数,去括号后各项的符号与原括号内相应各项的符号改变。
五、解方程的一般步骤1. 去分母(方程两边同乘各分母的最小公倍数)2. 去括号(按去括号法则和分配律)3. 移项(把含有未知数的项移到方程一边,其他项都移到方程的另一边,移项要变号)4. 合并(把方程化成ax = b (a≠0)形式)5. 系数化为1(在方程两边都除以未知数的系数a,得到方程的解x=).六、列一元一次方程解应用题的一般步骤1.列方程解应用题的基本步骤注意:(1)初中列方程解应用题时,怎么列简单就怎么列(即所列的每一个方程都直接的表示题意),不用担心未知数过多,简化审题和列方程的步骤,把难度转移到解方程的步骤上。
初中数学《一元一次方程》知识梳理+练习题讲解
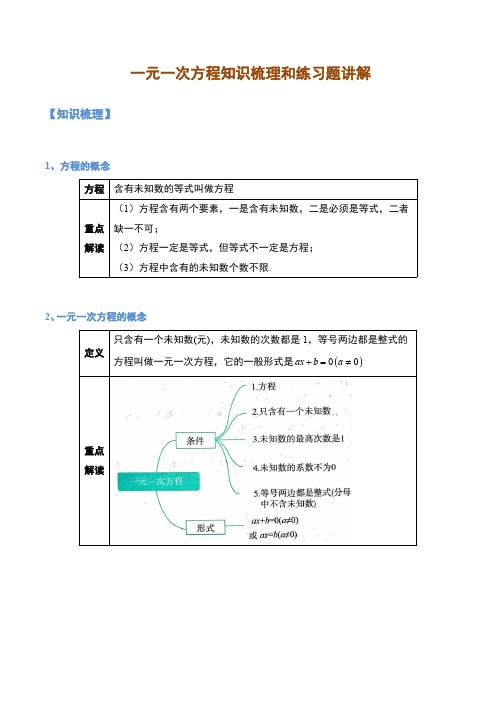
一元一次方程知识梳理和练习题讲解【知识梳理】1、方程的概念方程含有未知数的等式叫做方程重点解读(1)方程含有两个要素,一是含有未知数,二是必须是等式,二者缺一不可;(2)方程一定是等式,但等式不一定是方程;(3)方程中含有的未知数个数不限.2、一元一次方程的概念定义只含有一个未知数(元),未知数的次数都是1,等号两边都是整式的方程叫做一元一次方程,它的一般形式是()00ax b a +=≠重点解读3、方程的解与解方程定义实质方程的解使方程等号左右两边相等的未知数的值叫做方程的解具体数值解方程求方程解的过程叫做解方程变形过程4、等式的性质语言叙述字母表示等式性质1等式两边加(或减)同一个数(或式子),结果仍相等如果ba=,那么cbca±=±等式性质2等式两边乘同一个数,或除以一个不为0的数,结果仍相等如果ba=,那么bcac=;如果ba=,那么()0≠=ccbca重点解读(1)注意等式左右两边同时加、减、乘或除以不能遗漏任一边,并且同时加、减、乘或除以的数必须是同一个数;(2)等式的两边除以一个数或整式时,这个数或整式不能为0;(3)等式还有以下性质:①如果ba=,cb=,那么ca=;②如果ba=,那么ab=5、解一元一次方程的一般步骤①去分母;②去括号;③移项;④合并同类项;⑤系数化为1。
变形名称依据具体做法注意事项去分母等式的性质2在等号两边都乘各分母的最小公倍数(1)不要漏乘不含分母的项;(2)若分子是一个多项式,需加上括号去括号乘法分配律、去括号法则先去小括号,再去中括号,最后去大括号(1)不要漏乘括号里的项;(2)不要弄错符号移项移项法则把含有未知数的项移动到方程的一边,其他的项移动到方程的另一边(1)移项要变号;(2)不要丢项合并同类项合并同类项法则把方程化为()0≠=abax的形式(1)字母及其指数不变,系数相加;(2)不要漏项系数化为1等式的性质2在方程()0≠=abax的两边都除以未知数的系数a,得到方程的解abx=切忌分子、分母位置颠倒6、方程(组)与实际问题解有关方程(组)的实际问题的一般步骤:第1步:审题。
一元一次方程知识点及经典例题

一、知识要点梳理知识点一:一元一次方程及解的概念 1、 一元一次方程:一元一次方程的标准形式是:ax+b=0(其中x 是未知数,a,b 是已知数,且a≠0)。
要点诠释:一元一次方程须满足下列三个条件: (1) 只含有一个未知数; (2) 未知数的次数是1次; (3) 整式方程. 2、方程的解:判断一个数是否是某方程的解:将其代入方程两边,看两边是否相等. 知识点二:一元一次方程的解法1、方程的同解原理(也叫等式的基本性质)等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等。
如果,那么;(c 为一个数或一个式子)。
等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
如果,那么;如果,那么要点诠释:分数的分子、分母同时乘以或除以同一个不为0的数,分数的值不变。
即:(其中m≠0)特别须注意:分数的基本的性质主要是用于将方程中的小数系数(特别是分母中的小数)化为整数,如方程:-=1.6,将其化为: -=1.6。
方程的右边没有变化,这要与“去分母”区别开。
2、解一元一次方程的一般步骤:解一元一次方程的一般步骤变形步骤 具 体 方 法 变 形 根 据注 意 事 项去分母方程两边都乘以各个分母的最小公倍数等式性质21.不能漏乘不含分母的项;2.分数线起到括号作用,去掉分母后,如果分子是多项式,则要加括号去括号先去小括号,再去中括号,最后去大括号 乘法分配律、去括号法则 1.分配律应满足分配到每一项 2.注意符号,特别是去掉括号移 项 把含有未知数的项移到方程的一边,不含有未知数的项移到另一边等式性质11.移项要变号;2.一般把含有未知数的项移到方程左边,其余项移到右边合并同 类 项 把方程中的同类项分别合并,化成“b ax =”的形式(0≠a )合并同类项法则合并同类项时,把同类项的系数相加,字母与字母的指数不变未知数的系数化成“1”方程两边同除以未知数的系数a ,得a b x = 等式性质2 分子、分母不能颠倒要点诠释:理解方程ax=b 在不同条件下解的各种情况,并能进行简单应用:①a≠0时,方程有唯一解;②a=0,b=0时,方程有无数个解;③a=0,b≠0时,方程无解。
一元一次方程概念及解法

一元一次方程的概念及解法4、等式的基本性质:(1)、等式的两边都加上(或减去)同一个数或同一个整式,所得结果仍是等式。
(2)、等式的两边都乘以(或除以)同一个数(除数不能是零),所得结果仍是等式。
5、解一元一次方程的基本步骤:【例题解析】那么a=bA . 2x 3yB . 7x 5 6x1C . 2、下列运用等式的性质对等式进行的变形中,正确的是【练习】:1、下列方程中是 元-次方程的是【知识点】: 1、一元一次方程的定义:只含有 未知数,并且未知数的次数都,这样的方程叫一元一次方程。
2、方程的解:使方程左右两边 的未知数的值叫方程的解。
3、解方程:求的过程叫做解方程。
(1):去分母;(2):去括号;(3):移项;(4):合并同类项;(5):系数化成 1。
例1、判断下列各式是不是一元 次方程,是的打“ V”,不是的打“X⑴ x+3y=4 2⑵ x -2x=6⑶-6x=0(4) 2m +n =0(5) 2x-y=8(6) 1 —+8=5yy例2、下列变形中, 正确的是A 、若 ac=bc ,那么 a=b 。
B 、a=b C 、b ,那么a=bD 、若 a 2 =b 2x 23、若x(n-2)+2n=0是关于x的方程一元一次方程,则n=—,此时方程的解是x= 。
其中变形正确的是((1) x + 2x +4x=140【练习】:1、下列叙述正确的是则a=b则a=b则a=b4、某数x 的43%比它的一半少 7,则列岀求x 的方程应是(A : 43%x 1B : 43%(x !) 7 C2 2 :43%X 7 43%x例3、给岀下面四个方程及其变形: ①4x 8 0变形为x 3x 变形为4x2 ③—x 3变形为2x515;4x2变形为x2; 3、解方程:(1)丄 y-3-5y= 1 ;、x X(2) =5;2 31(3 )0.6x- —x-3=032 4 例5、解方程:(利用去括号、移项等步骤解方程)(1) 2x 1 4 ;2(2)2( X — 2) - (4 X —1)=3(1—x )____________ ,根据是例6、解方程:(利用去分母、去括号、移项、合并同类项及系数化成1解方程)A .①③④B •①②④C.②③④D .①②③例4、解方程:(利用移项、合并同类项及系数化成1来解方程)(2) 3x + 20=4x-25①若a=b ,则 a+c=b+ c②若 a=b ,贝U a-c=b- c ③若a+c=b+ c ,则 a=b ④若,a-c=b- c ,⑤若a=b ,则 ac=bc ⑥若 ac=bc ,贝U a=b⑦若a=b ,则-ca b ⑧若—_,c c⑨若a=b ,则⑩若b ,则 a=b(11)若 a=b ,贝U a 2=b 2 (12)若 a 2=b 2,(13)若 a=b ,则 a 3=b 3(14)若 a 3=b 3,贝U a=b2、方程2y-6=y+7变形为 2y-y=7+6 ,这种变形叫解:去分母,得 _____________________________________ 依据 ________________去括号,得 ______________________________________ 依据 ____________________移项,得 ________________________________________ 依据 ____________________合并同类项,得 __________________________________ 依据 ___________________系数化为1,得x 6例7、数学小诊所:小马虎的解法对吗如果不对,应怎么改正解方程专=1-专 解:去分母 2 ( 2x-1)=1-4x-1 去括号4x-仁1-4x-1移项 4x+4x=1-1+1系数化为1x=8【练习】:解方程:归纳:解一元一次方程的步骤:依据合并8x=12x —1x+2 (1)=T +13x 1 4x 2 15(3) 4-3(2-x)=5x例7、已知关于x 的方程13x 2的解互为倒数,求m 的值.3 31、解方程2(x3)5(1x) 3(x1),去括号正确的是().(A) 2x 6 55x3x3(B) 2x 35x3x 3 (C) 2x 6 55x3x3(D) 2x 35x3x 13x 7 2、解方程3x 721x31的步骤中,去分母一项正确的是().(A)3(3x 7)22x6(B)3x 7(1x)1 (C)3(3x 7)2(1x)1(D)3(3x7)2(1x) 6 3x 1 2x 23、若的值比的值小1,则X的值为()23/ 1313_5/ 5(A)(B)- (C) (D)-—5513134、解方程4(x 1)x2(x1)步骤下:①去括号,得4x 4 x2x 1 ②移项,得4x x 2x 1 4③合并同类项,得3x 55④系数化为1,得x -检验知:x —不是原方程的根,说明解题的四个步骤有错,其中做错的一步是35、当x= _____ 时,2x 8的值等于一-的倒数.46、已知3x 6 (y 3) 0,则3x 2y 的值是 _____________7、当x = _____ 时,式子1(1 2x)与式子2(3x 1)的值相等8、解方程:9、已知 A=2x-5,B=3x+3,求A 比B 大7时的x 值.x 4x 210、如果方程8的解与方程4x (3a 1) 6x 2a 1的解相同,求式子321a 的值.a111、已知x 1是关于x 的方程1」(m3m(y 3) 2 m(2y 5).12,已知方程 4x 2m 3x 1与方程3x 2m 6x 1的解相同.3(A )①(B )② (C )③ (D )④1)、2x 3(2x 1) 16 (x 1)2x 3 4x 1.3)、142 51x [2 -(x 4)]2x 3、2x 110x 1 2x 1 ,)、 1 36 4x) 2x 的解,解关于y 的方程:(1)求m的值; (2)求代数式(m 3)2010 (2m 2)2011的值.。
人教版九年级数学中考一元一次方程及其应用专项练习及参考答案

人教版九年级数学中考一元一次方程及其应用专项练习专题知识回顾知识点1:一元一次方程的概念1.一元一次方程:一元一次方程的标准形式是:ax+b=0(其中x是未知数,a,b是已知数,且a≠0)。
要点诠释:一元一次方程须满足下列三个条件:(1)只含有一个未知数;(2)未知数的次数是1次;(3)整式方程.注意:方程要化为最简形式,且一次项系数不能为零。
2.方程的解:判断一个数是否是某方程的解,将其代入方程两边,看两边是否相等.知识点2:一元一次方程的解法1.方程的同解原理(也叫等式的基本性质)性质1:等式的两边都加上(或减去)同一个数或同一个整式,所得结果仍是等式。
性质2:等式的两边都乘以(或除以)同一个数(除数不能是零),所得结果仍是等式。
要点诠释:分数的分子、分母同时乘以或除以同一个不为0的数,分数的值不变。
2.解一元一次方程的一般步骤:(1)去分母在方程两边都乘以各分母的最小公倍数,依据等式基本性质2,注意防止漏乘(尤其整数项),注意添括号。
(2)去括号一般先去小括号,再去中括号,最后去大括号,依据去括号法则、分配律,注意变号,防止漏乘。
(3)移项把含有未知数的项都移到方程的一边,其他项都移到方程的另一边(记住移项要变号),依据等式基本性质1,移项要变号,不移不变号。
(4)合并同类项把方程化成ax =b(a≠0)的形式,依据合并同类项法则,计算要仔细,不要出差错。
(5)系数化为1在方程两边都除以未知数的系数a ,得到方程的解x =b/a ,依据等式基本性质2,计算要仔细,分子分母勿颠倒。
要点诠释:理解方程ax=b 在不同条件下解的各种情况,并能进行简单应用: ①a≠0时,方程有唯一解x =b/a ; ②a=0,b=0时,方程有无数个解; ③a=0,b≠0时,方程无解。
知识点3:列一元一次方程解应用题 1.列一元一次方程解应用题的一般步骤:(1)审—审题:认真审题,弄清题意,找出能够表示本题含义的相等关系。
一元一次方程概念及求解专题复习(知识点+基础应用+能力提高+中考真题).doc

一元一次方程一.等式和方程1.等式:含有的式子2.等式的性质①等式两边都同一个数或同一个整式,所得结果仍是等式。
②等式两边都同一个数(除数不能是0),所得结果仍是等式。
3.方程:含有未知数的等式叫方程。
(1)能够使方程左右两边相等的未知数的值,叫方程的解。
要检验未知数的某一个值是不是方程的解,就把这个值代入方程,看左、右两边的值是否相等。
必须注意方程的解和解方程这两个概念的区别。
方程的解是演算的结果,即求出的适合方程的未知数的值;解方程是求方程的解的演算过程。
4.方程的解一--使得方程左右两边相等的未知数的值5.检验:把未知数的值分别代入方程的左右两边。
6.等式的性质等式的性质①等式两边加(或减)同一个数(或式),结果仍相等。
即如果a = b,那么a±c = b±c等式的性质②等式两边乘同一个数,或除以同一不为0的数,结果仍相等。
即如果a=b,那么ac=bca _b如果a=b (cHO)那么c c二.一元一次方程的解法和应用(一)元一次方程的求解(1)一元一次方程:①只有一个未知数,②未知数的次数都是1的方程叫做一元一次方程。
(2)一元一次方程的最简形式2. (3)解一元一次方程的一般步骤。
一元一次方程的应用(二)一元一次方程的应用“1、类型:1.销售、利润问题2.工程问题3.行程问题4•比例问题5.其他问题(数字问题、等积变形、日历问题、人数问题、储蓄问题等)2、列方程解应用题的一般步骤:①审题,弄清题意找出题屮的等量关系②设未知数③列出方程④解方程⑤检验⑥答元一次方程常见题型类型一:利用方程的有关概念,等式性质等解决问题7. 如果Q 与一3互为相反数,那么Q 等于( )•c. 138. ___________________________________________________________ 求作一个一元一次方程使它的解为x=-2,这个一元一次方程为 ________________________________________【能力提高】1.己知方程(m+l)x lml 4-3-0.是关于x 的一元一次方程,则m 的值是( )A. ± 1B. 1C.-1D.O 或 12. 使(«-l)x-6 = 0为关于兀的一元一次方程的 ______________ (写出一个你喜欢的数即可).3. 若关于兀的方程U-2)/-,l +5^ = O 是一元一次方程,则“ _____________ .C. x=0 丄 二12x + 33. 下列方程小是一元一次方程的是( A. 2x = 3yB. 7% + 5 = 6(x-l)C ・ X 2= 1D. --2 = xX4•下列方程是一元一次方程的有哪些? x+2y 二9X 2—3x=l— = 1 x2x=l 3x - 5 3+7=10x 2+x=l5.根据下列条件列出方程(1)比x 大2的数等于7(2) x 比它的2倍小34 5(3) x 比它的上大丄5 166•只列方程,不解方程1) 3x + 5的值等于3, 求x 的值2) 当x 取何值时,3x + 5与4 —x 的值相等3) 当a 为何值量,式子2(3a-4)的值比2a + 7的值大34) 3x4-5与3-x 互为相反数,x 取何值A. 3B. —3 1. 【基础练习】 下列各式不是方程的是( )A. y2_y=4B. m - 2nC. p 2-2pq + q 2D. x = 02. 下列等式中是一元一次方程的是(A. S=Xab2B. x —y=04.若关于x的方程伙+ 2庆+4尬-5£ =()是一元一次方程,则方程的解x二___________・5.已知(2加一3庆一(2-3加)兀=1是关于x的一元一次方程,则加= _______ .6. 已知方程(ci - 2)丿"卜’ +4 = 0是一元一次方程,则a = ___ ; x = _______ .7. 若关于兀的方程伙-2)』刊+5" 0是一元一次方程,贝〃二 __________ .若关于x 的方程(k + 2)x 2 + 4kx-5k = 0是一元一次方程,则方程的解兀二 ______ . &如果@ + 1)』“珂_2 = 0是一元一次方程,那么。
专题04一元一次方程的概念和解法复习(原卷版)

专题04 一元一次方程的概念和解法复习(原卷版)第一部分典例剖析+变式训练知识点1:一元一次方程的概念(只含有一个未知数,并且所含未知数的项的最高次数是一次的整式方程.)1.(2022春•淅川县期中)下列方程中:①x﹣2=2x;②x=6;③2−y4=y−15;④x2﹣4x=3;⑤0.3x=1;⑥x+2y=0,其中一元一次方程的个数是()A.3B.4C.5D.6变式训练1.(2022春•安溪县期中)若x m+1+1=0是关于x的一元一次方程,则m的值为.2.(2022•定远县模拟)方程(7﹣a)x2+ax﹣8=0是关于x的一元一次方程,那么a的值是()A.0B.7C.8D.103.(2022春•仁寿县期中)已知(m﹣2)x|m|﹣1=5是关于x的一元一次方程,则m的值为()A.﹣2B.±2C.2D.0知识点2: 方程的解(能够使方程左右两边相等的未知数的值;只含有一个未知数的方程的解,也叫方程的根)典例2检验下列各数是不是方程4x﹣3=2x+3的解:(1)x=3;(2)x=﹣3.变式训练1.(2021秋•兴庆区校级期末)如果关于x的方程a﹣x=x2+3a的解是x=4,则a的值为()A.﹣3B.3C.﹣5D.52.(2022春•奉贤区校级期末)如果关于x的方程(a+1)x=a2+1无解,那么a的取值范围是()A.a=−1B.a>−1C.a≠−1D.任意实数3.(2022春•丰泽区期末)若x=3是关于x的方程ax﹣b=5的解,则6a﹣2b﹣2的值为()A.2B.8C.﹣3D.﹣84.(2021秋•肥西县月考)已知x=3是关于x的方程2x﹣a=4的解,则a的值是()A.﹣2B.0C.2D.35.(2022秋•市南区期末)方程2x ﹣1=3与方程1−3a−x3=0的解相同,则a 的值为( ) A .3B .2C .1D .536.(2021春•杨浦区期末)关于x 的一元一次方程ax =3,下列对于该方程的解的说法中,正确的是( ) A .该方程一定有实数解 B .该方程一定没有实数解C .该方程不一定有实数解D .上述说法都不对知识点3:等式的性质:1.等式的两边都加上或减去同一个数或同一个整式,所得的结果仍是等式;2.等式两边都乘(或除以)同一个数(除数不为零),所得的结果仍是等式.)典例3用适当的数或整式填空,使所得的结果仍是等式,并说明根据等式的哪一条性质以及怎样变形的: (1)若5x =4x +7,则5x ﹣ =7; (2)若2a =1.5,则6a = ; (3)若﹣3y =18,则y = ; (4)若a +8=b +8,则a = ; (5)若﹣5x =5y ,则x = . 变式训练1.(2021秋•玄武区期末)下列等式的变形中,错误的是( ) A .如果a =2,那么a +2=4 B .如果a =﹣3,那么﹣2a =6C .如果3a =5,那么a =35D .如果a =﹣2,那么a 2=42.(2021秋•罗源县期末)下列根据等式的性质正确变形的是( ) A .由x2=2,得x =1 B .由3(x ﹣2)=6,得x ﹣2=2C .由x ﹣2=6,得x ﹣2+2=6D .由2x +3=x ﹣1,得2x +x =﹣1﹣3知识点4: 解一元一次方程的一般步骤(去分母、去括号、移项、合并同类项、化系数为1) 典例4(2022春•郸城县校级月考)解下列方程:(1)4x ﹣3(20﹣x )=3; (2)12(x −1)=2−15(x +2);(3)x+24−2x−36=1; (4)0.3x−0.50.2−0.12−0.05x0.03=x .变式训练1.(2021秋•南关区校级期末)解下列方程:(1)10x +9=12x ﹣1; (2)12x ﹣3(x ﹣2)=4;(3)5(x ﹣1)=8x ﹣2(x +1); (4)2x+13−5x−16=1.2.(2021秋•新民市期末)当x 取什么值时,代数式2x+32的值与1−x−13的值相等?知识点5: 一元一次方程解的情况讨论(对于方程b ax =,⑴若0≠a ,则方程只有惟一解abx =;⑴若0,0≠=b a ,则原方程无解;⑴若0,0==b a ,则原方程有无数个解.) 典例5 已知关于x 的方程x−23−mx2+3=113. (1)当m 取何值时,方程有解? (2)当m 取何整数时,方程的解是整数?(3)在(2)的条件下,a ,b 在数轴上对应的点位于原点两侧,且到原点的距离相等,求(a +b +m )2013. 变式训练1.(2022秋•石景山区期末)设m 为整数,且关于x 的一元一次方程(m ﹣5)x +m ﹣3=0. (1)当m =2时,求方程的解; (2)若该方程有整数解,求m 的值.第二部分 一元一次方程的概念和解法复习配套作业1.(2022•美兰区校级二模)代数式﹣2a +1与a ﹣2的值相等,则a 等于( ) A .0B .1C .2D .32.(2021秋•滕州市期末)如果关于x 的方程6n +4x =7x ﹣3m 的解是x =1,则m 和n 满足的关系式是( ) A .m +2n =﹣1B .m +2n =1C .m ﹣2n =1D .3m +6n =113.(2021秋•开县期末)关于x 的方程2x +m =1的解是方程3x ﹣2=2x ﹣1的解的3倍,则m 的值是( ) A .﹣5B .﹣17C .1D .34.(2022春•唐河县月考)若﹣5x 2y m﹣3与x n ﹣1y 是同类项,则方程nx ﹣m =5的解是( )A .x =4B .x =3C .x =2D .x =15.(2021秋•朝阳区校级期中)写出一个满足“未知数的系数是﹣2,方程的解为3”的一元一次方程: . 6.(2021秋•阜新县校级期末)当x = 时,单项式5a 2x +1b 2与8a x +3b 2是同类项.7.(2021秋•银川校级期末)已知:x =4是关于x 的一元一次方程3a ﹣x =x2+3的解,则a = . 8.(2021秋•兴庆区校级期末)若12a +1与2a−73互为相反数,则a 的值为 .8.(2021秋•罗源县期末)已知2x m ﹣2+3=0是关于x 的一元一次方程,则m = .9.(2021秋•巩义市期末)关于x 的一元一次方程2x +m =6,其中m 是正整数.若方程有正整数解,则m 的值为 .10.(2021秋•西宁期末)已知x =1是关于x 的方程ax +3x =2的解,则a = . 11.(2022春•朝阳区期中)若x =4是关于x 的方程2x ﹣3a =2的解,则a = . 12.(2022秋•宣州区校级月考)关于x 的方程x−43=−1的解是x = .13.(2022•南京模拟)若关于x 的方程ax +2x =1的解为1,则a = . 14.(2022•南京模拟)已知关于x 的一元一次方程12020x +3=2x +b 的解为x =19,那么关于y 的一元一次方程12020(2y +1)+3=2(2y +1)+b 的解y = .15.(2022春•沙坪坝区期末)若2x n ﹣1=3是关于x 的一元一次方程,则n = . 16.(2021秋•河西区期末)已知关于x 的方程a (a ﹣2)x ﹣4(a ﹣2)=0. 当此方程有唯一的解时,a 的取值范围是 . 当此方程无解时,a 的取值范围是 . 当次方程有无数多解时,a 的取值范围是 .17.(2021秋•溧阳市期末)解下列方程:(1)2x ﹣5=x +4; (2)32x =7+13x ;(3)5(2x ﹣1)=2(1+2x )+x ﹣2; (4)x −x+26=x2−1.18.(2021春•奉贤区期中)解关于x 的方程:ax ﹣x =﹣2(x +2).19.(2021秋•海城区校级月考)已知y =1是方程2−13(m ﹣y )=2y 的解,求关于x 的方程m (x ﹣3)﹣2=m (2x +5)的解.20.(2022春•封丘县月考)已知代数式x4与代数式2−x 3.(1)当x 为何值时,这两个代数式的值相等? (2)当x 为何值时,代数式x4的值比代数式2−x 3的值大2?(3)是否存在x ,使得这两个代数式的值互为相反数?若存在,请求出x 的值;若不存在,请说明理由,21.(2020秋•白云区月考)当m 取什么整数时,关于x 的方程12mx −53=12(x −43)的解是整数?22.(2021秋•鹿邑县期末)在有理数范围内定义运算“※”,其规则为a ※b =a−b2. (1)求2021※2022的值;(2)求方程x ※3=2的解.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一元一次方程
知识点一:一元一次方程及解的概念
1、一元一次方程:
一元一次方程的标准形式是:ax+b=0(其中x是未知数,a,b是已知数,且a≠0)。
要点诠释:
一元一次方程须满足下列三个条件:
(1)只含有一个未知数;
(2)未知数的次数是1次;
(3)整式方程.
例:
直接判定一元一次方程
1、下列方程中,是一元一次方程的是()
A、x2﹣4x=3
B、x=0
C、x+2y=1
D、x﹣1=
2、下列方程中是一元一次方程的是()
A、B、+4=3x
C、y2+3y=0
D、9x﹣y=2
3、下列各方程中,是一元一次方程的是()
A、3x+2y=5
B、y2﹣6y+5=0
C、x﹣3=
D、3x﹣2=4x﹣7
4、下列方程中,属于一元一次方程的是()
A、x﹣3
B、x2﹣1=0
C、2x﹣3=0
D、x﹣y=3
5、下列方程中,是一元一次方程的是()
A、﹣1=2
B、x2﹣1=0
C、2x﹣y=3
D、x﹣3=
已知是一元一次方程,求参数的值
1、若方程3x2m﹣1+1=6是关于x的一元一次方程,则m的值是_________ .
2、已知等式5x m+2+3=0是关于x的一元一次方程,则m= _________ .
3、已知方程(m﹣2)x|m|﹣1+3=m﹣5是关于x的一元一次方程,则m= _________ .
4、关于x的方程(a+2)x|a|﹣1﹣2=1是一元一次方程,则a= _________ .
5、若方程3x4n﹣3+5=0是一元一次方程,则n= _________ .
6、已知2x m﹣1+4=0是一元一次方程,则m= _________ .
7、若4x m﹣1﹣2=0是一元一次方程,则m= _________ .
8、已知(m2﹣1)x2﹣(m+1)x+8=0是关于x的一元一次方程,求代数式199(m+x)(x﹣2m)+m的值.
9、若关于x的方程3(x-1)+a=b(x+1)是一元一次方程,则().
A.a,b为任意有理数B.a≠0 C.b≠0 D.b≠3
2、方程的解:
判断一个数是否是某方程的解:将其代入方程两边,看两边是否相等.
题型一
1、在下列方程中,解是2的方程是()
A、3x=x+3
B、﹣x+3=0
C、2x=6
D、5x﹣2=8
2、下列方程中,解是x=2的是()
A、2x=4
B、x=4
C、4x=2
D、x=2
题型二
1、如果x=﹣2是方程2x+m﹣4=0的解,那么m的值为()
A、﹣8
B、0
C、2
D、8
2、已知x=2是关于x的方程3x+a=0的一个解,则a的值是()
A、﹣6
B、﹣3
C、﹣4
D、﹣5
3、若x=2是方程9﹣2x=ax﹣3的解,则a= _________ .
4、x=是方程|k|(x+2)=3x的解,那么k= _________ .
知识点二:等式的基本性质 等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等。
如果,那么;(c 为一个数或一个式子)。
等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
如果,那么;如果,那么
要点诠释:
分数的分子、分母同时乘以或除以同一个不为0的数,分数的值不变。
即:(其中m≠0)
特别须注意:分数的基本的性质主要是用于将方程中的小数系数(特别是分母中的小数)化为整数,如方程:-=1.6,将其化为: -=1.6。
方程的右边没有变化,这要与“去分母”区别开。
例题:
1、列结论正确的是( )
A .若x+3=y-7,则x+7=y-11;
B .若7y-6=5-2y,则7y+6=17-2y;
C .若0.25x=-4,则x=-1;
D .若7x=-7x,则7=-7.
2、列说法错误的是( ).
A .若a
y a x ,则x=y; B .若x 2=y 2,则-4x 2=-4y 2
; C .若-41x=6,则x=-23; D .若6=-x,则x=-6.
3、知等式ax=ay,下列变形不正确的是( ).
A .x=y
B .ax+1= ay+1
C .ay=ax
D .3-ax=3-ay
4、列说法正确的是( )
A .等式两边都加上一个数或一个整式,所得结果仍是等式;
B .等式两边都乘以一个数,所得结果仍是等式;
C .等式两边都除以同一个数,所以结果仍是等式;
D .一个等式的左、右两边分别与另一个等式的左、右两边分别相加,所得结果仍是等式;
5、下列等式变形错误的是( )
A.由a=b 得a+5=b+5;
B.由a=b 得- a 9 =- b 9
C.由x+2=y+2得x=y;
D.由-3x=-3y 得x=-y
6、运用等式性质进行的变形,正确的是( )
A.如果a=b,那么a+c=b-c;
B.如果 a c = b c
,那么a=b; C.如果a=b,那么a c = b c
; D.如果a2=3a,那么a=3
7、等式2-3
1-x =1变形,应得( ) A .6-x+1=3 B .6-x-1=3 C .2-x+1=3 D .2-x-1=3
知识点三:解方程
解一元一次方程的一般步骤
常用步骤
具体做法 依据 注意事项 去分母 在方程两边都乘以各分
母的最小公倍数
等式基本性质2 防止漏乘(尤其整数项),注意添括号; 去括号 一般先去小括号,再去
中括号,最后去大括号
去括号法则、分配律 注意变号,防止漏乘;
移项 把含有未知数的项都移
到方程的一边,其他项
都移到方程的另一边
(记住移项要变号)
等式基本性质1 移项要变号,不移不变号; 合并同类项 把方程化成ax =
b(a≠0)的形式
合并同类项法则 计算要仔细,不要出差错; 系数化成1 在方程两边都除以未知
数的系数a ,得到方程
的解x = 等式基本性质2 计算要仔细,分子分母勿颠倒 要点诠释:理解方程ax=b 在不同条件下解的各种情况,并能进行简单应用:
①a≠0时,方程有唯一解;
②a=0,b=0时,方程有无数个解;
③a=0,b≠0时,方程无解。
题型一:直接解方程
解下列方程:
(1)2(3)15(23)t t +-=- (2)54324
x x -=
(3)21101136x x ---= (4)12225x x x -+-=-
(5)30.4110.50.3
x x ---= (6)32[23(x-21)-3]-2=4x
题型二:
1、当x =________时,式子322x -与23x
-互为相反数.
2、在解方程123123x x -+-=时,去分母正确的是( )
A .3(1)2(23)1x x --+=
B .3(1)2(23)6x x --+=
C .31431x x --+=
D .31436x x --+=
3、已知下面两个方程
3(x+2)=5x ,①
4x ﹣3(a ﹣x )=6x ﹣7(a ﹣x ) ②
有相同的解,试求a 的值.
4、已知关于x 的方程a (2x ﹣1)=3x ﹣2无解,试求a 的值.
5、a 为何值时,方程有无数个解?无解?
6、当k 取何值时,关于x 的方程3(x+1)=5﹣kx 分别有(1)正数解;(2)负数解;(3)不大于1的解.。
