微积分方法建模1飞机的降落曲线--数学建模案例分析
数学建模 飞机管理模型

Air Traffic ControlAbstract本文讨论了如何对新进入区域内的飞机是否会与区域内原有的飞机碰撞的问题,和如若碰撞,调整各架飞机方向角,使得飞机均能安全飞出正方形区域的问题。
针对判断飞行的飞机之间是否发生碰撞亦即可碰撞问题,把各架飞机的运动轨迹端点坐标用时间表示后,就可以写出第六架飞机与其它五架飞机的距离表达式,判断这个最小距离是否小于8km,如果小于,则碰撞,否则不碰撞。
这一过程的实现可通过MATLAB编程动态模拟飞机在区域内的飞行过程。
在时间轴上连续取样,最后得出第六架飞机和第五架相碰,碰撞时事件飞机的坐标位(),相碰时刻为?针对检测到碰撞的存在并采取措施进行规避,即碰撞规避问题。
需要对各架飞机的方向角进行调整,并且使得飞机方向角调整幅度最小。
建立非线性规划模型,利用MATLAB求得第i架飞机)6,5,4,3,2,1i调整的角度分别为:(关键字:飞机碰撞方向角最优解非线性规划ContentsI. IntroductionGrow inside 160 kilometers of exact square districts in the about 10,000 meters high empty some side, usually how many the airplane make level flight.Position and speed vector of each airplane inside the district are recorded its data by the calculator, so that they carry on a flight management.When desire gets into the airplane of the district to arrive a district edge, after recording its data, immediately compute and judge whether meeting and airplane occurrence in the district collision.If will collide, then should compute how to adjust each(including is lately ingoing) direction Cape that the airplane flies.To avoid collision.Now suppose a condition as follows:1)The standard that don't collide is more than 8 kilometers for the distance of arbitrarily two airplanes.2)The airplane flies the range that the direction Cape adjusts to be higher than 30 degrees.3)All airplane airspeeds are all per hours are 800 kilometers.4)The airplane that gets into the district while arriving a district edge, with the distance of airplane inside the district in response to above 60 kilometers.5)At most need to consider 6 airplanes.6)Need not consider that the airplane leaves the condition of this empress in the district.Please to the problem establishment mathematics model of the flight management that avoid collision.List to compute a step, carry on a calculation to the following data.(direction Cape the error margin isn't higher than 0.01 degrees)Requesting airplane to fly the range that the direction Cape adjusts is as far as possible small.The coordinates that establishes the district's 4 tops (0,0),(160,0) , (160,160) , (0,160)Airplane serial number Abscissa x Ordinate yDirectionCape(degree)1 150 140 2432 85 85 2363 150 155 220.54 145 50 1595 130 150 230 New 0 0 52Note:The direction Cape points to fly direction and X stalk just to of clip Cape. Try to carry on evaluation and expansion to your model according to the actual application background.II. The Description of the Problem2.1The analysis of the problem background在一个确切的广场区,每架飞机的位置和速度矢量飞机到达区的边缘.其数据记录,计算器立即计算和判断飞机发生碰撞的区域.如果发生碰撞然后计算如何调整各方向开普敦的飞机飞以避免碰撞,.程序如下:In an exact square district, position and speed vector of each airplane are recorded its data by the calculator.When the airplane arrives the edge of district, the calculator immediately computes and judge whether meeting and airplane occurrence in the district collision.If the occurrence collides and computes then how adjust each direction Cape that the airplane flies to avoid collision.Process such as figure a show:accessleave2.2 on the analysis to problem 1由于模型假设飞机是在同一高度飞行,故可以认为飞机是在同一水平面上,这样只需讨论二维平面管理飞机不相碰撞的管理和调节问题。
数学建模-降落伞的选择

降落伞的选择摘要本文讨论并确定了降落伞的最佳选购方案,使费用最低。
通过对问题的分析,以牛顿第二定律建立微分方程模型,通过以救灾物资2000kg,5种不同半径的降落伞的最大载重量为限制条件,建立优化模型。
通过优化模型最终解出最佳方案,以及最小费用。
继而我们继续讨论了在投放降落伞与救灾物资时,风速、偏角对降落伞下降时绳索拉直的影响。
在绳索拉直的情况下,我们才能确保救灾物资能在已有的约束条件下到达目的地。
所以最后我们通过数据的拟合,找出了最适合投放降落伞的风速及偏角范围,以此来增加救灾物资到达灾区的可靠性。
首先,我们要确定阻力系数。
通过对表二的数据分析,以牛顿第二定律建立微分方程模型,运用matlab插点作图进行数据拟合,得到半径为3m,载重为500kg 的降落伞从500m高度下落的运动曲线,发现物体在运动后期做了直线运动,通过对图形的分析得出了阻力系数2.959,.落地速度为17.5794m/s.其次,我们要确定不同半径的降落伞的最大载重。
通过对表一的数据分析,以牛顿第二定律建立微分方程模型,通过以空投高度为500m,以降落伞落地的速度不能超过20m/s为约束条件,代入阻力系数及相关数据求的每种半径下的降落伞最大载重。
运用优化模型的解题方法,我们得出最低费用为4932元,降落伞的最佳选购方案为半径为3m的降落伞数量为6个,其他半径的降落伞不予选购。
最后,我们根据查找数据,得到风速、偏角与降落伞下降时绳索拉直的关系,得到相关图片,然后进行拟合得到,从而在已选条件下,选择降落伞最好的投放地点(该地点要符合风速、偏角对绳索拉直的最佳状态)。
关键字:降落伞的选择、拉直问题、微分方程、matlab、数据拟合问题重述为了向灾区空投救灾物资,需要选择不同类型的降落伞。
降落伞根据半径不同分为半径为2米、2.5米、3米、3.5米、4米五种型号,降落伞的造价由伞面费用,绳索费用和固定费用三部分组成。
每个降落伞均是半径为的球形,并且用长为l的16跟绳索连接重物,重物位于球心正下方的球面处,降落伞在下降过程中除了受到重力的影响外,还受到空气的阻力。
上海虹桥机场的数学建模问题解决

一、问题背景与重述1.1问题背景虹桥国际机场采用的是东西两条跑道分工进行飞机起降的任务,所以大多数飞机的起降都要实现跑道穿越的过程,同时在飞机起降的高峰时期,此时人工指挥进行飞机调度就存在着一定的困难和安全隐患。
1.2问题重述1.设计一个跑道的智能调度模型,内容包括:飞机降落时间及落地后的运动规划,飞机起飞前的运动规划和起飞时间,所有航班的起降(次序、时间、地面滑行路径)。
在保证跑道上飞机安全的基础上,考虑准点率和起降效率的提高;2.对附件2的航班起降时间重新编排,在安全的基础上,计算出所有航班起降完需要的最短时间和调度安排(次序、时间、地面滑行路径)。
二、问题分析进近道对于参数较多,图形结构复杂的虹桥机场使用树状图,将其简化为三条主跑道与多条进近道,在此基础上,由南向北的行进过程中分析可能存在的道路,并考虑单一支路上的冲突情况与交叉冲突情形,并将多条可能的选择路线转化为时间效率,接着分析转弯节点处的约束条件与单一跑道的约束条件,将两者结合。
每次选定不同的覆盖航班数,在覆盖范围内唯一确定已经按计划起飞的航班,在此基础上,再对剩余的航班进行规划即可得到目标函数的最佳效益,通过改变每次覆盖的航班数量与可移动覆盖的航班数量,由此得到不同的目标效益最值。
三、模型假设所有斜进近跑道长度相等;飞机的机头调转不能超过90°;飞机在南北方向跑道上是匀速滑行的。
四、符号说明符号说明J第i架飞机的效益值iR最小尾流间隔i表示转弯角iv表示初始速度't起飞客机滑行时间''t降落客机的滑行时间五、模型建立与求解5.1 动态调度模型的建立与求解5.1.1 对虹桥机场跑道的简化(1)飞机起飞上海虹桥机场的跑道图显示,起飞飞机滑行的终点是指定的起飞跑道,此时飞机需要等待跑道被清空后才能完成飞行过程。
根据以上对飞机起飞过程的描述,可得到起飞图5-2 起飞飞机状态图为了简化问题,本文规定由T2机场起飞的飞机只能由H6与H7进近跑道进入滑行跑道,而由T1机场起飞的飞机只能由H7进近跑道进入滑行跑道,并且此时的飞机始终保持匀速滑行。
微积分方法建模2经济增长模型--数学建模案例分析
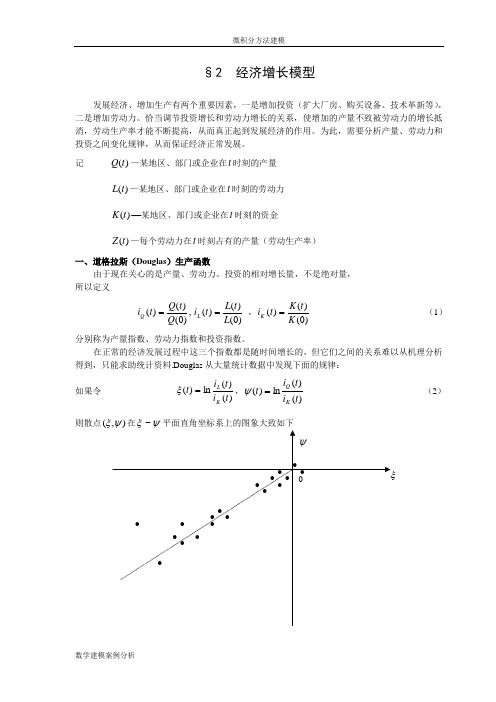
§2 经济增长模型发展经济、增加生产有两个重要因素,一是增加投资(扩大厂房、购买设备、技术革新等),二是增加劳动力。
恰当调节投资增长和劳动力增长的关系,使增加的产量不致被劳动力的增长抵消,劳动生产率才能不断提高,从而真正起到发展经济的作用。
为此,需要分析产量、劳动力和投资之间变化规律,从而保证经济正常发展。
记 )(t Q —某地区、部门或企业在t 时刻的产量)(t L —某地区、部门或企业在t 时刻的劳动力)(t K −某地区、部门或企业在t 时刻的资金)(t Z —每个劳动力在t 时刻占有的产量(劳动生产率)一、道格拉斯(Douglas )生产函数由于现在关心的是产量、劳动力、投资的相对增长量,不是绝对量,所以定义,)0()()(Q t Q t i Q =)0()()(L t L t i L = ,)0()()(K t K t i K = (1)分别称为产量指数、劳动力指数和投资指数。
在正常的经济发展过程中这三个指数都是随时间增长的,但它们之间的关系难以从机理分析得到,只能求助统计资料.Douglas 从大量统计数据中发现下面的规律:如果令 )()(ln )(t i t i t K L =ξ,)()(ln )(t i t i t K Q =ψ (2)则散点),(ψξ在ψξ~平面直角坐标系上的图象大致如下即大多数点靠近一条过原点的直线,这提示ξ和ψ的关系为)10(<<=γγξψ (3) 上式代入得)()()(1t i t i t i K L Q γγ-= (4) 记)0()0()0(1--=γγK L Q a ,则由(1)、(4),可得)0,10(),()()(1><<=-a t K t aL t Q γγγ (5)这就是经济学中著名的Douglas 生产函数,它表明产量与劳动力、投资之间的关系。
由(5)有K K L L Q Q )1(γγ-+= (6)(6)表明年相对增长量Q Q 、L L 、KK 之间呈线性关系。
纸飞机的飞行原理数学建模

纸飞机的飞行原理数学建模我们可以将纸飞机看作一个质点,忽略其形状和空气阻力对其运动的影响。
假设纸飞机在平面上运动,我们可以使用二维坐标系表示其位置,其中 (x, y) 表示飞机在水平和垂直方向上的位移。
我们需要确定纸飞机的初始条件。
这包括初始位置 (x0, y0) 和初始速度 (v0x, v0y),其中 v0x 和 v0y 分别表示飞机在水平和垂直方向上的速度。
然后,我们考虑纸飞机所受到的力。
在空气中,纸飞机主要受到重力和升力的作用。
重力可以用以下公式表示:Fg = m * gm 表示纸飞机的质量,g 表示重力加速度。
在这个模型中,我们可以忽略纸飞机的质量,即 m 取为常数。
升力可以使用简化的数学模型进行描述。
根据流体力学的基本原理,升力与速度的平方成正比,与气流的密度和机翼的面积有关。
我们可以使用以下公式表示升力:Fl = 0.5 * ρ * A * v^2Fl 表示升力,ρ 表示空气密度,A 表示机翼的有效面积,v 表示纸飞机的速度。
接下来,我们考虑纸飞机的运动方程。
根据牛顿第二定律,加速度与力的关系为:F = m * a在这个模型中,我们同时考虑了纸飞机受到的重力和升力,因此可以得到以下运动方程:ma = Fg - Fl由于我们忽略了纸飞机的质量 m,因此可以简化为:a = g - (0.5 * ρ * A * v^2)我们可以使用差分方程对纸飞机的运动进行数值模拟。
假设我们将时间间隔取为Δt,我们可以使用以下差分方程更新纸飞机的位置和速度:x[i+1] = x[i] + v[i] * Δty[i+1] = y[i] + v[i] * Δtv[i+1] = v[i] + a[i] * Δti 表示时间步数。
通过以上的数学建模,我们可以分析纸飞机在不同条件下的飞行轨迹和速度变化。
可以进一步讨论如何设计纸飞机的机翼面积和形状,以最大限度地提高其飞行距离和时间。
我们也可以通过调整纸飞机的初始条件来探讨其对飞行性能的影响。
高等数学模型—微积分模型(数学建模课件)

2、假设易拉罐是一个正圆柱体,什么是它的最优设计?其结果是
否可以合理地说明你们所测量地易拉罐地形状和尺寸。
二、数据测量
罐直径、罐高、罐壁厚、顶盖厚、圆台高、
顶盖直径、圆柱体高、罐底厚、罐内体积等。
该如何测量?
二、数据测量
1、直接测量
①用软皮尺环绕易拉罐相关部位一圈
(罐桶直径、罐
测得周长。
高、圆台高、顶
速度、出手角度和出手高度)
作定性和定量研究并得到明
确结论。
森林救火问题
微积分模型
知识点
一、问题的提出
二、模型分析与假设
三、模型建立与求解
四、模型应用
一、问题的提出
一、问题的提出
森林失火了!消防站接到火警后,立即决定派消防队员前去救火。队
员多,火被扑灭的快,森林损失小,但救援费用大;队员少,救援费用小,
118.0 123.5 136.5 142.0 146.0 150.0 157.0 158.0];
y1=[44 45 47 50 50 38 30 30 34 36 34 41 45 46 43 37 33 28 32 65 55 54 52 50 66 66 68];
y2=[44 59 70 72 93 100 110 110 110 117 118 116 118 118 121 124 121 121 121 122 116 83 81 82 86
四、模型建立与求解
一、问题的提出
运动员单手托住铅球,在投掷圆内将铅球掷出并使铅
球落入有效区内,以铅球投掷的远度评定运动员的成绩。
问题:
建模分析如何使铅球投掷的最远?
二、问题分析
• 铅球投掷中,影响投掷距离的因素有哪些?
数学建模作业

数学建模作业题目:客机水面迫降时的姿态指导老师:尚寿庭小组成员:日期:客机水面迫降时的姿态2009 年1 月15 日下午(美国东部时间),US Airways 所属第1549 航班(空中客车A320 客机)在起飞后不久在纽约哈德逊河紧急迫降。
经及时救助,机上155 人(其中包括两名机师和三名乘务人员)在飞机沉没之前全部获救。
该起事故造成78 人受伤,无人死亡。
这架客机从纽约长岛拉瓜迪亚机场起飞约90 秒后遭飞鸟撞击,导致两个发动机损坏。
机长萨伦伯格凭借着出色的驾驶技术和冷静的判断使飞机迫降在哈德逊河河面。
而飞机上的乘客在乘务员的指挥下,有秩序地逃出紧急舱门并全部获救。
问题:大型客机因为失去动力而进行的迫降具有相当大的危险性。
请你建立合理的数学模型,对客机在平静水面上的迫降进行分析,指出客机在河面上迫降时,以何种姿态接触水面是相对最好的选择。
解答:最佳襟翼位置①襟翼放下−着陆布局②放下襟翼到全开位置。
除非风速极高, 否则降落应平行于次涌浪而不应迎风。
如果存在次涌浪, 应力图在涌浪的顶部而不在背面着水。
起落架的收放状态①起落架收起。
②在降落前的燃油耗损尽可能多断开空调组件, 关闭放气活门冲压空气冷却门和发动机气管。
飞机的降落状态试验和理论分析以及实际水上迫降表明, 飞机要具有良好的漂浮性, 其降落应该是柔和的,没有俯冲或跳跃、向前减速度不太大、撞击压力和滑行压力也不太大,因为俯冲会给飞机结构造成灾难性破坏, 跳跃会使飞机失去操纵, 第二次着水也会给飞机结构造成灾难性破坏,着水时向前速度太大也会直接伤害乘员, 过大的撞击压力和滑行压力会引起飞机结构的严重破坏,所以最佳降落状态是11°,取纵向波涛.水上迫降过程中的冲击力水上迫降过程中, 飞机受到平行于x 轴的纵向力Fx 、平行于y 轴的法向力Fy 以及绕重心的俯仰力矩M 。
将上述冲击力无量纲化, 得到相应的冲击力系数如下:其中, U0 为飞机着水时刻的速度, S 为机翼面积, cA 为机翼平均气动弦长。
数学建模之微积分的应用

微积分的应用1.跳伞运动员由静止状态向地面降落,人和伞共重161磅(1磅=0.45359273kg ),在降落伞张开以前,空气阻力等于 v 2 ,在开始降落5s 后降落伞张开,这时空气阻力为 v 22 ,试求降落伞张开后跳伞员的速度v(t),并讨论极限速度。
问题分析:本题题目比较好懂,只要理解阻力的速度的关系,再根据物理关系进行列方程即可求解。
所以问题主要在于模型的建立于求解。
具体解题过程如下。
(1) 分析求解从t=0到t=5s 之间跳伞员的运动状态 由已知可得空气阻力f=v/2,故根据力学知识可以得到如下方程:mg-f=ma即 mg-v/2=m dv dt此为一元微分方程。
由高数知识,先解该方程对应的齐次微分方程-v/2=m dv dtdv v =−dt 2m 两边同时积分 ∫ dv v v t v 0=∫−dt 2m t 0 得 v t =v 0∗e −t2m由常数变异法令 v t =h(t)∗e −t 2m则 v t ’=h(t)’∗e −t2m + h(t)*(-12m ) ∗e −t2m 带回原方程得:h(t)’=g ∗e −t 2mh(t)=2mg ∗e−t2m +C (C 为常数)所以v t =h (t )∗e −t 2m = (2mg ∗e −t 2m +C) ∗e −t 2m又 v 0= 0,所以C= -2mg所以 v t = = 2mg (1−e −t 2m )带入数值,t=5s ,则可得到v 5=48.17m/s 。
且由方程的解的表达形式,利用MATLAB 可以得到如下v-t 曲线。
由于该曲线是在5s 内的,则e −t 2m 随t 的变花近似为线性的,所以看起来近似直线,实际则不是的。
(2) 分析求解从t=5s 到t=t 之间跳伞员的运动状态同以上的分析过程,可以列出在该时间段内的方程:mg- v 22 =m dv dt即 dvdt =2mg−v 22m dv 2mg−v 2=12m dt令√2mg =a ,对上式两边同时积分得:∫dva2−v2=∫12mdtt5v tv5查的积分表公式,上式继续得到:∫dva2−v2=12a∫(1a−v+1a+v)v tv5dv=v t v512aln|a+v ta−v t∗a−v5a+v5| =t−52m直接对该式进行定性分析:如果不考虑跳伞员的高度问题,当t ∞时,上式右边∞,所以可以得到绝对值部分为无穷大;所以有v t=a=√2mg=37.826 m/s。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 微积分方法建模
现实对象涉及的变量多是连续的,所以建立连续模型是很自然的,而连续模型一般可以用微积分为工具求解,得到的解析解便于进行理论分析,于是有些离散对象,如人口的演变过程,也可以构造连续模型。
当我们描述实际对象的某些特性随时间(或空间)而演变的过程,分析它的变化规律,预测它的未来性态时,通常要建立对象的动态模型。
建模时首先要根据建模目的和对问题的具体分析作出简化假设,然后按照对象内在的或可以类比的其它对象的规律列出微分方程,求出方程的解并将结果翻译回实际对象,就可以进行描述、分析或预测了。
§1 飞机的降落曲线
根据经验,一架水平飞行的飞机,其降落曲线是一条三次抛物线(如图)。
在整个降落过程中,飞机的水平速度保持为常数u ,出于安全考虑,飞机垂直加速度的最大绝对值不得超过10/g (这里g 是重力加速度)。
已知飞机飞行高度h (飞临机场上空时),要在跑道上O 点着陆,应找出开始下降点0x 所能允许的最小值。
一、 确定飞机降落曲线的方程
设飞机的降落曲线为
d cx bx ax y +++=23
由题设有 h x y y ==)(,0)0(0。
由于曲线是光滑的,所以y(x)还要满足0)(,0)0(0='='x y y 。
将上述的四个条件代入y 的 表达式
⎪⎪⎩
⎪⎪⎨⎧=++='=+++==='==023)()(0)0(0)0(020*******
c bx ax x y h
d cx bx ax x y c y d y 得 ,0,0,3,22030===-=d c x h b x h
a
飞机的降落曲线为 )32(230
20x x x x h y --
= 二、 找出最佳着陆点
飞机的垂直速度是y 关于时间t 的导数,故
dt dx x x x x h dt dy )66(20
20--= 其中dt
dx 是飞机的水平速度,,u dt dx = 因此 )(60
2
20x x x x hu dt dy --= 垂直加速度为
)12(6)12(6020
202022--=--=x x x hu dt dx x x x hu dt y d 记 ,)(22dt y d x a =则126)(0
202-=x x x hu x a ,[]0,0x x ∈ 因此,垂直加速度的最大绝对值为 202
6)(max x hu x a = []0,0x x ∈
设计要求 106202
g x hu ≤,所以g
h u x 600⋅≥ (允许的最小值) 例如:小时/540km u =,m h 1000=,则0x 应满足:
)(117378
.9100060360010005400m x =⨯⨯≥ 即飞机所需的降落距离不得小于11737米。
