博弈论66个经典例子
博弈论66个经典例子 python

博弈论66个经典例子 python在博弈论中,有许多经典的例子可以用Python来实现。
以下是其中的一些例子:1. 石头剪刀布游戏:两个玩家依次出手,根据规则判断胜负。
```pythondef rock_paper_scissors(player1, player2):if player1 == player2:return "Tie"elif (player1 == "rock" and player2 == "scissors") or (player1 == "scissors" and player2 == "paper") or (player1 == "paper" and player2 == "rock"):return "Player 1 wins"else:return "Player 2 wins"print(rock_paper_scissors("rock", "scissors")) # 输出 Player 1 wins ```2. 井字棋游戏:两个玩家轮流在3x3的棋盘上放置棋子,先连成一条线的玩家获胜。
```pythondef tic_tac_toe(board):# 检查行for i in range(3):if board[i][0] == board[i][1] == board[i][2] != "-":return board[i][0]# 检查列for i in range(3):if board[0][i] == board[1][i] == board[2][i] != "-":return board[0][i]# 检查对角线if board[0][0] == board[1][1] == board[2][2] != "-":return board[0][0]if board[0][2] == board[1][1] == board[2][0] != "-":return board[0][2]# 平局if all(board[i][j] != "-" for i in range(3) for j in range(3)): return "Tie"# 游戏未结束return "No winner"board = [["X", "-", "O"],["O", "X", "-"],["-", "O", "X"]]print(tic_tac_toe(board)) # 输出 X```3. 囚徒困境:两个囚徒面临合作或背叛的选择,根据选择和对方的选择获得不同的奖励。
经典博弈论

这个故事讲的道理是,尽管所罗门王不知道 两位妇人中谁是婴儿的母亲,但他知道婴儿真正 的母亲是宁愿失去孩子也不会让孩子被劈成两半 的。所罗门王正是利用这一点,一下就识别出谁 是婴儿的真正的母亲了。所罗门王的这种方法在 博弈论中被称为“ 机制设计 ” ,即设计一套博弈 “ 机制设计” 的规则,令不同类型的人作出不同的选择,尽管 每个人的类型可能是隐藏的,别人观察不到,但 他们所作出的不同选择却是可以观察到的。观察 者可以通过观察不同人的选择而反过来推演出他 们的真实类型。
而事实上是,村子里的这100对夫妇的男人都 不忠,但由于女人不会将她知道的事实告诉不 忠男人的妻子,每个女人都不知道自己的男人 不忠。因此,该村子一直很稳定,而没有发生 妻子杀死丈夫的行为。 村子里有一个辈分很高的老太太,她德高望重, 诚实可敬。因每个人都向她汇报村里的情况, 因此她对村里的情况了如指掌,她知道每个男 人都不忠。
5、走出囚徒困境的机制设计 、 冻结价格战的博弈机制
美国有两家销售音像商品的商店“疯狂 艾 迪 ( Crazy Eddie ) 和 纽 马 克 与 露 易 斯 (Newmark&Lewis),它们之间在市场上 存在竞争。当它们进行合谋时,如何保证对 方不会背叛而降价的一个前提就是如何能迅 速查出对方的背叛行为并给予惩罚。
飞机或轮船公司为了将这些在经济学 中被称为具有不同支付意愿的人区分开来, 让能支付较高价格的人支付较高价格,就设 计了一种“信息甄别”的机制,这种机制就 是设立头等舱、二等舱、三等舱……等等。 这种机制发挥作用的道理是这样的,我们可 以用著名的“ 所罗门王断案 ” 的故事来说 “ 所罗门王断案” 明。所罗门王是古代以色列国的一位以智慧 著称的君主。
3、信号传递博弈例子 、 有N个电视剧,其中有一个情节是一位武林豪 杰在交通要道边开了一个酒馆。生意十分兴隆, 引起另一位武林高手的垂涎。这位武林高手决定 打败那位豪杰然后霸占酒馆。两强相遇,武林豪 杰和武林高手相互之间不知对方底细,于是来一 番比试。本来,他们俩可以通过打斗来解决问题, 但打斗一场双方都会有所损伤,不如通过其他方 式比较武功高低。豪杰拿来5块砖,一掌将其击碎, 高手也不示弱,照样击碎5块砖。于是,豪杰又拿 来十块砖,同样是一掌击个粉碎,高手见之,心 中没底,于是明白自己武功较豪杰还差一截。于 是,这位武林高手甘拜下风,放弃了原来的计划, 弃剑而去。
博弈论的例子

博弈论的例子
1. 下棋不就是典型的博弈论例子嘛!就像你和朋友下棋,每一步都要思考怎么才能赢,这不就是在算计和对方的较量吗?
2. 还有在拍卖会上,大家互相竞价,这简直就是一场激烈的博弈啊!每个人都在权衡自己的出价,试图用最合适的价格得到想要的东西,难道不是吗?
3. 股票市场不也一样嘛!投资者们都在根据各种信息做出决策,和其他投资者进行无形的博弈,哎呀呀,那可真是惊心动魄呢!
4. 选举不也是一种博弈呀!候选人都在争取选民的支持,各种策略手段都用上了,这竞争可太激烈了!
5. 谈恋爱有时候也像博弈论呢!双方都在试探彼此的心意,决定自己要付出多少,这可不是一场微妙的较量嘛!
6. 商业谈判更是博弈论的舞台呀!双方为了达成对自己有利的协议,不断讨价还价,就像一场没有硝烟的战争,厉害吧!
我觉得博弈论在我们生活中无处不在,它让我们更清楚地看到各种互动中的策略和竞争,真的很有意思呢!。
博弈论的经典案例

智猪博弈
按钮 食槽
智猪博弈
假设食物进入食槽后, 1.大猪先吃,吃9个食物; 2.小猪先吃,吃4个食物; 3.同时吃,大猪吃7个食物,小 猪吃3个食物。
智猪博弈
小猪
按 按 大猪 等待 5, 1 9,-1 等待 4,4 0,0
智猪博弈
大猪按按钮。
Nash均衡——(按,等待)。
结果——(4,4)。
斗鸡博弈
性别战和斗鸡博弈引出的问题:
当存在多个Nash均衡时,如 何选择,即如何达到一致性预测。
5 猜硬币
甲乙两人玩猜硬币游戏。甲出正反, 乙猜正反。若乙猜对,则甲给乙一元钱; 否则,乙给甲一元钱。
猜硬币
B 正 反
1,-1
正
A 反
- 1 ,1
1,-1 -1,1
猜硬币
不存在前面所讨论的Nash均衡。
斗鸡博弈
B 进 退
2, 0 0, 0
进
A 退
-3,-3 0, 2
斗鸡博弈
斗鸡博弈存在两个Nash均衡——(进, 退)和(退,进)。
博弈结果——(2,0)和(0,2)。
斗鸡博弈
斗鸡博弈实例:
1.公共产品提供; 2.美苏争霸; 3.警察与游行队伍; 4.夫妻吵架; 5. 古巴导弹危机。
斗鸡博弈
现实生活中的象骑虎难下、进退 两难的局面都可看成是斗鸡博弈的具 体体现。
3 性别战
女 足球 足球 男 芭蕾 芭蕾
2,1 0,0
0,0 1,2
性别战
性别战博弈中存在两个Nash均衡— —(足球,芭蕾)和(芭蕾,足球)。
博弈结果——(2,1)和(1,2)。
4 斗鸡博弈
设想两个勇士举着火棍从独木桥两端冲向 中央进行火拼。
十大博弈论经典案例

十大博弈论经典案例1.《囚徒困境》。
囚徒困境是博弈论中最著名的案例之一。
在这个案例中,两名囚犯被捕,但检察官没有足够的证据来判定他们犯罪。
如果两名囚犯都沉默,他们将被判处较轻的刑罚;如果其中一人选择交代,而另一人保持沉默,那么交代的囚犯将获得豁免,而另一人将被判处重刑;如果两人都交代,他们将被判处较重的刑罚。
在这种情况下,每个囚犯都面临着一个困境,无论对方选择什么,自己都会受到损失。
2.《合作博弈》。
合作博弈是指参与者之间可以进行合作的博弈。
在合作博弈中,参与者可以通过合作来获得更好的结果。
例如,两家公司可以通过合作来共同开发新产品,从而获得更大的利润。
合作博弈强调参与者之间的合作和协调,以实现共同的利益。
3.《竞争博弈》。
竞争博弈是指参与者之间存在竞争关系的博弈。
在竞争博弈中,参与者的利益往往是相互对立的。
例如,两家公司在市场上竞争销售同一种产品,它们的利润往往是相互竞争的。
竞争博弈强调参与者之间的竞争和对抗,以争取最大的利益。
4.《博弈的策略》。
在博弈中,参与者可以选择不同的策略来影响结果。
策略是参与者在博弈中可以采取的行动。
不同的策略选择会导致不同的结果,而博弈论就是研究参与者如何选择最优策略以达到最大利益的学科。
5.《信息不对称博弈》。
信息不对称博弈是指参与者在博弈中拥有不同的信息。
在这种情况下,有一方可能掌握更多的信息,从而在博弈中占据优势。
信息不对称博弈强调信息的重要性,以及如何在信息不对称的情况下做出最优决策。
6.《博弈的均衡》。
博弈的均衡是指在博弈中参与者达到一种稳定状态的结果。
在这种状态下,参与者不会再改变自己的策略,因为任何单方面的改变都不会给自己带来更好的结果。
博弈的均衡是博弈论中非常重要的概念,它可以帮助我们预测参与者的行为和结果。
7.《博弈的合作与对抗》。
在博弈中,合作和对抗是两种常见的行为方式。
合作可以带来共同的利益,而对抗则是为了争取最大的利益。
在实际的博弈中,参与者往往需要权衡合作和对抗之间的关系,以达到最优的结果。
精编博弈论经典案例资料

精编博弈论经典案例资料在我们的生活中,博弈无处不在。
无论是在商业竞争、政治决策,还是日常的人际关系中,人们都在不断地进行着各种形式的博弈。
博弈论作为一门研究决策主体相互作用时的决策以及这种决策的均衡问题的学科,为我们理解和应对这些复杂的情况提供了有力的工具。
下面,让我们一起来看看一些经典的博弈论案例。
案例一:囚徒困境假设有两个犯罪嫌疑人 A 和 B 被警方抓获,但警方没有足够的证据指控他们。
于是,警方将两人分别关押在不同的房间进行审讯,并向他们分别提出了相同的条件:如果两人都保持沉默(即不坦白),那么他们都会被判刑 1 年;如果其中一人坦白而另一人保持沉默,坦白的人将被无罪释放,而沉默的人将被判刑 10 年;如果两人都坦白,那么他们都会被判刑 8 年。
对于 A 和 B 来说,他们都面临着两种选择:坦白或沉默。
从 A 的角度来看,如果 B 坦白,那么自己坦白会被判刑 8 年,沉默会被判刑10 年,所以坦白是更好的选择;如果 B 沉默,那么自己坦白会被无罪释放,沉默会被判刑1 年,还是坦白更好。
同样的逻辑对于B 也适用。
最终,两人都会选择坦白,尽管从整体上看,如果他们都保持沉默,结果会更好(两人总共判刑2 年),但由于他们无法相互信任和协调,最终都选择了坦白(两人总共判刑 16 年)。
囚徒困境揭示了个体理性与集体理性之间的冲突。
在很多情况下,人们从自身利益出发做出的决策,并不一定能带来整体的最优结果。
案例二:智猪博弈假设猪圈里有一头大猪和一头小猪,猪圈的一头有一个猪食槽,另一头安装着控制猪食供应的按钮。
按一下按钮会有 10 个单位的猪食进槽,但谁按按钮就会首先付出 2 个单位的成本。
若大猪先到槽边,大猪吃到 9 个单位,小猪只能吃到 1 个单位;若同时到槽边,大猪吃 7个单位,小猪吃 3 个单位;若小猪先到槽边,大猪吃 6 个单位,小猪吃 4 个单位。
那么,对于小猪来说,无论大猪是否去按按钮,等待都是它的最优选择。
博弈论66个经典例子之六
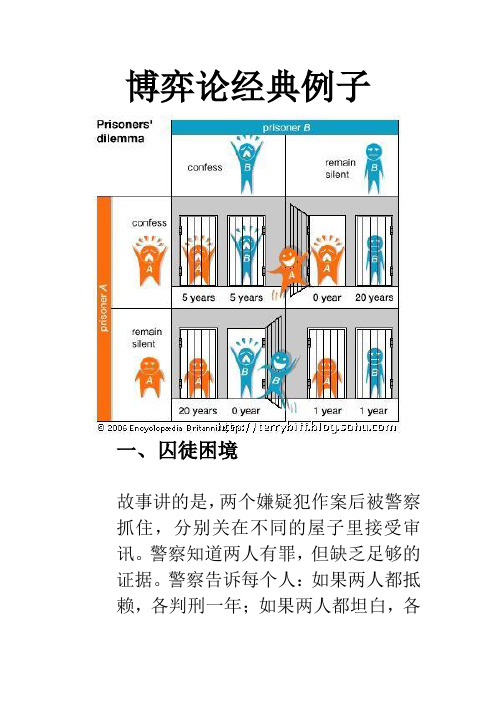
博弈论经典例子一、囚徒困境故事讲的是,两个嫌疑犯作案后被警察抓住,分别关在不同的屋子里接受审讯。
警察知道两人有罪,但缺乏足够的证据。
警察告诉每个人:如果两人都抵赖,各判刑一年;如果两人都坦白,各判八年;如果两人中一个坦白而另一个抵赖,坦白的放出去,抵赖的判十年。
于是,每个囚徒都面临两种选择:坦白或抵赖。
然而,不管同伙选择什么,每个囚徒的最优选择是坦白:如果同伙抵赖、自己坦白的话放出去,不坦白的话判一年,坦白比不坦白好;如果同伙坦白、自己坦白的话判八年,不坦白的话判十年,坦白还是比不坦白好。
结果,两个嫌疑犯都选择坦白,各判刑八年。
如果两人都抵赖,各判一年,显然这个结果好。
但这个帕累托改进办不到,因为它不能满足人类的理性要求。
囚徒困境所反映出的深刻问题是,人类的个人理性有时能导致集体的非理性——聪明的人类会因自己的聪明而作茧自缚。
二、旅行者困境两个旅行者从一个以出产细瓷花瓶著称的地方旅行回来,他们都买了花瓶。
提取行李的时候,发现花瓶被摔坏了,于是他们向航空公司索赔。
航空公司知道花瓶的价格大概在八九十元的价位浮动,但是不知道两位旅客买的时候的确切价格是多少。
于是,航空公司请两位旅客在100元以内自己写下花瓶的价格。
如果两人写的一样,航空公司将认为他们讲真话,就按照他们写的数额赔偿;如果两人写的不一样,航空公司就认定写得低的旅客讲的是真话,并且原则上按这个低的价格赔偿,同时,航空公司对讲真话的旅客奖励2元,对讲假话的旅客罚款2元。
为了获取最大赔偿而言,本来甲乙双方最好的策略,就是都写100元,这样两人都能够获赔100元。
可是不,甲很聪明,他想:如果我少写1元变成99元,而乙会写100元,这样我将得到101元。
何乐而不为?所以他准备写99元。
可是乙更聪明,他算计到甲要算计他写99元,于是他准备写98元。
想不到甲还要更聪明一个层次,估计到乙要写98元来坑他,于是他准备写97元……大家知道,下象棋的时候,不是说要多“看”几步吗,“看”得越远,胜算越大。
博弈论经典案例

博弈论经典案例1. 恶魔的游戏 (Devil's game)这是一种博弈论的思想实验,假设有两个玩家 A 和 B 同时选择一个数字,如果两个数字相等,则 A 赢;如果两个数字不相等,则 B 赢。
问题在于,无论 A 和B 怎样选择,是否存在一种策略,使得 A 有必胜的把握?答案是不存在这样的必胜策略。
因为无论 A 和 B 怎样选择,都有 50% 的概率两个数字相等,这个概率不受选择策略的影响。
所以,这个游戏是一个“随机游戏”,任何一方都没有必胜策略。
2. 囚徒困境 (Prisoner's dilemma)囚徒困境是最著名的博弈论案例之一。
在这个游戏里,有两个人被抓住了,被判处各自坐牢20 年。
检察官给他们一个选择:如果两个人都认罪,那么各坐8 年;如果其中一个人认罪,而另一个人不认罪,那么认罪的人不用坐牢,而不认罪的人要坐 30 年;如果两个人都不认罪,那么各坐 20 年。
问题在于,两个人应该做什么选择才能最大化自己的利益?这个游戏的特殊之处在于,两个人之间的合作可以带来更大的利益,但是他们又互相不信任。
如果两个人都认罪,那么他们的利益是最小的,但是这么做可以避免另一个人的背叛,因此是一种安全策略。
如果两个人都不认罪,那么他们的利益也不是最大的,因为他们错失了合作的机会。
最终,由于信任问题,两个人可能会都选择认罪,而得到不太理想的结果。
3. 鸽子和猫 (Pigeon and Cat)这是一个有趣的案例。
假设有一个狭长的走廊,有一只鸽子和一只猫在两端等待。
如果鸽子朝左走,那么猫就会朝右走;如果鸽子朝右走,那么猫就会朝左走。
如果两只动物在同一个地方相遇,那么鸽子就会被吃掉。
问题在于,这个走廊有多长时,鸽子才有足够的概率逃脱?答案是 2/3。
如果走廊长度小于等于 2/3,那么猫可以直接守在鸽子的对面,而鸽子无法逃脱。
如果走廊长度大于 2/3,那么猫不得不冒着追错方向的风险前进,这就给了鸽子逃脱的机会。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
博弈论66个经典例子博弈论66个经典例子XXX:《博弈论三大经典案例》经典的囚徒困境是博弈论中最为著名的例子之一。
它由XXX和XXX在1950年提出,后来由顾问XXX以囚徒方式阐述,并命名为“囚徒困境”。
在这个困境中,警方逮捕了甲、乙两名嫌疑犯,但是没有足够的证据来指控他们。
警方将他们分开囚禁,并向他们提供以下相同的选择:如果一个人认罪并检举对方,而对方保持沉默,那么这个人将被立即释放,而对方将被判监10年。
如果两个人都保持沉默,那么他们都将被判监半年。
如果两个人都检举对方,那么他们都将被判监2年。
在这个博弈中,每个参与者都是利己的,即都寻求最大自身利益,而不关心另一参与者的利益。
参与者某一策略所得利益,如果在任何情况下都比其他策略要低的话,此策略称为“严格劣势”,理性的参与者绝不会选择。
另外,没有任何其他力量干预个人决策,参与者可完全按照自己意愿选择策略。
那么,囚徒应该选择哪种策略才能将自己的刑期缩短到最短呢?两名囚徒由于隔绝监禁,并不知道对方选择;而即使他们能交谈,还是未必能够尽信对方不会反口。
就个人的理性选择而言,检举背叛对方所得刑期,总比沉默要来得低。
因此,两个理性的囚徒都会选择背叛,这是两种策略中的支配性策略。
因此,这场博弈中唯一可能达到的纳什均衡,就是双方都背叛对方,结果二人同样服刑2年。
在博弈论中,智猪博弈是一个著名的例子。
猪圈里有一头大猪和一头小猪,猪圈的一头有猪食槽,另一头安装着控制猪食供应的按钮。
按一下按钮会有10个单位的猪食进槽,但是谁按按钮就会首先付出2个单位的成本。
若大猪先到槽边,大小猪吃到食物的收益比是9∶1;同时到槽边,收益比是7∶3;小猪先到槽边,收益比是6∶4.在两头猪都有智慧的前提下,最终结果是小猪选择等待。
实际上,小猪选择等待,让大猪去按控制按钮,而自己选择“坐船”或搭便车的原因很简单:在大猪选择行动的前提下,小猪也行动的话,小猪可得到1个单位的纯收益,而小猪等待的话,则可以获得4个单位的纯收益,等待优于行动;在大猪选择等待的前提下,小猪如果行动的话,小猪的收入将不抵成本,纯收益为-1单位,如果小猪也选择等待的话,那么小猪的收益为零,成本也为零,总之,等待还是要优于行动。
在小企业经营中,学会如何搭便车是一个精明的职业经理人最为基本的素质。
在某些时候,如果能够注意等待,让其他大的企业首先开发市场,是一种明智的选择。
这时候有所不为才能有所为!高明的管理者善于利用各种有利的条件来为自己服务。
搭便车实际上是提供给职业经理人面对每一项花费的另一种选择,对它的留意和研究可以给企业节省很多不必要的费用,从而使企业的管理和发展走上一个新的台阶。
这种现象在经济生活中十分常见,却很少为小企业的经理人所熟识。
斗鸡博弈实际上是一种误译。
XXX在美国口语中是懦夫之意,Chicken Game本应译成懦夫博弈。
不过这个错误并不算太严重,非要把chicken game叫作斗鸡博弈,也不是不可以。
试想有两人狭路相逢,每人有两个行动选择:一是退下来,一是进攻。
如果一方退下来,而对方没有退下来,对方获得胜利,这人就很丢面子;如果对方也退下来,双方则打个平手;如果自己没退下来,而对方退下来,自己则胜利,对方则失败;如果两人都前进,那么则两败俱伤。
因此,对每个人来说,最好的结果是,对方退下来,而自己不退。
赢利矩阵如下:甲/乙前进后退前进 (-2,-2) (1,-1)后退 (-1,1) (-1,-1)上表中的数字表示两个选手在博弈中的不同选择所对应的支付。
如果两个选手都选择“前进”,则两败俱伤,都会获得-2的支付;如果一个选手选择“前进”,另一个选择“后退”,则前进者获得1的支付,赢得了面子,而后退者获得-1的支付,输掉了面子,但是两者均“前进”受到的损失更大,都会获得-2的支付;如果两个选手都选择“后退”,则两者都输掉了面子,获得-1的支付。
当然,表中的数字只是相对的值。
这个博弈存在两个纯策略纳什均衡:一方前进,另一方后退;或一方后退,另一方前进。
但是关键是谁前进谁后退。
当然,该博弈也存在一个混合策略均衡,即大家随机选择前进或后退。
但相对而言,我们更关注纯策略均衡。
如果一个博弈有唯一的纳什均衡点,那么这个博弈是可预测的,即这个纳什均衡点就是事先知道的惟一的博弈结果。
但是如果一个博弈有多个纳什均衡,则要预测结果就必须附加另外的有关博弈的细节信息。
比如,在这个博弈中,谁前进谁后退,可能需要附加额外的细节信息才能做出判断。
选择坦白招供,原本对双方都有利的策略,即不招供从而均被释放,不会出现。
因此,两人都选择坦白的策略,最终被判8年的结果,挑战了纳什均衡首先对XXX的“看不见的手”的原理:按照XXX的理论,在市场经济中,每个人都从利己的目的出发,最终全社会达到利他的效果。
但是我们可以从“纳什均衡”中引出“看不见的手”原理的一个悖论:从利己的目的出发,结果损人不利己,既不利己也不利他。
智猪博弈是指在猪圈里有两头猪,一头大猪,一头小猪。
猪圈的一边有一个踏板,每踩一下踏板,远离踏板的猪圈的另一边的投食口就会落下少量的食物。
如果一只猪去踩踏板,另一只猪就有机会抢先吃到另一边落下的食物。
当小猪踩动踏板时,大猪会在小猪跑到食槽之前刚好吃光所有的食物;若是大猪踩动了踏板,则还有机会在小猪吃完落下的食物之前跑到食槽,争吃到另一半残羹。
那么,两只猪各会采取什么策略呢?答案是:小猪将选择“搭便车”策略,也就是舒舒服服地等在食槽边;而大猪则会不知疲倦地奔忙于踏板和食槽之间。
为什么会这样呢?因为小猪踩踏板将一无所获,不踩踏板反而能吃到食物。
对小猪而言,无论大猪是否踩动踏板,不踩踏板总是最好的选择。
反观大猪,已经明白XXX不会去踩动踏板,自己亲自去踩踏板总比不踩更好,所以只好自己亲力亲为。
博弈论是一门应用数学的分支,已成为经济学等多个学科的标准分析工具之一。
它主要研究激励结构间的相互作用,是研究具有斗争或竞争性质现象的数学理论和方法。
博弈论的应用范围广泛,包括生物学、经济学、国际关系、计算机科学、政治学、军事战略等多个领域。
在博弈论中,策略是指一局博弈中每个局中人可行的自始至终全局筹划的一个行动方案,而得失则是一局博弈结局时的结果。
每个局中人在一局博弈结束时的得失与该局中人自身所选择的策略以及全局中人所取定的一组策略有关。
博弈论中还有一个重要概念是次序,各博弈方的决策有先后之分,且一个博弈方要作不止一次的决策。
在实际应用中,博弈论可以帮助我们更好地制定经济管理的游戏规则。
例如,在公司的激励制度设计中,奖励力度过大会导致成本过高,而奖励力度过小又会降低员工的积极性。
因此,最好的激励机制设计应该是针对个人的奖励,既能节约成本,又能消除“搭便车”现象,实现有效的激励。
然而,许多人并未深入了解博弈论,却在实际应用中使用了小猪的策略。
例如,在股市中,等待庄家抬轿的散户;在产业市场中,等待出现具有赢利能力的新产品,然后大举仿制牟取暴利的游资;在公司中,分享成果但不创造效益的人等等。
因此,对于制订各种经济管理的游戏规则的人,必须深谙博弈论的原理,避免出现不必要的风险和损失。
囚徒困境反映了个人理性和集体理性的矛盾。
如果A和B都选择抵赖,各判刑1年,显然比都选择坦白各判刑8年好得多。
当然,A和B可以在被警察抓到之前订立一个攻守同盟,但这可能无用,因为它不构成纳什均衡,没有人有积极性遵守这个协定。
在海盗分金币问题中,5个强盗商定了分配金币的规则。
假设每个强盗都足够聪明且能做出理性的选择,那么强盗一该提出什么样的分配方案,才能使自己得到最大的收益?采用方向推导方法,如果1至3号强盗都被扔进了海里,只剩4号和5号,5号会投反对票让4号喂鲨鱼,以独吞全部金币。
所以,4号必须支持3号才能保命。
3号知道这一点,就会提出“100.”的分配方案,对4号、5号一毛不拔,将全部金币归为已有,因为他知道4号一无所获但还是会投赞成票,再加上自己一票,他的方案即可通过。
不过,2号推知3号的方案,就会提出“98.1,1”的方案,即放弃3号,而给予4号和5号各一枚金币。
由于该方案对于4号和5号来说比在3号分配时更为有利,他们将支持他而不希望他出局而由3号来分配。
这样,2号将拿走98枚金币。
同样,2号的方案也会被1号所洞悉,1号并将提出(97.1,2,)或(97.1.2)的方案,即放弃2号,而给3号一枚金币,同时给4号(或5号)2枚金币。
由于1号的这一方案对于3号和4号(或5号)来说,相比2号分配时更优,他们将投1号的赞成票,再加上1号自己的票,1号的方案可获通过,97枚金币可轻松落入囊中。
答案是:1号强盗分给3号1枚金币,分给4号或5号强盗2枚,自己独得97枚。
在“海盗分金”游戏中,分配者需要事先考虑挑战者的分配方案,并用最小的代价获取最大收益,拉拢挑战者分配方案中最不得意的人们。
两个旅行者因为花瓶被摔坏向航空公司索赔,航空公司要求他们写下花瓶的价格,如果两人写的一样,就按照他们写的数额赔偿;如果两人写的不一样,航空公司就认定写得低的旅客讲的是真话,并且原则上按这个低的价格赔偿,同时,航空公司对讲真话的旅客奖励2元,对讲假话的旅客罚款2元。
为了获取最大赔偿,甲乙双方最好的策略是都写100元,但甲想到如果他少写1元,而乙会写100元,这样他将得到101元,于是他准备写99元。
但乙更聪明,他算计到甲要算计他写99元,于是他准备写98元。
甲估计到乙要写98元来坑他,于是他准备写97元。
在理性的假设下,这个博弈唯一的纳什均衡是每个人都只写一两元的地步。
甲、乙、丙三个枪手准备决斗,甲枪法最好,十发八中;乙枪法次之,XXX;丙枪法最差,XXX。
合乎推理的结论是,枪法最糟糕的丙活下来的几率最大。
甲一定要对乙先开枪,因为乙对甲的威胁要比丙对甲的威胁更大,乙的最佳策略是第一枪瞄准甲。
一旦将甲干掉,乙和丙进行对决,乙胜算的概率自然大很多。
XXX A's。
XXX faces B.Let'XXX of the three gunmen in the first round of the shootout under the above :A: 24% (shot by B and C together at 40% X 60% = 24%)B: 20% (shot by A at 100% - 80% = 20%)C: 100% (no one shoots C)The survival probabilities of A。
B。
and C in the second round of the shootout can be XXX:1) Assuming A and C duel: A'XXX 60%。
and C's XXX 20%.2) Assuming B and C duel: B'XXX 60%。
