激光器的速率方程理论
激光原理-4.2 典型激光器的速率方程

f2 f1
B21
在辐射场 的作用下的总受激跃迁几率 W21 中,
分配在频率 处单位频带内的受激跃迁几率为:
W21 B21 B21 g% ,0
太原理工大学物理与光电工程学院
4、公式的修正
dn21 dt
sp
n2 A21
d
n2 A21g% , 0
d n2 A21
' '
'
此时有: '
激光器中的情形即 是如此!
0 '
太原理工大学物理与光电工程学院
g%
',
0
'
d
'
中的被积函数
只在辐射场中心频率 附近很窄范围内才不为零。
g% ',0 g% ,0
' ' 且:
因 ' 很小,则有:
'
0
' '
'
d
' 1
太原理工大学物理与光电工程学院
物理意义: 由于谱线加宽, 外来光的频率 并不 一定要精确等于原子发光的中心频率 0 才能产生 受激跃迁,而是主要在=0 附近的一个频率范围内 都能产生受激辐射。当ν偏离中心频率ν0时,跃 迁几率急剧下降。
太原理工大学物理与光电工程学院
6、受激辐射、受激吸收几率的其它表达形式
W21
B21 g% ,0
—吸收截面
中心频率处发射截面和吸收截面最大!
太原理工大学物理与光电工程学院
均匀加宽工作物质中心频率发射截面
21 0
A21 2
4
2
2 0
H
非均匀加宽工作物质中心频率发射截面
激光原理(4)-速率方程

= n2 ∫
+∞ −∞
A21 g (ν ,ν 0 )dν
= n2 A21
谱线加宽对单位时间内自发辐射跃迁的原子数没有影响 3. n2 数 个原子中单位时间内发生受激辐射跃迁的原子总
+∞ dn21 ( ) st = ∫ n2W21 (ν )dν −∞ dt
2. 线宽
1 = = g (ν 1 ,ν 0 ) g (ν 2 ,ν 0 ) g (ν 0 ,ν 0 ) 2
∆ν = ν 2 − ν 1
线宽:光谱线的宽度
FWHM = Full width at half maximum 半幅线宽
NJUPT
谱线加宽的机理
自然加宽(Natural broadening) 这种谱线加宽是不可避免的 (1) 经典理论 处于激发态的发光粒子,在自发辐射的发光过程中, 辐射功率不断衰减,导致光谱线有一定宽度。 经典电子理论:原子是一个正电中心和 一个负电中心组成的偶极子 γt − 2 i 2πν 0 t 0
③ 全量子理论。本质上是量子电动力学体系,其特点是,将激光场看成是 遵循量子化规律的光子群的集合,将与激光场发生作用的工作物质看成是遵循 量子力学规律的微观粒子的集合,在此基础上进而将两者看成是一个统一的体 系而加以量子理论处理。这种理论体系的主要优点,是它能对涉及到激光与物 质相互作用过程中出现的各种现象与效应,给出严格而又全面的物理描述;其 不足之处,是这种理论的数学处理过程过于繁杂而不便求解。基于全量子理论, 在一定前提下还可派生出一些往往是十分简洁有用的专门理论。如在忽略量子 化激光场的位相特性(或光子数目起伏)的前提下,可简化为速率方程理论, 能非常方便地用它来描述激光的产生、振荡与放大等过程中的粒子数输运和激 光功率方面的动态特性。
激光器速率方程

思路小结
• 爱因斯坦采用唯象法得到光和物质相互作用 的关系式 • 考虑线型函数后必要的修正:几率按频率的 分布函数 • 原子和准单色光相互作用 • 单模振荡速率方程组(三能级系统和四能级 系统) • 多模振荡速率方程组
R1、R2为单位体积中,在单位时间内激励至E1 、E2能级的粒子数(激励速率);τ1、τ2为E1 、E2能级的寿命; τ21为E2能级由于至E1能级 跃迁造成的有限寿命。
• In Figure we show the ground state 0 as well as the two laser levels 2 and 1 of a four-level laser system. The density of atoms pumped per unit time into level 2 is taken as R2, and that pumped into 1 is R1. Pumping into 1 is, of course, undesirable since it leads to a reduction of the inversion. In many practical situations it cannot be avoided. The actual decay lifetime of atoms in level 2 at the absence of any radiation field is taken as t2. This decay rate has a contribution tspont which is due to spontaneous (photon emitting)2→1 transition as well as to additional non-radiative relaxation from 2 to 1. The lifetime of atoms in level 1 is t1.
半导体激光器设计理论I._速率方程理论3_突变同型异质结的库莫(Kumer)理论
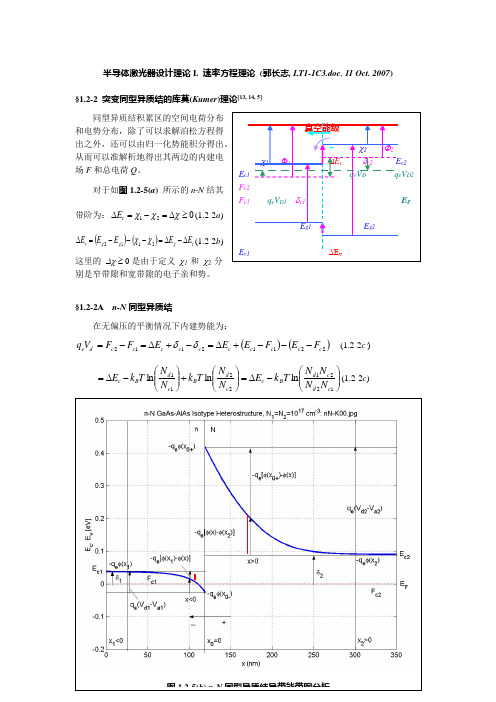
半导体激光器设计理论I. 速率方程理论 (郭长志, LT1-1C3.doc , 11 Oct. 2007)§1.2-2 突变同型异质结的库莫(Kumer )理论[13, 14, 5]同型异质结积累区的空间电荷分布和电势分布,除了可以求解泊松方程得 出之外,还可以由归一化势能积分得出。
从而可以准解析地得出其两边的内建电 场F 和总电荷Q 。
对于如图1.2-5(a ) 所示的n-N 结其 带阶为:021≥∆=-=∆χχχc E (1.2-2a )()()c g g g v E E E E E ∆-∆=---=∆2112χχ(1.2-2b )这里的 ∆χ ≥ 0是由于定义 χ1 和 χ2 分 别是窄带隙和宽带隙的电子亲和势。
§1.2-2A n-N 同型异质结在无偏压的平衡情况下内建势能为:2112c c c c c d e E F F V q δδ-+∆=-=()()2211c c c c c F E F E E ---+∆= (1.2-2c ')⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛-∆=2211ln ln c d B c d B c N N T k N N T k E ⎪⎪⎭⎫⎝⎛-∆=1221ln c d c d B c N N N N T k E (1.2-2c )真空能级- + χ2 Φ2χ1 Φ1 ∆E c δc2 E c2 E c1 q e V D q e V D2 F c2F c1 q e V D1 δc1 E FE g1 E g2E v1 ∆E v其中后两式采用了非简并统计近似。
由(1.2-2c ',b ),远离结区的带边之差分别为:()0211221<+∆-=∆-=∆--=-d e c d e c d e c c c c c V q E V q E V q E F F E E (1.2-2d )()()()v d e d e v d e g c c g c g c v v E V q V q E V q E E E E E E E E E ∆++=∆+=∆+-=---=-2121221121 (1.2-2e )电荷密度分布为:()[]p n N q x de +-=+ρ[]⎥⎥⎦⎤⎢⎢⎣⎡--=-≈-1T k E F d c d e d e B cc e N N N q n N q (1.2-2f ) 电势方程为:()+=-=dxd F dx dF F dx d dx d F εεεϕ,g ) 泊松方程为:()()⎥⎥⎦⎤⎢⎢⎣⎡-=-=→=-1022T k E F d c de B cc e N N N q x dx xd dx d εερϕε (1.2-2h ) n -和N -半导体接触并达到平衡时,其能带图将如图1.2-5(b )所示。
激光原理-4.2 典型激光器的速率方程

太原理工大学物理与光电工程学院
1、三能级系统的能级跃迁特点和跃迁示意图
W13
A31
S31
E3 泵浦上能级
S32(热弛豫)
E2
激光上能级 (亚稳态)
A21
S21
W21
W12
S31, A31 S32; S31 A31
E1(激泵光浦下下能能级级)
S21 A21
太原理工大学物理与光电工程学院
F
太原理工大学物理与光电工程学院
思考:分别求洛仑兹线型和高斯线型下简
化线型函数对应的等效谱宽 。
21 , 0
A21 2
8
h
2 0
g% ,0
21 l , 0 Nl 21 Nl 21 N
l
l
太原理工大学物理与光电工程学院
根据简化模型, 四能级多模速率方程
dn3 dt
n0W03
' '
'
此时有: '
激光器中的情形即 是如此!
0 '
太原理工大学物理与光电工程学院
g%
',
0
'
d
'
中的被积函数
只在辐射场中心频率 附近很窄范围内才不为零。
g% ',0 g% ,0
' ' 且:
因 ' 很小,则有:
'
0
' '
'
d
' 1
太原理工大学物理与光电工程学院
n2
f2 f1
n1
21
,
0
Nl
R1,R2为单位体积中,在单位时间内激励至 E1,E2能级的粒子数;τ1,τ2为E1, E2能级的寿命; τ21为E2能级由于至E1能级的跃迁造成的有限寿命。
激光原理(4)-速率方程

均匀加宽线型函数
∆ν H 2π
2
g H (ν ,ν 0 ) =
∆ν H 2 (ν − ν 0 ) + ( ) 2
1 1 1 ∆ν H = ( + ) = ∆ν N + ∆ν L 2π τ s τ L
一般气体激光器:
NJUPT
非 均 匀 加 宽
气体激光器的非均匀加宽往往只有多普勒加宽
gi (ν ,ν 0 ) = g D (ν ,ν 0 ) ∆ν i = ∆ν D
原子和准单色光辐射场的相互作用 在频率为 ν 的单色辐射场作用下,受激跃迁(吸收与发射)几率:
W21 = B21 g (ν ,ν 0 ) ρ W12 = B12 g (ν ,ν 0 ) ρ
g (ν ,ν 0 )
ρ = N l hν
发自发辐射线型函数 在v处的函数值 N l ——第 l 模式的光子数密度
x( t ) = x e
e
γ ——衰减因子(阻尼系数)
NJUPT
谱线加宽的机理
自然加宽(Natural broadening)
g N (ν ,ν 0 ) =
4 最大值: ν ν= = g (ν 0 ,ν 0 ) 0,
( )2 + 4π 2 (ν − ν 0 )2 2
γ
γ
γ 1 线宽:ν = g N (ν ,ν 0 ) ν 0 ± , g N (ν ,ν 0 ) = 4π 2
= n2 B21 ∫
+∞ −∞
g (ν ,ν 0 ) ρν dν
NJUPT
原子和准单色光辐射场的相互作用
∆ν ′ ∆ν
在 ∆ν ′ 作不变
g (ν ′,ν )
范围内: 近似看
激光原理与技术 第18讲 速率方程、小信号增益系数

当粒子从E2能级跃迁到E1 能级后,必须使其迅速的
回到基态,即要求S10较大, S10称为下能级抽空速率;
5
18.1 单模振荡速率方程
四能级 系统速 率方程
dn3
dt
n0W03
n3
S32 A30
dn2
dt
n2
g2 g1
n1 21
, 0
21
此式是一个具有普遍意义的公式;
10
18.2 小信号增益系数
2、小信号反转粒子数n
从前面得到的式子:
dn3
dt
n0W03
n3
S32 A30
G n 21可知G与
dn2
dt
n 21
, 0
cNl n2
A21 S21
n3 S32
n成正比,即n具 有的特性,G就具
dn0
而不涉及具体的激励及跃迁过程,而前面给出的速率方程则忽
略了激光下能级的激励过程。
7
连续激光器的增益和工作特性
增益特性是分析激光器振荡条件、模式竞争、输出功 率和激光放大器净增益系数的基础。 激光器可以运行于连续和脉冲工作方式,连续运行即 稳定运行,也就是各能级的粒子数目以及腔内的辐射 场有稳定分布,而增益饱和是形成稳定振荡的关键。 具有均匀加宽谱线和具有非均匀加宽谱线的工作物质 的增益饱和行为有很大差别,由此构成的激光器的工 作特性也有很大差别。
dt
n1 S10
n0W03
n3 A30
S10 W03 , S32 W03 ,
有,因此G的特性
n0 n1 n2 n3 n
n3 A30可忽略
同n紧密联系起来。
n如何求?
激光物理简答题

第一章激光器的基本原理1、问:产生激光的条件是什么?(戴大鹏)答: 1.受激辐射是激光产生的必要条件; 2.要形成激光,工作物质必须具有亚稳态能级,这是产生激光的第二个条件; 3.选择适当的物质,使其在亚稳态能级上的电子比低能级上的电子还多,即形成粒子束反转,这是形成激光的第三个条件;4.激光中开始产生的光子是自发辐射产生的,其频率和方向是杂乱无章的。
要使得频率单纯,方向集中,就必须有一个谐振腔,这是形成激光的第四个条件;5. 只有使光子在腔中振荡一次产生的光子数比损耗掉的光子要多得多,才能有放大作用,这是产生激光的第五个条件。
2、问:什么是粒子数反转?(钟双金)粒子数反转 (population inversion )是激光产生的前提。
两能级间受激辐射几率与两能级粒子数差有关。
在热平衡状态下,粒子数按能态的分布遵循玻耳兹曼分布律,这种情况得不到激光。
为了得到激光,就必须使高能级 E2 上的原子数目大于低能级 E1 上的原子数目,因为 E2 上的原子多,发生受激辐射,使光增强(也叫做光放大) 。
为了达到这个目的,必须设法把处于基态的原子大量激发到亚稳态 E2,处于高能级 E2 的原子数就可以大大超过处于低能级 E1 的原子数。
这样就在能级 E2 和 E1 之间实现了粒子数的反转。
实现粒子数反转的条件:通常实现粒子数反转要依靠两个以上的能级:低能级的粒子通过比高能级还要高一些的泵浦能级抽运到高能级。
一般可以用气体放电的办法来利用具有动能的电子去激发激光材料,称为电激励;也可用脉冲光源来照射光学谐振腔内的介质原子,称为光激励;还有热激励、化学激励等。
各种激发方式被形象化地称为泵浦或抽运。
为了使激光持续输出,必须不断地“泵浦”以补充高能级的粒子向下跃迁的消耗量。
3、什么叫纵模、横模?由谱线宽度和腔长来估算可能振荡的纵模数目答案:光场在腔内的纵向和横向分布分别叫做纵模和横模。
横模数目 n=谱线宽度/c纵模数目 n=谱线宽度/ (c/2*腔长 L)第二章激光器的速率方程理论答案:第三章 密度矩阵1:考虑衰减过程、原子的泵浦或激发过程,写出在初始光场为零时的光学布洛 赫方程并说明各项含义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
aNa
WDn
dNb dt
b
bNb
WDn
绝热近似
a ? b ?
dNa dNb 0 dt dt dn 0 dt
dNa dt
a
a Na
WDn 0
dNb dt
b
b Nb
WDn 0
D
D0
1 nW (1/ a 1/ b )
dn WDn n
dt
当激光器在阈值之上不太高时,激光光子数不太大,有
1. 在激励源的作用下,基态E0上的粒子被抽运到能级E3 上,其跃迁几率用W0表示。
2. 到达E3能级的粒子将主要以非辐射跃迁的形式极为迅 速地转移到激光上能级E2,其跃迁几率用S32表示。
3. 处在E2能级的粒子,能通过自发辐射、非辐射跃迁和 受激辐射,跃迁到激光下能级E1,其跃迁几率分别用A21, S21和W21表示。
dN1 dt
N2W21
N2 A21
N2S21 N1W12
N1S10
dN0 dt
N1S10
ቤተ መጻሕፍቲ ባይዱ
N0W0
dn dt
N2W21
N1W12
作业:求解以下速率方程
dne dt
ne
epnenp
dnp dt
epnenp
npnnnp
dnn dt
ne
npnnnp
ne , np , nn 分别为电子,正离子和负离子的密度
D 临界反转粒子数
D
D0
1 nW (1/ a 1/ b )
D0 a / a b / b
引入
R nW
Rs
(1/ a
1/
b
)1
a
a b
b
a b 2 ab
ab
1 (
2
a
b)
D D0 1 R / Rs
G G0 1 R / Rs
增益饱和
dn WDn n
dt
dN a dt
a
q qc / 2L
q
q1
q
c 2L
激光器阈值 增益饱和 均匀加宽 多模振荡
均匀加宽
dn WDn n
dt
W
c3
8 2
A21g( )
c3
1
W
2 2
A21
2
(0 )2 (V / 2)2
第 个模的光场与第 个原子作用的受激辐射速率为
W
c3
2 2
A21
2
(
2
)2
2
sin2 k z
考虑泵浦过程以及激光作用
D Na Nb W c
dn WDn n
dt
dN a dt
a
aNa
WDn
dNb dt
b
bNb
WDn
定态时
. ..
Na Nb n 0
WDn n 0
a a Na WDn 0 b b Nb WDn 0
得到
WD
定态工作的激光器的增益等于损耗
4. 处在E1能级的粒子,能通过受激吸收到达E2,或非辐 射跃迁到E0,其跃迁几率分别用 W12和S10表示。
各能级上的粒子数密度N0,N1,N2,N3如果变化? 光子数密度n如果变化?
速率方程:
dN3 dt
N0W0
S32 N3
dN2 dt
N3S32
N2W21 N2 A21 N2S21 N1W12
dt dD 2WDn dt
对于四能级系统的激光器
dn WDn n
dt
dD WDn dt
已知初始条件 t 0
n ni
D Di 在脉冲开始建立的时间内,光子数和反转粒子数为
n(t) niet ( WDi )
D(t)
Di{1
Wni
[1
et
]}
2.5 均匀加宽的激光器的多模振荡
纵模
谱线线型
小信号增益 自饱和参数
dn dt
(G0
)n
Cn2
G0 D0W
C W 2 D0 (1/ a 1/ b )
2.4 调Q激光器的速率方程
Q开关 损耗
光强 增益
t
调Q激光器的速率方程
dn WDn n
dt
略去泵浦项和衰减项
dNa dt
a
a Na
WDn
dNb dt
b
bNb
WDn
dn WDn n
为电子和中性分子的吸附速率系数
ep 电子与正离子的复合系数 np 正离子与负离子的复合系数
6.2 107s1 ep np 2.21013 m3 / s
整体为电中性
初值
ne nn np
ne (0) np (0) 1017 cm3
求 ne (t) ?
1. 激光器的速率方程
激发与衰减的速率方程(还未产生激光)
定态时
dNa dt
a
aNa
dNb dt
b
bNb
..
Na Nb 0
Ea
a
Eb
aNa
Na a / a
b
bNb
Nb b / b
只考虑泵浦过程而激光场为零时的定态反转粒子数,记为
D0 a / a b / b
激光器的速率方程
N0 ( a
b )] /
( a
b)
2
引入
||
1 2
(
a
b
)
dD dt
|| (D
D0 )
2WDn
dd dt
|| (d
d0 ) 2Wd n
dd
dt
|| (d d0 ) 2
W d n
对于四能级系统 E3 W0 E0
S32 W21 A21 S21
S10
E2 W12
E1
对于四能级系统
第 个模的光子数的速率方程是
dn
dt
n
W d n
单模振荡的粒子数方程
dNa dt
a
a Na
WDn
dNb dt
b
bNb
WDn
D Na Nb
N0 Na Nb
dD dt
(a
b )
1 2
N0 ( a
b)
1 2
D( a
b)
2WDn
n 0, dD 0 dt
D0
[(a
b )
1 2
