初三数学证明题(含答案)
初三几何证明练习题和答案

初三几何证明练习题和答案几何证明是初中数学中的重要内容,通过练习不同类型的几何证明题,可以帮助学生理解并掌握几何证明的基本方法与技巧。
本文将为大家提供一些初三几何证明的练习题和答案,希望对同学们的学习有所帮助。
1. 题目:已知ABCD是平行四边形,证明∠ABC + ∠ADC = 180°。
证明:解:连接AC,根据平行四边形的性质可知∠ADC = ∠ACB,所以要证明∠ABC + ∠ADC = 180°,只需证明∠ABC + ∠ACB = 180°。
由角的内外(对顶、同旁)定理可知∠ACB + ∠ABC = 180°,即∠ABC + ∠ACB = 180°。
所以,∠ABC + ∠ADC = 180°得证。
2. 题目:已知直角三角形ABC中,∠ACB = 90°,AC = 5cm,BC= 12cm,证明AB = 13cm。
证明:解:根据勾股定理可得AB² = AC² + BC²。
代入已知条件,即可得AB² = 5² + 12² = 25 + 144 = 169。
开方可得AB = 13cm。
所以,AB = 13cm得证。
3. 题目:已知直角三角形ABC中,∠ACB = 90°,AC = BC,证明∠ABC = 45°。
证明:解:连接AB,根据等腰直角三角形的性质可知∠ACB = ∠CAB。
所以,∠ABC = 180° - ∠ACB - ∠CAB = 180° - ∠ACB - ∠ACB = 180° - 2∠ACB。
由于∠ACB = 90°,代入得∠ABC = 180° - 2 × 90° = 0°。
所以,∠ABC = 0°,即∠ABC = 45°得证。
4. 题目:已知ABCD是一个平行四边形,E为AD的中点,证明BE平分∠CBD。
初三数学初中数学人教版试题答案及解析

初三数学初中数学人教版试题答案及解析1.如图,△ABC的边AB上有一点D,边BC的延长线上有一点E,且AD=CE,DE交AC于点F,试证明AB·DF=BC·EF.【答案】见解析【解析】要证AB·DF=BC·EF,即证.由于EF、DF是同一直线上的两条线段,为此,可考虑转化线段的比,即作DG∥CE交AC于点G,则,而AD=CE,所以,即只需证,很显然△ABC∽△ADG,从而问题得到证明.证明:如图,过点D作DG∥BC交AC于点G,∴△DGF∽△ECF,△ADG∽△ABC.∴,,∵AD=CE,∴,∴,即AB·DF=BC·EF.2. (2014广西玉林)△ABC与△A′B′C′是位似图形,且△ABC与△A′B′C′的位似比是1︰2.已知△ABC的面积是3,则△A′B′C′的面积是( )A.3B.6C.9D.12【答案】D【解析】∵△ABC与△A′B′C′是位似图形,且△ABC与△A′B′C′的位似比是1︰2,△ABC的面积是3,∴△ABC与△A′B′C′的面积比为1︰4,故△A′B′C′的面积是12.故选D.3.如图所示,点A的坐标为(4,3),C为OA上一点,且AC=2,AB⊥x轴于点B,CD⊥x轴于点D.则△AOB与△COD的相似比为________.【答案】5︰3【解析】因为,AC=2,所以OC=3,所以OA︰OC=5︰3,即△AOB与△COD的相似比为5︰3.4.如图所示,一段街道的两边缘所在直线分别为AB,PQ,并且AB∥PQ,建筑物的一端DE所在的直线MN⊥AB于点M,交PQ于点N,小亮从胜利街的A处,沿着AB的方向前进,小明一直站在点P的位置等候小亮.(1)请你在图中画出小亮恰好能看见小明时的视线,以及此时小亮所在的位置(用点C标出);(2)已知MN=20m,MD=8m,PN=24m,求(1)中的点C到胜利街口的距离CM.【答案】见解析【解析】解:(1)如图所示,CP为视线,点C为所求位置.(2)因为AB∥PQ,MN⊥AB于M,所以∠CMD=∠PND=90°.又∠CDM=∠PDN,所以△CDM∽△PDN,所以.因为MN=20m,MD=8M,PN=24m,所以,所以CM=16m,故点C到胜利街口的距离CM为16m.5.某市经济开发区建有B,C,D三个食品工厂,这三个工厂和开发区A处的自来水厂正好在一个矩形的四个顶点上,它们之间有公路相通,且AB=CD=900m,AD=BC=1700m,自来水公司已经修好一条自来水主管道AN,B,C两厂之间的公路与自来水主管道交于E处,EC=500m.若修建自来水主管道到各工厂的自来水管道由各厂负担,每米造价800元.(1)要使修建自来水管道的造价最低,这三个工厂的自来水管道路线应怎样设计?并在图中画出.(2)各厂所修建自来水管道的最低造价各是多少元?【答案】见解析【解析】解:(1)过B,C,D分别作AN的垂线BH,CF,DG,分别交AN于H,F,G,则BH,CF,DG即为所求的造价最低的管道路线.如图所示.(2)由题意,得BE=BC-CE=1700-500=1200(m),(m).因为∠ABE=∠CFE=90°,∠AEB=∠CEF,所以△ABE∽△CFE,所以,所以(m).同理易知△BHE∽△CFE,所以,所以(m).易知△ABE∽△DGA,所以,所以(m),所以B,C,D三厂所建自来水管道的最低造价分别是:720×800=576000(元),300×800=240000(元),1020×800=816000(元).6.(2014浙江绍兴)课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长是多少mm?小颖解得此题的答案为48mm,小颖善于反思,她又提出了如下的问题.(1)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成的,如图①,此时,这个矩形零件的两条边长又分别为多少mm?请你计算.(2)如果原题中所要加工的零件只是一个矩形,如图②,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.【答案】(1)矩形零件的两条边长分别为mm,mm(2)PN=60mm,PQ=40(mm)【解析】解:(1)设矩形的长PN=2ymm,则PQ=ymm,由条件可得△APN∽△ABC,∴,即,解得,∴(mm),答:这个矩形零件的两条边长分别为mm,mm.(2)设PN=xmm,由条件可得△APN∽△ABC,∴,即,解得.∴,∴S的最大值为2400mm2.此时PN=60mm,(mm)7.已知△ABC∽△A′B′C′,AB=5,AC=12,BC=13,A′B′=8,那么△A′B′C′的周长为________.【答案】48【解析】∵AB=5,AC=12,BC=13,∴△ABC的周长为5+12+13=30.∵△ABC∽△A′B′C′,∴,即.∴△A′B′C′的周长为48.8.某工程队接受一项开挖水渠的工程,所需时间y(天)与每天完成的工作量x(米/天)之间的函数关系如图所示.(1)共需开挖水渠多少米?(2)如果为了防汛工作的需要,必须在35天内完成该项任务,那么每天至少完成多少米?(保留一位小数)【答案】(1)共需开挖水渠1200米;(2)每天至少完成约34.3米。
初三数学精选试题及答案

初三数学精选试题及答案一、选择题1. 下列哪个数是无理数?A. 2B. πC. 0.5D. √4答案:B2. 如果一个三角形的两边长分别为3和4,那么第三边长x的取值范围是?A. 1 < x < 7B. 0 < x < 7C. 1 < x < 7 或 x > 7D. 0 < x < 7 或 x > 7答案:A3. 一个数的平方根是2,那么这个数是?A. 4B. -4C. 2D. -2答案:A二、填空题4. 计算:(2x - 3)(x + 4) = _______。
答案:2x² + 5x - 125. 一个圆的直径是14cm,那么它的半径是 _______ cm。
答案:7三、解答题6. 已知一个二次函数的图像经过点(1, 2)和(-1, 10),求这个二次函数的解析式。
答案:设二次函数的解析式为y = ax² + bx + c。
将点(1, 2)和(-1, 10)代入得到方程组:\[\begin{cases}a +b +c = 2 \\a -b +c = 10\end{cases}\]解得a = 4, b = -3, c = 1。
因此,二次函数的解析式为y = 4x² - 3x + 1。
7. 一个长方体的长、宽、高分别为a、b、c,已知长方体的体积为V,求长方体的表面积S。
答案:长方体的体积V = abc,表面积S = 2(ab + bc + ac)。
四、证明题8. 证明:勾股定理。
答案:在直角三角形ABC中,∠C为直角,设a、b为直角边,c为斜边。
根据勾股定理,有a² + b² = c²。
可以通过构造一个边长为a+b的正方形,将其划分为两个直角三角形和一个边长为c的正方形,从而证明a² + b² = c²。
五、应用题9. 一个水池的长、宽、高分别为4m、3m、2m,现在要将水池装满水,需要多少立方米的水?答案:水池的体积V = 长× 宽× 高= 4m × 3m × 2m = 24立方米。
初三数学圆试题答案及解析

初三数学圆试题答案及解析1.如图,AB是⊙O的直径,点C,D是半圆O的三等分点,过点C作⊙O的切线交AD的延长线于点E,过点D作DF⊥AB于点F,交⊙O于点H,连接DC,AC.(1)求证:∠AEC=90°;(2)试判断以点A,O,C,D为顶点的四边形的形状,并说明理由;(3)若DC=2,求DH的长.【答案】(1)证明见解析;(2)四边形AOCD为菱形;(3)DH=2.【解析】(1)连接OC,根据EC与⊙O切点C,则∠OCE=90°,由题意得,∠DAC=∠CAB,即可证明AE∥OC,则∠AEC+∠OCE=180°,从而得出∠AEC=90°;(2)四边形AOCD为菱形.由(1)得,则∠DCA=∠CAB可证明四边形AOCD是平行四边形,再由OA=OC,即可证明平行四边形AOCD是菱形(一组邻边相等的平行四边形是菱形);(3)连接OD.根据四边形AOCD为菱形,得△OAD是等边三角形,则∠AOD=60°,再由DH⊥AB于点F,AB为直径,在Rt△OFD中,根据sin∠AOD=,求得DH的长.试题解析:(1)连接OC,∵EC与⊙O切点C,∴OC⊥EC,∴∠OCE=90°,∵点CD是半圆O的三等分点,∴,∴∠DAC=∠CAB,∵OA=OC,∴∠CAB=∠OCA,∴∠DAC=∠OCA,∴AE∥OC(内错角相等,两直线平行)∴∠AEC+∠OCE=180°,∴∠AEC=90°;(2)四边形AOCD为菱形.理由是:∵,∴∠DCA=∠CAB,∴CD∥OA,又∵AE∥OC,∴四边形AOCD是平行四边形,∵OA=OC,∴平行四边形AOCD是菱形(一组邻边相等的平行四边形是菱形);(3)连接OD.∵四边形AOCD为菱形,∴OA=AD=DC=2,∵OA=OD,∴OA=OD=AD=2,∴△OAD是等边三角形,∴∠AOD=60°,∵DH⊥AB于点F,AB为直径,∴DH=2DF,在Rt△OFD中,sin∠AOD=,∴DF=ODsin∠AOD=2sin60°=,∴DH=2DF=2.【考点】1.切线的性质2.等边三角形的判定与性质3.菱形的判定与性质4.解直角三角形.2.如图,AB是⊙O的直径,点C是圆上一点,,则 °.【答案】20.【解析】∵AB是⊙O的直径,∴.∵OA=OC,,∴.∴.【考点】1.圆周角定理;2.等腰三角形的性质.3.已知一个圆锥的底面半径为3 cm,母线长为10 cm,则这个圆锥的侧面积为 ()A.15π cm2B.30π cm2C.60π cm2D.3cm2【答案】B【解析】圆锥的侧面积=π×3×10=30π cm2.故选B.4.如图,⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长是A.4cm B.6cm C.8cm D.10cm【答案】C.【解析】连接OB;∵CD=10cm,∴OC=5cm;∵OM:OC=3:5,∴OM=3cm;Rt△OCP中,OC=OA=5cm,OM=3cm;由勾股定理,得:所以AB=2AM=8cm,故选C.考点: 1.垂径定理;2.勾股定理.5.如图,点A是半圆上一个三等分点,点B是的中点,点P是直径MN上一动点,若⊙O的半径为1,则AP+BP的最小值是.【答案】.【解析】本题是要在MN上找一点P,使PA+PB的值最小,设A′是A关于MN的对称点,连接A′B,与MN的交点即为点P.此时PA+PB=A′B是最小值,可证△OA′B是等腰直角三角形,从而得出结果.试题解析:作点A关于MN的对称点A′,连接A′B,交MN于点P,则PA+PB最小,连接OA′,AA′.∵点A与A′关于MN对称,点A是半圆上的一个三等分点,∴∠A′ON=∠AON=60°,PA=PA′,∵点B是弧AN^的中点,∴∠BON=30°,∴∠A′OB=∠A′ON+∠BON=90°,又∵OA=OA′=1,∴A′B=.∴PA+PB=PA′+PB=A′B=.考点: 1.垂径定理;2.勾股定理;3.圆心角、弧、弦的关系;4.轴对称-最短路线问题.6.如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A→B→A方向运动,设运动时间为t(秒)(0≤t<3),连结EF,当t值为________秒时,△BEF是直角三角形.【答案】t=1或或.【解析】∵AB是⊙O的直径,∴∠C=90°.∵∠ABC=60°,∴∠A=30°.又BC=3cm,∴AB=6cm.则当0≤t<3时,即点E从A到B再到O(此时和O不重合).若△BEF是直角三角形,则当∠BFE=90°时,根据垂径定理,知点E与点O重合,即t=1;当∠BEF=90°时,则BE=BF=,此时点E走过的路程是或,则运动时间是s或s.故答案是t=1或或.【考点】圆周角定理.7.如图,边长为1的小正方形构成的网格中,⊙O的半径为1,则图中阴影部分两个小扇形的面积之和为(结果保留π)【答案】.【解析】如图,根据正方形和圆的对称性,上方的小扇形与下方的红色小扇形面积相等,所以图中阴影部分两个小扇形的面积之和为四分之一半径为1的圆的面积,即.【考点】1.网格问题;2. 正方形和圆的对称性;3. 扇形的面积;4.转换思想的应用.8.如图,从A地到B地有两条路可走,一条路是大半圆,另一条路是4个小半圆.有一天,一只猫和一只老鼠同时从A地到B地.老鼠见猫沿着大半圆行走,它不敢与猫同行(怕被猫吃掉),就沿着4个小半圆行走.假设猫和老鼠行走的速度相同,那么下列结论正确的是A.猫先到达B地;B.老鼠先到达B地;C.猫和老鼠同时到达B地;D.无法确定.【答案】C.【解析】以AB为直径的半圆的长是:•AB;设四个小半圆的直径分别是a,b,c,d,则a+b+c+d=AB.则老鼠行走的路径长是:a+b+c+d=(a+b+c+d)=•AB.故猫和老鼠行走的路径长相同.故选C.【考点】弧长公式.9.如图,已知在⊙O中,弦AB的长为8cm,半径为5 ㎝,过O作OC AB求点O与AB的距离.【答案】3cm.【解析】连接OA.根据垂径定理求得AC的长,再进一步根据勾股定理即可求得OC的长.试题解析:连接OA.如图:∵OC⊥AB,弦AB长为8cm,∴AC=4(cm).根据勾股定理,得OC=考点: 1.垂径定理;2.勾股定理.10.如图所示,内接于,,,则______.【答案】.【解析】由圆周角定理知:,由于,得到,所以:.故答案是.【考点】圆周角定理.11.如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.(1)求证:CD为⊙O的切线;(2)若DC+DA=6,⊙O的直径为10,求AB的长度.【答案】(1)详见解析;(2)6【解析】(1)连接OC,根据题意可证得∠CAD+∠DCA=90°,再根据角平分线的性质,得∠DCO=90°,则CD为⊙O的切线;(2)过O作OF⊥AB,则∠OCD=∠CDA=∠OFD=90°,得四边形OCDF为矩形,设AD=x,在Rt△AOF中,由勾股定理得(5-x)2+(6-x)2=25,从而求得x的值,由勾股定理得出AB的长.试题解析:(1)连接OC,∵OA=OC,∴∠OCA=∠OAC,∵AC平分∠PAE,∴∠DAC=∠CAO,∴∠DAC=∠OCA,∴PB∥OC,∵CD⊥PA,∴CD⊥OC,CO为⊙O半径,∴CD为⊙O的切线;(2)过O作OF⊥AB,垂足为F,∴∠OCD=∠CDA=∠OFD=90°,∴四边形DCOF为矩形,∴OC=FD,OF=CD.∵DC+DA=6,设AD=x,则OF=CD=6-x,∵⊙O的直径为10,∴DF=OC=5,∴AF=5-x,在Rt△AOF中,由勾股定理得AF2+OF2=OA2.即(5-x)2+(6-x)2=25,化简得x2-11x+18=0,解得x1=2,x2=9.∵CD=6-x大于0,故x=9舍去,∴x=2,从而AD=2,AF=5-2=3,∵OF⊥AB,由垂径定理知,F为AB的中点,∴AB=2AF=6.【考点】1.切线的判定和性质;2.勾股定理;3.矩形的判定和性质4.垂径定理12.如图MN=10是⊙O的直径,AE⊥MN于E,CF⊥MN于F,AE=4,CF=3,(1)在MN上找一点P,使PA+PC最短;(2)求出PA+PC最短的距离。
初三数学常考试题及答案

初三数学常考试题及答案一、选择题1. 已知一个二次函数的图像经过点A(-1,0)和点B(3,0),且函数的开口向上,则该二次函数的对称轴是()。
A. x = 0B. x = 1C. x = 2D. x = -1答案:B解析:二次函数的对称轴是其顶点的x坐标,由于函数图像经过点A(-1,0)和点B(3,0),且开口向上,根据二次函数的性质,对称轴是这两点x坐标的平均值,即x = (-1 + 3) / 2 = 1。
2. 下列哪个选项是不等式2x - 3 > 0的解集?A. x > 3/2B. x < 3/2C. x > 3D. x < 3答案:A解析:将不等式2x - 3 > 0移项得到2x > 3,再除以2得到x > 3/2,因此选项A是正确的。
二、填空题3. 计算绝对值:|-7| = _______。
答案:7解析:绝对值表示一个数距离0的距离,因此|-7|表示-7距离0的距离,即7。
4. 计算平方根:√9 = _______。
答案:±3解析:平方根是一个数的平方等于给定数的那个数,9的平方根是3,因为3的平方是9。
同时,-3的平方也是9,所以9的平方根是±3。
三、解答题5. 已知一个直角三角形的两条直角边长分别为3和4,求斜边的长度。
答案:5解析:根据勾股定理,直角三角形的斜边长度等于两直角边长度的平方和的平方根。
即斜边长度= √(3² + 4²) = √(9 + 16) = √25 = 5。
6. 某工厂生产一种零件,每件成本为10元,售价为15元,若该工厂希望获得的利润不低于1000元,问至少需要生产多少件零件?答案:100件解析:设需要生产的零件数量为x件,则总利润为(15 - 10)x = 5x元。
根据题意,5x ≥ 1000,解得x ≥ 200。
因此,至少需要生产200件零件。
四、证明题7. 证明:如果一个三角形的两边之和大于第三边,那么这个三角形是存在的。
初三圆的证明专题训练(答案)

初三圆的证明专题训练(答案)初三圆的证明专题训练(答案)下载试卷⽂档前说明⽂档:1、试题左侧⼆维码为该题⽬对应解析;2、请同学们独⽴解答题⽬,⽆法完成题⽬或者对题⽬有困惑的,扫描⼆维码查看解析,杜绝抄袭;3、只有⽼师通过组卷⽅式⽣成的⼆维码试卷,扫描出的解析页⾯才有“求⽼师讲解”按钮,菁优⽹原有的真题试卷、电⼦书上的⼆维码试卷扫出的页⾯⽆此按钮。
学⽣点击该按钮以后,下载试卷教师可查看被点击的相关统计数据。
4、⾃主组卷的教师使⽤该⼆维码试卷后,可在“菁优⽹->我的空间->我的收藏 ->我的下载”处点击重点。
5、在使⽤中有任何问题,欢迎在“意见反馈”提出意见和建议,感谢您对菁优⽹的⽀持。
图标查看学⽣扫描的⼆维码统计图表,以便确定讲解第1页 xx年04⽉19⽇九年级数学组的初中数学组卷 (扫描⼆维码可查看试题解析)⼀、解答题1、如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=∠CAB、求证:直线BF是⊙O的切线;若AB=5,sin∠CBF= ,求BC和BF的长、2、如图,四边形OABC是平⾏四边形,以O为圆⼼,OA为半径的圆交AB于点D,延长AO交⊙O于点E,连接CD,CE,若CE 是⊙O的切线,解答下列问题:求证:CD是⊙O的切线;若BC=3,CD=4,求平⾏四边形OABC的⾯积、3、如图,点D为⊙O上⼀点,点C在直径BA的延长线上,且∠CDA=∠CBD、判断直线CD和⊙O的位置关系,并说明理、过点B作⊙O的切线BE交直线CD于点E,若AC=2,⊙O的半径是3,求BE 的长、第2页4、如图,已知⊙O的半径为1,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于B点,四边形BCOE是平⾏四边形、求AD的长; BC是⊙O的切线吗?若是,给出证明;若不是,说明理、5、如图,BC是⊙O的直径,A是⊙O上⼀点,过点C作⊙O的切线,交BA的延长线于点D,取CD的中点E,AE的延长线与BC 的延长线交于点P、求证:AP是⊙O的切线; OC=CP,AB=6,求CD的长、6、如图,AB是⊙O的直径,AF是⊙O切线,CD是垂直于AB 的弦,垂⾜为E,过点C作DA的平⾏线与AF相交于点F,CD=四边形FADC是菱形; FC是⊙O的切线、,BE=2、求证:第3页7、已知:如图,AB是⊙O的直径,C是⊙O上⼀点,OD⊥B C 于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE、求证:BE与⊙O相切;连接AD并延长交BE于点F,若OB=9,sin∠ABC=,求BF的长、8、如图,AB是⊙O的直径,AC是弦,OD⊥AC于点D,过点A 作⊙O的切线AP,AP与OD的延长线交于点P,连接PC、BC、猜想:线段OD与BC有何数量和位置关系,并证明你的结论、求证:PC是⊙O的切线、9、如图,已知点C是以AB为直径的⊙O上⼀点,CH⊥AB于点H,过点B作⊙O的切线交直线AC于点D,点E为CH的中点,连接AE并延长交BD于点F,直线CF交AB的延长线于G、求证:AE?FD=AF?EC;求证:FC=FB;若FB=FE=2,求⊙O的半径r 的长、第4页10、已知:如图,点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A、求证:CD为⊙O的切线;过点C作CE⊥AB于E、若CE=2,cosD=,求AD的长、11、如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP、求证:直线CP是⊙O的切线、若BC=2 ,sin∠BCP= ,求点B 到AC的距离、在第的条件下,求△ACP的周长、12、如图,在△ABC中,BA=BC,以AB为直径作半圆⊙O,交AC于点D,过点D作DE⊥BC,垂⾜为点E、求证:DE为⊙O的切线;2 求证:BD=AB?BE、第5页13、如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上⼀点,且AC平分∠PAE,过C作CD丄PA,垂⾜为D、求证:CD为⊙O的切线;若DC+DA=6,⊙O的直径为10,求AB的长度、14、如图,已知△ABC,以BC为直径,O为圆⼼的半圆交AC 于点F,点E为的中点,连接BE交AC于点M,AD为△ABC的⾓平分线,且AD⊥BE,垂⾜为点H、求证:AB是半圆O的切线;若AB=3,BC=4,求BE的长、15、如图,D为⊙O上⼀点,点C在直径BA的延长线上,且∠CDA=∠CBD、求证:CD是⊙O的切线;过点B作⊙O的切线交CD的延长线于点E,若BC=6,tan∠CDA=,求BE的长、第6页16、如图所⽰,P是⊙O外⼀点,PA是⊙O的切线,A是切点,B是⊙O 上⼀点,且PA=PB,连接AO、BO、AB,并延长BO与切线PA相交于点Q、求证:PB是⊙O的切线;求证:AQ?PQ=OQ?BQ;设∠AOQ=α,若,OQ=15,求AB的长、17、如图,C是以AB为直径的⊙O上⼀点,过O作OE⊥AC于点E,过点A作⊙O的切线交OE的延长线于点F,连接CF并延长交BA的延长线于点P、求证:PC是⊙O的切线、若AF=1,OA=,求PC的长、第7页 xx年04⽉19⽇九年级数学组的初中数学组卷参考答案与试题解析⼀、解答题1、如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=∠CAB、求证:直线BF是⊙O的切线;若AB=5,sin∠CBF= ,求BC和BF的长、考点:切线的判定与性质;勾股定理;圆周⾓定理;相似三⾓形的判定与性质;解直⾓三⾓形、专题:⼏何综合题、分析:连接AE,利⽤直径所对的圆周⾓是直⾓,从⽽判定直⾓三⾓形,利⽤直⾓三⾓形两锐⾓相等得到直⾓,从⽽证明∠ABF= 90、利⽤已知条件证得△AGC∽△ABF,利⽤⽐例式求得线段的长即可、解答:证明:连接AE,∵AB是⊙O的直径,∴∠AEB=90,∴∠1+∠2=90、∵AB=AC,∴∠1=∠CAB、∵∠CBF=∠CAB,∴∠1=∠CBF ∴∠CBF+∠2=90 即∠ABF=90 ∵AB是⊙O的直径,∴直线BF是⊙O的切线、解:过点C作CG⊥AB于G、第8页∵sin∠CBF=∴sin∠1=,,∠1=∠CBF,∵在Rt△AEB中,∠AEB=90,AB=5,∴BE=AB?sin∠1=,∵AB=AC,∠AEB=90,∴BC=2BE=2,在Rt△ABE中,勾股定理得AE=∴sin∠2===,cos∠2===, =2,在Rt△CBG中,可求得GC=4,GB=2,∴AG=3,∵GC∥BF,∴△AGC∽△ABF,∴∴BF= = 点评:本题考查常见的⼏何题型,包括切线的判定,⾓的⼤⼩及线段长度的求法,要求学⽣掌握常见的解题⽅法,并能结合图形选择简单的⽅法解题、2、如图,四边形OABC是平⾏四边形,以O为圆⼼,OA为半径的圆交AB于点D,延长AO交⊙O于点E,连接CD,CE,若CE 是⊙O的切线,解答下列问题:求证:CD是⊙O的切线;若BC=3,CD=4,求平⾏四边形OABC的⾯积、考点:切线的判定与性质;全等三⾓形的判定与性质;平⾏四边形的性质、专题:证明题、第9页分析:连接OD,求出∠EOC=∠DOC,根据SAS推出△EOC≌△DOC,推出∠ODC=∠OEC=90,根据切线的判定推出即可;根据全等三⾓形的性质求出CE=CD=4,根据平⾏四边形性质求出OA=3,根据平⾏四边形的⾯积公式求出即可、解答:证明:连接OD,∵OD=OA,∴∠ODA=∠A,∵四边形OABC 是平⾏四边形,∴OC∥AB,∴∠EOC=∠A,∠COD=∠ODA,∴∠EOC=∠DOC,在△EOC和△DOC中∴△EOC≌△DOC,∴∠ODC=∠OEC=90,即OD⊥DC,∴CD是⊙O的切线;解:∵△EOC≌△DOC,∴CE=CD=4,∵四边形OABC是平⾏四边形,∴OA=BC=3,∴平⾏四边形OABC的⾯积S=OACE=34= 12、点评:本题考查了全等三⾓形的性质和判定,切线的判定,平⾏四边形的性质的应⽤,解此题的关键是推出△EOC≌△DOC、3、如图,点D为⊙O上⼀点,点C在直径BA的延长线上,且∠CDA=∠CBD、判断直线CD和⊙O的位置关系,并说明理、过点B作⊙O的切线BE交直线CD于点E,若AC=2,⊙O的半径是3,求BE 的长、第10页考点:切线的判定与性质、专题:⼏何图形问题、分析:连接OD,根据圆周⾓定理求出∠DAB+∠DBA=90,求出∠CDA+∠ADO=90,根据切线的判定推出即可;根据勾股定理求出DC,根据切线长定理求出DE=EB,根据勾股定理得出⽅程,求出⽅程的解即可、解答:解:直线CD和⊙O的位置关系是相切,理是:连接OD,∵AB是⊙O的直径,∴∠ADB=90,∴∠DAB+∠DBA=90,∵∠CDA=∠CBD,∴∠DAB+∠CDA=90,∵OD=OA,∴∠DAB=∠ADO,∴∠CDA+∠ADO=90,即OD⊥CE,∴直线CD是⊙O的切线,即直线CD和⊙O的位置关系是相切;∵AC=2,⊙O 的半径是3,∴OC=2+3=5,OD=3,在Rt△CDO中,勾股定理得:CD=4,∵CE切⊙O于D,EB切⊙O于B,∴DE=EB,∠CBE=90,设DE=EB=x,在Rt△CBE中,勾股定理得:CE=BE+BC,222则=x+,解得:x=6,即BE=6、222第11页点评:本题考查了切线的性质和判定,勾股定理,切线长定理,圆周⾓定理,等腰三⾓形的性质和判定的应⽤,题⽬⽐较典型,综合性⽐较强,难度适中、4、如图,已知⊙O的半径为1,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于B点,四边形BCOE是平⾏四边形、求AD的长; BC是⊙O的切线吗?若是,给出证明;若不是,说明理、考点:切线的判定与性质;直⾓三⾓形斜边上的中线;平⾏四边形的性质、专题:计算题、分析:连接BD,ED为圆O的直径,利⽤直径所对的圆周⾓为直⾓得到∠DBE为直⾓,BCOE为平⾏四边形,得到BC与OE平⾏,且BC=OE=1,在直⾓三⾓形ABD中,C为AD的中点,利⽤斜边上的中线等于斜边的⼀半求出AD的长即可;连接OB,BC与OD平⾏,BC=OD,得到四边形BCDO为平⾏四边形,AD为圆的切线,利⽤切线的性质得到OD垂直于AD,可得出四边形BCDO 为矩形,利⽤矩形的性质得到OB垂直于BC,即可得出BC为圆O的切线、解答:解:连接BD,∵DE是直径∴∠DBE=90,∵四边形BCOE为平⾏四边形,∴BC∥OE,BC=OE=1,在Rt△ABD中,C为AD的中点,∴BC=AD=1,则AD=2;是,理如下:如图,连接OB、∵BC∥OD,BC=OD,∴四边形BCDO为平⾏四边形,∵AD 为圆O的切线,∴OD⊥AD,第12页∴四边形BCDO为矩形,∴OB⊥BC,则BC为圆O 的切线、点评:此题考查了切线的判定与性质,直⾓三⾓形斜边上的中线性质,以及平⾏四边形的判定与性质,熟练掌握切线的判定与性质是解本题的关键、5、如图,BC是⊙O的直径,A是⊙O上⼀点,过点C作⊙O的切线,交BA的延长线于点D,取CD的中点E,AE的延长线与BC 的延长线交于点P、求证:AP是⊙O的切线; OC=CP,AB=6,求CD的长、考点:切线的判定与性质;解直⾓三⾓形、分析:连接AO,AC、欲证AP是⊙O的切线,只需证明OA⊥AP即可;利⽤中切线的性质在Rt△OAP中利⽤边⾓关系求得∠ACO=60、然后在Rt△BAC、Rt△ACD中利⽤余弦三⾓函数的定义知AC=2,CD=4、解答:证明:连接AO,AC、∵BC是⊙O的直径,∴∠BAC=∠CAD=90、∵E是CD的中点,∴CE=DE=AE、∴∠ECA=∠EAC、∵OA=OC,∴∠OAC=∠OCA、∵CD是⊙O的切线,∴CD⊥OC、∴∠ECA+∠OCA=90、∴∠EAC+∠OAC=90、∴OA⊥AP、∵A是⊙O上⼀点,∴AP是⊙O的切线;第13页解:知OA⊥AP、在Rt△OAP中,∵∠OAP=90,OC=CP=OA,即OP=2OA,∴sinP==,∴∠P=30、∴∠AOP=60、∵OC=OA,∴∠ACO=60、在Rt△BAC中,∵∠BAC=90,AB=6,∠ACO=60,∴AC==2,⼜∵在Rt△ACD中,∠CAD=90,∠ACD=90﹣∠ACO=30,∴CD===4、点评:本题考查了切线的判定与性质、解直⾓三⾓形、注意,切线的定义的运⽤,解题的关键是熟记特殊⾓的锐⾓三⾓函数值、6、如图,AB是⊙O的直径,AF是⊙O切线,CD是垂直于AB 的弦,垂⾜为E,过点C作DA的平⾏线与AF相交于点F,CD=,BE=2、求证:四边形FADC是菱形; FC是⊙O的切线、考点:切线的判定与性质;菱形的判定、专题:压轴题、分析:⾸先连接OC,垂径定理,可求得CE的长,⼜勾股定理,可求得半径OC的长,然后勾股定理求得AD的长,即可得AD=CD,易证得四边形FADC是平⾏四边形,继⽽证得四边形FADC是菱形;第14页⾸先连接OF,易证得△AFO≌△CFO,继⽽可证得FC 是⊙O的切线、解答:证明:连接OC,∵AB是⊙O的直径,CD⊥AB,∴CE=DE=CD=4=2,设OC=x,∵BE=2,∴OE=x﹣2,222在Rt△OCE中,OC=OE+CE,222∴x=+,解得:x=4,∴OA=OC=4,OE=2,∴AE=6,在Rt△AED中,AD=∴AD=CD,∵AF是⊙O切线,∴AF⊥AB,∵CD⊥AB,∴AF∥CD,∵CF∥AD,∴四边形FADC是平⾏四边形,∵AD=CD,∴平⾏四边形FADC是菱形;连接OF,AC,∵四边形FADC是菱形,∴FA=FC,∴∠FAC=∠FCA,∵AO=CO,∴∠OAC=∠OCA,∴∠FAC+∠OAC=∠FCA+∠OCA,即∠OCF=∠OAF=90,即OC⊥FC,∵点C在⊙O上,∴FC是⊙O的切线、 =4,第15页点评:此题考查了切线的判定与性质、菱形的判定与性质、垂径定理、勾股定理以及全等三⾓形的判定与性质、此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应⽤、7、已知:如图,AB是⊙O的直径,C是⊙O上⼀点,OD⊥BC 于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE、求证:BE与⊙O相切;连接AD并延长交BE于点F,若OB=9,sin∠ABC=,求BF的长、考点:切线的判定与性质;相似三⾓形的判定与性质;解直⾓三⾓形、专题:⼏何综合题、分析:连接OC,先证明△OCE≌△OBE,得出EB⊥OB,从⽽可证得结论、过点D作DH⊥AB,根据sin∠ABC=,可求出OD=6,OH=4,HB=5,然后△ADH∽△AFB,利⽤相似三⾓形的性质得出⽐例式即可解出BF的长、解答:证明:连接OC,第16页∵OD⊥BC,∴∠COE=∠BOE,在△O CE和△OBE 中,∵,∴△OCE≌△OBE,∴∠OBE=∠OCE=90,即OB⊥BE,∵OB 是⊙O半径,∴BE与⊙O相切、过点D作DH⊥AB,连接AD 并延长交BE于点F,∵∠DOH=∠BOD,∠DHO=∠BDO=90,∴△ODH∽△OBD,∴== ⼜∵sin∠ABC=,OB=9,∴OD=6,易得∠ABC=∠ODH,∴sin∠ODH=,即∴OH=4,∴DH==2, =,⼜∵△ADH∽△AFB,∴=,=,第17页∴FB=、点评:此题考查了切线的判定与性质、相似三⾓形的判定与性质,解答本题的关键是掌握切线的判定定理,在第⼆问的求解中,⼀定要注意相似三⾓形的性质的运⽤、8、如图,AB是⊙O的直径,AC是弦,OD⊥AC于点D,过点A 作⊙O的切线AP,AP与OD的延长线交于点P,连接PC、BC、猜想:线段OD与BC有何数量和位置关系,并证明你的结论、求证:PC是⊙O的切线、考点:切线的判定与性质;全等三⾓形的判定与性质;三⾓形中位线定理;圆周⾓定理、分析:根据垂径定理可以得到D是AC的中点,则OD是△ABC的中位线,根据三⾓形的中位线定理可以得到OD∥BC,CD=BC;连接OC,设OP与⊙O交于点E,可以证得△OAP≌△OCP,利⽤全等三⾓形的对应⾓相等,以及切线的性质定理可以得到:∠OCP=90,即OC⊥PC,即可等证、解答:猜想:OD∥BC,OD=BC、证明:∵OD⊥AC,∴AD=DC ∵AB是⊙O的直径,∴OA=OB…2分∴OD是△ABC的中位线,∴OD∥BC,OD=BC 证明:连接OC,设OP与⊙O交于点E、∵OD⊥AC,OD经过圆⼼O,∴,即∠AOE=∠COE 在△OAP和△OCP中,,∴△OAP≌△OCP,∴∠OCP=∠OAP第18页∵PA是⊙O的切线,∴∠OAP=90、∴∠OCP=90,即OC⊥PC ∴PC是⊙O的切线、点评:本题考查了切线的性质定理以及判定定理,三⾓形的中位线定理,证明圆的切线的问题常⽤的思路是根据切线的判定定理转化成证明垂直的问题、9、如图,已知点C是以AB为直径的⊙O上⼀点,CH⊥AB于点H,过点B作⊙O的切线交直线AC于点D,点E为CH的中点,连接AE并延长交BD于点F,直线CF交AB的延长线于G、求证:AE?FD=AF?EC;求证:FC=FB;若FB=FE=2,求⊙O的半径r 的长、考点:切线的判定与性质;等腰三⾓形的性质;等腰三⾓形的判定;直⾓三⾓形斜边上的中线;勾股定理;圆周⾓定理;相似三⾓形的判定与性质、专题:证明题;⼏何综合题;压轴题、分析:BD是⊙O的切线得出∠DBA=90,推出CH∥BD,证△AEC∽△AFD,得出⽐例式即可;连接OC,BC,证△AEC∽△AFD,△AHE∽△ABF,推出BF=DF,根据直⾓三⾓形斜边上中线性质得出CF=DF=BF即可;求出EF=FC,求出∠G=∠FAG,推出AF=FG,求出AB=BG,求出∠FCB=∠CAB22推出CG是⊙O切线,切割线定理得出=BGAG=2BG,在Rt△BFG中,2222勾股定理得出BG=FG﹣BF,推出FG﹣4FG﹣12=0,求出FG即可、解答:证明:∵BD是⊙O的切线,∴∠DBA=90,∵CH⊥AB,∴CH∥BD,第19页∴△AEC∽△AFD,∴=,∴AE?FD=AF?EC、证明:连接OC,BC,∵CH∥BD,∴△AEC∽△AFD,△AHE∽△ABF,∴=∴=,==,,∵CE=EH,∴BF=DF,∵AB为⊙O的直径,∴∠ACB=∠DCB=90,∵BF=DF,∴CF=DF=BF,即CF=BF、解:∵BF=CF=DF,EF=BF=2,∴EF=FC,∴∠FCE=∠FEC,∵∠AHE=∠CHG=90,∴∠FAH+∠AEH=90,∠G+∠GCH=90,∵∠AEH=∠CEF,∴∠G=∠FAG,∴AF=FG,∵FB⊥AG,∴AB=BG,∵BF切⊙O于B,∴∠FBC=∠CAB,∵OC=OA,CF=BF,∴∠FCB=∠FBC,∠OCA=∠OAC,∴∠FCB=∠CAB,∵∠ACB=90,∴∠ACO+∠BCO=90,∴∠FCB+∠BCO=90,即O C⊥CG,∴CG是⊙O切线,∵GBA是⊙O割线,AB=BG, FB=FE=2,22∴切割线定理得:=BGAG=2BG,第20页在Rt△BFG中,勾股定理得:BG=FG﹣BF,2∴FG﹣4FG﹣12=0,解得:FG=6,FG=﹣2,勾股定理得:AB=BG=∴⊙O的半径是2=4、,222 点评:本题考查了切线的性质和判定,相似三⾓形的性质和判定,等腰三⾓形的性质和判定,直⾓三⾓形斜边上中线的性质,圆周⾓定理,勾股定理等知识点的综合运⽤,题⽬综合性⽐较强,有⼀定的难度、10、已知:如图,点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A、求证:CD为⊙O的切线;过点C作CE⊥AB于E、若CE=2,cosD=,求AD的长、考点:切线的判定与性质;圆周⾓定理;解直⾓三⾓形、分析:先连接CO,根据AB是⊙O直径,得出∠1+∠OCB=90,再根据AO=CO,得出∠1=∠A,最后根据∠4=∠A,证出OC⊥CD,即可得出CD为⊙O的切线;根据OC⊥CD,得出∠3+∠D=90,再根据CE⊥AB,得出∠3+∠2=90,从⽽得出cos∠2=cosD,再在△OCD中根据余弦定理得出CO的值,最后根据⊙O的半径为,即可得出AD 的长、解答:证明:连接CO,∵AB是⊙O直径∴∠1+∠OCB=90,∵AO=CO,∴∠1=∠A、第21页∵∠4=∠A,∴∠4+∠OCB=90、即∠OCD=90、∴OC⊥CD、⼜∵OC是⊙O半径,∴CD为⊙O的切线、∵OC⊥CD于C,∴∠3+∠D=90、∵CE⊥AB于E,∴∠3+∠2=90、∴∠2=∠D、∴cos∠2=cosD,在△OCD中,∠OCD=90,∴cos∠2=,∵cosD=,CE=2,∴=,tanD=∴CO=,∴⊙O的半径为、 =,∴OD===, AD=、点评:本题考查了切线的判定与性质,要证某线是圆的切线,已知此线过圆上某点,连接圆⼼与这点,再证垂直即可,同时考查了三⾓函数的知识、11、如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP、求证:直线CP是⊙O的切线、第22页若BC=2,sin∠BCP=,求点B到AC的距离、在第的条件下,求△ACP的周长、考点:切线的判定与性质;等腰三⾓形的性质;勾股定理;相似三⾓形的判定与性质;解直⾓三⾓形、专题:⼏何综合题;压轴题、分析:根据∠ABC=∠ACB且∠CAB=2∠BCP,在△ABC中∠ABC+∠BAC+∠BCA=180,得到2∠BCP+2∠BCA=180,从⽽得到∠BCP+∠BCA=90,证得直线CP是⊙O的切线、作BD⊥AC于点D,得到BD∥PC,从⽽利⽤sin∠BCP=sin∠DBC===,求得DC=2,再根据勾股定理求得点B到AC的距离为4、先求出AC的长度,然后利⽤BD∥PC的⽐例线段关系求得CP的长度,再勾股定理求出AP的长度,从⽽求得△ACP的周长、解答:解:∵∠ABC=∠ACB且∠CAB=2∠BCP,在△ABC中,∠ABC+∠BAC+∠BCA=180 ∴2∠BCP+2∠BCA=180,∴∠BCP+∠BCA=90,⼜C点在直径上,∴直线CP是⊙O的切线、如右图,作BD⊥AC于点D,∵PC⊥AC ∴BD∥PC∴∠PCB=∠DBC ∵BC=2,sin∠BCP==, =,∴sin∠BCP=sin∠DBC=解得:DC=2,∴勾股定理得:BD=4,∴点B到AC的距离为4、如右图,连接AN,∵AC为直径,∴∠AN C=90,第23页∴Rt△ACN中,AC==5,⼜CD=2,∴AD=AC﹣CD=5﹣2=3、∵BD∥CP,∴∴CP=,、 ==20,,在Rt△ACP中,AP=AC+CP+AP=5++∴△ACP的周长为20、点评:本题考查了切线的判定与性质等知识,考查的知识点⽐较多,难度较⼤、12、如图,在△ABC中,BA=BC,以AB为直径作半圆⊙O,交AC于点D,过点D作DE⊥BC,垂⾜为点E、求证:DE为⊙O的切线;2 求证:BD=AB?BE、考点:切线的判定与性质;圆周⾓定理;相似三⾓形的判定与性质、专题:证明题、分析:连接OD、BD,根据圆周⾓定理可得∠ADB=90,继⽽得出点D是AC 中点,判断出OD是三⾓形ABC的中位线,利⽤中位线的性质得出∠ODE=90,这样可判断出结论、2根据题意可判断△BED∽△BDC,从⽽可得BD=BC?BE,将BC替换成AB即可第24页得出结论、解答:证明:连接OD、BD,则∠ADB=90,∵BA=BC,∴CD=AD,⼜∵AO=OB,∴OD是△ABC的中位线,∴OD∥BC,∵∠DEB=90,∴∠ODE=90,即OD⊥DE,故可得DE为⊙O的切线;。
初中数学证明题练习5套(含答案)
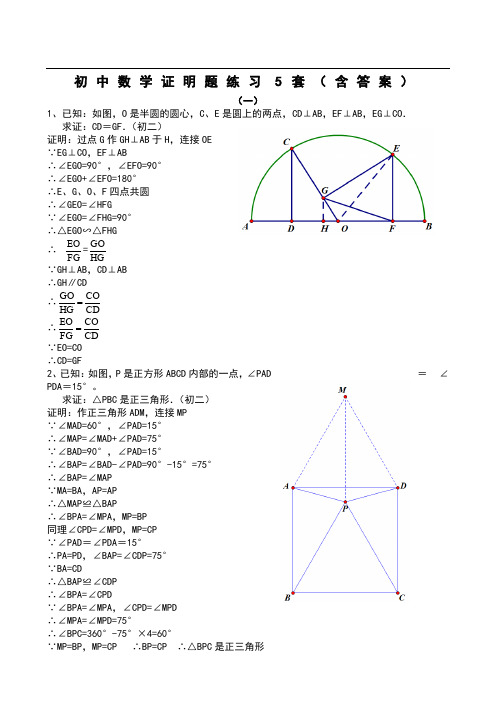
初中数学证明题练习5套(含答案)(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO .求证:CD =GF .(初二)证明:过点G 作GH ⊥AB 于H ,连接OE ∵EG ⊥CO ,EF ⊥AB∴∠EGO=90°,∠EFO=90° ∴∠EGO+∠EFO=180° ∴E 、G 、O 、F 四点共圆 ∴∠GEO=∠HFG∵∠EGO=∠FHG=90° ∴△EGO ∽△FHG∴FG EO =HGGO∵GH ⊥AB ,CD ⊥AB ∴GH ∥CD ∴CD CO HG GO = ∴CD CO FG EO = ∵EO=CO ∴CD=GF 2、已知:如图,P 是正方形ABCD 内部的一点,∠PAD =∠PDA =15°。
求证:△PBC 是正三角形.(初二) 证明:作正三角形ADM ,连接MP ∵∠MAD=60°,∠PAD=15° ∴∠MAP=∠MAD+∠PAD=75° ∵∠BAD=90°,∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75° ∴∠BAP=∠MAP ∵MA=BA ,AP=AP ∴△MAP ≌△BAP∴∠BPA=∠MPA ,MP=BP 同理∠CPD=∠MPD ,MP=CP ∵∠PAD =∠PDA =15°∴PA=PD ,∠BAP=∠CDP=75° ∵BA=CD∴△BAP ≌∠CDP ∴∠BPA=∠CPD∵∠BPA=∠MPA ,∠CPD=∠MPD ∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP ,MP=CP ∴BP=CP ∴△BPC 是正三角形3、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .证明:连接AC ,取AC 的中点G,连接NG 、MG ∵CN=DN ,CG=DG∴GN ∥AD ,GN=21AD∴∠DEN=∠GNM ∵AM=BM ,AG=CG∴GM ∥BC ,GM=21BC∴∠F=∠GMN ∵AD=BC ∴GN=GM∴∠GMN=∠GNM ∴∠DEN=∠F(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)证明:(1)延长AD 交圆于F ,连接BF ,过点O 作OG ⊥AD 于G∵OG ⊥AF ∴AG=FG ∵AB ⌒ =AB⌒ ∴∠F=∠ACB又AD ⊥BC ,BE ⊥AC ∴∠BHD+∠DBH=90° ∠ACB+∠DBH=90° ∴∠ACB=∠BHD ∴∠F=∠BHD∴BH=BF 又AD ⊥BC ∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2(GH+DH )=2GD 又AD ⊥BC ,OM ⊥BC ,OG ⊥AD ∴四边形OMDG 是矩形 ∴OM=GD ∴AH=2OM (2)连接OB 、OC∵∠BAC=60∴∠BOC=120° ∵OB=OC ,OM ⊥BC∴∠BOM=21∠BOC=60°∴∠OBM=30°∴BO=2OM由(1)知AH=2OM ∴AH=BO=AO2、设MN 是圆O 外一条直线,过O 作OA ⊥MN 于A ,自A 引圆的两条割线交圆O 于B 、C 及D 、E ,连接CD 并延长交MN 于Q ,连接EB 并延长交MN 于P. 求证:AP =AQ .证明:作点E 关于AG 的对称点F ,连接AF 、CF 、QF ∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF 即∠PAE=∠QAF∵E 、F 、C 、D 四点共圆 ∴∠AEF+∠FCQ=180° ∵EF ⊥AG ,PQ ⊥AG ∴EF ∥PQ∴∠PAF=∠AFE ∵AF=AE∴∠AFE=∠AEF ∴∠AEF=∠PAF ∵∠PAF+∠QAF=180° ∴∠FCQ=∠QAF ∴F 、C 、A 、Q 四点共圆 ∴∠AFQ=∠ACQ 又∠AEP=∠ACQ ∴∠AFQ=∠AEP3、设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)证明:作OF ⊥CD 于F ,OG ⊥BE 于G ,连接OP 、OQ 、OA 、AF 、AG ∵C 、D 、B 、E 四点共圆 ∴∠B=∠D ,∠E=∠C ∴△ABE ∽△ADC∴DF BG FD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF ∴∠AGB=∠AFD ∴∠AGE=∠AFC ∵AM=AN , ∴OA ⊥MN 又OG ⊥BE ,∴∠OAQ+∠OGQ=180° ∴O 、A 、Q 、E 四点共圆 ∴∠AOQ=∠AGE 同理∠AOP=∠AFC ∴∠AOQ=∠AOP在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQ又∠OAQ=∠OAP=90°,OA=OA ∴△OAQ ≌△OAP ∴AP=AQ4、如图,分别以△ABC 的AB 和AC 为一边,在△ABC 的外侧作正方形ABFG 和正方形ACDE ,点O 是DF 的中点,OP ⊥BC 求证:BC=2OP (初二)证明:分别过F 、A 、D 作直线BC 的垂线,垂足分别是L 、M 、N ∵OF=OD ,DN ∥OP ∥FL∴PN=PL∴OP 是梯形DFLN 的中位线 ∴DN+FL=2OP ∵ABFG 是正方形 ∴∠ABM+∠FBL=90° 又∠BFL+∠FBL=90° ∴∠ABM=∠BFL又∠FLB=∠BMA=90°,BF=AB ∴△BFL ≌△ABM ∴FL=BM同理△AMC ≌△CND ∴CM=DN∴BM+CN=FL+DN ∴BC=FL+DN=2OP(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)证明:连接BD 交AC 于O 。
初三数学上学期第三章证明(三)试题

1-3】(2004、重庆北碚,10分)如图1-已知四边形ABCD是等腰梯形,AB=DC,AD PB=PC.求证:PA=PD..已知:如图 l -3-6,E 是□MABCD 的对角线上的两点,A E =CF .求证:(1)△ABE ≌△CDF ;(2)BE ∥DF ..如图1-3-8,已知等腰梯形ABCD ,AD ∥为梯形内一点,且 EA=ED ,求证:EB=EC.在梯形ABCD中,AB∥CD,E、F、G、BC、CD、DA边上的中点,当梯形___________条件时,四边形EWIH是菱形.-3-13,边长为3的正方形ABCD.已知:如图1-3-l5,在矩形ABCD中,点边上,且BE=CF,AF、DE交于点AM=DM。
年新课标中考题一网打尽★★★)在备用图中,画出满足上述条件的图形,记为图⑵试用刻度尺在图1-3-17⑴⑵中量得AQ的长度,估计AQ、B Q间的关系,并填入下表.由上表可猜测AQ、BQ间的关系是______________.2)上述问)中的猜测AQ,BQ间的关系成立吗?3】(2005、温州,8分)如图1-3-ABCD是平行四边形,对角线AC、BD过点O画直线EF,分别交AD、BC于点OE=OF.【回顾4】(2005、南充,3分)如图1-3-21是边长为1的菱形ABCD对角线AC上一个动点绕正方形ABCDFC=HB:EC,顺次连结四边形ABCD各要使四边形EFGH为矩形,90°D、33【备考7】如图l-3-28,在□ABCD中,E为DC边的中点,AE交BD于点O.若SΔDOE= 9,则SΔAOB等于()A.18 B.27 C.36 D.45【备考10】如图l-3-30,在□ABCD中,AB=10AD=6,E是AD的中点,在AB上取一点F,使△CBF∽△CDE,则BF的长是()A.5 B.8.2 C.6.4 D.1.8【备考14】(动手操作题)在给定的锐角三角形中,求作一个正方形DEFG,使D、E落在F、G分别落在AC、AB边上,作法如下:第一步:画一个有三个顶点落在△ABC15】(探究题)如图l-3-35,矩形ABCDAC与BD的交点,过O点的直线EF与的延长线分别交于E、F.(l)求证:△BOE≌△)当EF与AC满足什么条件时,四边形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2010哈尔滨)5.如图,、是O 的切线,切点分别是A 、B ,如果∠P =60°,那么∠等于( ) DA.60°B.90°C.120°D.150°(2010台州市)如图,正方形边长为4,以为直径的半圆O 交对角线于E .则直线与⊙O 的位置关系是 ▲ ,阴影部分面积为(结果保留π) ▲ .答案:相切(2分),-6π(桂林2010)25.(本题满分10分)如图,⊙O 是△的外接圆,是⊙O 的切线,切点为F ,∥,连结交于E ,∠的平分线交于D ,连结.(1)证明:平分∠;(2)证明:=;(3)若=4,=3,求的长.25.(本题10 分)证明(1)连结 ∵是⊙O 的切线∴⊥ ……………1分∵∥ ,∴垂直平分 ………2分∴BF FC =∴平分∠ …………3分(2)证明:由(1)及题设条件可知∠1=∠2,∠4=∠3,∠5=∠2 ……………4分 ∴∠1+∠4=∠2+∠3∴∠1+∠4=∠5+∠3 ……………5分 ∠∠∴ ………………6分(3)解: 在△和△中∵∠5=∠2=∠1,∠∠F∴△∽△ ………………7分∴BF AFFE BF=, ……………8分 ∴2BF FE FA =⋅∴2BF FA FE= ……………………9分A B C D EOA BCDE O12345ABCD EO 12A BD OE (第15题)∴274944 FA==∴4974-214…………………10分(2010年兰州)6.已知两圆的半径R、r分别为方程0652=+-xx的两根,两圆的圆心距为1,两圆的位置关系是A.外离 B.内切 C.相交D.外切答案 B(2010年兰州)10.如图,正三角形的内切圆半径为1,那么这个正三角形的边长为A.2 B.3 C.3 D.23答案 D(2010年无锡)6.已知两圆内切,它们的半径分别为3和6,则这两圆的圆心距d的取值满足(▲)A.9d>B.9d=C.39d<<D.3d=答案 D(2010年无锡)27.(本题满分10分)如图,已知点(63,0),(0,6)A B,经过A、B的直线l以每秒1个单位的速度向下作匀速平移运动,与此同时,点P从点B出发,在直线l上以每秒1个单位的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.(1)用含t的代数式表示点P的坐标;(2)过O作⊥于C,过C作⊥x轴于D,问:t为何值时,以P为圆心、1为半径的圆与直线相切?并说明此时P与直线的位置关系.BAOPDClxy答案解:⑴作⊥于H ﹙如图1﹚,∵=6,=36,∴∠=30°∵=t ,∠=30°,∴=12t ,=t 23 ; ∴=t t t 236216-=--,∴P ﹙t 23,t 236-﹚⑵当⊙P 在左侧与直线相切时﹙如图2﹚, ∵=t -6,∠=30°∴=)6(21t -t 213-= ∴t t t 233213-=--=由1233=-t ,得34=t ﹙s ﹚,此时⊙P 与直线相割.当⊙P 在左侧与直线相切时﹙如图3﹚,323)6(21-=--=t t t由1323=-t ,得38=t ﹙s ﹚,此时⊙P 与直线相割. 综上,当s t 34=或s 38时,⊙P 与直线相切,⊙P 与直线相割.(2010年兰州)26.(本题满分10分)如图,已知是⊙O 的直径,点C 在⊙O 上,过点C 的直线与的延长线交于点P ,,∠2∠. (1)求证:是⊙O 的切线;(2)求证:21;(3)点M 是弧的中点,交于点N ,若4,求·的值. 答案(本题满分10分)解:(1)∵,∴∠∠∵∠2∠A ,∠2∠∴∠∠∠ ……………………………………………………1分∵是⊙O 的直径∴∠∠90° …………………………………………………2分∴∠∠90°,即⊥ …………………………………………3分∵是⊙O 的半径∴是⊙O 的切线 …………………………………………………4分(2)∵ ∴∠∠P ∴∠∠∠∠P ∵∠∠∠,∠∠∠∴∠∠ ……………………………………………5分∴∴21………………………………………………………6分(3)连接 ∵点M 是弧的中点∴弧弧 ∴∠∠ ………7分 ∵∠∠ ∴∠∠∵∠∠∴△∽△∴BM MNMC BM =∴2· ……………………8分∵是⊙O 的直径,弧弧 ∴∠90°∵4 ∴22 ………………………………………………………9分∴·2=8 ……………………………………………………10分(2010宁波市)6.两圆的半径分别为3和5,圆心距为7,则两圆的位置关系是 A .内切 B .相交 C .外切 D .外离13. (2010年金华) 如果半径为3的⊙O 1与半径为4的⊙O 2内切,那么两圆的圆心距O 1O 2= ▲ . 答案:1;6.(2010年长沙)已知⊙O 1、⊙O 2的半径分别是12r =、24r =,若两圆相交,则圆心距O 1O 2可能取的值是 B A .2 B .4C .6D .8(2010年成都)8.已知两圆的半径分别是4和6,圆心距为7,则这两圆的位置关系是( ) (A )相交 (B )外切 (C )外离 (D )内含 答案:A(2010年眉山)4.⊙O 1的半径为3,⊙O 2的半径为5,圆心距O 1O 2=2,这两圆的位置关系是A .外切B .相交C .内切D .内含 答案:C 毕节24.(本题12分)如图,已知是△中边上的高,以为直径的⊙O 分别交、于点E 、F ,点G 是的中点.求证:是⊙O 的切线.24.证明:(证法一)连接OE DE ,. 1分 ∵CD 是⊙O 的直径,∴90AED CED ∠=∠=.2分∵G 是AD 的中点,∴12EG AD DG ==. 4分∴12∠=∠. 6分 ∵34OE OD =∴∠=∠,. 8分 ∴1324∠+∠=∠+∠.即90OEG ODG ∠=∠=. 10分 ∴GE 是⊙O 的切线.12分(证法二)连接OE OG ,. 1分 ∵AG GD CO OD ==,, ∴OG AC ∥.2分 ∴1234∠=∠∠=∠,. 4分∵.∴∠2=∠4. ∴∠1=∠3.6分又OE OD OG OG ==,,∴OEG ODG △≌△. 8分 ∴90OEG ODG ∠=∠=. 10分 ∴GE 是⊙O 的切线.12分15.(10重庆潼南县)如图,在矩形中,6 ,4,⊙O 是以为直径的圆,则直线与⊙O 的位置关系是.相离1、(2010年杭州市)如图,台风中心位于点P ,并沿东北方向移动,已知台风移 动的速度为30千米/时,受影响区域的半径为200千米,B 市位 于点P 的北偏东75°方向上,距离点P 320千米处. (1) 说明本次台风会影响B 市;(2)求这次台风影响B 市的时间.答案:(1) 作⊥于点H , 在△中,由条件知, = 320, ∠ = 30°, 得 = 32030° = 160 < 200,∴ 本次台风会影响B 市. (2) 如图, 若台风中心移动到P 1时, 台风开始影响B 市, 台风中心移动到P 2时, 台风影响结束.由(1)得 = 160, 由条件得12 = 200,∴所以P 1P 2 = 222160200 =240, ∴台风影响的时间t =30240= 8(小时). (2010陕西省)23.如图,在△中∠90°,斜边的垂直平分线交与D点,交与E 点,连接(1)若是△的外接圆的切线,求∠C 的大小? (2)当12是求△外界圆的半径解:(1)∵ 垂直平分∴∠90°∴ 为△外接圆的直径 ∴的中点 O 即为圆心 连结又知是圆O 的切线 ∴∠∠90°在△ 中 E 斜边 的中点 ∴ ∴∠∠C 又∵∠2∠C ∴∠2∠90°∴∠30°(2)在△中= ∴12 ∵∠∠90° ∴△∽△ ∴AC BC DC EC =∴54△ 外接圆半径为58(2010年天津市)(22)(本小题8分)已知AB 是⊙O 的直径,AP 是⊙O 的切线,A 是切点,BP 与⊙O 交于点C . (Ⅰ)如图①,若2AB =,30P ∠=︒,求AP 的长(结果保留根号); (Ⅱ)如图②,若D 为AP 的中点,求证直线CD 是⊙O 的切线.解:(Ⅰ)∵ AB 是⊙O 的直径,AP 是切线,∴ 90BAP ∠=︒.在△PAB 中,2AB =,30P ∠=︒, ∴ 2224BP AB ==⨯=.由勾股定理,得AP ==..................5分 (Ⅱ)如图,连接OC 、AC ,∵ AB 是⊙O 的直径, ∴ 90BCA ∠=︒,有90ACP ∠=︒. 在△APC 中,D 为AP 的中点, ∴ 12CD AP AD ==. ∴ DAC DCA ∠=∠. 又 ∵OC OA =, ∴OAC OCA ∠=∠.A图①AD图②第(22)题AD∵ 90OAC DAC PAB ∠+∠=∠=︒, ∴ 90OCA DCA OCD ∠+∠=∠=︒. 即 OC CD ⊥.∴ 直线CD 是⊙O 的切线. ..............................8分(2010山西22.(本题8分)如图,四边形是平行四边形,以为直径的⊙O 经过点D ,E 是⊙O 上一点,且∠=45º.(1)试判断与⊙O 的关系,并说明理由.(2)若⊙O 的半径为3,=5 cm .求∠的正弦值.1.(2010宁德).如图,在8×4的方格(每个方格的边长为1个单位长)中,⊙A 的 半径为1,⊙B 的半径为2,将⊙A 由图示位置向右平移1个单位长后, ⊙A 与静止的⊙B 的位置关系是( ).DA.内含B.内切C.相交D.外切2.(2010黄冈)6分)如图,点P 为△的内心,延长交△的外接圆于D ,在延长线上有一点E ,满足2=·,求证:是⊙O 的切线.ABE(第22题)O第9题图 ABO 第22题图x yA B P C D第20题图证明:连结,并延长交⊙O 于F ,连结.∵2=·,∠=∠,∴△∽△,∴∠=∠E. 又∵∠=∠,∴∠=∠E ,∥,∴∠=∠=∠=∠,又∵∠=∠,∴∠=∠∠=∠∠=∠=90°,故是⊙O 的切线1.(2010山东济南)如图所示,菱形的顶点A 、B 在x 轴上,点A 在点B 的左侧,点D 在y 轴的正半轴上,∠60°,点A 的坐标为(-2,0).⑴求线段所在直线的函数表达式.⑵动点P 从点A 出发,以每秒1个单位长度的速度,按照A →D →C →B →A 的顺序在菱形的边上匀速运动一周,设运动时间为t 秒.求t 为何值时,以点P 为圆心、以1为半径的圆与对角线相切?答案:1 解:⑴∵点A 的坐标为(-2,0),∠60°,∠90°,∴·60°=23∴点D 的坐标为(0,3, ················································ 1分 设直线的函数表达式为y kx b =+,2023k b b -+=⎧⎪⎨=⎪⎩,解得323k b ⎧=⎪⎨=⎪⎩ ∴直线的函数表达式为323y x +. ····································· 3分 ⑵∵四边形是菱形, ∴∠∠60°,∴∠1=∠2=∠3=∠4=30°, 4, ················································································· 5分第22题图 如图所示:①点P 在上与相切时, 1=22, ∴t 1=2. ·············································································· 6分②点P 在上与相切时,2=22,∴2=6,∴t 2=6. ······························ 7分③点P 在上与相切时,3=22, ∴3=10,∴t 3=10. ······························ 8分④点P 在上与相切时, 4=22, ∴4=14, ∴t 4=14,∴当2、6、10、14时,以点P 为圆心、以1为半径的圆与对角线相切. ···············································9分1.(2010四川宜宾)若⊙O 的半径为4cm ,点A 到圆心O 的距离为3cm ,那么点A 与⊙O 的位置关系是( )A .点A 在圆内B .点A 在圆上C .点A 在圆外D .不能确定 2.(2010山东德州)已知三角形的三边长分别为3,4,5,则它的边与半径为1的圆的公共点个数所有可能的情 况是(A)0,1,2,3 (B)0,1,2,4 (C)0,1,2,3,4 (D)0,1,2,4,53.(2010山东德州)如图,在△中,,D 是中点,平分∠交于点E ,点O 是上一点,⊙O 过A 、E 两点, 交于点G ,交于点F . (1)求证:与⊙O 相切; (2)当∠120°时,求∠的度数.第20题图答案:1.A 2、C 3.(1)证明:连接,1分∵且D 是中点, ∴⊥. ∵平分∠, ∴∠∠.3分 ∵, ∴∠∠. ∴∠∠. ∴∥. ∴⊥.∴是⊙O 的切线.6分 (2)∵,∠120°,∴∠∠30°.7分 ∴∠ =60°.8分 ∴∠ =∠ =30°.9分 ∴∠ =30°.10分(2010年常州)6.若两圆的半径分别为2和3,圆心距为5,则两圆的位置关系为A.外离B.外切C.相交D.内切 (2010株洲市)15.两圆的圆心距5d =,它们的半径分别是一元二次方程2540x x -+=(2010河北省)23.(本小题满分10分)观察思考某种在同一平面进行传动的机械装置如图14-1,图14-2 是它的示意图.其工作原理是:滑块Q 在平直滑道l 上可以 左右滑动,在Q 滑动的过程中,连杆也随之运动,并且 带动连杆绕固定点O 摆动.在摆动过程中,两连杆的接点P 在以为半径的⊙O 上运动.数学兴趣小组为进一步研究其中所蕴含的数学知识,过点O 作 ⊥l 于点H ,并测得 =4分米, = 3分米, = 2分米.解决问题图14-1(1)点Q 与点O 间的最小距离是 分米;点Q 与点O 间的最大距离是 分米;点Q 在l 上滑到最左端的位置与滑到最右端位置间 的距离是 分米. (2)如图14-3,小明同学说:“当点Q 滑动到点H 的位置时,与⊙O 是相切的.”你认为他的判断对吗? 为什么?(3)①小丽同学发现:“当点P 运动到上时,点P 到l的距离最小.”事实上,还存在着点P 到l 距离最大 的位置,此时,点P 到l 的距离是 分米;②当绕点O 左右摆动时,所扫过的区域为扇形, 求这个扇形面积最大时圆心角的度数.解:(1)4 5 6;(2)不对.∵ = 2, = 3, = 4,且42≠32 + 22,即2≠2 + 2, ∴与不垂直.∴与⊙O 不相切. (3)① 3;②由①知,在⊙O 上存在点P ,P '到l 的距离为3,此时,将不能再向下转动,如图3.在绕点O 左右摆动过程中所扫过的最大扇形就是P '.连结P 'P ,交于点D .∵,P 'Q '均与l 垂直,且 =P '3Q '=,∴四边形Q 'P '是矩形.∴⊥P P ', P '. 由 = 2, = - = 1,得∠ = 60°.∴∠P ' = 120°.∴°.(2010河南)11.如图,切⊙O 于点A ,交⊙O 于点C ,点D 是⌒CmA 上异于点C 、A 的一点,若∠32°,则∠的度数是. 29°OmDCBA(第11题)l图14-3lQ图14-2l图3(2010广东中山)14.如图,与⊙O 相切于A点,弦⊥,垂足为C ,与⊙O 相交于D 点,已知2,4。
