直线插补与圆弧插补程序设计
实验一 逐点比较法圆弧和直线插补实验
Y B(xe,ye)
M(xm,ym)
Rm R
A(x0,y0)
O 图3 圆弧插补原理图 X
圆弧插补原理参见上图，对于第一象限逆圆，设圆弧的起点为 A(x0,y0)，终点为 B(xe,ye)， 圆弧半径为 R。加工点为 M(xm,ym)，它与圆心的距离为 Rm，则
（1）偏差计算
Fm
=
Rm2
− R2
=
xm2
p102=p102-p104 p101=p101+1 x-0.1 else p102=p102+p103 p101=p101+1 y0.1
；计算新的偏差值（Fi+1=Fi－ya） ；步数计数器加一 ；X方向进分别是（-0.1 -0.5 -1.0） ；偏差判别（若P102小于0表示刀具在直线下方） ；计算新的偏差值（Fi+1=Fi＋xa） ；步数计数器加一 ；Y方向进给分别是（0.1 0.5 1.0）
endif
endwhile
close
（3）根据直线插补编成格式，编写所给圆弧插补程序。 各组的圆弧的插补任务是： u 第一组：圆弧半径 50，第二象限顺圆；
第二组：圆弧半径 50，第二象限逆圆； 第三组：圆弧半径 60，第三象限顺圆； 第四组：圆弧半径 60，第三象限逆圆； 第五组：圆弧半径 70，第四象限顺圆； 第六组：圆弧半径 70，第四象限逆圆； open prog7 clear linear inc p101=0 p102=0 p103=0 p104=50 while(p101!>100) if(p102!<0) y0.5 p101=p101+1 p102=p102-2*p104+1 p104=p104-1 else -x0.5 p101=p101+1 p102=p102-2*p103+1 p103=103-1 endif endwhile close
G02 G03圆弧插补指令编程
圆弧终点坐标
确定圆心位置 进给速度
绝对值 X、Z 增量值 U、W 混合编程 X、W
α≤180° 用＋R 360°＞α＞180° 用－R
车床刀架前后置，圆弧顺逆不相同 刀架后置为标准，前置顺逆方向反
教学重点
圆弧顺、逆的判断和圆心位置R正负的确定。
教学难点
圆弧顺逆的判断。
主目录
能力训练题：
YHCNC实 习 卡 片
N78 G01X21
（切断工件 ）
N80 G00X100
（X轴方向退刀）
N82 Z120 M09 （回换刀点，切削液关 ）
N84 M30
（程序结束，返回第一条程序段 ）
四、典型零件加工演示
（用YHCNC仿真软件）
课堂小结
G02（G03）X（U）——Z（W）—— R—— F——
圆弧顺、逆
刀架后置 刀架前置
N62 T0404
（换切断刀）
N64 G00X82S400M03（点定位到φ82,正转,400r/min ）
N66 Z－44
（快速点定位到离端面44处）
N68 G01X75F200 （切槽 ）
N70 G00X82
（退刀到φ82 ）
N72 W2
（增量移动2mm ）
N74 G01X80F200 （进刀到φ80 ） N76 G？03X76W－2R2 （车R2圆弧 ）
模块 学习单元
FANUC-0i数控车
G02、G03圆弧插补 指令编程
考核项目 考 核 标 准 配 分 得 分 总 分
编程考核 任错一处扣5分 70
设 YHCNC 学时
软件操作考核 任错一处扣10分 30
备 仿真软件 件数 1 记 事
直线与圆弧插补实验
实验一工作台直线插补运动1 实验目的1.了解工作台直线插补原理和算法；2.在掌握直线插补原理的基础上实现平面绘图。
2 实验设备1.直线／旋转工作台；2.工作台控制箱一台；3.笔架夹持器、画笔及画板。
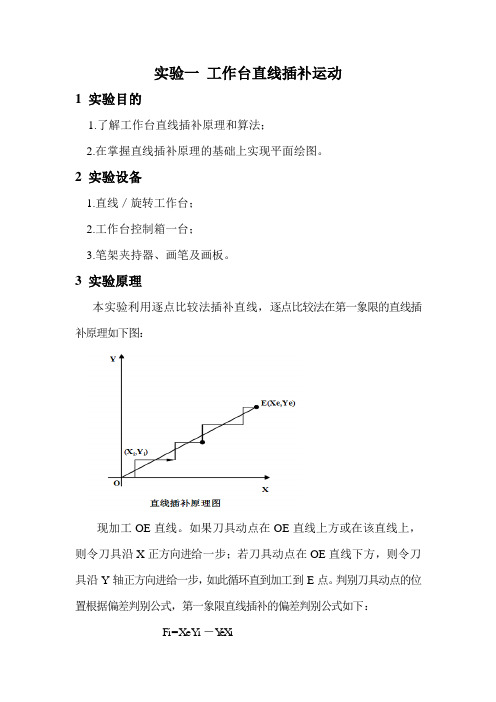
3 实验原理本实验利用逐点比较法插补直线，逐点比较法在第一象限的直线插补原理如下图：现加工OE直线。
如果刀具动点在OE直线上方或在该直线上，则令刀具沿X正方向进给一步；若刀具动点在OE直线下方，则令刀具沿Y轴正方向进给一步，如此循环直到加工到E点。
判别刀具动点的位置根据偏差判别公式，第一象限直线插补的偏差判别公式如下：Fi = Xe Y i －Y e X iFi≥0时，偏差判别公式为F i+1=F i -Ye 向X正方向进给Fi<0时，偏差判别公式为F i+1= F i＋Xe，向Y正方向进给逐点比较法插补节拍：逐点比较法插补需要四个节拍，即偏差判别、进给、偏差计算和终点判别。
4.4 实验步骤1.按使用说明书上将工作台组合成二自由度直线工作台，安装好笔架夹持器，放置好画板，并正确连接电缆。
2.安装上笔架夹持器及画笔，在桌面相应位置放好画板，使笔尖接触到画板；3.接通控制箱电源；4.启动计算机，运行工作台控制软件；5.在“工作台组合方式”界面中选择X直线工作台和Y直线工作台；6.单击主界面“工作台复位”按钮，工作台进行回零运动，运动完成后工作台处于零点位置；7.把画笔安装到笔架夹持器上，使笔尖接触到画板；8.单击“直线插补”按钮；9.加速方式选择“梯形”，插补目标X轴填写0，Y轴填写-30，点击“运动”按钮，画出一条直线，10.插补目标X轴填写30，Y轴填写30，点击“运动”，11.插补目标X轴填写30，Y轴填写0，点击“运动”，12.插补目标X轴填写0， Y轴填写0，点击“运动”，13.几条直线在画板上组成一个梯形，14.单击“工作台复位”按钮，使工作台回到零点位置；15.关闭计算机；16.断开控制箱电源。
直线插补与圆弧插补程序设计
直线插补与圆弧插补程序设计一．直线插补1.直线插补程序流程图直线插补程序流程图2.直线插补程序设计#include <stdio.h>#include <graphics.h>#include <stdlib.h>void cb_line(int x1, int y1, int x2, int y2) {int dx, dy, n, k, i, f;int x, y;dx = abs(x2-x1);dy = abs(y2-y1);n = dx + dy;if (x2 >= x1) {k = y2 >= y1 ? 1: 4;x = x1;y = y1;} else {k = y2 >= y1 ? 2: 3;x = x2;y = y2;}putpixel(x, y, 1);for (i = 0, f = 0; i < n; i++)if (f >= 0)switch (k) {case 1:putpixel(x++, y, 1);f -= dy;break;case 2:putpixel(x, y++, 1);f -= dx;break;case 3:putpixel(x--, y, 1);f -= dy;break;case 4:putpixel(x, y--, 1);f -= dx;break;}elseswitch (k) {case 1:putpixel(x, y++, 1);f += dx;break;case 2:putpixel(x--, y, 1);f += dy;break;case 3:putpixel(x, y--, 1);f += dx;break;case 4:putpixel(x++, y, 1);f += dy;break;}}int main(){cb_line(0,0,15,20); /* <--- you forgot ; here */return 0;}二.圆弧插补2.1.四象限圆弧插补程序流程图2.1四象限圆弧插补程序设计#include <stdio.h>#include <math.h>int ArcXY(double dfx0,double dfy0,double dfrx, double dfry,int angle); int symbol(double number);main(){ArcXY(0,0,-3,5,360);getch();}int ArcXY(double dfx0,double dfy0,double dfrx, double dfry,int angle) {FILE *f1;double i,j,dx,dy,dfr,x,y,ang,step,f = 0.01;int flag,tempx,tempy,statex,statey,direction = 1;dfr = sqrt((dfrx - dfx0) * (dfrx - dfx0) + (dfry - dfy0) * (dfry - dfy0));if(dfx0 == 0){dfx0 = 1;dfrx = dfrx + 1;statex =1;}if(dfy0 == 0){dfy0 = 1;dfry = dfry + 1;statey =1;}dfrx = 2 * dfx0 - dfrx;i = dfx0 - dfrx;j = dfy0 - dfry;x = dfx0 ;y = dfy0 ;step = ang = 180 * 2 * asin(f/(2*dfr))/3.1415926;if(((dfx0 > 0) && (dfy0 > 0)) || ((dfx0 < 0) && (dfy0 < 0))){flag = direction;}if(((dfx0 < 0) && (dfy0 > 0)) || ((dfx0 > 0) && (dfy0 < 0))) {flag = -direction;}f1=fopen("c:\\c.txt","w+");if(statex ==1){x = x - 1;}if(statey ==1){y = y - 1;}fprintf(f1,"%f,",x);fprintf(f1,"%f\n",y);while(ang < angle){dx = f * (j + flag*(f * i)/(2 * dfr))/dfr;dy = f * (i - flag*(f * j)/(2 * dfr))/dfr;tempx = symbol(x);tempy = symbol(y);x = x + dx;y = y + dy;fprintf(f1,"%f,",x);fprintf(f1,"%f\n",y);if( (tempx !=symbol(x)) || (tempy != symbol(y)) ){flag = -flag;}i = i - dx;j = j + dy;ang = ang + step;}return 0;}int symbol(double number) {if(number > 0){return 1;}else{return -1;}}。
数控实验报告(模板)
实验三数控插补原理与实现一、实验目的（1）了解直线插补、圆弧插补原理和实现方法。
（2）利用运动控制器基本控制指令实现直线插补和圆弧插补。
（3）掌握运动控制卡的编程方法。
二、实验设备（1）两维直线运动数控教学实验系统一套。
（2） MPC02运动控制卡一块。
（3）辅助设备：台式计算机一台，安装Windows 98或以上操作系统，安装VC++ 或VB 开发环境。
三、实验内容根据插补计算原理，利用运动控制器基本位臵控制指令，在VC++或VB环境下编写插补程序，并在X-Y平台上进行验证。
四、实验步骤1. 直线插补根据逐点比较法直线插补原理进行编程，然后编译运行，并按图2.6给定坐标进行实验，观察画笔运动轨迹是否如图2.6所示。
图2.6 直线插补运动轨迹设有一工件，其廓形为三角形。
建立工件X-Y坐标系如图2.6所示。
以点A为坐标原点，则点1的坐标为(20, 0)，点2的坐标为(45, 50)，点3的坐标为(70, 0)。
设在X-Y运动平台归零时，画笔在A点。
此时，X-Y运动平台的坐标系与工件坐标系是一致的。
画笔运动轨迹如图2.6所示。
2. 圆弧插补根据逐点比较法圆弧插补原理进行编程，并编译运行。
按图2.7给定坐标进行实验，观察画笔运动轨迹是否如图2.7所示。
图2.7 圆弧插补运动轨迹设有一工件，如图 2.7所示，其廓形曲线由两段圆弧组成，两段圆弧半径分别为40和20。
设在X-Y运动平台归零时，画笔在A点。
在X-Y运动平台坐标系中，坐标原点在A点。
工件上的1、2、3点坐标分别为：点1(0,15)、点2(40,15)、点3(60,15)。
画笔运动轨迹如图2.7所示。
五、实验总结（1）简述常见的插补算法。
（2）根据实验分析逐点插补算法的精度和局限性。
实验五数控代码编程一、实验目的了解从运动控制器的基本控制指令到数控代码库的实现过程。
二、实验设备（1）两维直线运动数控教学实验系统，三维直线运动数控铣教学实验系统各一套。
数控系统中直线与圆弧插补算法的探讨
数控系统中直线与圆弧插补算法的探讨导言数控系统是一种广泛应用于机械加工领域的自动化控制系统。
其中，直线与圆弧插补算法是数控系统中的核心算法之一。
本文将深入探讨直线与圆弧插补算法的原理、方法以及应用。
直线插补算法直线插补是数控系统中最基本的插补运动方式之一。
它的目标是实现两个给定点之间的直线路径。
在直线插补算法中，我们需要考虑以下几个方面：1.起始点和终点的坐标：为了实现直线插补，我们需要明确起始点和终点的空间坐标。
2.运动速度和加速度：直线插补需要考虑加速度和速度的变化，以实现平滑而又快速的运动。
3.插补精度：直线插补的精度决定了运动轨迹的平滑度和误差控制的能力。
直线插补算法的基本思路是将插补路径划分为多个小段，然后通过控制每个小段的加速度和速度，以达到平滑运动的效果。
常用的直线插补算法包括线性插补算法和B样条插补算法。
线性插补算法线性插补算法是最简单和最基础的直线插补算法之一。
它假设插补路径是一条直线，并根据起始点和终点的坐标以及插补周期，计算出每个插补周期点的位置。
线性插补算法的优点是计算简单，实现容易，但缺点是对于曲线路径的插补效果较差。
B样条插补算法B样条插补算法是一种基于样条曲线的插补算法。
在B样条插补算法中，我们将插补路径表示为一条样条曲线，并通过控制样条曲线的控制点来实现运动轨迹的控制。
B样条插补算法的优点是对曲线路径的插补效果较好，但是计算复杂度较高。
圆弧插补算法除了直线插补，圆弧插补算法也是数控系统中常用的插补方式之一。
圆弧插补用于实现两个给定点之间的圆弧路径。
与直线插补类似，圆弧插补算法也需要考虑起始点和终点的坐标、运动速度和加速度等因素。
圆弧插补算法的基本思路是通过指定起始点、终点和圆心，计算出圆弧路径上每个插补点的位置。
常用的圆弧插补算法包括圆心法和半径法。
圆心法圆心法是一种基于圆心坐标的圆弧插补算法。
在圆心法中，我们通过指定起始点、终点和圆心的坐标，计算出圆弧路径上每个插补点的位置。
数控系统中直线与圆弧插补算法的探讨
数控系统中直线与圆弧插补算法的探讨
数控系统中直线与圆弧插补算法的探讨
数控系统是现代制造业中不可或缺的一部分，它的主要功能是将数字
化的指令转化为机器能够理解的运动控制信号，从而实现对机器的精
确控制。
在数控系统中，直线与圆弧插补算法是非常重要的一部分，
它们决定了机器在加工过程中的精度和效率。
直线插补算法是数控系统中最简单的插补算法之一，它的原理是将直
线分割成若干个小段，然后通过控制机器在每个小段上的运动来实现
整条直线的加工。
在实际应用中，直线插补算法的精度和效率都非常高，因此被广泛应用于各种数控加工设备中。
与直线插补算法相比，圆弧插补算法则更加复杂。
圆弧插补算法的原
理是将圆弧分割成若干个小段，然后通过控制机器在每个小段上的运
动来实现整个圆弧的加工。
在实际应用中，圆弧插补算法的精度和效
率都非常高，但是由于其复杂性，需要更高的计算能力和更复杂的控
制算法来实现。
在实际应用中，直线和圆弧插补算法经常会同时使用。
例如，在加工
一个复杂的零件时，可能需要使用直线插补算法来加工一些直线部分，
而使用圆弧插补算法来加工一些曲线部分。
在这种情况下，数控系统需要能够自动切换不同的插补算法，并且保证整个加工过程的精度和效率。
总的来说，直线和圆弧插补算法是数控系统中非常重要的一部分，它们决定了机器在加工过程中的精度和效率。
在实际应用中，直线和圆弧插补算法经常会同时使用，数控系统需要能够自动切换不同的插补算法，并且保证整个加工过程的精度和效率。
3.5.2 直线和圆弧DDA法插补原理
JY-1 JY 5
5 5 5 5-1=4 4-1=3 3-1=2 2-1=1
终点判 别 NX NY
+Y +Y +Y -X,+Y 10-8=2 -X,+Y 10-8=2 -X -X 12-8=4 9-8=1
10-8=2 12-8=4 9-8=1 11-8=3 11-8=3
2012-5-30
数字积分法直线插补运算过程（前五步）
累加 次数 X积分器 Y积分器 终点计 数 器 JE 000
JRX+JVX
1 0+101=101
溢出 △X 0 1
0 1 1
JRY+JVY
0+010=010
溢 出 △Y 0 0
0 1 0
2
3 4 5
101+101=010
010+101=111 111+101=100 100+101=001
一 插补的基本概念； 二 插补方法的分类； 三 逐点比较法； 四 数字积分法； 五 数据采样法（时间分割法）； 六 插补算法中的速度处理。
2012-5-30
四 数字积分法插补
特点：
易于实现多坐标联动插补 Y 1 数字积分法的工作原理 如右图，函数在[t0 , tn ]的定 积分，即为函数在该区间 的面积： O t0 t1 t2 如果从t=0开始，取自变量 t的一系列等间隔值为△t， 当△t足够小时，可得
2 设圆弧AB为第一象限逆圆弧，起点A (3,0),终点为B(0,3)，用DDA法加工圆弧 AB。
2012-5-30
逐点比较法第一象限直线圆弧插补
逐点比较法第一象限直线，圆弧插补编程逐点比较法是以折线来逼近给定的轨迹，就是每走一步控制系统都要将加工点与给定的图形轨迹相比较，以决定下一步进给的方向，使之逼近加工轨迹。
逐点比较法以折线来逼近直线或圆弧，其最大的偏差不超过一个最小设定单位。
只要将脉冲当量取得足够小，就可以达到精度要求。
逐点比较插补法在脉冲当量为0.01mm，系统进给速度小于3000mm/min时，能很好的满足要求。
一、逐点比较法直线插补如下图所示设直线 oA 为第一象限的直线，起点为坐标原点o (0 ， 0) ，终点坐标为， A( ) ， P() 为加工点。
若 P 点正好处在直线 oA 上，由相似三角形关系则有即点在直线 oA 上方 ( 严格为直线 oA 与 y 轴正向所包围的区域 ) ，则有即若 P 点在直线 oA 下方 ( 严格为直线 oA 与 x 轴正向所包围的区域 ) ，则有图 3 — 1 逐点比较法第一象限直线插补即令则有：①如，则点 P 在直线 oA 上，既可向 +x 方向进给一步，也可向 +y 方向进给一步；②如，则点 P 在直线 oA 上方，应向 +x 方向进给一步，以逼近oA 直线；③如，则点 P 在直线 oA 下方，应向 +y 方向进给一步，以逼近 oA 直线一般将及视为一类情况，即时，都向 +x 方向进给一步。
当两方向所走的步数与终点坐标相等时，停止插补。
这即逐点比较法直线插补的原理。
对第一象限直线 oA 从起点 ( 即坐标原点 ) 出发，当 F 时， +x 向走一步；当 F<0 时，y 向走一步。
特点：每一步都需计算偏差，这样的计算比较麻烦。
递推的方法计算偏差：每走一步后新的加工点的偏差用前一点的加工偏差递推出来。
采用递推方法，必须知道开始加工点的偏差，而开始加工点正是直线的起点，故。
下面推导其递推公式。
设在加工点 P( ) 处，，则应沿 +x 方向进给一步，此时新加工点的坐标值为新加工点的偏差为即若在加工点 P( ) 处，，则应沿 +y 方向进给一步，此时新加工点的坐标值为，新加工点的偏差为即综上所述，逐点比较法直线插补每走一步都要完成四个步骤 ( 节拍 ) ，即：(1) 位置判别根据偏差值大于零、等于零、小于零确定当前加工点的位置。
数控车床 直线插补G01 圆弧插补G02,G03
精车A--J点的轮廓
快速返回刀具起点 主轴停止，换2号切断刀，刀宽为3 mm 主轴正转，转速500r/min
G00 X45 Z-33; G01 X40 F50; G02 X20 W-10 R10; G01 Z-60; X40;
精车K—I的轮廓
上一页
下一页
返回
参考程序 G00 X80 Z80; T0100 M05; M30;
注释 快速返回刀具起点 主轴停止，换回基准刀 程序结束
1． 由于T0100偏刀加工F-H的轮廓时刀具与工件有干涉,所以采用T0202切 槽刀来加工。 2．本程序G02/G03的程序段采用混合坐标编程。 3．刀具精加工时应根据刀具的性能采用不同的转速。 4． 本例切槽刀对刀时以左刀位点为基准，在定位加工时,应考虑刀宽与定 位点的位置。
程序名 快速定位至安全换刀点（刀具起点） 使用1号基准刀，主轴正转，转速600r/min 靠近工件
快速返回刀具起点 主轴停止 程序结束
上一页
下一页
返回
下一页 上一页
返回
如图所示，工件已粗加工完毕，各位置留有余量 0.2mm，要求重新编写精加工程序，不切断。
参考程序
注释
O....； G00 X100 Z100； M03 S800 T0101； G00 X20 Z2； G01 Z0 F60； X26 Z-3 ； Z-48； X60 Z-58 ； X80 W-73 ； G00 X100 Z100； M05 T0100； M30;
程序名 快速定位至安全换刀点（刀具起点） 使用1号基准刀，主轴正转，转速800r/min 靠近工件 快速定位到A点 加工到B点（顺圆弧加工） 加工到C点 加工到D点（逆圆弧加工） 加工到E点（顺圆弧加工） 加工到F点 快速返回刀具起点 主轴停止 程序结束
直线插补,圆弧插补
数控技术第三次作业题目【1】：第一象限的逆圆插补。
1.取该圆弧的圆心坐标为（0，0），起点坐标为（4，0），终点坐标为（0，4），圆弧半径为4.2.采用逐点比较法的C程序如#include <stdio.h>void main(){int n=8,x,y,f,g;scanf("%d,%d",&x,&y);f=x^2+y^2-16;if (f>=0)g=f-2x+1,x--,n--;printf("%d,%d,%d\n",x,y,n);elseg=f+2y+1,y++,n--;printf("%d,%d,%d\n",x,y,n);if (g>=0)g=g-2x+1,x--,n--;printf("%d,%d,%d\n",x,y,n);elseg=g+2y+1,y++,n--;printf("%d,%d,%d\n",x,y,n);while (n==0)printf("it is over");}3.程序流程图如下：4.程序运行后得到一系列插补点，连接插补点得到插补轨迹如下图所示：5.综上，第一象限的逆圆采用逐点插补法的插补过程及其解决算法如上所述。
题目【2】：第一象限的直线插补取第一象限的直线方程为Y=X，起点坐标为原点（0，0），终点坐标为（4，4）。
1．基于MATLAB的插补程序如下：Xe = input('输入终点横坐标X\nXe = ');Ye = input('输入终点纵坐标Y\nYe = ');h = input('输入步长\nh = ');Tstep= (abs(Xe)+abs(Ye))/h;Step=0;F=0;Xi=0;Yi=0;x = 0;y = 0;Xi=Xi+h; x = [x Xi]; y = [y Yi];endStep=1;while (Step<Tstep)F=Xe*Yi-Xi*Ye;if (F>=0)Xi=Xi+h;elseYi=Yi+h;endx = [x Xi];y = [y Yi];Step = Step+1;hold onendplot(x,y)2.MATLAB程序运行得到的插补图形及其轨迹如下图：综上，用逐点比较法完成了第一象限的逆圆插补和直线插补。
C语言模拟直线插补与圆弧插补程序设计
C语言模拟直线插补与圆弧插补程序设计(总17页)-本页仅作为预览文档封面，使用时请删除本页-数控技术课程设计说明书设计题目直线插补与圆弧插补程序设计机械设计以及自动化专业机械工程学院机械102班设计者青岛理工大学 2013年6月20日目录1.设计题目 (1)2.目录 (2)3.直线插补流程图 (3)4.直线插补程序 (4)5.程序结果 (8)6.圆弧插补流程图 (9)7.圆弧插补程序 (10)8.程序结果 (21)一．直线插补1.直线插补程序流程图2.直线插补程序设计#include ""int i,X,Y,X0,Y0,Xe,Ye,F,N;int a[30][2];void main(){int m;int menu();void yi();void er();void san();void si();void te();void shuchu();m=menu();a[0][0]=X0;a[0][1]=Y0;switch(m){case 1:yi();shuchu();break;case 2:er();shuchu();break;case 3:san();shuchu();break;case 4:si();shuchu();break;case 5:te();shuchu();break;default:printf("无法插补\n");}}int menu(){int t;printf("输入起点坐标\n");scanf("%d,%d",&X0,&Y0);printf("输入终点坐标\n");scanf("%d,%d",&Xe,&Ye);if (Xe>=X0&&Ye>=Y0)t=1;else if (Xe<=X0&&Ye>=Y0)t=2;else if (Xe<=X0&&Ye<=Y0)t=3;else if (Xe>=X0&&Ye<=Y0)t=4;else if (Xe==X0&&((Ye>Y0&&Y0>=0)||(Ye<Y0&&Y<=0))) t=5;elset=6;return(t); }void yi(){F=0;N=Xe-X0+Ye-Y0; X=X0;Y=Y0;for(i=1;i<=N;i++) { if(F>=0){X++;a[i][0]=X;a[i][1]=Y;F-=Ye-Y0;}else{Y++;a[i][0]=X;a[i][1]=Y;F+=Xe-X0;}}}void er(){F=0;N=X0-Xe+Ye-Y0; X=X0;Y=Y0;for(i=1;i<=N;i++) {if(F>=0){ X--;a[i][0]=X;a[i][1]=Y;F-=Ye-Y0;}else{Y++;a[i][0]=X;a[i][1]=Y;F+=X0-Xe;}}}void san(){F=0;N=X0-Xe+Y0-Ye; X=X0;Y=Y0;for(i=1;i<=N;i++) {if(F>=0){X--;a[i][0]=X;a[i][1]=Y;F-=Y0-Ye;}else{Y--;a[i][0]=X;a[i][1]=Y;F+=X0-Xe;}}}void si(){F=0;N=Xe-X0+Y0-Ye; X=X0;Y=Y0;for(i=1;i<=N;i++) {if(F>=0){X++;a[i][0]=X;a[i][1]=Y;F-=Y0-Ye;}else{ Y--;a[i][0]=X;a[i][1]=Y;F+=Xe-X0;}}}void te(){N=Ye-Y0; for(i=1;i<=N;i++) {if(Ye>0){Y++;a[i][0]=X;a[i][1]=Y;}else if(Ye<0){Y--;a[i][0]=X;a[i][1]=Y;}}}void shuchu(){for(i=0;i<=N;i++){printf("%d ",i);printf("%d,%d\n",a[i][0],a[i][1]);}}3．程序结果例如起点（0,0）终点（6,4）步数坐标1 1,02 1,13 2,14 2,25 3,26 4,27 4,38 5,39 6,310 6,4二.圆弧插补1.圆弧插补程序流程图2.圆弧插补程序#include ""#include ""int X0,Y0,X1,Y1,X2,Y2,X3,Y3,X4,Y4; int i=1,r,f,s;void main(){int m;int menu();void yishun();void yini();void ershun();void erni();void sanshun();void sanni();void sishun();void sini();void shuchu();m=menu();switch(m){case 1:yishun();break;case 2:yini();break;case 3:ershun();break;case 4:yini();break;case 5:sanshun();break;case 6:yini();break;case 7:sishun();break;case 8:yini();break;default:printf("无法插补\n"); }}int menu(){int t;printf("输入原点坐标\n");scanf("%d,%d",&X0,&Y0);printf("输入起点坐标\n");scanf("%d,%d",&X3,&Y3);printf("输入终点坐标\n");scanf("%d,%d",&X4,&Y4);printf("1:顺时针圆弧\n");printf("2:逆时针圆弧\n");scanf("%d",&s);X1=X3-X0;Y1=Y3-Y0;X2=X4-X0;Y2=Y4-Y0;r=X1*X1+Y1*Y1;if (X1>=0&&Y1>0&&s==1)t=1;else if (X1>0&&Y1>=0&&s==2) t=2;else if (X1<0&&Y1>=0&&s==1) t=3;else if (X1<=0&&Y1<0&&s==2) t=4;else if (X1<=0&&Y1<0&&s==1) t=5;else if (X1<0&&Y1<=0&&s==2) t=6;else if (X1>0&&Y1<=0&&s==1)t=7;else if (X1>=0&&Y1<0&&s==2)t=8;elset=9;return(t);}void yishun(){do{f=X1*X1+Y1*Y1-r;if(f>=0){Y1--;f-=2*Y1+1;i++;printf("%d ",i);printf("%d,%d\n",X1,Y1);}else{X1++;f+=2*X1+1;i++;printf("%d ",i);printf("%d,%d\n",X1,Y1);}}while(Y1!=0&&(X1!=X2||Y1!=Y2)); if(Y1==0){void sishun();sishun();}}void yini(){do{f=X1*X1+Y1*Y1-r;if(f>=0){X1--;f-=2*X1+1;i++;printf("%d ",i);printf("%d,%d\n",X1,Y1);}else{Y1++;f+=2*Y1+1;i++;printf("%d ",i);printf("%d,%d\n",X1,Y1);}}while(X1!=0&&(X1!=X2||Y1!=Y2)); if(X1==0){void erni();erni();}}void ershun(){do{f=X1*X1+Y1*Y1-r;if(f>=0){X1++;f+=2*X1+1;i++;printf("%d ",i);printf("%d,%d\n",X1,Y1);}else{Y1++;f+=2*Y1+1;i++;printf("%d ",i);printf("%d,%d\n",X1,Y1);}}while(X1!=0&&(X1!=X2||Y1!=Y2)); if(X1==0){void yishun();yishun();}}void erni(){do{f=X1*X1+Y1*Y1-r;if(f>=0){Y1--;f-=2*Y1+1;i++;printf("%d ",i);printf("%d,%d\n",X1,Y1);}else{X1--;f-=2*X1+1;i++;printf("%d ",i);printf("%d,%d\n",X1,Y1);}}while(Y1!=0&&(X1!=X2||Y1!=Y2)); if(Y1==0){void sanni();sanni();}}void sanshun(){do{f=X1*X1+Y1*Y1-r;if(f>=0){Y1++;f+=2*Y1+1;i++;printf("%d ",i);printf("%d,%d\n",X1,Y1);}else{X1--;f-=2*X1+1;i++;printf("%d ",i);printf("%d,%d\n",X1,Y1);}}while(Y1!=0&&(X1!=X2||Y1!=Y2)); if(Y1==0){void ershun();ershun();}}void sanni(){do{f=X1*X1+Y1*Y1-r;if(f>=0){X1++;f+=2*X1+1;i++;printf("%d ",i);printf("%d,%d\n",X1,Y1);}else{Y1--;f+=2*Y1+1;i++;printf("%d ",i);printf("%d,%d\n",X1,Y1);}}while(X1!=0&&(X1!=X2||Y1!=Y2)); if(X1==0){void sini();sini();}}void sishun(){do{f=X1*X1+Y1*Y1-r;if(f>=0){X1--;f-=2*X1+1;i++;printf("%d ",i);printf("%d,%d\n",X1,Y1);}else{Y1--;f-=2*Y1+1;i++;printf("%d ",i);printf("%d,%d\n",X1,Y1);}}while(X1!=0&&(X1!=X2||Y1!=Y2));if(X1==0){void sanshun();sanshun();}}void sini(){do{f=X1*X1+Y1*Y1-r;if(f>=0){Y1++;f+=2*Y1+1;i++;printf("%d ",i);printf("%d,%d\n",X1,Y1);}else{X1++;f+=2*X1+1;i++;printf("%d ",i);printf("%d,%d\n",X1,Y1);}}while(Y1!=0&&(X1!=X2||Y1!=Y2));if(Y1==0){void yini();yini();}}3.程序结果例如圆心（0,0）起点（4,3）终点（4,3）步数坐标0 4,31 3,32 3,43 2,44 2,55 1,56 0,57 0,48 -1,49 -2,410 -3,411 -3,312 -4,313 -4,214 -5,215 -5,116 -5,017 -4,018 -4,-119 -4,-220 -4,-321 -3,322 -3,-423 -2,-424 -2,-525 -1,-526 0,-527 0,-428 1,-429 2,-430 3,-431 3,-332 4,-333 4,-234 5,-235 5,-136 5,037 4,038 4,139 4,240 4,3。
第三章插补原理及控制方法
及
控
终点判别
N
终点？
制
方
法
结束
25
二、逐点比较法圆弧插补---其它象限
y
F>0
y
F>0
第
F<0
F<0
三 章
o
x
o
x
插
补
原
理
逆圆
顺圆
及 控
各象限插补进给方向， 各象限插补进给方向，远
制
远离原点坐标值加一接 离原点坐标值加一，接近
方
近原点坐标值减一。
原点坐标值减一。
法
26
作业
试推导逐点比较法第一象限顺圆弧 第 插补的递推公式，并画出程序流程图。
逐点比较插补计算法（简称逐点比较法）
第
三 章
数字积分插补计算法（简称数字积分法）
插 时间分割插补计算法（简称时间分割法）
补
原
理 及
样条插补计算方法等。
控
制
方
法
2
3-1 逐点比较法插补
逐点比较插补计算法（简称逐点比
第 较法）又称区域判别法。
三
章
其原理是：计算机在控制加工轨迹过
插 程中逐点计算和判断加工偏差以控制坐
章
当M点在直线上时， + Δ X
y
插 补
(αi= α)
原
M (x i y j )
A
理
及 控
tg αi= tg α
制
方 法
αi
oα
x
6
其中 tg αi= y j / xi
tgα= y e / x e
tg αi -tgα= y j / xi - y e / x e
数控技术数控机床的插补原理直线插补与圆弧插补计算原理
就结束该插补运算；如未到达再重复上述的 循环步骤。
（七）直线插补例题
图中的OA是要加工的直线。直线的起点在坐标原 点，终点为A（5，3）。试用逐点比较法对该直线 段进行插补，并画出补轨迹。
Y A（5,3）
O X
图2-5 逐点比较法直线插补轨迹
插补分类：（插补采用的原理和计算方法）
基准脉冲插补：(又称为行程标量插补或脉冲增量插补) 每次插补结束，向每个运动坐标输出基准脉冲序列。 脉冲序列的频率代表了运动速度，而脉冲的数量表示 移动量。
①逐点比较法；②数字积分法；③数字脉冲乘法器插补法；④矢 量判别法；⑤比较积分法；⑥最小偏差法；⑦目标点跟踪法；⑧ 单步追踪法；⑨直接函数法。
（五）逐点比较法直线插补源自2. 算法分析（第Ⅰ象限） 总结
第一拍 判别 第二拍 进给 第三拍 运算 第四拍 比较
Fm≥0 Fm<0
+△x +△y
Fm+1=Fm-ye Fm+1=Fm+xe
m=m+1
（六）插补运算过程
方向判定：根据偏差值判定进给方向； 坐标进给：根据判定的方向，向该坐标方向
发一进给脉冲； 偏差计算：每走一步到达新的坐标点，按偏
特点：以折线逼近直线、圆弧或各类曲线。
精度高：最大偏差不超过一个脉冲当量。
（四）逐点比较法
插补开始 方向判定
逐点比较法 工作循环过程
坐标进给
偏差计算
终点到？
N
插补结束
Y
（五）逐点比较法直线插补
y A(xe,ye)
o
x
每次插补计算输出一个脉冲，不是进给到X轴 方向，就是进给到Y轴方向，不可能两个坐标轴都进给
数控技术数控机床的插补原理直线插补与圆弧插补计算原理
（三）、插补方法的种类与特点
插补器： 插补是数控系统必备功能， NC中由硬件完成，
CNC中由软件实现，两者原理相同。
硬件 通过硬件逻辑电路 插补速度快 插补器 来实现插补
软件 利用CNC系统的微 插补器 处理器执行相应的
插补程序来实现
结构简单、灵活易变、可
靠性好，大部分CNC系统 采用了软件插补方式
偏差判别函数：Fm = ymxe-xmye
（五）逐点比较法直线插补
2. 算法分析（第Ⅰ象限）
终点比较：
判别是否到达终点，若到达终点就结束该插 补运算；如未到达再重复上述的循环步骤。
方法一 方法二
用Xe+Ye作为计数器，每走一步对计 数器进行减 1计算，直到计数器为零 时，便到达终点。
用通常根据刀具沿X、Y两轴所走的 总步数m来判断直线是否加工完毕， 总步数为：N=|xA|+|yA|
部分高档CNC：软件插补实现粗插补，硬件插补实现精插补
（三）、插补方法的种类与特点
插补分类：（插补采用的原理和计算方法）
基准脉冲插补：(又称为行程标量插补或脉冲增量插补) 每次插补结束，向每个运动坐标输出基准脉冲序列。 脉冲序列的频率代表了运动速度，而脉冲的数量表示 移动量。
①逐点比较法；②数字积分法；③数字脉冲乘法器插补法；④矢 量判别法；⑤比较积分法；⑥最小偏差法；⑦目标点跟踪法；⑧ 单步追踪法；⑨直接函数法。
Fm Fm
（五）逐点比较法直线插补
2. 算法分析（第Ⅰ象限）
新偏差计算：
每走一步到达新的坐标点，按偏差公 式计算新的偏差
+△x进给 +△y进给
xm+1 = xm+1, ym+1 =ym Fm+1=ym+1xe-xm+1ye=ymxe-(xm+1)ye=Fm-ye
直线、圆弧插补指令编程
说 明
① 用绝对值编程时，圆弧终点坐标为圆弧终点在工件坐标系中的坐标值，用X、Z 表 示。当用增量值编程时，圆弧终点坐标为圆弧终点相对于圆弧起点的增量值，用U、W表示。 ② 圆心坐标（I, K）为圆弧起点到圆弧中心点所作矢量分别在X、Z坐标轴方向上分矢 量（矢量方向指向圆心）。本系统I、K为增量值，并带有“±”号，当矢量的方向与坐标轴 的方向不一致时取“−”号。 ③ R为圆弧半径，不与I、K同时使用。当用半径R指定圆心位置时，由于在同一半径R 的情况下，从圆弧的起点到终点有两个圆弧的可能性，为区别两者，规定圆心角α ≦180° 时，用“+R”表示，α ≧180°时，用“−R”表示。用半径R指定圆心位置时，不能描述整圆。
图5-1 G00定位轨迹图
5-2 绝对、相对、混合编程实例
表5-1 绝对、相对、混合编程方法表 绝对编程（G90） 相对编程 混合编程 G00 G00 G00 G00 X70 U40 U40 X70 Z40
W−60
Z40
W−60
直线插补
G01直线插补 直线插补
G01代码用于刀具直线插补运动。功能：G01指令使刀具以一定的进给速度，从所在点出 发，直线移动到目标点。 指令格式：G01 X（U）_ Z（W）_ F 式中：X、Z：为绝对编程时目标点在工件坐标系中的坐标； U、W：为增量编程时目标点 坐标的增量；F：进给速度。
图5-7 倒角指令示意图
顺/逆时针圆弧插补
圆弧顺、 圆弧顺、逆的判断
圆弧插补的顺、逆可按如图5-9所示的方向判断 （点击箭头进入 ）
G02/G03指令编程格式 指令编程格式
① 用I、K指定圆心位置： 指令格式：G02/G03 X（U）Z（W） I K F ② 用圆弧半径R指定圆心位置： 指令格式：G02/G03 X（U）Z（W） R F
3,4---第二章 数控机床的插补原理――直线插补与圆弧插补计算原理
直线上
=
YmXe―XmYe=0
直线上方
>
YmXe―XmYe>0
直线下方
<
YmXe―XmYe<0
｛ 偏差判别函数：Fm = ymxe-xmye
= 0 在直线上； >0在直线上方
< 0 在直线下方
（五）逐点比较法直线插补
2. 算法分析（第Ⅰ象限）
坐标进给：
根据判定的进给方向，向该坐标 方向发一进给脉冲
特点：以折线逼近直线、圆弧或各类曲线。
精度高：最大偏差不超过一个脉冲当量。
（四）逐点比较法
插补开始 方向判定
逐点比较法 工作循环过程
坐标进给
偏差计算
终点到？
N
插补结束
Y
（五）逐点比较法直线插补
y A(xe,ye)
o
x
每次插补计算输出一个脉冲，不是进给到X轴 方向，就是进给到Y轴方向，不可能两个坐标轴都进给
数据采样插补:(又称为时间标量插补或数字增量插 补,8ms，10.24ms)数控装置产生的不是单个脉冲，而 是采样周期内，各坐标的位移量
①直线函数法；②扩展数字积分法；③二阶递归扩展数字积分插 补法；④双数字积分插补法；⑤角度逼近圆弧插补法。
（四）逐点比较法
思想：“走一步看一步”：就是每走一步都要和给定 轨迹上的坐标值进行一次比较，视该点在给定轨迹 的上方或下方，或者给定轨迹的里面或者外面，从 而决定下一步的进给方向，使之趋近加工轨迹。
（五）逐点比较法直线插补
1.基本原理：
在刀具按要求轨迹运动加工零件轮廓的过程中， 不断比较刀具与被加工零件轮廓之间的相对位置，并 根据比较结果决定下一步的进给方向，使刀具向减小 误差的方向进给。其算法最大偏差不会超过一个脉冲 当量δ。