数字信号处理-答案-第二章
数字信号处理第2章习题解答

e
n 0
e
j ( 0 )
n
1 1 e e j (0 )
当 e 1 0
2-9 求 x(n) R5 (n) 的傅里叶变换 解:X (e j )
5 j 2
n
j
x ( n )e j n e j n
1 1 1 z 2
1 1 1 2 1 z z 2 4 1
1 1 1 2 X ( z) 1 z z 2 4 n 1 n z 2 n 0
1 x(n ) u(n ) 2
n
1 1 1 z 2 1 1 z 2 1 1 1 2 z z 2 4 1 2 z 4
解:
1 由x1 ( n ) u( n ) 2
1 z 2
n
1 得 X 1 ( z ) ZT [ x1 ( n )] 1 1 1 z 2 n 1 由x2 ( n ) u( n ) 3 1 得 X 2 ( z ) ZT [ x2 ( n )] 1 1 1 z 3
1 z 3
z3 z 3z 5 1 1 1 1 1 z 1 z z 3 z 2 3 2
1 z 3 2
j x ( n ) X ( e ): 2-7 求以下序列 的频谱
(1) (n n0 )
X ( e j )
n j n ( n n ) e 0
0
1/ 4 Re[ z ]
当 n 1 时, F ( z )在围线c内有一 (n 1)阶极点 z 0 在围线c外有单阶极点 z 1/ 4, 且分母阶次高于分子阶次二阶以上
数字信号处理(方勇)第二章习题答案

2-1 试求如下序列的傅里叶变换: (1))()(01n n n x -=δ (2))1(21)()1(21)(2--++=n n n n x δδδ (3)),2()(3+=n u a n x n10<<a(4))4()3()(4--+=n u n u n x(5)∑∞=-⎪⎭⎫⎝⎛=05)3(41)(k nk n n x δ(6)()6cos ,14()0,n n x n π⎧-≤≤=⎨⎩其他解: (1) 010()()j n j j nn X e n n ee ωωωδ∞--=-∞=-=∑(2) 2211()()122j j nj j n X e x n e e e ωωωω∞--=-∞==+-∑ωsin 1j +=(3) 2232()(2)1j j nj nn j nj n n a e X e a u n ea eaeωωωωω-∞∞---=-∞=-=+==-∑∑, 10<<a(4) []4()(3)(4)j j nn X e u n u n eωω∞-=-∞=+--∑∑-=-=33n nj e ω∑∑==-+=313n n j n nj e eωωωωωωωj j j j j e e e e e --+--=--111134=⎪⎭⎫ ⎝⎛⎪⎭⎫⎝⎛=----ωωωω21sin 27sin 1137j j j e ee(5) 3350011()(3)44n kj jn j k n k k X e n k e e ωωωδ∞∞+∞--=-∞==⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭∑∑∑∑∞+=--⎪⎭⎫⎝⎛-=⎪⎭⎫⎝⎛=033411141k j kj e e ωω(6) 44336441()cos 32j j j jn jn n n X e nee e e ππωωωπ---=-=-⎛⎫==+ ⎪⎝⎭∑∑994()()4()()3333001122j j n j j n n n e e e e ππππωωωω--++===+∑∑ ()9()9334()4()33()()3311112211j j j j j j e e e e e e ππωωππωωππωω-+-+-+⎡⎤⎡⎤--⎢⎥⎢⎥=+⎢⎥⎢⎥++⎢⎥⎢⎥⎣⎦⎣⎦2-2 设信号}1,2,3,2,1{)(---=n x ,它的傅里叶变换为)(ωj e X ,试计算(1)0()j X e (2)()j X ed πωπω-⎰(3)2()j X e d πωπω-⎰。
(完整word版)数字信号处理答案第二章

第二章2.1 判断下列序列是否是周期序列。
若是,请确定它的最小周期.(1)x (n )=Acos(685ππ+n ) (2)x (n)=)8(π-ne j(3)x (n)=Asin(343ππ+n ) 解 (1)对照正弦型序列的一般公式x (n )=Acos (ϕω+n ),得出=ω85π。
因此5162=ωπ是有理数,所以是周期序列。
最小周期等于N=)5(16516取k k =。
(2)对照复指数序列的一般公式x (n )=exp[ωσj +]n,得出81=ω。
因此πωπ162=是无理数,所以不是周期序列。
(3)对照正弦型序列的一般公式x (n)=Acos(ϕω+n ),又x (n)=Asin (343ππ+n )=Acos (-2π343ππ-n )=Acos(6143-n π),得出=ω43π.因此382=ωπ是有理数,所以是周期序列。
最小周期等于N=)3(838取k k =2.2在图2.2中,x (n )和h(n)分别是线性非移变系统的输入和单位取样响应。
计算并列的x (n )和h (n)的线性卷积以得到系统的输出y(n ),并画出y(n)的图形。
(a)1111(b)(c)111110 0-1-1-1-1-1-1-1-1222222 33333444………nnn nnnx(n)x(n)x(n)h(n)h(n)h(n)21u(n)u(n)u(n)a n ===22解 利用线性卷积公式y(n )=∑∞-∞=-k k n h k x )()(按照折叠、移位、相乘、相加、的作图方法,计算y(n)的每一个取样值。
(a ) y (0)=x (O)h (0)=1y (l )=x (O )h(1)+x (1)h (O)=3y (n)=x(O)h (n )+x (1)h(n-1)+x(2)h (n —2)=4,n ≥2 (b) x(n )=2δ(n )-δ(n-1)h(n)=-δ(n)+2δ(n —1)+ δ(n —2)y(n )=-2δ(n)+5δ(n —1)= δ(n-3) (c ) y (n )=∑∞-∞=--k kn k n u k u a)()(=∑∞-∞=-k kn a=aa n --+111u (n )2。
(完整word版)数字信号处理第二章习题解答
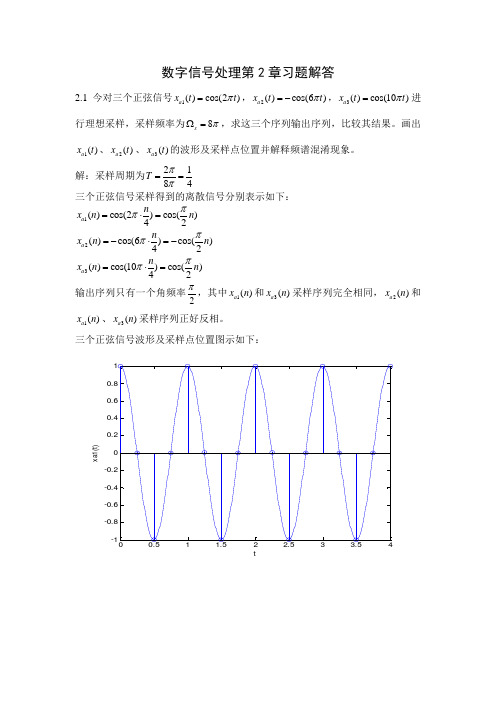
数字信号处理第2章习题解答2.1 今对三个正弦信号1()cos(2)a x t t π=,2()cos(6)a x t t π=-,3()cos(10)a x t t π=进行理想采样,采样频率为8s πΩ=,求这三个序列输出序列,比较其结果。
画出1()a x t 、2()a x t 、3()a x t 的波形及采样点位置并解释频谱混淆现象。
解:采样周期为2184T ππ== 三个正弦信号采样得到的离散信号分别表示如下:1()cos(2)cos()42a n x n n ππ=⋅=2()cos(6)cos()42a n x n n ππ=-⋅=-3()cos(10)cos()42a n x n n ππ=⋅=输出序列只有一个角频率2π,其中1()a x n 和3()a x n 采样序列完全相同,2()a x n 和1()a x n 、3()a x n 采样序列正好反相。
三个正弦信号波形及采样点位置图示如下:tx a 1(t )tx a 2(t )tx a 3(t )三个正弦信号的频率分别为1Hz 、3Hz 和5Hz ,而采样频率为4Hz ,采样频率大于第一个正弦信号频率的两倍,但是小于后两个正弦信号频率的两倍,因而由第一个信号的采样能够正确恢复模拟信号,而后两个信号的采样不能准确原始的模拟信号,产生频谱混叠现象。
2.3 给定一连续带限信号()a x t 其频谱当f B >时,()a X f 。
求以下信号的最低采样频率。
(1)2()a x t (2)(2)a x t (3)()cos(7)a x t Bt π解:设()a x t 的傅里叶变换为()a X j Ω(1)2()a x t 的傅里叶变换为22()[()]Ba a BX j X j d ππωωω-⋅Ω-⎰因为22,22B B B B πωππωπ-≤≤-≤Ω-≤ 所以44B B ππ-≤Ω≤即2()a x t 带限于2B ,最低采样频率为4B 。
数字信号处理习题答案

n
2π [ ( 0 2kπ) δ( 0 2kπ)]
式中
k
ω0=Ω0T=0.5π rad 上式推导过程中, 指数序列的傅里叶变换仍然不存在, 只有引入奇异函
数δ函数才能写出它的傅里叶变换表示式。
解: (1) x(n)序列的波形如题2解图(一)所示。 (2) x(n)=-3δ(n+4)-δ(n+3)+δ(n+2)+3δ(n+1)+6δ(n) +6δ(n-1)+6δ(n-2)+6δ(n-3)+6δ(n-4)
第1章 时域离散信号与时域离散系统
(3) x1(n)的波形是x(n)的波形右移2位,再乘以2, 画出图形如题2解图 (二)所示。
n
1=n+1
m0
3
1=8-n
mn4
④ n>7时, y(n)=0
题8解图(1)
最后结果为 0 n<0或n>7
y(n)= n+1 0≤n≤3 8-n 4≤n≤7
y(n)的波形如题8解图(1)所示。 (2) y(n) =2R4(n)*[δ(n)-δ(n-2)]=2R4(n)-2R4(n-2) = 2[δ(n)+δ(n-1)-δ(n+4)-δ(n+5)
y(n)=(2-0.5n)R5(n)+31×0.5nu(n-5)
第1章 时域离散信号与时域离散系统
13. 有一连续信号xa(t)=cos(2πft+j), 式中, f=20 Hz, j=π/2
(1) 求出xa(t)
(2) 用采样间隔T=0.02 s对xa(t)进行采样, 试写出采样信号xˆa (t)
数字信号处理第二章答案 朱冰莲

(1)
(2)
由(1)得:
由(2)得:
以上两式相乘得:
(1)
零点:z= ,极点z=0.5
(2)
零点:z=-2,极点:z=0.5
因为此系统是一个因果稳定系统;所以其收敛
2-22
解:
(1)根据DTFT的线性、反折、移位等性质,有
(3)
(5)
(7)
2-23
(2)对于线性移不变系统,若输入序列为 ,则系统输出为
(1)
(2)
(3)
(4)
(5)
(6)
2-18
解:根据离散时间傅里叶逆变换公式
2-19
解:根据离散时间傅里叶变换定义,有
得证。
2-20
解:
若 ,则 ,那么 , ,为线性相位;
若 ,则 ,那么 , ,为线性相位;得证。
相位谱:若令 (其实就是单位圆),那么 就变成了 ,而 就是频率响应。通过 可以得到幅度谱和相位谱(也就是幅值和相位角随 的变化情况)。由于是一个复数(复数就有幅值和相位嘛),所以必然能够变换成: 这种形式,而 就是相位谱了,它是数字频率w的函数。
参考答案说明:以下为教材第二章部分习题参考答案,未经朱老师审核,综合了本人、以前助教、同学们交上来的作业的答案,其中有些不是作业。现发给大家,仅供参考,可能有错误之处,大家要及时相互讨论,弄懂原理才是最重要的。
第一次:
2-1求以下序列的Z变换、收敛域及零级点分布图。
(1)
解:
当 时,收敛域为|Z|>0,极点为Z=0,无零点。
8后的结果上下同乘32n212212222132?22?12?32112132?22?23112?121121112?11111112n1z1?221?1221?1212112111111211?1121?21??????????????????????????n??n??????????????z??z??????z????n?????????nzznznznzzznzznzznznzzznzznzznznnzznznnzzzzzzdzdzzzznzzzdzdzznnunnunznznnununznxzxnnnnnnnnnnnnnnnnnnnnnnnnnnnnn通过验证知上式分子中包含21?z故在z1处零极点抵消
数字信号处理答案
第二章 离散时间信号与系统1. 为什么数字角频率为π时表示正弦信号变化最快?2. 确定下列序列的周期18[]3[]cos 78j n x n e x n n πππ⎛⎫- ⎪⎝⎭=⎛⎫=- ⎪⎝⎭ 3. 证明 [][]xy yx r n r n =-4. 判断系统的线性、时不变性、因果性和稳定性{}21[]sin []2n T x n n x n +⎛⎫= ⎪⎝⎭5. 证明LTI 系统满足[][][]y n x n h n =*6. LTI 系统的线性常系数差分方程和卷积表示间的关系是什么?7. 比较FIR 和IIR 在以下几方面的异同:单位取样响应的长度、卷积表示是否是有限项求和、差分方程是否与卷积一致、直接实现是否有反馈。
8. 为什么傅立叶变换会得到负频率?9. 傅立叶变换以2π为周期与π为正弦序列的最高频率间的关系。
10. 什么是稳态响应?FIR 和IIR 系统达到稳态响应的时间长短有何区别?为什么?11.用特征函数法、时域或频域卷积法求LTI系统的输出。
其中系统的频响和输入序列分别为:()24112[]sin4jjjeH eenx nωωωπ---=+⎛⎫= ⎪⎝⎭第二章答案1.因为数字信号两个点间采样间隔不为0,如果两点间变换频率高于π看起来就和变化频率低于π是一样的效果。
2.1(1) 2/2/()16,8314(2) 2/2/(),1473NNπωπππωππ===∞===3.][]'[]'[][][][nrnkxkynkykxnryx kkxy-=-=+=∑∑∞-∞=∞-∞=4.线性,时变,因果,稳定。
5.][*][][][]}[{][][][][nhnxknhkxknTkxknkxTnykkk=-=-=⎥⎦⎤⎢⎣⎡-=∑∑∑∞-∞=∞-∞=∞-∞=δδ6.差分方程求和项数有限,可以有输出的递归存在;卷积表示求和项数可能无限,没有输出的递归;对于FIR,两者可以是一致的。
数字信号处理知到章节答案智慧树2023年温州医科大学
数字信号处理知到章节测试答案智慧树2023年最新温州医科大学第一章测试1.由离散信号x[k]经基本运算得到离散信号x[-5k+3],不需要的运算为()。
参考答案:内插2.已知某模拟信号最高频率为fm,若要求能恢复原信号,则抽样频率至少为()。
参考答案:2*fm3.正弦序列总是周期的。
()参考答案:错4.一个离散系统的因果性和稳定性无关。
()参考答案:对5.序列的周期是()。
参考答案:4第二章测试1.三点有限长序列的DFT矩阵为()参考答案:2.某实系数奇对称序列以4点为周期,其中x[1]=2,则()参考答案:x[3]=-2,x[4]=03.DFT矩阵与FFT的系数矩阵完全相同。
()参考答案:对4.如果希望信号的DFT是实偶函数,则原序列也应当是实偶函数()参考答案:对5.下列关于DFT的论述错误的是()参考答案:DFT可以对连续信号频谱进行变换第三章测试1.对8点序列采取基2频率抽取FFT算法,其序列排布为()参考答案:x[0]、x[1]、x[2]、x[3]、x[4]、x[5]、x[6]、x[7]2.使用FFT算法所需的乘法次数与()成正比参考答案:3.FFT变换要求序列为某个整数的整数幂次方,否则需补零()参考答案:错4.FFT算法的基本运算单元是蝶形运算()参考答案:对5.基2频率算法先与旋转矩阵相乘后与系数矩阵相乘。
()参考答案:错第四章测试1.要实现同样的性能指标,以下滤波器中阶数最低的是()。
参考答案:椭圆型2.数字滤波器是一种离散时间系统,可以根据需要有选择性地滤除输入信号中的某些频率成分,从而实现对输入信号的处理。
()参考答案:对3.脉冲响应不变法是一种将模拟滤波器转换为数字滤波器的方法,其基本思想是使数字滤波器的单位脉冲响应等于模拟滤波器冲激响应的等间隔抽样。
()参考答案:对4.双线性变换法存在频谱混叠现象,不适合设计高通滤波器。
()参考答案:错5.在相同设计指标下,BW型滤波器的阶数最高,因此在滤波器的实现过程中,BW型滤波器不易实现。
数字信号处理(第三版)第2章习题答案
第2章 时域离散信号和系统的频域分析
2.3
求信号与系统的频域特性要用傅里叶变换。 但分析频 率特性使用Z变换却更方便。 我们已经知道系统函数的极、 零点分布完全决定了系统的频率特性, 因此可以用分析极、 零点分布的方法分析系统的频率特性, 包括定性地画幅频 特性, 估计峰值频率或者谷值频率, 判定滤波器是高通、 低通等滤波特性, 以及设计简单的滤波器(内容在教材第5 章)等。
X e (e j ) FT[xr (n)]
Hale Waihona Puke 1 1 ej2 1 e j2 1 (1 cos 2)
24
4
2
因为 所以
Xe
(e j
)
1 2
[X
(e j
)
X
(e j
)]
X(ejω)=0π≤ω≤2π
X(e-jω)=X(ej(2π-ω))=0 0≤ω≤π
第2章 时域离散信号和系统的频域分析
当0≤ω≤π时,
用留数定理求其逆变换, 或者将z=ejω代入X(ejω)中, 得到X(z)函数, 再用求逆Z变换的方法求原序列。 注意收 敛域要取能包含单位圆的收敛域, 或者说封闭曲线c可取 单位圆。
第2章 时域离散信号和系统的频域分析
例如, 已知序列x(n)的傅里叶变换为
X
(e
j
)
1
1 ae
j
a 1
1 求其反变换x(n)。 将z=ejω代入X(ejω)中, 得到 X (z) 1 az 1
三种变换互有联系, 但又不同。 表征一个信号和系统 的频域特性是用傅里叶变换。 Z变换是傅里叶变换的一种推 广, 单位圆上的Z变换就是傅里叶变换。
第2章 时域离散信号和系统的频域分析
数字信号处理作业(第二章答案)蔡坤宝英文版版
Chapter 2 Problem Answers2.1 Two sequences and are, respectively, given by)(1n x )(2n x and .⎩⎨⎧-<-≥=+1 01 2)(1)(11n ,n ,/n x n ⎩⎨⎧≥+<=0 10(2))(2n ,n n ,n x n Find the sequence of the sample-added sum of two sequences.)(n y Solution: The sample-added sum is given by.⎪⎩⎪⎨⎧≥++-=-<=+=+0)1((1/2)12312)()()(121n ,n n ,/n ,n x n x n y n n 2.2 Find the sample-accumulated sequence of a given sequence)(n y .⎩⎨⎧-<-≥=+1 012)(1)(1n ,n ,/n x n Solution: For , the sample-accumulated sequence is given by1-<n .0)()(==∑-∞=nk k x n y For , we have1-≥n .1211)21(2)21(1)21(1 )21()()(++-=+-∞=-=--===∑∑n n nk k n k ////k x n y Thus, the sample-accumulated sequence is.⎪⎩⎪⎨⎧-<-≥⎪⎭⎫ ⎝⎛-=+1 01 212)(1n ,n ,n y n 2.3 Assume that a sequence is the same as that in problem 2.2. Determine the first-)(n x order forward and backward difference sequences of , respectively.)(n x Solution: The first-order forward difference sequence is given by,⎪⎩⎪⎨⎧->--=-<=-+=+2)21(2120)()1()(2n ,/n ,n ,n x n x n x n ∆and the first-order backward difference sequence is given by.⎪⎩⎪⎨⎧->--=<=--=∇+1)21(1110,)1()()(1n ,/n ,-n n x n x n x n 2.4 Determine whether or not each of following signals is periodic. If a signal, in the case, is periodic, specify its fundamental period.(1) )010cos()(n .n x π=(2) )3sin()(πn n x =(3) 873cos()(πn πA n x -=(4) )8()(πn j en x -=Solution: (1) Considering,min min min k k ./k /N )200()0102()2(0===ππωπand taking , we see that the sequence is periodic with period .1=min k 200=N Solution: (2) This sequence is periodic. Since,min min min k /k /k /N )32()32()2(0===ππωπwe can take and obtain the period of the sequence as .3=min k 2=N Solution: (3) Considering,min min min k /k //k /N )314()]73(2[)2(0===ππωπand taking , we see that the period of the sequence is .3=min k 14=N Solution: (4) Since,min min min k k //k /N )16()]81(2[)2(0ππωπ=== is not an integer for any integer value of . Thus, the given sequence is nonperiodic.N min k 2.10 For each of the following systems, determine whether the system is (a) stable, (b) causal, (c) linear, (d) time invariant, and (e) memoryless.下列系统,确定系统是否(a)稳定,(b )因果,(C )线性,(D )时不变,和(E )无记忆。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数字信号处理-答案-第二章第二章2.1 判断下列序列是否是周期序列。
若是,请确定它的最小周期。
(1)x(n)=Acos(685ππ+n ) (2)x(n)=)8(π-nej(3)x(n)=Asin(343ππ+n ) 解 (1)对照正弦型序列的一般公式x(n)=Acos(ϕω+n ),得出=ω85π。
因此5162=ωπ是有理数,所以是周期序列。
最小周期等于N=)5(16516取k k =。
(2)对照复指数序列的一般公式x(n)=exp[ωσj +]n,得出81=ω。
因此πωπ162=是无理数,所以不是周期序列。
(3)对照正弦型序列的一般公式x(n)=Acos(ϕω+n ),又x(n)=Asin(343ππ+n )=Acos(-2π343ππ-n )=Acos(6143-n π),得出=ω43π。
因此382=ωπ是有理数,所以是周期序列。
最小周期等于N=)3(838取k k =2.2在图2.2中,x(n)和h(n)分别是线性非移变系统的输入和单位取样响应。
计算并列的x(n)和h(n)的线性卷积以得到系统的输出y(n),并画出y(n)的图形。
(a)1111(b)(c)111110 0-1-1-1-1-1-1-1-1222222 33333444………nnn nnnx(n)x(n)x(n)h(n)h(n)h(n)21u(n)u(n)u(n)a n ===22解 利用线性卷积公式y(n)=∑∞-∞=-k k n h k x )()(按照折叠、移位、相乘、相加、的作图方法,计算y(n)的每一个取样值。
(a) y(0)=x(O)h(0)=1y(l)=x(O)h(1)+x(1)h(O)=3y(n)=x(O)h(n)+x(1)h(n-1)+x(2)h(n-2)=4,n ≥2 (b) x(n)=2δ(n)-δ(n-1)h(n)=-δ(n)+2δ(n-1)+ δ(n-2) y(n)=-2δ(n)+5δ(n-1)= δ(n-3)(c) y(n)= ∑∞-∞=--kkn knuku a)()(=∑∞-∞=-kkna=aa n--+111u(n)2.3 计算线性线性卷积(1) y(n)=u(n)*u(n)(2) y(n)=λn u(n)*u(n)解:(1) y(n)= ∑∞-∞=-kknuku)()(=∑∞=-)()(kknuku=(n+1),n≥0即y(n)=(n+1)u(n)(2) y(n)=∑∞-∞=-kk knuku)()(λ=∑∞=-)()(kk knukuλ=λλ--+111n,n≥0即y(n)=λλ--+111n u(n)2.4 图P2.4所示的是单位取样响应分别为h1(n)和h2(n)的两个线性非移变系统的级联,已知x(n)=u(n),h1(n)=δ(n)-δ(n-4), h2(n)=a n u(n),|a|<1,求系统的输出y(n).解ω(n)=x(n)*h1(n)=∑∞-∞=k ku)([δ(n-k)-δ(n-k-4)] =u(n)-u(n-4)y(n)=ω(n)*h2(n)=∑∞-∞=k k k ua)([u(n-k)-u(n-k-4)]=∑∞-=3nk ka,n≥32.5 已知一个线性非移变系统的单位取样响应为h(n)=a n-u(-n),0<a<1 用直接计算线性卷积的方法,求系统的单位阶跃响应。
2.6 试证明线性卷积满足交换率、结合率和加法分配率。
证明(1)交换律X(n) * y(n) = ∑∞-∞=-kknykx)()(令k=n-t,所以t=n-k,又-∞<k<∞,所以-∞<t<∞,因此线性卷积公式变成` x(n) * y(n) =∑∞-∞=---ttnnytnx)]([)(=∑∞-∞=-ttytnx)()(=y(n) * x(n)交换律得证.(2)结合律[x(n) * y(n)] * z(n)=[∑∞-∞=-kknykx)()(] * z(n)=∑∞-∞=t [∑∞-∞=-kktykx)()(]z(n-t)=∑∞-∞=k x(k) ∑∞-∞=ty(t-k)z(n-t)=∑∞-∞=k x(k) ∑my(m)z(n-k-m)=∑∞-∞=k x(k)[y(n-k) * z(n-k)]=x(n) * [y(n) * z(n)] 结合律得证. (3)加法分配律x(n) * [y(n) + z(n)]= ∑∞-∞=k x(k)[y(n - k) +z(n - k)]=∑∞-∞=k x(k)y(n-k)+ ∑∞-∞=k x(k)z(n - k)=x(n) * y(n) + x(n) *z(n) 加法分配律得证.2.7 判断下列系统是否为线性系统、非线性系统、稳定系统、因果系统。
并加以证明 (1)y(n)=2x(n)+3(2)y(n)= x(n)sin[32πn+6π] (3)y(n)= ∑∞-∞=k k x )( (4)y(n)=∑=nn k k x 0)((5)y(n)= x(n)g(n)解 (1)设y 1(n)=2x 1(n)+3,y 2(n)=2x 2(n)+3,由于y(n)=2[x1(n)+x2(n)]+3≠y1(n)+ y2(n)=2[x1(n)+x2(n)]+6故系统不是线性系统。
由于y(n-k)=2x(n-k)+3,T[x(n-k)]=2x(n-k)+3,因而y(n-k) = T[x(n-k)]故该系统是非移变系统。
设|x(n)|≤M,则有|y(n)|=|2x(n)+3|≤|2M+3|<∞故该系统是稳定系统。
因y(n)只取决于现在和过去的输入x(n),不取决于未来的输入,故该系统是因果系统。
(2)设 y1(n)=ax1(n)sin[32πn+6π]y2(n)=bx2(n)sin[32πn+6π]由于 y(n)=T[ax1(n)+ bx2(n)]=[ax1(n)+bx2(n)]sin[32πn+6π]=ax1(n)sin[32πn+6π]+bx2(n)sin[32πn+6π]=ay1(n)+by2(n)故该系统是线性系统。
由于 y(n-k)=x(n-k)sin[32π(n-k)+6π] T[x(n-k)]=x(n-k)sin[32πn+6π] 因而有 T[x(n-k)]≠y(n-k) 帮该系统是移变系统。
设 |x(n)|≤M ,则有|y(n)|=|x(n)sin[32π(n-k)+6π]| =|x(n)|| sin[32π(n-k)+6π]| ≤M|sin[32π(n- k)+6π]|≤M 故系统是稳定系统。
因y(n)只取决于现在和过去的输入x(n),不取决于未来的输入,故该系统是因果系统。
(3)设 y 1(n)=∑-∞=n k k x )(1,y 2(n)=∑-∞=nk k x )(2,由于y(n)=T[ax 1(n)+ bx 2(n)]= ∑-∞=+nk k k )](bx )(ax [21=a ∑-∞=n k k x )(1+ b ∑-∞=nk k x )(2=ay 1(n)+by 2(n)故该系统是线性系统。
因 y(n-k)= ∑--∞=tn k k x )(= ∑-∞=-nm t m x )(=T[x(n-t)]所以该系统是非移变系统。
设 x(n)=M<∞ y(n)= ∑-∞=nk M =∞,所以该系统是不稳定系统。
因y(n)只取决于现在和过去的输入x(n),不取决于未来的输入,故该系统是因果系统。
(4)设 y 1(n)=∑=n n k k x 01)( ,y 2(n)=∑=nn k k x 02)(,由于y(n)=T[ax 1(n)+ bx 2(n)]= ∑=+nn k k k 021)](bx )(ax [= a ∑=n n k k x 01)(+b ∑=nn k k x 02)(=ay 1(n)+by 2(n)故该系统是线性系统。
因 y(n-k)= ∑-=tn n k k x 0)(= ∑+=-ntn m t m x 0)(≠T[x(n-t)]=∑=-nn k t m x 0)(所以该系统是移变系统。
设x(n)=M,则lim n →∞y(n)= lim n →∞(n-n 0)M=∞,所以该系统不是稳定系统。
显而易见,若n ≥n 0。
则该系统是因果系统;若n<n 0。
则该因果系统是非因果系统。
(5)设y 1(n)=x 1(n)g(n),y 2(n)=x 2(n)g(n),由于y(n)=T[ax 1(n)+bx 2(n)]=(ax 1(n)+bx 2(n))g(n)=ax 1(n)g(n)+b 2(n)=ay 1(n)+by 2(n)故系统是线性系统。
因y(n-k)=x(n-k),而T[x(n-k)]=x(n-k)g(n)≠y(n-k) 所以系统是移变系统。
设|x(n)|≤M<∞,则有|y(n)|=|x(n)g(n)|=M|g(n)| 所以当g(n)有限时该系统是稳定系统。
因y(n)只取决于现在和过去的输入x(n),不取决于本来的输入,故该系统是因果系统。
2.8 讨论下列各线性非移变系统的因果性和稳定性 (1)h(n)=2nu(-n) (4) h(n)=(12)nu(n) (2) h(n)=-a nu(-n-1) (5) h(n)=1nu(n) (3) h(n)=δ(n+n 0), n 0≥0 (6) h(n)= 2nR nu(n)解 (1)因为在n<0时,h(n)= 2n≠0,故该系统不是因果系统。
因为S=n ∞=-∞∑|h(n)|= 0n ∞=∑|2n|=1<∞,故该系统是稳定系统。
(2) 因为在n<O 时,h(n) ≠0,故该系统不是因果系统。
因为S=n ∞=-∞∑|h(n)|= 1n -=-∞∑| a n|=n ∞=∞∑a n-,故该系统只有在|a|>1时才是稳定系统。
(3) 因为在n<O 时,h(n) ≠0,故该系统不是因果系统。
因为S=n ∞=-∞∑|h(n)|= n ∞=-∞∑|δ(n+n 0)|=1<∞,故该系统是稳定系统。
(4) 因为在n<O 时,h(n)=0,故该系统是因果系统 。
因为S=n ∞=-∞∑|h(n)|= 0n ∞=∑|(12)n|<∞,故该系统是稳定系统。
(5) 因为在n<O 时,h(n)=1n u(n)=0,故该系统是因果系统 。
因为S=n ∞=-∞∑|h(n)|= n ∞=-∞∑|1nu(n)|= 0n ∞=∑1n=∞,故该系统不是稳定系统。
(6) 因为在n<O 时,h(n)=0,故该系统是因果系统 。
因为S=n ∞=-∞∑|h(n)|= 1N n -=∑|2n|=2N-1<∞,故该系统是稳定系统。
2.9 已知y(n)-2cosβy(n-1)+y(n-2)=0,且y(0)=0,y(1)=1,求证y(n)=sin()sin n ββ证明 题给齐次差分方程的特征方程为α2-2cos β·α+1=0由特征方程求得特征根α1=cos β+jsin β=e j β,α2=cos β-jsin β= e j β-齐次差分方程的通解为 y(n)=c1α1n +c2α2n =c 1e j n β+c 2ej nβ-代入初始条件得 y(0)=c 1+c 2=0y(1)= c 1e j n β+c 2ej nβ-=1由上两式得到 c 1=1j nj nee ββ--=12sin β,c 2=- c 1=-12sin β将c 1和c 2代入通解公式,最后得到 y(n) =c 1e j n β+c 2ej nβ-=12sin β( e j nβ+ e j nβ-)=sin()sin n ββ2.10 已知y(n)+2αy(n-1)+β(n-2)=0,且y(0)=0,y(1)=3,y(2)=6,y(3)=36,求y(n) 解 首先由初始条件求出方程中得系数a 和b 由(2)2(1)(0)660(3)2(2)(1)361230y ay by a y ay by a b ++=+=⎧⎨++=++=⎩可求出 a=-1,b=-8 于是原方程为y(n)-2y(n-1)-iy(n-2)=0 由特征方程α2-2α-8=0求得特征根α1=4 ,α2=-2齐次差分方程得通解为 y(n)=c1α1n +c2α2n = c 14n+c 2(-2n)代入初始条件得 y(n)= c1α1+c2α2= 4α1+2α2=3由上二式得到c 1=12,c 2=-12将c 1和c 2代入通解公式,最后得到y(n)=c 1α1n +c2α2n =12[4n-(-2) n]2.11 用特征根法和递推法求解下列差分方程: y(n)-y(n-1)-y(n-2)=0,且y(0)=1,y(1)=1解 由特征方程α2-α-1=0求得特征根α1=152,α2=152通解为y(n)=c1α1n +c2α2n =c 1(152+)n+c 2(152-)n代入初始条件得121211515(()122c c c c +=⎧⎪⎨-+=⎪⎩求出 c 11525+,c 21525-最后得到通解y(n)= c 11525+)n+ c 21525-)n5525)1n +5251n +]2.12 一系统的框图如图P2.12所示,试求该系统的单位取样响应h(n)和单位阶跃响应 解由图可知+x-1ßx(n)y(n)=x(n)+ βy(n-1)为求单位取样响应,令x(n)=δ(n),于是有 h(n)= δ(n)+ βh(n-1) 由此得到h(n)=()1n Dδβ-=βnu(n) 阶跃响应为y(n)=h(n)*u(n)=0nk =∑βky(k)u(n-k)=111n ββ+--u(n)2.13 设序列x(n)的傅立叶变换为X(e jw),求下列各序列的傅立叶变换解 (1)F[ax 1(n)+bx 2(n)]=aX 1(e jw)+bX 2(e jw)(2)F[x(n-k)]=ejwk-X(e jw)(3)F[e 0jw nx(n)]=X[e0()j w w -](4)F[x(-n)]=X(e jw-) (5)F[x *(n)]=X *(e jw-) (6)F[x *(-n)]= X *(e jw)(7)(8)jIm[x(n)]=12[X(e jw)-X *(e jw-)] (9)12πX(e j θ)*X(e jw) (10)j ()jw dx e dw2.14 设一个因果的线性非移变系统由下列差分方程描述y(n)-12y(n-1)=x(n)+ 12x(n-1) (1) 求该系统的单位取样响应h(n)(2) 用(1)得到的结果求输入为x(n)=e jwn时系统的响应(3) 求系统的频率响应(4) 求系统对输入x(n)=cos(2πn+4π)的响应解 (1)令X (n )=δ(n),得到h(n)-h(n-1)/2=δ(n)+ δ(n-1)/2由于是因果的线性非移变系统,故由上式得出 h(n)=h(n-1)/2+δ(n)+ δ(n-1)/2 ,n ≥0 递推计算出h(-1)=0h(0)=h(-1)/2+δ(0)=1 h(1)=h(0)/2+1/2=1h(2)=h(1)/2=1/2 h(3)=21h(2)=(21)2 h(4)= 21h(2)=(21)3 . ..h(n)=δ(n)+ (21)n-1u(n-1) 或 h(n)= (21)n [u(n)-u(n-1)]也可将差分方程用单位延迟算子表示成(1-D)h(n)=(1+D)δ(n)由此得到h(n)=[(1+21D)/(1-21D)]δ(n) =[1+D+21D 2+ (21)2 D 3+…+(21)k-1 D 3+…] δ(n) =δ(n)+ δ(n-1)+ 21δ(n-2)+21δ(n-3)+... +(21)k-1δ(n-1)+… =δ(n)+ (21)n u(n-1)2)将jwn e n X =)(代入)(*)()(n h n x n y =得到[]()jwjwjwnjwn jw jwnnn jwnjwn e e e e e e D D D D e D D n D De n y ------+=-+=⎥⎥⎦⎤⎢⎢⎣⎡••••+⎪⎭⎫ ⎝⎛+••••+⎪⎭⎫ ⎝⎛+++=-+=-+=2112112112121211211211)(211211*)(11322δ(3)由(2)得出()jw jwjw e e e H ---+=211211 (4)由(3)可知121121121212=-+=⎪⎪⎭⎫ ⎝⎛--wj w j w j e e e H ⎪⎭⎫ ⎝⎛-=⎥⎦⎤⎢⎣⎡--⎥⎦⎤⎢⎣⎡+=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛--21arctan 2211arctan 211arctan arg 222ππj j w j e e e H故:()()()[]⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛-+=⎥⎦⎤⎢⎣⎡++=21arctan242cosarg42cosππππneHneHny jwjw2.15 某一因果线性非移变系统由下列差分方程描述y(n)-ay(n-1)=x(n)-bx(n-1)试确定能使系统成为全通系统的b值(b≠a),所谓全通系统是指其频率响应的模为与频率ω无关的常数的系统。
