高中数学立体几何学科老师辅导讲义
立体几何专题讲义
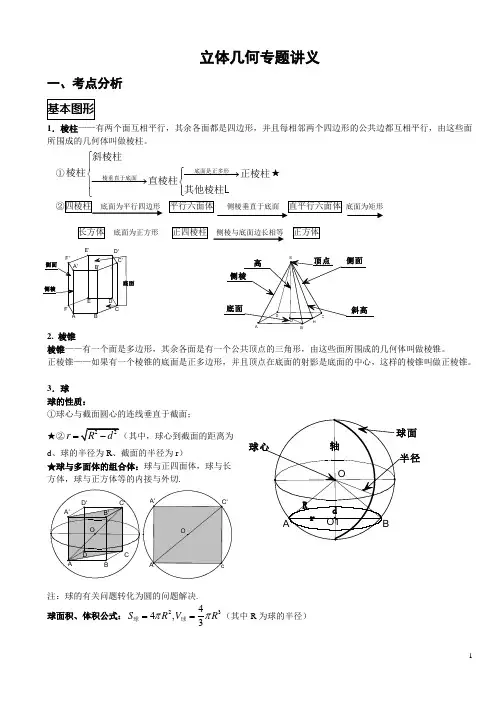
立体几何专题讲义一、考点分析1．棱柱——有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的几何体叫做棱柱。
①⎧⎪⎧−−−−−→⎨⎪−−−−−→⎨⎪⎪⎩底面是正多形棱垂直于底面斜棱柱棱柱正棱柱直棱柱其他棱柱★ 底面为矩形底面为正方形 侧棱与底面边长相等 2. 棱锥棱锥——有一个面是多边形，其余各面是有一个公共顶点的三角形，由这些面所围成的几何体叫做棱锥。
正棱锥——如果有一个棱锥的底面是正多边形，并且顶点在底面的射影是底面的中心，这样的棱锥叫做正棱锥。
3．球球的性质：①球心与截面圆心的连线垂直于截面；★②r =d 、球的半径为R 、截面的半径为r ）★球与多面体的组合体：球与正四面体，球与长 方体，球与正方体等的内接与外切.注：球的有关问题转化为圆的问题解决. 球面积、体积公式：2344,3S R V R ππ==球球（其中R 为球的半径）1．求异面直线所成的角(]0,90θ∈︒︒：解题步骤：一找（作）：利用平移法找出异面直线所成的角；（1）可固定一条直线平移 另一条与其相交；（2）可将两条一面直线同时平移至某一特殊位置。
常用中位线平移法 二证：证明所找（作）的角就是异面直线所成的角（或其补角）。
常需要证明线线平行； 三计算：通过解三角形，求出异面直线所成的角；2求直线与平面所成的角[]0,90θ∈︒︒：关键找“两足”：垂足与斜足解题步骤：一找：找（作）出斜线与其在平面内的射影的夹角（注意三垂线定理的应用）； 二证：证明所找（作）的角就是直线与平面所成的角（或其补角）（常需证明线面垂直）；三计算：常通过解直角三角形，求出线面角。
3求二面角的平面角[]0,θπ∈解题步骤：一找：根据二面角的平面角的定义，找（作）出二面角的平面角； 二证： 证明所找（作）的平面角就是二面角的平面角（常用定义法，三垂线法，垂面法）； 三计算：通过解三角形，求出二面角的平面角。
俯视图二、典型例题1．_________________.第1题2.若某空间几何体的三视图如图2所示，则该几何体的体积是________________.第2题 第3题3．一个几何体的三视图如图3所示，则这个几何体的体积为 .4．若某几何体的三视图（单位：cm ）如图4所示，则此几何体的体积是 .第4题 第5题5．如图5是一个几何体的三视图，若它的体积是 a侧(左)视图 正(主)视图 3 俯视图6．已知某个几何体的三视图如图6，根据图中标出的尺寸（单位：cm ），可得这个几何体的体积是 .第6题 第7题7.若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是 3cm 8.设某几何体的三视图如图8（尺寸的长度单位为m ），则该几何体的体积为_________m 3。
高中数学立体几何讲义
高中数学立体几何讲义(一)(总13页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--平面与空间直线(Ⅰ)、平面的基本性质及其推论1、空间图形是由点、线、面组成的。
点、线、面的基本位置关系如下表所示：图形符号语言文字语言（读法） AaA a ∈ 点A 在直线a 上。
AaA a ∉点A 不在直线a 上。
AαA α∈点A 在平面α内。
AαA α∉点A 不在平面α内。
b a Aa b A =直线a 、b 交于A 点。
aαa α直线a 在平面α内。
aαa α=∅直线a 与平面α无公共点。
aAαa A α=直线a 与平面α交于点A 。
l αβ=平面α、β相交于直线l 。
α⊄a （平面α外的直线a ）表示a α=∅或a A α=。
2、平面的基本性质公理1： 如果一条直线的两点在一个平面内，那么这条直线上的所有点都在这个平面内推理模式：A AB B ααα∈⎫⇒⎬∈⎭。
如图示：应用：是判定直线是否在平面内的依据，也是检验平面的方法。
BA α公理2：如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线。
推理模式：A l A ααββ∈⎫⇒=⎬∈⎭且A l ∈且l 唯一如图示：应用：①确定两相交平面的交线位置；②判定点在直线上。
例1．如图，在四边形ABCD 中，已知AB ∥CD ，直线AB ，BC ，AD ，DC 分别与平面α相交于点E ，G ，H ，F ．求证：E ，F ，G ，H 四点必定共线． 解：∵AB ∥CD ，∴AB ，CD 确定一个平面β．又∵AB α＝E ，AB ⊂β，∴E ∈α，E ∈β， 即E 为平面α与β的一个公共点．同理可证F ，G ，H 均为平面α与β的公共点．∵两个平面有公共点，它们有且只有一条通过公共点的公共直线， ∴E ，F ，G ，H 四点必定共线．说明：在立体几何的问题中，证明若干点共线时，常运用公理2，即先证明这些点都是某二平面的公共点，而后得出这些点都在二平面的交线上的结论．例2．如图，已知平面α，β，且α β＝l ．设梯形ABCD 中，AD ∥BC ，且AB ⊂α，CD ⊂β，求证：AB ，CD ，l 共点（相交于一点）．α D C B A EFHGA证明∵梯形ABCD中，AD∥BC，∴AB，CD是梯形ABCD的两条腰．∴AB，CD必定相交于一点，设AB CD＝M．又∵AB⊂α，CD⊂β，∴M∈α，且M∈β．∴M∈α β．又∵α β＝l，∴M∈l，即AB，CD，l共点．说明：证明多条直线共点时，一般要应用公理2，这与证明多点共线是一样的．公理3：经过不在同一条直线上的三点，有且只有一个平面。
(完整)高中数学第一二章立体几何复习讲义人教版必修二.doc(2)
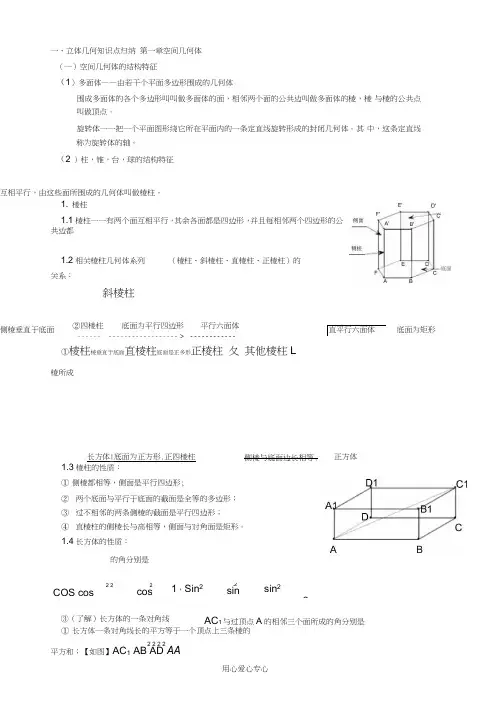
一、立体几何知识点归纳 第一章空间几何体 （一）空间几何体的结构特征（1）多面体——由若干个平面多边形围成的几何体围成多面体的各个多边形叫叫做多面体的面，相邻两个面的公共边叫做多面体的棱，棱 与棱的公共点叫做顶点。
旋转体一一把一个平面图形绕它所在平面内的一条定直线旋转形成的封闭几何体。
其 中，这条定直线称为旋转体的轴。
（2 ）柱，锥，台，球的结构特征1. 棱柱1.1棱柱一一有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都1.2相关棱柱几何体系列（棱柱、斜棱柱、直棱柱、正棱柱）的关系：斜棱柱①棱柱棱垂直于底面直棱柱底面是正多形正棱柱 夂 其他棱柱L长方体|底面为正方形.正四棱柱 1.3棱柱的性质：① 侧棱都相等，侧面是平行四边形;② 两个底面与平行于底面的截面是全等的多边形； ③ 过不相邻的两条侧棱的截面是平行四边形；④ 直棱柱的侧棱长与高相等，侧面与对角面是矩形。
1.4长方体的性质：① 长方体一条对角线长的平方等于一个顶点上三条棱的 2 2 2 2平方和；【如图】AC 1 AB AD AA互相平行，由这些面所围成的几何体叫做棱柱。
②四棱柱 底面为平行四边形 平行六面体 ------ _ ------------------ > ------------侧棱垂直于底面 直平行六面体 底面为矩形棱所成的角分别是2 2COS cos2cos1，Sin 2.2sinsin 22③（了解）长方体的一条对角线AC 1与过顶点A 的相邻三个面所成的角分别是侧棱与底面边长相等.正方体底面②（了解）长方体的一条对角线AG与过顶点A的三条贝V cos2cos2cos22，sin2 sin2 sin21.1.5侧面展开图：正n 棱柱的侧面展开图是由 n 个全等矩形组成的以底面周长和侧棱长为邻 边的矩形.c h（其中c 为底面周长，hc h 2S底，V 棱柱S 底h为棱柱的高）2•圆柱2.1圆柱——以矩形的一边所在的直线为旋转轴，其余各边旋转而形成的曲面所围成的几何体叫圆柱•2.2圆柱的性质：上、下底及平行于底面的截面都是 等圆；过轴的截面（轴截面）是全等的矩形2.3侧面展开图：圆柱的侧面展开图是以底面周长和 母线长为邻边的矩形. 2.4面积、体积公式② 正棱锥各侧棱相等，各侧面是全等的等腰三角形；1.6面积、体积公式:S 圆柱侧=2 rh ； S 圆柱全= 2 rh22 r ， V 圆柱=S 底h=2r h （其中r 为底面半径,h 为圆柱高）3.棱锥 3.1棱锥一一有一个面是多边形， 其余各 面是有一个公共顶点的三角形，侧棱底面顶点侧面斜高轴母线轴截面侧面底面OVSOB,VSOH,VSBH,VOBH为直角三角形）1 1 1 ,3.4面积、体积公式：S正棱锥侧=ch ，S正棱锥全=ch S底，V棱锥=—S底h .（其中c为底面2 2 3周长，h侧面斜高，h棱锥的高）4.圆锥4.1圆锥一一以直角三角形的一直角边所在的直线为旋转轴，其余各边旋转而形成的曲面所围成的几何体叫圆锥。
高一数学立体几何讲义
I. 基础知识要点一、 平面.1. 经过不在同一条直线上的三点确定一个面.注：两两相交且不过同一点的四条直线必在同一平面内.2. 两个平面可将空间分成3或4部分.（①两个平面平行，②两个平面相交）3. 过三条互相平行的直线可以确定1或3个平面.（①三条直线在一个平面内平行，②三条直线不在一个平面内平行）[注]：三条直线可以确定三个平面，三条直线的公共点有0或1个.4. 三个平面最多可把空间分成 8 部分.（X 、Y 、Z 三个方向）二、 空间直线.1. 空间直线位置分三种：相交、平行、异面. 相交直线——共面有且仅有一个公共点；平行直线——共面没有公共点；异面直线——不同在任一平面内[注]：①两条异面直线在同一平面内射影一定是相交的两条直线.（×）（可能两条直线平行，也可能是点和直线等）②直线在平面外，指的位置关系：平行或相交③若直线a 、b 异面，a 平行于平面α，b 与α的关系是相交、平行、在平面α内. ④两条平行线在同一平面内的射影图形是一条直线或两条平行线或两点.⑤在平面内射影是直线的图形一定是直线.（×）（射影不一定只有直线，也可以是其他图形） ⑥在同一平面内的射影长相等，则斜线长相等.（×）（并非是从平面外一点．．向这个平面所引的垂线段和斜线段）⑦b a ,是夹在两平行平面间的线段，若b a =，则b a ,的位置关系为相交或平行或异面.2. 异面直线判定定理：过平面外一点与平面内一点的直线和平面内不经过该点的直线是异面直线.（不在任何一个平面内的两条直线）3. 平行公理：平行于同一条直线的两条直线互相平行.4. 等角定理：如果一个角的两边和另一个角的两边分别平行并且方向相同，那么这两个角相等（如下图）.（二面角的取值范围[) 180,0∈θ） （直线与直线所成角(] 90,0∈θ）（斜线与平面成角() 90,0∈θ）（直线与平面所成角[] 90,0∈θ） 推论：如果两条相交直线和另两条相交直线分别平行，那么这两组直线所成锐角（或直角）相等.5. 两异面直线的距离：公垂线的长度.空间两条直线垂直的情况：相交（共面）垂直和异面垂直.21,l l 是异面直线，则过21,l l 外一点P ，过点P 且与21,l l 都平行平面有一个或没有，但与21,l l 距离相等的点在同一平面内. （1L 或2L 在这个做出的平面内不能叫1L 与2L 平行的平面）三、 直线与平面平行、直线与平面垂直.1. 空间直线与平面位置分三种：相交、平行、在平面内.2. 直线与平面平行判定定理：如果平面外一条直线和这个平面内一条直线平行，那么这条直线和这个平面平行.（“线线平行，线面平行”）[注]：①直线a 与平面α内一条直线平行，则a ∥α. （×）（平面外一条直线）②直线a 与平面α内一条直线相交，则a 与平面α相交. （×）（平面外一条直线） 12方向相同12方向不相同③若直线a 与平面α平行，则α内必存在无数条直线与a 平行. （√）（不是任意一条直线，可利用平行的传递性证之）④两条平行线中一条平行于一个平面，那么另一条也平行于这个平面. （×）（可能在此平面内）⑤平行于同一直线的两个平面平行.（×）（两个平面可能相交）⑥平行于同一个平面的两直线平行.（×）（两直线可能相交或者异面）⑦直线l 与平面α、β所成角相等，则α∥β.（×）（α、β可能相交）3. 直线和平面平行性质定理：如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行.（“线面平行，线线平行”）4. 直线与平面垂直是指直线与平面任何一条直线垂直，过一点有且只有一条直线和一个平面垂直，过一点有且只有一个平面和一条直线垂直.● 若PA ⊥α，a ⊥AO ，得a ⊥PO （三垂线定理）， 得不出α⊥PO . 因为a ⊥PO ，但PO 不垂直OA .● 三垂线定理的逆定理亦成立.直线与平面垂直的判定定理一：如果一条直线和一个平面内的两条相交直线都垂直，那么这两条直线垂直于这个平面.（“线线垂直，线面垂直”）直线与平面垂直的判定定理二：如果平行线中一条直线垂直于一个平面，那么另一条也垂直于这个平面.推论：如果两条直线同垂直于一个平面，那么这两条直线平行.[注]：①垂直于同一平面．．．．的两个平面平行.（×）（可能相交，垂直于同一条直线．．．．．的两个平面平行）②垂直于同一直线的两个平面平行.（√）（一条直线垂直于平行的一个平面，必垂直于另一个平面）③垂直于同一平面的两条直线平行.（√）5. ⑴垂线段和斜线段长定理：从平面外一点．．向这个平面所引的垂线段和斜线段中，①射影相等的两条斜线段相等，射影较长的斜线段较长；②相等的斜线段的射影相等，较长的斜线段射影较长；③垂线段比任何一条斜线段短.[注]：垂线在平面的射影为一个点. [一条直线在平面内的射影是一条直线.（×）]⑵射影定理推论：如果一个角所在平面外一点到角的两边的距离相等，那么这点在平面内的射影在这个角的平分线上四、 平面平行与平面垂直.1. 空间两个平面的位置关系：相交、平行.2. 平面平行判定定理：如果一个平面内有两条相交直线都平行于另一个平面，哪么这两个平面平行.（“线面平行，面面平行”）推论：垂直于同一条直线的两个平面互相平行；平行于同一平面的两个平面平行.[注]：一平面间的任一直线平行于另一平面.3. 两个平面平行的性质定理：如果两个平面平行同时和第三个平面相交，那么它们交线平行.（“面面平行，线线平行”）4. 两个平面垂直性质判定一：两个平面所成的二面角是直二面角，则两个平面垂直.两个平面垂直性质判定二：如果一个平面与一条直线垂直，那么经过这条直线的平面垂直于这个平面.（“线面垂直，面面垂直”）注：如果两个二面角的平面对应平面互相垂直，则两个二面角没有什么关系.5. 两个平面垂直性质定理：如果两个平面垂直，那么在一个平面内垂直于它们交线的直线也垂直于另一个平面.P OA a P αβ推论：如果两个相交平面都垂直于第三平面，则它们交线垂直于第三平面.证明：如图，找O 作OA 、OB 分别垂直于21,l l ，因为ααββ⊥⊂⊥⊂OB PM OA PM ,,,则OB PM OA PM ⊥⊥,.五、 棱锥、棱柱.1. 棱柱.⑴①直棱柱侧面积：Ch S =（C 为底面周长，h 是高）该公式是利用直棱柱的侧面展开图为矩形得出的.②斜棱住侧面积：l C S 1=（1C 是斜棱柱直截面周长，l 是斜棱柱的侧棱长）该公式是利用斜棱柱的侧面展开图为平行四边形得出的.⑶棱柱具有的性质：①棱柱的各个侧面都是平行四边形，所有的侧棱都相等；直棱柱的各个侧面都是矩形．．．．．．．．；正棱柱的各个侧面都是全等的矩形．．．．．.②棱柱的两个底面与平行于底面的截面是对应边互相平行的全等．．多边形. ③过棱柱不相邻的两条侧棱的截面都是平行四边形.注：①棱柱有一个侧面和底面的一条边垂直可推测是直棱柱. （×）（直棱柱不能保证底面是钜形可如图）②（直棱柱定义）棱柱有一条侧棱和底面垂直.[注]：①有两个侧面是矩形的棱柱是直棱柱.（×）（斜四面体的两个平行的平面可以为矩形） ②各侧面都是正方形的棱柱一定是正棱柱.（×）（应是各侧面都是正方形的直．棱柱才行） ③对角面都是全等的矩形的直四棱柱一定是长方体.（×）（只能推出对角线相等，推不出底面为矩形） ④棱柱成为直棱柱的一个必要不充分条件是棱柱有一条侧棱与底面的两条边垂直. （两条边可能相交，可能不相交，若两条边相交，则应是充要条件）2. 棱锥： [注]：①一个棱锥可以四各面都为直角三角形.②一个棱柱可以分成等体积的三个三棱锥；所以棱柱棱柱3V Sh V ==.⑴①正棱锥定义：底面是正多边形；顶点在底面的射影为底面的中心.[注]：i. 正四棱锥的各个侧面都是全等的等腰三角形.（不是等边三角形）ii. 正四面体是各棱相等，而正三棱锥是底面为正△侧棱与底棱不一定相等iii. 正棱锥定义的推论：若一个棱锥的各个侧面都是全等的等腰三角形（即侧棱相等）；底面为正多边形. ②正棱锥的侧面积：'Ch 21S =（底面周长为C ，斜高为'h ） ⑵棱锥具有的性质：①正棱锥各侧棱相等，各侧面都是全等的等腰三角形，各等腰三角形底边上的高相等（它叫做正棱锥的斜高）.②正棱锥的高、斜高和斜高在底面内的射影组成一个直角三角形，正棱锥的高、侧棱、侧棱在底面内的射影也组成一个直角三角形.⑶特殊棱锥的顶点在底面的射影位置：①棱锥的侧棱长均相等，则顶点在底面上的射影为底面多边形的外心.②棱锥的侧棱与底面所成的角均相等，则顶点在底面上的射影为底面多边形的外心. ③棱锥的各侧面与底面所成角均相等，则顶点在底面上的射影为底面多边形内心. ④棱锥的顶点到底面各边距离相等，则顶点在底面上的射影为底面多边形内心.⑤三棱锥有两组对棱垂直，则顶点在底面的射影为三角形垂心.⑥三棱锥的三条侧棱两两垂直，则顶点在底面上的射影为三角形的垂心.⑦每个四面体都有外接球，球心0是各条棱的中垂面的交点，此点到各顶点的距离等于球半径；⑧每个四面体都有内切球，球心I 是四面体各个二面角的平分面的交点，到各面的距离等于半径.[注]：i. 各个侧面都是等腰三角形，且底面是正方形的棱锥是正四棱锥.（×）（各个侧面的等腰三角形不知是否全等）3. 球：⑴球的截面是一个圆面.①球的表面积公式：24R S π=. ②球的体积公式：334R V π=. 附：①圆柱体积：h r V 2π=（r 为半径，h 为高） ②圆锥体积：h r V 231π=（r 为半径，h 为高） ③锥形体积：Sh V 31=（S 为底面积，h 为高） 侧面积公式S 直棱柱侧＝ch ( c －底面周长，h －高 )S 正棱锥侧＝1/2 ch ( c －底面周长，h －斜高 )S 正棱台侧＝1/2 (c ＋c')h (c ，c'－上、下底面周长，h －斜高)S 圆柱侧＝cl ＝2πrl (c －底面周长，l －母线长 ，r －底面半径) S 圆锥侧＝1/2cl ＝πrl (c －底面周长，l －母线长 ，r －底面半径) S 圆台侧＝1/2(c ＋c')l ＝π(r ＋r')l(c ，c' －上、下底面周长，r ，r －上、下底面半径)体积公式V 柱体＝Sh ( S －底面积，h －高 )V 椎体=1/3Sh ( S －底面积，h －高 )()h ss s s V '31'++=台体 (S ，S －上下底面积，h －高 ) 3R 34π=球V (R 为球的半径) 24R S π=球。
立体几何的体积和表面积辅导讲义
旋转体 (3)圆台可以由直角梯形绕直角腰所在直线或等腰梯形绕上、下底中点连
线所在直线旋转得到，也可由平行于底面的平面截圆锥得到.
(4)球可以由半圆或圆绕直径所在直线旋转得到.
2.三视图与直观图
三视图
画法规则：长对正，高平齐，宽相等
空间几何的直观图：常用斜二测画法来画.
基本步骤是：
(1)原图形中 x 轴、y 轴、z 轴两两垂直，直观
第 5 页（共 14 页）
综上可得，S1∶S2∶S3＝1∶2∶3. 思维升华 (1)解决组合体问题关键是分清该几何体是由哪些简单的几何体组成的以及这些简单的几何体的 组合情况；(2)由三视图求几何体的面积、体积，关键是由三视图还原几何体，同时还需掌握求体积的常用 技巧如：割补法和等价转化法．
(2)把边长为 1 的正方形 ABCD 沿对角线 BD 折起，使得平面 ABD⊥平面 CBD，形成三棱锥 C－ABD 的正视 图与俯视图如图所示，则侧视图的面积为( )
空间几何体的表面积和体积
1．空间几何体的结构特征
(1)棱柱的侧棱都平行且相等，上、下底面是全等的多边形.
多面体 (2)棱锥的底面是任意多边形，侧面是有一个公共顶点的三角形.
(3)棱台可由平行于底面的平面截棱锥得到，其上、下底面是相似多边形.
(1)圆柱可以由矩形绕其任一边所在直线旋转得到.
(2)圆锥可以由直角三角形绕其直角边所在直线旋转得到.
17
5
10
1
A.27
B.9
C.27
D.3
第 4 页（共 14 页）
(2)一个多面体的三视图如图所示，则该多面体的体积为( )
23
47
A. 3
B. 6
C．6
最新人教A版必修2高中数学 第一章《立体几何》复习讲义1
1 1
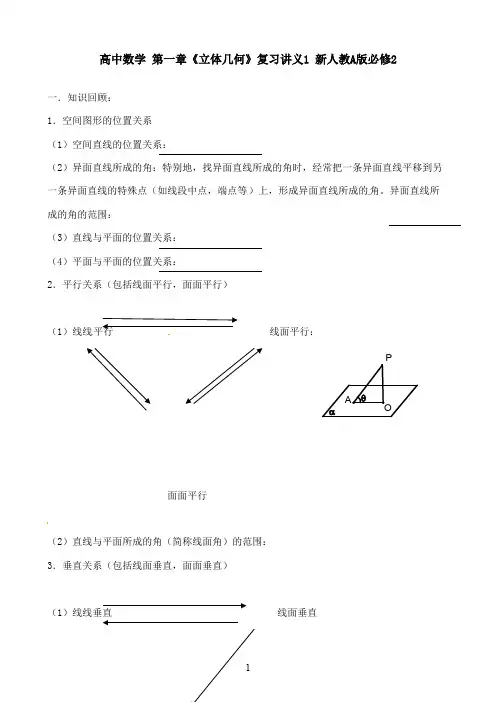
④ , // ，说法正确的序号是：_________________ E A 例2、如右图，在正方体ABCD－A1B1C1D1中，E、F为棱AD、AB的中点． （1）求证：EF∥平面CB1D1； 2 D F B C
（2）求证：B1D1⊥平面CAA1C1
练习： 如图，已知矩形ABCD中，AB=10，BC=6，将矩形沿对角线BD把△ABD折起，使A移到 A1 点，且 A1 在平面BCD上的射影O恰好在CD上． （1）求证： BC A1 D ； （2）求证：平面 A1 BC 平面
A1 BD ；
（3）求三棱锥 A1 BCD 的体积
（1）线线 平行
线面平行：
P
A
O
面面平行
（2）直线与平面所成的角（简称线面角）的范围： 3．垂直关系（包括线面垂直，面面垂直）
（1）线线垂直
线面垂直
1
面面垂直
（2）二面角：二面角的平面角的范围： 二．立体几何常见题型归 纳例讲 1、概念辨析题： （1）此题型一般出现在填空题，选择题中，解题方法可采用排除法，筛选法等。 （2）对于判断线线关系，线面关系，面面关系等方面的问题，必须在熟练掌握有关的定理 和性质的前提下，利用长方体，正方体，实物等为模型来进行判断。你认为正确的命 题需要证明它，你认为错误的命题必须找出反例。 （3）相关例题：课本和报纸上出现很多这样的题型，举例说明如下： 2、证明 题：证明平行关系，垂直关系等方面的问题。 三、例题分析 例1、设m，n是两条不同的直线， , , 是三个不同的平面，给出下 列四个说法：① m , n // m n ；②
【精】高中数学：立体几何优质讲义.docx
高中数学：立体几何优质讲义姓名:指导：日期：立体几何证平行（一）甄蟻平有＜■图丄E）--------------- K如果两条蛾切平行于第三条最，那么这两条蛾相互平行.2.如果一条蛛平行于另一个平面，那么这条蟻就平行于这这条地的平面与已知平而的交蟻. 图丄】3 .血果商个平面平行，那玄另一个平血虹诳两个平血的交妹互制平行.4如果两喪直蟻都制另一•个平而垂直.那么这两条直蟻平有.5一在同T面内，如果两条直或垂直于同一条直墟，那么这两条直慟'成.，程茜师中学亞建化L.如果平而外一条直絞平行于平面内的一条直銭，那衣宜城与平而干径 :!.如果两个平部平行，一个平薊内的任何一条直域平行于另一个平面. 3 .州果平血*了平而如一条如果干时垂直于另--条直邑, 4 一如果平面与平面外一条直理同时垂直于另一个平面,I. 如果一个平而内有两果闵全平f li 平有于另一个平而,丄如果两个平面揺平行于第三个平潮，那互这两个平面平有. 3.如果两个平面问畦垂直于同一条面雄，那么这两个平ffii 平行.证塔直大部分毎是通过隼直证垂直:下能ii 史旳时榛.平移到另i 一个位置证垂直. （一） 或蟻垂西如果一案直蛾垂直于一个平St 那佥谊条宜戒垂直于这个平ifi 内的任何一条直銭一 （二） 蜷海垂苴【一如果一条直蜷垂直于平而内两条招交的部，那么这条直坡就垂直于两条相交直域所在的平面. 丄如果睥个平而常有，在其中一个 平血內，垂森于公芯検的il 注垂立于yi-t-Tni!. t 三）而而垂直（■囲At ）【.辻一个平而垂洼旳平而垂辻于巳辻平而. 土二部南为直请的两个平面垂直.〈理科）（四〉不能祝匿征垂直的情况L 把已知蟻成ffii 平秽到容駐证照垂直的位置 2.询和已知蟻或面平行的蟻凍海证垂直一那么场面平有. 图卩二.求相疔，求距离，成求体根〈一）求術》〈理我丄技线爾.絞血曲•和二而跆歩L建系，崖可能il.薮将计算的点落在抽我和軸而L坐株系可以任意拆向*凡是角度渉成的面都要至少已如（SU出）3个点，肅度演及的絞都要至少巳知《成求出）£个点.歩，标期段坐标，不能表廚的可以持定字毋系数，当盧坐岳中只舍有一个未知字毋时可以直接代入下一歩求解：当点坐标中含有£个以上未知字毋盹需要握据以下三点列式求字母取住.①前量垂成a ijj =>^15 +y L k'i + -^i = u囲向量其蟻，"Jj2n W =虹2.乂 =加.=切崖向0模，何|=巧了「了歩丄表航向量，终点跋起点歩4:朮法曲丽1也（歩I上（如丄"I'""（歩3丄不姉妨X."中一一个字辱为。
高三数学立体几何专题复习讲义资料
1平行关系例题讲解：例1：已知四面体ABCD 中：M 、N 分别是△ABC 和△ACD 的重心：求证：(1)MN ∥平面ABD ： (2)BD ∥平面CMN 。
答案与提示：连CM 、CN 分别交AB 、AD 于E 、F ：连EF ：易证 MN ∥EF ∥BD例2.已知边长为10的等边三角形ABC 的顶点A 在平面α内：顶点B 、C 在平面α的上方：BD 为AC 边上的中线：B 、C 到平面α的距离BB 1=2：CC 1=4． (1)求证：BB 1∥平面ACC 1 (2)求证：BD ⊥平面ACC 1 (3)求四棱锥A -BCC 1B 1的体积 答案与提示：（3）307例3.已知P A ⊥平面ABCD ：四边形ABCD 是矩形：M 、N 分别是AB 、PC 的中点.(1) 求证：MN ∥平面P AD ： (2) 求证：MN ⊥CD ：(3) 若平面PCD 与平面ABCD 所成二面角为θ：问能否确定θ的值：使得MN 是异面直线AB 与PC 的公垂线.答案与提示：（3）45°备用题如图,在三棱锥P -ABC 中：P A ⊥面ABC ：△ABC 为正三角形： D 、E 分别为BC 、AC 的中点：设AB =2P A =2：(1)如何在BC 上找一点F ：使AD ∥平面PEF ？说明理由： (2)对于(1)中的点F ：求二面角P -EF -A 的大小： 答案与提示：（1）F 为CD 中点（2）arctan2作业D CB M AN P在正四棱柱ABCD -A 1B 1C 1D 1中：AA 1=12 AB ：点E 、M 分别为A 1B 、C 1C 的中点：过A 1：B ：M 三点的平面交C 1D 1于点N 。
(1)求证：EM ∥平面ABCD ： (2)求二面角B -A 1N -B 1的正切值。
答案与提示：（2）arctan542垂直关系例题讲解：例1：如图,在三棱锥P -ABC 中：AB =BC =CA ：P A ⊥底面ABC ：D 为AB 的中点．(1)求证：CD ⊥PB ：(2)设二面角A -PB -C 的平面角为α：且tan α=7：若底面边长为1：求三棱锥P -ABC 的体积． 答案与提示：（2）18例2：已知ABCD —A 1B 1C 1D 1是棱长为a 的正方体：E 、F 分别是棱AA 1和CC 1的中点：G 是A 1C 1的中点．(1)求证平面BFD 1E ⊥平面BGD 1： (2)求点G 到平面BFD 1E 的距离： (3)求四棱锥A 1-BFD 1E 的体积．答案与提示：（2）66a (3) 16a 3例3：四边形ABCD 中．AD ∥BC ：AD =AB ：∠BCD =45°：∠BAD =90°：将△ABD 沿对角线BD 折起：记折起点A 的位置为P ：且使平面PBD ⊥平面BCD ． (1)求证：CD ⊥平面PBD ：(2)求证：平面PBC ⊥平面PDC ： (3)求二面角P —BC —D 的大小．答案与提示：(2)先证PB ⊥面PCD (3)arctan 2备用题在三棱锥S -ABC 中：已知SA =4：AB =AC ：BC =3 6 ,∠SAB =∠SAC =45°,SA 与底面ABC 所的角为30°.BA PD CE(1)求证：SA ⊥BC ：(2)求二面角S —BC —A 的大小： (3)求三棱锥S —ABC 的体积． 答案与提示：(2)arctan 23 3 (3)9 2作业1.在四棱锥P -ABCD 中：已知PD ⊥底面ABCD ：底面ABCD 为等腰梯形,且∠DAB =60°：AB =2CD ：∠DCP =45°：设CD =a ．(1)求四棱锥P -ABCD 的体积． (2)求证：AD ⊥PB ． 答案与提示：(1)34a 32.如图：正三角形ABC 与直角三角形BCD 成直二面角：且∠BCD =90°：∠CBD =30°.（1）求证：AB ⊥CD ：（2）求二面角D —AB —C 的大小： 答案与提示：(2)arctan 233 空间角例1、如图1：设ABC -A 1B 1C 1是直三棱柱：F 是A 1B 1的中点：且SC CBAAAB(1)求证：AF ⊥A 1C ： (2)求二面角C -AF -B 的大小．解：(1)如图2：设E 是AB 的中点：连接CE ：EA 1．由ABC -A 1B 1C 1是直三棱柱：知AA 1⊥平面ABC ：而CE 平面ABC ：所以CE ⊥AA 1：∵AB =2AA 1=2a ：∴AA 1=a ：AA 1⊥AE ：知AA 1FE 是正方形：从而AF ⊥A 1E ．而A 1E 是A 1C 在平面AA 1FE 上的射影：故AF ⊥A 1C ：(2)设G 是AB 1与A 1E 的中点：连接CG ．因为CE ⊥平面AA 1B 1B ：AF ⊥A 1E ：由三垂线定理：CG ⊥AF ：所以∠CGE 就是二面角C -AF -B 的平面角．∵AA 1FE 是正方形：AA 1=a ：∴11222EG EA a ==： ∴2216222CG a a =-=： ∴tan ∠CGE =6232CG EG a ===：∠CGE ＝60：从而二面角C -AF -B 的大小为60。
高中数学讲义 第七章 立体几何初步(超级详细)
分析：证明两条直线异面通常采用反证法。
证明：(1)（反证法）假设AC与BD不是异面直线，则AC与BD共面，
所以A、B、C、D四点共面
这与空间四边形ABCD的定义矛盾
所以对角线AC与BD是异面直线
(2)解：∵E,F分别为AB,BC的中点,∴EF//AC,且EF= AC.
（1）求圆锥的母线与底面所成的角；
（2）求圆锥的全面积．
解: （1）设圆锥的底面半径为R，母线长为l，
由题意得： ,
即 ,
所以母线和底面所成的角为
(2)设截面与圆锥侧面的交线为MON，
其中O为截面与AC的交点，则OO1//AB且
在截面MON内，以OO1所在有向直线为y轴，O为原点，建立坐标系，
则O为抛物线的顶点，所以抛物线方程为x2=－2py，
同理HG//AC,且HG= AC.∴EF平行且相等HG,∴EFGH是平行四边形.
又∵F,G分别为BC,CD的中点,∴FG//BD,∴∠EFG是异面直线AC与BD所成的角.
∵AC⊥BD,∴∠EFG=90o.∴EFGH是矩形.
(3)作法取BD中点E,AC中点F,连EF,则EF即为所求.
点评：在空间四边形中我们通常会遇到上述类似的问题，取中点往往是很有效的方法，特别是遇到等腰三角形的时候。
3．抓主线，攻重点。针对一些重点内容加以训练，平行和垂直是位置关系的核心，而线面垂直又是核心的核心，角与距离的计算已经降低要求。
4．复习中要加强数学思想方法的总结与提炼。立体几何中蕴含着丰富的思想方法，如：将空间问题转化成平面图形来解决、线线、线面与面面关系的相互转化、空间位置关系的判断及角与距离的求解转化成空间向量的运算。
高二立体几何数学讲义1.doc
高二立体几何数学讲义（一）一、空间几何体的结构特征及三视图和直观图知识点回顾1.空间几何体的结构特征2.空间几何体的三视图三视图：用得到，这种投影下与投影面的平面图形留下的影子与平面图形的形状和大小是的.三视图包括、、.3.空间几何体的直观图空间几何体的直观图常用画法来画，基本规则是：(1)原图形中x轴、y轴、z轴两两垂直，直观图中，x′轴、y′轴的夹角为，z′轴与x′轴和y′轴所在平面.(2)原图形中平行于坐标轴的线段，直观图中. 平行于x轴和z轴的线段长度在直观图中，平行于y轴的线段长度在直观图中.巩固练习1.下列有关棱柱的命题中正确的是()A.有两个面平行，其余各面都是四边形的几何体叫棱柱B.有两个面平行，其余各面都是平行四边形的几何体叫棱柱C.一个棱柱至少有五个面、六个顶点、九条棱D.棱柱的侧棱长有的都相等，有的不都相等2.用任意一个平面截一个几何体，各个截面都是圆，则这个几何体一定是()A.圆柱B.圆锥C.球体D.圆柱，圆锥，球体的组合体3.如图所示，下列几何体各自的三视图中，有且仅有两个视图相同的是() A.①② B.①③ C.①④ D.②④4.如图所示，图①、②、③是图④表示的几何体的三视图，其中图①是，图②是，图③是(说出视图名称).5.下面有四个命题：(1)各个侧面都是等腰三角形的棱锥是正棱锥；(2)三条侧棱都相等的棱锥是正三棱锥；(3)底面是正三角形的棱锥是正三棱锥；(4)顶点在底面上的射影是底面多边形的内心，又是外心的棱锥必是正棱锥.其中正确命题的个数是()A.1B.2C.3D.4二、平面的基本性质1.下列命题：①两两相交的三条直线共面；②两条相交直线上的三个点可以确定一个平面；③梯形是平面图形；④一条直线和一个点可以确定一个平面；⑤两条相交直线可以确定一个平面；⑥若点P不在平面α内，A,B,C三点都在平面α内，则P、A、B、C四点不在同一平面内.其中正确的有.2.下列命题中不正确的是.①若一条直线上有一点在平面外，则直线上有无穷多点在平面外；②若点,,A B C ABαα∈∈∈,则Cα∈；③若,,,a b l a A l b Bαα⊂⊂==,则lα⊂；④若一条直线上有两点在已知平面外，则直线上所有点在平面外。
高三立体几何讲义
立体几何讲义一、空间几何体 球与正方体的组合体问题(1)正方体的内切球： 球与正方体的每个面都相切，切点为每个面的中心，显然球心为正方体的中心。
设正方体的棱长为a ，球半径为R 。
如图3，截面图为正方形EFGH 的内切圆，得2aR =； (2)与正方体各棱相切的球：球与正方体的各棱相切，切点为各棱的中点，如图4作截面图，圆O 为正方形EFGH 的外接圆，易得a R 22=。
(3)正方体的外接球：正方体的八个顶点都在球面上，如图5，以对角面1AA 作截面图得，圆O 为矩形C C AA 11的外接圆，易得a O A R 231==。
例1．某三棱锥的三视图如图所示,该三棱锥的表面积是().ABCD例2.（1） 在球面上有四个点P 、A 、B 、C .如果PA 、PB 、PC 两两互相垂直，且a PC PB PA ===,那么这个球的表面积是______.(2)正四棱锥S ABCD -，点S 、A 、B 、C 、D 都在同一个球面上，则该球的体积为_________。
二、平行关系例3. 如图,直三棱柱ABC-A'B'C',∠BA点M,N 分别为A'B 和B'C'的中点.图3图4图5证明:MN ∥平面A'ACC';三、垂直关系例4.如图，三棱柱ABC －A 1B 1C 1中，侧棱垂直底面，∠ACB=90°，AC=BC=12AA 1，D 是棱AA 1的中点证明：平面BDC 1⊥平面BDC（2）. 如图,三棱柱ABC-A 1B 1C 1中,CA=CB,AB=A A 1,∠BA A 1=60°.证明AB ⊥A 1C; 如图,三棱柱ABC-A 1B 1C 1中,CA=CB,AB=A A 1,∠BA A 1=60°.(Ⅰ)证明AB ⊥A 1C;(Ⅱ)若平面ABC⊥平面AA 1B 1B,AB=CB=2,求直线A 1C 与平面BB 1C 1C 所成角的正弦值.B 1CB A DC 1A 1（3）如图,AB 是圆的直径,PA 垂直圆所在的平面,C 是圆上的点.(I)求证:PAC PBC ⊥平面平面；(II)2.AB AC PA C PB A ===--若，1，1，求证：二面角的余弦值练习题1. 一个长方体全面积是20cm 2，所有棱长的和是24cm ，求长方体的对角线长.2．如图所示是一个几何体的三视图，根据图中标出的尺寸(单位：cm)，可得该几何体的表面积为________cm 2.3. 如图，某三棱锥的三视图都是直角边为2的等腰直角三角形，则该三棱锥的体积是(A)43 (B) 83(C) 4 (D) 8 4．一个长方体共一顶点的三个面的面积分别是6,3,2，这个长方体对角线的长是（ ） A ．23B ．32C ．6D ．65. 如图，已知四棱锥P －ABCD 的底面为等腰梯形，AB ∥CD ，AC ⊥BD ，垂足为H ，PH 是四棱锥的高．(1)证明：平面PAC ⊥平面PBD ；(2) )若AB ＝6，∠APB ＝∠ADB ＝60°,求面APD 与面BPC 所成二面角的余弦值。
高中数学空间立体几何讲义
第1讲 空间几何体高考《考试大纲》的要求：① 认识柱、锥、台、球及其简单组合体的结构特征，并能运用这些特征描述现实生活中简单物体的结构.② 能画出简单空间图形（长方体、球、圆柱、圆锥、棱柱等的简易组合）的三视图，能识别上述的三视图所表示的立体模型，会用斜二测法画出它们的直观图.③ 会用平行投影与中心投影两种方法，画出简单空间图形的三视图与直观图，了解空间图形的不同表示形式.④ 会画某些建筑物的视图与直观图（在不影响图形特征的基础上，尺寸、线条等不作严格要求）. ⑤ 了解球、棱柱、棱锥、台的表面积和体积的计算公式（不要求记忆公式）. （一）例题选讲：例1.四面体ABCD 的外接球球心在CD 上，且CD ＝2，AB ＝3，在外接球面上两点A 、B 间的球面距离是（ ）A ．6π B ．3πC ．32πD ．65π例2.如果圆台的母线与底面成60°角,那么这个圆台的侧面积与轴截面面积的比为( )A ．π2B ．π23C ．π332D ．π21例3.在正三棱柱ABC —A 1B 1C 1中，侧棱长为2，底面三角形的边长为1，则BC 1与侧面ACC 1A 1所成的角是 .例4.如图所示，等腰△ABC 的底边AB =66,高CD =3，点B 是线段BD 上异于点B 、D 的动点.点F 在BC 边上，且EF ⊥AB .现沿EF 将△BEF 折起到△PEF 的位置，使PE ⊥AE .记BE ＝x ，V (x )表示四棱锥P-ACFE 的体积.（1）求V (x )的表达式；（2）当x 为何值时，V (x )取得最大值？（3）当V (x )取得最大值时，求异面直线AC 与PF 所成角的余弦值。
（二）基础训练：1．下列几何体各自的三视图中，有且仅有两个视图相同的是（ ）A ．①②B ．①③C ．①④D ．②④2．设地球半径为R ，若甲地位于北纬045东经0120，乙地位于南纬度075东经0120，则甲、乙两地球面距离为（ ）（A ）3R (B) 6R π(C)56R π(D) 23R π①正方形 ②圆锥 ③三棱台 ④正四棱锥C3．若一个底面边长为2的正六棱柱的所有顶点都在一个球的面上，则此球的体积为 ．4. 已知,,A B C 三点在球心为O ，半径为R 的球面上，AC BC ⊥，且AB R =，那么,A B 两点的球面距离为___________，球心到平面ABC 的距离为________ 5．如图，四棱锥P —ABCD 中，底面ABCD 为矩形，AB=8，AD=43，侧面PAD 为等边三角形，并且与底面所成二面角为60°. （Ⅰ）求四棱锥P —ABCD 的体积； （Ⅱ）证明PA ⊥BD.（三）巩固练习：1．若一个圆锥的轴截面是等边三角形，其面积为3，则这个圆锥的全面积是（ ）（A ）π3 （B ）π33 （C ）π6 （D ）π92、已知各顶点都在一个球面上的正四棱柱高为4，体积为16，则这个球的表面积是（ ）A ．16πB ．20πC ．24πD ．32π3.一个圆锥和一个半球有公共底面，如果圆锥的体积恰好与半球的体积相等，那么，这个圆锥轴截面顶角的余弦值是( ) A.34 B.45 C.35 D.－35 4．已知球O 的半径为1，A 、B 、C 三点都在球面上，且每两点间的球面距离为2π，则球心O 到平面ABC 的距离为（ ）（A ）31 （B ）33 （C ）32 （D）36 5.表面积为的正八面体的各个顶点都在同一个球面上,则此球的体积为（）A ．3 B ．13π C．23π D ．36.已知正四棱锥的体积为12，底面对角线的长为，则侧面与底面所成的二面角等于________7．请您设计一个帐篷。
立体几何复习讲义全解
圆梦教育1对1个性化辅导讲义学员姓名 学校 年级和科目教师课 题 空间点、直线、平面之间的位置关系授课时间教学目标掌握平面的基本性质，在充分理解本讲公理、推论的基础上结合图形理解点、线、面的位置关系和等角定理．教学内容【基础知识回顾】 1．平面的基本性质公理1：如果一条直线上的 在一个平面内，则这条直线在此平面内． 公理2：过的三点，有且只有一个平面．公理3：如果两个不重合的平面有一个公共点，则它们过该点的公共直线． 2．直线与直线的位置关系(1)位置关系的分类(2)异面直线所成的角①定义：设a ，b 是两条异面直线，经过空间任一点O 作直线a ′∥a ，b ′∥b ，把a ′与b ′所成的锐角或直角叫做异面直线a ，b 所成的角(或夹角)．②范围：0,2π⎛⎤ ⎥⎝⎦.④若直线l1、l2是异面直线，则与l1、l2都相交的两条直线是异面直线．其中假命题的个数( )A．1 B．2C．3 D．47．若三个平面两两相交，有三条交线，且三条交线互相平行，则这三个平面把空间分成( )A．5部分B．6部分C．7部分D．8部分8．如下图所示，点P，Q，R，S分别在正方体的四条棱上，且是所在棱的中点，则直线PQ与RS是异面直线的一个图是( )9．三个不重合的平面可以把空间分成n部分，则n的可能取值为________．5．如下图所示，正方体ABCD—A1B1C1D1中，(1)求A1C1与B1C所成角的大小；(2)若E、F分别为AB、AD的中点，求A1C1与EF所成角的大小．【考点探究】考点一平面的基本性质例1正方体ABCDA1B1C1D1中，P、Q、R分别是AB、AD、B1C1的中点，则，正方体的过P、Q、R的截面图形是( )．A．三角形B．四边形C．五边形D．六边形画几何体的截面，关键是画截面与几何体各面的交线，此交线只需两个公共点即可确定．作图时充分利用几何体本身提供的面面平行等条件，可以更快的确定交线的位置．【训练1】下列如图所示是正方体和正四面体，P、Q、R、S分别是所在棱的中点，则四个点共面的图形是________．考点二异面直线例2如图所示，正方体ABCDA1B1C1D1中，M、N分别是A1B1、B1C1的中点．问：(1)AM和CN是否是异面直线？说明理由；(2)D1B和CC1是否是异面直线？说明理由．【训练2】在下图中，G、H、M、N分别是正三棱柱的顶点或所在棱的中点，则表示直线GH、MN是异面直线的图形有________(填上所有正确答案的序号)．考点三异面直线所成的角例3(2014·宁波调研)正方体ABCD-A1B1C1D1中．(1)求AC与A1D所成角的大小；(2)若E、F分别为AB、AD的中点，求A1C1与EF所成角的大小．【训练3】A是△BCD平面外的一点，E，F分别是BC，AD的中点．(1)求证：直线EF与BD是异面直线；(2)若AC⊥BD，AC＝BD，求EF与BD所成的角．例4正方体ABCD-A1B1C1D1中，E、F分别是AB和AA1的中点．求证：(1)E、C、D1、F四点共面；(2)CE、D1F、DA三线共点．【训练4】如图所示，已知空间四边形ABCD中，E、H分别是边AB、AD的中点，F、G分别是边BC、CD上的点，且CFCB ＝CGCD＝23，求证：三条直线EF、GH、AC交于一点．【作业】[知能演练]一、选择题1．已知a，b是异面直线，直线c∥直线a，则c与b( )C.35 D.45二、填空题5．如图所示，在三棱锥C－ABD中，E、F分别是AC和BD的中点，若CD＝2AB ＝4，EF⊥AB，则EF与CD所成的角是________．6．在正方体上任意选择4个顶点，它们可能是如下各种几何体的4个顶点，这些几何体是________．(写出所有正确结论的编号)．①矩形②不是矩形的平行四边形③有三个面为等腰直角三角形，有一个面为等边三角形的四面体④每个面都是等边三角形的四面体⑤每个面都是直角三角形的四面体三、解答题7．有一矩形纸片ABCD，AB＝5，BC＝2，E，F分别是AB，CD上的点，且BE＝CF＝1，如下图(1)．现在把纸片沿EF折成图(2)形状，且∠CFD＝90°.(1)求BD的距离；(2)求证：AC，BD交于一点且被该点平分．[高考·模拟·预测]1．正方体ABCD－A1B1C1D1的棱上到异面直线AB，CC1的距离相等的点的个数为( ) A．2 B．3C．4 D．52．已知三棱柱ABC—A1B1C1的侧棱与底面边长都相等，A1在底面ABC上的射影为BC的中点，则异面直线AB与CC1所成的角的余弦值为( )A.34B.54C.74 D.34。
立体几何讲义(前7讲)
新高中讲义01.平面性质及两直线的位置关系1.平面性质(1.1)平面概念,平面的表示法将水平的平面画成一个平行四边形,用平行四边形表示平面,如图(1),平行四边形的锐角通常画成45°,且横边长等于其邻边长的2倍.如果一个平面被另一个平面遮住,为了增强它的立体感,常把被遮挡部分用虚线画出来,如图(2).注.立体几何中的虚线总表示被遮住的线条而不是辅助线.若添加的辅助线是未被遮住的,则要画成实线.把希腊字母,,αβγ等写在代表平面的平行四边形的一个角上,如平面α,平面β;也可以用代表平四边形的四个顶点,或者相对的两个顶点的大写英文字母作为这个平面的名称,图(1)的平面α,也可以记为:平面ABCD ,平面AC 或者平面BD .面内有无数个点,平面可以看成点的集合.如图(3),点A 在平面α内,记作A α∈;点B 在平面α外,记作B α∉.(1.2)平面公理及推论公理1.若一条直线上的两点在一个平面内,则这条直线在此平面内.点P 在直线l 上,记作P l ∈;点P 在直线l 外,记作P l ∉.若直线l 上的所有点都在平面α内,就说直线l 在平面α内,或者说平面α经过直线l ,记作l α⊂;否则就说直线l 在平面α外,记作l α⊄.公理1也可以用符号表示:,A l ∈B l ∈且,A α∈B α∈l α⇒⊂.公理2.若两个平面有一个公共点,则它们有且只有一条过该点的公共直线.公理2表明,如果两个平面有一个公共点,则它们有无限多个公共点,所有公共点构成一条直线,称为两个平面相交,这条由公共点组成的直线称为这两个平面的交线.若已知两个平面有两个公共点,A B ,则它们的 其他公共点都在直线AB 上.这一结论可用于证明三点共线.平面,αβ的交线是l ,记为l αβ⋂=.注.本讲义中的“两点”,“两条直线”,“两个平面”等,如无特别申明,均指不同两点,不同两直线及不同两平面.例1.用α表示平面,l 表示直线,,A B 表示点,以下关系式中正确的是A.A αβ⋂=B.l α∈C.AB α⊂D.A α⊂公理3. 过不在同一直线上的三点,有且只有一个平面.公理3简述:不在同一直线上的三点确定一个平面.不在同一直线上的三点,,A B C 所确定的平面,可以记成“平面ABC ”.推论1.过一条直线及直线外一点的平面有且只有一个.推论2.过两条相交直线的平面有且只有一个.推论3.过两条平行直线的平面有且只有一个.例2.(1)证明两两相交而不共点的4条直线在同一平面内.(2)空间4条线段首尾相连,这4条线段在同一平面内吗?例3.正方体1111ABCD A B C D -中,1,O O 分别是上下底面的中心,判断下列命题是否正确,说明理由.(1)直线1AC ⊂平面11CC B B .(2)直线1OO 是平面11AAC C 与平面11BB D D 的交线.(3)由,,A O C 可确定一个平面.(4)由11,,A C B 确定的平面是11ADC B .(5)直线l ⊂平面AC ,直线m ⊂平面1D C 且,l m 交于P ,则P ∈直线CD .(6)由11,,A C B 确定的平面与由1,,A C D 确定的平面是同一平面.例4.三个平面两两相交,若其中两条交线有公共点,证明第三条交线也过此点.例5.如图,正方体1111ABCD A B C D -中,O 为面ABCD 的中心,直线1AC 与面1C BD 交于M ,求证:(1)1,,C M O 共线.(2)M 为1C BD ∆的重心.2.空间两直线的位置关系(2.1)空间两直线的位置关系分类既不相交也不平行的两条直线称为异面直线.(2.2)空间两直线平行公理4.平行于同一直线的两直线互相平行.定理.若一个角的两边分别平行于另一个角的两边,则这两个角相等或互补.空间图形F 作一次平移是指F 的所有点都沿同一方向平移相同距离.顺次连接不共面4点得到的四边形称为空间四边形.例6.空间四边形ABCD 中,,,,E F G H 分别在边,,,AB BC CD DA 上,AE AH EB HD =且CF CG FB GD=,证明:(1)//EH FG .(2)三直线,,AC EF GH 平行或共点.注.顺次连接空间四边形四边中点的四边形是平行四边形.(2.3)异面直线定义.设,a b 是两直线,若不存在平面π满足,a b ππ⊂⊂,则称,a b 为一对异面直线. 直观描述:永远不在同一平面内的两直线称为一对异面直线.定理.过平面内一点和平面外一点的直线,与平面内不过该点的直线是异面直线.异面直线的另一种画图法.例7.正方体的12条棱所在的直线中有多少异面直线对?例8.设,,,m a b a m A αβαβ⋂=⊂⊂⋂=.(1)若//b m ,证明,a b 异面.(2)若b m ⋂ B =,则,a b 能否异面?两条异面直线所成的角.设直线,a b 异面,任取空间一点O ,过O 作两直线//,//a a b b '',称,a b ''所夹的(不超过直角的)角为异面直线,a b 所成的角.异面直线,a b 所成角θ的范围是(0,]2π.若2πθ=,则称,a b 互相垂直,记为a b ⊥.空间两直线垂直有两种可能:共面垂直(有垂足)和异面垂直(无公共点).求异面直线所成角,一般可平移直线构造三角形,再用余弦定理解出.注意该三角形的内角可能恰为两异面直线所成角,也可能是其补角.例9.空间四边形ABCD 中,AB BC CD DA AC BD =====,,M N 分别是BC 和DA 的中点,直线,AM CN 所成的角是θ,求cos θ的值.例10.正方体1111ABCD A B C D -中,,M N 分别是11A B 和1BB 的中点,求直线AM 与1C N 所成角的余弦值.例11.正方体1111ABCD A B C D -中,E 为BC 的中点,求异面直线1,AC DE 所成角的正切值.例12.设异面直线,a b 成080,过点P 且与,a b 都成050角的直线有条?将050改成060呢?两条异面直线的距离.设,a b 是一对异面直线,与,a b 都垂直的直线有无限多条,但与,a b 都垂直且都相交的直线有且仅有一条,两垂足间的线段称为,a b 的公垂线段,公垂线段的长称为两异面直线,a b 的距离.例13.设正方体1111ABCD A B C D -的棱长为1,则异面直线11,AC A B 的距离为1,异面直线1,AB CC 的距离为1,异面直线1,AC BD 的距离是多少?练习题1.有如下命题:①三个平面两两相交,则这三条交线共面.②一条直线与两平行线都相交,则这三直线共面;③四边形内角和为0360;④空间四点中有三点共线,则这四点共面;⑤若,a b ππ⊂⊄,则,a b 异面.其中正确命题的序号是__________.2.直线,a b 交于平面π内一点P 用符号表示,不正确的是A.,,a b P a b ππ⋂=⊂⊂B.a b P ππ⋂=⋂=C.,a b P P π⋂=∈D.,a P P B π⋂=∈3.下列各图都是正方体或正四面体,,,,P Q R S 分别是所在棱的中点,则,,,P Q R S 不共面的是4.若直线,a b 与直线c 所成的角相等,则,a b 的位置关系是A.平行B.相交C.异面D.不能确定5.已知,,c a b αβαβ=⋂⊂⊂且,a b 异面,则直线c A.与直线,a b 都相交 B.可与直线,a b 都不相交C.至少与,a b 之一相交D.至多与,a b 之一相交6.三个平面可将空间划分成m 个互和重叠的部分,则m 的值的集合为___________.7.正方体1111ABCD A B C D -中,与1AB 成060角的面对角线的条数是_______.8.空间四边形ABCD 中,,M N 分别是,BD AC 的中点,2,AB CD MN ===求,AB CD 所成角的大小.9.空间四边形ABCD 中,32,22AB BD AD BC CD AC ======,延长BC 到E ,使得CE BC =,F 是BD 的中点,求,AF DE 所成角的大小.新高中讲义02.线面平行与面面平行1.直线与平面平行(1.1)直线和平面的位置关系分类直线在平面内(无限多个公共点);直线与平面相交(唯一公共点);直线与平面平行(无公共点).(1.2)直线与平面平行定理1.若平面外的一条直线平行于平面内的一条直线,则这条直线与该平面平行.符号表示(注意是三个条件,缺一不可): ,,////j l j l j ααα⊄⊂⇒.定理2.若直线l 与平面α平行,过l 的平面β与平面α相交,则l 与两平面的交线平行.例 1.(1)证明:过平面内一点且平行于平面的一条平行线的直线在该平面内.(2)若直线a 平行于平面π的一条平行线,判断a 与π的位置关系.例2.如图,两个全等的正方形ABCD 与ABEF 不在同一平面内,,M AC N FB ∈∈且AM FN =,求证://MN 平面BCE .a kj例3.已知,AB CD 都是平面α的平行线且分居α两侧,,AC E BD F αα⋂=⋂=.(1)求证AE BF EC FD=.*(2)若,AB CD AB CD EF ⊥===,求(1)中的比值.例4.证明:过两异面直线中的一条,有且仅有一个平面平行于另一条.例5.证明:若两相交平面平行于同一直线,则它们的交线平行于该直线.2.平行平面(2.1)两平面的位置关系:平行(无公共点);相交(有公共点).(2.2)两平面平行的性质和判定定理1.若两平面平行,则其中一平面内的任何直线平行于另一平面.定理2.若两个平行平面都与第三个平面相交,则两条交线平行.例6.求证:夹在两平行平面间的平行线段的长相等.定理3.若一平面内有两条相交直线平行于另一平面,则这两个平面平行.推论1.若一平面内有两条相交直线分别平行于另一平面内的两条直线,则这两平面平行.推论2.平行于同一平面的两平面互相平行.例7.如图,,AB CD 是异面直线,//,AB CD αα⊂,,M N 分别是,AC BD 的中点,求证://MN α.例8.正方体1111ABCD A B C D -的棱长为a ,1,M A B N AC ∈∈且1A M AN =,求证: //MN 平面11BB C C .例9.正方体1111ABCD A B C D -中,,E F 分别是11,AA CC 的中点,(1)求证:平面//BDF 平面11B D E .(2)求证:1DFB E 是平行四边形.例10.设,AB CD 是夹在两个平行平面,αβ间的线段,,M N 分别是,AB CD 的中点,求证://MN α.(2.3)斜二测画法平面图形的斜二测画法:在原图F 上建立平面直角坐标系xOy ,任取点O ',作仿射坐标系x O y ''',使得045x O y '''∠=;作F 上点(,)A x y 在新图形F '上的对应点1(,)2A x y ';连接相应线段并擦去坐标系x O y ''',就得到F 的按斜二测画法作出的直观图F '. 例11.用斜二测画法画出正6边形的直观图. 注.由画法直接得到:若F '是平面图形F 由斜二测画法画出的直观图,则F '的面积与F 的面积的比为4. 空间图形的斜二测画法:在原图F 上取水平平面及互相垂直的轴,Ox Oy ,再取轴Oz 使之与,Ox Oy 都互相垂直;作平面仿射坐标系x O y '''如前,作出F 的水平平面上图形的直观图;再取O z ''使之垂直于面x O y ''',将F 中与Oz 平行的线段画成与O z ''平行的线段并保持长度不变例12.用斜二测画法画出正方体的直观图.练习题1.设,a b 为直线,π为平面,下列说法正确的是A.若a 平行于π内的无数条直线,则//a πB.若a π⊄,则//a πC.若//,a b b π⊂,则a 平行于π内的无数条直线D.若//,a b b π⊂,则//a π2.过两异面直线外一点且与这两直线都平行的平面A.可能不存在B.有且仅有一个C.有无限个D.至少一个3.设,a b 为异面直线,a π⊂,则过b 且与平面π平行的平面A.不存在B.至多一个C.恰有一个D.有无数个4.正方体1111ABCD A B C D -中,,,E F G 分别是,,AD DC1CC 的中点,则平面EFG 截正方体表面所得图形为A.等腰三角形B.等腰梯形C.正五边形D.正六边形5.平面//αβ,直线,,//,//a b a b αββα⊂⊂,则直线,a b 的位置关系是____________.6.设,m n 是平面α外的两条直线,给出:①//m n ;②//m α;③//n α,以其中两个为条件另一个为结论的正确命题是______________.7.设平面//αβ,,,,A C B D αβ∈∈,AB CD S ⋂=,若5,8,21AS BS CD ===,且060ASB ∠=,则CS 的长为_________.8.如图,正方体1111ABCD A B C D -的棱长为a ,1111,,M AB N AC A N AM ∈∈=.(1)求证//MN 平面11BB C C .(2)求MN 长的最小值.9.设平面l αβ⋂=,直线,,//a b a b αβ⊂⊂,求证//a l .新高中讲义03.线面垂直与线面角1.线面垂直与线面角(1.1)直线与平面垂直定义:若一条直线垂直于一个平面内的所有直线,则称这条直线与这个平面垂直. 直线l 与平面α垂直,记为l α⊥.例 1.(1)证明过一点且垂直于已知平面的直线有且只有一条.(2)证明过一点且垂直于已知直线的平面有且只有一个.定理1.若一条直线垂直于一个平面内的两条相交直线,则这条直线垂直于这个平面.推论1.若两条平行线中的一条垂直于一个平面,则另一条也垂直于该平面.若一直线垂直于两个平行平面中的一个,则必垂直于另一个.推论2.垂直于同一平面的两条直线互相平行.垂直于同一直线的两个平面互相平行. 例2.四面体ABCD 中,,AB CD AC BD ⊥⊥,求证:AD BC ⊥.例 3.(1)设直线l ⊥平面α,垂足A ,证明过A 且垂直于l 的直线必在平面α内.(2)若已知,l l m α⊥⊥,则,l α有何关系?例4.如图,PA ⊥平面ABC ,090ABC ∠=,AE PB ⊥于,E AF PC ⊥于F .(1)证明PB BC ⊥.(2)三棱锥P ABC -的4个面中有几个直角三角形?(3)证明PC ⊥面AEF .(1.2)正射影与三垂线定理自点P 向平面α作垂线,垂足P '叫做点P 在平面α内的正射影(简称射影).线段PP '的长叫做点P 到平面α的距离,是集合{}PQ Q α∈中长度最小者.若图形F 的点在平面α内的正射影构成图形F ',则称F '为F 在平面α内的射影. 与平面相交但不垂直的直线称为平面的斜线,交点叫斜足.任何直线在平面上的射影是一个点或一条直线.设点P 在平面α内的射影P ',又,A B α∈,则PA PB P A P B ''>⇔>.例5.设,,,P A B C αα∉∈.(1)PA PB PC ==⇔P 在α内的射影是ABC ∆的外心.(2),PA BC PB AC ⊥⊥⇔P 在α内的射影是ABC ∆的垂心.(3)P 到直线,,BC CA AB 的距离(垂线段的长)相等P ⇔在α内的射影是ABC ∆的内心或旁心.三垂线定理.设平面α的斜线l 在α内的射影是l ',m α⊂,则l m l m '⊥⇔⊥.例6.如图,梯形ABCD 中,090,,2DAB ABC AB BC a AD a ∠=∠====,PA ⊥平面,ABCD PA a =.(1)求证:PC CD ⊥.(2)求点B 到直线PC 的距离.例7.正方体1111ABCD A B C D -中,,,M N P 分别是1,,AB BC DD 的中点,证明PB ⊥ 平面1B MN .2.直线与平面所成的角定义.平面的斜线与它在平面内的射影所夹的角,称为斜线与平面所成的角.规定平面的垂线与平面所成角为直角;规定平面内的直线或平面的平行线与平面所成的角为零.直线与平面所成角的范围是[0,]2π;斜线与平面所成角的范围是(0,)2π. 直线与平面所成的角是直线与平面内所有直线所成角中的最小者.例8.(三余弦公式)直线l 在平面α内的射影是l ',直线m α⊂.若,l l '所成角为0θ,,l m 所成角为2θ,,l m '所成角为1θ,则201cos cos cos θθθ=.例9.COB ∠在平面α内,OA 是α的一条斜线,060AOB AOC ∠=∠=,OA OB =OC a ==,BC =,求OA 与α所成的角.例10.如图,平面α内线段AB 的长为3,CA α⊥,BD 与α所成角为030,,BD AB ⊥,C D 在α同侧,4CA BD ==.(1)求CD 长.(2)求直线CD 与α所成角的正切值.例11.四面体PABC 中,,,PA PB PC 两两互相垂直.(1)证明ABC ∆是锐角三角形.(2)设H 是P 在平面ABC 内的射影,证明22221111PH PA PB PC =++.(3)证明ABC ∆的面积的平方等于,,PBC PCA PAB ∆∆∆的面积的平方和.(4)证明,,PA PB PC 与平面ABC 所成的角的正弦的平方和为定值.例12.如图,已知AB ⊥平面BCD ,AB BC =且090BCD ∠=,又AD 与平面BCD 所成角为030.(1)求AD 与平面ABC 所成角的大小.(2)求AC 与平面ABD 所成角的正弦.练习题1.设直线l 交平面α于点P ,则平面α内A.存在平行于l 的直线B.存在两条相交直线都垂直于lC.有无数条直线垂直于lD.存在与l 成030角的直线2.若不共线三点到平面α的距离相等且大于0,则这三点确定的平面与α的关系是A.平行B.相交C.平行或相交D.前面答案都不对3.正方体1111ABCD A B C D -中,1O 是11AC 的中点,则与直线1CO 垂直的是A.ACB.BDC.1A DD.1A A4.,a b 是两条相交直线,直线,c d 与,a b都垂直,则直线,c d 的关系是________.5.设P 是正方体1111ABCD A B C D -的中心,则APC ∆在其表面的射影的可能图形的序号是___________.6.P 是边长为3的正ABC ∆所在平面α外一点,2PA PB PC ===,则PC 与平面α 所成角的度数是_________.7.Rt ABC ∆的斜边AB 在平面α内,,AC BC 与α所成角分别为0030,45,则AB 边上的高与α所成角的度数是__________.8.如图,已知ABCD 为正方形,SA ⊥平面ABCD ,过A 且垂直于SC 的平面分别交,SB ,SC SD 于,,E F G ,求证:,AE SB AG SD ⊥⊥.9.ABC ∆中,090,3,4,A AB AC PA ∠===是平面ABC 的斜线,PAB PAC ∠=∠ 060=.(1)求PA 与平面ABC 所成角的大小.(2)若P 在平面ABC 上的射影恰在BC 上,求PA 的长.新高中讲义04.二面角及两平面互相垂直1.二面角平面内一条直线将平面分成两部分,每部分都叫做一个半平面,这条直线称为半平面的端线.定义.有公共端线的两个半平面构成的空间图形叫做二面角,这两个半平面叫做二面角的面,公共端线叫做二面角的棱.棱为l ,两个半平面分别为,αβ的二面角记为l αβ--.注.二面角也可看成是一个半平面(始面)绕其端线旋转到一定位置(终面)所形成的空间图形.二面角的度量.垂直于二面角l αβ--的棱的平面γ分别与面,αβ交于射线OA 和OB ,则AOB ∠称为二面角l αβ--的平面角,显然平面角的大小只与二面角l αβ--有关而与平面γ的选择(即点O l ∈的选择)无关.规定二面角的度数等于其平面角的度数.二面角的范围是00[0,180]:当终面与始面重合时,认为该二面角为00;当终面与始面互为反向延伸面(合成一平面)时,认为该二面角为0180.例1.如图,三棱锥S ABC -中,SA ⊥面ABC ,AB BC ⊥,,SA AB SB BC ==,又E 为SC 中点,D AC ∈且DE SC ⊥,求二面角C BD E --的大小.例2.如图,已知ABCD 是正方形,PA ⊥平面ABCD ,且S BC D --和S CD B --都是045的二面角,求二面角B SC D --的大小.求二面角大小的一般方法第一步:先从其一个面内任一点P (一般选择现成的特殊点)向另一面所在平面作垂线,由垂足Q 的位置可判断该二面角是锐角还是钝角:若Q 在另一面上,则该二面角是锐二面角;若Q 在另一面的反向延伸面上,则该二面角为钝二面角.第二步:作QH l ⊥于H ,连PH ,由三垂线定理知PH l ⊥,故PHQ ∠为所论二面角的平面角(解题时这步要书写到位).第三步:在Rt PHQ ∆中由已知条件算出PHQ ∠的某三角函数值进而求出PHQ ∠. 例3.正方体1111ABCD A B C D -中,P 为AB 中点,求二面角1P AC B --的大小.例4.自二面角l αβ--的棱l 上一点A ,在平面β引射线AC ,与棱l 成045角,与面α成030角,求二面角l αβ--的大小.例5.空间一点P 到二面角l αβ--的两个面的距离分别为1到棱的距离为2,求此二面角的大小.例 6.如图,锐二面角l αβ--的大小为θ,,(,)AC BD A B l αβ∈∈∈都垂直于l .(1)求证,AC BD 所成的角等于θ.(2)若060θ=,4,6,8AB AC BD ===,求CD 的长.面积射影定理.设二面角l αβ--的大小为θ,平面α内一图形的面积为0S ,它在β内的射影的面积为1S ,则10cos S S θ=.立得:正四面体的所有二面角的余弦都是13. 2.平面与平面垂直定义.平面角是直角的二面角叫做直二面角,若两平面相交成直二面角,则称这两平面互相垂直.平面,αβ互相垂直,记为αβ⊥.注.研究直线与平面的位置关系时,是先定义直线与平面垂直,再利用射影定义直线与平面所成的角;研究平面与平面的位置关系时,是先定义二面角,再用直二面角定义两平面垂直.能先定义两平面垂直再定义二面角吗?定理.若一平面过另一平面的一条垂线,则这两平面互相垂直.推论.若一平面平行于另一平面的一条垂线,则这两平面互相垂直.定理2.若两平面互相垂直,则一平面内垂直于交线的直线垂直于另一平面.推论.若l αβ--是直二面角,直线m β⊥,则m α⊂,或//m α.例7.求证:若一平面垂直于两相交平面,则此平面垂直于那两平面的交线.例8.如图,将菱形ABCD 平移得一个平行六面体1111ABCD A B C D -,已知1A AB ∠=1A AD ∠,求证平面11ACC A ⊥平面ABCD .例9.如图,A 是0120的二面角EF αβ--内一点,,AB AC αβ⊥⊥,垂足,B C .(1)求证:,αβ都垂直于平面ABC .(2)若4,6AB AC ==,求BC 长及A 到EF 的距离.例10.如图,ABC ∆是正三角形,,EC DB 都垂直于平面ABC ,2EC AB DB ==,M 为AE 中点.求证: (1)DE DA =.(2)平面BDM ⊥平面EAC .(3)平面DEA ⊥平面EAC .例11.平行四边形ABCD 中,02,60AB AD BAD =∠=,O 为对角线交点,沿BD 将其折成直二面角.(1)求证:CB ⊥平面BAD .(2)求证:平面ACD ⊥平面CBD .(3)求二面角C AO B --的大小.练习题1.设,a b 是直线,,αβ是平面,,a b αβ⊂⊂,则A.a b αβ⊥⇒⊥B.////a b αβ⇒C.a βαβ⊥⇒⊥D.a b αβ⊥⇒⊥2.设,a b 是异面直线,所成角为060,若,a b βα⊥⊥,则二面角l αβ--的大小为A.030B.060C.0120D.060或01203.设l αβ--是直二面角,直线,a b αβ⊂⊂,且,a b 都不垂直于l ,则A.,a b 可能垂直,但不可能平行B.,a b 既可能垂直,也可能平行C.,a b 不可能垂直,但可能平行D.,a b 既不可能垂直,也不可能平行4.设,m l 为直线,,,αβγ是平面,,//,,l l m m βγααγ=⋂⊂⊥,则A.αγ⊥且l m ⊥B.//αγ且//m βC.//m β且l m ⊥D.//αβ且αγ⊥5.设,m l 为直线,,αβ是平面,命题:①若l 垂直于α内的两条相交直线,则l α⊥;②若//l α,则l 平行于α内所有直线;③,m l αβ⊂⊂且m l ⊥,则m β⊥;④,m l αβ⊂⊂且m l ⊥,则l α⊥.其中正确命题的序号是________.6.设P 是二面角AB αβ--的棱AB 上一点,分别在,αβ上作射线,PM PN ,使得0045,60BPM BPN MPN ∠=∠=∠=,则二面角AB αβ--的大小是_______.7.四面体ABCD 中,C AB D --是直二面角,090,ACB AC BC ∠==,又ABD ∆是正三角形,则二面角C BD A --的正切值为_______.8.如图,已知ABCD 是矩形,SA ⊥平面ABCD ,1,SA AB AD ===求二面角 A SC B --的正弦值.9.正方体1111ABCD A B C D -中,,,,K L M N 分别是111111,,,A B BC C D B C 的中点.(1)求证平面MNL ⊥平面KNL .(2)求二面角K ML N --的正切值.新高中讲义05.简单多面体和球1.多面体由若干个平面多边形围成的空间图形叫多面体,围成多面体的各个多边形叫多面体的面,两个面的公共边叫多面体的棱,两条棱的公共点叫做多面体的顶点,连接不在同一面上两顶点的线段叫多面体的对角线.将一个多面体的任一面延展成平面,若多面体其余面都在这个平面的同一侧,这样的多面体叫凸多面体.一个多面体有几个面就称为几面体,如四面体,五面体,六面体等.多面体的Euler 公式:2v e f -+=,其中,,v e f 分别是多面体的顶点数,棱数和面数. 正多面体:每个面都是有相同边数的正多边形,且每个顶点为端点都有相同的棱数的凸多面体叫正多面体.由多面体的Euler 公式可推得正多面体只有5种:正四面体,正六面体,正八面体,正十二面体及正二十面体.2.棱柱有两个面互相平行,其余每相邻两面的交线互相平行的多面体叫棱柱,两个互相平行的面叫棱柱的底面,简称底,其余各面叫棱柱的侧面,两侧面的公共边叫棱柱的侧棱,两个底面所在平面的公垂线段叫棱柱的高.侧棱垂直于底面的棱柱叫直棱柱,底面是正多边形的直棱柱叫正棱柱.侧棱不垂直于底面的棱柱叫斜棱柱.棱柱的底面是几边形就被称为几棱柱,如三棱柱,四棱柱,五棱柱等.棱柱用代表底面各顶点的字母来表示,如三棱柱111ABC A B C -等.棱柱的体积等于底面积乘以高.棱柱性质:(1)棱柱的各侧面都是平行四边形,所有侧棱都相等;直棱柱的各侧面都是矩形,正棱柱的各侧面是全等的矩形.(2)棱柱的两底面与平行于底面的截面是对应边互相平行的全等的多边形.(3)过棱柱不相邻的两侧棱的截面是平行四边形.例1.下列各几何体中,哪些是棱柱?若是棱柱,指出其底面.例2.如图,正三棱柱111ABC A B C -中,11AB BC ⊥,求证11BC CA ⊥.例3.如图,正三棱柱111ABC A B C -中,D 是AC 中点.(1)求证:1//AB 平面1DBC .(2)若还有11AB BC ⊥,求二面角1D BC C --的大小.平行六面体与长方体:底面是平行四边形的四棱柱叫平行六面体,侧棱与底面垂直的平行六面体叫直平行六面体,底面是矩形的直平行六面体叫长方体,棱长都相等的长方体叫正方体.换个说法:底面是矩形的直四棱柱叫长方体.定理1.平行六面体的四条对角线共点且互相平分.定理2.(1)长方体的对角线长的平方等于同一顶点处三棱长的平方和.(2)长方体的对角线与同一顶点处三棱所成角的余弦的平方和等于1,与同一顶点处三面所成角的余弦的平方和等于2.例 4.长方体1111ABCD A B C D -中,15,4,3AB AC AA ===,沿长方体表面从A 到1C 的最小路径长是多少?例5.如图是三个几何体的侧面展开图,它们的原图各是什么几何体?3.棱锥和棱台一个面是多边形,其余各面是有公共顶点的三角形的多面体叫棱锥,这些有公共顶点的三角形叫棱锥的侧面,两个相邻侧面的公共边叫棱锥的侧棱,各侧面的公共顶点叫棱锥的顶点,顶点对面的多边形叫棱锥的底面,顶点到底面所在平面的垂线段叫棱锥的高.底面是正多边形且顶点在底面的射影是底面中心的棱锥叫正棱锥.(也可说成:底面是正多边形,各侧面是全等的等腰三角形的棱锥叫正棱锥.)棱锥性质:棱锥被平行于底面的平面所截的截面与底面相似.正棱锥性质:正棱锥的高,斜高(锥顶到底面边的距离),斜高在底面的射影(底面正多边形边心距)构成一个直角三角形;正棱锥的高,侧棱,侧棱在底面的射影(底面正多边形半径)也构成一个直角三角形.棱锥的体积等于等底等高的棱柱体积的三分之一.例6.如图所示的长方体中,以,,,,O A B C D 为顶点的几何体是A.三棱锥B.四棱锥C.五棱锥D.六棱锥例7.正三棱锥S ABC -中,O 是底面中心,SO =且SA ,BC 的公垂线段的长是3,求ASB ∠的大小.例7.如图,正四棱锥P ABCD -,过AC 且平行于PB 的截面交PD 于点E ,求截面EAC 与底面所成较小二面角的大小.用平行于棱锥底面的平面去截棱锥,截面与底面之间的部分叫棱台.棱台有两个平行的面,称为棱台的底面,是两个相似而不全等的多边形,其余各面都是梯形,称为棱台的侧面,梯形的腰称为棱台的侧棱.棱台的所有侧棱延长相交于同一点.设棱台的两底面积分别为12,S S ,高为h ,则棱台的体积为12()3h V S S =.两底是对应边分别平行的相似多边形,且两底中心连线垂直于底面的棱台叫正棱台.正棱台的各侧棱长相等,各侧面是全等的等腰梯形.例8.下列命题中错误的是________.①用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台;②两个底面平行且相似,其余各面都是梯形的多面体是棱台;③有两面互相平行,其余四面都是等腰梯形的六面体是棱台;④仅有两个面互相平行的五面体是棱台.例9.对右图有描述:①是六面体;②是四棱台;③是四棱柱;④可由三棱柱截去一个小三棱柱而得;⑤可由四棱柱截去一个小三棱柱而得.其中描述正确的是___________.4.圆柱,圆锥,圆台以矩形一边所在直线为旋转轴,其余三边旋转所生成的面围成的旋转体叫圆柱,旋转轴叫圆柱的轴,垂直于轴的边旋转生成的面叫圆柱的底面,平行于轴的边旋转生成的面叫圆柱的侧面,平行于轴的边的任何位置都叫圆柱的母线.以直角三角形一条直角边所在直线为旋转轴,其余两边旋转生成的面所包围的旋转体叫圆锥,相仿地可定义圆锥的轴,侧面及母线.相仿地可定义圆台及相关概念.计算圆柱,圆锥和圆台的侧面积可用曲面展开法:圆柱的侧面可展开为一个矩形,其一边等于圆柱的母线长,另一边等于圆柱的底面周长;圆锥的侧面可展开为一个扇形,其半径等于圆锥的母线长,弧长等于圆锥的底面周长;圆台的侧面展开图是一个扇环(如上最后一图).5.球到定点的距离等于定长的点的集合叫球面,到定点的距离不大于定长的点的集合叫球体(简称球),其中定点叫球心,定长叫半径.一个球或球面用表示其球心的字母表示,如球O等.另一表述:半圆绕其直径旋转一周所形成的曲面叫球面,球面所包围的几何体叫球体.用一个平面去截一个球面,截面是一个圆.若此平面过球心,则得到的截面称为大圆;若此平面不过球心,则截面称为小圆.。
高中数学立体几何学科老师辅导讲义
北辰教育学科老师辅导讲义学员姓名：年级: 高二辅导科目: 数学学科教师:授课日期3月19日授课时段授课主题几何体表面积与体积教学内容知识回顾：知识梳理一．要求：了解球、棱柱、棱锥表面积和体积的计算公式(不要求记忆公式)。
二．考点总结：考试中不仅有直接求多面体、旋转体的面积和体积问题，也有已知面积或体积求某些元素的量或元素间的位置关系问题。
即使考查空间线面的位置关系问题，也常以几何体为依托.因而要熟练掌握多面体与旋转体的概念、性质以及它们的求积公式.同时也要学会运用等价转化思想，会把组合体求积问题转化为基本几何体的求积问题，会等体积转化求解问题，会把立体问题转化为平面问题求解，会运用“割补法"等求解。
三．考点精讲1．多面体的面积和体积公式名称侧面积（S侧）全面积(S全）体积（V）棱棱柱直截面周长×l S侧+2S底S底·h=S直截面·h北辰教育·教学部柱直棱柱 ch S 底·h棱 锥棱锥 各侧面积之和S 侧+S 底31S 底·h 正棱锥21ch ′ 表中S 表示面积,c ′、c 分别表示上、下底面周长，h 表斜高，h ′表示斜高，l 表示侧棱长。
2．旋转体的面积和体积公式 名称圆柱 圆锥 圆台 球 S 侧 2πrlπrlπ（r 1+r 2)lS 全2πr （l+r ） πr(l+r) π(r 1+r 2）l+π(r 21+r 22）4πR 2Vπr 2h （即πr 2l ）31πr 2h 31πh(r 21+r 1r 2+r 22） 34πR 3表中l 、h 分别表示母线、高，r 表示圆柱、圆锥与球冠的底半径，r 1、r 2分别表示圆台 上、下底面半径，R 表示半径.四．题型解析：题型1：柱体的体积和表面积例1．一个长方体全面积是20cm 2，所有棱长的和是24cm ，求长方体的对角线长。
北辰教育· 教学部点评：涉及棱柱面积问题的题目多以直棱柱为主,而直棱柱中又以正方体、长方体的表面积多被考察.我们平常的学习中要多建立一些重要的几何要素（对角线、内切)与面积、体积之间的关系.例2．如图1所示，在平行六面体ABCD —A 1B 1C 1D 1中,已知AB=5，AD=4，AA 1=3，AB ⊥AD ，∠A 1AB=∠A 1AD=3。
高二年级文科立体几何复习讲义教师版
高二文科立体几何复习讲义一、基础知识梳理：1、柱、锥、台、球的结构特征（1）棱柱：定义：有两个面互相平行，其余各面都是四边形，且每相邻两个四边形的公共边都互相平行，由这些面所围成的几何体。
分类：以底面多边形的边数作为分类的标准分为三棱柱、四棱柱、五棱柱等。
表示：用各顶点字母，如五棱柱'''''EDCBAABCDE-或用对角线的端点字母，如五棱柱'AD几何特征：两底面是对应边平行的全等多边形；侧面、对角面都是平行四边形；侧棱平行且相等；平行于底面的截面是与底面全等的多边形。
（2）棱锥定义：有一个面是多边形，其余各面都是有一个公共顶点的三角形，由这些面所围成的几何体分类：以底面多边形的边数作为分类的标准分为三棱锥、四棱锥、五棱锥等表示：用各顶点字母，如五棱锥'''''EDCBAP-几何特征：侧面、对角面都是三角形；平行于底面的截面与底面相似，其相似比等于顶点到截面距离与高的比的平方。
（3）棱台：定义：用一个平行于棱锥底面的平面去截棱锥，截面和底面之间的部分分类：以底面多边形的边数作为分类的标准分为三棱态、四棱台、五棱台等表示：用各顶点字母，如五棱台'''''EDCBAP-几何特征：①上下底面是相似的平行多边形②侧面是梯形③侧棱交于原棱锥的顶点（4）圆柱：定义：以矩形的一边所在的直线为轴旋转,其余三边旋转所成的曲面所围成的几何体几何特征：①底面是全等的圆；②母线与轴平行；③轴与底面圆的半径垂直；④侧面展开图是一个矩形。
（5）圆锥：定义：以直角三角形的一条直角边为旋转轴,旋转一周所成的曲面所围成的几何体几何特征：①底面是一个圆；②母线交于圆锥的顶点；③侧面展开图是一个扇形。
（6）圆台：定义：用一个平行于圆锥底面的平面去截圆锥，截面和底面之间的部分几何特征：①上下底面是两个圆；②侧面母线交于原圆锥的顶点；③侧面展开图是一个弓形。
高中数学复习讲义 第七章 立体几何初步
高中数学复习讲义第七章立体几何初步【知识图解】【方法点拨】立体几何研究的是现实空间，认识空间图形，可以培养学生的空间想象能力、推理论证能力、运用图形语言进行交流的能力以及几何直观能力。
空间的元素是点、线、面、体，对于线线、线面、面面的位置关系着重研究它们之间的平行与垂直关系，几何体着重研究棱柱、棱锥和球。
在复习时我们要以下几点：1．注意提高空间想象能力。
在复习过程中要注意：将文字语言转化为图形，并明确已知元素之间的位置关系及度量关系；借助图形来反映并思考未知的空间形状与位置关系；能从复杂图形中逻辑的分析出基本图形和位置关系，并借助直观感觉展开联想与猜想，进行推理与计算。
2．归纳总结，分门别类。
从知识上可以分为：平面的基本性质、线线、线面、面面的平行与垂直、空间中角与距离的计算。
3．抓主线，攻重点。
针对一些重点内容加以训练，平行和垂直是位置关系的核心，而线面垂直又是核心的核心，角与距离的计算已经降低要求。
4．复习中要加强数学思想方法的总结与提炼。
立体几何中蕴含着丰富的思想方法，如：将空间问题转化成平面图形来解决、线线、线面与面面关系的相互转化、空间位置关系的判断及角与距离的求解转化成空间向量的运算。
第1课 空间几何体【考点导读】1．观察认识柱、锥、台、球及其简单组合体的结构特征，并能运用这些特征描述现实生活中简单物体的结构；2．能画出简单空间图形（长方体、球、圆柱、圆锥、棱柱等的简易组合）的三视图，能识别上述的三视图所表示的立体模型，会用斜二侧法画出它们的直观图；3．通过观察用两种方法（平行投影与中心投影）画出的视图与直观图，了解空间图形的不同表示形式；4.了解球、棱柱、棱锥、台的表面积和体积的计算公式。
【基础练习】1．一个凸多面体有8个顶点，①如果它是棱锥，那么它有 14 条棱， 8 个面；②如果它是棱柱，那么它有 12 条棱 6 个面。
2.（1）如图，在正四面体A －BCD 中，E 、F 、G 分别是三角形ADC 、ABD 、BCD 的中心，则△EFG 在该正四面体各个面上的射影所有可能的序号是 ③④ 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
北辰教育学科老师辅导讲义
V
πr 2
h(即πr 2
l)
31πr 2
h 31πh(r 21+r 1r 2+r 2
2) 3
4πR 3
表中l 、h 分别表示母线、高，r 表示圆柱、圆锥与球冠的底半径，r 1、r 2分别表示圆台 上、下底面半径，R 表示半径。
四．题型解析：
题型1：柱体的体积和表面积
例1．一个长方体全面积是20cm 2，所有棱长的和是24cm ，求长方体的对角线长.
点评：涉及棱柱面积问题的题目多以直棱柱为主，而直棱柱中又以正方体、长方体的表面积多被考察。
我们平常的学习中要多建立一些重要的几何要素（对角线、内切）与面积、体积之间的关系。
例2．如图1所示，在平行六面体ABCD —A 1B 1C 1D 1中，已知AB=5，AD=4，AA 1=3，AB ⊥AD ，∠A 1AB=∠A 1AD=
3。
（1）求证：顶点A 1在底面ABCD 上的射影O 在∠BAD 的平分线上； （2）求这个平行六面体的体积。
图1 图2
题型2：柱体的表面积、体积综合问题
例3．一个长方体共一顶点的三个面的面积分别是6,3,2，这个长方体对角线的长是（ ） A ．2
3
B ．3
2
C ．6
D ．
6
图
图
图图
题型8：球的体积、表面积
例15．已知过球面上,,A B C 三点的截面和球心的距离为球半径的一半，且2AB BC CA ===，求球的表面积。
点评： 正确应用球的表面积公式，建立平面圆与球的半径之间的关系。
例16．如图所示，球面上有四个点P 、A 、B 、C ，如果PA ，PB ，PC 两两互相垂直，且PA=PB=PC=a ，求这个球的表面积。
点评：本题也可用补形法求解。
将P —ABC 补成一个正方体，由对称性可知，正方体内接于球，则球的直径就是正方体的对角线，易得球半径R=
2
3
a ,下略。
，底面半径为r，则
P-PA ABCD。