《数值分析》中文教材勘误表
统计学第八版贾俊平指导书勘误

《统计学第八版贾俊平指导书勘误》序统计学作为一门重要的应用数学学科,对于理解和处理数据具有至关重要的地位。
而贾俊平编著的《统计学第八版》作为一本经典教材,被广泛应用于统计学教学和研究中。
然而,即使是经典之作也难免存在一些错误或疏漏,因此勘误也就显得至关重要。
本文将对《统计学第八版贾俊平指导书》进行全面评估,并提供相关的勘误内容,以帮助读者更好地理解和应用该教材。
一、对于《统计学第八版贾俊平指导书》的全面评估在对《统计学第八版贾俊平指导书》进行全面评估时,我们首先需要对其内容进行深入理解和分析。
该教材系统全面地介绍了统计学的基本概念、原理和方法,涵盖了概率论、数理统计和应用统计等内容,对于统计学初学者和进阶者都具有很大的参考价值。
然而,在阅读过程中,我们也发现了一些可能存在的错误或疏漏,这就需要我们进行勘误和修正。
二、《统计学第八版贾俊平指导书》的勘误内容1. 第xx页,第x行:“xxx”应更正为“xxx”。
在该页面和行数处出现了一个概念或术语的错误使用,正确的表述应当是“xxx”。
2. 第xx页,第x段,第x句:“xxx”应更正为“xxx”。
在该段落中出现了一个公式或推导的错误,正确的表述应当是“xxx”。
3. 第xx页,第x章,第x节:“xxx”应更正为“xxx”。
在该章节中出现了一个概念或原理的错误理解,正确的表述应当是“xxx”。
通过以上勘误内容的整理,我们可以更好地理解和应用《统计学第八版贾俊平指导书》,避免在学习和研究中出现错误或误解。
三、对于《统计学第八版贾俊平指导书》的个人观点和理解作为我个人来说,《统计学第八版贾俊平指导书》是一本非常重要的统计学教材,它系统地介绍了统计学的基本概念和方法,对于我在统计学领域的学习和研究具有很大的指导作用。
通过对该教材进行勘误和修正,我可以更加准确地理解和应用其中的知识,从而提高自己在统计学领域的能力和水平。
总结通过本文对《统计学第八版贾俊平指导书》的全面评估和勘误内容的整理,我们可以更好地理解和应用该教材,避免在学习和研究中出现错误或误解。
统计学第八版贾俊平指导书勘误

统计学第八版贾俊平指导书勘误
摘要:
1.统计学第八版贾俊平指导书勘误的背景和重要性
2.勘误内容的详细列举和解释
3.对勘误的反思和建议
正文:
统计学是一门非常重要的学科,它被广泛应用于各个领域,包括自然科学、社会科学和商业等。
贾俊平所著的《统计学》第八版是一本非常受欢迎的教材。
然而,无论多么仔细的编写,书籍中总会存在一些错误。
因此,对书籍进行勘误是非常必要的。
根据我们的统计,贾俊平的《统计学》第八版中存在一些错误。
这些错误主要包括数据错误、公式错误、表述错误等。
例如,在某一章节中,一个重要的数据被错误地标记为零,这可能导致读者对这一章节的理解产生误解。
在另一个章节中,一个关键的公式被错误地写成了另一个公式,这可能导致读者无法理解这一部分的内容。
此外,还有一些表述错误,如语句不通顺、用词不准确等。
对于这些错误,我们建议贾俊平先生及时进行勘误。
这不仅可以帮助读者更好地理解书中的内容,也可以提高书籍的质量。
我们希望贾俊平先生能够重视这个问题,并在未来的工作中更加仔细地审核书籍的内容。
总的来说,对书籍进行勘误是一项非常重要的工作。
这不仅可以帮助读者更好地理解书中的内容,也可以提高书籍的质量。
《高等数学(经管类)》(上)勘误
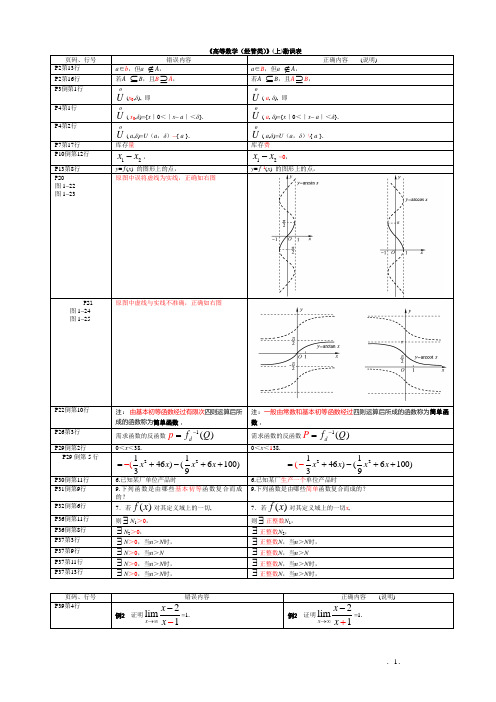
4.(1)-40
4.(1)-20
P208倒第8行
5.(2)减少13.9%
5.(2)增加13.9%
P208倒第7行
6.(1)
6.(1)
P208倒第6行
P208倒第5行
P208倒第4行
P208倒第2行
(2)-0.8,价格上涨1%,需求减少0.8%.
(2)-1,价格上涨1%,需求减少1%.
P208倒第1行
(3)增加0.2%;
(3)不变;
页码、行号
错误内容
正确内容(说明)
P209倒第4行
P209第6行
8.-3, 0,1
8.3, 3,2
P211第1行
P213倒第1行
2.(1)
2.(1)
P214第2行
(4)
(4)
P217倒第4行
(2)
(2)
P178第10行
P179倒第8行
P181第9行
例4设函数 在区间 上连续,
例4设函数 在区间 上连续,
P182倒第5行
牛顿-莱布尼茨公式
牛顿-莱布尼兹公式
P185倒第6行
上式(6-5)表明定积分
上式表明定积分
P187倒第4行
图6-7中:
图6-7中:
P193第2行
(7)
(7)
P194倒第2行
比如,对于例24有:
N>0,当n>N
正整数N,当n>N
P37第11行
N>0,当n>N时,
正整数N,当n>N时,
P37第13行
N>0,当n>N时,
正整数N,当n>N时,
页码、行号
错误内容
正确内容(说明)
P39第4行
(运筹学)教材勘误表

(以下勘误表1错误在第4次印刷后已改正)勘误表1CH11. P11倒数第6行,(0<α<0),改为:(0<α<1)2.P27第20行,阅读本书第13章附录,改为:阅读本书附录A3.P35 习题1.12第(3)小题123,,0x x x ≥,改为,12,0x x ≥CH21.P42第1行,YA ≤C ,改为:YA ≥C2. P42倒数第11行,一个问题有可行解时,另一个问题可能有可行解(此时具有无界解)也可能无可行解 改为:一个问题无可行解时,另一个问题可能有可行解(此时具有无界解)也可能无可行解 2.P49第9行,表2-8(2)中x 5=-6,改为:表2-8(2)中x 4=-6 3. P49倒数第1行,B -1P i ,改为:B -1P j4.P50第5行,当j j c λ'∞<≤-时最优解不变,改为:当j j j c c λ'∞<≤-+时最优解不变5. P57倒数第13行,111()B b b B b B b μμ---'''''=+=+,改为:8.P62习题2.2第(4)题,1510x -≤≤,改为:1510x ≤≤ 8.P62习题2.5,123,0,x x x ≤无约束 改为:123,0,x x x ≥无约束CH31.P68图3-4中去掉小三角形的阴影部分:1.P76习题3.9印掉了。
请补上,放在P77的第一行。
(1)⎪⎩⎪⎨⎧==≤++≥-++=3,2,11072462534max 321321321j x x x x x x x x x x Z j,或+ (2)⎪⎪⎩⎪⎪⎨⎧==≤+++≥-+-≥+++-++-=4,3,2,1107423422335434min 4321432143214321j x x x x x x x x x x x x x x x x x Z j ,或 CH41.P84倒数第4行,满意解就是点A(20,40)。
(参考)数学实验教程勘误表

(mod m)
B
*1250
175 180
J
加上一横线
!= abc+def>400
下列二行
144
4
y x2
y x2 (x 0)
209
3
Windows95/98
209
14
双击
210
6
圆括号(和)
210
8
下划线“-”
210
-5
exp(1), E
210 10,12,25
以及其它
‘
页等多处
211
75
-8
两个:GoldRatio LCD Sin(x)
…,200},{901,902,
x3 x 1
几个曲面
GoldenRatio
LCM Sin[x] …200}, …, {901,902,
x2 x 1
几个曲面(线)
89
9
x
3
94
-2
x1, x2 , , xm
xm , xm1, , x1
95
-4
bk ak
-8
fyuan 两个:GoldRatio
LCD Sin(x) …,200},{901,902,
x3 x 1
几个曲面
fywan
GoldenRatio
LCM Sin[x] …200}, …, {901,902,
x2 x 1
几个曲面(线)
9
5 -9 -2 -4
-6
5 7, 18 16 -12
-6 7
18 7、8 间
缺少一横线
加上一横线
119
11
<=
!=
《概率论与数理统计》本科教材勘误表
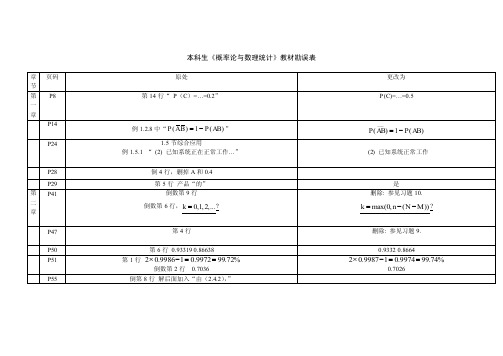
P( AB) 1 P( AB)
(2) 已知系统正常工作
___
P28 P29 第 二 章 P41
是 删除: 参见习题 10.
k max(0, n ( N M )) ?
删除: 参见习题 9. 0.9332 0.8664
P47 P50 P51 P55
第4行 第 6 行 0.93319 0.86638 第 1 行 2 0.9986 1 0.9972 99.72% 倒数第 2 行 0.7036 倒第 8 行 解后面加入“由(2.4.2) , ”
f ( x, y )
P72 第 10 行 P77
1 21 2
2 ( x 1 )( y 2 ) ( y 2 ) 2 1 ( x 1 ) exp 2 2 2 2 2 ( 1 ) 1 1 1 2 2
2
2. (2)
建议删除。
七 章
) 1 ( x , x e f ( x, , ) 0, 其他
( 0, 和未知) ;
倒数第 4 行, 的概率 依概率
X lim P n x n / n
P125 P126
6. 假设某生产线上组装每件成品的时间服从指数分布, 统计资料表明该生产线每件 6.假设某生产线上组装每件成品的时间服从指数分布,统计资料表明 成品的组装时间平均为 15 分钟,各件产品的组装时间相互独立。 该生产线每件成品的组装时间平均为 10 分钟,各件产品的组装时间相 互独立。
问: 参数λ 为平均寿命 400 小时的倒数 空消耗 1 千瓦电将损失 0.12 元。 而当用户用电量超过供电量时, 公司需 要从别处补电, 每 1 千瓦电反而赔 0.20 元。求在指定时间内,该公司获 利润的期望值。
勘误表
《数据结构及算法》勘误表P6 图1-5修改,其正确形式如下(注意单实线和双实线)P13 算法1-1代码正数第2行将“void MatrixMultiply(int A[a], int B[n][n], int C[n][n]) {”改为“void MatrixMultiply(int A[n][n], int B[n][n], int C[n][n]) {”P29 算法2-11,正数第15行将“p=L; j=0;”改为“p=L->next; j=1;”P29 正数第16行将“while((p->next)&&(j<i)) { p=p->next; ++j; }”改为“while(p&&(j<i)) { p=p->next; ++j; }”P29 正数第17行将“if(!(p->next)||(j>=i)) ErrorMessage("输入的i值不合理!");”改为“if(!(p->next)||(j>i)) ErrorMessage("输入的i值不合理!");”P34 正数第7行将“④将p结点赋给新结点的后向指针域;”改为“④将p结点的指针赋给新结点的后向指针域;”P37 倒数第4行将“while((i<=A.length)&&(j<=B.length))”改为“while((i<A.length)&&(j<B.length))”P38 正数第4行将“while(i<=A.length)”改为“while(i<A.length)”P38 正数第7行将“while(j<=B.length)”改为“while(j<B.length)”P38 算法2-20代码开始正数第3行将“while((j<=A.length)&&(j<=B.length))”改为“j=0;while((j<A.length)&&(j<B.length))”P52 算法3-7代码开始正数第3行将“S=new LNode;”改为“S=new S Node;”P53 算法3-10代码开始正数第3行将“if(S->next) EmptyMessage("链栈S空!");”改为“if(!(S->next)) EmptyMessage("链栈S空!");”P54 算法3-12代码开始正数第3行将“if(S->next) EmptyMessage("链栈S空!");”改为“if(!(S->next)) EmptyMessage("链栈S空!");”P61 算法3-22代码开始正数第3行将“if(Q.front->next) EmptyMessage("链队列Q空!");”改为“if(!(Q.front->next)) EmptyMessage("链队列Q空!");”P61 算法3-24代码开始正数第3行将“if(Q.front==Q.rear) EmptyMessage("链队列Q空!");”改为“if(!(Q.front->next)) EmptyMessage("链队列Q空!");”P63 算法3-26代码开始正数第16行将“if(k=1) return 1;”改为“if(k==1) return 1;”P76 正数22行将“(2) 确定两个串的最大相等前缀子串,"s1 s1 … s k "="t1 t1 … t k"(其中1≤k≤m,1≤k≤n)。
数值分析(清华大学出版社)第1,2章
2.
x 的相对误差是
x x d x er ( x ) d ln x x x
它是对数函数的微分。
设 u = xy , 则 lnu=lnx+lny , 因而 dlnu = dlnx + dlny
e r ( u ) e r ( x ) e r ( y ) r ( u ) r ( x ) r ( y )
即 m- n = - 2, m=1, n = 3, 所以 x = 3.14 作为 近似值 时, 就有3 位有效数字。
16
四、 相对误差限与有效数字的关系
定理1
设近似值
x 0.a1a2 an 10m
有n 位有效数字, a1 0 。则其相对误差限为 1 n 1 r (x ) 10 2a1 x 0.a1a2 an 10m 故 证明
a1 10
m 1
| x | (a1 1) 10
m 1
r (x )
x x x
0 .5 10m n 1 10 n1 a1 10m 1 2a1
17
定理2 设近似值 x 0.a1a2 an 10 的相对误差限
m
1 10 n1 ,则它至少有n 位有效数字。 不大于 2( a 1) 1
25
对多元函数 y f ( x1 , x2 , , xn ), 自变量的近似值为 x1 , x2 ,, xn , y 的近似值为 y f ( x1 , x2 , , xn ),
y 的运算误差为 函数值
e ( y ) e[ f ( x1 , x2 , , xn )] df ( x1 , x2 , , xn )
统计学——教材勘误表
n n0 n 1 0 N
修改为
n
n0
1
n0 N
89 页
X i
1 r X ij , (i=1,2,„, r j 1
r) (5-13)
X i
1
s
1
X ij j
1
s
X j
1 X ij , (j=1,2,„, s i 1
去掉,表述有错误。
135 页 155 页
② 判定系数为 0.997
ˆ F bl Y T l t t
ቤተ መጻሕፍቲ ባይዱ
l 1,2,
Yˆ t l F t b tl
l 1,2,
另外,107 页最后一段关于单侧检验 p 值的结果没有错误。按照相关定义在这里计算 Z 值时必定取负值,由此给很多学生造成了一些困扰,提醒请各位老师注意。
s) (5-14)
s
X j
r
X ij i
1
r
91 页 第1行 94 页 第2行 105 页 倒 数 第6行 131 页 倒 数 第 2、 3 行 134 页
( )11 12 ( )ss 0
兴趣作为因子 根据表 6-3,计算出的 Dmax 统计量的值为 0.960(表中的 Kolmogorov-Smirnov Z), 相应的 p 值(渐近显著性)为 0.315。 „„99.7%„„99.7%„„
( ) 11 12 ( ) rs 0
采伐状况作为因子 根据表 6-3,计算出的 Dmax 统计量的值 为 0.096,相应的 p 值(渐近显著性) 为 0.315。 „„99.4%„„99.4%„„
„„, “在 p 个自变量中,只要有一个自 变量同因变量的线性关系不显著,F 检验 就不能通过,因此 F 检验是对方程整体线 性关系的检验” 。 ② 修正自由度的判定系数为 0.997
勘误表 整理
22. p.185 最后一段第二行“整个规划期界界”删去一个“界”字。
23. p.197 式 (8.9) 下方一行“在稳态或稳态处”删去“或稳态”三字。
2
24. p.197 式 (8.10) 下方一行“为了从方程 (8.9)7 值函数的近似计算”下方一段第二行“这里其中”改为“这里介绍其中” 26. p.206 模型 (8.23) 下方一行“劳动 N 为常数时”改为“劳动为常数 N 时” 27. p.209 式 (8.28) 上方一行“问题 (8.25)”改为“问题 (8.27)”。同一段落的后两个公式之
勘误表
September 13, 2012
2011-12-25
1. p.181 第三行及第二段中“Euler 方程”均改为“共态方程” 2. p.182 第三段中“2.Euler 方程”改为“2. 共态方程” 3. p.183 例 7.5 中“2.Euler 方程”改为“2. 共态方程” 4. p.195 第三段 Lagrange 函数
13. p143 定义 6.3 第一行末尾“如果在存”删去“在”字
14. p162 倒数第二段第三行“转移方程'' 改为“状态方程”。
15. p.169 第一段式 (7.9c) 右边“x˙ ∗ = f (t, x∗, u∗)”改为“x˙ ∗ = g (t, x∗, u∗)”
16.
p.169 第三段式 (7.10)
20. p. 181 倒数第二段在公式 “λ (T ) = 0, λ (T )=[K∗ (T ) − Kmin]” 后加入 “这意味着, 若 K∗ (T ) > Kmin, 则 λ (T ) = 0, 因而施加在终结期资本存量上的约束不起作用。但若 λ (T ) >0, 则最低资本约束 Kmin 的确起作用,因为它防止厂商在接近终结期时耗光大部分资本,厂商 留下的资本恰好等于最低要求水平 Kmin。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第20行d(k) = a (k,k)-t (k,1:k-1)*L(k,1:k-1)';
第21行t(k+1:n,k) = a (k+1:n,k)-t (k+1:n,1:k-1)*L(k,1:k-1)';
第14行function x = mpfg (A,b)
第15行[n, n] = size (A)
第16、18行
fhtx(0,1, 0.00001,1)
输出结果是:
0.35913928448364
216
倒数第8行
h=(b-a)/n;
x=a:h:b;
S1=0;
倒数第8行
h=(b-a)/n;
S1=0;
217
第4行
例7.8.3已知函数 的下列数值
0
0
0.1119
0.2054
0.2886
0.3664
0.4422
k=k+1;
112
倒数第2行
warning('已迭代次数上限');
倒数第2行
warning('已达迭代次数上限');
112
第7-10行
x=
1.3247
k=
7
第7-10行
x=
1.3259
k=
3
112
倒数第6行
break;
倒数第6行
break
112
倒数第1行
warning('已迭代次数上限');
倒数第1行
《数值分析》勘误表
页码
误
正
3
倒数第6行
倒数第6行
3
倒数第5行
倒数第5行
3
倒数第2行
对数据进行四舍五入后产生的误差称为舍入误差(roundoff error).
倒数第2行
由于计算机的字长有限,进行数值计算的过程中,对计算得到的中间结果数据要使用“四舍五入”或其他规则取近似值,因而使计算过程有误差。这种误差称为舍入误差(roundoff error).
0
0
0.1119
0.2054
0.2886
0.3664
0.4422
0.5185
0.5971
0.6796
利用所给数值,用复化梯形公式计算积分 .
第8行
例7.8.2用复化梯形公式的递推公式计算积分 .
216
第16、18行
fhtx(0,1, 0.00001, 9)
输出结果是:
0.35913269479387
第13行
6.已知函数 的数值表
1234
0-5-63
试分别求出 的三次Newton向前和向后插值公式;并分别计算当 和 时 的近似值.
164
倒数第1行
用多项式 逼近 的,问题
倒数第1行
用多项式 逼近 的问题
166
第10、11行
第10、11行
177
第13行
倒数第2行
第13行
倒数第2行
168
第3行
第3行
187
第13行function f = Newtonbackward(x,y,x0)
154
倒数第6行f2=Newtonback(x,y,2.5)
倒数第6行f2=Newtonbackward(x,y,2.5)
161
第13行
6.已知函数 的数值表
0 1 2 3
1 2 17 64
试分别求出 的三次Newton向前和向后插值公式;并分别计算当 和 时, 的近似值.
77
第1行
disp('请注意:Jacobi迭代次数已经超过最大迭代次数max1.')
第1行
disp('请注意:Gauss-Seidel迭代次数已经超过最大迭代次数max1.')
78
第15行
disp('请注意:Jacobi迭代次数已经超过最大迭代次数max1.')
第15行
disp('请注意:SOR迭代次数已经超过最大迭代次数max1.')
warning('已达迭代次数上限');
113
倒数第7行
break;
倒数第7行
break
114
第9-12行
x=
0.347296357208033
k=
4
第7-10行
x=
0.34729635533386
k=
5
115
倒数第11行这个根,使误差界不超过 .
倒数第11行这个根,使误差限不超过 .
127
倒数第2、1行
5.将原方程组调整成等价方程组
因为调整后的方程组的系数矩阵是严格对角占优的,所以其Gauss-Seidel迭代格式收敛;迭代6次后得满足精度要求的近似解
333
倒数第13行
2.1.324,9次,13次.
倒数第3行
3.(1), (2)收敛,(3)发散;用(2)计算 .
倒数第13行
2.1.32031,9次,13次.
(5)若 是一个关于 的 次多项式,则
倒数第2、1行
(5)若 是一个关于 的 次多项式,则
137
第3行(2)
第3行(2)
137
第6、7行
(5.5.10)
第6、7行
(5.5.10)
145
第3行
(5.7.19)
第3行
(5.7.19)
146
第6行
(5.7.21)
第6行
(5.7.21)
148
倒数第8行
l = l*(t-x(j))/(x(i)-x(j)); %计算Lagrange基函数
,
其中
第10、11行
,
其中
197
第14行
第14行
198
第7行
倒数第7行
201
第1、2行
(7.4.11)
其中
第1、2行
(7.4.11)
其中
201
第6行
.(7.4.12)
第6行
.(7.4.12)
204
第12行
定理7.5.2设 ,则复化Simpson公式的余项为
第12行
定理7.5.2设 ,则复化Simpson公式的余项为
0.5185
0.5971
0.6796
利用所给数值,用复化Simpson公式计算积分 .
第4行
例7.8.3用复化Simpson公式计算积分 .
223
第4行 (8.2.1)
第4行 (8.2.1)
225
第6行
第6行
228
第12行这样得到的 与准确值 的
第12行这样得到的 与准确值 的
229
倒数第6行
倒数第6行
80
第3行
5.对线性方程组
进行调整,使得用Gauss-Seidel迭代法求解时收敛,并用该方法求近似解,使得 取 .
第3行
5.对线性方程组
进行调整,使得用Gauss-Seidel迭代法求解时收敛,并用该方法求近似解,使得 取 .
83
第12行
第12行
84
第3行
第3行
90
第10行
第10行
92
第14、15行
例4.3.2中迭代法(3)的 ,而 ,
第14、15行
例4.3.3中迭代法(3)的 ,而 ,
99
第15行
,
第15行
,
99
倒数第7行
(2)此时 ,代人(4.4.3),取初值 ,得
倒数第7行
(2)此时 ,代人(4.4.3),取初值 ,得
99
倒数第5行
与 得精确值相比较, 是具有10位有效数的近似值.
倒数第5行
195
|
196
P195倒数第1行、P196第1行
容易验证,该公式对 也精确成立,但对 ,求积公式不能精确成立,因此,该求积公式具有2阶代数精度.
P195倒数第1行、P196第1行
容易验证,该公式对 也精确成立,但对 ,求积公式不能精确成立,因此,该求积公式具有5次代数精度.
197
第8行
第8行
197
第10、11行
104
倒数第8行
倒数第8行
111
第17行
%用迭代法求非线性方程f(x)=0的根,fun为函数f(x)的表达式
第17行
%用迭代法求非线性方程f(x)=0的根,fun为迭代函数φ(x)的表达式
111
倒数第5、6行
x0=x;x=feval(fun,x0)
k=k+1
倒数第5、6行
x0=x;x=feval(fun,x0);
倒数第7行
以 为例,已知
倒数第7行
以 为例,已知
188
第5行
类似上述推导,在等距节点的情形,即
第5行
类似上述推导,在等距节点的情形,即
189
倒数第5行
倒数第5行
194
倒数第15行
则称式(7.3.1),称
倒数第15行
则称式(7.3.1)为求积公式(numerical quadrature formula),称
205
第8行
第10行
第8行
第10行
205
倒数第9行
倒数第9行
214
倒数第18行if(n==1)
倒数第18行ifn==1
215
第2、3行
7.8.2复化梯形公式求积分
%复化梯形公式求积分
第2、3行
7.8.2用复化梯形公式的递推公式求积分
