第2章平面汇交力系与平面力偶系优秀课件

2）几何平衡条件：力的多边形自行封闭
Fn
FR
F3
F2
F1
Fn
F3
F2
F1
例2-1 压路碾子，自重P=20 kN，半径R=0.6m，障碍物高
h=0.08m。碾子中心O处作用一水平拉力F。试求：
（1）当水平拉力F=5 kN时，碾子对地面及障碍物的压力；
（2）欲将碾子拉过障碍物，水平拉力至少应为多大；
（3）力F沿什么方向拉动碾子最省力，此时力F为多大。
FA
F
由： FBsin F
FA FBcos P
解得： FA=11.34 kN , FB=10 kN
F
O
BP
FB
A
FA
（2）碾子能越过障碍物的力学条件 是FA=0，作出此时封闭的力三角形。
由几何关系可得
FP ta n1.5 15 kN
FB
P 23.09
cos
kN
（3）当拉力与FB垂直时，拉动 碾子的力最小。由几何关系可得
n i 1
FRyY1Y2 Yn Yi Y
i1
三. 平面汇交力系的平衡
FR 0
FRx 0
FRy 0
X0 Y0
平衡方程由两个方程组成，可解两个未知量
四. 解题步骤
1）取研究对象，画受力图； 2）建立坐标系，列方程 ； 3）解未知量； 4）重复以上步骤。
例2-3 已知 AC=CB ，杆 DC 与水平线成 450 角；载荷 P=10 kN ，作用于 B 处。梁与杆的重量忽略不计，试 用解析法求铰链 A 的约束反力和杆 DC 所受的力。
第2章平面汇交力系 与平面力偶系
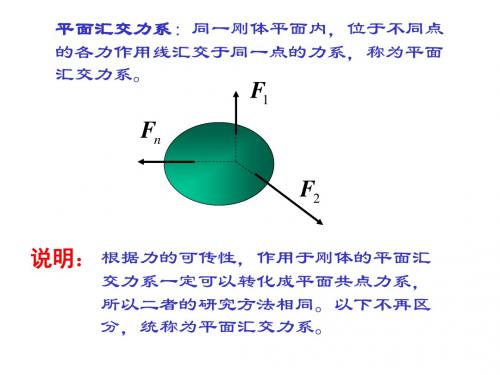
平面汇交力系：同一刚体平面内，位于不同点 的各力作用线汇交于同一点的力系，称为平面 汇交力系。
F1
Fn
F2
说明： 根据力的可传性，作用于刚体的平面汇
交力系一定可以转化成平面共点力系， 所以二者的研究方法相同。以下不再区 分，统称为平面汇交力系。
二、工程中的平面汇交力系问题举例：
E
B
FA
A
C
P
A
B
C
D
FC
P
解： 取梁为研究对象。 注意：这里所设力 FA 的方向与
画受力图。
实际方向相反。
解：取横梁为研究对象。画受力图。 y
建立图示直角坐标系。
由平面汇交力系的平衡条件列方程 A
X 0 , FAco sF Cco 4s 050 Y 0 , F A sin F csi4n 05 P0
FR F1 F2 Fn Fi
Fn
FR F 3
F2
F1
力
多 合力为力多边形的
边 封闭边
形
说明：力系的合成与力序无关
矢量方程为： F R F 1 F 2 F nF i
合力：如果一个力和一个力系等效，则此力称为 该力系的合力。
二、 平面汇交力系的平衡 平衡条件
1）从方程上说： FR 0
几何法的优缺点
（1）各力之间的关系很清楚、直观，便于定性地处理问题。
（2）不便于精确地处理有较多力或各力间几何关系较复杂 的力系平衡问题。一般对于由二力或三力组成的力系的平 衡问题，且当几何关系简单时才应用。
§2-2 解析法
解析法是通过力矢量在坐标轴上的投影来分析力系 的合成和平衡条件
一. 力的解析表示法
1）三个共点力的合成
设 {F1,F2,F3}为作用在A点的力系
F 3 F2
A
F1
F F3
R FR12
F2
F1
FR12 F1 F2 FR FR12 F3
FR F 3
F2
F1
FR F1 F2 F3
2）多个共点力的合成 设 {F1,F2, Fn}为作用在A点的汇交力系
则该力系的合力为 {F R }{F 1,F 2, F n}
B
A
C
P
A D
解： 取梁为研究对象。 画受力图。
FA
C
FC
E B
P
根据平面汇交力系平衡的几何条 件，可作出封闭的力三角形
FA
P 450 FC
E
FA
A
B
C
FC
Q
按比例尺量得或由几何关系经计算可得
FC 28.3 kN FA22.4kN
注： 若作出其它形式的力三角形， 可以解出同样的结果。
FC
P
FA
例 已知：三铰刚架受力如图 求：A,B两处的反力
X ,Y是力F在两个坐标轴上 的投影(代数量)
力Fx ，Fy 是力F沿着两个坐标轴 方向的两个分力(矢量)
设x、y轴上单位矢量为i 和 j
投影与分力 Fy Y j
间的关系 Fx Xi
Y
y
Fy
F
Fx
j
Oi
x
x
y
Y
Fy
Fx
O X
仿射坐标系中分力 与投影间并没有上
F 述的特殊关系。
x
二.ຫໍສະໝຸດ Baidu平面汇交力系的合成
解：（1）取碾子为研究对 象。 画受力图。
F
O
B
P
A
F
O
B
P
A
FB
FA
（2）根据力系平衡的几何条件，作封闭的力多边形。
按比例，先画已知力，各力矢首位相接。
a.从图中按比例量得
FA=11.4 kN , FB=10 kN
5 kN
b.也可由几何关系计算
cos R h 0.866 300
R
FB
P
解：①分别取AC部分,BC部分 为 分离体
②分画受力图 Fc C
B FB
P A
P A
FA
C
B
a
a
C FC '
③应用几何法求解 力 P, F A , F C ' 构成封闭力多边形
FA
F
' C
45 0
P
FA F'C
P 2
FC F'C
P 2
几何法解题步骤：
①取分离体
②画受力图，做力多边形
③ 按比例测量，或应用几何关系计算
E
FA
45 0
B
C
FC
xP
其中：cos 2 sin 1
三、三力平衡汇交定理
定理： 若刚体在三 个力的作用下保持平 FC 衡，其中两个力汇交
FA A O
于一点，那么第三个
力的作用线也必通过 FBC
FB
汇交点。
O
FAy
FA
Q
A
FAx C
B
Q
FC
四、本章的研究内容
分别用几何法和解析法研究平面汇交力系的 合成与平衡
§2-1 几何法（矢量法）
一、 平面汇交力系的合成—力的多边形法则
F R F 1 F 2 F n F R i x F Rjy F R ( X 1 i Y 1 j ) ( X 2 i Y 2 j ) ( X n i Y n j )
( X 1 X 2 X n ) i ( Y 1 Y 2 Y n ) j
比较上式：
n
F Rx X 1X2 Xn Xi X
Fmi nPsin10 kN
FB
P
Fmin
F
FB
P
FA
F
例2-2 支架的横梁 AB 与斜杆 DC 彼此以铰链 C 相连 接，并各以铰链 A、D 连接于铅直墙上。已知 AC=CB ； 杆 DC 与水平线成 450 角；载荷 P=10 kN ，作用于 B 处。梁与杆的重量忽略不计，求铰链 A 的约束反力和 杆 DC 所受的力。