平面汇交力系与平面力偶系习题课

合集下载

工程力学课件：平面力系的简化与平衡

Fx 0 二矩式： M A ( F ) 0 M ( F ) 0 B M A ( F ) 0 三矩式： M B ( F ) 0 M ( F ) 0 C
Fx 0 Fy 0 即： M o ( F ) 0
例 2 利用铰车绕过定滑轮B的绳子吊起一重P=20kN的货物，滑轮由两端铰链的水平刚杆AB 和斜刚杆BC 支持于点B [图(a) ]。不计铰车的自重，试求杆AB 和BC 所受的力。
解： 1）取滑轮B 轴销作为研究对象。 2）画出受力图（b)。
3）列出平衡方程：
Fx 0 Fy 0
机械工程基础 ——工程力学
第二章
平面力系
第一讲：平面汇交力系、平面力偶系的简化与平衡第二讲：平面任意力系的简化与平衡第三讲：考虑摩擦时的平衡问题和重心习题课
第一讲：平面汇交力系、平面力偶系的简化与平衡
目的要求：掌握利用平面汇交力系、平面力偶系平衡方程
基本形式求解平衡问题。
F Fx2 Fy2
tan Fy Fx
多个力组成的力系在坐标轴上的投影合力公式为：
FRx F1x F2 x Fnx Fx
FRy F1y F2 y Fny Fy
FR F F
2 Rx
2 Ry

F F
可见，静摩擦力就是接触面对物体作用的切向约束反力，它的方向与物体相对滑动趋势相反，它的大小需用平衡条件确 G 定。
此时有：可见，静摩擦力的大小随拉力F的增大而增大，
F
F
Fs
FN
G
（2）最大静滑动摩擦力静摩擦力与一般约束反力不同，它并不是随力F的增加而无限度的增加。当力F的大小达到一定数值时物体处于将要滑动，但尚未开始滑动的临界状态。这时，力 F 再增大一点，物体将开始滑动。当物体处于平衡的临界状态时，静摩擦力达到最大值，即为最大静滑动摩擦力，简称为最大静摩擦力，以 Fmax表示。此后，如果F 再继续增大。但静摩擦力不能再随之增大，物体将失去平衡而滑动。静摩擦力的大小随主动力的情况而改变，但介于零和最大值之间，即0< Fs < Fmax 实验证明：最大静摩擦力大小与两种物体间的正压力（即法向反力）成正比，即：

第2章平面汇交力系与第3章平面力偶系

F
x
0
F
y
0
FA F sin 45 sin( 180 90 1 ) 10 FA F 7.9 N 4
FA
F
1
FN B FA
FNB
2-10
解2: 解析法研究AB杆，画受力图
F F
X
0 FA cos 1 F cos 0 0 FA sin 1 FN B F sin 0
d
d
m1 F1d1;
m2 F2 d 2
又m1 P 1d
m2 P2d
' RA P P 1 2 ' RB P 1 P 2
合力矩 M RA d ( P1 P2' )d P1d P2' d m1 m2
2-23
m 即合力偶矩等于各个力偶矩的代数和。 2. 平衡： m m 0
方向：以逆时针为正，顺时针为负。
若用矢量表示： m BA F
2-18
注：力偶无合力，即不能与某力作等效变换，其是一个基本的力素。证明： FR=F-F'=0
由合力距定理，可知
M
C
0, F 'CB F CA 0 CB F 1 CA F '
FR
若CB CB d成立, 必有CB
A
1
Y
O
10 FA F 7.9 N 4
F
C
45°
B
FA
FNB
2-11
§2-3 力矩、力偶的概念及其性质
力对物体可以产生移动效应--取决于力的大小、方向转动效应--取决于力矩的大小、方向一、力对点的矩

第2章 2.2平面力偶系

1、合理确定研究对象并画该研究对象的受力图；
2、由平衡条件建立平衡方程；
3、由平衡方程求解未知力。
目录
2.2.1力矩 2.2.2力偶 2.2.3平面力偶系的合成与平衡
单元学习目标
1、理解力对点之矩的概念； 2、掌握力矩的计算方法，学会应用合力矩定理； 3、理解力偶的概念，掌握其性质； 4、掌握平面力偶系的合成方法与平衡条件。
2.2.1 力矩
2、力矩的性质 1）力对点之矩，不仅取决于力的大小，还与矩心的位置有
关。力矩随矩心的位置变化而变化。 2）力对任一点之矩，不因该力的作用点沿其作用线移动而
改变。 3）力的大小等于零或其作用线通过矩心时，力矩等于零。
2.2.1 力矩
3、合力矩定理
平面汇交力系的合力对该平面上任一点之矩等于各个分力对该点之矩的代数和。
解法二：应用合力矩定理计算。
将力F在C点分解为两个正交的分力，由合力矩定理可得： MA(F)=MA(Fx)+MA(Fy)=－Fxb+Fya =－Fbcosα ＋Fasinα =F(asinα -bcosα )
例3 如图所示，求力对A点之矩。
解：将力F沿坐标轴方向分解为两个分力，由合力矩定理得：
M A Fxdx +Fyd y
将其推广到平面内n个力偶的情形平面力偶系可以合成为一个力偶，即合力偶，其合力偶矩等于各分力偶矩的代数和。合力偶矩计算公式：
M M1 M2
Mn Mi
例4 某物体受三个共面力偶的作用,试求其合力偶。已知F1=9kN,d1=1m， F2=6kN,d2=0.5m， M3=-12kN·m
2.2 平面力偶系的计算
2.2.1力矩 1、力对点之矩的概念力对刚体的作用效应——运动效应

理论力学02习题课

M F d 1 2 F d 2ABC 2
平面内两个力偶，如果力偶矩相等，则两个力偶等效
8
主要内容和方法
平面力偶系的合成和平衡条件
平面力偶系:作用在物体同一平面的许多力偶叫平面力偶系
平面力偶系合成结果还是一个力偶,其力偶矩为各力偶矩的代数和。
M FR d F1d F2 d M1 M 2
例题7:在刚体的A、B、C、D四点作用有四个大小相等的力,此四力沿四个边恰好组成封闭的力多边形,如图所示.此刚体是否平衡?选择其中一对平行力，同时改变方向,此刚体是否平衡? 答:图示情况下刚体不平衡，依然存在顺时针方向力矩，选择其中一对平行力，同时改变方向,此时刚体平衡。
14
典型题目
例题8:在下面各图中,力或力偶对点A的矩都相等,它们引起的支座约束力是否相同?
解：
F 0 F F 0 M 0 F l M 0
x A B A B
M M FA ; FB l l
23
作业题
2-12已知梁上作用有力偶，重量不计，在下面三种情况下，计算之作的约束力
解：
F 0 F cos F cos 0 M 0 F l cos M 0
Fx 0 F FA
2 5 0 FA F 2 5
Fy 0 FD FA
19
1 1 0 FD F 2 5
支座A点的约束力与假设的方向相反
作业题
2-6如图所示，输电线重量沿AB均匀分布，求电线中点和两端拉力 f 1m, AB 40m, P 400 N
0 M 2 F cos r2 0 M1 r cos r2 M 1 2 cos r1 r1

理论力学作业二

平面汇交力系与平面力偶系作业1．四力作用于一点，其方向如图所示。

已知各力的大小为：F1=50N，F2=80N，F3=60N，F4=100N。

求力系的合力。

2．一均质球重P=1000N，放在两个相交的光滑斜面之间如图示。

如斜面AB的倾角ϕ =45º，而斜面BC的倾角θ =60º。

求两斜面的约束力F D和F E的大小。

3．以吊斗运物过河，吊斗系用小车C挂在钢丝绳AB上，如图所示。

如欲将小车拉向左岸，则利用一跨过滑车A而绕在绞盘D上的绳索C AD；如欲将小车拉向右岸，则可利用一跨过滑车B而绕在铰盘E上的绳索C BE。

A、B两点在同一水平线上，距离AB=100m，钢索ACB长102m，吊斗重5kN。

如略去钢索和绳子的重量以及小车C沿钢索的摩擦，求当AC=20m时绳子C AD和钢索A C B的张力。

4．均质杆AB长l，置于销子C与铅垂面间，如图所示。

不计摩擦力，求平衡时杆与铅垂线间的夹角θ。

5．三个相同的光滑圆柱放置如图示，求圆柱不至于倒塌时θ 角的最小值。

6．杆AB以铰链A及弯杆BC支持，杆AB上作用一力偶，其力偶矩大小为M，顺时针转向，如图所示。

所有杆件的重量不计，求铰链A与C的约束力。

7．图示机构中杆AB 上有一导槽，套在CD 杆的销子E 上，在AB 和CD 杆上各有一力偶作用，如图所示。

己知M 1=1000N ·m ，不计杆重及摩擦。

求机构在图示位置平衡时力偶矩M 2的大小。

8．水平杆AB 由铰链A 与连杆CD 支持于铅垂转轴EF 上，在AB 杆的一端作用有一力偶（F ，F ′）其矩的大小为M 。

设所有杆件的重量不计，求CD 杆的内力及轴承E 与F 处的约束力。

平面汇交力系与平面力偶系(2)a

y
F1
F2
FR
A
F3
F4
O
x
2. 合力之矩定理
平面汇交力系合力对于平面内一点之矩等于所有各分力对于该点之矩的代数和。
MO (FR ) MO (F1) MO (F2 ) MO (Fn ) MO (Fi )
3. 力矩与合力矩的解析表达式
y
Fy
xA y
O
F
Fx
x
MO (F ) MO (Fx ) MO (Fy ) xFy yFx
M
C
F2
B
P
问刚体在四个力的作用下是否平衡，若改变F1和F1′的方向，则结果又如何。
当 M=PR 时，系统处于平衡，因此力偶也可以与一个力平衡，这种说法对吗。
B
M
C
M
A
图示系统平衡否，若平衡，A、B 处约束反力的方向应如何确定。
思考题2 ? 图示四连杆机构，在A、B点分别作用
FA,FB，求：机构平衡时FA与FB力的关係。
墙接触，在F力作用使C块压紧物体D，求：物体D所受压力。
h B L
F A L
y FAB F
FAC
x [A]
y
[C] FCA x
FC
FD
D
C 解:[点A] Fix=0; – FABcos – FACcos – F=0 （1）
Fiy=0; FABsin–FACsin =0 （2）
从（2）可得：FAB=FAC，代（1）得：FAC=F/（2 cos）
A d
F
F
B xO
MO (F , F ) MO (F ) MO (F ) F(d x) Fx Fd

理论力学作业答案

解：力系对O点的主矩在轴上的投影为
M Ox M x F F2 cos a .100 F3 sin .300 51.8 N .m M Oy M y F F1 .200 F2 sin a .100 36.64 N .m M Oz M z F F2 cos a .200 F3 cos .300 103.6 N .m
FCy
P1
FDx
解得： FCy 4550 N
P
3、研究杆ABC
FCy
C
M F F
y
C
0
M A 6FAx 3FBx 0 0
B
FCx
FBy
FAy FBy FCy P3 0
x
0
FBx
FAx FBx FCx 0
MA P3 FAy
A
解得： FBx 22800, FBy 17850
M M FAx tan , FAy , M A M a a
3-9(b)
已知：q, M, a,. 不计梁自重，求支座A、B、C约束反力。 FNC FBy FBx

解：BC段梁受力分析如图，平面任意力系平衡方程为
F F
解得：
FNC
x y
0 FBx FNC sin 0 0 FBy qa FNC cos 0
解得： FAx 0, FAy 1 F M , FNB 1 3F M 2 a 2 a
3-5(b)
已知：F, M, q, a, 求支座A、B约束反力。
q
M
解：梁受力分析如图，平面任意力系平衡方程为
FAx

理论力学第二章

扭矩扳手
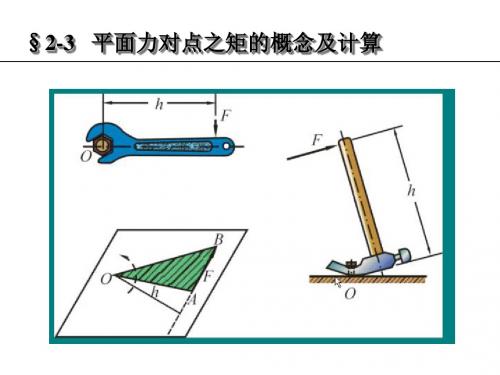
2-3 平面力对点之矩的概念及计算
一、力对点的矩（力矩）力对点的矩（力矩）
M O ( F ) = ± F ⋅ d ，单位N•m或KN•m 单位N KN•
→
→
① ②
是代数量。 M O ( F ) 是代数量。
M O ( F ) 正负判定：正负判定：
→
→
M O (F ) (F
+
→ →
-
③ 当F=0或d=0时， O (F ) =0。 =0或 =0时 M =0。点O为矩心，d为力臂。为矩心，为力臂。角形面积，或是矢量积的模。面积，或是矢量积的模。 ④ M O (F ) = ± 2⊿AOB= r × F 2⊿AOB= 力对点0矩的大小等于2 力对点0矩的大小等于2倍三
Fx = X i , F y = Y j
F = X +Y
2 2
→
→ →
→
X cos α = F
Y cos β = F
2-2 平面汇交力系合成与平衡的解析法
区分力沿轴的分力和力在两轴上的投影：区分力沿轴的分力和力在两轴上的投影：力沿轴的分力和力在两轴上的投影 • 分力是矢量，投影是代分力是矢量，数量，二者性质不同。数量，二者性质不同。 • 在直角坐标系中，投影在直角坐标系中，的大小与分力的大小相但在斜角坐标系中，同，但在斜角坐标系中，二者不等。二者不等。
∑F = 0 ix
− FBA + F cos60 − F2 cos30 = 0 1
o o
∑F =0 iy
FBC − F cos30 − F cos60 = 0 1 2
o o
F = F2 = P 1
解得： FC = 27 32kN 解得： B .

第二章-1 平面汇交力系与平面力偶系

第二章-1 平面汇交力系与平面力偶系一、判别题（正确和是用√，错误和否×，填入括号内。

）2-1 平面汇交力系平衡的充分与必要的几何条件是：力多边形自行封闭。

（√）2-2 力在某一固定面上的投影是一个代数量。

（×）2-3 两个力F1、F2大小相等，则它们在同一轴上的投影也相等。

（×）2-4 一个力不可能分解为一个力偶；一个力偶也不可能合成一个力。

（√）2-5 力偶无合力、不能用一个力来等袒代替，也不能用一个力来平衡；（√）2-6 力偶无合力，也就是说力偶的合力等于零。

（×）2-7 力偶矩和力对点之矩本质上是二样的，讲的是一回事。

（×）2-8 力偶的作用效果取决于力偶矩的大小和转向。

（√）2-9 只要两力偶的力偶矩代数值相等，就是等效力偶。

（√）2-10 力偶中的两个力对同平面内任一点之矩的代数和等于力偶矩。

（√）2-11 力偶只能用力偶来平衡。

（√）2-12 平面力偶系可简化为一个合力偶。

（√）2-13 力偶可任意改变力的大小和力偶臂的长短。

（×）2-14 力偶的两力在其作用面内任意轴上的投影的代数和都等于零。

（√）2-15 若两个力F1、F2在同一轴上的投影相等，则这两个力相等，即F1 = F2。

（×）2-16 若两个力F1、F2大小相等，则在同一轴Ox上投影相等，即F1x = F2x。

（×）2-17 若两个力F1、F2大小、方向、作用点完全相同，则这两个力在任一轴上的投影相等。

（√）2-18 若两个力大小相等、方向相反，则在任一轴Ox上的投影大小相等。

（√）2-19 若两个力平行，则它们在任一轴上的投影相等。

（×）2-20 若两个力在某轴上的投影均为零，则该两力平行。

（√）2-21 图示为分别作用在刚体上A、B、C、D点的4个共面力，它们所构成的力多边形自行封闭且为平行四边形。

由于力多边形自行封闭，所以是平衡的。

第2章平面汇交力系和平面力偶系

9
例题 1
解：
1. 选碾子为研究对象，受力分析如图b所示。
F
R O
各力组成平面汇交力系，根据平衡的几何条
件，力P ， F ， FA和FB组成封闭的力多边形。
qP
B
由已知条件可求得
A
h
cos q R h 0.866
(a)
R
q 30
FO
再由力多边形图c 中各矢量的几何关系可得
解得
FB sin q F FA FB cosq P
（2）应用合力矩定理
MO (F ) MO (Fx ) MO (Fy )
F cosq l cosj F sinq l sinj Fl cos(q j)
22
§2—4 平面力偶 1．力偶与力偶矩
由两个大小相等、方向相反且不共线的平行力组成的力系，
称为力偶。如图所示，记作（F，F'）。力偶的两力之间
如图轧路碾子自重P = 20
kN，半径 R = 0.6 m，障碍物高
h = 0.08 m碾子中心O处作用一
水平拉力F，试求: (1)当水平拉力F = 5 kN时，碾子对地面和
R
FO
障碍物的压力；(2)欲将碾子拉
q
过障碍物，水平拉力至少应为多
B
大；(3)力F 沿什么方向拉动碾
A
h
子最省力，此时力F为多大。
大小取决于力的大小与力臂的乘积，平面力对点之矩是一个代数量。它的转向人为规定一般取逆时针转向时为正，反之为负。
F对矩心点O之矩
MO(F) r
ห้องสมุดไป่ตู้Oh
B F A
M O (F ) Fh 2 AOAB
式中 AOAB为三角形OAB 的面积，如图所示。单位为 N•m或kN •m。

第二章平面汇交力系与平面力偶系

第2章平面汇交力系与平面力偶系一、是非题(正确的在括号内打“√”、错误的打“×”)1．力在两同向平行轴上投影一定相等，两平行相等的力在同一轴上的投影一定相等。

( √ )2．用解析法求平面汇交力系的合力时，若选取不同的直角坐标轴，其所得的合力一定相同。

( √ )3．在平面汇交力系的平衡方程中，两个投影轴一定要互相垂直。

( × )4．在保持力偶矩大小、转向不变的条件下，可将如图2.18(a)所示D处平面力偶移到如图2.18(b)所示E处，而不改变整个结构的受力状态。

( × )图2.185．如图2.19所示四连杆机构在力偶的作用下系统能保持平衡。

( × )6．如图2.20所示皮带传动，若仅是包角发生变化，而其他条件均保持不变时，使带轮转动的力矩不会改变。

( √ )图2.19 图2.20 二、填空题1．平面汇交力系的平衡的充要条件是平面汇交力系的合力等于零，利用它们可以求解2个未知的约束反力。

2．三个力汇交于一点，但不共面，这三个力不能相互平衡。

3．如图2.21所示，杆AB自重不计，在五个力作用下处于平衡状态。

则作用于点B的四个力的合力=，方向沿与F的方向相反。

4．如图2.22所示结构中，力对点O的矩为。

5．平面汇交力系中作力多边形的矢量规则为：各分力的矢量沿着环绕力多边形边界的某一方向首尾相接，而合力矢量沿力多边形封闭边的方向，由第一个分力的起点指向最后一个分力的终点。

图2.21 图2.22 6．在直角坐标系中，力对坐标轴的投影与力沿坐标轴分解的分力的大小相等，但在非直角坐标系中，力对坐标轴的投影与力沿坐标轴分解的分力的大小不相等。

三、选择题1．如图2.23所示的各图为平面汇交力系所作的力多边形，下面说法正确的是( C )。

(A) 图(a)和图(b)是平衡力系 (B) 图(b)和图(c)是平衡力系(C) 图(a)和图(c)是平衡力系 (D) 图(c)和图(d)是平衡力系图2.232. 关于某一个力、分力与投影下面说法正确的是( B )。

工程力学ppt 2平面汇交力系和平面力偶系

FR F1 F2 Fn Fi
i 1
(2-1)
a
b 图2.1
c
● 2.1.2 平面汇交力系合成的几何法
由力多边形法则知，平面汇交力系的合成结果为一合力，显然，平面汇交力系平衡的必要和充分条件是该力系的合力等于零。如果用矢量形式表示，即
FR
F
i 1
n
i
0
（2-2）
由力的合成的几何法可知，平面汇交力系的合力是由力多边形的封闭边来表示的。在平衡的情形下合力为零，也就是力多边形中最后一力终点与第一个力的起点重合，此时的力多边形称为封闭的力多边形。于是得到如下结论：平面汇交力系平衡的必要和充分条件是力多边形自行封闭。这就是平面汇交力系平衡的几何条件。运用平面汇交力系平衡的几何条件求解问题时，需要首先按比例画出封闭的力多边形，然后用尺和量角器在图上量得所要求的未知量；也可根据图形的几何关系，用三角公式计算出所要求的未知量，这种解题方法称为几何法。
FA 22.4kN，FC 28.3kN
根据作用力和反作用力的关系，作用于杆DC在端C的力FC与 FC 的大小相等，方向相反，由此可知杆DC是受压杆，如图2.3(b)所示。
应该指出，封闭的力的多边形也可以根据三角几何关系，作成如图2.3(d)所示的力三角形，同样可求得力 FA 和 FC ，且结果相同。通过以上例题，可知用几何法求解平衡问题的主要步骤如下： (1) 选取研究对象。根据题意，分析已知量与待求量，选取恰当的平衡物体作为研究对象，并画出分离体简图。 (2) 分析研究对象的受力情况，正确地画出其相应的受力图。在研究对象上，画出其所受的全部外力。若某个约束反力的作用线不能根据约束特性直接确定，而物体又只受三个力作用时，则可根据三力平衡汇交的条件来确定未知力的作用线方位。 (3) 作封闭的力多边形图，求解未知量。可以应用比例尺直接量出待求的未知量，也可以根据几何三角关系计算出来。

第2章平面汇交力系与平面力偶理论

且在同一平面内，由平面力偶系的合成理论．其合力偶矩为
式中，负号表示合力偶的转向为顺时针方向转动。
欲求作用在A、B处的水平力，应以工件为研究对象，受力分析如图 2—13所示，由于工件在水平面内受四个力偶和两个螺栓的水平反力的作用下而平衡。因为力偶只能与力偶平衡，故两个螺栓的水平反力N一和jv”必然组成一个力偶。由平面力偶系的平衡方程
二、平面汇交力系合成与平衡的解析法
根据合力投影定理，可计算出合力R的投影Rx和Ry
合力R与x轴正向间的夹角为
平面汇交力系平衡的充要条件是该力系的合力R等于0，则有
上式成立，必须同时满足
平面汇交力系解析法平衡的必要与充分条件是：力系中所有各力在两个坐标轴上投影的代数和分别等于零。
例2-2 图2-5(a)所示圆柱体A重Q，在中心上系着两条绳AB和 AC，并分别经过滑轮B和C，两端分别挂重为P和2P的重物，试求平衡时绳AC和水平线所构成的角α及D处的约束反力。解选圆柱为研究对象，取分离体画受
（2）作用在同一平面内的两个力偶，只要它的力偶矩的大小相等、转向相同，则该两个力偶彼此等效。这就是平面力偶的等效定理。
定理的推论
(1)力偶可以在其作用面内任意移动，而不影响它对刚体的作用效应。 (2)只要保持力偶矩大小和转向不变，可以任意改变力偶中力的大小和相应力偶臂的长短。而不改变它对刚体的作用效应上述推论表明，在研究同一平面内有关力偶问题时，只需考虑力偶矩的代数值，而不必研究其中力的大小和力偶臂的长短。
从而解得
所以
例图a 所示结构中，各构件自重不计。在构件AB 上作用1力偶矩为M 的力偶，求支座A 和C 的约束力。
解（1）BC为二力杆： F c= −F B（图c）（2）研究对象AB，受力如图b 所示， F AFB' 构成力偶，则

理论力学训练题集(终)

第一章静力学公理和物体的受力分析一、选择题1、三力平衡定理是﹍﹍﹍﹍。

①共面不平行的三个力互相平衡必汇交于一点；②共面三力若平衡,必汇交于一点；③三力汇交于一点，则这三个力必互相平衡。

2、三力平衡汇交定理所给的条件是﹍﹍﹍﹍。

①汇交力系平衡的充要条件;②平面汇交力系平衡的充要条件;③不平行的三个力平衡的必要条件；④不平行的三个力平衡的充分条件；3、图示系统只受作用而平衡。

欲使Ａ支座约束力的作用线及ＡＢ成30°角,则斜面的倾角应为﹍﹍﹍﹍。

①0°②30°③45°④60°4、作用在一个刚体上的两个力、，满足=－的条件，则该二力可能是﹍﹍﹍﹍.①作用力和反作用或是一对平衡的力；②一对平衡的力或一个力偶；③一对平衡的力或一个力和一个力偶；④作用力和反作用力或一个力偶。

二、填空题1、已知力沿直线ＡＢ作用，其中一个分力的作用线及ＡＢ成30°角，若欲使另一个分力的大小在所有分力中为最小，则此二分力间的夹角为﹍﹍﹍﹍﹍﹍﹍﹍度。

2、作用在刚体上的两个力等效的条件是﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍。

3、将力沿Ｘ、Ｙ方向分解，已知Ｆ＝100Ｎ，在Ｘ轴上的投影为86。

6Ｎ,而沿Ｘ方向的分力的大小为115。

47Ｎ，则的Ｙ的方向分量及Ｘ轴的夹角为﹍﹍﹍﹍,在Ｙ轴上的投影为﹍﹍﹍﹍。

4、若不计各物体重量，试分别画出各构杆和结构整体的受力图。

第二章平面汇交力系和平面力偶系一、选择题1、已知、、、为作用于刚体上的平面共点力系，其力矢关系如图所示为平行四边形,由此可知﹍﹍﹍﹍﹍﹍﹍。

（1）力系可合成为一个力偶；（2）力系可合成为一个力；（3）力系简化为一个力和一个力偶；（4）力系的合力为零，力系平衡。

2、汇交于Ｏ点的平面汇交力系，其平衡方程式可表示为二力矩形式。

即（）＝0,（)＝0,但必须﹍﹍﹍﹍﹍﹍﹍。

①Ａ、Ｂ两点中有一点及Ｏ点重合；②点Ｏ不在Ａ、Ｂ两点的连线上；③点Ｏ应在Ａ、Ｂ两点的连线上；3、由n个力组成的空间平衡力系，若其中（n－1）个力相交于Ａ点，则另一个力﹍﹍﹍﹍﹍﹍﹍。

工程力学课后详细答案

第一章静力学的基本概念受力图第二章平面汇交力系2-1解：由解析法，23cos 80RX F X P P Nθ==+=∑12sin 140RY F Y P P Nθ==+=∑故：22161.2R RX RY F F F N=+=1(,)arccos2944RYR RF F P F '∠==2—2解：即求此力系的合力，沿OB 建立x 坐标,由解析法，有123cos45cos453RX F X P P P KN==++=∑13sin 45sin 450RY F Y P P ==-=∑故： 223R RX RY F F F KN=+= 方向沿OB 。

2—3 解：所有杆件均为二力杆件,受力沿直杆轴线。

(a) 由平衡方程有：0X =∑sin 300AC AB F F -=0Y =∑cos300AC F W -=0.577AB F W=（拉力）1.155AC F W=(压力)（b ）由平衡方程有:0X =∑ cos 700AC AB F F -=0Y =∑sin 700AB F W -=1.064AB F W=（拉力）0.364AC F W=（压力)（c ）由平衡方程有：0X =∑cos 60cos300AC AB F F -=0Y =∑sin 30sin 600AB AC F F W +-=0.5AB F W= （拉力）0.866AC F W=(压力）（d) 由平衡方程有:0X =∑sin 30sin 300AB AC F F -=0Y =∑cos30cos300AB AC F F W +-=0.577AB F W= (拉力）0.577AC F W= (拉力）2-4 解：(a ）受力分析如图所示：由x =∑ 22cos 45042RA F P -=+15.8RA F KN∴=由Y =∑22sin 45042RA RB F F P +-=+7.1RB F KN∴=(b)解：受力分析如图所示:由x =∑3cos 45cos 45010RA RB F F P ⋅--=0Y =∑1sin 45sin 45010RA RB F F P ⋅+-=联立上二式,得:22.410RA RB F KN F KN==2—5解：几何法:系统受力如图所示三力汇交于点D ，其封闭的力三角形如图示所以：5RA F KN= （压力）5RB F KN=（与X 轴正向夹150度）2—6解：受力如图所示:已知，1R F G = ,2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-⋅=--2—7解：受力分析如图所示，取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=0Y =∑sin 45sin 450CBRA F F '-=联立后，解得：0.707RA F P=0.707RB F P=由二力平衡定理0.707RB CB CBF F F P '===2-8解:杆AB,AC 均为二力杆，取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=0Y =∑sin 30sin 600AB AC F F W +-=联立上二式,解得：7.32AB F KN=-(受压）27.3AC F KN=（受压）2—9解：各处全为柔索约束，故反力全为拉力,以D,B 点分别列平衡方程（1）取D 点,列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==（2）取B 点列平衡方程：由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2—10解：取B 为研究对象：由0Y =∑sin 0BC F P α-=sin BC PF α∴=取C 为研究对象:由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式，且有BCBC F F '= 解得：2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象：由0Y =∑ cos 0NH CEF F α'-=CECE F F '= 故有：22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2—11解:取A 点平衡:x =∑sin 75sin 750AB AD F F -=0Y =∑cos 75cos 750AB AD F F P +-=联立后可得： 2cos 75AD AB PF F ==取D 点平衡，取如图坐标系：x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD P F F F KN'∴===⋅=2-12解：整体受力交于O 点，列O 点平衡由x =∑cos cos300RA DC F F P α+-=0Y =∑sin sin 300RA F P α-=联立上二式得：2.92RA F KN=1.33DC F KN=(压力）列C 点平衡x =∑405DC AC F F -⋅=0Y =∑ 305BC AC F F +⋅=联立上二式得： 1.67AC F KN=（拉力）1.0BC F KN=-(压力）2-13解：（1)取DEH 部分，对H 点列平衡x =∑05RD REF F '= 0Y =∑05RD F Q =联立方程后解得: 5RD F Q =2REF Q '=（2）取ABCE 部分,对C 点列平衡x =∑cos 450RE RA F F -=0Y =∑sin 450RB RA F F P --=且RE REF F '=联立上面各式得： 22RA F Q =2RB F Q P=+（3）取BCE 部分。

习题解答(平面力系)

② 受力如图 ③ 选坐标、取矩点B点 ④ 列方程为:
X 0 X B 0; Y 0 YB P 0; YB P
M B 0 M B P DE 0
解方程得
M B 100011000( Nm 7 )
① 再研究CD杆 ② 受力如图
o M 0 , S sin 45 CE P ED 0 E CA ③ 取E为矩心，列方程
FB
FAx 0 FAy FB F 0 FB 2a M F 3a 0
17
习题2-14
解答要点:
q
D A
M
B
F
C
F
1.取整体为研究对象
q
FAX
2.受力分析如图
FAY
D 3.列平衡方程如下:
A
M
B
C
F F
FB
x y
0, 0,
FAx 0 FAy FB F qa 0
M A
FA
B
FB
对于c图
M M 0, FBl cos M 0 FB l cos
16
习题2-14
解答要点: 1.取整体为研究对象 2.受力分析如图 3.列平衡方程如下:
A
M
B
F
FAX
A
FAY
M
B
F
F 0, F 0, M ( F ) 0,
x y A
19
习题2-20
解答要点一: 1.先取BC为研究对象
A
B
FBY
M
y C
x

M
FC
2.受力分析如图
3.列平衡方程如下:

山东大学《理论力学》教案第2章平面汇交力系与平面力偶系

第2章平面汇交力系与平面力偶系一、目的要求1．平面汇交力系（多个力）合成与平衡的几何法，并能应用平衡的几何条件求解平面汇交力系的平衡问题。

2.能正确地将力沿坐标轴分解和求力在坐标轴上的投影，对合力投影定理有清晰的理解，掌握汇交力系合成的解析法和平衡方程，并能熟练的应用平衡方程求解汇交力系的平衡问题。

3. 理解力对点之矩的概念，并能熟练地计算。

4．深入理解力偶和力偶矩的概念，明确平面力偶的性质和平面力偶的等效条件。

二、基本内容1．平面汇交力系合成的几何法·力多边形法则平面汇交力系可合成为通过汇交点的合力，其大小和方向等于各分力的矢量和。

即∑==+++=n i i 11F F F F F n 2R 或 ∑=F F R合力R F 的大小和方向可用力三角形法则或力多边形法则得到。

作出图示首尾相接的开口的力多边形，封闭边矢量即所求的合力。

2．平面汇交力系平衡的几何条件平面汇交力系平衡的必要和充分条件是：力系的合力等于零。

其矢量表达式为∑==0F F R （2-2）力系平衡的几何条件是：力系的力多边形自行封闭。

如图2-4所示。

3．力在正交坐标轴系的投影与力的解析表达式力F 在y x ,轴上的投影分别为cos cos sin x y F F F F F αβα=⎫⎪⎬==⎪⎭力的投影是代数量。

4．平面汇交力系合成的解析法合力投影定理：合力在某轴上的投影等于各分力在同一轴上投影的代数和。

平面汇交力系平衡的必要和充分条件是：各力在两个坐标轴上的投影的代数和分别为零。

即00x y F F ⎫=⎪⎬=⎪⎭∑∑ 两个独立的平衡方程，可解两个未知量。

5.平面内的力对点O 之矩是代数量，记为M o (F )ABO Fh M o ∆±=±=2)(F其中F 为力的大小，h 为力臂，∆ABO 为力矢AB 与矩心O 组成三角形的面积。

一般以逆时针转向为正，反之为负。

力矩的解析表达式为：合力矩定理： 6.力偶和力偶矩：·大小相等，方向相反，作用线平行的两个力称为力偶。

理论力学习题及答案

第2章平面汇交力系与平面力偶系2-1(2-3) 物体重P=20 kN，用绳子挂在支架的滑轮B上，绳子的另一端接在绞车D上，如图a所示。

转动绞车，物体便能升起。

设滑轮的大小、杆AB与CB自重及摩擦略去不计，A，B，C三处均为铰链连接。

当物体处于平衡状态时，求拉杆AB和支杆CB所受的力。

(a) (b)图2-3解取支架、滑轮及重物为研究对象，坐标及受力图b。

由平衡将F T=P=20 kN代入上述方程，得（拉），（压）2-2(2-5) 在图a所示刚架的点B作用一水平力F，刚架重量不计。

求支座A，D的约束力。

(a) (b)图2-5解研究对象：刚架。

由三力平衡汇交定理，支座A的约束力F A必通过点C，方向如图b。

取坐标系，由平衡（1）（2）式(1)，(2)联立，解得，2-3(2-7) 图a所示液压夹紧机构中，D为固定铰链，B，C，E为活动铰链。

已知力F，机构平衡时角度如图，求此时工件H所受的压紧力。

(a) (b) (c)(d)图2-7解（1）轮B，受力图 b。

由平衡（压）（2）节点C，受力图c。

由图c知，，由平衡，（3）节点E，受力图d即工件所受的压紧力2-4(2-9) 铰链4杆机构CABD的CD边固定，在铰链A、B处有力F1，F2作用，如图a所示。

该机构在图示位置平衡，不计杆自重。

求力F1与F2的关系。

(a) (b) (c)图2-9解(1) 节点A，坐标及受力图b，由平衡，（压）（2）节点B，坐标及受力图c，由平衡即﹕2-5(2-13) 图a所示结构中，各构件自重不计。

在构件AB上作用一力偶矩为M的力偶，求支座A和C的约束力。

(a) (b)(c)图2-13解（1）BC为二力杆：（图c）（2）研究对象AB，受力图b，构成力偶，则，，2-6(2-15) 直角弯杆ABCD与直杆DE及EC铰接如图a，作用在杆DE上力偶的力偶矩,不计各杆件自重，不考虑摩擦，尺寸如图。

求支座A，B处的约束力和杆EC 受力。

(a) (b) (c)图2-15解（1）EC为二力杆，杆DE受力图b（2）整体，受力图c。

平面汇交力系与平面力偶系习题及解答

3-1 杆AC 、BC 在C 处铰接，另一端均与墙面铰接，如图所示，F 1和F 2作用在销钉C 上，F 1=445 N ，F 2=535 N ，不计杆重，试求两杆所受的力。

解：(1) 取节点C 为研究对象，画受力图，注意AC 、BC 都为二力杆，(2) 列平衡方程：12140 sin 600530 cos 6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。

3-2 水平力F 作用在刚架的B 点，如图所示。

如不计刚架重量，试求支座A 和D 处的约束力。

解：(1) 取整体ABCD 为研究对象，受力分析如图，画封闭的力三角形：(2)F 1F FDF F AF D211 1.122D A D D A F F FF F BC AB AC F F F F =====∴===3-3 在简支梁AB 的中点C 作用一个倾斜45o 的力F ，力的大小等于20KN ，如图所示。

若梁的自重不计，试求两支座的约束力。

解：(1) 研究AB ，受力分析并画受力图：(2) 画封闭的力三角形：相似关系：B A F F FCDE cde CD CE ED∆≈∆∴== 几何尺寸：11 22CE BD CD ED =====求出约束反力：12010 22010.4 45arctan 18.4B A o oCE F F kNCDED F F kN CDCECDα=⨯=⨯==⨯===-=3-4 如图所示结构由两弯杆ABC 和DE 构成。

构件重量不计，图中的长度单位为cm 。

已知F =200 N ，试求支座A 和E 的约束力。

FF BF A dce解：(1) 取DE 为研究对象，DE 为二力杆；F D = F E(2) 取ABC 为研究对象，受力分析并画受力图；画封闭的力三角形：'15166.7 23A D E F F F F N ===⨯= 3-5 在四连杆机构ABCD 的铰链B 和C 上分别作用有力F 1和F 2，机构在图示位置平衡。