电学 1-4 环路定理、电势、电势差
静电场的环路定理 电势

静电场的环路定理 电势
式中,Uab为静电场中任意两点 a、b间的电势差,也称为电压.式( 8-22)表明,静电场中a、b两点的 电势之差等于把单位正电荷从a点沿 任意路径移到b点电场力所做的功.电 势差是绝对的.
静电场的环路定理 电势
四、 电势的计算 1. 点电荷电场的电势
设在真空中有一点电荷q,其周围的电场分布为
(8- 21)
式(8-21
a的电势在数值上等
于把单位正电荷从a点沿任意路径移到无限远电场力所做的功.在
许多实际问题中,也常选地球为电势零点.
电势是标量,在国际单位制中,电势的单位为伏特(V).
静电场的环路定理 电势
2. 电势差
从电场力做功的角度引入电势能的概念,由式(8-19) 和式(8-20)可以看出,电势能Wa不仅与a点的电场性质有 关,还与试验电荷q0有关,因而不能用来描述电场中某场 点的性质.但是,人们发现电势能与试验电荷q0的比值与试 验电荷q0无关,仅与a点电场的性质有关.因此,用电势描 述电场的能量特征.a、b两点的电势分别用Va、Vb表示.由 式(8-18),定义
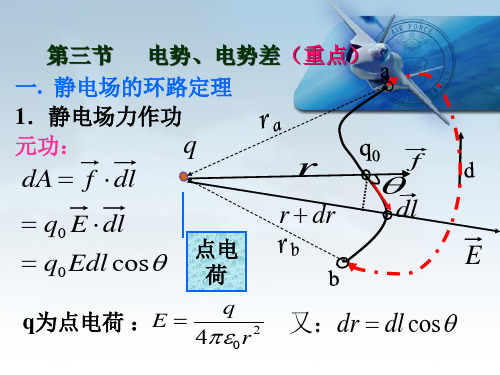
dW=F·dl=q0E·dl=q0Edlcosθ
静电场的环路定理 电势
式中,θ为E与dl的夹角.由图8-20可以看出,元位移dl在电场力 方向的投影为dlcosθ=dr,则元功可写成
静电场的环路定理 电势
既然每个点电荷的电场力对q0所做 的功都与路径无关,那么它们的代数和 也必然与路径无关.由此可以得到以下结 论:在任意带电体的电场中,电场力对 试验电荷q0所做的功只与试验电荷q0及 其始末位置有关,而与路径无关.
静电场的环路定理 电势
2. 电势叠加原理
设场源电荷是由分布在有限区域内的点电荷系q1、q2、q3、 …、qn组成,根据场强叠加原理,任一点P处的场强等于各个点电 荷在该点产生场强的矢量和,即
物理学精品课件之电势、电势差
3. 电势叠加原理
在点电荷系q1.q2.q3
a点的电场:
qn 的电场中q,n
E E1 E2 En q0
q3
a点的电势:
q2
Ua a E dl
q1
E1 dl E2 dl En dl
的功。---物理意义
讨论: 标量,有正、负;单位:J·C-1 ; V; 与电势零点的选择有关。
一般情况选 U 0
2. 电势差 U ab
设:U a
E dl
a
U b b E dl
则a、b两点的电势之差
b
U ab U aU b
E dl
a
试探电荷从a b 电场力作功:
Aab Wa Wb q0 (Ua Ub )
二. 电势能
静电场是保守场,静电场力是保守力。
重力场
静电场
重力势能mgh 类比 电势能W
重力做功=重力势能 的变化,即
电场力做功=电势 能的变化,即
AG mgh mgh1 mgh2
Aab Wa Wb
b vv
Wa Wb a q0E dl
b vv
Aab a q0E dl
q
q0 f
---电场力做功的特点
2. 静电场的环路定理
a
q0沿acbda闭合
路径运动一周,
q
电场力做功:
A l f dl
r
r dr
f
dl
c E
l q0 E dl q0
E dl 0
l
E dl 0
l E dl 0
静电场 是保守场
Ao q0 (U Uo ) 1.0109 (81010) 80(J )
第 2 章 电势

四、电势梯度 例题
五、电势能
1.定义
静电场是保守场,可引进静电势能的概念。检验
电荷 q0 在静电场中从 a 点移到 b 点电场力作正
功,电势能减少。
定义电势能增量Δ W
W Wb Wa dA
L rb ra
E P mgh
q0 E dl
b a
x2 r 2
r
O
R
x
P
dS
4 0 x 2 r 2
S
dS 2rdr R 2 rdr ( x 2 R2 x) 0 4 0 x 2 r 2 2 0
三、电势叠加原理 讨论
(1) x R时 R2 1 1 R2 2 ( x R ) x(1 2 ) 2 x(1 ) 2 x 2 x R2 x 2x R2 R2 Q (x x) 2 0 2x 40 x 40 x
rb
ra
E dl
q0 (b a )
五、电势能 定义电势能
W q0
即:一个电荷在电场中某点的电势能等于它的电 量与电场中该点电势的乘积。 一般取 r→∞ 时为势能零点,则空间任一点的电 势能为
W q0
r
E dl
五、电势能
2.注意
(1)电势能是属于系统的,为场源电荷和电荷
第 2 章
电势
一、静电场环路定理 二、电势差和电势 三、电势叠加原理 四、电势梯度 五、电势能 六、静电场的能量
一、静电场环路定理
1.静电场力所作的功
与引力场相类似,静电场也是保守场,静电力
是保守力,即静电力作功与具体路径无关。 点电荷电场: dA q0 E dl q0 cos1 dl q E b E e 2 r 40 r q0 Edr
电磁学讲课电势

4 0 r r
r– r r+
–
–q
O
+
l +q
x
对于离电偶极子比较远的点,r >> l,有
rr r2, r r l cos
则
V
q l co s 40r 2
p cos 40r 2
p r co s 4 0 r 3
pr
4 0 r 3
例5 利用书中例 7-11 结果计算均匀带电圆盘 (R, )
轴线上任一点电势。
得
V
px
40 (x2
y2 )3/2
x x2 y2
–
–q
p O
+
+q
x
所以
Ex
V x
p(2x2 y2)
40 (x2 y2 )5/ 2
Ey
V y
3 pxy
40 (x2 y2 )5/ 2
E Exi Ey j
静电场与万有引力场的比较
静电力
F
40r 2
er
电场强度
F
Q
E q 40r2 er
(对比地图上等高线、等温线、等压线等)
特点 (1) 等势面 电场线 证明:取很近的两点 a和 b,
Vab Va Vb E l El cos
Δ l
b
a
E
若在同一等势面 Va = Vb,则 cos = 0 即 = /2,得证。
(2) 等势面越密的地方,电场线越密,场强越大。
证明:作等势面时,按规定任意两
b
dA
q0q
a
40
rb dr r ra 2
q0q
40
1 ra
高中物理竞赛初级讲义 电学电势及电势能

半径为R、电荷为q的均匀带电球壳内外,距球心r处的电势:
【例1】试求电偶极子周围的电势分布.
【例2】试求均匀带电圆环轴线上电势和电场分布。设圆环半径为R,电荷线密度为η。
【例3】半径为R的半球形薄壳,其表面均匀分布面电荷密度为σ的电荷,求该球开口处圆面上任一点的电势.
【例7】如图所示,AB=2l,OCD是以B为中心,l为半径的半圆。A点有正点电荷q,B点有负点电荷-q。
(1)把单位正电荷从O点沿OCD移到D点,电场力对它作了多少功?
(2) 把单位负电荷从D点沿AB的延长线移到无穷远,电场力对它作了多少功?
(3)电荷q均匀分布在半球面ACB上,球面半径为R,CD为通过半球顶点C和球心O的轴线,如图所示.P、Q为CD轴线上相对O点对称的两点,已知P点的电势为φP,试求Q点的电势φQ.
【例6】有人设想了一种静电场:电场的方向都垂直于纸面并指向纸里,电场强度的大小自左向右逐渐增大,如图所示.这种分布的静电场是否可能存在?试述理由.
电势差:电场中两点电势的差值叫电势差。
匀强电场中,沿场强方向两点间的电势差:
2.等势面
等势面:静电场中电势相同的点组成的面叫等势面。
判断电势高低的方法:
等量异种点电荷和等量同种点电荷连线上与中垂线上场强及电势的变化规律
3.电势的计算
(1)由定义 ,B点为电势零点,一般为无穷远处
(2)点电荷的电势: ,其中r是场点到电荷q的距离。
电磁学第3讲电势及电势能
一、电势能
1.静电场的环路定理
静电场力是保守力,静电场是保守场。
静电场的环路定理:静电场中场强沿场力对电荷所做功等于电荷电势能的改变量:
简述静电场的环路定理

简述静电场的环路定理静电场的环路定理是电磁学中的基本定理之一,它描述了静电场中电场强度的分布以及其与电荷分布之间的关系。
本文将对静电场的环路定理进行简述,重点介绍定理的含义和应用。
静电场的环路定理,又称为库仑定律或环路定理,是由法国物理学家库仑在18世纪末提出的。
定理的核心思想是在闭合路径上,电场强度沿着路径的积分等于路径内电荷的代数和与真空介电常数的乘积。
简单来说,静电场的环路定理可以用以下公式表示:∮E·dl = q/ε₀其中,∮E·dl表示电场强度沿闭合路径的环路积分,q表示路径内的总电荷,ε₀表示真空介电常数。
根据静电场的环路定理,可以推导出一些重要的结论和应用。
首先,对于闭合路径上没有电荷的情况,环路积分必然等于零。
这意味着在没有电荷存在的区域,电场强度沿着任意闭合路径的环路积分都等于零。
这个结论可以用来验证电场的无旋性,即电场强度的旋度为零。
对于闭合路径上存在电荷的情况,环路积分不等于零。
根据路径内电荷的正负情况以及电场强度的方向,可以确定环路积分的正负。
如果路径内的总电荷为正,则环路积分为正,表示电场强度沿路径的方向与路径的方向一致;如果路径内的总电荷为负,则环路积分为负,表示电场强度沿路径的方向与路径的方向相反。
静电场的环路定理可以应用于计算电场强度、电势差等物理量。
例如,在计算电场强度时,可以通过选择合适的闭合路径,利用环路定理求解电场强度的大小和方向。
在计算电势差时,可以利用环路定理将电场强度的环路积分转化为电势差的差值,从而简化计算过程。
静电场的环路定理还可以应用于电场的分布和电势的计算。
通过选择合适的闭合路径,可以根据路径内的电荷分布和已知的电场强度,求解路径上任意点的电场强度和电势。
同时,环路定理也为电场强度的计算提供了一种简便的方法,避免了直接积分计算的繁琐过程。
静电场的环路定理是电磁学中的重要定理之一,它描述了静电场中电场强度与电荷分布之间的关系。
电磁学公式

电磁学公式
电磁学公式主要包括以下几个方面:
1. 库伦定律(Coulomb's Law):
F = k * (q1 * q2) / r^2
其中,F为两个电荷之间的静电力,q1和q2为两个电荷的电荷量,r为两个电荷之间的距离,k为库伦常数。
2. 电场强度(Electric Field Strength):
E =
F / q
其中,E为电场强度,F为电荷所受的力,q为电荷量。
3. 电势差(Electric Potential Difference):
V = W / q
其中,V为电势差,W为电势能,q为电荷量。
4. 安培环路定理(Ampere's Law):
∮B·dl = μ0 * I
其中,B为磁场强度,dl为路径微元长度,μ0为真空中
的磁导率,I为通过闭合路径的电流。
5. 法拉第电磁感应定律(Faraday's Law):
ε = - dΦ / dt
其中,ε为感应电动势,Φ为磁通量,t为时间。
6. 电感(Inductance):
L = N * Φ / I
其中,L为电感,N为线圈匝数,Φ为磁通量,I为电流。
这只是电磁学公式的一部分,电磁学公式还包括磁场强度、电磁波传播等方面的公式。
实际应用中,还会结合物理常
数和其他公式一起使用。
4 静电场的环路定理

高压发生器
静电力做正功, 电势能减少; 静电力做正功, ∆A > 0, WA > WB , 电势能减少; 静电力做负功, 电势能增加。 静电力做负功, ∆A < 0, WA < WB , 电势能增加。
电势能和重力势能一样,是一个相对量, 电势能和重力势能一样,是一个相对量,先要规定电 势能为0的参考点 如果参考点p0确定 的参考点。 确定, 势能为 的参考点。如果参考点 确定,则
R2 q1 R1 o Ⅰ Ⅱ
V=
1
r ≤ R1 R1 ≤ r ≤ R2
Ⅲ
r ≥ R2
无限长均匀带电圆柱面的电场。圆柱半径为R, 例6 无限长均匀带电圆柱面的电场。圆柱半径为 ,单 试求其电势分布。 位长度上的带电量为 + λ ,试求其电势分布。 解:电场分布也应有柱对称性 (1) r <R (2) r >R (2) r >R
∞ r r r r r r = ∫ E1 ⋅ dl + ∫ E2 ⋅ dl + ....... + ∫ En ⋅ dl P P
P ∞ P ∞ ∞
= u1 + u2 + ...... + un = ∑ ui = ∑
i =1
n
P
4πε 0 ri
qi
各点电荷单独存在时在该点电势的代数和 各点电荷单独存在时在该点电势的代数和, 代数和 注意(电势是一个标量) 电势是一个标量 注意 电势是一个标量
无旋场
2. 电势(Electric potential) )
2.1 电势能
由环路定理知,静电场是保守场。 由环路定理知,静电场是保守场。 保守场必有相应的势能, 保守场必有相应的势能,对静电场 则为电势能。 则为电势能。 静电力的功,等于静电势能的减少。 静电力的功,等于静电势能的减少。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§1.4.1 静电场的环路定理 §1.4.2 静电势能 §1.4.3 电势和电势差 §1.4.4 电势的计算 §1.4.5 等势面 §1.4.6 电势梯度
从功和能的角度研究静电场的性质
§1.4.1 静电场的环路定理
一、什么是保守力 ?
力所做的功只与物体的始末位置有关,而与所经历的
qE cos
a
b dl qlEcos
pE cos
W pE
当 p 和 E 同向时,W 取最小值 -pE,电偶极子达到稳
定平衡,即外电场的作用总是使电偶极子转向外场方向
§1.4.4 电势的计算
一、点电荷电场中的电势
选无限远为电势零点,点q电荷电量为 q,其场强为
E 40r 2 er
离点电荷为 r 的 P 点的电势为 积分路径沿径向
只与路径的起点和终点的位置有关,而与路径无关。
静电力是保守力,静电力场是保守力场。
式中
Aab
b E dr
称为场强沿任意路径
L 的线积分
q0
a
三、静电场环路定理
考察:试验电荷在电场中运动经过闭合路径回到原来
位置时,电场力做功 ?
A
F
L
b
dr
q0
E dr
L a
L1
b
q0 q0
例 4 两无限长同轴圆柱面,半径分别为 R1 和 R2。圆
柱面均匀带电,线电荷密度分别为 1 和 2 。
求:1)电势分布;2)两圆柱面之间电压。
解:1) 由高斯定理可得场强分布
E
0
1
2 0r
(r R1 ) (R1 r R2 )
方向 垂直 于圆
R1 2 1 R2
P0
r
1 2 2 0r
(r R2 )
当 r R2 时,选类似积分路径
R2
E
dr
R2 1 2dr
r
r 2 0r
1 2 ln R2 0 20 r
2) 两圆柱面之间电压
U R1 R2
R2
E
dr
R2
1
dr
R1
R1 2 0r
1 ln R2 2 0 R1
R1 2 1 R2
P0
r
P’ P
0 R1 R2
r
例 5 一无限大均匀带电平面,电荷面密度为 。若
1. 定义:从点 a 到点 b 移动单位正电荷时静电场力
所作的功,或电场中单位正电荷在 a, b 两点的电
势能之差称为 a, b 两点的电势差。
b
电势差(电压)
Uab a b
E dr
a
2. 电场中任意两点 a, b 的电势差等于把单位正电荷 从 a 点沿任意路径移动到 b 点静电场力所做的功, 即等于场强沿任意路径从 a 点到 b 点的线积分。
以该平面为电势零点,求平面周围空气电势分布
解:
E
2 0
20
x0 x0
O
x
在 x 0 区域
0 dx x
x 20
2 0
在 x 0 区域
0
dx
x
x 20
2 0
例 6 半径为 R 的无限长圆柱形带电体,电荷体密度为 Ar(r ≤ R),r 为距轴线距离,A 为常数。选距轴线距 离为 L(L > R)处为电势零点。计算圆柱体内外各点的 电势。
通常:理论计算有限带电体电势时选无限远为参考点; 实际应用或研究电路问题时取大地、仪器外壳 等为电势零点。
3. 电势和电势能的关系
点电荷 q0 在电场中的电势能为
电势能零点
电势能 Wa q0 a
E dr
W q0
Байду номын сангаас
电势零点即电势能零点
4. 电势单位 SI 单位:伏[特] (V)
注意 电势是描述电场能量性质的 物理量,与试验电荷无关
路径无关,这类力称为保守力。
例如:万有引力、弹性力、静电力等
b
二、静电场保守性的证明
1. 点电荷产生的电场
q
电场力所做 的功
dA F dr F dr cos dr cos r'r dr
a
dA
Fdr
q0 Edr
qq0
4 r
2
dr
0
dr
c
q0
θ
c’dr F
dA
Fdr
q0 Edr
qq0
4 r 2
E dr
q
r
4 0r
(r R)
若 P 点在球面内(r < R),由于球面内外场强的表达
式不同,所以电势的定义式中的积分要分成两段
E dr
r R
E
dr
E dr
r
R
q
O R
r
P
0
q
R 4 0r
2
dr
q
(r R)
4 0 R
OR
r
均匀带电球面内各点电势相等并等于球面上电势
例 8 一均匀带电直线,长为 L,线电荷密度为 ,求
直线延长线上到其一端距离为 d 的一点 P 的电势。
解:在直线上取电荷元 dl ,它到 P 点 距离为 l ,在 P 点产生的电势为
d dq dl 4 0l 4 0l
d dL dl
40 d l
L dl
d P
l
ln d L 4 0 d
3. 把电荷 q0 从 a 沿任意路径移动到 b 静电场力所做
的功为
Aab q0 (a b )
电势
1. 定义:电场中任一点电势等于把单位正电荷自该点 沿任意路径移动到电势零点静电场力所做的功,或
等于场强从该点沿任意路径到电势零点的线积分
a
电势零点 E dr
a
2. 电势零点的选择 原则:任意,视研究问题的方便而定;
E dr
r
r
q
4 0r
2
er
dr
r
q
4 0
dr r2
q
4 0r
点电荷 的电势
q 4 0r
q 为正, 为正,r 越小, 越大;
q 为负, 为负,r 越小, 越小
二、任意带电体电场中的电势
1. 场强积分法(由定义)
步骤:(1) 计算场强; (2) 选择合适的路径 L; (3) 分段积分(计算)。
力所做的功。
b
b
W
Aab
a F dr q0
E dr
a
q0 在电场中 a, b 两点的电势能之差等于把 q0 从 a 点移至 b 点过程中电场力所做的功。
3. 单位:SI 单位:焦[耳] (J) 其他常用单位:电子伏特 (eV)
b
电势能差 Wa Wb Aab q0 a E dr
例 9 均匀带电球层,内半径为 R1,外半径为 R2,体电荷密度为 。求图中 a 点和 b 点电势
解:取薄球壳,半径为 r,厚为 dr,可视为均匀带电球面, 其带电量为
dq 4r 2dr
对 a 点,此带电球面产生的电势为
R2
a
O R1
r
ra br
rb dr
d dq 4r 2dr rdr 4 0r 4 0r 0
(2) 根据点电荷电势公式由 dq 求出 d
(3) 根据电势叠加原理由 d 求出 d
例 7 点电荷 q1、q2、q3、q4 均为 4.0109C 放在一正方 形的四个顶点上,各顶点与正方形中心 O 的距离均为
5.0cm. (1) 计算 O 点的电势; (2) 将试验电荷 q0 1.0109C 从无限远处移到 O 点,电场力做的功为多少?(3) 电势
柱面
P
因电荷分布不局限于有限 空间范围,如果仍选无限远为
电势零点,则由积分
(
P
E
)
dr
,可知电势为无限大而失
去意义。把电势零点选在有限远处,可得到空间各点的
电势值。例如我们选 r = R2 处的 P0 点作为电势零点
当
r
P0RE1
时,选如图所示积分路径
dr
P' E dr
P0
E
解:内部场强,取半径为 r < R,
R
高为 l 的同轴圆柱面为高斯面
2rlE q 0
r l
q
r
Ar2rldr
0
2Alr 3
3
E 1 Ar 2 (r R)
3 0
外部场强,取半径为 r > R,长 为 l 的同轴圆柱面为高斯面
R r
2rlE q 0
l
q R Ar2rldr 2AlR3
结果违反环路定理 E d r 0,故而假设不成立。 L
所以,均匀电场具有平行而等间距的电场线。
§1.4.2 静电势能
1. 因为静电场的保守性,或静电场力作功与路径无关, 故任一电荷在静电场中都具有势能,称为电势能
2. 静电力作功和电势能增量的关系:
q0 在静电场中移动时,它的电势能的减少等于电场
a
电势零点 E dr
a
例 3 求均匀带电球面的电势分布。设球面半径为 R, 带电量为 q
解:场强已由高斯定律 求得
E
0
q
4 0r
2
er
(r R) (r R)
选无限远为电势零点。由于在球面外直到无穷远处场
强的分布都和电荷集中在球心处的点电荷的场强分布
一样,因此球面外任一点的电势与点电荷的结果相同
dr
0
Aab
b
dA
qq0
a
4 0
b1 a r2
dr
q
qq0 ( 1 1 )
