环路定理电势
静电场的环路定理 电势

· · a O
2
均匀带电球体内、外的场强: E内 r 3 0 均匀带电球体内某点的电势
2 腔内电势: U ( r ) U 1 U 2 [( 3 R12 r 2 ) ( 3 R2 r 2 )] 6 0
对O2点,r a, r 0
U r
(2) 点电荷系的电势
qi UA i 4 π ε0 ri
推广:
E Ei
A
U Ui
i
r1
q1
r2 ri
qi
rN
qN
电势叠加原理 (标量叠加)
q2
§3-1-4 静电场的环路定理 电势
(3) 有限连续带电体
【方法一】微元分割+积分法
Q
dq
e
带电体
r
A
UA ? dU 4 0 r
但在工程技术中,取大地、仪器外壳等为电势零点; (2)电场的电势分布确定后,电场力做功
W AB q0 (U A U B )
§3-1-4 静电场的环路定理 电势
2、电势的计算 (1) 点电荷的电势
q
+
A
积分至无穷远
r
E
q U (r ) 4πε0 r
§3-1-4 静电场的环路定理 电势
3 解:取如图所示C点(0,3R/2) 0, R r 2 根据对称性 U B U C O A x C 补上下半球面成为完整球面后 y B Q R U A 4 0 R 0 R U U UC AC A 3 0 Q 2R UC 4 0 ( 3 R / 2) 3 0 1 R 再由根据对称性 U AB U AC U AC 2 6 0
6-3 静电场的环路定理和电势

V(r>R)
1
4 0
q r
练习 在点电荷 +2q 的电场中,如果取图中P点处 为电势零点,则 M点的电势为
2q P M
a
a
(A) q
2π 0a
(C)
q
8π
0
a
q
(B)
4π 0a
(D) q
4π 0a
练习 在点电荷q的电场中,选取以q为中心,R为半 径的球面上一点P处作电势零点,则与点电荷q距离 为r的P’点电势为
A
(D)电场力作的功 W 0
电势的求解方法
(1)利用电势叠加原理
VP
dq
4π0r
使用条件:有限大带电体且选无限远处为电势零点.
(2)利用电势的定义
V 0点
VA E dl
A
使用条件:场强分布已知或很容易确定.
均匀带电球面:
V( r R )
1
4 0
q R
四 电势
1、电势
VA
EpA q0
E dl
AB
(VB 0)
q0
A
B E
物理意义:描述电场能的性质,某点的电势在数值上等于将单 位正电荷从该点沿着任意路径移到零势能点时电场力所做的功.
B
电势差(电压):U AB VA VB
E dl
A
WAB q0 (VA VB ) (EPB EPA)
位置有关,与路径无关.
B
dr
dl
q0
E
二 静电场的环路定理
q0 E dl q0 E dl
电势能 电势

r
37.
讨论: 讨论:
q
4πε0R 结论 V = q 4πε0r
(r < R)
V
Q 4πε0 R
(r ≥ R) (记住 记住) 记住
Q 4πε 0 r
o a. r < R 等势体 ; r >> R“点电荷” 点电荷”
电势分布?(设V∞= 0 ) 电势分布? 设 Ⅰ法 叠加法
利用上述结论 V = ∑Vi
v E
v v q0 ( ∫ E ⋅ dl +
ABC
v v v v ∫ E⋅ dl ) = q0 ∫ E⋅ dl =0
L CDA
即
v v v 的环流为零) ∫ E⋅ dl = 0 ( E 的环流为零)
l
说明:静电力 保守力, 说明:静电力——保守力,静电场 保守力 静电场——保守场 保守场
29 .
三. 电势能
q dl 任取点电荷 dq = o 2πR dq dV = 4πε0r 积分中: 与 积分中:r与d q 选取无关 常量
b. 线积分法 利用P.159例1结论 例 结论 利用 积分路径 P
x轴 轴
R
P
x
x
无穷远
35.
讨论 结论
V=
q 4πε0 x + R
2 2
记住) (记住)
q 4 πε0 R
V
q 4πε0 x2 + R2
a. E 的分布函数已知, 用线 积分法较方便
R
rA
r r
rB
b. 选径向为积分路径 v v v v 则 dl = dr er ⋅ dr = dr oA B R r c. 对球面内一点B : 分段积分 dr A v R ∞ v ∞ VB = ∫ E ⋅ dl = ∫ E1 ⋅ dr + ∫ E2 ⋅ dr
09-4静电场的环路定理和电势

19
19
J
一个电子伏特的能量
9.4 静电场的环路定理和电势
9.4.3 电势的计算
一、点电荷q的电场中任一场点的电势
无穷远处为电势零点
V ( P)
P
E dl E dr P Edr P
q q dr 2 r 4 πε r 4πε 0 r 0
电场指向电势降落方向
沿电场线方向移动正电荷,电场力做正功, 正电荷的电势能减少,故电势减小。
9.4 静电场的环路定理和电势
我们的心脏附近 的等电势线(类似于 电偶极子)
9.4 静电场的环路定理和电势
电势差
9.5.2 电场强度与电势梯度 E
U AB VA VB V
U AB E l El cos
9.4 静电场的环路定理和电势
电势是相对的,电势差是绝对的
电势差 U V V PQ P Q
单位:1V=1J/C
P
Q
E dl
二、电势零点 1、电荷只分布在有限区域时,电势零点通常选在无 穷远处。 VP E dl 设Q点在无限远,VQ=0
P
2、 电荷分布延伸到无限远;可选取场中任一点, 合理选择电势零点可使问题简化。
y
P( x, y)
p cos V 4 π 0 r 2
在图示的Oxy坐标系中
q
r
O
r
r
q
r x y
2 2
2
l
x
cos
x x2 y 2
px V 2 2 3/ 2 4 π 0 ( x y )
9.4 静电场的环路定理和电势
【大学物理】静电场的环路定理 电势 等势面 电势梯度
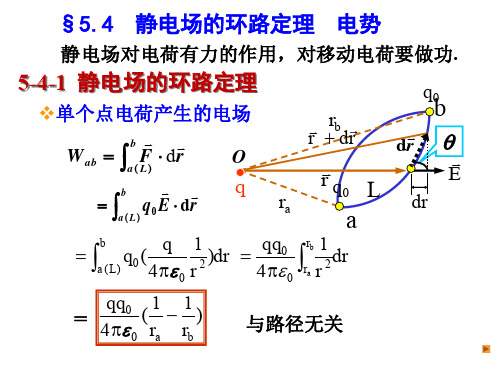
r r r r- r l cos
r
r
r+
q l
q+
3. 连续分布电荷电场中的电势 利用电势叠加原理:
dV
dq
dq VP 4 π 0 r
r
P
使用此公式的前提条件为有限大带电体且选无限远 处为电势零点;积分是对整个带电体的积分。 E 利用电势定义式: dl “ 0 ” P
qr E1 3 4 π 0 R
r
q E2 2 4 π 0 r
V1 E1dr E 2 dr
r R
R
q R
R
r
qr q dr dr 3 2 R 4 π r 4 π 0 R 0
2
q q q (3 R r ) 2 2 (R r ) 3 8 π 0 R 4 π 0 R 8 π 0 R
与路径无关
a
dr
任意带电体系产生的电场
任意带电体系都可以看成电荷系 q1、q2、…,移动q0, 静电力所作功为: b b q E •b dr W F dr 0
ab
q0 a• q0 ( E1 E 2 E n ) dr a( L) n b q 0 E i d r = qi q0 ( 1 1 ) a( L) i 1 rbi i 4 0 rai
注意:
• 电势能的零点可以任意选取,但是在习惯上, 当场源电荷为有限带电体时,通常把电势能的零 点选取在无穷远处。 这时,空间a点的电势能:
E pa
a
q0 E dl
• 电势能为电场和位于电场中的电荷这个系统所 共有。
电场环路定理

电场环路定理
一、电场环路定理:
电场环路定理是物理学中有关电场的一种重要定理。
它指明在任一给定的电场中,环绕任一闭合环路的电势差总和为零。
电场环路定理的准确表达形式是:
若在环路上沿着任意方向行走,那么绕该环路的电场E和磁场B 的积分结果都等于零。
二、电场环路定理的证明:
根据电势场的定义:
电势V=∫ E·dr
其中E和dr分别表示点P处电场和从点A到点B的空间线段之间的路径积分。
因此,沿着环路行走,电势不变,电势差为0,即:
∫ E·dr=0
综上,电场环路定理的证明就完成了。
- 1 -。
所有分类 环路定理 电势能 电势

Wq0a b Ed clo s
dcl o s dr
Wq0ab Edr
点电荷的场
q
Wq0ab 410rq2dr
q0q 1 1
40 ra rb
b
rb
dl r
ra
q0 a
dr F
E
W q0q 1 1
40 ra rb
电场力的功只与始末位置有关,而与路径无关,电场力为保守力,静电场为保守场。
电场力是保守力,可引入势能的概念。
引力是保守力,作功为
W 引[Gm1 rm b2(Gm1 rm a2)]
取无穷远为零势能点,则引力势能为:
电场力作功
Ep
G m1m2 r
W q0q 1
40 ra
r1b (4q0q0rb
q0q )
40ra
1.电势能Ep
定义: 单位:焦耳,J
EP
q0q
40r
为点电荷电势能(选无穷远为零势能点)
r
r
r
0R E2dr d l/d /r/E / 高斯面
R410 rq2dr
q
4 0 R
•II区:球壳外电势
II
rR
选无穷远为电势 0 点,
U2 r E2dl
I
qo RE
r
r
r
rE2dr d l/d /r/E / 高斯面
1
r 40
rq2dr
q
4 0 r
II
I
qoR
II
I
qoR
qE
4 0 R 2
qV 4 0 R
oR
r oR
r
例3 如图,两个同心的均匀带电球壳,半径分别
大学物理电磁学部分04-环路定理电势

Ua
Ub
Epa Epb q0
Aab q0
b E dl
a
意义:把单位正电荷从a点沿任意路径移到b点时电
场力所作的功。
电势差和电势的单位相同,在国际单位制中,电势 的单位为:焦耳/库仑(记作J/C),也称为伏特(V) ,即1V=1J/C。
7
注意几点:
1.电势是标量,只有正负之分。U a
E pa q0
设在静电场中,将检验电荷 q0 从 a 点沿任意路 径移动到 b 点,电场力作功为Aab。
因为保守力所作的功等于势能增量的负值。
电荷 q0 在静电场中从 a 点沿任意路径移动到 b 点时, 电场力所作的作功Aab与这两点电势能Ea、Eb的关系为:
Aab
E p
b
(E
pb
E pa
b
Aab
F dl
(2)连续带电体:将带电体分割成无限多个电荷元,
将每个电荷元看成点电荷,根据点电荷电势公式求电
荷元的电势,迭加归结于积分。
U
dU
dq
4 0r
注意电荷元的选取!
11
例1:均匀带电圆环,半径为 R,带电为 q,求 圆环轴线上一点的电势 U。
解:将圆环分割成无限多个电荷元:
dU dq
4 0r
环上各点到轴线等距。
一、静电场的保守性——环路定理
1.电场力的功
1.点电荷的场
点电荷q0所受电场力为:F q0E 点电荷的场中移动点电荷q0从 r
到 r dr,电场做的功:
dA F dl q0E dl
q
q0Edl dr dl c
dA q0
cos
os , E
q
4 0r 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
环路定理 电势
- 选择题
题号:30411001 分值:3分 难度系数等级:1
1. 下列关于场强和电势的关系的说法中,正确的是:
()A 已知某点的场强E ,就可以确定该点电势U ;()B 已知某点的电势U ,就可以确定该点场强E ; ()C 在某空间内的场强不变,则U 也一定不变; ()D 在等势面上,场强E 不一定处处相等。
答案:()D
题号:30411002 分值:3分 难度系数等级:1
下列关于静电场的说法中,正确的是:
()A 电势高的地方场强就大; ()B 带正电的物体电势一定是正的; ()C 场强为零的地方电势一定为零; ()D 电场线与等势面一定处处正交。
答案:()D
题号:30413003 分值:3分 难度系数等级:3
在均匀电场中各点,下列诸物理量中:(1)电场强度、(2)电势、(3)电势梯度,哪些是大小相等的?
()A (1)、(2)、(3)都相等; ()B (1)、(2)相等; ()C (1)、(3)相等; ()D (2)、(3)相等。
答案:()C
题号:30412004 分值:3分 难度系数等级:2
图中实线为某电场中的电场线,虚线表示等势面,由图可看出:
()A ,A B C A B C E E E U U U >>>>; ()B ,A B C A B C E E E U U U <<<<; ()C ,A B C A B C E E E U U U >><<; ()D ,A B C A B C E E E U U U <<>>。
答案:()D
题号:30413005
分值:3分
难度系数等级:3
关于静电场的保守性的叙述可以表述为:
()A静电场场强沿任一曲线积分时,只要积分路径是某环路的一部分,积分结果就一定为零;
()B静电场场强沿任意路径的积分与起点和终点的位置有关,也要考虑所经历的路径;
()
C当点电荷q在任意静电场中运动时,电场力所做的功只取决于运动的始末位置而与路径无关。
()
D静电场场强沿某一长度不为零的路径做积分,若积分结果为零,则路径一定闭合。
答案:()C
题号:30412006
分值:3分
难度系数等级:2
静电场中,电场线为平行直线的区域内
()A场强E处处相同,电势U可以存在不同;()B场强E可以处处不同,电势U可以处处相同;
()
C场强E可以处处不同,电势U可以处处不同;()D场强E处处相同,电势U也处处相同。
答案:()A
题号:30413007
分值:3分
难度系数等级:3
关于等势面正确的说法是
()A电荷在等势面上移动时不受电场力作用,所以不做功;()B等势面上各点的场强大小相等;()C等势面的方向指示电场强度的减小;()D两等势面不能相交
答案:()D
题号:30413008
分值:3分
难度系数等级:3
关于等势面,下列的说法中错误的有
()A等势面上各点的场强的方向一定与等势面垂直;
()B在同一等势面上移动电荷,电场力一定不做功;
()
C等量异号点电荷连线的中垂线一定是等势线;
()
D在复杂的电场中,不同电势的等势面可以在空间相交。
答案:()D
题号:30413009 分值:3分
N
U1U2U3
难度系数等级:3
一个电场等势面与纸面的交线称等势线。
若某电场的等势线如图,已知123U >U >U ,在2U 上有点M 、
N ,则关于M 、N 两点的电势M ϕ、N ϕ及电场强度M E 、N E 的关系,下列的说法中正确的有
()A M N ϕϕ=,M E 一定小于N E ; ()B M N ϕϕ=,M E 一定大于N E ; ()C M N ϕϕ=, M E 等于N E ; ()D M N ϕϕ=,M E 和N E 哪个大不能确定。
答案:()B
题号:30412010 分值:3分 难度系数等级:2
在以下公式中,E v
是电场强度,可以说明静电场保守性的是 ()A
⎰
=⋅L
q
l d E 0
int εϖϖ; ()B
0=⋅⎰
l d E L
ϖ
ϖ; ()C
⎰
=⋅L
S d E 0ϖ
ϖ; ()D
⎰
=⋅L
q S d E 0
int εϖϖ。
答案:()B
二 判断题
题号:30422001 分值:2分 难度系数等级:2
静电场的环路定理和高斯定理都是说明静电场特性的。
其中环路定理说明静电场的电场线不闭合。
答案:对
题号:30422002 分值:2分 难度系数等级:2
静电场中,若在电场区域内电场线是平行的,则该区域内电场强度和电势都相等。
答案:错
题号:30421003 分值:2分 难度系数等级:1
静电场的保守性体现在电场强度的环流等于零。
答案:对
题号:30423004 分值:2分 难度系数等级:3 静电场的环路积分0=⋅⎰
l d E L
ϖ
ϖ,表明静电场是非保守场,可以引入电势的概念。
答案:错
题号:30422005 分值:2分 难度系数等级:2
在电势不变的空间,场强处处为零。
答案:对
题号:30423006 分值:2分 难度系数等级:3
当知道空间某区域的电势分布时,对该电势求梯度就是该区域的电场强度。
答案:错
题号:30422007 分值:2分 难度系数等级:2
均匀带电球面的外部,等势面是同心球面。
答案:对
题号:30421008 分值:2分 难度系数等级:1
当静电场的分布很复杂时,电场线可能闭合。
答案:错
题号:30424009 分值:2分 难度系数等级:4
有人说:只要知道电场中的一个等势面,就可以确定它周围的电场。
答案:错
题号:30421010 分值:2分 难度系数等级:1
场强弱的地方电势一定低、电势高的地方场强一定强。
答案:错
三 填空题
题号:30432001 分值:2分 难度系数等级:2 静电场的环路积分0=⋅⎰
l d E L
ϖ
ϖ,表明静电场是 场,可以引入电势来描述静电场。
答案:保守
题号:30433002 分值:2分
难度系数等级:3
如图所示,在静电场中,一电荷0q 沿正三角形的一边从a 点移动到b 点再移
动到c 点后回到a 点,电场力作功等于零。
这个结论可以由静电场的 定理直接说明。
答案:环路
题号:30434003 分值:2分
a
b
c
难度系数等级:4
一静电场的电势分布是2
4(V)U xy
=-,其中x 和y 的单位均以米记。
则电场强度的分布是
E v
= 。
答案:21
48(V m )E y i xyj -=+⋅v v v
题号:30433004 分值:2分 难度系数等级:3
求电场强度的方法有两种,一种是采用电场叠加原理直接求解,另一种就是用电势叠加原理求出空间电势的分布(,)U x y ,然后对(,)U x y 求 运算即可。
答案:梯度
题号:30432005 分值:2分 难度系数等级:2
均匀带电球面内部的电场强度等于零,则说明球面内部的电势是 的。
答案:相等的
题号:30331006 分值:2分 难度系数等级:1
描述静电场性质的两个基本定律是高斯定理和 定理。
答案:环路定理
题号:30432007 分值:2分 难度系数等级:2
静电场的环路定理的数学表示式为:______________________。
答案:0=⋅⎰
l d E L
ϖϖ
题号:30432008
分值:2分
难度系数等级:2
电场强度是矢量,用电场线的疏密表示其大小。
在等势面已经确定的情况下,画出电场线时,必须注意电场线_等势面。
答案:垂直于
题号:30433009
分值:2分
难度系数等级:3
电荷在等势面上移动时,电场力作功为零,电荷是否受到电场力的作用?___________
答案:受到
题号:30432010
分值:2分
难度系数等级:2
电场强度的大小与电势的高低没有必然的联系,但由电场强度的方向可以判断电势的高低。
沿着电场强度的方向,电势总是不断的。
答案:降低。
