求线段和的最小值
线段和的最小值 万能方法

M1 A1
A2
N1
提高
例2:如图,已知AB是⊙OB中AC的 30直0 径,
,点D是线段AC上的任意一点1 C(DO不D 含端点),
连接OD,当
的最小2值为6时,求AB的
长。
在RtOO1F中
O1 D1 C
O1OF 600
DE
OO1 4 3
A
FB
AB 8 3
O
线段和的最小值
方法策略
初中数学经常遇到求PA+PB最小值问题,或 者是求△ABC的周长最小值。 1.题型:①两定一动
②一定两动 2.万能方法: ①作一定点关于动点所在直线的对称点
定点作了对称点后不用,对称点即为定点
②如果是两个定点则利用“两点之间,线段最 短”
如果是一个定点则利用“垂线段最短”
常见的数学模
存在一点P,使得△ABP的周长最
小A.B请 求BP出点APP的坐标. y 分析:因为AB的
长是确定的,故 △ABP的周长最 小时AP与BP的和
AO
x
P
为最小,所以可作 出右图所示的图
B
B
’
例3、已知:如图,AB是⊙O的直 径,AB=4,点C是半圆的三等份点, 点D是弧BC的中点,AB上有一动点 P,连接PC,PD,则PC+PD的最小 值是多2 2少?并画出点P的位置C .
型1、(浙教版数学课本八上,P50 例2)l 如
图,直线 表示草原上的一条河流。一骑
马少年从A地出发,去河边让马饮水,然后
返回位于B地的家中。他沿怎样的路线行走, 能使路程最短?作出这条最B 短路P线'A P'B
直线l A为A'
线
的中垂
线段和的最小值万能方法

总结
1.万能方法: ①作一定点关于动点所在直线的对称点
定点作了对称点后不用,对称点即为定点
②如果是两个定点则利用“两点之间,线段最短” 如果是一个定点则利用“垂线段最短”
2.本质就是想方设法换含定点的已知线段
典型例题例1作Fra bibliotek点关于动点所在直线的对称点 作对称点的垂线
例2、(2010东营)如图,已知二次函数y=ax2-4x+c的 图象与坐标轴交于点A(-1, 0)和点B(0,-5).
C
D
A
O P P’ B
D’
例1
提高
例2:如图,已知AB是⊙O中的直径, 的任意一点(不含端点),连接OD,当 求AB的长。
,点D是线段AC上 的最小值为6时,
精品文档 欢迎下载
读书破万卷,下笔如有神--杜甫
线段和的最小值
方法策略
初小中 值数 。学经常遇到求PA+PB最小值问题,或者是求△ABC的周长最 1.题型:①两定一动
②一定两动 2.万能方法: ①作一定点关于动点所在直线的对称点
定点作了对称点后不用,对称点即为定点
②如果是两个定点则利用“两点之间,线段最短” 如果是一个定点则利用“垂线段最短”
常见的数学模型
(1)求该二次函数的解析式;
(2)已知该函数图象的对称轴上存在一点P, 使得△ABP的周长最小.请求出点P的坐标.
分析:因为AB的长是确 定的,故△ABP的周长 最小时AP与BP的和为最 小,所以可作出右图所 示的图
y AO
B
x P
B’
例3、已知:如图,AB是⊙O的直径,AB=4,点 C是半圆的三等份点,点D是弧BC的中点,AB上 有一动点P,连接PC,PD,则PC+PD的最小值是 多少?并画出点P的位置.
用轴对称知识求线段和的最小值

浅析用轴对称知识求线段和的最小值求线段和的最小值问题,在初中数学中经常会遇到,利用轴对称知识可以比较简单的解决。
我们先通过一个非常典型的例题来推导一个性质:一、性质推导例题:如图所示,在河岸L的一侧有两个村庄A、B,现要在河岸L上修建一个供水站,问供水站应建在什么地方,才能到A,B两村庄的距离之和最短?首先,我们来推导一个轴对称的性质,如图,作B点关于L的对称点B1, 在直线L上任意定一点M,连接B B1,BM,B1M,根据轴对称知识,我们可以求证BM=B1M,所以,我们可以得出这样的性质:成轴对称的两个对应点到对称轴上任意一点的距离相等。
在该例题中,利用这一性质,我们可得出:点B到河岸L上任意点M的距离等于对称B1到点M的距离。
要使AM+ B1M最小,必须使A、M、B1三点共线,也就是说,必须使点M,与A B1连线和L的交点N重合,所以,河岸上的N点为到A、B的距离之和最小的点。
B1证明:M为L上的任意点因为BM=B1M所以,BM+AM=B1M+AM,而B1M+AM大于B1A,所以,结论成立二、应用1:在图(1)中,若A到直线L的距离AC是3千米,B到直线L的距离BD是1千米,并且CD的距离4千米,在直线L上找一点P,使PA+PB的值最小。
求这个最小值。
解:作出A1B(作法如上图)过A1点画直线L的平行线与BD的延长线交于H,在Rt△A1BH中,A1H=4千米,BH=4千米,用勾股定理求得A1B的长度为42千米,即PA+PB的最小值为42千米。
A1 Array2、如图(1),在直角坐标系XOY中,X轴上的动点M(x,0)到定点P(5,5)和到Q(2,1)的距离分别为MP和MQ,那么当MP+MQ取最小值时,点M的横坐标x=__________________。
解:如图(2),只要画出点Q关于x轴的对称点Q1(2,-1),连结PQ1 交x轴于点M,则M点即为所求。
点M的横坐标只要先求出经过PQ1两点的直线的解析式,(y=2x-5),令y=0,求得x=5/2。
求线段之和的最小值问题的常用方法

求线段之和的最小值问题的常用方法嘿,咱今儿个就来唠唠求线段之和的最小值问题的那些常用法子!这可是数学里挺有意思的一块儿呢!你想想啊,就好像咱要在一个迷宫里找最短的路一样。
比如说,有两个固定的点 A 和 B,然后还有一条线,咱得找到从 A 到这条线再到B 的最短路径,这就是求线段之和最小值的一种常见情况。
先来说说对称法吧。
这就好比是给线段照镜子,通过找到某个点关于某条线的对称点,然后把问题转化一下,一下子就变得简单明了啦!就好像你本来要绕一大圈才能到的地方,突然发现有条捷径就在眼前。
再讲讲三角形三边关系法。
这就像是三根小棍儿,两边之和肯定得大于第三边呀,那咱就利用这个道理来找最小值。
就好比你知道走哪几条路组合起来最短,嘿,就是这么神奇!还有一种呢,就是利用一些特殊的几何图形的性质。
就像正方形、圆形之类的,它们都有自己独特的地方。
比如说在正方形里,对角线就是个很关键的线索,能帮咱找到那些最短的线段组合。
咱举个例子哈,想象有只小蚂蚁要从一个角落爬到另一个角落,但是中间有好多障碍,那咱就得开动脑筋,想想怎么让这小蚂蚁走最短的路呀!这时候这些方法就派上用场啦。
有时候啊,做这种题就跟玩游戏一样,一点点去探索,去发现其中的奥秘。
你得仔细观察题目中的条件,看看能不能找到那个关键的点或者线,然后运用合适的方法去求解。
哎呀,数学的世界就是这么奇妙!这些求线段之和最小值的方法就像是一把把钥匙,能打开各种难题的大门。
咱可得把这些宝贝方法好好记住,以后遇到问题就不怕啦!你说是不是?总之呢,求线段之和的最小值问题虽然有时候会让人觉得有点头疼,但只要咱掌握了这些常用方法,再加上一点点耐心和细心,那都不是事儿!相信自己,咱都能在数学的海洋里畅游,找到那些隐藏的宝藏!所以啊,别害怕这些问题,大胆去尝试,去探索,你会发现其中的乐趣无穷呢!。
例说利用几何变换求线段和的最小值

例说利用几何变换求线段和的最小值作者:张海华潘从清来源:《教育界·中旬》2015年第05期新课程改革及新中考改革,都要求学生学会自主学习,尝试探疑,发现知识,寻找规律。
故近年各地中考热点之一是动手操作性的探索问题,即通过已知条件,结合数学经验,经过几何图形变换探索其内在联系,发现规律,得出结论。
利用几何变换求线段和的最小值,就属于此类题型。
本文结合具体的例子说明如何利用几何变换求线段和的最小值。
一、利用图形的对称变换1.求两条线段和的最小值例1.如图1已知AB为⊙O的直径,AB=4,OC⊥AB于O,点D在弧BC上,2倍的弧BD等于弧DC,点P是OB上一动点,则PC+PD的最小值为。
解析:由OC⊥AB于O知,延长CO交⊙O于点E,则点C、点E关于AB对称,连接DE交OB于P,则PC=PE,此时PC+PD=DE最小,连接DC,则∠CDE=90°,又因为2倍的弧BD等于弧DC,所以∠E=30°,则DE=CE·cos30°=4×=,则PC+PD的最小值为。
例2.(2004年黑龙江省中考试题)如图2,已知正方形ABCD的边长为8,点M在DC边上,且DM=2,N是AC上的动点,则DN+MN的最小值为。
解析:注意到正方形关于对角线AC对称性,连接BN、BM,则DN+MN=BN+MN≥BM (B、M、N共线时等号成立)。
又根据两点间线段最短知,当B、M、N共线时,DN+MN转化为线段BM,此时最短,由条件可得BM=10。
所以DN+MN的最小值为10。
2.求几条线段和的最小值例3.(初中数学奥林匹克竞赛教程)如图3,∠AOB=45°,角内有一点P,PO=10,两边上各有点Q、R(均不同于O),则△PQR周长的最小值为。
解析:作P关于OA、OB的对称点,根据对称性质可知PQ=P1Q,PR=P2R。
即求P1Q+QR+ P2R的最小值,由两点间直线距离最短,可知当Q、R分别为P1 P2与OA、OB的交点时,P1Q+QR+ P2R值最小。
线段和的最小值问题

课堂小结
学习目标
1.了解并掌握解决两定一动求线段和的最小 值问题的方法。
2.能够运用相关知识和方法解决两定两动求 线段和的最小值问题。
达标检测
已知平面直角坐标系内两点A(1,2), B(2,-1),点P在y轴上运动,求当PA+PB取 得最小值时P点的坐标。
(第 1 题)
能力提升:已知A(0,5),EF=2,且EF在x轴 上平行移动,当AE+AF最小时求E、F 坐标。
典例一:两定一动,求和最小
例1:如图矩形顶点O在坐标原 点,OA=6,OB=8,D为OB边的 中点,若E为OA边上的一个动 点,当△DCE的周长最小时, 在图中画出E点的位置并求点 E的坐标;
变式练习1:已知平面直角坐标系中的两点A (1,2),B(4,2),点P在x轴上运动,则 PA+PB的最小值是_5__。
典例二:两定两动,求和最小
作图2:已知线段EF=1且EF在直线a上平行 移动,A 、B为两个定点,E点在什么位置 时,使得AE+BF最小,请在图中画出点来
• 变式练习2:如图矩形OACB,OA=6, OB=8,D为OB边的中点,若E、F为OA边 上的两个动点,且EF=2,当四边形CDEF 的周长最小时,求点E、F的坐标。
学习目标
1.了解并掌握解决两定一动求线段和的最小 值问题的方法。
2.能够运用相关知识和方法解决两定两动求 线段和的最小值问题。
自主学习
作图1:已知直线l,在直线l同侧 有两点A、B,在直线l上找一点P, 使+PB的值最小。
·B A﹒
l
知识点拨:
1、轴对称性; 2、三角形两边之和大于第三边。
线段差的最大值与线段和的最小值问题
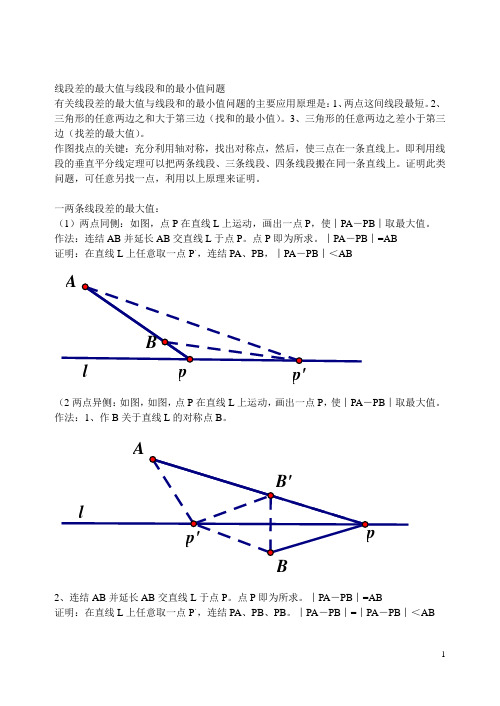
线段差的最大值与线段和的最小值问题有关线段差的最大值与线段和的最小值问题的主要应用原理是:1、两点这间线段最短。
2、三角形的任意两边之和大于第三边(找和的最小值)。
3、三角形的任意两边之差小于第三边(找差的最大值)。
作图找点的关键:充分利用轴对称,找出对称点,然后,使三点在一条直线上。
即利用线段的垂直平分线定理可以把两条线段、三条线段、四条线段搬在同一条直线上。
证明此类问题,可任意另找一点,利用以上原理来证明。
一两条线段差的最大值:(1)两点同侧:如图,点P在直线L上运动,画出一点P,使︱PA-PB︱取最大值。
作法:连结AB并延长AB交直线L于点P。
点P即为所求。
︱PA-PB︱=AB证明:在直线L上任意取一点P。
,连结PA、PB,︱PA-PB︱<ABp'(2两点异侧:如图,如图,点P在直线L上运动,画出一点P,使︱PA-PB︱取最大值。
作法:1、作B关于直线L的对称点B。
B2、连结AB并延长AB交直线L于点P。
点P即为所求。
︱PA-PB︱=AB证明:在直线L上任意取一点P。
,连结PA、PB、PB。
︱PA-PB︱=︱PA-PB︱<AB(三角形任意两边之差小于第三边)二、两条线段和的最小值问题:(1))两点同侧:如图,点P在直线L上运动,画出一点P使P A+PB取最小值。
(三角形的任意两边之和大于第三边(找和的最小值),P A+PB=AB(2)两点异侧:如图,点P在直线L上运动,画出一点P使P A+PB取最小值。
(两点之间线段最短)三、中考考点:08年林金钟老师的最后一题:如图,在矩形ABCO中,B(3,2),E(3,1),F(1,2)在X轴与Y轴上是否分别存在点M、N,使得四边形EFNM的周长最小?若存在,请求出周长的最小值,若不存在,请说明理由。
提示:EF长不变。
即求F N+NM+MF的最小值。
利用E关于X轴的对称点E,F的对称点F,把这三条线段搬到同一条直线上。
一、以正方形为载体,求线段和的最小值例1. 如图1,四边形ABCD 是正方形,边长是4,E 是BC 上一点,且CE =1,P 是对角线BD 上任一点,则PE +PC 的最小值是_____________。
线段和的最小值问题

线段和的最小值问题一直以来,“线段和的最小值问题”是中考的热点和难点问题之一。
学生在这方面常常出现丢分,问题是找不到解题的突破口。
怎样解决这个突破口呢?本人把它们归结为两个“典型题型”进行“发散式”的概括和引申,是解决此类问题的一个捷径。
所谓“典型题型”,就是某些题例它不是公理或定理,却可以举一反三地运用于其他相关的系列问题解答。
下面就“线段和的最值”问题,运用两个“典型题型”的原命题进行探讨。
1.关于线段和的最小值问题例1:如图1所示,要在河边修建一个水站,向A、B区的居民提供自来水,水站应建在什么地方,才能使A、B区的居民到它的距离之和最短?本题的解答是:作出点B的轴对称点 ,连接交直线于点P,则点P就是所求的水站位置。
利用这一题例的结论,可以解决类似的关联题。
图1[ 类型1:]如图2,菱形ABCD的两条对角线的长分别是6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、AC的中点,则PM+PN的最小值是________。
分析:根据菱形的对称性,在AD上找出的M关于AC的对称点(即AD的中点),连结交AC于P,则PM+PN的最小值就是线段的长,等于菱形的边长5. 图2[ 类型2:]如图3,MN是的直径,MN=2,点A在上,∠AMN=,B为弧AN的中点,P是直径MN上一个动点,则PA+PB的最小值是________。
分析:连结OA,由∠AMN=得∠AON=,取点B关于MN的对称点 ,连结 , ,则交MN于点P,则的长为PA+PB的最小值,且∠ ,即△为等腰直角三角形,故。
图3[ 类型3:]如图4,在等腰△ABC中,∠ABC=,点P是底边AC上一个动点,M、N分别是AB、BC的中点,若PM+PN的最小值为2,则△ABC的周长是()。
A.2 B. C.4 D.分析:把等腰△ABC沿AC翻折可得一个菱形,由上面[类型:1]的解图4答可知,PM+PN的最小值就是菱形的边AB的长,故AB=2,由AB=BC=2,∠ABC=120°,易求得AC=,因此△ABC的周长是。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三门九年制学校 温晓艳
一、复习回顾
一牧童在A处牧马,牧童的家在B处,A、B处距河岸的距离分别是 AC=500m,BD=700m,且C、D两地间距离也为500m,天黑前牧童 从A点将马牵到河边去饮水,再赶回家,为了使所走的路程最短.牧童 应将马赶到河边的什么地点?请你在图中画出来.并求出最短路程。
O
P M A’
5、在二次函数图象中求线段和的最小值
(7)、抛物线 y
1 2 x x 2 顶点为A,与Y轴交点为 4
B。点P是x轴上的一个动点,则PA+PB的最小值是多少?
解:易得A(2,1),B(0,2), 作点B关于x轴的对称点B’(0,-2) 连接AB’交x轴于点P,此时PA+PB最小为 AB’= 13
y B O B’ P
A x
检测:
1、如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD =4,AB=5,BC=6,点P是AB上一个动点,当PC+PD的和最 小时,PB的长为______. 2、如图,菱形ABCD中,AB、AD的中点E、F,P为BD上任一点, 当P在何处时,PE+PF最小,最小值是多少? 3、如图,已知正方形ABCD的边长为8,点M在DC上,且DM=2, N是AC上的一个动点,则DN+MN的最小值为 .
A E 2 M 6
法二:过点E作EF ⊥AD,垂足为F。
A E 2 F M B 6
B
F D
C
D
C
由 AEF ~ ABD, 可得 EF=1,AF=
3
在Rt△BEF中,∠ B=60°,BE=4.可得
EF= 2 3 ,BF=2. 在Rt △EFC中,FC=4,因此CE=
,FD= 2 3 .
由 MEF ~ MCD
A’ 500m D
P
C A E
700m
B
500m
(易知Rt △ABC ,A’E=1200m,BE=500m, 可得A’B=1300m。)
模型:
①一条直线l; ②线同侧有两个不同点A、B, 要求:在线l上找一点,满足 PA+PB 最短。
A’ P A B
l
方法:选择合适的一点A, 作其关于直线l的对称点 A’,连接A’B,交直线 l于点P,此时PA+PB最短。
析:△PBQ周长=PB+PQ+BQ=PB+PQ+1, 要求△PBQ周长的最小值即求PB+PQ的 最小值。 由图知,B关于AC的对称点为D, 连接DQ交AC于点P,此时PB+PQ值最小 为DQ。
A D
P B Q C
解:在Rt △DQC中,DC=2,QC=1, 可得DQ= 5 ,则△PBQ的周长最小值 为( 5+1 )cm。
D
析:由图知,B关于AC的对称点 为D,连接DE交AC于点P,此时 PE+PB值最小为DE。
2 A E B
P
C
解: ∵ ∠BAD=60 °,菱形ABCD ∴ △ ADB为等边三角形, ∵ E为AB中点 ∴ DE ⊥ AB, 在Rt △DEA中,DA=2,∴DE= 3
(4)、如图,在边长为2cm的正方形ABCD中,点Q为BC边的 中点,点P为对角线AC上一动点,连接PB、PQ,则△PBQ周长 的最小值为 ___cm.(结果不取近似值).
1 S OM AM 1, OM AM 2 k OAM 解: ①、 2 2 y x B(1, 2),
y B
A x
②、
1 y x x 2 2 A(2,1) 2 y 1 y x 作点A关于x轴的对称点A '(2, 1), 连接A ' B交x轴于点P, 即为所求。 5 可得l A ' B : y=-3x+5 P( , 0). 3
二、教学过程 1、在三角形中求线段和的最小值
(1)如图,等边△ABC的边长为6,AD是BC边上的中线,M 是AD上的动点,E是AB边上一点.若AE=2,EM+BM的最小值 为 .
A
E
M
析:由图知,B关于AD的 对称点为C,连接EC交AD于点 M,此时EM+BM最小为EC.
C
B
D
法一: 过点E作EF ⊥BC,垂足为F。
y M N A
E
B
O P
F
B
O
x
3、在圆中求线段和的最小值 (5)、如图,MN是半径为1的⊙O的直径,点A在⊙O上, ∠AMN=30°,B为AN弧的中点,P是直径MN上一动点, 则PA+PB的最小值为( )
析:作点A关于MN的对称点A’, 连接A’B交MN于点P,此时 PA+PB最小为A’B. 解:连接OB、OA’, ∵ ∠AMN=30° ∴ ∠AON=60°= ∠A ’ON, ∵B为弧AN中点,∴ ∠BON=30 °, ∴ ∠BOA’=90 °. △OBA’为等腰直角三角形,因此 A’B= 2 .
2 7
3 3 3 可得FM= ,MD = 2 . 2
在
RtMFE和RtMDC 中,
,MC=
3 7 2
7 可得EM= 2
.
因此CE=
2 7
.
2、在四边形中求线段和的最小值
(2)、如图,等腰梯形ABCD中,AB=AD=CD=1, ∠ABC=60°,P是上底,下底中点EF直线上的一点,则 PA+PB的最小值为 .
A E P B C D
析:由图知,B关于EF的对称点 为C,连接AC交EF于点P,此时 PA+PB值最小为AC。 解,由题得∠D= ∠ DAB=120 °, ∵DA=DC, ∴ ∠ DAC=∠DCA=30 °, ∴ ∠BAC=90 °. 在Rt △ABC中,AC= 3
F
(3)、如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB 的中点,P是对角线AC上的一个动点,则PE+PB的最小值 为 ___.
M 30 ° A B
O
P
N
A’
4、在反比例函数图象中求线段和的最小值
1 k y= (6)、如图,正比例函数 2 x 的图象与反比例函数 y= (k≠0) x
在第一象限的图象交于A点,过A点作X轴的垂线,垂足为M,已知三 角形OAM的面积为1. ①求反比例函数的解析式; ②如果B为反比例函数在第一象限图象上的点(点B与点A不重合), 且B点的横坐标为1,在X轴上求一点P,使PA+PB最小.
A A P B C E B A F P C B D D N C M
4、如图,AB、CD是半径为5的⊙O的两条弦,AB=8, CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上 的任意一点,则PA+PC的最小值为( )。 5、如图,在平面直角坐标系中,点A的坐标为 (1, )△AOB的面积是 . ①求点B的坐标;②求过点A、O、B的抛物线的解析式; ③在(2)中抛物线的对称轴上是否存在点C,使△AOC的 周长最小?若存在,求出点C的坐标;若不存在,请说明 理由;A
