线段和最小值问题
“求两线段长度之和的最小值”问题全解析
“求两线段长度之和的最小值”问题全解析“求两线段长度值和最小”问题全解析在近几年的中考中，经常遇到求PA+PB最小型问题，为了让同学们对这类问题有一个比较全面的认识和了解，我们特此编写了“求两线段长度值和最小”问题全解析，希望对同学们有所帮助．一、在三角形背景下探求线段和的最小值1.1 在锐角三角形中探求线段和的最小值例1如图1，在锐角三角形ABC中，AB=4,∠BAC=45°，∠BAC的平分线交BC于点D，M,N分别是AD和AB上的动点，则BM+MN的最小值为．第 2 页第 3 页解：因为等边△ABC的边长为6,AD是BC边上的中线,所以点C与点B关于AD对称，连接BE交AD于点M，这就是EM+CM最小时的位置，如图5所示，因为CM=BM，所以EM+CM=BE，过点E作EF⊥BC，垂足为F，因为AE=2，AC=6，所以EC=4，在直角三角形EFC中，因为EC=4, ∠ECF=60°，∠FEC=30°，所以FC=2,EF==2．因为BC=6，FC=2，所以BF=4．在直角三角形BEF中，BE==.二、在四边形背景下探求线段和的最小值2.1在直角梯形中探求线段和的最小值例3（2010江苏扬州）如图3，在直角梯形ABCD中，∠ABC＝90°，AD∥BC，AD＝4，AB＝5，BC＝6，点P是AB上一个动点，当PC＋PD的和最小时，PB的长为__________．第 4 页第 5 页分析：在这里有一个动点，两个定点符合对称点法求线段和最小的思路，所以解答时可以用对称法．解：如图3所示，作点D 关于直线AB 的对称点E ，连接CE ，交AB 于点P ，此时PC ＋PD 和最小，为线段CE ．因为AD ＝4，所以AE=4．因为∠ABC ＝90°，AD ∥BC ，所以∠EAP ＝90°．因为∠APE ＝∠BPC,所以△APE ∽△BPC ，所以.因为AE=4，BC ＝6，所以，所以，所以,因为AB ＝5，所以PB=3.2.2在等腰梯形中探求线段和的最小值例4 如图4，等腰梯形ABCD 中，AB=AD=CD=1，∠ABC=60°，P 是上底，下底中点EF 直线上的一点，则PA+PB的最小值第 6 页 为 ．分析：根据等腰梯形的性质知道，点A 的对称点是点D ，这是解题的一个关键点．其次运用好直角三角形的性质是解题的又一个关键．解：如图4所示，因为点D 关于直线EF 的对称点为A ，连接BD ，交EF 于点P ，此时PA ＋PB 和最小，为线段BD ．过点D 作DG ⊥BC ，垂足为G ，因为四边形ABCD 是等腰梯形，且AB=AD=CD=1，∠ABC=60°，所以∠C=60°，∠GDC=30°，所以GC=,DG=．因为∠ABC ＝60°，AD ∥BC ，所以∠BAD ＝120°．因为AB=AD ，所以∠ABD=∠ADB=30°，所以∠ADBC=30°，所以BD=2DG=2×=．所以PA+PB的最小值为．2.3在菱形中探求线段和的最小值例5如图5菱形ABCD中，AB=2，∠BAD=60°，E是AB的中点，P是对角线AC 上的一个动点，则PE+PB的最小值为．分析：根据菱形的性质知道，点B的对称点是点D，这是解题的一个关键点．解：如图5所示，因为点B关于直线AC的对称点为D，连接DE，交AC于点P，此时PE ＋PB和最小，为线段ED．因为四边形ABCD 是菱形，且∠BAD=60°，所以三角形ABD是等边三角形．因为E是AB的中点，AB=2，所以AE=1，DE⊥AB，所以ED==．所以PE＋PB的最小值为．2.4在正方形中探求线段和的最小值第 7 页第 8 页 例6 如图6所示，已知正方形ABCD 的边长为8，点M 在DC 上，且DM=2，N 是AC 上的一个动点，则DN+MN 的最小值为 ．分析：根据正方形的性质知道，点B 的对称点是点D ，这是解题的一个关键点．解：如图6所示，因为点D 关于直线AC 的对称点为B ，连接BM ，交AC 于点N ，此时DN ＋MN 和最小，为线段BM ．因为四边形ABCD 是正方形，所以BC=CD=8．因为DM=2，所以MC=6，所以BM==10.所以DN+MN 的最小值为10. 例7（2009?达州）如图7，在边长为2cm 的正方形ABCD 中，点Q 为BC 边的中点，点P为对角线AC 上一动点，连接PB 、PQ ，则△PBQ周长的最小值为 cm ．（结果不取近似值）．第 9 页分析：在这里△PBQ 周长等于PB+PQ+BQ ，而BQ 是正方形边长的一半，是一个定值1，所以要想使得三角形的周长最小，问题就转化成使得PB+PQ 的和最小问题．因为题目中有一个动点P ，两个定点B,Q 符合对称点法求线段和最小的思路，所以解答时可以用对称法．解:如图7所示，根据正方形的性质知道点B 与点D 关于AC 对称，连接DQ ，交AC 于点P ，连接PB ．所以BP=DP ，所以BP+PQ=DP+PQ=DQ ．在Rt △CDQ 中，DQ== ，所以△PBQ 的周长的最小值为：BP+PQ+BQ=DQ+BQ=+1．故答案为+1．三、在圆背景下探求线段和的最小值例8（2010年荆门）如图8，MN 是半径为1的⊙O的直径，点A在⊙O上，∠AMN＝30°，B为AN弧的中点，P是直径MN上一动点，则PA＋PB的最小值为( )(A)2(B)(C)1 (D)2分析：根据圆的对称性，作出点A的对称点D，连接DB，则线段和的最小值就是线段DB 的长度．解：如图8，作出点A的对称点D，连接DB，OB,OD．因为∠AMN＝30°，B为AN弧的中点，所以弧AB的度数为30°，弧AB的度数为30°，弧AN的度数为60°．根据圆心角与圆周角的关系定理得到：∠BON＝30°．由垂径定理得：弧DN的度数为60°．所以∠BOD＝∠BON +∠DON= 30°+60°=90°.所以DB==.所以选择B．第 10 页四、在反比例函数图象背景下探求线段和的最小值例9（2010山东济宁）如图9，正比例函数y=x 的图象与反比例函数y=（k≠0）在第一象限的图象交于A点，过A点作x轴的垂线，垂足为M，已知三角形OAM的面积为1.（1）求反比例函数的解析式；（2）如果B为反比例函数在第一象限图象上的点（点B与点A不重合），且B点的横坐标为1，在x轴上求一点P，使PA+PB最小.分析：利用三角形的面积和交点坐标的意义，确定出点A的坐标是解题的第一个关键．要想确定出PA+PB的最小值，关键是明白怎样才能保证PA+PB的和最小，同学们可以联想我们以前学过的对称作图问题，明白了最小的内涵，解题的过程就迎刃而解了．解：（1）设点A的坐标为（x，y），且点A在第一象限，所以OM=x,AM=y．因为三角形OAM的面积为1，所以所以xy=2，所以反比例函数的解析式为y=．（2）因为y=x与y=相交于点A，所以=x，解得x=2，或x=-2.因为x＞0，所以x=2，所以y=1，即点A的坐标为（2，1）．因为点B的横坐标为1，且点B在反比例函数的图像上，所以点B的纵坐标为2，所点B的坐标为（1，2），所以点B关于x轴的对称点D的坐标为（1，-2）．设直线AD的解析式为y=kx+b，所以，解得k=3，b=-5，所以函数的解析式为y=3x-5，当y=0时，x=，所以当点P在（，0）时，PA+PB 的值最小．五、在二次函数背景下探求线段和的最小值例10（2010年玉溪改编）如图10，在平面直角坐标系中，点A的坐标为（1，），△AOB 的面积是.（1）求点B的坐标；（2）求过点A、O、B 的抛物线的解析式；（3）在（2）中抛物线的对称轴上是否存在点C，使△AOC的周长最小？若存在，求出点C 的坐标；若不存在，请说明理由；分析：在这里△AOC周长等于AC+CO+AO，而A,O是定点，所以AO是一个定长，所以要想使得三角形的周长最小，问题就转化成使得AC+CO的和最小问题．因为题目中有一个动点C，两个定点A,O符合对称点法求线段和最小的思路，所以解答时可以用对称法．解：（1）由题意得:所以OB=2．因为点B在x轴的负半轴上，所以点B的坐标为（-2，）；（2）因为B(-2,0),O(0,0),所以设抛物线的解析式为：y=ax（x+2），将点A的坐标为（1，）代入解析式得：3a=，所以a=，所以函数的解析式为y=+x．（3）存在点C. 如图10，根据抛物线的性质知道点B与点O是对称点，所以连接AB与抛物线的对称轴x= - 1交AC于点C，此时△AOC 的周长最小.设对称轴与x轴的交点为E．过点A作AF垂直于x轴于点F，则BE=EO=EF=1.因为△BCE∽△BAF,所以,所以，所以CE=．因为点C在第二象限，所以点C的坐标为（-1，）．六、在平面直角坐标系背景下探求线段和的最小值例11（2010年天津）如图11，在平面直角坐标系中，矩形的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，OA=3，OB=4，D为边OB的中点.（1）若E为边OA上的一个动点，当△CDE 的周长最小时，求点E的坐标；（2）若E、F为边OA上的两个动点，且EF=2，当四边形CDEF的周长最小时，求点E、F的坐标.分析：本题的最大亮点是将一个动点求最小值和两个动点求最小值问题糅合在一起，并很好的运用到平面直角坐标系中．解：（1）如图12，作点D关于x轴的对称点，连接C与x轴交于点E，连接DE.若在边OA上任取点（与点E不重合），连接C、D、.由D+ C=+ C＞C= D+CE=DE+CE，所以△的周长最小.因为在矩形OACB中，OA=3,OB=4, D为OB的中点，所以BC=3，DO=O=2.所以点C的坐标为（3，4），点的坐标为（0，-2），设直线C的解析式为y=kx+b，则，解得k=2，b=-2，所以函数的解析式为y=2x-2，令y=0，则x=1，所以点E的坐标为（1，0）；（2）如图13，作点D关于x轴的对称点，在CB边上截取CG=2，连接G与x轴交于点E，在EA上截EF=2.因为GC∥EF，GC=EF，所以四边形GEFC为平行四边形，有GE=CF.又DC、EF的长为定值，所以此时得到的点E、F使四边形CDEF的周长最小.因为在矩形OACB中，OA=3,OB=4, D为OB的中点，CG=2,所以BC=3，DO=O=2,BG=1.所以点G的坐标为（1，4），点的坐标为（0，-2），设直线G的解析式为y=kx+b，则，解得k=6，b=-2，所以函数的解析式为y=6x-2，令y=0，则x=，所以点E的坐标为（，0）,所以点F的坐标为（+2，0）即F的坐标为（，0）。
线段和的最小值 万能方法
M1 A1
A2
N1
提高
例2：如图，已知AB是⊙OB中AC的 30直0 径，
，点D是线段AC上的任意一点1 C（DO不D 含端点），
连接OD，当
的最小2值为6时，求AB的
长。
在RtOO1F中
O1 D1 C
O1OF 600
DE
OO1 4 3
A
FB
AB 8 3
O
线段和的最小值
方法策略
初中数学经常遇到求PA+PB最小值问题，或 者是求△ABC的周长最小值。 1.题型：①两定一动
②一定两动 2.万能方法： ①作一定点关于动点所在直线的对称点
定点作了对称点后不用，对称点即为定点
②如果是两个定点则利用“两点之间，线段最 短”
如果是一个定点则利用“垂线段最短”
常见的数学模
存在一点P，使得△ABP的周长最
小A．B请 求BP出点APP的坐标． y 分析：因为AB的
长是确定的，故 △ABP的周长最 小时AP与BP的和
AO
x
P
为最小，所以可作 出右图所示的图
B
B
’
例3、已知：如图，AB是⊙O的直 径，AB=4，点C是半圆的三等份点， 点D是弧BC的中点，AB上有一动点 P，连接PC，PD，则PC+PD的最小 值是多2 2少？并画出点P的位置C .
型1、（浙教版数学课本八上，P50 例2）l 如
图，直线 表示草原上的一条河流。一骑
马少年从A地出发，去河边让马饮水，然后
返回位于B地的家中。他沿怎样的路线行走， 能使路程最短？作出这条最B 短路P线'A P'B
直线l A为A'
线
的中垂
线段和最小值问题整理
线段和最小值问题是一类数学问题，通常涉及到在给定的线段上找到使某个函数取得最小值的点。
这类问题在数学建模、优化问题和几何学中都有应用。
下面是对线段和最小值问题的整理：
1. 定义线段：线段是由两个端点确定的一段连续的直线部分。
2. 定义函数：线段和最小值问题通常需要定义一个函数，该函数将线段上的点映射到一个实数上。
3. 最小值问题：线段和最小值问题的目标是找到线段上使函数取得最小值的点。
4. 解决方法：解决线段和最小值问题的方法通常包括数学分析和优化算法。
a. 数学分析：通过分析函数的性质、导数和极值点等，可以找到函数取得最小值的点。
b. 优化算法：如果函数较为复杂或者无法通过数学分析得到解析解，可以使用优化算法，如梯度下降法、遗传算法等，来搜索最小值点。
5. 约束条件：线段和最小值问题中，通常会存在一些约束条件，如线段的端点范围、函数的可行域等。
这些约束条件需要考虑在解决问题时。
线段和最小值问题的具体形式和解决方法会因具体情况而异，可以根据具体问题的特点来选择合适的方法进行求解。
(完整版)初中几何中线段和与差最值问题
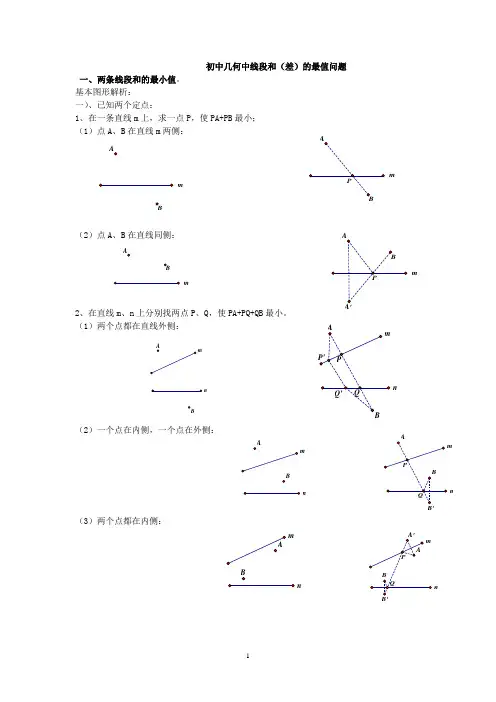
三、其它非基本图形类线段和差最值问题
1、求线段的最大值与最小值需要将该条线段转化到一个三角形中，在该三角形中，其他两边是已知的，则所求线段的最大值为其他两线段之和，最小值为其他两线段之差。
点B在直线n上运动，在直线m上找一点P，使PA+PB最小（在图中画出点P和点B）
1、两点在直线两侧：
2、两点在直线同侧：
（二）动点在圆上运动
点B在⊙O上运动，在直线m上找一点P，使PA+PB最小（在图中画出点P和点B）
1、点与圆在直线两侧：
2、点与圆在直线同侧：
三）、已知A、B是两个定点，P、Q是直线m上的两个动点，P在Q的左侧,且PQ间长度恒定,在直线m上要求P、Q两点，使得PA+PQ+QB的值最小。(原理用平移知识解)
压轴题
1、如图，正比例函数 的图象与反比例函数 （k≠0）在第一象限的图象交于A点，过A点作x轴的垂线，垂足为M，已知三角形OAM的面积为1.
（1）求反比例函数的解析式；
（2）如果B为反比例函数在第一象限图象上的点（点B与点A不重合），且B点的横坐标为1，在x轴上求一点P，使PA+PB最小.
2、如图，一元二次方程 的二根 ， （ ＜ ）是抛物线 与x轴的两个交点B，C的横坐标，且此抛物线过点A（3，6）．
（1）求点D的坐标；
（2）过O，C，D三点作抛物线，在抛物线的对称轴上是否存在一点P，使线段PO与PD之差的值最大？
若存在，请求出这个最大值和点P的坐标．若不存在，请说明理由．
线段和的最小值问题
课堂小结
学习目标
1.了解并掌握解决两定一动求线段和的最小 值问题的方法。
2.能够运用相关知识和方法解决两定两动求 线段和的最小值问题。
达标检测
已知平面直角坐标系内两点A(1，2), B(2，-1),点P在y轴上运动，求当PA+PB取 得最小值时P点的坐标。
（第 1 题）
能力提升：已知A(0,5),EF=2,且EF在x轴 上平行移动，当AE+AF最小时求E、F 坐标。
典例一：两定一动,求和最小
例1：如图矩形顶点O在坐标原 点，OA=6，OB=8，D为OB边的 中点，若E为OA边上的一个动 点，当△DCE的周长最小时， 在图中画出E点的位置并求点 E的坐标；
变式练习1：已知平面直角坐标系中的两点A （1，2），B（4,2），点P在x轴上运动，则 PA+PB的最小值是_5__。
典例二：两定两动,求和最小
作图2：已知线段EF=1且EF在直线a上平行 移动，A 、B为两个定点，E点在什么位置 时，使得AE+BF最小，请在图中画出点来
• 变式练习2：如图矩形OACB，OA=6， OB=8，D为OB边的中点，若E、F为OA边 上的两个动点，且EF=2，当四边形CDEF 的周长最小时，求点E、F的坐标。
学习目标
1.了解并掌握解决两定一动求线段和的最小 值问题的方法。
2.能够运用相关知识和方法解决两定两动求 线段和的最小值问题。
自主学习
作图1：已知直线l，在直线l同侧 有两点A、B，在直线l上找一点P， 使+PB的值最小。
·B A﹒
l
知识点拨：
1、轴对称性； 2、三角形两边之和大于第三边。
线段差的最大值与线段和的最小值问题
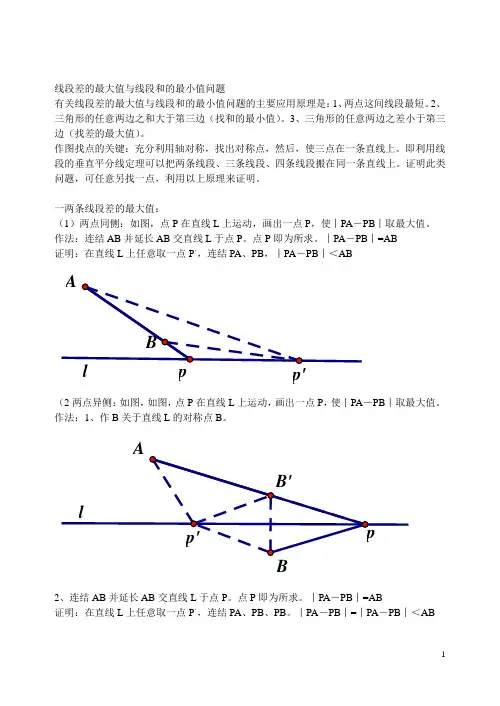
线段差的最大值与线段和的最小值问题有关线段差的最大值与线段和的最小值问题的主要应用原理是：1、两点这间线段最短。
2、三角形的任意两边之和大于第三边（找和的最小值）。
3、三角形的任意两边之差小于第三边（找差的最大值）。
作图找点的关键：充分利用轴对称，找出对称点，然后，使三点在一条直线上。
即利用线段的垂直平分线定理可以把两条线段、三条线段、四条线段搬在同一条直线上。
证明此类问题，可任意另找一点，利用以上原理来证明。
一两条线段差的最大值：（1）两点同侧：如图，点P在直线L上运动，画出一点P，使︱PA－PB︱取最大值。
作法：连结AB并延长AB交直线L于点P。
点P即为所求。
︱PA－PB︱=AB证明：在直线L上任意取一点P。
，连结PA、PB，︱PA－PB︱＜ABp'（2两点异侧：如图，如图，点P在直线L上运动，画出一点P，使︱PA－PB︱取最大值。
作法：1、作B关于直线L的对称点B。
B2、连结AB并延长AB交直线L于点P。
点P即为所求。
︱PA－PB︱=AB证明：在直线L上任意取一点P。
，连结PA、PB、PB。
︱PA－PB︱=︱PA－PB︱＜AB（三角形任意两边之差小于第三边）二、两条线段和的最小值问题：（1））两点同侧：如图，点P在直线L上运动，画出一点P使P A＋PB取最小值。
（三角形的任意两边之和大于第三边（找和的最小值），P A＋PB=AB（2）两点异侧：如图，点P在直线L上运动，画出一点P使P A＋PB取最小值。
（两点之间线段最短）三、中考考点：08年林金钟老师的最后一题：如图，在矩形ABCO中，B（3，2），E（3，1），F（1，2）在X轴与Y轴上是否分别存在点M、N，使得四边形EFNM的周长最小？若存在，请求出周长的最小值，若不存在，请说明理由。
提示：EF长不变。
即求F N＋NM＋MF的最小值。
利用E关于X轴的对称点E，F的对称点F，把这三条线段搬到同一条直线上。
一、以正方形为载体，求线段和的最小值例1. 如图1，四边形ABCD 是正方形，边长是4，E 是BC 上一点，且CE ＝1，P 是对角线BD 上任一点，则PE ＋PC 的最小值是_____________。
线段和的最小值问题
练习
A’
P
C
B
A
E
P
D
C
DE
5
出题背景变式有：
1
角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等。
2
解题思路：
3
找点关于线的对称点，实现“折”转“直”。
----线段和的最小值问题
单击添加副标题
单击此处添加文本具体内容，简明扼要地阐述你的观点
如图，要在街道旁修建一个奶站P，向居民区A、B提供牛奶，奶站P应建在什么地方，才能使从A，B到它的距离之和最短？为什么？
A
B
街道
P
P’
A B A’ P 如图，要在街道旁修建一个奶站P，向居民区A、B提供牛奶，奶站P应建在什么地方，才能使从A，B到它的距离之和最短？为什么？ 街道 P’
4
变式1（2008 年湖北荆门市中考题） 如图，菱形ABCD 的两条对角线分别长6 和8，点P是对角线AC 上的一个动点，点M、N 分别是边AB、BC 的中点，则PM+PN 的最小值是_____________．
A
D
C
B
M
N
P
M’
P’
5
练习 (2011广西试题改编） 如图所示，在边长为2的正三角形ABC中，E、F、G分别为AB、AC、BC的中点，点P线段EF上一个动点，连接BP、GP，则（1）PB+PG的最小值是 （2）△BPG周长的最小值是 。
线段和的最小值
本节课我们学习了 问题， 这类问题的解题方法是怎样的？
线段和的最小值问题
线段和的最小值问题一直以来，“线段和的最小值问题”是中考的热点和难点问题之一。
学生在这方面常常出现丢分，问题是找不到解题的突破口。
怎样解决这个突破口呢？本人把它们归结为两个“典型题型”进行“发散式”的概括和引申，是解决此类问题的一个捷径。
所谓“典型题型”，就是某些题例它不是公理或定理，却可以举一反三地运用于其他相关的系列问题解答。
下面就“线段和的最值”问题，运用两个“典型题型”的原命题进行探讨。
1.关于线段和的最小值问题例1：如图1所示，要在河边修建一个水站，向A、B区的居民提供自来水，水站应建在什么地方，才能使A、B区的居民到它的距离之和最短？本题的解答是：作出点B的轴对称点 ,连接交直线于点P，则点P就是所求的水站位置。
利用这一题例的结论，可以解决类似的关联题。
图1[ 类型1：]如图2，菱形ABCD的两条对角线的长分别是6和8，点P是对角线AC上的一个动点，点M、N分别是边AB、AC的中点，则PM+PN的最小值是________。
分析：根据菱形的对称性，在AD上找出的M关于AC的对称点（即AD的中点）,连结交AC于P，则PM+PN的最小值就是线段的长，等于菱形的边长5. 图2[ 类型2：]如图3，MN是的直径，MN=2，点A在上，∠AMN=，B为弧AN的中点，P是直径MN上一个动点，则PA+PB的最小值是________。
分析：连结OA，由∠AMN=得∠AON=，取点B关于MN的对称点 ,连结 , ,则交MN于点P,则的长为PA+PB的最小值，且∠ ,即△为等腰直角三角形，故。
图3[ 类型3：]如图4，在等腰△ABC中，∠ABC=，点P是底边AC上一个动点，M、N分别是AB、BC的中点，若PM+PN的最小值为2，则△ABC的周长是（）。
A.2 B. C.4 D.分析：把等腰△ABC沿AC翻折可得一个菱形，由上面[类型：1]的解图4答可知，PM+PN的最小值就是菱形的边AB的长，故AB=2，由AB=BC=2,∠ABC=120°，易求得AC=，因此△ABC的周长是。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
线段和最小值问题
问题模型：如下图，、是直线同旁的两个定点．
问题：在直线上确定一点，使的值最小．
方法：作点关于直线的对称点，连结交于点，则的值最小（不必证明）．
题型一：两定一动一线
例1：如图，在菱形ABCD中，对角线AC=6，BD=8，点E、F分别是边AB、BC的中点，点P在AC上运动，在运动过程中，存在PE+PF的最小值，则这个最小值是______．
方法总结：当有两个定点时，做任一定点关于线的对称点，连接另一点和
对称点，和线的交点即为所求。
跟踪练习：
如图，在边长为4的正方形ABCD中，E是AB边上的一点，且AE=3，点Q为对角线AC 上的动点，则△BEQ周长的最小值为______．
题型二：一定两动一线
例2：如图，在矩形ABCD中，AB=10 , BC=5 ．若点M、N
分别是线段ACAB上的两个动点，则BM+MN的最小值为______．
方法总结：点P在AD上运动，则作线段AD关于线AE的对称线段，结合垂线段最短求最
小值。
跟踪练习
如图，正方形ABCD的边长为4，∠DAC的平分线交DC于点E，若点P、Q分别是AD和
AE上的动点，则DQ+PQ的最小值是______．
拓展提升
题型三：三动一线（做法参照题型二）
例3：如图，菱形ABCD中，AB=2，∠BAD=60°，E、F、P分别是AB、BC、AC上的动点，PE+PF的最小值等于______．
题型四：一定两动两线
例4：如图，∠AOB=45°，角内有一动点P ，PO=10，在AO，BO上有两动点Q，R，求
△PQR周长的最小值______．
方法总结：分别作定点关于两线的对称点，连接两对称点所得线段即为线段和的最小值。
题型五：两定两动两线
例5：如图，∠AOB＝30°，点M、N分别在边OA、OB上，且OM=1，ON=3，点P、Q分别在边OB、OA上，则MP＋PQ＋QN的最小值是_______.
方法总结：分别作两定点关于两线的对称点，连接两对称点所得线段即为线段和的最小值。
随堂练习：
1.如图，正方形ABCD的边长为7，点E、F分别在AB、BC上，AE=3，CF=1，P是对角线AC上的个动点，则PE+PF的最小值是______．
2.如图，等边△ABC的边长为6，AD是BC边上的中线，M是AD上的动点，E是AC边上
一点，若AE=2，EM+CM的最小值为______．
3.如图所示，正方形ABCD的面积为12，是等边三角形，点E
在正方形ABCD内，在对角线AC上有一点P，使的和最小，则PD+PE这个最小值为______．
4.如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，
AD是∠BAC的平分线．若P，Q分别是AD和AC上的动点，则PC+PQ的最小值是______．
5.如图，五边形ABCDE中，∠BAE=120°，∠B=∠E=90°，AB=BC=1，AE=DE=2，在BC、DE上分别找一点M、N，使△AMN的周长最小，则△AMN的周长最小值为______．。